
 , 魏小梅, 汪嘉杨, 张小丽
, 魏小梅, 汪嘉杨, 张小丽成都信息工程大学, 资源环境学院, 成都 610225
收稿日期: 2019-11-05; 修回日期: 2020-02-20; 录用日期: 2020-02-20
基金项目: 国家自然科学基金(No.51679155);四川省科技厅项目(No.19JDJQ0006);四川省社科规划项目(No.SC18B027)
作者简介: 李祚泳(1944-), 男, 教授, E-mail:lizuoyong@cuit.edu.cn
通讯作者(责任作者): 李祚泳
摘要:为了建立适用于广义环境系统评价的普适指数公式,针对传统的环境评价指数公式不具有普适、规范和通用的局限,提出适用于广义环境系统任意指标的参照值和规范变换式的设计原则和方法;该变换要求变换后的任意指标的各分级标准规范值都能被限定在各自的较小区间内,从而用规范值表示的任意指标皆"等效"于同一个规范指标;再分别用不同限定区间内生成的随机数模拟任意指标的不同分级标准的规范值,不同区间内生成的所有随机数组成不同分级标准的全部训练(学习)样本,借助免疫进化算法优化不同评价指数公式中的参数,得到适用于广义环境系统评价的9个(广义)普适指数公式,并论证了公式的可靠性.分别将9个普适指数公式用于北京市朝阳区19个监测井的9项指标的地下水水质的综合评价,以及用于郑州、西安、上海三市2000年可持续发展评价.结果表明:9个普适指数公式用于同一监测井水质的评价结果几乎完全相同,也与传统评价方法的评价结果基本一致;用于郑州、西安、上海三市可持续发展评价的结果分别是3级、3级、2级,比传统评价法更符合实际情况.9个普适指数公式使广义环境系统的评价变得简洁、规范、统一和通用;基于指标规范变换的评价指数公式的建模思想和方法对建立广义环境系统的普适智能评价模型有借鉴作用.
关键词:广义环境系统环境评价指标规范变换普适指数公式
Universal index formula for generalized environmental system assessment based on normal transformation of indicators
LI Zuoyong

 , WEI Xiaomei, WANG Jiayang, ZHANG Xiaoli
, WEI Xiaomei, WANG Jiayang, ZHANG XiaoliCollege of Resources and Environment, Chengdu University of Information Technology, Chengdu 610225
Received 5 November 2019; received in revised from 20 February 2020; accepted 20 February 2020
Abstract: the purpose of this study is to establish a universal index formula for the evaluation of generalized environmental systems. In view of the limitation of traditional environmental evaluation index formula that is not universal, standard and general, the design principle and method of reference value and normative transformation formula suitable for any index of generalized environmental system are proposed. The transformation requires that the standard values of each grade of any index after transformation can be limited to their own smaller cells, so that any index represented by the standard value is "equivalent" to the same standard index. Then the random numbers generated in different limited intervals are used to simulate the standard values of different classification standards for any index. All the random numbers generated in different intervals constitute all training (learning) samples of different classification standards. By using immune evolutionary algorithm to optimize the parameters in different evaluation index formulas, nine (generalized) universal index formulas for the evaluation of generalized environmental systems are obtained, and the reliability of the formulas is demonstrated. Nine universal index formulas are applied to the comprehensive evaluation of groundwater quality of 19 monitoring wells in Chaoyang District, Beijing, and to the evaluation of sustainable development of Zhengzhou, Xi'an and Shanghai in 2000. The results showed that:The evaluation results of nine universal index formulas used in the same monitoring well water quality are almost the same, and also basically consistent with the evaluation results of traditional evaluation methods. The results of their evaluation for the sustainable development of the three cities are all level 3, 3 and 2, which is more in line with the actual situation than the traditional evaluation methods. nine universal index formulas make the evaluation of the generalized environmental system simple, standardized, unified and universal. The modeling ideas and methods of the evaluation index formula based on the transformation of the index specifications are useful for building the universal intelligent evaluation model of the generalized environmental system.
Keywords: generalized environmental systemenvironmental assessmentindex specification transformationuniversal index formula
1 引言(Introduction)迄今为止, 国内外****已提出了数10种可用于环境评价的模型和方法, 主要有指数评价公式(Sanchez et al., 2007;Jie et al., 2012;Yang et al., 2012)、统计分析法(Liou et al., 2005;Shrestha et al., 2007; 周丰等, 2007;Zhang et al., 2011;富天乙等, 2014)、不确定性分析评价法(Zhu et al., 2007;IP et al., 2009; 王文圣等, 2009;Pai et al., 2010;Xu et al., 2011;Li et al., 2012; Liu et al., 2012;Wang et al., 2014;Huang et al., 2015;王建军等, 2015;Yan et al., 2016;方运海等, 2018)和各种智能评价模型(Wang et al., 2004;Wu et al., 2007;Singh et al., 2009;李祚泳等, 2013; 2015;Liu et al., 2015), 以上方法各有其特点(Osawa et al., 2009;Yan et al., 2013).由于不同环境评价对象所依据的指标及其分级标准、指标数目都不相同, 因而对不同的环境系统, 传统的各种评价公式、模型和方法的共同局限是不能规范、普适、统一和通用.因此, 探索建立适用于不同指标及其分级标准和不同指标数目的广义环境系统(即任意环境系统)评价的普适、规范、简洁、通用的公式、模型和方法, 具有十分重要的理论意义和实用价值.
从实用角度出发, 指数评价公式是最简单、实用的评价方法, 但传统的单指标指数评价公式或多指标综合指数评价公式同样不具有规范、普适、统一和通用的特点.虽然文献(李祚泳等, 2012)提出了适用于指标规范变换的地表水、地下水和富营养化水体的共72项指标的水环境评价的6个普适指数公式, 但它们对广义环境系统的任意评价指标并不普适、通用.所谓广义环境系统是指地球表面生物的和非生物的各种环境因素及其相互关系的总和, 其包括通常所说的空气环境、噪声环境、水环境(地表水、地下水、富营养化水体)、海洋环境、生态环境等传统(狭义)意义的环境系统和水文水资源(径流量、水资源利用、水资源承载力)环境、自然资源环境、安全与灾害环境、天气环境、人类社会与经济可持续发展等非传统意义的环境系统.因此, 广义环境系统是由人口、社会、经济、资源、环境等构成的复杂系统.不过, 对由上述不同环境系统组成的广义环境系统, 虽然不同指标的属性及其分级标准不尽相同, 但总可以按照一定的普适原则和方法, 通过适当设置指标参照值及指标规范变换式, 并对指标的各分级标准值进行规范变换, 使规范变换后的广义环境系统任意指标的各级标准规范值都能被限定在各自的较小区间内, 从而用规范值表示的任意指标皆“等效”于同一个规范指标, 因而广义环境系统的任意指标的各个评价指数公式都可以用该“等效”规范指标的相应评价指数公式“等效”替代.并在满足一定的优化目标准则条件下, 采用免疫进化算法分别对各指数公式中的参数进行优化, 得到适用于任意指标规范值的广义环境系统评价的普适指数公式, 为广义环境系统的规划、管理的科学决策提供理论基础和技术手段.
2 广义环境系统指标参照值及规范变换式的设置(Setting of index reference value and normative transform formula for generalized environmental system)通过对多种不同环境系统指标的国标或非国标分级标准值的观察、分析、归纳表明, 对广义环境系统(实际上即是任意环境系统), 不论评价指标的数目、量纲、单位、分级标准和数据分布特性及变化规律(线性或非线性、正态或非正态、独立或相关、正向或逆向等)之间存在多大差异, 皆能按cj0、nj和cjb设定的普适原则和方法, 构建式(1)的幂函数变换式和式(2)的对数函数变换式组成的规范变换式, 使不同环境系统的任意指标的同级标准值cjk, 经规范变换后的同级标准规范值x′jk都能被限定在如表 1所示的较小区间内, 从而可以认为, 用规范值表示的不同环境系统的任意指标皆“等效”于同一个规范指标.此“等效”指标的某级标准规范值即是该级标准的不同指标规范值的均值, 因而对“等效”规范指标建立的评价指数公式亦适用于不同环境系统的任意指标规范值的评价, 从而使不同环境系统的评价指数公式得到规范、普适、统一、通用和简化.
表 1(Table 1)
| 表 1 广义环境系统指标分级标准规范值的平均值、标准差及变化范围 Table 1 Average value, standard deviation and range of change of standard value for index classification of generalized environmental systems | ||||||||||||||||||||||||||||
表 1 广义环境系统指标分级标准规范值的平均值、标准差及变化范围 Table 1 Average value, standard deviation and range of change of standard value for index classification of generalized environmental systems
| ||||||||||||||||||||||||||||
式中, cj为指标实际值或分级标准值;cj0为设置的指标参照值;cjb为设定的指标的阈值;Xj和x′j分别为指标的变换值和规范值;k代表分级标准数目;nj为指标j变换式的幂指数.式(1)右边1~4行适用于正向类指标的变换, 5~8行适用于逆向类指标的变换.nj、cj0和cjb的确定原则和步骤如下:
① 确定幂指数nj.首先, 计算指标j分级标准值中的最大值与最小值的比值
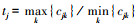

② 确定阈值cjb.只有当tj < 2(k≥5级)或tj < 1.5(k≤4级)的指标才需要确定阈值cjb.
③ 初设指标参照值cj0.当nj和cjb确定后, 初设变换式(1)中各指标的cj0, 使由式(1)和式(2)计算得到的指标j的最低一级标准规范值x′j和最高一级标准规范值x′j5能在表 1所示的相应级标准规范值的限定范围内.
④ 最终确定指标参照值cj0.检查由式(1)和式(2)计算的指标j的其余各级标准规范值是否处于表 1所示的相应各级标准规范值限定范围内.若是, 则cj0确定;否则, 需对初步设定的cj0作微调, 使得各级标准规范值x′jk尽可能都在表 1所示的限定范围内即可.为使建立的评价模型具有更好的适应能力, 表 1中相邻两级分级标准指标规范值x′jk的变化范围容许有少部分交叉、重叠.
3 适用于指标规范值的广义环境系统评价的普适指数公式(A universal index formula for generalized environmental system assessment with normal value of indicators)3.1 训练样本的随机生成为使建立的评价普适指数公式具有真正意义上的“广义”普适性和规范性, 在表 1中的广义环境系统指标各级标准规范值x′jk限定变化范围内, 分别用各自随机生成的100个随机数值, 模拟广义环境系统任意指标的不同分级标准的规范值.5级标准共生成500个随机数值, 各级标准生成的100个随机数值的均值和标准差见表 1.同级标准生成的100个随机数值可视为“等效”指标的该级标准的100个规范值标准样本;5级标准共生成的500个随机数值则组成“等效”指标的5级标准的500个规范值标准样本.
3.2 评价指数公式的选取为了适应各种线性和非线性不同环境系统评价的需要及满足简单、实用的特点, 提出了以下9个不同形式的评价指数公式.
① W-F韦伯费希纳(W-F)指数公式:
 | (3) |
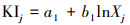 | (4) |
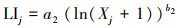 | (5) |
 | (6) |
 | (7) |
 | (8) |
 | (9) |
 | (10) |
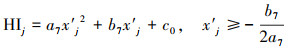 | (11) |
3.3 评价指数公式中参数的优化为了优化式(3)~(11)中的参数, 使评价指数公式对广义环境系统的任意指标规范值皆适用, 需要设计如式(12)或式(13)所示的优化目标函数式.
 | (12) |
 | (13) |
表 2(Table 2)
| 表 2 9个普适指数公式的设定目标值XIk0、目标函数值Q0、参数优化结果及各分级标准值XIk Table 2 Setting target value XIk0, objective function value Q0, parameter optimization result and grading standard XIk of 9 universal index formulas | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
表 2 9个普适指数公式的设定目标值XIk0、目标函数值Q0、参数优化结果及各分级标准值XIk Table 2 Setting target value XIk0, objective function value Q0, parameter optimization result and grading standard XIk of 9 universal index formulas
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
在满足式(12)或式(13)优化目标函数值条件下, 将表 1中生成的500个随机数值作为5级标准的500个训练样本, 分别代入式(3)~(11)中, 用免疫进化算法(Immune Evolutionary Algorithm, IEA)对9个普适公式中的参数(a0, a1, …, a7;b1, …, b7;λ0;c0)进行迭代优化.IEA算法的基本思想和实现过程详见文献(倪长健等, 2003).当算法迭代100次后, 分别得到优化后的9个普适指数公式(3)~(11)的目标函数值Q0及参数优化值, 亦见表 2.从而得到适用于基于指标规范值的广义环境系统评价的9个普适指数公式, 分别如式(14)~(22)所示.
① W-F(韦伯费希纳)指数公式:
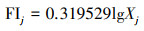 | (14) |
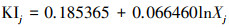 | (15) |
 | (16) |
 | (17) |
 | (18) |
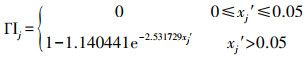 | (19) |
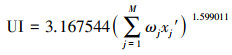 | (20) |
 | (21) |
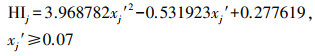 | (22) |
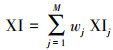 | (23) |
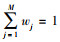
 | (24) |
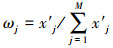 | (25) |
3.5 普适指数公式的可靠性分析由于任何数学模型(公式也是模型)都是构筑在若干模型参数基础上的, 这些模型参数又是依据模型的多组输入/输出数据来确定的.而获得的输入/输出数据(环境系统评价指标值cj)都会由于受多种因素的影响, 存在着一定的误差, 故用式(1)和式(2)计算得到的指标规范值x'j不可避免地亦存在着一定的误差.这样必然会导致所估计的模型(文中的指数公式)参数存在一些不确定性, 这些参数的不确定性对模型评价结果的可靠性和稳定性当然会有一定的影响.因此, 需要对模型的可靠性进行分析, 而模型的可靠性可通过对优化得到的模型参数的灵敏度分析来验证.以普适卡森指数公式(4)的可靠性分析为例说明如下.
卡森指数的相对误差ΔKIk/KIk0与参数a1、b1的相对误差Δa1/a1、Δb1/b1及其灵敏度Sa1、Sb1之间的关系如式(26)所示.
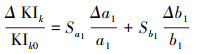 | (26) |
 | (27) |
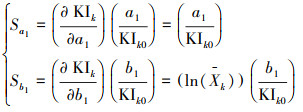 | (28) |
表 3(Table 3)
| 表 3 9个普适指数公式中参数的可靠性分析结果 Table 3 Reliability analysis results of parameters in 9 universal exponential formulas | ||||||||||||||||||||||||||||||
表 3 9个普适指数公式中参数的可靠性分析结果 Table 3 Reliability analysis results of parameters in 9 universal exponential formulas
| ||||||||||||||||||||||||||||||
从表 3可以看出, 9个公式中, 除多参数组合算子普适指数公式的参数λ和二次函数普适公式参数b的相对误差绝对值>5%以外, 其余普适公式的参数相对误差绝对值均 < 5%.从而表明优化得到的9个普适指数公式(14)~(22)具有可靠性.
3.6 普适指数公式的评价步骤步骤1:由具体评价对象给定的指标分级标准, 依据nj、cj0、cjb和指标变换式设计原则和方法, 设置如式(1)所示的各指标的变换式, 要求满足由规范变换式(1)和式(2)计算得到各指标的各级标准规范值分别处于表 1所示的各自标准规范值限定范围内.
步骤2:由设置的各指标的规范变换式, 计算出各指标的各级标准值的变换值Xjk和规范值x′jk及评价对象指标实际数据的变换值Xj和规范值x′j.
步骤3:分别将各指标的各级标准的变换值Xjk或规范值x′jk代入参数优化得到的9个普适指数公式(14)~(22)中, 计算得到各个指数公式的各指标的各级标准的分级指数值, 并视式(23)各指标等权情况下, 计算得到各指数公式的综合指数分级标准值;类似的, 将实际评价对象各指标的变换值Xj或规范值x′j代入参数优化得到的9个普适指数公式(14)~(22)中, 计算得到评价对象各个指数公式的各指标的分指数值, 并用加权综合指数式(23)~(25)计算得到实际评价对象的各指数公式的加权综合指数值.
步骤4:依据各指数公式的综合指数分级标准值, 对计算得到的实际评价对象的加权综合指数值, 做出等级评价结果.
4 普适指数公式的效果验证(Validation of the universal index formula)4.1 普适指数公式用于地下水质评价4.1.1 设置指标参照值和指标值的规范变换式以北京市朝阳区地下水水质综合评价的实例数据验证9个普适指数公式的实用性.19个水质监测井的9项地下水指标总硬度(C1)、溶解性总固体(C2)、硫酸盐(C3)、氯化物(C4)、CODMn(C5)、NO3--N(C6)、NO2--N(C7)、NH3-N(C8)、氟化物(C9)的监测数据及其地下水质级别分类标准参见文献(巩奕成等, 2015).依据表 1对指标的各级标准规范值的限定范围及nj、cj0、cjb和指标变换式的设计原则和方法, 设置如式(29)所示的变换式(步骤1).由式(29)及式(2)计算得到9项地下水质指标的5级标准变换值和规范值(步骤2), 结果如表 4所示.同样, 由式(29)及式(2)计算得到19个监测井的9项地下水质指标的监测数据的变换值和规范值(步骤2), 如表 5所示.再由各监测井的9项地下水指标的规范值, 用式(25)计算各监测井的各指标分指数加权值Wj, 如表 5所示.
表 4(Table 4)
| 表 4 9项地下水指标的5级分级标准的变换值Xjk和规范化值x′jk Table 4 The conversion value Xjk and normalized value x′jk of 5 grading standards for 9 groundwater indicators | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
表 4 9项地下水指标的5级分级标准的变换值Xjk和规范化值x′jk Table 4 The conversion value Xjk and normalized value x′jk of 5 grading standards for 9 groundwater indicators
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
表 5(Table 5)
| 表 5 19个地下水监测井的9项指标的监测数据变换值Xj、规范值x′j及其权值Wj Table 5 The transformation value Xj, standard value x′j and weight value Wj of monitoring data for 9 indexes of 19 groundwater monitoring wells | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
表 5 19个地下水监测井的9项指标的监测数据变换值Xj、规范值x′j及其权值Wj Table 5 The transformation value Xj, standard value x′j and weight value Wj of monitoring data for 9 indexes of 19 groundwater monitoring wells
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 | (29) |
4.1.2 综合指数分级标准值及评价结果分别将表 4中各级标准的9项评价指标的变换值Xjk或规范值x′jk代入9个普适指数公式(14)~(22)中, 计算得到各级标准的各指标的指数公式的分指数值, 并求算术平均値, 得到各指数公式的各分级标准综合指数值(步骤3), 如表 6所示.同样, 由式(14)~(22)及(23)和式(25)计算得到9个指数公式对19个水质监测井的加权综合指数值(步骤3), 如表 7所示.依据表 6各指数公式的综合指数的分级标准值, 得出用9个普适指数公式对19个水质监测井的水质评价结果(步骤4), 如表 8所示.表 8中还列出笔者用基于指标规范变换的广义环境系统评价的投影寻踪回归(NV-PPR)模型对19个监测井的水质指数PI评价结果, 以及文献(巩奕成等, 2015)用RAGAP和FAPP两种传统方法对19个监测井的水质评价结果.需要指出的是:①综合指数λI的计算:需将指标x′j按从小到大(或从大到小)排序, 按排好的序从第1个x′[1]开始, 计算x′[1]与x′[2]组成的λI1指数, 再计算x′[2]与x′[3]组成的λI2指数, 直到计算x′[9]与x′[1]组成的λI9指数为止;然后再对9个λIj值加权平均, 即是λI综合指数值.②NV-PPR的综合指数PI的计算:指标x′j不用大小排序, 只需从第1个指标的x′1开始, 依次将相邻两个指标的规范值代入PI指数公式中, 计算分指数值PIj, 直到最后用x′9和x′1代入PI指数公式中, 计算分指数值PI9为止;然后对计算得到的9个PIj求平均值即可.
表 6(Table 6)
| 表 6 适用于北京市地下水质评价的9个普适指数公式的综合指数的分级标准值XIk Table 6 Grading standard value XIk of comprehensive index of 9 universal index formulas for groundwater quality assessment in Beijing | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
表 6 适用于北京市地下水质评价的9个普适指数公式的综合指数的分级标准值XIk Table 6 Grading standard value XIk of comprehensive index of 9 universal index formulas for groundwater quality assessment in Beijing
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
表 7(Table 7)
| 表 7 北京市19个监测井的9个评价指数公式的综合指数值 Table 7 Comprehensive index values of 9 evaluation index formulas for 19 monitoring wlls in Beijing | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
表 7 北京市19个监测井的9个评价指数公式的综合指数值 Table 7 Comprehensive index values of 9 evaluation index formulas for 19 monitoring wlls in Beijing
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
表 8(Table 8)
| 表 8 多种评价方法用于19个监测井的地下水质评价结果 Table 8 Evaluation results of groundwater quality in 19 monitoring wells by various evaluation methods | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
表 8 多种评价方法用于19个监测井的地下水质评价结果 Table 8 Evaluation results of groundwater quality in 19 monitoring wells by various evaluation methods
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
4.1.3 评价结果分析与比较由表 8可见, 19个水质监测井中, 除2、4、17号3个监测井有少数几个公式评价等级相差1级外, 其余16个监测井的9个普适指数公式和NV-PPR模型评价结果完全一致.即使不一致的2、4、17号3个监测井, 也只是因为计算得到的指数值都处于相邻两类标准的分界值的附近, 因而两种评价结果都是可以接受的.
19个水质监测井中, 9个普适指数公式、NV-PPR模型评价结果与传统的评价方法RAGAPP、FAPP的评价结果完全相同的也有14个监测井;评价结果有差异的也只有3、4、7、8和17号5个监测井.其中, 3号监测井9项指标中, 分别有3项和6项指标处于1类和2类水质标准, 因此, 9个普适指数公式和NV-PPR模型综合评价皆为2类水比RAGAPP和FAPP综合评价为1类水更适当;4号监测井9项指标中, 处于1类、2类和3类水质标准的各有3项, 依据取大不取小原则, 有7个普适指数公式和NV-PPR模型综合评价为3类水是适当的;7、8两个监测井9项指标中, 分别有6项和7项指标处于1类水质标准, 因此, 9个普适指数公式和NV-PPR模型综合评价为1类水是合理的;17号监测井分别有2项、4项、2项和1项指标处于1类、3类、4类和5类水质标准, 因此, 多数普适指数公式和NV-PPR模型综合评价为4类水比评价为3类水更适当.
4.2 普适指数公式用于城市可持续发展评价由于郑州、西安、上海三市的可持续发展评价指标众多, 而且指标中包括人文、社会、经济、自然资源、生态环境、环境保护和治理等多种不同类型的指标, 属于典型的广义环境系统.因此, 选择对此三市的可持续发展评价验证9个普适指数公式对广义环境系统评价的普适性和可行性.
4.2.1 设置指标参照值和指标值的规范变换郑州、西安、上海三市2000年可持续发展评价的28项指标的分级标准值cjk及三市各指标值cji如表 9所示(陈媛等, 2010).依据表 1对指标的各级标准规范值的限定范围及nj、cj0和指标变换式设计原则和方法, 设置如表 9所示的指标参照值cj0和指标变换式(30)(步骤1).由式(30)及式(2)计算得到28项指标的3级标准变换值和规范值(步骤2), 结果如表 9所示;同样, 由式(30)及式(2)计算得到郑州、西安、上海三市的28项可持续发展指标实际数据的变换值和规范值(步骤2), 具体见表 9.
表 9(Table 9)
| 表 9 可持续发展评价指标分级标准值cjk及其标准规范值x′jk和郑州、西安、上海三市指标值cji及其规范值x′ji(2000年) Table 9 Classification standard value cjk of sustainable development evaluation index and its standard value x′jk, as well as index value cji and its standard value x′ji of Zhengzhou, Xi′an and Shanghai (2000) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
表 9 可持续发展评价指标分级标准值cjk及其标准规范值x′jk和郑州、西安、上海三市指标值cji及其规范值x′ji(2000年) Table 9 Classification standard value cjk of sustainable development evaluation index and its standard value x′jk, as well as index value cji and its standard value x′ji of Zhengzhou, Xi′an and Shanghai (2000)
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
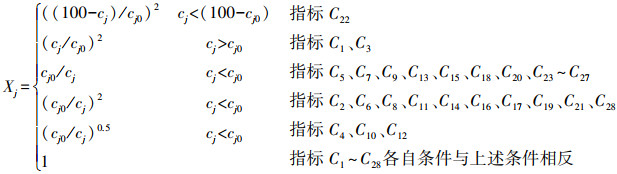 | (30) |
表 10(Table 10)
| 表 10 9个指数公式计算得到的郑州、西安、上海三市可持续发展评价的综合指数分级标准值XIk Table 10 Comprehensive index grading standard value XIk of three cities′ sustainable development evaluation calculated by 9 index formulas | |||||||||||||||||||||||||||||||||||||||||||||||||
表 10 9个指数公式计算得到的郑州、西安、上海三市可持续发展评价的综合指数分级标准值XIk Table 10 Comprehensive index grading standard value XIk of three cities′ sustainable development evaluation calculated by 9 index formulas
| |||||||||||||||||||||||||||||||||||||||||||||||||
表 11(Table 11)
| 表 11 9个指数公式计算得到的郑州、西安、上海三市可持续发展评价的综合指数值及评价结果比较 Table 11 Comprehensive index value of sustainable development evaluation of three cities and comparison of evaluation results calculated by 9 index formulas | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
表 11 9个指数公式计算得到的郑州、西安、上海三市可持续发展评价的综合指数值及评价结果比较 Table 11 Comprehensive index value of sustainable development evaluation of three cities and comparison of evaluation results calculated by 9 index formulas
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
实际情况是:郑州市28项指标中分别有1项、11项和16项指标处于1级(强可持续)、2级(基本可持续)和3级(弱可持续), 因此, 评价为3级比评价为2级更适当;西安市28项指标中分别有6项和22项指标处于2级和3级, 因此, 评价为3级比评价为2级更适当;上海市28项指标中分别有8项、12项和8项指标处于1级、2级和3级, 因此, 评价为2级比评价为1级更适当.由上述分析结果可知, 9个普适指数公式和NV-PPR模型对郑州、西安、上海三市可持续发展的评价结果比用集对分析法、灰色分析法和模糊分析法的评价结果更符合实际情况, 而且计算相对简便.
5 讨论(Discussion)① 9个指数评价公式都不受指标数多少的限制;对同一个评价对象, 不同指数公式的评价结果多数情况下是完全一致的.因此, 只需用任何一个或几个公式评价即可, 若用多个评价公式, 其评价结果可作为相互印证.笔者也将9个指数评价公式用于具有不同指标数的空气环境、各种水环境、生态环境、海洋环境、水安全环境、水文水资源环境、可持续发展环境等10余个实例进行评价检验, 评价结果与实际相符.
② 虽然依据指标参照值和指标值的变换式的设置原则和方法, 设置评价对象的指标参照值cj0和指标值的变换式(1)的具体形式也有一定程度的不确定性, 但由于都是用设置的同一个指标规范变换式和相同的参照值cj0及同一个指数公式, 计算得到综合指数的分级标准值和评价样本的综合指数值, 因而依据普适指数公式的各综合指数分级标准值对评价样本做出的评价等级是确定性的, 不存在差异.
③ 分类环境(比如水环境)系统评价的普适指数公式(李祚泳等, 2012)与广义环境系统评价的普适指数公式的显著不同之处为:1).两者的参数优化所依据的训练样本不同:前者是以分类环境指标的各级标准规范值组成训练样本, 对指数公式中的参数进行优化, 因此, 优化得到的指数公式仅适用于该类环境系统指标的评价, 而不能用于不同类环境系统指标的评价;后者是以不同限定区间内生成的随机数组成不同分级标准的全部训练(学习)样本(其与任何一类环境系统的具体指标分级标准无关), 对指数公式中的参数进行优化, 因此, 优化得到的指数公式适用于任意类环境系统(即广义环境系统)的任意指标的评价.2).两者综合评价依据的分级标准不同:对任何具体评价对象, 前者都是以各指数公式的该类环境所有指标的各级标准的分指数值的均值作为各指数公式的综合指数分级标准值, 因而对该类环境的任意指标组成的具体评价对象, 综合指数分级标准值是共同的;而后者则是由具体评价对象给定的指标分级标准, 计算得到各指数公式的综合指数作为该具体评价对象的综合指数分级标准值, 因而评价指数公式的综合指数分级标准值随问题的指标分级标准不同而不同.
④ 用优化得到的9个评价普适指数公式评价与传统的模糊数学评价法、物元分析评价法、灰色系统评价法、集对分析评价法等不确定性评价法相比, 不需要构造众多的评价函数, 与传统的神经网络(BP网络、RBF网络、FNN网络、PNN网络)、投影寻踪回归(PPR)、支持向量机(SVM)等智能评价模型相比, 不再需要编程优化计算, 因而十分简便.
6 结论(Conclusions)1) 指数公式的指标参照值和指标规范变换式的设置具有可操作性、规范性和简单性.
2) 9个普适指数公式的评价结果彼此具有兼容性和协调性.
3) 与传统的评价指数公式相比, 广义环境系统评价的普适指数公式的最大优势是使任意环境系统的评价指数公式得到普适、规范、统一和通用.
4) 基于指标规范变换的广义环境系统评价指数公式的建模思想和方法, 对建立广义环境系统的神经网络评价模型和支持向量机评价模型具有参考意义.
参考文献
| 陈媛, 王文圣, 汪嘉杨, 等. 2010. 基于集对分析的城市可持续发展评价[J]. 人民黄河, 32(1): 11-13. DOI:10.3969/j.issn.1000-1379.2010.01.005 |
| 方运海, 郑西来, 彭辉, 等. 2018. 基于模糊综合与可变模糊集耦合的地下水质量评价[J]. 环境科学学报, 38(2): 546-552. |
| 巩奕成, 张永祥, 丁飞, 等. 2015. 基于萤火虫算法的投影寻踪地下水水质评价方法[J]. 中国矿业大学学报, 44(3): 566-572. |
| 富天乙, 邹志红, 王晓静. 2014. 基于多元统计和水质标识指数的辽阳太子河水质评价研究[J]. 环境科学学报, 34(2): 473-480. |
| Huang H, Liang X J, Xiao C L, et al. 2015. Analysis and assessment of confined and phreatic water quality using a rough set theory method in Jilin City, China[J]. Water Science and Technology, Water Supply, 15(4): 773-783. DOI:10.2166/ws.2015.031 |
| IP W C, Hu B Q, Wong H, et al. 2009. Application of grey relational method to river environment quality evaluation in China[J]. Journal of Hydrology, 379: 284-290. DOI:10.1016/j.jhydrol.2009.10.013 |
| Jie C, Qing L, Hui Q. 2012. Application of improved Nemerow index method based on entropy weight for groundwater quality evaluation[J]. International Journal of Environmental Sciences, 2(3): 1284-1290. |
| Li P Y, Wu J H, Qian H. 2012. Groundwater quality assessment based on rough set attribute reduction and TOPSIS method in a semi-arid area[J]. Environmental Monitoring and Assessment, 184(8): 4841-4854. DOI:10.1007/s10661-011-2306-1 |
| 李祚泳, 张正健, 汪嘉杨, 等. 2012. 基于水环境信息规范变换的水质普适指数公式[J]. 环境科学学报, 32(3): 668-677. |
| 李祚泳, 张正健. 2013. 基于回归支持向量机的指标规范值的水质评价模型[J]. 中国环境科学, 33(8): 1502-1508. |
| 李祚泳, 徐源蔚, 汪嘉杨, 等. 2015. 基于前向神经网络的广义环境系统评价普适模型[J]. 环境科学学报, 35(9): 2996-3005. |
| Liou Y T, Lo S L. 2005. A fuzzy index model for trophic status evaluation of reservoir water[J]. Water Research, 39(7): 1415-1423. DOI:10.1016/j.watres.2005.01.014 |
| 倪长健, 丁晶, 李祚泳. 2003. 免疫进化算法[J]. 西南交通大学学报, 38(1): 87-91. DOI:10.3969/j.issn.0258-2724.2003.01.020 |
| Liu D J, Zou Z H. 2012. Water quality evaluation based on improved fuzzy matter-element method[J]. Environmental Sciences, 24(7): 1210-1216. DOI:10.1016/S1001-0742(11)60938-8 |
| Liu S Y, Xu L Q, Li D L. 2015. Water quality early warning model based on support vector machine optimized by rough set algorithm[J]. Systems Engineering Theory and Practics, 35(6): 1617-1724. |
| Osawa H, Hayashi M. 2009. Status of the indoor air chemical pollution in Japanese houses based on the nationwide field survey from 2000 to 2005[J]. Building and Environment, 44: 1330-1336. DOI:10.1016/j.buildenv.2008.06.022 |
| Pai P F, Lee F C. 2010. A rough set based model in water quality analysis[J]. Water Resources Management, 24(11): 2405-2418. DOI:10.1007/s11269-009-9558-3 |
| Sanchez E, Colmenarejo M F, Vicente J, et al. 2007. Use of the water quality index and dissolved oxygen deficit as simple indicators of watersheds pollution[J]. Ecological Indicators, 7(2): 315-328. DOI:10.1016/j.ecolind.2006.02.005 |
| Shrestha S, Kazama F. 2007. Assessment of surface water quality using multivariate statistical technique:A case study of the Fuji river basin, Japan[J]. Environmental Modelling and Software, 22(4): 464-475. DOI:10.1016/j.envsoft.2006.02.001 |
| Singh K P, Basant A, Malik A, et al. 2009. Artificial neural network modeling of the river water quality:a case study[J]. Ecological Modeling, 220(6): 888-895. DOI:10.1016/j.ecolmodel.2009.01.004 |
| 王文圣, 金菊良, 丁晶, 等. 2009. 水资源系统评价新方法-集对评价法[J]. 中国科学(E集技术科学), 39(9): 1529-1534. |
| 王建军, 李建平, 杜仕甫. 2015. 基于模糊聚类的无权值风险综合评判算法[J]. 系统工程理论与实践, 35(8): 2137-2143. |
| Wang X G, Tang Z, Tamura H, et al. 2004. An improved back-propagation algorithm to avoid the local minima problem[J]. Neurocomputing, 56(1): 455-460. DOI:10.1016/j.neucom.2003.08.006 |
| Wang W, Xu D, Chan K, et al. 2014. Assessment of river water quality based on theory of variable fuzzy sets and fuzzy binary comparison method[J]. Water Resources Mangement, 28(12): 4183-4200. DOI:10.1007/s11269-014-0738-4 |
| Wu Z L, Li C H, Joseph K, et al. 2007. Location estimation via support vector regression[J]. IEEE Trans on Mobile Computing, 6(3): 311-321. DOI:10.1109/TMC.2007.42 |
| Xu L, Liu Z H, Du J. 2011. Study on evaluation of water ecological carrying capacity[J]. Energy Procedia, 11: 3530-3538. DOI:10.1016/S1876-6102(14)00453-6 |
| Yang D F, Zheng L, Song W P, et al. 2012. Evaluation indexes and methods for water quality in ocean dumping areas[J]. Procedia Environmental Sciences, 16: 112-117. DOI:10.1016/j.proenv.2012.10.015 |
| Yan S H, Dong S C, Li Z H, et al. 2013. Carrying Capacity of water resources for Three-North shelterbelt construction in China[J]. Journal of Resources and Ecology, 4(1): 50-55. |
| Yan F, Liu L, Zhang Y, et al. 2016. The research of dynamic variable fuzzy set assessment model in water evaluation[J]. Water Resources Mangement, 30(1): 63-78. DOI:10.1007/s11269-015-1146-0 |
| Zhu C Hi, Li N P, Re D, et al. 2007. Uncertainty in indoor air quality and grey system method[J]. Building and Environment, 42(4): 1711-1717. DOI:10.1016/j.buildenv.2006.01.015 |
| Zhang X, Wang Q S. 2011. Application of multivariate statistical technique in the assessment of water quality in the Southwest New Territories and Kowloon, Hong Kong[J]. Environment Monitoring and Assessment, 173: 17-27. DOI:10.1007/s10661-010-1366-y |
| 周丰, 郭怀成, 刘永, 等. 2007. 基于多元统计分析和RBFNNs的水质评价方法[J]. 环境科学学报, 27(5): 846-853. DOI:10.3321/j.issn:0253-2468.2007.05.023 |
