 , 刘朝顺1,2
, 刘朝顺1,2
 , 焦鹏龙1
, 焦鹏龙11. 华东师范大学地理科学学院, 上海 200241;
2. 华东师范大学地理信息科学教育部重点实验室, 上海 200241
收稿日期: 2018-11-22; 修回日期: 2019-01-08; 录用日期: 2019-01-08
基金项目: 上海市自然科学基金(No.17ZR1408600);国家理科基地科研训练及科研能力提高项目(No.J1310028)
作者简介: 李珂(1997-), 女, E-mail:L_K_971206@163.com
通讯作者(责任作者): 刘朝顺, E-mail:csliu@re.ecnu.edu.cn
摘要: 随着工业化和城市化的迅速发展,中国面临着越来越严重的大气污染危机,以细颗粒物(PM2.5)为标志的区域性大气复合污染问题已经成为我国大气环境污染治理的核心工作.目前,传统的地面监测站监测PM2.5浓度的方法空间分辨率较差且耗费人力物力,而卫星遥感数据监测PM2.5浓度的方法大部分只能应用于白天.由于PM2.5浓度在时间上存在周期性变化,因此利用卫星遥感数据监测的夜间PM2.5浓度可以作为表征PM2.5日变化规律的重要补充.本研究采用Suomi National Polar-orbiting Partnership(Suomi NPP)卫星搭载的可见红外成像辐射计套件(Visible Infrared Imaging Radiometer Suite,VIIRS)中Day/Night波段(DNB)夜间灯光影像数据,依据大气气溶胶消光原理和站点气象数据,建立PM2.5浓度的预测模型,基于多元线性回归分析对上海地区9个空气质量监测站在2014-2018年冬季无月无云的晴朗夜间的PM2.5浓度值进行估计,并对PM2.5浓度的空间分布进行模拟.结果表明,在研究时段上海地区PM2.5实际浓度与模型估算PM2.5浓度之间R2=0.767,均方根误差(RMSE)为19.210 μg·m-3,验证了VIIRS/DNB夜间灯光影像数据在估算PM2.5浓度方面有巨大潜力.
关键词:夜间灯光遥感VIIRS/DNB多元线性回归空气质量PM2.5
Estimation of nighttime PM2.5 concentration in Shanghai based on NPP/VIIRS Day_Night Band data
LI Ke1
 , LIU Chaoshun1,2
, LIU Chaoshun1,2
 , JIAO Penglong1
, JIAO Penglong1 1. School of Geographic Sciences, East China Normal University, Shanghai 200241;
2. Laboratory of Geographic Information Science of Ministry of Education, East China Normal University, Shanghai 200241
Received 22 November 2018; received in revised from 8 January 2019; accepted 8 January 2019
Abstract: With rapid development of industrialization and urbanization, China has currently suffered from increasingly serious air pollution, in particular the fine particulate matter (PM2.5) related haze pollution episodes. Ground-level PM2.5 concentrations are routinely measured via sparsely distributed ground monitors, which is always costly and labor-intensive. Although satellite-based PM2.5 mapping is capable of providing PM2.5 measurements over large spatial area, the output data sets are largely limited to daytime concentrations. To better characterize the daily variability of PM2.5 concentration, this study estimated nighttime PM2.5 concentrations over Shanghai for the period of 2014-2018 in winter using Day/Night band image data (DNB) collected from the Visible Infrared Imaging Radiometer Suite (VIIRS) on board Suomi National Polar-orbiting Partnership satellite (Suomi-NPP). The results showed that the predicted PM2.5 data agreed well with the co-located ground-based PM2.5 measurements, with a correlation coefficient of 0.767 and root mean square error of 19.210 μg·m-3, thereby indicating large potential of VIIRS/DNB data in nighttime PM2.5 mapping.
Keywords: night lighting remote sensingVIIRS/DNBmultiple linear regressionair quality PM2.5
1 引言(Introduction)大气污染已成为21世纪中国面临的最严重的危机之一.研究发现, 我国细粒子背景浓度较高, 远远高于世界卫生组织WHO的指导限值(PM2.5年均标准10 μg·m-3)和美国大气质量标准(PM2.5年均标准12.5 μg·m-3), 也远高于WHO于2011年10月公布的全球38个国家567个城市的平均浓度(Gao et al., 2016).而且, PM2.5占PM10的比例达到60%~80%左右(Wei et al., 1999; Wang et al., 2006; Wang et al., 2013).这说明在霾气溶胶污染中, 主要是细粒子污染.这正是近年来能见度恶化的根本原因.为贯彻落实国务院《大气污染防治行动计划》, 2012年新发布的《环境空气质量标准》, 提高了PM2.5的阈值标准, 增加了环境质量评价的污染物因子, 用以更好地表征我国环境空气质量状况, 反映当前复合型大气污染形势.以细颗粒物(PM2.5)为标志的区域性大气复合污染问题已经成为我国大气环境污染治理的核心工作之一.
传统的地面空气质量站点对PM2.5浓度监测方法有:手工颗粒物采样重量法、微量振荡天平法等(蔡艳等, 2012).这些方法虽然精度高、能够实时在线监测, 但是由于成本限制, 通过区域内有限数量的空气质量站点来表征PM2.5浓度空间分布存在一定局限性.卫星遥感技术的发展为区域霾污染监测带来了新的机遇, 使得利用卫星数据监测大范围空间分布的PM2.5浓度成为可能.通过搭载在卫星的传感器可以对污染物来源、扩散等空间上的变化进行宏观监测, 在很大程度上弥补了地面观测的不足. Wang等(2003)提出了利用卫星观测产品——气溶胶光学厚度(Aerosol Optical Depth, AOD)建立与地面PM2.5浓度关系模型的想法. Lee等(2011)使用中分辨率成像光谱仪(Moderate Resolution Imaging Spectroradiometer, MODIS)产品建立了一种气溶胶光学厚度(AOD)定标方法, 实现了对新英格兰地区地面日PM2.5浓度较为准确的估算. Zheng等(2016)利用线性混合效应(Linear Mixed-Effects, LMEs)模型, 同样使用MODIS相关产品对京津冀、长三角、珠三角地区白天的PM2.5浓度进行了估算.
但在先前的研究中, 利用到的卫星遥感数据大多数都是采用基于可见光观测反演的AOD产品, 进而估计白天PM2.5浓度.根据李名升等(2016)研究表明, PM2.5浓度的日变化具有较强的规律性. Zhang等(2008)的研究指出利用地球表面人造光来监测夜间粒子光学特性的可能, 并且寄希望于将来升空的NPOESS-JPSS卫星所搭载的高空间分辨率VIIRS传感器可以为此研究提供重要数据支持. 2012年, 美国新一代国家极轨业务环境卫星系统预备项目(NPOESS)的首颗卫星NPP的发射.随后, Wang等(2016)提出了利用VIIRS中DNB波段的夜间灯光辐射值作为辐射源, 依据气溶胶消光原理反演大气气溶胶光学厚度, 建立与PM2.5浓度的多元线性回归模型来估算美国亚特兰大地区5个空气质量监测站的PM2.5浓度, 其中使用光学模型估算精度R达到0.671, 而使用气象要素所构建模型的估算精度仅为0.501.在Wang等(2016)的研究中, 对于PM2.5吸湿增长因子的拟合采用了Malm et al.(1994)所提出的多项式模型, 但该多项式模型没有区分因季节变化而导致的参数差异, 同时用来拟合上海地区大气颗粒物吸湿增长特性也存在一定局限性.类似的方法在估算北京地区夜间空气质量方面也得到了应用. 赵笑然等(2017)对Wang等(2016)使用的模型进行精简, 并基于支持向量机方法建立北京地区PM2.5浓度反演模型, 模型估算PM2.5浓度与实际PM2.5浓度的相关系数R达到0.950, 但在赵笑然等(2017)的研究中, 由于选取研究样本量过少, 因此需要进一步的研究来证明该方法的可行性. Fu等(2018)利用混合效应模型建立夜间灯光数据VIIRS/DNB与PM2.5浓度之间的关系, 研究选取了北京35个空气质量监测站点作为PM2.5实测数据, 重点关注了所建立混合效应模型在城市市区与郊区应用中存在的差异, 经过交叉验证方法训练模型, 结果在北京城区估算精度R可达到(0.950±0.020), 郊区估算精度R可达(0.880±0.060), 再次证明了VIIRS/DNB数据估算PM2.5浓度的可行性.
本研究参考Wang等(2016)所使用的光学模型, 将模型中原有的吸湿增长因子替换为更适合上海地区冬季的指数型吸湿增长因子(庄雯雯, 2015), 并引入气象要素——相对湿度和风速对模型进行优化.本研究使用VIIRS/DNB夜间灯光影像数据, 选取上海地区9个空气质量国控站点的PM2.5实测数据, 基于多元线性回归对上海地区的夜间PM2.5浓度进行估算, 并对估算结果进行相关统计分析, 验证相关方法在该地区的可行性, 最后对PM2.5浓度的空间分布进行模拟, 分析上海地区PM2.5浓度的空间分布规律.
2 数据与方法(Data and methods)2.1 研究区域概况上海(30°40′~31°53′N和120°52′~122°12′E)位于中国东部沿海的长江三角洲地区, 面积约6340 km2, 平均海拔10 m以下, 地形起伏小, 属于亚热带季风气候.该地区风场有明显的季节变化规律.在冬季受到西伯利亚高压的影响, 来源于蒙古、中国华北或东北地区的气流, 途径黄海海域或东部沿海地区的山东、江苏等地抵达上海(陈镭等, 2016), 由于冬季北方燃煤燃气供暖的缘故, 以PM2.5为主的大气污染物也会随之扩散到上海地区, 造成上海冬季环境空气污染等一系列问题.上海是中国的经济金融中心.尽管人类活动促进了经济的繁荣, 但随着汽车保有量的不断攀升, 汽车尾气的排放也在不断加剧.除此之外, 周边城市工业废气污染问题也日益显著.为了能够更好地帮助相关部门制定环境治理政策, 对于环境空气质量标准中的重要污染物PM2.5浓度的监测就显得尤为重要.
2.2 数据2.2.1 地面站点——PM2.5浓度数据和气象数据本研究时段为2014—2018年冬季12月、1月、2月, 使用上海9个空气质量国控站点所提供的逐小时实测PM2.5浓度数据.国控站点数据由于监测技术和标准统一, 保证了研究数据的准确性.上海虹桥机场站的逐小时数据作为本研究的气象要素相对湿度和风速数据, 考虑到气象要素在小范围区域的均一性(Murano et al., 2016), 因此在后期估算分析中, 9个空气质量监测站将采用统一的气象观测数据. 表 1显示了上海9个空气质量监测站和虹桥机场气象台站的地理位置信息, 其中空气质量监测站编号为国控站点记录编号. 图 1给出这些站点在上海地区的分布情况.
表 1(Table 1)
| 表 1 上海市空气质量监测站和气象台站信息概况 Table 1 General information of air-quality stations and meteorological station in Shanghai | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
表 1 上海市空气质量监测站和气象台站信息概况 Table 1 General information of air-quality stations and meteorological station in Shanghai
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||
图 1(Fig. 1)
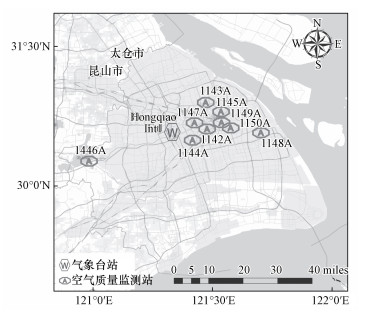 |
| 图 1 空气质量监测站和气象台站在上海地区空间分布 Fig. 1Spatial distribution of air-quality stations and meteorological station in Shanghai |
2.2.2 NPP-VIIRS卫星数据本研究采用的卫星遥感数据来自美国新一代国家极轨业务环境卫星系统预备项目(NPOESS)的首颗卫星Suomi National Polar-orbiting Partnership (NPP).该卫星搭载可见红外成像辐射计VIIRS在内的5个对地观测仪器. VIIRS可扫描幅宽3040 km, 拥有22个波段, 其中5个高分辨率图像波段(Imagery Bands, I-Bands)、16个中等分辨率波段(Moderate Resolution Bands, M-Bands)和1个DNB波段. 表 2给出了NPP卫星22个对地观测通道的详细信息.本研究数据来源于其中DNB波段, DNB是一个全色波段, 对可见光和近红外十分敏感, 可以观测到夜间辐射强度相对较小的城市灯光.
表 2(Table 2)
| 表 2 NPP/VIIRS卫星对地观测通道 Table 2 NPP/VIIRS satellite earth observation channel | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
表 2 NPP/VIIRS卫星对地观测通道 Table 2 NPP/VIIRS satellite earth observation channel
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
本研究采用VIIRS的Sensor Data Records(SDR)和Environmental Data Records(EDR)数据进行处理, SDR已将原始计数转换为辐射值、反射率或亮度温度等数据, EDR是通过有限数量的SDR文件处理得到.研究所需要的数据分别是其中的:VIIRS/DNB SDR数据(SVDNB)——提供夜间灯光辐射值的信息; VIIRS地理SDR数据(GDNBO)——提供相应的经度、纬度、月相角、卫星观测天顶角等地理信息; VIIRS Cloud Cover/Layers EDR(VCCLO)数据——作为识别云体的数据来筛选晴朗无云的夜空(Johnson et al., 2013).
卫星数据的处理包括:①排除人文因素导致的夜间灯光异常情况, 如春节节日庆典等导致夜间灯光辐射值异常增大; ②根据GDNBO字段中月相角数据, 认为月相角大于120°即为月球光照度可忽略的无月光数据(赵笑然等, 2017); ③根据GDNBO数据中太阳天顶角字段剔除杂散光; ④利用DNB字段中Quality Flag进行质量判断, 对于质量过差的数据进行排除, 获取高质量的辐射值数据; ⑤利用VCCLO数据获取无云区域, 与经过上述处理得到的数据进行叠乘, 获取无云区域DNB数据.经上述5个步骤处理后得到上海地区无云无月的夜间灯光辐射数据.
2.3 理论基础在上海地区, 常见的户外灯光有高压钠灯、荧光灯和二极管灯(light-emitting diode, LED).通过研究3种灯光的光谱曲线可以发现, 大部分的透射是在可见光小于0.65 μm的波段, 它们在大气中传输过程不受主要气体吸收线的影响(宋佳音, 2012).但高压钠灯在0.82 μm有一个辐射峰恰好在水蒸气柱的吸收峰附近.经过进一步研究, 水蒸气的变化对大气中DNB辐射传递的影响可以忽略不计(Wang et al., 2016).因此, 在整合灯光光谱强度和DNB光谱响应函数后, 可以认为DNB对气溶胶的变化很敏感, 这为在复杂地表条件下建立光传输模型提供了理论支持.
为了方便研究, 假设在研究期间, 地表灯光强度I0是一个恒定不变的值, 但不否认在同一时间不同地点之间存在差异(Fu et al., 2018).在本研究中, 为了抵消因时间跨度大而导致城市灯光的整体改变, 选取4年研究期间每年的一个晴朗夜晚(共4个)的DNB均值作为I0.假设气溶胶的多次散射效应可以忽略不计, 根据比尔定律, 到达卫星的夜间灯光辐射强度I:
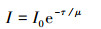 | (1) |
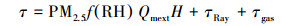 | (2) |
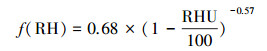 | (3) |
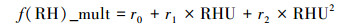 | (4) |
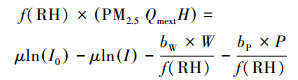 | (5) |
2.4 回归分析在Saunders等(2014)的研究中, 使用MODIS的AOD产品估算PM2.5浓度, 发现基于多元线性回归拟合模型要比简单线性回归能更好的解释地面PM2.5浓度变化, 并且证明估算精度提高并不依赖于特征参数的增加. Li等(2017)比较了线性修正回归、半经验回归和多元线性回归的优劣, 发现多元线性回归要优于线性修正回归, 而与半经验回归表现相对持平.使用同样策略对PM2.5进行估算在Kamarul等(2017)和Upadhyay等(2018)的研究中也有体现.为了寻找合适的回归模型, 本研究遵循了Wang等(2016)的基本方法, 同样利用多元线性回归模型来拟合方程(5).
为了更好地说明多元线性回归模型在本研究的可行性, 首先探究各变量与实测PM2.5之间的线性相关关系, 根据式(5)所提及的变量, 表 3(其中将每一列最大值和最小值加粗表示, 下文表格遵循同样规则)显示了9个站点的变量PM2.5×f (RH)与μln (I)、RHU/ f(RH)之间的相关系数, 其中RHU替代上文中大气中水蒸气含量(W).可以发现PM2.5×f(RH)与μln (I)之间存在较强的负相关关系, 其中平均相关系数为-0.662; PM2.5×f(RH)与RHU/f(RH)之间存在较强的正相关关系, 其中平均相关系数为0.609;另外, 研究发现PM2.5×f (RH)与WIN/ f(RH)存在一定的负相关关系(WIN代表风速), 平均相关系数为-0.342.依据Mukherjee等(2018)在研究中提出风速对大气颗粒物沉降的影响机制, 认为风速大小与PM2.5浓度之间存在负相关关系, 所以尝试在模型(5)中加入“风速”这一回归变量来进一步提高模型精度.至此, 本研究所建立的多元线性回归模型共有3个回归变量, 分别为μln (I)、RHU/f(RH)、WIN/ f(RH), 和1个常量μln (I0).
表 3(Table 3)
| 表 3 空气质量站点PM2.5×f(RH)与不同变量之间的相关系数 Table 3 Correlation coefficients between PM2.5×f(RH) and different variables at air-quality stations | ||||||||||||||||||||||||||||||||||||||||||||
表 3 空气质量站点PM2.5×f(RH)与不同变量之间的相关系数 Table 3 Correlation coefficients between PM2.5×f(RH) and different variables at air-quality stations
| ||||||||||||||||||||||||||||||||||||||||||||
在利用最小二乘法原理对式(5)进行参数求解时, 为了能够充分利用已有的数据所包含的信息(Fu et al., 2018), 本研究使用交叉验证方式进行模型训练, 最后利用随机预留的测试数据对模型泛化能力进行检验. 图 2为本研究采用的技术流程图.
图 2(Fig. 2)
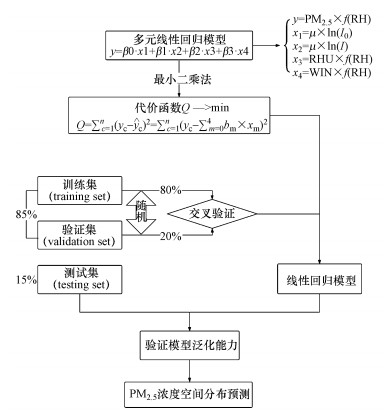 |
| 图 2 多元线性回归模型建立、训练、测试流程图 Fig. 2The flowchart of establishment, training and testing of multiple linear regression model |
3 结果与讨论(Result and discussion)3.1 NPP卫星过境时刻PM2.5浓度与日平均浓度关系对比不同站点2014—2018年冬季逐小时平均PM2.5浓度波动情况(图 3), 其中水平实线代表日平均PM2.5浓度, 可以发现PM2.5浓度日变化存在较强的规律性.上海冬季PM2.5浓度有明显的双峰分布(李名升等, 2016), 双峰分别发生在11:00—12:00和21:00—23:00, 峰值与谷值的绝对差值平均约为11 μg·m-3.在7:00—10:00时段, 大气混合层高度较低, 近地面大气也易出现逆温层, 不利于颗粒污染物的扩散, 造成了PM2.5浓度在此时段的持续增高, 并在正午附近出现了一天内的第一个PM2.5高峰; 午后交通排放污染物有所减少, 且大气层的对流运动逐渐增强, 有利于污染物扩散, 在16:00左右出现一天内PM2.5浓度的谷值; 在17:00—20:00时段, 下班高峰交通工具尾气排放叠加餐饮油烟排放, 会导致PM2.5浓度再次升高, 直至22:00左右出现一天内的第二个PM2.5浓度小高峰; 午夜, 由于太阳辐射消失, 温度在不断降低, 大气湍流运动减弱, 从而使PM2.5浓度稳定在一个较为平均的范围内.
图 3(Fig. 3)
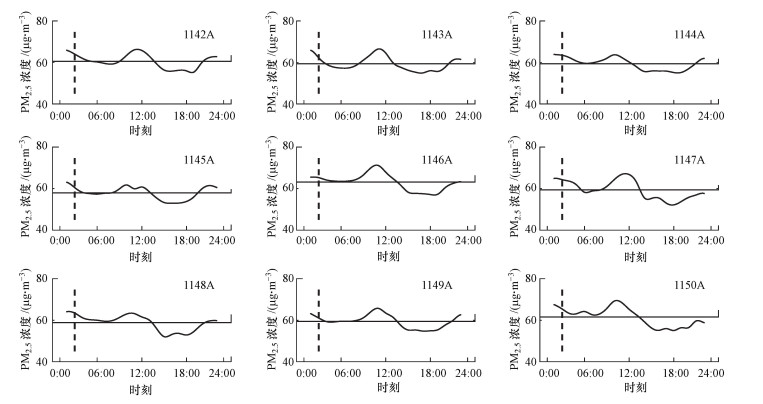 |
| 图 3 上海地区空气质量监测站冬季PM2.5浓度日变化曲线 Fig. 3Daily change curve of PM2.5 concentration in winter at the air-quality stations in Shanghai |
NPP卫星过境时刻为上海凌晨2:00左右, 夜间大气正处于相对稳定的环境.根据图 3所示, 在卫星过境时刻(垂直虚线)的PM2.5浓度值处于向夜间平稳状态过渡阶段.结合图 4发现, 卫星过境时刻PM2.5浓度与PM2.5浓度日均值之间R2可达0.664.由此可见, NPP卫星过境时刻的PM2.5浓度值与PM2.5浓度的日均值存在较强的线性关系.因此, 使用NPP/VIIRS卫星数据估算PM2.5浓度值, 除了可以反映卫星过境时刻所对应的浓度值以外, 也可用来描述PM2.5的日均值, 对反映PM2.5浓度日变化也是重要补充.
图 4(Fig. 4)
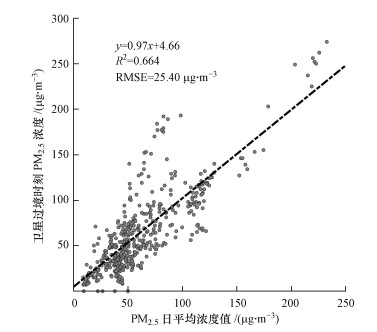 |
| 图 4 PM2.5日平均浓度值与上海地区卫星过境时刻浓度值对比 Fig. 4Comparison between daily average and satellite transit time concentration of PM2.5 in Shanghai |
3.2 提取站点DNB辐射值为了提取站点有效的辐射值, 本研究首先试采用以站点为中心的1.5、2.0、2.5 km圆形缓冲区, 计算缓冲区内栅格的DNB辐射值均值, 作为该站点DNB辐射值.不同半径缓冲区生成DNB均值时, 分别对栅格的计数为12~16个、20~25个、30~36个.经过模型拟合分析后, 模型训练精度如表 4所示.采用不同半径缓冲区进行DNB辐射值统计, 对本研究的估算精度存在一定影响, 因此在接下来模型验证与分析中, 一致采用2.0 km缓冲区所提取的DNB辐射均值.
表 4(Table 4)
| 表 4 不同半径圆形缓冲区下的模型训练精度R2 Table 4 Fitting Precision of Circular Buffer with Different Radius | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
表 4 不同半径圆形缓冲区下的模型训练精度R2 Table 4 Fitting Precision of Circular Buffer with Different Radius
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||
3.3 模型验证与分析卫星数据经过处理后, 共得到可用数据55 d 488条记录.将这55 d数据按照85%:15%的比例分为模型训练数据和模型验证数据, 其中模型测试数据构成的测试集(testing set)在2014—2018年冬季的12月—2月中随机抽取.
在回归分析的过程中, 将模型训练数据按照80%:20%的比例随机分成训练集(training set)和验证集(validation set), 对上述多元线性模型参数进行拟合(图 2).利用交叉验证的策略, 对模型进行训练后, 使用验证集对训练模型进行评估, 得到模型验证精度R2稳定在0.810±0.050, 验证均方根误差RMSE稳定在(17.500±0.500)μg·m-3.
为了验证模型的泛化能力, 防止模型的过拟合现象, 将之前留作估算的测试集代入模型中进行测试. 图 5是根据测试集数据得到的PM2.5浓度估算值和实测值对比图.可以看出, 在测试样本序列中, 两者变化趋势基本一致, 可进一步对结果进行统计分析.
图 5(Fig. 5)
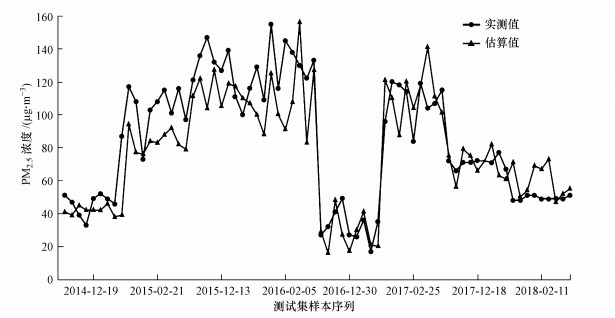 |
| 图 5 测试样本序列PM2.5浓度实测值与估算值对比 Fig. 5Comparison of Measured and Estimated Values of PM2.5 Concentration in the Sample Sequences of The Testing Set |
表 5给出了上海9个空气质量监测站PM2.5浓度的模型估算统计分析结果. PM2.5浓度实测值与估算值均值的偏差稳定在±11.000 μg·m-3, 其中站点1150A的偏差最大, 为14.001 μg·m-3; 站点1142A偏差最小, 为2.425 μg·m-3; 而所有站点实测均值和估算值均值分别为84.003 μg·m-3和77.181 μg·m-3, 偏差为6.822 μg·m-3.由此可见该模型具有较好的泛化能力, 说明使用该模型来估算上海地区PM2.5均值是可信的.进一步分析发现, 各站的均方根误差稳定在(20.000±3.000)μg·m-3, 实测值与估算值R2稳定在(0.800±0.100), 其中R2最大值由站点1143A所得, 均方根误差最小的站点为1145A.然而, 1146A站点实测值与估算值的R2 0.669为最小, 同时均方根误差24.904 μg·m-3为最大, 结合表 5的数据, 可以认为1146A站点在估计PM2.5浓度的精度上与其他站点存在一定差距.主要原因是1146A站点地处淀山湖地区, 远离上海市区, 夜间灯光明显弱于其他站点. Wang等(2016)在研究中也指出, 该模型在农郊地区应该慎重使用.因此1146A站点的估算精度低于其他站点.
表 5(Table 5)
| 表 5 上海地区9个站点PM2.5浓度实测值与估算值统计分析结果 Table 5 results of statistical analysis of measured and estimated PM2.5 concentrations at nine stations in Shanghai | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
表 5 上海地区9个站点PM2.5浓度实测值与估算值统计分析结果 Table 5 results of statistical analysis of measured and estimated PM2.5 concentrations at nine stations in Shanghai
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
图 6给出了模型验证数据的实测PM2.5浓度(横轴)和估算PM2.5浓度(纵轴)的散点图, 并得到回归方程.可以看出, 该模型估算的PM2.5浓度与地面站点实测的PM2.5浓度具有较好的线性关系, 拟合精度R2可达0.767, 回归拟合方程为y = 0.778x + 11.833.
图 6(Fig. 6)
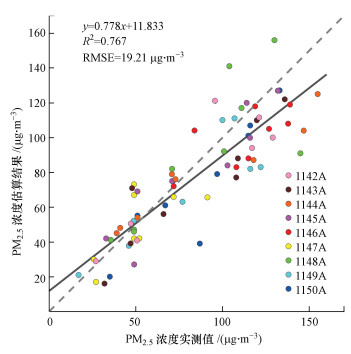 |
| 图 6 PM2.5浓度实测值与估算值散点分布图 Fig. 6Scatterplot of Measured and Estimated PM2.5 Concentration |
为验证修改回归变量吸湿增长因子和引入回归变量风速, 使得PM2.5浓度反演模型精度有了进一步的提高, 本研究使用相同数据对未优化的原始PM2.5反演模型进行图 2所示流程的回归分析.模型估算PM2.5浓度值的精度评价如表 6所示, R2与均方根误差均由PM2.5实测值与估算值计算得出, 其中模型Ⅰ代表本研究所使用的优化模型, 模型Ⅱ代表使用多项式型吸湿增长因子的模型, 模型Ⅲ代表移除回归变量风速的模型, 模型Ⅳ代表移除回归变量相对湿度的模型.根据表 6所示的信息, 本研究对模型进行的优化使其估算上海地区冬季PM2.5浓度的精度得到提高.
表 6(Table 6)
| 表 6 不同模型对估算PM2.5浓度值的精度评价 Table 6 Accuracy evaluation of PM2.5 concentration estimation by different models | |||||||||||||||
表 6 不同模型对估算PM2.5浓度值的精度评价 Table 6 Accuracy evaluation of PM2.5 concentration estimation by different models
| |||||||||||||||
3.4 PM2.5浓度空间分布估算鉴于上述模型估算结果有较好的精度, 本研究尝试通过上海地区夜间灯光数据对该地区的PM2.5浓度空间分布进行估算, 从而进一步研究PM2.5浓度的空间分布规律.
图 7a和图 7b分别是上海地区2017-12-19和2016-02-05卫星过境时刻(2:00 am左右)的灯光辐射值, 成像时刻卫星观测天顶角分别为52.68°和47.28°, 其中图 7a所代表的卫星过境时刻PM2.5浓度均值13.440 μg·m-3, 处于一个相对较低的范围; 图 7b所代表的卫星过境时刻PM2.5浓度均值为104.220 μg·m-3, 处于一个相对较高的范围.对比图 7a、7b可以发现, 在卫星观测天顶角值相近的前提下, 由于较高浓度的PM2.5颗粒物削弱了传输路径上灯光的辐射强度, 使得图像上表现出灯光辐射强度变低, 成像亮度降低、昏暗不清.
图 7(Fig. 7)
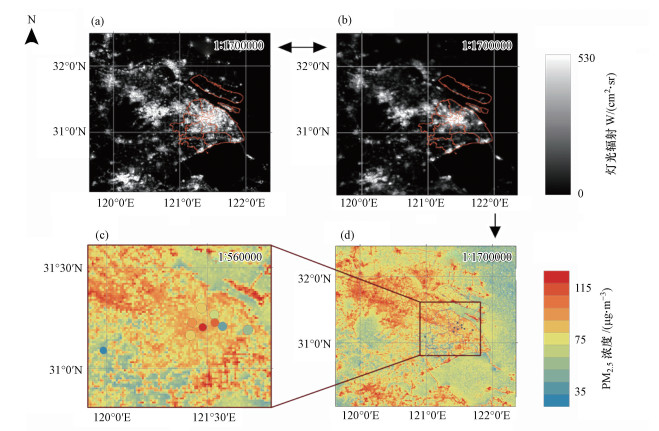 |
| 图 7 上海地区灯光辐射示意图与PM2.5浓度空间分布图 Fig. 7Lighting Radiation Map and Spatial Distribution Map of PM2.5 Concentration in Shanghai |
图 7c和图 7d是2016年2月5日卫星过境时刻PM2.5空间分布估算的结果图.该结果是基于上述多元线性回归模型而估算得到的, 其中图 7c的圆形符号代表 9个空气质量监测站的分布情况, 不同颜色代表各站点不同的PM2.5浓度实测值, 圆形符号的半径对应表 4第4列的R2站点PM2.5估算值与实测值R2越高, 站点的圆形符号半径越大.结果表明, 当站点符号尺寸越大, 即PM2.5估算值与实测值R2越高时, 站点PM2.5浓度实测值所代表的颜色能更好的与背景融合.进一步分析2016年2月5日这一日的PM2.5浓度的空间分布规律, 由图 7d可知, 该日空气质量较差地区集中在上海中心城区(黄浦区、静安区等中心城区)并覆盖嘉定区、宝山区至昆山、苏州等太湖北部地区, 严重地区污染等级可达“中度污染”.而上海南部闵行区、松江区至太湖南部地区空气质量相对较好, 污染等级以“良”为主.综上所述, 利用该模型进行的PM2.5浓度空间估算可信度是较高的, 能够进一步掌握地区PM2.5浓度分布规律, 更好地帮助相关部门做出相应污染治理决策.
4 结论(Conclusions)本研究将VIIRS/DNB夜间灯光数据估算PM2.5浓度的方法应用到上海地区, 利用2014—2018年冬季无云无月的VIIRS/DNB夜间灯光数据和相对湿度等气象数据建立物理模型, 基于多元线性回归使用交叉验证方法对模型进行训练, 并随机选取在研究时期未参与模型训练的8 d数据来验证模型泛化能力.
结果显示, PM2.5实际浓度与模型估算PM2.5浓度之间R2为0.767, 均方根误差RMSE为19.210 μg·m-3.因此, 利用夜间灯光遥感数据估算PM2.5浓度在本研究中表现出了很好的潜力.同时本研究将地面空气质量监测站点数据与灯光遥感影像数据进行结合, 利用训练模型对上海地区PM2.5浓度分布进行空间分析, 结果在一定程度上反映了PM2.5浓度的空间分布.
本研究同样也存在一些问题, 需要在接下来的工作中进一步解决: ①由于上海地区经济发达, 部分地区所得到的灯光辐射值达到阈值, 因此进一步提高模型精度, 还需要更强大的传感器作支持; ②进一步提高气象要素数据的空间精度; ③考虑将土地利用类型作为可能提高模型精度的要素.
致谢:本研究部分数据来源于美国海洋与大气管理局(National Oceanic and Atmospheric Administration, NOAA).其中, NPP卫星VIIRS数据下载网站——美国国家地理数据中心(https://download.class.ngdc.noaa.gov/download); 上海逐小时气象要素数据下载网站——美国国家气象数据中心(http://gis.ncdc.noaa.gov/map/viewer).感谢对本研究的数据支持.
参考文献
| 蔡艳, 张懿华, 沙斐, 等. 2012. 手工法与自动监测法测定PM2.5质量浓度比对研究[J]. 环境科学与管理, 2012, 37(7): 110–113.DOI:10.3969/j.issn.1673-1212.2012.07.029 |
| 陈镭, 马井会, 甄新蓉, 等. 2017. 上海地区空气污染变化特征及其气象影响因素[J]. 气象与环境学报, 2017, 33(3): 59–67.DOI:10.3969/j.issn.1673-503X.2017.03.008 |
| Fu D, Xia X, Duan M, et al. 2018. Mapping nighttime PM2.5 from VIIRS DNB using a linear mixed-effect model[J]. Atmospheric Environment, 178: 214–222.DOI:10.1016/j.atmosenv.2018.02.001 |
| Gao J, Peng X, Chen G, et al. 2016. Insights into the chemical characterization and sources of PM2.5 in Beijing at a 1-h time resolution[J]. Science of the Total Environment, 542: 162–171.DOI:10.1016/j.scitotenv.2015.10.082 |
| Johnson R S, Zhang J, Hyer E J, et al. 2013. Preliminary investigations toward nighttime aerosol optical depth retrievals from the VIIRS Day/Night Band[J]. Atmospheric Measurement Techniques, 6(5): 1245–1255.DOI:10.5194/amt-6-1245-2013 |
| Kamarul Zaman N A F, Kanniah K D, Kaskaoutis D G. 2017. Estimating particulate matter using satellite based aerosol optical depth and meteorological variables in Malaysia[J]. Atmospheric Research, 193: 142–162.DOI:10.1016/j.atmosres.2017.04.019 |
| Lee H J, Liu Y, Coull B A, et al. 2011. A novel calibration approach of MODIS AOD data to predict PM2.5 concentrations[J]. Atmospheric Chemistry and Physics, 11(15): 7991–8002.DOI:10.5194/acp-11-7991-2011 |
| 李名升, 任晓霞, 于洋, 等. 2016. 中国大陆城市PM2.5污染时空分布规律[J]. 中国环境科学, 2016, 36(3): 641–650.DOI:10.3969/j.issn.1000-6923.2016.03.001 |
| Li T, Shen H, Zeng C, et al. 2017. Point-surface fusion of station measurements and satellite observations for mapping PM2.5 distribution in China:Methods and assessment[J]. Atmospheric Environment, 152: 477–489.DOI:10.1016/j.atmosenv.2017.01.004 |
| Malm W C, Sisler J F, Huffman D, et al. 1994. Spatial and seasonal trends in particle concentration and optical extinction in the United States[J]. Journal of Geophysical Research, 99(D1): 1347–1370.DOI:10.1029/93JD02916 |
| Mukherjee A, Agrawal M. 2018. Assessment of local and distant sources of urban PM2.5 in middle Indo-Gangetic plain of India using statistical modeling[J]. Atmospheric Research, 213: 275–287.DOI:10.1016/j.atmosres.2018.06.014 |
| Murano G, Corrado V, Dirutigliano D. 2016. The new italian climatic data and their effect in the calculation of the energy performance of buildings[J]. Energy Procedia, 101: 153–160.DOI:10.1016/j.egypro.2016.11.020 |
| 宋佳音. 2012.基于行人穿行的LED道路照明功效研究[D].天津: 天津大学http://cdmd.cnki.com.cn/Article/CDMD-10056-1013039519.htm |
| Saunders R O, Kahl J D W, Ghorai J K. 2014. Improved estimation of PM2.5 using Lagrangian satellite-measured aerosol optical depth[J]. Atmospheric Environment, 91: 146–153.DOI:10.1016/j.atmosenv.2014.03.060 |
| Upadhyay A, Dey S, Goyal P, et al. 2018. Projection of near-future anthropogenic PM 2.5 over India using statistical approach[J]. Atmospheric Environment, 186: 178–188.DOI:10.1016/j.atmosenv.2018.05.025 |
| Wang J. 2003. Intercomparison between satellite-derived aerosol optical thickness and PM2.5 mass:Implications for air quality studies[J]. Geophysical Research Letters, 30(21): 2095.DOI:10.1029/2003GL018174 |
| Wang J, Aegerter C, Xu X, et al. 2016. Potential application of VIIRS Day/Night Band for monitoring nighttime surface PM2.5 air quality from space[J]. Atmospheric Environment, 124: 55–63.DOI:10.1016/j.atmosenv.2015.11.013 |
| Wang X, Bi X, Sheng G, et al. 2006. Chemical composition and sources of PM10 and PM2.5 aerosols in Guangzhou, China[J]. Environmental Monitoring and Assessment, 119(1/3): 425–439. |
| Wang X, Chen R, Meng X, et al. 2013. Associations between fine particle, coarse particle, black carbon and hospital visits in a Chinese city[J]. Science of the Total Environment, 458-460: 1–6.DOI:10.1016/j.scitotenv.2013.04.008 |
| Wei F, Teng E, Wu G, et al. 1999. Ambient concentrations and elemental compositions of PM10 and PM2.5 in Four Chinese Cities[J]. Environmental Science & Technology, 33(23): 4188–4193. |
| 杨景梅, 邱金桓. 1996. 我国可降水量同地面水汽压关系的经验表达式[J]. 大气科学, 1996, 20(5): 620–626.DOI:10.3878/j.issn.1006-9895.1996.05.14 |
| Zhang J, Reid J S, Miller S D, et al. 2008. Strategy for studying nocturnal aerosol optical depth using artificial lights[J]. International Journal of Remote Sensing, 29(16): 4599–4613.DOI:10.1080/01431160802020528 |
| 赵笑然, 石汉青, 杨平吕, 等. 2017. NPP卫星VⅡPS微光资料反演夜间PM2.5质量浓度[J]. 遥感学报, 2017, 21(2): 291–299. |
| Zheng Y, Zhang Q, Liu Y, et al. 2016. Estimating ground-level PM2.5 concentrations over three megalopolises in China using satellite-derived aerosol optical depth measurements[J]. Atmospheric Environment, 124: 232–242.DOI:10.1016/j.atmosenv.2015.06.046 |
| 庄雯雯. 2015.基于地面MPL研究上海霾天气及吸湿增长的影响[D].上海: 东华大学. 38-52http://cdmd.cnki.com.cn/Article/CDMD-10255-1015042067.htm |
