 , 刘延安1,2
, 刘延安1,2
 , 施润和1,2
, 施润和1,2
 , 郭春颖1, 窦新宇1
, 郭春颖1, 窦新宇11. 华东师范大学地理科学学院, 上海 200241;
2. 华东师范大学地理信息科学教育部重点实验室, 上海 200241
收稿日期: 2018-02-08; 修回日期: 2018-03-23; 录用日期: 2018-03-23
基金项目: 国家理科基地科研训练及科研能力提高项目(No.J1310028);上海市卫计委环境卫生与劳动卫生重点学科建设项目(No.15GWZK0201)
作者简介: 许悦蕾(1997-), 女, E-mail:xll102012@163.com
通讯作者(责任作者): 刘延安, E-mail:lya163@126.com
施润和, E-mail:shirunhe@163.com
摘要: 地面监测得到的近地面细颗粒物PM2.5浓度较为精确,但数据覆盖范围相对较小,卫星遥感反演的气溶胶光学厚度(AOD)数据可以反映污染物浓度分布,具有范围大且速度快的特点,因此,大多数****通过建立PM2.5-AOD模型来实现卫星遥感监测PM2.5浓度,并通过引入气象要素来优化模型.然而,气象要素的选择与引入往往对模型的精度有较大的影响,如何有效地选择对PM2.5浓度影响较大的气象要素一直是PM2.5-AOD模型中的关键问题.因此,本文基于华东地区2014-2015年的MODIS AOD和地面监测站的PM2.5浓度数据,结合再分析气象资料,利用多元逐步线性回归方法建立PM2.5-AOD模型,从由特定时刻、高度上的气象要素与随时间、高度变化的气象要素组成的气象要素集中,筛选出对因变量PM2.5浓度有显著影响的关键气象要素.结果表明:在地域与季节双重尺度下的PM2.5-AOD模型精度更高;相较于特定时刻高度的气象要素,随时间和高度变化的气象要素对PM2.5-AOD模型的影响更为显著;在地域与季节双重尺度下,1000~850 hPa经向风速差、世界时0:00-6:00近地面温度差、850~600 hPa温度差、6:00边界层高度、12:00-18:00近地面压强差、1000~850 hPa温度差对模型影响较大,但应依据不同季节和不同地区的具体影响程度作为选择标准.
关键词:多元逐步线性回归气象要素集AODPM2.5
Impact of meteorological elements on estimation of PM2.5 by aerosol optical depth
XU Yuelei1
 , LIU Yan'an1,2
, LIU Yan'an1,2
 , SHI Runhe1,2
, SHI Runhe1,2
 , GUO Chunying1, DOU Xinyu1
, GUO Chunying1, DOU Xinyu1 1. School of Geographic Sciences, East China Normal University, Shanghai 200241;
2. Laboratory of Geographic Information Science of Ministry of Education, East China Normal University, Shanghai 200241
Received 8 February 2018; received in revised from 23 March 2018; accepted 23 March 2018
Supported by the Scientific Research Training and Scientific Research Ability Improvement Project of National Science Base (No.J1310028) and the Shanghai Municipal Key Discipline Construction Project of Commission of Health and Family Planning Environmental Health and Occupational Health (No.15GWZK0201)
Biography: XU Yuelei(1997—), female, E-mail:xll102012@163.com
*Corresponding author: LIU Yan′an, E-mail:lya163@126.com
SHI Runhe, E-mail:shirunhe@163.com
Abstract: The fine particulates (PM2.5) concentrations obtained from the surface monitoring are relatively accurate but with smaller data coverage, while aerosol optical depth (AOD) data from the satellite remote sensing retrievals can reflect the concentration distribution of atmospheric pollutants, with a wide range and fast data acquisition. To effectively monitor the changes of near-surface PM2.5 concentrations using the satellite remote sensing, therefore, various PM2.5-AOD models have been established and optimized by introducing meteorological elements. However, the selection and introduction of the meteorological elements often has a great impact on the model accuracy, and how to determine the critical meteorological element(s) has always been a key issue in developing the PM2.5-AOD model. Therefore, based on the AOD data derived from the Moderate Resolution Imaging Spectroradiometer (MODIS) and the ground-level PM2.5 station observations in East China from 2014 to 2015, this study established the relationship between PM2.5 and AOD using the multivariable stepwise linear regression model in combination with meteorological reanalysis data. In constructing this PM2.5-AOD model, a meteorological element dataset was built, and meteorological elements at specific time and heights were then selected to compare with other elements highly varying with time and heights in order to determine the key meteorological factors that have significant impacts on the ground-level PM2.5 concentrations. The main results are as follows:①The accuracy of the PM2.5-AOD model is higher when both regional and seasonal dependences are considered.②Compared with the meteorological elements at a particular time or level, the meteorological elements that change with time and levels have greater impacts on the PM2.5-AOD model; ③Several key meteorological factors are found to have prominent influence on the model, including the difference in meridional wind speed between 1000 hPa and 850 hPa, the near-surface temperature difference between 00 and 06 UTC, the temperature difference at 850~600 hPa and at 1000~850 hPa, the planetary boundary layer height at 06UTC, and the surface pressure difference between 12 and 18UTC. These factors should be selected in the model according to their specific impacts in different seasons and regions.
Keywords: multivariable stepwise linear regressionmeteorological element datasetAODPM2.5
1 引言(Introduction)近年来, 由工业化和城市化的迅猛发展所导致的空气污染, 特别是由高浓度PM2.5形成的大气灰霾(吴健生等, 2017), 已引起政府和公众的普遍关注和高度重视(徐晓斌, 2016).PM2.5对大气环境造成的不良影响已严重危害到公众的生活和健康(Pope et al., 2002; Li et al., 2013; 穆泉等, 2013), 因此, PM2.5的监测工作显得尤为重要和迫切.地面监测站点能够较为精确地测得近地面PM2.5污染情况, 但地面监测站点分布不均, 无法全面地反映地区内污染情况, 且耗费大量的人力物力.而通过遥感卫星获得AOD来反映近地面污染情况具有连续性好、传输速度快的特点, 可弥补地面监测的不足.因此, 建立AOD与PM2.5的关系模型对高效地利用卫星遥感监测PM2.5浓度有较大的现实意义.
已有不少研究表明, 气溶胶光学厚度(Aerosol Optical Depth, AOD)与PM2.5有较高相关性(Li et al., 2005; Kumar et al., 2007; Guo et al., 2009; Wang et al., 2010; Tsai et al., 2011).但AOD与PM2.5的相关系数存在不稳定性, 易受到时空因素及其他因素的影响.国内外众多****在PM2.5-AOD关系研究的过程中发现, 加入气象要素有助于二者相关关系的优化.Gupta等(2006)在评估风速、云量等气象要素对二者关系的影响过程中发现, 在气溶胶集中、云量稀少、湿度低的情况下, PM2.5-AOD相关性显著.Liu等(2009)通过建立广义加性模型发现气象要素在运用AOD预测PM2.5中发挥着重要作用.Zheng等(2014)利用北京市2001—2012年PM2.5数据, 在PM2.5-AOD的线性回归模型中加入大气边界层高度和相对湿度, 使得二者相关关系有所提高.王静(2016)从污染物日变化、天气特征、AOD空间分布等方面对上海市一次雾霾事件分析发现, 早晚的近地层出现的逆温与污染物浓度指标较高的时段基本吻合, 表明气象要素和天气形势在雾霾事件中扮演着重要角色.
目前探究关于PM2.5-AOD关系模型中不同气象要素的重要程度的依据不足.以风速小、高压、低湿、低边界层高度等为特征的静稳天气易导致雾霾(邓君俊, 2011), 以往的研究中通常使用风速、温度、湿度等常见的气象要素来提升PM2.5-AOD模型拟合度, 但缺少对气象要素的系统判断.且现有的地面监测站点实测的气象数据存在可共享的气象数据指标较少、气象数据之间时间间隔较大、气象数据类型较为单一等缺陷.相比之下, 再分析的气象数据类型丰富、覆盖范围广, 在一定程度上能够弥补地面监测站点实测气象数据的不足, 因而能充分发挥气象要素在PM2.5-AOD关系中的优化作用.搭载在Terra和Aqua卫星上的MODIS传感器提供了全球范围的气溶胶产品, 已被广泛应用于PM2.5-AOD关系的研究中.由于Terra卫星和Aqua卫星在中国境内的时间分别为10:30和13:30, 因而MODIS传感器只能提供中国范围内的10:30和13:30气溶胶产品.但气溶胶的日变化比较明显, 若在PM2.5-AOD关系模型中只使用日平均值气象数据与MODIS数据对应, 这将会在一定程度上造成误差.
华东地区在经济高速发展的同时, PM2.5浓度也呈现以增大为主的变化趋势(郁珍艳等, 2017), 而目前我国关于PM2.5的研究主要集中在京津冀地区及上海、南京、杭州等局部城市, 有关长江以南的大范围研究仍然较少.因此, 本文以华东地区6省1市为研究区域, 基于MODIS气溶胶光学厚度和地面监测的PM2.5质量浓度监测资料及气象要素资料, 结合所创建的包括变温变压等气象要素在内的再分析气象要素集, 运用多元逐步线性回归方法, 从再分析气象要素集中选出能够对应气溶胶日变化的气象要素参与PM2.5-AOD模型, 建立华东地区PM2.5遥感反演模型, 探究最优模型中气象要素的入选情况, 以期为日后利用气象要素提高PM2.5-AOD模型精度提供依据.
2 数据与方法(Data and methods)本文研究的区域为我国华东地区(图 1), 位于长江中下游及沿海地区, 其经纬度范围为23.5°~38.38°N, 113.57°~122.2°E, 区域内共有1个直辖市(上海市)、6个省(山东省、江苏省、安徽省、浙江省、福建省、江西省)、93个地级市(区).华东地区人口稠密, 城市化水平高, 是我国重要的经济区.城市化过程中恶化的生态环境与高楼阻碍季风环流(周峤, 2015)、秸秆燃烧排放大量PM2.5(靳全锋等, 2017)、建筑施工扬尘(赵普生等, 2009)、机动车尾气排放(孙友敏等, 2017)和工业化排放(顾为东, 2014)都是影响区域空气质量的主要人为原因.近年来, 华东地区的快速发展引发了人们对该地区空气环境质量的极大关注.分析研究该区域PM2.5-AOD模型, 实现该区域PM2.5浓度的预测和预报, 对开展减灾防灾工作具有重要的现实意义.
2.1 PM2.5地面监测数据本次研究使用国家环境保护部发布的空气质量指数实时数据, 共选取华东地区217个国控监测站点于Aqua卫星过境时刻的每小时PM2.5浓度, 其中, 上海10个站点, 江苏省62个站点, 浙江省41个站点, 安徽省18个站点, 福建省12个站点, 江西省12个站点, 山东省62个站点, 具体空间分布如图 1所示.
图 1(Fig. 1)
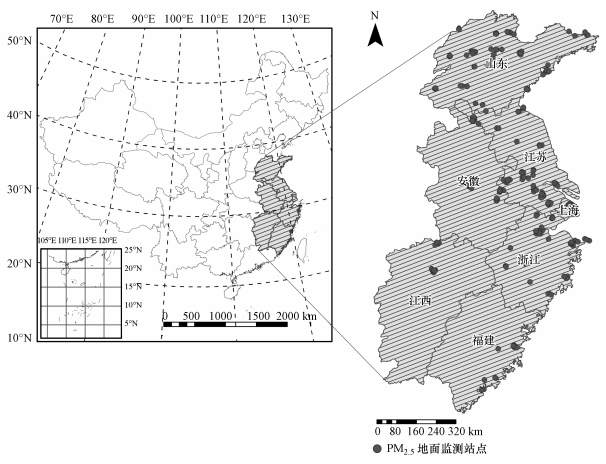 |
| 图 1 研究区范围及PM2.5地面监测站点分布 Fig. 1Range of studying area and distribution of PM2.5 ground monitoring sites |
2.2 MODIS气溶胶产品本次研究选取的是NASA发布的来自Aqua卫星的MYD04 Level2的0.55 μm通道的气溶胶产品, 空间分辨率为10 km, 时间范围为2014年1月1日—2015年12月31日, 共计730 d, 经纬度范围为23.5°~38.38°N, 113.57°~122.2°E, MODIS气溶胶产品数据采用分层数据的格式(HDF)储存.
2.3 气象资料在雾霾形成过程中, 除了人类活动因素外, 气象要素的影响也不可忽视.气象要素对污染物的聚集、传输和扩散有显著影响.气溶胶辐射效应(张悦等, 2016)、持续高压(陈朝晖等, 2007)、大气边界层高度降低(王耀庭等, 2012)、低空大气逆温层(杜荣光等, 2011)、较高的近地面相对湿度和较低的风速(马艳等, 2018)等都在一定程度上降低了大气的扩散能力, 影响污染物浓度.
因此, 本研究采用欧洲中期气象预报中心(ECMWF)的再分析数据中的近地面和不同高度层(1000~7 hPa, 以25 hPa为间隔, 共37层)的气象数据:温度、湿度、压强、经向风速、纬向风速, 每一种气象要素分别包含UTC0:00、6:00、12:00、18:00的数据, 空间分辨率为0.125°×0.125°, 数据格式为NetCDF文件(NC文件).由于Aqua卫星每天过境时间约为地方时间13:30, 所以在不同高度层的气象要素上本次研究只选择了UTC6:00的数据.获得的数据经过预处理后得到包含73个元素的再分析气象要素集(表 1).
表 1(Table 1)
| 表 1 73种气象要素清单 Table 1 List of 73 meteorological elements | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
表 1 73种气象要素清单 Table 1 List of 73 meteorological elements
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
2.4 数据预处理首先使用ENVI-IDL软件读取下载后的MODIS数据并投影转换, 将影像转换成UTM_51N投影坐标, 大地基准系统WGS_1984, 再利用已有的217个PM2.5国控监测站点的经纬度点坐标信息, 使用ArcMap软件提取相应位置的AOD值;其次使用Matlab程序对下载后的NC气象文件进行时间格式转换和坐标投影转换, 并依据PM2.5国控监测站点的经纬度点坐标信息提取相应位置的气象要素;最后对以上经过预处理后的AOD、气象要素和PM2.5使用ENVI-IDL软件进行基于每日1次的时间匹配, 生成同站点同时间的数据对, 完成基本的预处理操作.
由于考虑到随时间和高度变化的气象要素在PM2.5与AOD关系的建立中有较大的影响, 因此, 本次研究对匹配完成后的气象数据, 再通过Excel差值计算获得随时间变化和随高度变化的气象要素.最终建立具有73个气象要素的集合, 其中包括24个特定高度的气象要素、17个特定时刻的气象要素, 以及由此得到的20个根据高度变化的气象要素差值和12个根据时间变化的气象要素差值.
2.5 多元回归统计分析多元逐步线性回归过程是以自变量对因变量作用的显著程度为选取依据, 由大到小依次将自变量加入方程中, 若已经引入的变量在引入新变量后重要性减弱, 将会被剔除出方程, 这一过程不断循环, 直到不再加入新变量和剔除旧变量, 最终获得包含一个因变量和若干个自变量的方程模型(游士兵等, 2017).多元逐步线性回归模型的形式如下:
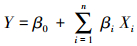 | (1) |
构建模型时, 为了既能达到所构建模型的准确性又要保证评估结果的保真性, 常见的做法是将大约2/3~4/5的样本用于构建模型, 剩余样本用于测试(周志华, 2016).因此, 本文在多元逐步线性回归分析中使用75%的样本构建PM2.5-AOD模型, 剩余25%的样本用于PM2.5-AOD模型的验证.在季节尺度、地域尺度及地域季节双重尺度下建立PM2.5和AOD关系模型的过程中, 利用多元逐步线性回归过程不断加入与剔除变量的特点, 从气象要素集中筛选出对模型的拟合度有较大影响的气象要素.
2.6 模型精度评估利用地面监测站点测得的PM2.5与模型反演所得的PM2.5的差异可以确定模型的均方根误差RMSE(Root Mean Square Error), 反映模型平均误差水平(黄思等, 2015).RMSE计算公式如下:
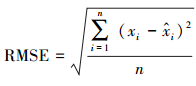 | (2) |
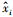
R2是以地面监测站点测得的PM2.5的样本点聚集在所建立的回归方程周围的密集程度反映回归方程对样本的代表程度, 完成回归方程的拟合优度检验(Bai et al., 2016).R2计算公式如下:
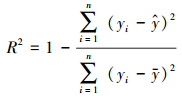 | (3) |
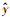
本文通过建立多元线性回归模型所计算出的RMSE和R2来综合评价回归模型的拟合优度.RMSE值越小, 表明拟合精度越高;R2取值范围介于0~1之间, 当R2越趋于1, 表示回归方程的拟合度越优.
3 结果与分析(Results and analysis)3.1 模型建立结果与分析从地域尺度上建立的AOD与PM2.5关系模型的7个线性结果中, 上海市的模型拟合度最高, R2为0.52, 而浙江省和江西省的模型拟合度相对较低, R2都约为0.35, 江苏省、安徽省、福建省、山东省的模型的R2约为0.42.总体而言, 在地域尺度上, 除上海市外, 其余各省市模型的R2均不超过0.5.
图 2(Fig. 2)
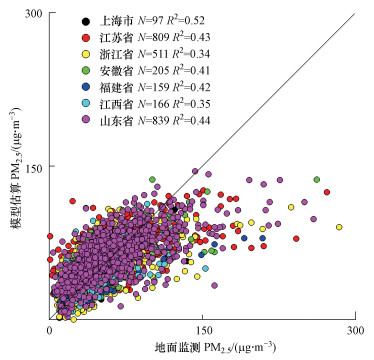 |
| 图 2 地域尺度模型拟合结果 Fig. 2Result of PM2.5-AOD model in regional scale |
从季节尺度上建立的AOD与PM2.5关系模型的4个线性结果中, 秋季模型的拟合度最高, R2为0.47, RMSE为22.81 μg·m-3, 而春季、夏季和冬季模型的拟合度不佳, 春季和冬季模型的R2大致都为0.37, 夏季模型的R2相对较高, 为0.44, RMSE分别为25.87、19.50、37.52 μg·m-3.总体而言, 在季节尺度上, 各季节模型的R2均不超过0.5.
图 3(Fig. 3)
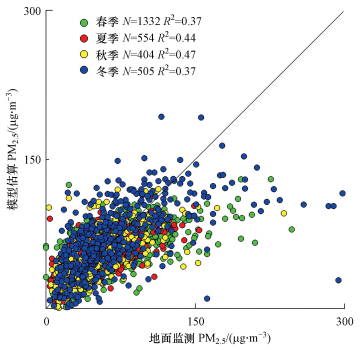 |
| 图 3 季节尺度模型拟合结果 Fig. 3Result of PM2.5-AOD model in seasonal scale |
在地域和季节双重尺度上建立的AOD与PM2.5关系模型的28个线性结果中, 上海市秋季模型的拟合度最高, R2为0.89, RMSE为8.17 μg·m-3(图 4).除安徽省、江西省、山东省秋季模型的R2略低之外, 其余各省的季节模型都表现为秋季最优, R2基本上都大于0.70, RMSE较小.相比之下, 春、夏季模型拟合度较低, R2大部分介于0.5~0.6.
图 4(Fig. 4)
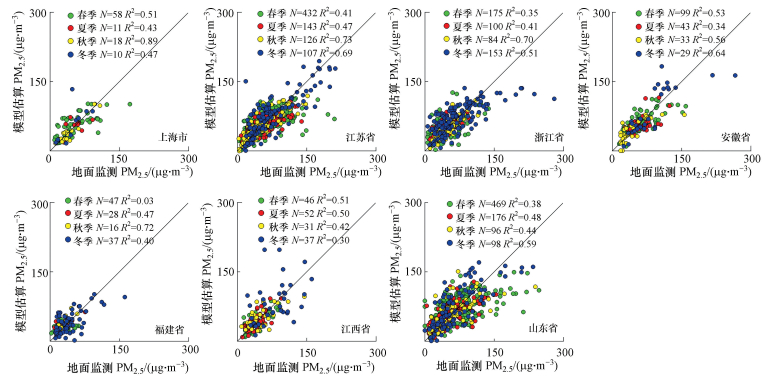 |
| 图 4 地域季节双重尺度模型拟合结果 Fig. 4Result of PM2.5-AOD model in regional and seasonal double scales |
通过R2和RMSE指标综合评估3种尺度模型拟合度, 结果表明, 相比于单一尺度而言, 在地域和季节双重尺度下建立的PM2.5-AOD模型结果更优.
3.2 气象要素筛选结果与分析在地域尺度上, 多元逐步线性回归生成的7个关系模型中, 被选入的气象要素共为45个, 其中, 变化的气象要素为30个.UTC0:00—6:00及12:00—18:00近地面的温度差在7个模型中均被选入, 变化的气象要素被选入次数基本上都大于3次, 而其余的被选入的非变化气象要素的次数都在1~2次不等.
在季节尺度上, 多元逐步线性回归生成的4个关系模型中, 除了春、秋季模型选入少量的非变化的气象要素以外, 夏、冬两季的模型中选入的气象参数均是变化的气象因素, 且1000~850 hPa和850~600 hPa的相对湿度差、UTC0:00—6:00近地面温度差、1000~850 hPa经向风速差在季节尺度模型中基本都被选入.该结果表明, 在季节尺度上, 相对湿度在高空中的变化幅度会影响AOD估算PM2.5, 这是因为气溶胶粒子的吸湿作用会使气溶胶粒子半径增大, 相对湿度在不同高度处的变化会影响气溶胶含量的分布, 进而影响对PM2.5的估算.
在地域和季节的双重尺度上, 通过多元逐步线性回归对73个气象要素集进行筛选, 包括24个特定高度的气象要素(X1)、17个特定时刻的气象要素(X2), 以及由此得到的20个根据高度变化的气象要素差值(X3)和12个根据时间变化的气象要素差值(X4).本文中, 定义气象要素的入选率为被选入次数与该类型气象要素总数的比值, 并用该指标评估各个气象要素类型对PM2.5-AOD模型的重要性程度.图 5是地域和季节双重尺度下气象要素入选结果, 从图中可以看出, 随高度和时间变化的气象要素差值(X3、X4)被选入PM2.5-AOD模型的频率较大, 而特定时刻和高度的气象要素(X1、X2)被选中的频率较小.该筛选结果表明, 选择随时间和高度变化的气象要素更有利于优化PM2.5-AOD模型, 特别是根据时间变化的气象要素差值对模型的影响更大.因此, 气象条件是否发生变化和发生变化的快慢在AOD估算PM2.5浓度的过程中都起到了不可或缺的作用.
图 5(Fig. 5)
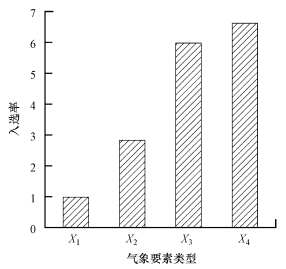 |
| 图 5 地域季节双重尺度下气象要素入选结果 Fig. 5Result of meteorological elements introduced in regional and seasonal double scales |
在地域和季节双重尺度下气象要素筛选的基础上, 对随高度和时间变化的气象要素差值(X3、X4)中的各气象要素类型进行统计分析(图 6).统计结果显示, 随时间和高度变化的温度、压强、湿度、纬向风速、经向风速在被选入的变化气象要素中所占比重有一定的差别, 温度与压强占比最大, 反映了温度要素与压强要素对模型构建的影响较大.温度随高度变化反映了逆温情况, 温度随时间变化是影响空气流动的基本因素, 温度较为突出的影响也与生活实际情况相符合.但从总体上看, 温度、压强、湿度、纬向风速、经向风速在被选入的变化气象要素中所占比重相差不大, 表明这5种变化的气象要素类型在AOD估算PM2.5过程中都会产生一定的影响.
图 6(Fig. 6)
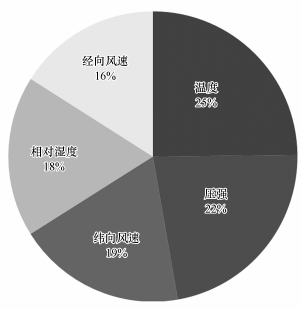 |
| 图 6 随时间和高度变化的气象要素入选气象各类型的比重 Fig. 6Proportions of various types of meteorological elements selected from those changing with time and height |
在地域和季节双重尺度下气象要素筛选的结果中, 表 2列出了入选次数最多的6个气象要素.针对表 2列出的6个气象要素, 地域和季节双重尺度模型的结果显示:1000~850 hPa经向风速差、UTC 0:00—6:00近地面温度差及1000~850 hPa温度差与PM2.5呈正相关, 表明卫星过境前温度随时间升高幅度越大, 空气流通导致外部污染物扩散至研究区, 研究区内PM2.5浓度上升;而UTC6:00的1000~850 hPa温度差反映该地区是否发生逆温, 进而影响污染物的扩散.UTC6:00边界层高度和UTC 12:00—18:00近地面压强差与PM2.5呈负相关, 表明边界层高度越低, 压强变化幅度越大, 将降低大气的扩散能力, 导致PM2.5浓度上升.850~600 hPa温度差与PM2.5的相关性随着季节和地域改变而呈现不同的相关性, 即从高度为850 hPa到高度为600 hPa的温度变化在不同的季节和地域会对AOD估算PM2.5产生不同的影响.
表 2(Table 2)
| 表 2 气象因素筛选结果 Table 2 Result of meteorological factors | ||||||||||||||||||||||||||||
表 2 气象因素筛选结果 Table 2 Result of meteorological factors
| ||||||||||||||||||||||||||||
图 7是在不同季节上对表 2中6个气象要素的入选次数情况的分布统计图.图中显示, 在春季, V1000~850对PM2.5-AOD模型影响更大.华东地区地处亚热带季风气候区, 冬、春季节的西北季风带来的外部空气污染物对区域内的PM2.5浓度影响较大.相比于其他季节, 这6个气象要素各自在夏季对AOD估算PM2.5浓度没有特别突出的影响.在秋季模型中侧重选入BLH和SP12~18, 表明秋季时大气边界层高度与大气压强变化幅度更能影响AOD估算PM2.5浓度的过程.在冬季, ST0~6和T850~600的入选次数最多, 表明温度变化导致的空气流通和逆温层对PM2.5浓度的影响在冬季更为突出.本研究结果表明, 在不同的季节, 选择影响AOD估算PM2.5过程的气象要素也应有所侧重.相比于季节尺度, 在不同地区上6个气象要素的入选次数情况没有显著的分布规律, 但仍然存在地域差异.因此, 在选择气象要素加入模型时, 需要考虑该气象要素在不同季节不同地区的影响程度.
图 7(Fig. 7)
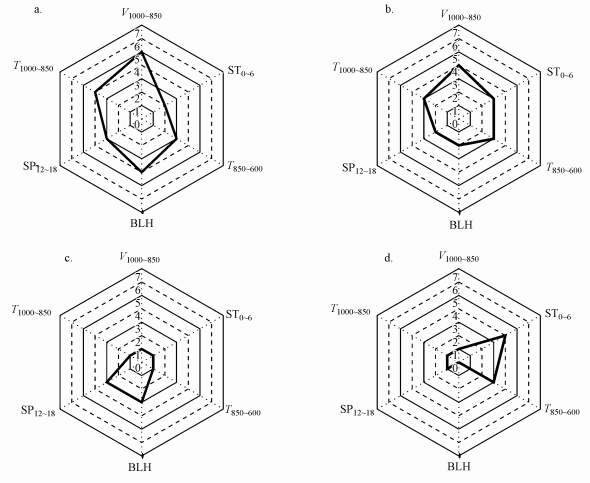 |
| 图 7 入选气象因素的季节分布图 (a.春季, b.夏季, c.秋季, d.冬季) Fig. 7Seasonal distribution of meteorological elements introduced |
4 结论(Conclusions)1) 本文利用2014—2015年华东地区内通过搭载在NASA的Aqua卫星上的MODIS传感器获得的气溶胶光学厚度和地面监测站点观测所得的PM2.5浓度值, 引入气象模式资料(ECMWF)中的温度、相对湿度、风速、压强、边界层高度等数据, 通过处理后获得随时间和高度层变化的各气象要素差值, 最终形成具有73个元素的气象要素集, 分别从地域尺度、季节尺度、地域与季节双重尺度构建线性回归关系模型, 结果表明:在地域与季节双重尺度下的PM2.5-AOD模型精度更高.
2) 本文在建立PM2.5-AOD模型的过程中, 采用多元逐步线性回归的方法筛选影响模型拟合度的若干气象要素.结果表明:随时间变化和随高度变化的气象要素被选入模型的入选率最高, 相较于特定时刻和特定高度的气象要素, 随时间变化和随高度变化的气象要素对建立PM2.5-AOD模型的影响更大, 效果更优.因此, 在未来关于建立二者关系的气象要素的选择中, 不应该仅仅局限于传统的气象要素, 应该更多地考虑变化的气象要素对二者关系的影响.
3) 本文在所建立的气象要素集中, 以随时间变化和随高度变化的若干气象要素对AOD估算PM2.5的过程影响较大为基础, 对随时间变化和随高度变化的若干气象要素进行进一步分析.结果表明:包括温度、压强、湿度、经向风速、纬向风速在内的5个气象要素类型对AOD估算PM2.5过程都会产生一定的影响, 在选入模型的占比相差不大;在28个地域季节模型中,1000~850 hPa经向风速差、UTC0:00—6:00近地面温度差、850~600 hPa温度差、UTC6:00边界层高度、UTC12:00—18:00近地面压强差、1000~850 hPa温度差这6个气象要素被选入次数最多, 表明其对模型影响较大, 这6个气象要素在不同季节不同地区对模型的影响程度也有所侧重, 在选择气象要素时也要具体考虑其在不同季节不同地区的影响程度.
参考文献
| Bai Y, Wu L X, Qin K, et al. 2016. A geographically and temporally weighted regression model for ground-level PM2.5 estimation from satellite-derived 500 m resolution AOD[J]. Remote Sensing, 8(3): 262.DOI:10.3390/rs8030262 |
| 陈朝晖, 程水源, 苏福庆, 等. 2007. 北京地区一次重污染过程的大尺度天气型分析[J]. 环境科学研究, 2007, 20(2): 99–105.DOI:10.3321/j.issn:1001-6929.2007.02.020 |
| 邓君俊.2011.长三角地区霾天气形成机理和预报方法研究[D]南京: 南京大学http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y2372276 |
| 杜荣光, 齐冰, 郭惠惠, 等. 2011. 杭州市大气逆温特征及对空气污染物浓度的影响[J]. 气象与环境学报, 2011, 27(4): 49–53.DOI:10.3969/j.issn.1673-503X.2011.04.009 |
| 顾为东. 2014. 中国雾霾特殊形成机理研究[J]. 宏观经济研究, 2014, 6(3): 3–7. |
| Guo J P, Zhang X Y, Che H Z, et al. 2009. Correlation between PM concentrations and aerosol optical depth in eastern China[J]. Atmospheric Environment, 43(37): 5876–5886. |
| 黄思, 唐晓, 徐文帅, 等. 2015. 利用多模式集合和多元线性回归改进北京PM10预报[J]. 环境科学学报, 2015, 35(1): 56–64. |
| 靳全锋, 马祥庆, 王文辉, 等. 2017. 华东地区2000-2014年间秸秆燃烧排放PM2.5时空动态变化[J]. 环境科学学报, 2017, 37(2): 460–468. |
| Li C, Mao J, Lau A K H, et al. 2005. Application of MODIS satellite products to the air pollution research in Beijing[J]. Science in China Series D(Earth Sciences), 48: 209–219. |
| Gupta P, Christopher S A, Wang J, et al. 2006. Satellite remote sensing of particulate matter and air quality assessment over global cities[J]. Atmospheric Environment, 40(30): 5880–5892. |
| Li P, Xin J, Wang Y, et al. 2013. The acute effects of fine particles on respiratory mortality and morbidity in Beijing, 2004-2009[J]. Environmental Science and Pollution Research, 20(9): 6433–6444.DOI:10.1007/s11356-013-1688-8 |
| Liu Y, Paciorek C J, Koutrakis P. 2009. Estimating regional spatial and temporal variability of PM2.5 concentrations using satellite data, meteorology, and land use information[J]. Environmental health perspectives, 117(6): 886–892. |
| Kumar N, Chu A, Foster A. 2007. An empirical relationship between PM2.5 and aerosol optical depth in Delhi Metropolitan[J]. Atmospheric Environment, 41(21): 4492–4503.DOI:10.1016/j.atmosenv.2007.01.046 |
| 马艳, 黄容, 时晓曚, 等. 2018. 青岛冬季持续PM2.5重污染天气的大气边界层特征[J]. 环境科学研究, 2018, 31(1): 42–52. |
| 穆泉, 张世秋. 2013. 2013年1月中国大面积雾霾事件直接社会经济损失评估[J]. 中国环境科学, 2013, 33(11): 2087–2094. |
| Pope Ⅲ C A, Burnett R T, Thun M J, et al. 2002. Lung cancer, cardiopulmonary mortality, and long-term exposure to fine particulate air pollution[J]. Jama, 287(9): 1132–1141. |
| Tsai T C, Jeng Y J, Chu D A, et al. 2011. Analysis of the relationship between MODIS aerosol optical depth and particulate matter from 2006 to 2008[J]. Atmospheric Environment, 45(27): 4777–4788. |
| 王静.2016.基于卫星遥感的长三角主要城市PM2.5估算[D].上海: 华东师范大学http://cdmd.cnki.com.cn/Article/CDMD-10269-1016126911.htm |
| 王耀庭, 李威, 张小玲, 等. 2012. 北京城区夏季静稳天气下大气边界层与大气污染的关系[J]. 环境科学研究, 2012, 25(10): 1092–1098. |
| Wang Z F, Chen L F, Tao J H, et al. 2010. Satellite-based estimation of regional particulate matter (PM) in Beijing using vertical-and-RH correcting method[J]. Remote Sensing of Environment, 114(1): 50–63.DOI:10.1016/j.rse.2009.08.009 |
| 吴健生, 王茜, 李嘉诚, 等. 2017. PM2.5浓度空间分异模拟模型对比:以京津冀地区为例[J]. 环境科学, 2017, 38(6): 2191–2201. |
| Zheng S, Pozzer A, Cao C X, et al. 2014. Long-term (2001-2012) fine particulate matter (PM2.5) and the impact on human health in Beijing, China[J]. Atmospheric Chemistry & Physics Discussions, 14(21): 5715–5725. |
| 孙友敏, 李少洛, 陈春竹, 等. 2017. 济南市机动车排气污染特征及对市区PM2.5的影响研究[J]. 环境科学学报, 2017, 37(4): 1384–1391. |
| 徐晓斌. 2016. 我国霾和光化学污染观测研究进展[J]. 应用气象学报, 2016, 27(5): 604–619. |
| 游士兵, 严研. 2017. 逐步回归分析法及其应用[J]. 统计与决策, 2017(14): 31–35. |
| 郁珍艳, 高大伟, 李正泉, 等. 2017. 华东区域PM2.5变化背景下浙江省人口经济暴露水平评估[J]. 环境科学, 2017, 38(12): 4924–4931. |
| 张悦, 樊曙先, 李皓, 等. 2016. 气溶胶辐射效应在华东地区一次雾霾过程中的作用[J]. 气象学报, 2016, 74(3): 465–478. |
| 赵普生, 冯银厂, 金晶, 等. 2009. 建筑施工扬尘特征与监控指标[J]. 环境科学学报, 2009, 29(8): 1618–1623. |
| 周峤. 2015. 雾霾天气的成因[J]. 中国人口资源与环境, 2015(S1): 211–212. |
| 周志华. 2016. 机器学习[M]. 北京: 清华大学出版社: 25–26. |
