 )
) 北京师范大学中国基础教育质量监测协同创新中心, 北京 100875
收稿日期:2018-06-07出版日期:2019-05-15发布日期:2019-03-20通讯作者:陈平E-mail:pchen@bnu.edu.cn基金资助:* 国家自然科学基金青年基金项目(31300862);东北师范大学应用统计教育部重点实验室开放课题(KLAS130028732);中国基础教育质量监测协同创新中心研究生自主课题资助(BJSM-2016A1-16004)Explanatory item response theory models: Theory and application
CHEN Guanyu, CHEN Ping( )
) Collaborative Innovation Center of Assessment toward Basic Education Quality, Beijing Normal University, Beijing 100875, China
Received:2018-06-07Online:2019-05-15Published:2019-03-20Contact:CHEN Ping E-mail:pchen@bnu.edu.cn摘要/Abstract
摘要: 解释性项目反应理论模型(Explanatory Item Response Theory Models, EIRTM)是指基于广义线性混合模型和非线性混合模型构建的项目反应理论(Item Response Theory, IRT)模型。EIRTM能在IRT模型的基础上直接加入预测变量, 从而解决各类测量问题。首先介绍EIRTM的相关概念和参数估计方法, 然后展示如何使用EIRTM处理题目位置效应、测验模式效应、题目功能差异、局部被试依赖和局部题目依赖, 接着提供实例对EIRTM的使用进行说明, 最后对EIRTM的不足之处和应用前景进行讨论。
图/表 3
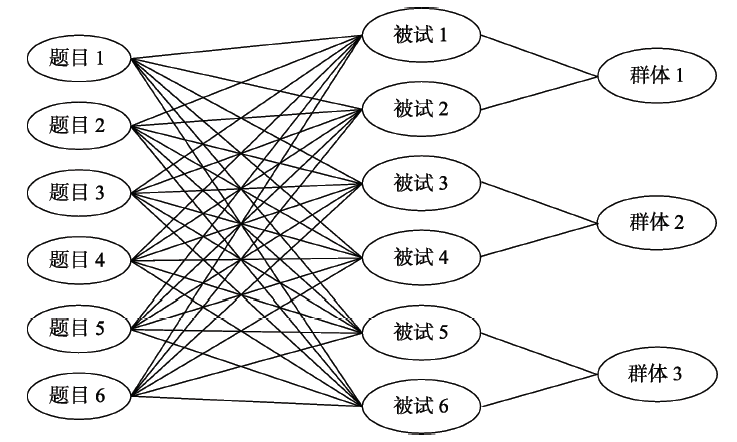
图1题目、被试和群体的层级关系图 注:图片翻译自Jiao, Kamata和Xie (2015, p. 145) 图5.3
 图1题目、被试和群体的层级关系图 注:图片翻译自Jiao, Kamata和Xie (2015, p. 145) 图5.3
图1题目、被试和群体的层级关系图 注:图片翻译自Jiao, Kamata和Xie (2015, p. 145) 图5.3表124道言语攻击题目
| 题目 | 行为模式 | 情境类型 | 行为类型 |
|---|---|---|---|
| 一辆公交车没有进站停靠, 我想诅咒。 | 想 | 他人责任 | 诅咒 |
| 一辆公交车没有进站停靠, 我想责备。 | 想 | 他人责任 | 责备 |
| 一辆公交车没有进站停靠, 我想怒骂。 | 想 | 他人责任 | 怒骂 |
| 因为工作人员给我错误的信息, 我错过了火车, 我想诅咒。 | 想 | 他人责任 | 诅咒 |
| 因为工作人员给我错误的信息, 我错过了火车, 我想责备。 | 想 | 他人责任 | 责备 |
| 因为工作人员给我错误的信息, 我错过了火车, 我想怒骂。 | 想 | 他人责任 | 怒骂 |
| 当我刚进入商店, 商店就关门了, 我想诅咒。 | 想 | 自己责任 | 诅咒 |
| 当我刚进入商店, 商店就关门了, 我想责备。 | 想 | 自己责任 | 责备 |
| 当我刚进入商店, 商店就关门了, 我想怒骂。 | 想 | 自己责任 | 怒骂 |
| 我与对方的通话断了, 因为我用完了话费, 我想诅咒。 | 想 | 自己责任 | 诅咒 |
| 我与对方的通话断了, 因为我用完了话费, 我想责备。 | 想 | 自己责任 | 责备 |
| 我与对方的通话断了, 因为我用完了话费, 我想怒骂。 | 想 | 自己责任 | 怒骂 |
| 一辆公交车没有进站停靠, 我会诅咒。 | 做 | 他人责任 | 诅咒 |
| 一辆公交车没有进站停靠, 我会责备。 | 做 | 他人责任 | 责备 |
| 一辆公交车没有进站停靠, 我会怒骂。 | 做 | 他人责任 | 怒骂 |
| 因为工作人员给我错误的信息, 我错过了火车, 我会诅咒。 | 做 | 他人责任 | 诅咒 |
| 因为工作人员给我错误的信息, 我错过了火车, 我会责备。 | 做 | 他人责任 | 责备 |
| 因为工作人员给我错误的信息, 我错过了火车, 我会怒骂。 | 做 | 他人责任 | 怒骂 |
| 当我刚进入商店, 商店就关门了, 我会诅咒。 | 做 | 自己责任 | 诅咒 |
| 当我刚进入商店, 商店就关门了, 我会责备。 | 做 | 自己责任 | 责备 |
| 当我刚进入商店, 商店就关门了, 我会怒骂。 | 做 | 自己责任 | 怒骂 |
| 我与对方的通话断了, 因为我用完了话费, 我会诅咒。 | 做 | 自己责任 | 诅咒 |
| 我与对方的通话断了, 因为我用完了话费, 我会责备。 | 做 | 自己责任 | 责备 |
| 我与对方的通话断了, 因为我用完了话费, 我会怒骂。 | 做 | 自己责任 | 怒骂 |
表124道言语攻击题目
| 题目 | 行为模式 | 情境类型 | 行为类型 |
|---|---|---|---|
| 一辆公交车没有进站停靠, 我想诅咒。 | 想 | 他人责任 | 诅咒 |
| 一辆公交车没有进站停靠, 我想责备。 | 想 | 他人责任 | 责备 |
| 一辆公交车没有进站停靠, 我想怒骂。 | 想 | 他人责任 | 怒骂 |
| 因为工作人员给我错误的信息, 我错过了火车, 我想诅咒。 | 想 | 他人责任 | 诅咒 |
| 因为工作人员给我错误的信息, 我错过了火车, 我想责备。 | 想 | 他人责任 | 责备 |
| 因为工作人员给我错误的信息, 我错过了火车, 我想怒骂。 | 想 | 他人责任 | 怒骂 |
| 当我刚进入商店, 商店就关门了, 我想诅咒。 | 想 | 自己责任 | 诅咒 |
| 当我刚进入商店, 商店就关门了, 我想责备。 | 想 | 自己责任 | 责备 |
| 当我刚进入商店, 商店就关门了, 我想怒骂。 | 想 | 自己责任 | 怒骂 |
| 我与对方的通话断了, 因为我用完了话费, 我想诅咒。 | 想 | 自己责任 | 诅咒 |
| 我与对方的通话断了, 因为我用完了话费, 我想责备。 | 想 | 自己责任 | 责备 |
| 我与对方的通话断了, 因为我用完了话费, 我想怒骂。 | 想 | 自己责任 | 怒骂 |
| 一辆公交车没有进站停靠, 我会诅咒。 | 做 | 他人责任 | 诅咒 |
| 一辆公交车没有进站停靠, 我会责备。 | 做 | 他人责任 | 责备 |
| 一辆公交车没有进站停靠, 我会怒骂。 | 做 | 他人责任 | 怒骂 |
| 因为工作人员给我错误的信息, 我错过了火车, 我会诅咒。 | 做 | 他人责任 | 诅咒 |
| 因为工作人员给我错误的信息, 我错过了火车, 我会责备。 | 做 | 他人责任 | 责备 |
| 因为工作人员给我错误的信息, 我错过了火车, 我会怒骂。 | 做 | 他人责任 | 怒骂 |
| 当我刚进入商店, 商店就关门了, 我会诅咒。 | 做 | 自己责任 | 诅咒 |
| 当我刚进入商店, 商店就关门了, 我会责备。 | 做 | 自己责任 | 责备 |
| 当我刚进入商店, 商店就关门了, 我会怒骂。 | 做 | 自己责任 | 怒骂 |
| 我与对方的通话断了, 因为我用完了话费, 我会诅咒。 | 做 | 自己责任 | 诅咒 |
| 我与对方的通话断了, 因为我用完了话费, 我会责备。 | 做 | 自己责任 | 责备 |
| 我与对方的通话断了, 因为我用完了话费, 我会怒骂。 | 做 | 自己责任 | 怒骂 |
表224道言语攻击题目的固定效应
| 题目 | 模型1 | 模型2 | 模型3 | 模型4 | |||
|---|---|---|---|---|---|---|---|
| βq | βq | 行为模式 | βq | DIF | 95%置信区间 | βq | |
| 1 | -1.162 | -1.148 | -1.196 | -0.101 | (-0.723, 0.549) | -1.248 | |
| 2 | -0.546 | -0.531 | -0.574 | -0.104 | (-0.717, 0.505) | -0.584 | |
| 3 | -0.091 | -0.074 | -0.134 | -0.171 | (-0.777, 0.431) | -0.101 | |
| 4 | -1.657 | -1.641 | -1.727 | -0.261 | (-0.934, 0.449) | -1.800 | |
| 5 | -0.681 | -0.667 | -0.729 | -0.182 | (-0.800, 0.433) | -0.746 | |
| 6 | -0.026 | -0.011 | -0.184 | -0.684 | (-1.293, -0.070) | -0.031 | |
| 7 | -0.512 | -0.496 | -0.495 | 0.103 | (-0.507, 0.721) | -0.617 | |
| 8 | 0.630 | 0.643 | 0.751 | 0.535 | (-0.067, 1.151) | 0.689 | |
| 9 | 1.430 | 1.451 | 1.338 | -0.455 | (-1.153, 0.240) | 1.610 | |
| 10 | -1.014 | -0.998 | -1.071 | -0.221 | (-0.853, 0.415) | -1.221 | |
| 11 | 0.312 | 0.329 | 0.362 | 0.231 | (-0.376, 0.826) | 0.354 | |
| 12 | 0.963 | 0.982 | 0.866 | -0.454 | (-1.104, 0.185) | 1.132 | |
| 13 | -1.145 | -1.580 | -0.465 | -1.066 | 0.426 | (-0.251, 1.108) | -1.225 |
| 14 | -0.383 | -0.820 | -0.465 | -0.215 | 0.792 | (0.156, 1.420) | -0.412 |
| 15 | 0.820 | 0.381 | -0.465 | 0.786 | -0.133 | (-0.767, 0.487) | 0.885 |
| 16 | -0.822 | -1.260 | -0.465 | -0.618 | 1.006 | (0.352, 1.706) | -0.895 |
| 17 | 0.035 | -0.404 | -0.465 | 0.263 | 1.019 | (0.409, 1.648) | 0.042 |
| 18 | 1.372 | 0.933 | -0.465 | 1.422 | 0.222 | (-0.417, 0.879) | 1.498 |
| 19 | 0.200 | -0.240 | -0.465 | 0.393 | 0.864 | (0.280, 1.481) | 0.199 |
| 20 | 1.390 | 0.956 | -0.465 | 1.579 | 0.750 | (0.093, 1.390) | 1.563 |
| 21 | 2.711 | 2.277 | -0.465 | 2.775 | 0.244 | (-0.615, 1.062) | 3.034 |
| 22 | -0.660 | -1.106 | -0.465 | -0.548 | 0.568 | (-0.068, 1.205) | -0.801 |
| 23 | 0.363 | -0.080 | -0.465 | 0.488 | 0.546 | (-0.059, 1.146) | 0.416 |
| 24 | 1.867 | 1.427 | -0.465 | 1.799 | -0.359 | (-1.138, 0.375) | 2.202 |
表224道言语攻击题目的固定效应
| 题目 | 模型1 | 模型2 | 模型3 | 模型4 | |||
|---|---|---|---|---|---|---|---|
| βq | βq | 行为模式 | βq | DIF | 95%置信区间 | βq | |
| 1 | -1.162 | -1.148 | -1.196 | -0.101 | (-0.723, 0.549) | -1.248 | |
| 2 | -0.546 | -0.531 | -0.574 | -0.104 | (-0.717, 0.505) | -0.584 | |
| 3 | -0.091 | -0.074 | -0.134 | -0.171 | (-0.777, 0.431) | -0.101 | |
| 4 | -1.657 | -1.641 | -1.727 | -0.261 | (-0.934, 0.449) | -1.800 | |
| 5 | -0.681 | -0.667 | -0.729 | -0.182 | (-0.800, 0.433) | -0.746 | |
| 6 | -0.026 | -0.011 | -0.184 | -0.684 | (-1.293, -0.070) | -0.031 | |
| 7 | -0.512 | -0.496 | -0.495 | 0.103 | (-0.507, 0.721) | -0.617 | |
| 8 | 0.630 | 0.643 | 0.751 | 0.535 | (-0.067, 1.151) | 0.689 | |
| 9 | 1.430 | 1.451 | 1.338 | -0.455 | (-1.153, 0.240) | 1.610 | |
| 10 | -1.014 | -0.998 | -1.071 | -0.221 | (-0.853, 0.415) | -1.221 | |
| 11 | 0.312 | 0.329 | 0.362 | 0.231 | (-0.376, 0.826) | 0.354 | |
| 12 | 0.963 | 0.982 | 0.866 | -0.454 | (-1.104, 0.185) | 1.132 | |
| 13 | -1.145 | -1.580 | -0.465 | -1.066 | 0.426 | (-0.251, 1.108) | -1.225 |
| 14 | -0.383 | -0.820 | -0.465 | -0.215 | 0.792 | (0.156, 1.420) | -0.412 |
| 15 | 0.820 | 0.381 | -0.465 | 0.786 | -0.133 | (-0.767, 0.487) | 0.885 |
| 16 | -0.822 | -1.260 | -0.465 | -0.618 | 1.006 | (0.352, 1.706) | -0.895 |
| 17 | 0.035 | -0.404 | -0.465 | 0.263 | 1.019 | (0.409, 1.648) | 0.042 |
| 18 | 1.372 | 0.933 | -0.465 | 1.422 | 0.222 | (-0.417, 0.879) | 1.498 |
| 19 | 0.200 | -0.240 | -0.465 | 0.393 | 0.864 | (0.280, 1.481) | 0.199 |
| 20 | 1.390 | 0.956 | -0.465 | 1.579 | 0.750 | (0.093, 1.390) | 1.563 |
| 21 | 2.711 | 2.277 | -0.465 | 2.775 | 0.244 | (-0.615, 1.062) | 3.034 |
| 22 | -0.660 | -1.106 | -0.465 | -0.548 | 0.568 | (-0.068, 1.205) | -0.801 |
| 23 | 0.363 | -0.080 | -0.465 | 0.488 | 0.546 | (-0.059, 1.146) | 0.416 |
| 24 | 1.867 | 1.427 | -0.465 | 1.799 | -0.359 | (-1.138, 0.375) | 2.202 |
参考文献 76
| [1] | 刘红云, 骆方 . ( 2008). 多水平项目反应理论模型在测验发展中的应用. 心理学报, 40( 1), 92-100. |
| [2] | 聂旭刚, 陈平, 张缨斌, 何引红 . ( 2018). 题目位置效应的概念及检测. 心理科学进展, 26( 2), 368-380. |
| [3] | 詹沛达, 王文中, 王立君 . ( 2013). 项目反应理论新进展之题组反应理论. 心理科学进展, 21( 12), 2265-2280. |
| [4] | Adams R. J., Wu M. L., & Wilson M. R . ( 1988). ACER ConQuest: Generalised item response modelling software [Computer software]. Melbourne, Victoria, Australia: Australian Council for Educational Research. |
| [5] | Baghaei P., Ravand H., . ( 2016). Modeling local item dependence in cloze and reading comprehension test items using testlet response theory. Psicologica: International Journal of Methodology and Experimental Psychology, 37( 1), 85-104. |
| [6] | Bates D., Mächler M., Bolker B. M., & Walker S. C ( 2015). Fitting linear mixed-effects models using LME4. Journal of Statistical Software, 67( 1), 1-48. |
| [7] | Bechger T. M Maris G ., ( 2015). A statistical test for differential item pair functioning. Psychometrika, 80( 2), 317-340. doi: 10.1007/s11336-014-9408-yURL |
| [8] | Binet A., & Simon T. , ( 1904). Méthodes nouvelles pour le diagnostic du niveau intellectuel des anormaux. L'année Psychologique, 11( 1), 191-244. |
| [9] | Birnbaum A., , ( 1968). Some latent trait models and their use in inferring an examinee’s ability. In F. M. Lord & M. R. Novick (Eds.), Statistical theories of mental test scores( pp. 392-479). Reading, MA: Addison-Wesley. |
| [10] | Bock R. D., & Aitkin M. , ( 1981). Marginal maximum likelihood estimation of item parameters: Application of an EM algorithm. Psychometrika, 46( 4), 443-459. |
| [11] | Bock R. D., & Lieberman M. , ( 1970). Fitting a response model for n dichotomously scored items. Psychometrika, 35(2), 179-197. |
| [12] | Bolker B. M., Brooks M. E., Clark C. J., Geange S. W., Poulsen J. R., Stevens M. H. H & White J. S. S ., ( 2009). Generalized linear mixed models: A practical guide for ecology and evolution. Trends in Ecology & Evolution, 24( 3), 127-135. |
| [13] | Bolt D. M . ( 2002). A Monte Carlo comparison of parametric and nonparametric polytomous DIF detection methods. Applied Measurement in Education, 15( 2), 113-141. doi: 10.1207/S15324818AME1502_01URL |
| [14] | Cosgrove J., & Cartwright F. , ( 2014). Changes in achievement on PISA: The case of Ireland and implications for international assessment practice. Large Scale Assessments in Education, 2( 2), 1-17. |
| [15] | Debeer D. & Janssen R. , ( 2013). Modeling item-position effects within an IRT framework. Journal of Educational Measurement, 50( 2), 164-185. doi: 10.1111/jedm.2013.50.issue-2URL |
| [16] | Debeer D., Buchholz J., Hartig J., & Janssen R . ( 2014). Student, school, and country differences in sustained test-taking effort in the 2009 PISA reading assessment. Journal of Educational and Behavioral Statistics, 39( 6), 502-523. doi: 10.3102/1076998614558485URL |
| [17] | De Boeck P., Bakker M., Zwitser R., Nivard M., Hofman A., Tuerlinckx F., & Partchev I . ( 2011). The estimation of item response models with the lmer function from the lme4 package in R. Journal of Statistical Software, 39( 12), 1-28. |
| [18] | De Boeck P., & Wilson M. , ( 2004). Explanatory item response models: A generalized linear and nonlinear approach. New York, NY: Springer. |
| [19] | De Boeck P., Wilson M. R . ( 2016). Explanatory response models. In W. J. van der Linden (Ed.), Handbook of Item Response Theory, Volume One: Models( pp. 565-580). New York, NY: Chapman and Hall/CRC. |
| [20] | Eyre J., Berg M., Mazengarb J., & Lawes E . ( 2017). Mode equivalency in PAT: Reading comprehension. Wellington: NZCER. |
| [21] | Fujimoto K. A . ( 2018). A general Bayesian multilevel multidimensional IRT model for locally dependent data. British Journal of Mathematical and Statistical Psychology, 71( 3), 536-560. doi: 10.1111/bmsp.2018.71.issue-3URL |
| [22] | Fukuhara H. & Kamata A. , ( 2011). A bifactor multidimensional item response theory model for differential item functioning analysis on testlet-based items. Applied Psychological Measurement, 35( 8), 604-622. doi: 10.1177/0146621611428447URL |
| [23] | Gamerman D., Gonçalves F. B., Soares T. M . ( 2018). Differential item functioning. In W. J. van der Linden (Ed.), Handbook of Item Response Theory, Volume Three: Applications( pp. 67-86). New York, NY: Chapman and Hall/CRC. |
| [24] | Gill J . ( 2000). Generalized linear models: A unified approach (Vol. 134). Thousand Oaks, CA: Sage Publications. |
| [25] | Hartig J., & Buchholz J. , ( 2012). A multilevel item response model for item position effects and individual persistence. Psychological Test and Assessment Modeling, 54( 4), 418-431. |
| [26] | Hohensinn C., Kubinger K. D., Reif M., Schleicher E., & Khorramdel L . ( 2011). Analyzing item position effects due to test booklet design within large-scale assessment. Educational Research and Evaluation, 17( 6), 497-509. doi: 10.1080/13803611.2011.632668URL |
| [27] | , , Hoskens M., & De Boeck P. , ( 1997). A parametric model for local dependence among test items. Psychological Methods, 2( 3), 261-277. |
| [28] | Ip E. H . ( 2000). Adjusting for information inflation due to local dependency in moderately large item clusters. Psychometrika, 65( 1), 73-91. doi: 10.1007/BF02294187URL |
| [29] | Janssen R .( 2016). Linear Logistic Models. In W. J. van der Linden (Ed.), Handbook of Item Response Theory, Volume One: Models ( pp. 211-224). New York, NY: Chapman and Hall/CRC. |
| [30] | Jeon M., Rijmen F., & Rabe-Hesketh S . ( 2013). Modeling differential item functioning using a generalization of the multiple-group bifactor model. Journal of Educational and Behavioral Statistics, 38( 1), 32-60. doi: 10.3102/1076998611432173URL |
| [31] | Jeon M., Rijmen F., & Rabe-Hesketh S . ( 2014). Flexible item response theory modeling with FLIRT. Applied Psychological Measurement, 38( 5), 404-405. |
| [32] | Jerrim J .( 2016). PISA 2012: How do results for the paper and computer tests compare? Assessment in Education: Principles, Policy & Practice, 23( 4), 495-518. |
| [33] | Jerrim J., Micklewright J., Heine J. H., Salzer C., & McKeown C . ( 2018). PISA 2015: How big is the ‘mode effect’ and what has been done about it? Oxford Review of Education, 44( 4), 476-493. |
| [34] | Jiao H., Kamata A., Wang S., & Jin Y . ( 2012). A multilevel testlet model for dual local dependence. Journal of Educational Measurement, 49( 1), 82-100. doi: 10.1111/jedm.2012.49.issue-1URL |
| [35] | Jiao H., Kamata A. & Xie C. , ( 2015). Multilevel cross-classified testlet model for complex item and person clustering in item response data analysis. In J. R. Harring, L. M. Stapleton & S. N. Beretvas (Eds.), Advances in multilevel modeling for educational research: Addressing practical issues found in real-world applications (pp. 139-161). Charlotte, NC: Information Age Publishing Inc. |
| [36] | Jiao H., Wang S. D., & Kamata A . ( 2005). Modeling local item dependence with the hierarchical generalized linear model. Journal of Applied Measurement, 6( 3), 311-321. |
| [37] | Jiao H.,Zhang Y , ( 2015). Polytomous multilevel testlet models for testlet-based assessments with complex sampling designs. British Journal of Mathematical and Statistical Psychology, 68( 1), 65-83. doi: 10.1111/bmsp.2015.68.issue-1URL |
| [38] | Jin Y.,Kang M , ( 2016). Comparing DIF methods for data with dual dependency. Large-scale Assessments in Education, 4( 1), 18. doi: 10.1186/s40536-016-0033-3URL |
| [39] | Kamata A. , ( 2001). Item analysis by the hierarchical generalized linear model. Journal of Educational Measurement, 38( 1), 79-93. doi: 10.1111/jedm.2001.38.issue-1URL |
| [40] | Kang C. , ( 2014). Linear and nonlinear modeling of item position effects (Unpublished master’s thesis). University of Nebraska-Lincoln. |
| [41] | Klein Entink R. H., Kuhn J. T., Hornke L. F., & Fox J. P . ( 2009). Evaluating cognitive theory: A joint modeling approach using responses and response times. Psychological methods, 14( 1), 54-75. |
| [42] | Koziol N. A . ( 2016). Parameter recovery and classification accuracy under conditions of testlet dependency: A comparison of the traditional 2PL, testlet, and bi-factor models. Applied Measurement in Education, 29( 3), 184-195. doi: 10.1080/08957347.2016.1171767URL |
| [43] | Lee Y .( 2004). Examining passage-related local item dependence (LID) and measurement construct using Q3 statistics in an EFL reading comprehension test. Language Testing, 21( 1), 74-100. doi: 10.1191/0265532204lt260oaURL |
| [44] | Logan T . ( 2015). The influence of test mode and visuospatial ability on mathematics assessment performance. Mathematics Education Research Journal, 27(4), 423-441. doi: 10.1007/s13394-015-0143-1URL |
| [45] | Mislevy R. J . ( 2016). How developments in psychology and technology challenge validity argumentation. Journal of Educational Measurement, 53( 3), 265-292. |
| [46] | OECD. ( 2017a). PISA 2015 technical report. Pairs: OECD Publishing. |
| [47] | OECD. ( 2017b). PISA 2015 assessment and analytical framework: Science, reading, mathematic, financial literacy and collaborative problem solving, Paris: OECD Publishing. Retrieved from http://dx.doiorg/10.1787/9789264281820-en. |
| [48] | Osterlind S. J., & Everson H. T . ( 2009). Differential item functioning (Vol. 161). Thousand Oaks, CA: Sage Publications. |
| [49] | Paek I., Fukuhara H . ( 2015). Estimating a DIF decomposition model using a random-weights linear logistic test model approach. Behavior Research Methods, 47( 3), 890-901. doi: 10.3758/s13428-014-0512-9URL |
| [50] | Plummer M . ( 2017). JAGS version 4. 3.0 user manual [Software manual]. Retrieved from |
| [51] | Rabe-Hesketh S., Skrondal A . ( 2016). Generalized linear latent and mixed modeling. In W. J. van der Linden (Ed.), Handbook of Item Response Theory, Volume One: Models( pp. 503-526). New York, NY: Chapman and Hall/CRC. |
| [52] | Rabe-Hesketh S., Skrondal A.Pickles, & Pickles A., , ( 2004). GLLAMM manual [Software manual]. (U. C. Berkeley Division of Biostatistics Working Paper Series, 160) |
| [53] | Raudenbush S. W., Bryk A. S., Cheong Y. F., Congdon Jr R. T., & Toit M. D . ( 2011). HLM7 hierarchical linear and nonlinear modeling manual [Software manual]. Lincolnwood, IL: SSI Scientific Software International Inc. |
| [54] | Ravand H . ( 2015). Assessing testlet effect, impact, differential testlet, and item functioning using cross-classified multilevel measurement modeling. SAGE Open, 5( 2). |
| [55] | Rijmen F . ( 2006). BNL: A Matlab toolbox for Bayesian networks with logistic regression( Tech. Rep.). Amsterdam, the Netherlands: VU University Medical Center. |
| [56] | Rijmen F., Tuerlinckx F., De Boeck P., & Kuppens P . ( 2003). A nonlinear mixed model framework for item response theory. Psychological Methods, 8( 2), 185-205. doi: 10.1037/1082-989X.8.2.185URL |
| [57] | SAS Institute . ( 2015). SAS/STAT 14.1: user's guide [Software manual]. Cary, NC: SAS Institute Inc. |
| [58] | Spiegelhalter D., Thomas A., Best N., & Lunn D. ( 2014). OpenBUGS (Version 3.2.3) [Software manual]. Retrieved from, . |
| [59] | Stroup W. W . ( 2012). Generalized linear mixed models: Modern concepts, methods and applications. Boca Raton, FL: CRC press. |
| [60] | Su Y, Yajima M ( 2015). R2jags: A Package for Running JAGS from R [Computer software]. Retrieved from |
| [61] | Teker G. T Dogan N ., ( 2015). The Effects of testlets on reliability and differential item functioning. Educational Sciences: Theory and Practice, 15( 4), 969-980. |
| [62] | Thissen D ., ( 1991). MULTILOG [Software manual]. Lincolnwood, IL: Scientific Software. |
| [63] | Trendtel M., Robitzsch A ., ( 2018). Modeling item position effects with a Bayesian item response model applied to PISA 2009-2015 data. Psychological Test and Assessment Modeling, 60( 2), 241-263. |
| [64] | Tutz G., Berger M ., ( 2016). Item-focussed trees for the identification of items in differential item functioning. Psychometrika, 81( 3), 727-750. doi: 10.1007/s11336-015-9488-3URL |
| [65] | Tutz G., Schauberger G ., ( 2015). A penalty approach to differential item functioning in Rasch models. Psychometrika, 80( 1), 21-43. doi: 10.1007/s11336-013-9377-6URL |
| [66] | van der Linden W.J, . ( 2016). Handbook of Item Response Theory, Volume One. New York, NY: Chapman and Hall/ CRC. |
| [67] | van der Linden W.J, . ( 2018). Handbook of Item Response Theory, Volume Three: Applications. New York, NY: Chapman and Hall/CRC. |
| [68] | Vansteelandt K, .( 2000). Formal models for contextualized personality psychology (Unpublished doctoral dissertation). K.U. Leuven, Belgium. |
| [69] | Wainer H., & Lukhele R. , ( 1997). How reliable are TOEFL scores? Educational and Psychological Measurement, 57( 5), 741-758. doi: 10.1177/0013164497057005002URL |
| [70] | Wainer H., Sireci S. G., & Thissen D . ( 1991). Differential testlet functioning definitions and detection (Research Rep. 91-21). Princeton NJ: ETS. |
| [71] | Wang W. C., & Wilson M. ,( 2005). Assessment of differential item functioning in testlet-based items using the Rasch testlet model. Educational and Psychological Measurement, 65( 4), 549-576. |
| [72] | Weirich S., Hecht M., Böhme K . ( 2014). Modeling item position effects using generalized linear mixed models. Applied Psychological Measurement, 38( 7), 535-548. doi: 10.1177/0146621614534955URL |
| [73] | Weirich S., Hecht M., Penk C., Roppelt A., Böhme K . ( 2017). Item position effects are moderated by changes in test-taking effort. Applied psychological measurement, 41( 2), 115-129. doi: 10.1177/0146621616676791URL |
| [74] | Wilson M., Zheng X. H., & McGuire L . ( 2012). Formulating latent growth using an explanatory item response model approach. Journal of Applied Measurement, 13( 1), 1-22. |
| [75] | Xie C . ( 2014). Cross-classified modeling of dual local item dependence (Unpublished doctoral dissertation). University of Maryland, College Park, MD. |
| [76] | Xie C., & Jiao H. , ( 2014, April). Cross-classified modeling of dual local item dependence. Paper presented at the Annual Meeting of the American Educational Research Association, Phliadelphia, PA. |
相关文章 2
| [1] | 王阳, 温忠麟, 付媛姝. 等效性检验——结构方程模型评价和测量不变性分析的新视角[J]. 心理科学进展, 2020, 28(11): 1961-1969. |
| [2] | 聂旭刚, 陈平, 张缨斌, 何引红. 题目位置效应的概念及检测[J]. 心理科学进展, 2018, 26(2): 368-380. |
PDF全文下载地址:
http://journal.psych.ac.cn/xlkxjz/CN/article/downloadArticleFile.do?attachType=PDF&id=4688
