陈鑫峰^,1,2, 王武^,1,*1.中国科学院计算机网络信息中心,北京 100190
2.中国科学院大学,北京 100049

An Effective Implementation of LDLT Decomposition of Sparse Symmetric Matrix on GPU

Chen Xinfeng^,1,2, Wang Wu^,1,*1. Computer Network Information Center, Chinese Academy of Sciences, Beijing 100190, China
2. University of Chinese Academy of Sciences, Beijing 100049, China

通讯作者: *王武（E-mail:wangwu@sccas.cn）

收稿日期:2021-02-1网络出版日期:2021-06-20

基金资助:

国家重点研发计划项目“复杂电磁环境高性能应用软件系统研制及应用示范”(2017YFB 0202502) 中国科学院“十三五”信息化专项“科研信息化应用工程”(XXH13506-405)

Received:2021-02-1Online:2021-06-20
作者简介 About authors

陈鑫峰,中国科学院计算机网络信息中心,在读硕士研究生,主要研究方向为高性能计算和并行计算。
本文承担工作：实/复数稀疏对称矩阵的LDL^T分解在GPU上的实现。
Chen Xinfeng is a master student at Computer Network Information Center, Chinese Academy of Sciences. His main research interests are high performance computing and parallel computing.
In this paper, he undertakes the following tasks: the implemen-tation and optimization of LDL^T decomposition of complex/real sparse symmetric matrix on GPU.
E-mail: chenxinfeng@cnic.cn


王武,中国科学院计算机网络信息中心,博士,副研究员,研究方向为并行算法、高性能计算。
本文承担工作为GPU上的稀疏矩阵分解的算法指导。
Wang Wu, Ph.D., is an associate researcher at Computer Network Information Center, Chinese Academy of Sciences. His main research interests are parallel algorithm and high performance computing. In this paper, he undertakes the following tasks: algorithm director of sparse matrix decomposi-tion on GPU.
E-mail: wangwu@sccas.cn



摘要
【目的】 LDL^T分解是求解很多稀疏对称线性系统的有效工具之一,尤其是对于迭代法难以收敛的问题。然而在GPU上实现LDL^T分解存在困难,因为分解过程中存在数据依赖和不规则的数据访问。【方法】 本文设计并实现了一个基于GPU的稀疏对称矩阵的LDL^T分解,它采用Cholesky的符号分解和右视分解算法、稀疏矩阵依赖图的层次划分,以及CUDA的动态并行核调度技术,算法的所有三层循环都并行化,从而获得更高的并行度。【结果】 实验结果表明,针对稀疏对称矩阵的一个典型的测试集,在GPU上实现的LDL^T分解相对于UMFPACK最高加速46.2倍。【结论】 LDL^T分解CUDA实现策略可为高性能GPU异构平台上开展稀疏矩阵的高性能数值算法研究与实现提供借鉴。
关键词： LDL^T 分解 ;右视算法;GPU;动态并行

Abstract
[Objective] LDL^T decomposition is an effective tool to solve many problems in sparse symmetric linear systems, especially for those problems which are hard to converge using iterative solvers. However, it is difficult to implement LDL^T on the GPU for data dependency and irregular data access during the factorization. [Methods] In this paper, an effective GPU-based LDL^T decomposition method of sparse symmetric matrix is designed and implemented based on Cholesky symbolic decomposition, right-looking decomposition algorithm and level partition of the dependency graph for the sparse matrix. By using controlled kernel launch for CUDA dynamic parallelism, all three loops of the algorithm are parallelized, so the proposed method can achieve higher parallelism.[Results] Experimental results show that the implementation of LDL^T on GPU can achieve a maximum speedup of 46.2 compared to UMFPACK for a typical collection of sparse symmetric matrix. [Conclusions] CUDA implementation of LDL^T can give reference to high performance numerical algorithm research and implementation for sparse matrix on GPU-based heterogeneous platforms.
Keywords：LDL^T decomposition ;right-looking algorithm;GPU;dynamic parallelism


PDF (8373KB)元数据多维度评价相关文章导出EndNote|Ris|Bibtex收藏本文
本文引用格式
陈鑫峰, 王武. 稀疏对称矩阵的LDL^T分解在GPU上的高效实现[J]. 数据与计算发展前沿, 2021, 3(3): 136-147 doi:10.11871/jfdc.issn.2096-742X.2021.03.012
Chen Xinfeng, Wang Wu. An Effective Implementation of LDLT Decomposition of Sparse Symmetric Matrix on GPU[J]. Frontiers of Data and Computing, 2021, 3(3): 136-147 doi:10.11871/jfdc.issn.2096-742X.2021.03.012

引言

稀疏对称矩阵的LDL^T分解对许多科学工程问题的有效求解非常重要。例如基于有限差分或有限元离散得到的稀疏线性系统,若采用迭代法难以奏效（迭代收敛很慢甚至不收敛）时,直接法LU分解便可有效解决问题。若矩阵具有对称性,则LU分解转化为LDL^T分解。直接法分解过程计算开销较大,如何提高其性能尤为重要。直接法的步骤可分为符号分解、数值分解和三角求解,其中数值分解最耗时。目前在多核或众核上并行实现稀疏矩阵分解比较困难,因为分解过程中有较多的数据依赖和不规则数据访问,导致难以充分利用这些多核CPU或加速卡,加速效果不佳,甚至无法加速。

基于CPU+GPU的并行异构架构已成为当今高性能计算机和服务器的主流体系结构之一。在GPU上稠密矩阵的计算已经具备很高的性能,如CUDA的cuBLAS库^[1],因为稠密问题有利于高效内存访问和存取,以及向量化计算指令集的应用。由于非零元素分布不规则的稀疏方程组难以高效访存和向量化计算,无法充分利用GPU的计算资源实现高效求解。目前有很多适用于CPU的稀疏矩阵直接法求解器,比如SuperLU、MKL的PARDISO、MUMPS、UMFPACK、HSL^[2]的MA57等,但是在GPU上有效实现稀疏矩阵分解的软件还很少。CUDA的cuSOLVER^[3]还没有提供GPU上稀疏LU分解的接口。加州大学Peng等^[4]开发了基于GPU的稀疏LU分解算法库GLU 3.0,并用于集成电路仿真。它的数值分解较快,但符号分解存在瓶颈。如何有效利用GPU计算能力提升稀疏矩阵分解的性能仍是需要研究的课题^[5]。

本文设计和实现了一种基于GPU的稀疏对称矩阵的LDL^T分解,该方法基于右视（right- looking）的LDL^T分解,使得该分解可以实现右视算法的三层循环并行,这极大的提高了LDL^T分解的并行度,并通过GPU动态并行技术提升了GPU的计算和访存效率。本文最后针对一般稀疏对称矩阵的一个典型测试集测试了该分解的性能。

实验结果表明,本文提出的LDL^T分解算法在NVIDIA TITAN V GPU测试平台上达到较高的计算性能,针对稀疏对称矩阵测试集,LDL^T数值分解的计算速度相对于UMFPACK最高加速46.2倍,加速倍数取决于稀疏矩阵在分解过程中的非零元填充比。

本文结构如下：第1部分介绍LDL^T的右视分解算法、符号分解和数值分解;第2部分重点介绍数值分解在GPU上的并行算法和实现;第3部分给出分解和求解算法在典型测试集上实现的性能,并与UMFPACK、MA57、cuSOLVER和GLU 3.0进行了性能对比。最后给出本文结论。

1 稀疏矩阵的LDL^T 分解算法

1.1 LDL^T分解的右视算法

阶对称矩阵A的LDL^T分解可表示为A = LDL^T,其中L是一个对角线元素为1的下三角矩阵,D是一个对角矩阵,而L^T表示L的转置。LDL^T分解是高斯消去法的一个变型,即：

$\left[\begin{array}{ll}a_{11} & a_{21}^{T} \\ a_{21} & A_{22}\end{array}\right]=\left[\begin{array}{cc}1 & 0 \\ l_{21} & L_{22}\end{array}\right] \cdot\left[\begin{array}{cc}d_{11} & 0 \\ 0 & D_{22}\end{array}\right] \cdot\left[\begin{array}{cc}1 & l_{21}^{T} \\ 0 & L_{22}^{T}\end{array}\right]$

其中l₁₁=1,d₁₁和a₁₁是标量,l₂₁和a₂₁是（n-1）×1的列向量,l₂₂和D₂₂以及A₂₂是（n-1）阶的子矩阵。由此可得到,d₁₁=a₁₁,l₂₁=a₂₁/d₁₁,L₂₂D₂₂L^T₂₂=A₂₂-l₂₁d₁₁l^T₂₂。一直重复该过程,直到求出L和D的所有元素,D的元素存储在L的主对角线上。

右视算法每次迭代时先求解D的一个元素,然后求解一列L的元素,最后更新剩下的子矩阵。从中可以看到很大的数据依赖性,即必须先分解前k-1列,才能分解第k列,这极大的限制了并行性。

为了节省存储空间,需要将稀疏矩阵压缩后存储,这导致稀疏矩阵非零元素的内存访问极不规则。由于处理器对内存的访问有空间局部性和时间局部性的特点,而LDL^T分解过程中经常不规则跳跃式访问数据,这与内存访问特点相悖,因此极大地降低了性能,所以选择一个适当的稀疏矩阵储存格式很重要,本文采用压缩稀疏列（Compressed Sparse Colum,CSC）格式,它一定程度上减少了不规则内存访问。

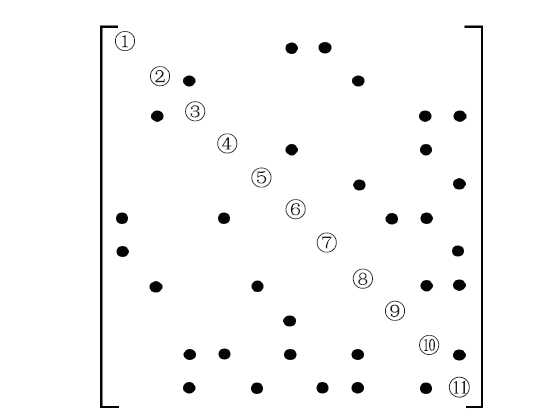
稀疏矩阵A的CSC格式由三部分组成,分别为Ai,Ap和Ax,其中Ai表示稀疏矩阵A的行索引,大小为nnz（A的非零元素个数）,Ap表示A的列指针,大小为n+1,n为A的维数,Ax表示A的非零元素值,大小为nnz。第k列元素的索引和值分别为Ai[Ap[k]],Ai[Ap[k]+1],…,Ai[Ap[k+1]-1]和Ax[Ap[k]],Ax[Ap[k]+1], …,Ax[Ap[k+1] - 1]。图1是某个稀疏矩阵的非零元分布结构,●表示非零元素的位置。

图1

新窗口打开|下载原图ZIP|生成PPT
图1稀疏矩阵分布

Fig.1The pattern of sparse matrix



算法1展示了右视LDL^T分解算法的伪代码,在这个伪代码中,L表示初始矩阵A被符号分解后的矩阵,包括重排序和非零元填充（fill-in）。k表示当前列的索引,j表示当前列右边的列。第k列被计算完成后,第j（j>k）列将会被立即更新。即第k列被计算完以后,该算法会向右看,使用算好的第k列更新第k列所有右边的列j（j>k）。所以主要的操作变成子矩阵更新,该过程具有较好的并行性。


算法1.
算法1.基于右视的LDL^T分解

1: for k = 1 to n do 2: //分解L的第k 列 3: for i = k + 1 to n where lik≠ 0 do 4: lik = liklkk 5: end for 6: //更新依赖第k列的子列 7: for j = k + 1 to n where lik≠ 0 do 8: for i = j to n where ljk≠ 0 do 9: lij = lij-likljklkk 10: end for 11: end for 12: end for

新窗口打开|下载CSV

分解过程有3层循环,最外层的循环表示正在被分解的列,中间一层循环表示将要被更新的列,而最内层的循环表示待更新列的某个元素。显而易见,最内层的两个循环完全可以并行计算,后面介绍如何通过图划分实现最外层循环并行。

1.2 符号分解方法

由于本文待求解的稀疏矩阵是对称的,并且符号分解不涉及任何具体的数值,所以本文使用稀疏Cholesky分解的符号分解^{[6,7,8,9,10,11]},这一部分时间很短,所以没有使用GPU加速。这一步结束以后会将矩阵重新排列,即C=P^TAP,其中P是排列矩阵,而且还会生成一个parent数组,表示列与列的依赖关系,即parent[i]=k表示第k列依赖第i列,也就表示必须先分解第i列,然后使用分解好的第i列更新第k列,最后才能分解第k列。这个parent数组也为后续的最外层循环并行提供基础。

符号分解也需要为下一步的数值分解确定L矩阵的结构,因为对称稀疏矩阵分解后,原先的零元素可能变成非零元素,即fill-in,所以需要尽可能的减少fill-in的数量。这就需要重排序算法,即减少fill-in的数量而提出的算法。符号分解主要包含以下4个步骤：

（1）重排序

该步骤通过对稀疏矩阵的非零元位置置换,即重排序来尽可能减少fill-in的数量。结束后会返回置换矩阵P,并使用该矩阵来重排序初始矩阵A,即C=PTAP。常用的重排序有近似最小度^[12]（Approximate Minimum Degree, AMD）排序和METIS软件包的图划分排序^[13],我们默认调用METIS重排序,对于规模较小的矩阵（比如n小于5000）,则使用AMD重排序。METIS的排序算法基于多层次递归二分切分法、多层K路划分法以及多约束划分机制,执行效率更高,填充数量更少。

（2）寻找依赖图

该步骤根据重排序后的矩阵C,寻找列与列之间的依赖关系,即依赖图parent,数组parent[i]=k表示第k列依赖第i列,必须先分解完第i列,然后使用第i列更新第k列,最后才能分解第k列。可通过构造etree函数实现^[14]。

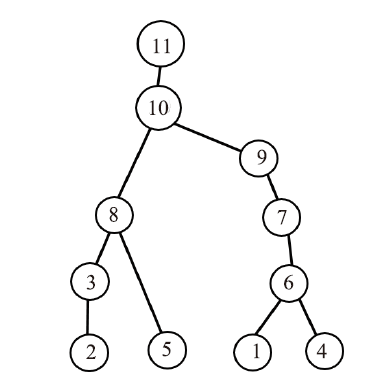
图2为图1稀疏矩阵符号分解过程的依赖图：其中节点表示列,边表示列与列之间的依赖关系,且位于上面的节点所代表的列依赖下面节点所代表的列。从该依赖图看出,分解完第1列后才能分解第6列;分解完第6列后才能分解第7列;分解完第7列后才能分解第9列;分解完第9列后才能分解第10列;分解完第10列后才能分解第11列。

图2

新窗口打开|下载原图ZIP|生成PPT
图2依赖图

Fig.2The dependency graph



依赖图为树结构,对于一个树节点,必须先分解完它的孩子节点所代表的列,然后使用它的孩子节点所代表的已分解好的列更新它自己所代表的列,最后才能分解它自己所代表的列。可见不同子树代表的子列分解完全独立,这进一步提升了并行度,即多层图划分并行。

（3）根据依赖图确定levels

根据以上分析,我们可以实现层划分并行。该步骤根据列与列的依赖关系,即依赖图数组parent确定可并行计算的列,即level[],同一个level中的列都可以并行分解,不同的level中的列有依赖关系,只能串行分解。

算法2为确定节点层划分的算法伪代码。其中叶子节点的层记作level 0,每个节点的层编号为它的左孩子节点的level值与右孩子节点的level值最大值取其较大者加1。level_i[]数组大小为n,它表示每一层包含的列编号,总层数为nlevel,数组level_p[]用于确定每层level_i的起始和终止列,大小为nlevel+1。例如第k层包含的列为level_i[level_p[k]],level_i[level_p[k]+1],…,level_i[level_p[k+1]-1]。这跟储存稀疏矩阵的CSC格式类似,因此可通过level_i[]和level_p[]索引快速定位每层节点包含的列编号。


算法2.
算法2.数据依赖图的划分

1: 为lev[]分配内存,初值设为0 2: nlevel = 1 3: for k = 0 to n - 1 do 4: if parent[k]≠ -1 then 5: lev[parent[k]] = max(lev[parent[k]], lev[k]+1); 6: end if 7: nlevel = max(nlevel, lev[k]+1); 8: end for 9: 为c[]分配内存, 大小为nlevel,初值设为0 10: for k = 0 to n- 1 do 11: c[lev[k]]++; 12: end for 13: 为level_p[]分配内存, 大小为nlevel+1 14: level_p[0] = 0; 15: for k = 1 to nlevel do 16: level_p[k] = level_p[k-1]+c[k-1]; 17: c[k-1] = level_p[k-1] 18: end for 19: 为level_i 分配内存空间, 大小为n 20: for k = 0 to n - 1 do 21: level_i[c[lev[k]]++] = k; 22: end for 23: 释放lev[]和c[]

新窗口打开|下载CSV

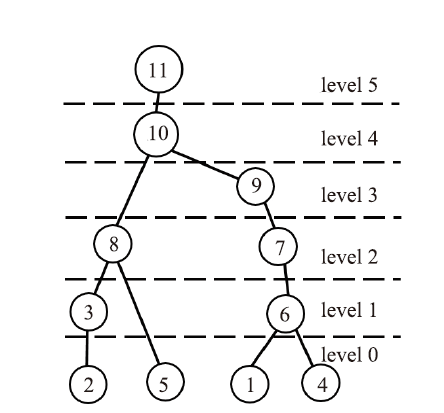
对图2进行多层划分后的依赖图见图3。其中属于level 0的为第1、2、4、5列,这些列可以被并行分解。属于level 1的为第3,6列,这些列必须等待level 0中的列被分解完以后才能被分解,同样这些列也可以被并行分解。属于level 2的为第7、8列,这些列必须等待level 1中的列被分解完以后才能被分解,同样这些列可以被并行分解。属于level 3的为第9列,这些列必须等待level 2中的列被分解完以后才能被分解,同样这些列可以被并行分解。属于level 4的为第10列,这些列必须等待level 3中的列被分解完以后才能被分解,同样这些列可以被并行分解。属于level 5的为第11列,这些列必须等level 4中的列被分解完以后才能被分解,同样这些列可以被并行分解。

图3

新窗口打开|下载原图ZIP|生成PPT
图3多层划分后的依赖图

Fig.3The dependency graph after level partition



（4）根据依赖图数组确定L的结构

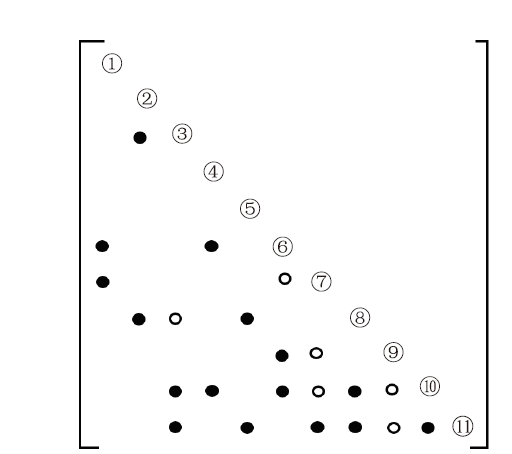
该步骤根据列与列之间的依赖关系,即依赖图parent数组,来为下一步的数值分解确定L的结构。确定L结构的算法基于Cholesky分解的上视分解^[6],算法3为确定填充元位置的伪代码,其中矩阵L第k行的非零元位置通过ereach函数^[6]得到。图4为图1的稀疏矩阵符号分解填充后的L矩阵结构,其中●表示非零元素的位置,○表示填充元的位置。

图4

新窗口打开|下载原图ZIP|生成PPT
图4填充后的L矩阵

Fig.4The L matrix after fill-in




算法3.
算法3.确定填充元的位置

1: // 为x和s分配内存,大小均为n 2: // c数组存储L矩阵每一列在Lx的起始位置 3: for k = 0 to n -1 do 4: Lp[k] = c[k]; 5: top = ereach(C, k, parent, s,c); //获取L矩阵第k行的非零结构 6: x[k] = 0 7: for p = Cp[k] to Cp[k + 1] do 8: if Ci[p] ≤ k then 9: x[Ci[p]] = Cx[p]; 10: end if 11: end for 12: // s[top...n-1] 为L矩阵第k行的非零结构 13: for top to n-1 do 14: i = s[top]; 15: p = c[i]++; 16: Li[p] = k; //在L矩阵的第i列存储Lki
17: Lx[p] = x[i]; 18: x[i] = 0; //为第k+1行清除x 19: end for 20: //存储Lkk 21: p = c[k]++; 22: Li[p] = k; 23: Lx[p] = x[k]; 24: x[k] = 0; 25: end for 26: Lp[n] = c[n-1];

新窗口打开|下载CSV

1.3 并行数值分解方法

基于右视的LDL^T分解算法见算法1,对应的并行数值分解过程的伪代码见算法4^[14]。


算法4.
算法4.并行化的LDL^T数值分解

1: for level = 1 to nlevel do 2: //分层划分级别的并行 3: for 当前level包含的所有列 do 4: 并行分解当前的列 5: end for 6: for 当前level的所有列 do 7: //并行更新子列 8: for 依赖当前列的所有子列do 9: //并行向量MAD操作 10: 并行更新一个子列 11: end for 12: end for 13: end for

新窗口打开|下载CSV

其中第一层循环是选择一个level的所有列,这些列可以被并行分解。

在第一层循环内部一共有两个阶段,第一阶段为通过使用向量标量除法来并行分解当前选中的列,可以看出这些被选中的列可以被完全并行分解。第二阶段为更新操作,即使用当前分解好的列来更新那些依赖该列的子列,这些子列很容易由以下方法定位：

假设当前被分解好的列为k,且l_ik ≠ 0, l_ik ≠ 0 ( i≥ j),根据算法1中的第9行l_ij = l_ij - l_ik * l _jk * l _kk 就可以知道l_ij ≠ 0。所以如果 l_ik ≠ 0,则第i 列依赖第k列。为了快速判断 l_ik是否等于零,采用临时非压缩数组temp,即temp[i] =l_ik,如果temp[i] ≠ 0,则表示l_ik ≠ 0,这样就可以快速定位和更新这些子列。从算法1的第9行也可以看到,该更新涉及到两次乘法,为了提高数值分解速度,用了两个临时数组： tmpMem1[i] =l_ik*l_kk,tmpMem[i] =l_ik。而且这些子列只是读取这些临时数组,并没有更新它们,所以更新某个子列并不会影响其它子列的更新。

从算法1中可以看到,这些子列只更新一次且更新相互独立,所以这些子列的更新完全可以被并行。第三层循环本质上是一个向量标量乘法和向量加法操作,即MAD操作,这个操作用来更新一个子列,算法1中子列每个元素的更新相互独立,完全可以并行进行。可以看到,算法1的三层循环通过算法2和算法3实现完全并行,这有利于在GPU上提升性能。

1.4 三角求解方法

完成重排序、符号分解和LDL^T数值分解之后,就可以求解线性方程组Ax = b,其中x可以是向量或矩阵,即同时求解多个有相同系数矩阵和不同右端向量b的线性方程组。因为C =P^TAP,且C = LDL^T,基于分解矩阵L、D和置换矩阵P,Ax = b的求解过程为：

(1) x =P^Tb;

(2) Ly= x;

(3) Dx = y;

(4) L^Ty =x;

(5) x = Py。

为了提高数值分解的并行度,没有采用动态选主元,而是假设主对角元不为零,在分解过程中,如果主对角元足够小,就将其赋值为常量,这会导致主对角元非常小的情况下数值分解后三角求解的计算结果有一定的误差,为减少误差,三角求解时使用迭代收敛^[15,16]方法提高精度。相对于数值分解,三角求解的计算时间很短,没有必要使用GPU加速。

2 LDL^T数值分解在GPU上的实现

2.1 GPU架构和CUDA编程

GPU在科学与工程计算的很多应用领域发挥着越来越重要的作用^{[17,18,19,20,21]},尤其是对于计算密集型的应用。GPU由一组线程化的流多处理器（SM）构成,它们共享全局内存。每个SM含多个标量处理器、L1缓存、常量缓存（C-Cache）、多线程指令获取(MT issue)以及共享内存等部件。线程是GPU的基本运算单元,多个线程构成线程块,一个SM上可同时运行多个块,块内以单指令多线程（SIMT）方式执行程序。块内的线程可实现同步。

CUDA作为GPU的编程模型,它支持核调用和核内存分配,从而充分利用GPU的并行计算能力。CUDA假设CPU和GPU有各自的内存空间,分别称为主机内存和设备内存。同一个块中所有线程可访问同一共享内存,全局内存所有线程均可访问。CUDA提供了blockIdx.x和threadIdx.x等内置变量,调用核函数时这些变量被自动确定,指引每个线程和块的索引,将数据映射到对应的线程上,从而每个线程可独立处理对应的数据。

2.2 LDL^T数值分解在GPU上的实现

LDL^T数值分解的算法伪代码见伪代码1,被重排序后的矩阵C=P^TAP的列被划分成了level层,即算法的最外层循环,每层的列可并行分解。前文已经表明,需要两个临时非压缩的内存空间来更新子列,但是GPU的全局内存有限,所以需要提前判断当前GPU还有多少全局内存可用。

在伪代码1的第3行,free表示剩下可用的全局内存,单位是字节。因为level中的每一列分解都需要nB=2*n*sizeof(数据类型)字节的内存（算例中的矩阵数据是单精度的,可以是实数也可以是复数）,而如果level中的列比free/nB还要大,尤其是n很大且level很小时,无法一次性全部并行分解完level中的所有列,必须分几次才能完这些列的并行分解。


伪代码1.
伪代码1.基于GPU的并行LDL^T数值分解

1: function LDLT(Lp, Li, Lx, level_p, level_i) 2:分配GPU内存,将数据从CPU端复制到GPU端 3: cudaMemGetInfo(&free, &total); 4: free -= 1024ull*1024ull*1024ull; //预留1GB的空闲内存 5: free /= (2*n*sizeof(数据类型)); 6: for level = 0 to nlevel - 1 do 7: //level 级别的并行 8: lev_size = level_p[level+1]-level_p[level]; 9: tmp = min(lev_size,free); 10: //GPU上为tmpMem1和tmpMem分配全局内存 11: offset = 0; 12: while lev_size >0 do 13: restCol = min(lev_size tmp); 14: dynamic<<<restCol, 1>>>(Lp, Li, Lx, level_p, level_i, tmpMem, tmpMem1, n,level,offset); 15: lev_size -= tmp; 16: offset += tmp; 17: end while 18: 释放tmpMem 19: end for 20:从GPU端到CPU端拷贝数据,释放GPU内存

新窗口打开|下载CSV

一旦确定了要并行分解的列,就要调用一个核函数（dynamic）来并行分解这些列,即伪代码1的第14行,其中restCol表示当前需要并行分解的列数,该核函数调用表示每个线程块负责分解一列,其伪代码如下：


伪代码2.
伪代码2.动态并行分解核函数

1: function dynamic(Lp, Li, Lx, level_p, level_i, tmpMem, tmpMem1, n, level, offset) 2: k = level_i[level_p[level]+offset+blockIdx.x]; 3: d = Lx[Lp[k]]; 4: if abs(d)<1e-5 then 5: Lx[Lp[k]]=1e-5; 6: d=1e-5; 7: end if 8: subColSize=Lp[k+1]-Lp[k]-1; 9: factorize<<<(subColSize+1023)/1024,1024>>> (Lp,Li,Lx,tmpMem,tmpMem1,d,n,k,blockIdx.x);
10: update<<<subColSize,1024>>>(Lp,Li,Lx, tmpMem,tmpMem1,n,k,blockIdx.x); 11: cleartmpMem<<<(subColSize+1023)/1024, 1024>>>(Lp,Li,tmpMem,tmpMem1,n,k,blockIdx.x); 12: end function

新窗口打开|下载CSV

在dynamic核函数中,每个线程首先确定当前被分解的列,然后再分别并行调用三个核函数factorize、update和clearTmpMem,它们分别表示分解当前列,用分解好的当前列更新依赖这一列的子列,以及清空分解当前列所使用的非压缩的内存空间,它们的伪代码分别为：


伪代码3.
伪代码3.当前列的多线程分解

1: function factorize(Lp, Li, Lx, tmpMem, tmpMem1, d, n, k, col) 2: id=blockIdx.x*blockDim.x+threadIdx.x; 3: if id < Lp[k+1]-Lp[k]-1 then 4: tmpMem1[n*col+Li[Lp[k]+1+id]] = Lx[Lp[k]+1+id]; // L(i,k)*L(k,k) 5: Lx[Lp[k]+1+id] = cuCdivf( Lx[Lp[k]+1+id], d); //A为复数矩阵 6: Lx[Lp[k]+1+id ] /= d; //A为实数矩阵 7: tmpMem[n*col+Li[Lp[k]+1+id]] = Lx[Lp[k]+1+id]; // L(i,k) 8: end if 9: end function

新窗口打开|下载CSV


伪代码4.
伪代码4.更新当前列的子列

1: function update(Lp, Li, Lx, tmpMem, tmpMem1, n, k, col) 2: j = Li[Lp[k]+1+blockIdx.x]; 3: s = tmpMem1[n*col+j]; 4: subColSize = Lp[j+1]-Lp[j]; 5: offset=0; 6: while offset<subColSize do 7: if threadIdx.x+offset < subColSize then 8: //A为复数矩阵 9: x = cuCmulf(s,tmpMem[n*col + Li[Lp[j] +offset+threadIdx.x]]); 10: atomicAdd(&(Lx[Lp[j] + offset + threadIdx.x].x), -x.x); 11: atomicAdd(&(Lx[Lp[j] + offset+threadIdx.x].y), -x.y); 12: //A为实数矩阵 13: x = s*tmpMem[n*col+Li[Lp[j] +offset+threadIdx.x]]);

14: atomicAdd(&(Lx[Lp[j]+offset+threadIdx.x]), -x); 15: end if 16: offset += blockDim.x; 17: end while 18: end function

新窗口打开|下载CSV


伪代码5.
伪代码5.清空当前列多线程分解所用内存

1: function cleartmpMem(Lp, Li, tmpMem, tmpMem1, n,k,col) 2: id=blockIdx.x*blockDim.x+threadIdx.x; 3: if id < Lp[k+1]-Lp[k]-1 then 4: tmpMem1[n*col+Li[Lp[k]+1+id]] = 0; 5: tmpMem[n*col+Li[Lp[k]+1+id]] = 0; 6: end if 7: end function

新窗口打开|下载CSV

本文使用了CUDA C的动态并行（dynamic parallel）技术^{[20, 22]}。它支持嵌套执行内核函数,即从内核中启动内核。动态并行的优势是等内核执行的时候再配置创建网格和线程块,这样就可以动态的利用GPU硬件调度器和加载平衡器,通过动态调整适应负载。并且在内核中启动内核可以减少一部分数据传输的开销。动态并行技术尤其适合嵌套调用和递归调用的内核函数^[22],但只支持Nvidia推出的计算能力大于3.5的GPU设备。

3 数值结果

算法实现基于C/C++和CUDA C,编译选项为-O3,其中GCC版本为4.8.5,CUDA的版本为11.1。测试平台包含2个20核的Intel Xeon Gold 6148 CPU和4个NVIDIA TITAN V GPU,CPU主频为2.4GHz,CPU端的内存为384GB,每张GPU卡的显存为12GB。操作系统为Red Hat Linux 4.8.5-16。

实验使用的测试集来自佛罗里达大学稀疏矩阵集^[23],它被广泛用于稀疏矩阵基准测试,评价稀疏矩阵相关算法的性能。用于对比本文求解器性能的UMFPACK-5.6.2是稀疏数学库SuiteSparse^[24]的一个子集,它同时支持复数和实数矩阵的数值分解和直接法求解。

用于性能对比的稀疏矩阵直接法求解器还有HSL的MA57、CUDA自带的cuSOLVER和加州大学Peng等开发的GLU。cuSPARSE只提供不完全LU分解,cuSOLVER的cusolverSp模块虽然实现了稀疏矩阵的LU分解、Cholesky分解和QR分解,但目前的版本还没有提供设备端的接口,因此无法通过GPU加速。GLU3.0在GPU上实现了稀疏矩阵的LU分解,并用于电路仿真,但只支持实数类型的稀疏矩阵。

利用CUDA实现的稀疏对称矩阵的LDL^T分解求解器在测试平台上分解和求解各阶段的运行时间见表1（其中数值分解在GPU上进行）;在CPU上采用UMFPACK、MA57和GPU上的LDL^T数值分解的时间见图5;采用UMFPACK、MA57、cuSOLVER和GPU上的LDL^T求解器求解各阶段的整体时间见图6;本文求解器相比UMFPACK的LDL^T数值分解的加速比和整个方程组求解时间的加速比见表2和图7。图表中的时间单位为毫秒（下同）。

Table 1
表1
表1基于本文的直接法求解、LDL^T分解和求解阶段的时间（ms）
Table 1Runtime (in ms) of LDLT decomposition and solving phases using our direct solver

matrix	n	nz	nnz	nnz/nz	symbolic	numeric	solve	total
windscreen	22692	752541	5545914	7.370	311.814	973.928	534.656	1820.398
crystk03	24696	887937	9221958	10.386	371.007	693.275	88.267	1152.549
bcsstk37	25503	583240	2996850	5.138	182.664	342.704	29.465	554.833
bcsstk35	30237	740200	3045171	4.114	178.499	354.06	31.053	563.612
t3dh	79171	2215638	45191167	20.396	3311.172	4136.49	440.249	7887.911
TEM152078	152078	3305720	57409931	17.367	4423.406	4893.649	556.43	9873.485
TEM181302	181302	4010156	70510354	17.583	5555.54	6092.029	689.041	12336.61
pwtk	217918	5926171	47124510	7.952	2570.829	2878.245	468.653	5917.727
BenElechi1	245874	6698185	52230259	7.798	2779.673	3193.183	176.464	6095.320

新窗口打开|下载CSV

Table 2
表2
表2UMFPACK的分解和求解各阶段的时间（ms）,以及本文求解器相对UMFPACK的加速比
Table 2Runtime (in ms) of LDLT decomposition and solving phases using UMFPACK solver, and the speedup of our solver compared with UMFPACK

matrix	symbolic	numeric	solve	T(umf)	Sp(ldlt)	Sp(total)
windscreen	603.154	13968.758	94.106	14666.018	14.342	8.056
crystk03	215.40	4951.943	34.575	5201.919	7.143	4.513
bcsstk37	54.54	1447.959	30.678	1533.177	4.224	2.763
bcsstk35	223.709	1661.172	31.031	1915.912	4.692	3.399
t3dh	7468.603	191216.956	443.984	199129.543	46.227	25.245
TEM152078	9288.08	200071.001	566.479	209925.56	40.884	21.262
TEM181302	11430.526	218608.984	288.069	230327.579	35.884	18.670
pwtk	1171.662	21133.883	211.081	22516.626	7.343	3.805
BenElechi1	1129.767	24923.273	211.145	26264.185	7.805	4.309

新窗口打开|下载CSV

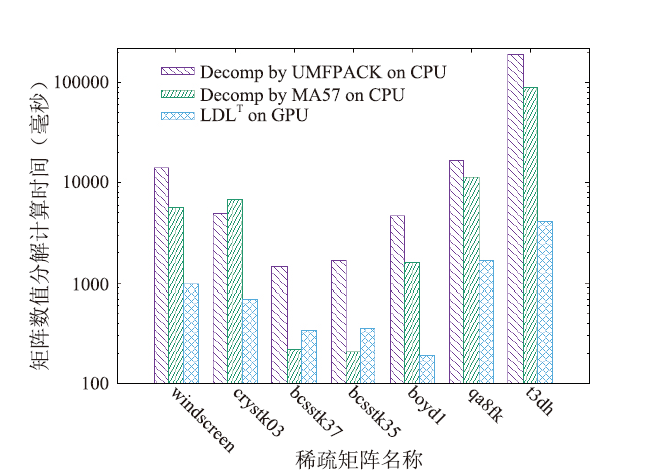
图5

新窗口打开|下载原图ZIP|生成PPT
图5不同软件数值分解的时间（毫秒）

Fig.5Runtime of LDLT (in ms)

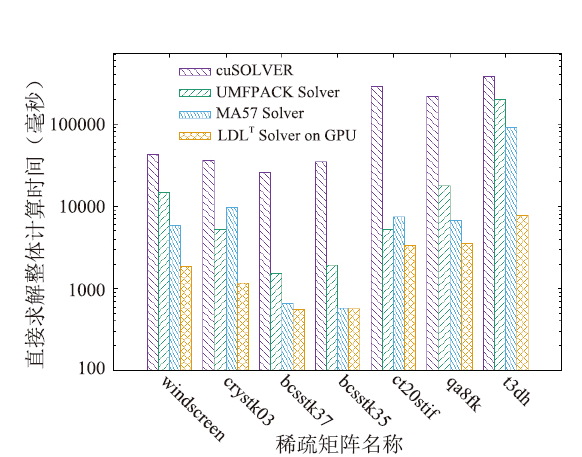
图6

新窗口打开|下载原图ZIP|生成PPT
图6不同求解器的整体求解时间（毫秒）

Fig.6Total runtime of different solvers (in ms)

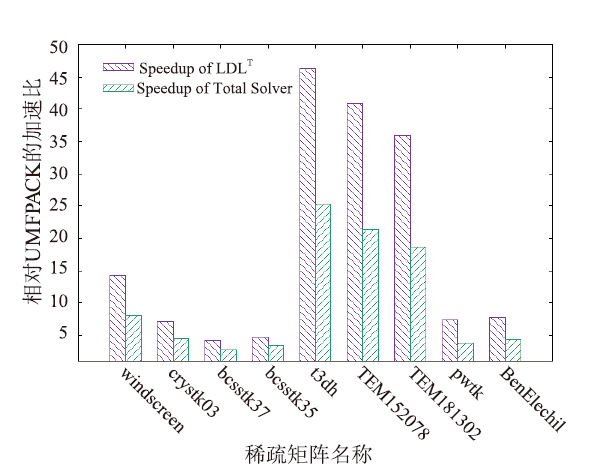
图7

新窗口打开|下载原图ZIP|生成PPT
图7数值分解和整体求解的加速比

Fig.7Speedup of LDLT and total solver



表中的稀疏对称矩阵以维数n排序的,考虑到并行度和内存限制,排除了1万阶以下和25万阶以上的矩阵集。其中matrix表示矩阵名称,n表示矩阵的维数,nz表示初始矩阵的非零元个数（只包含了下三角部分）,nnz表示本文求解器符号分解后的L矩阵的非零元个数。

nnz/nz表示fill-in的倍数。symbolic表示符号分解运行时间,numeric表示数值分解运行时间,solve表示三角求解运行时间,total表示本文求解器总的运行时间,为符号分解和数值分解以及三角求解运行时间之和,T(umf)表示UMFPACK总的运行时间,即符号分解和数值分解以及三角求解运行时间之和,Sp(ldlt)表示数值分解的加速比,Sp(total)表示总运行时间的加速比。

针对表1中列举的矩阵,从表2可以看出,三角求解的运行时间远少于数值分解的运行时间,因此表1中只对LDL^T分解进行GPU加速。从表1和表2还可以看出,非零元填充比越高（即nnz/nz越大）,LDL^T数值分解的性能提升越明显,因为更高的非零元填充比可以更好地利用右视分解算法的三层循环并行性,而且计算访存比更高。

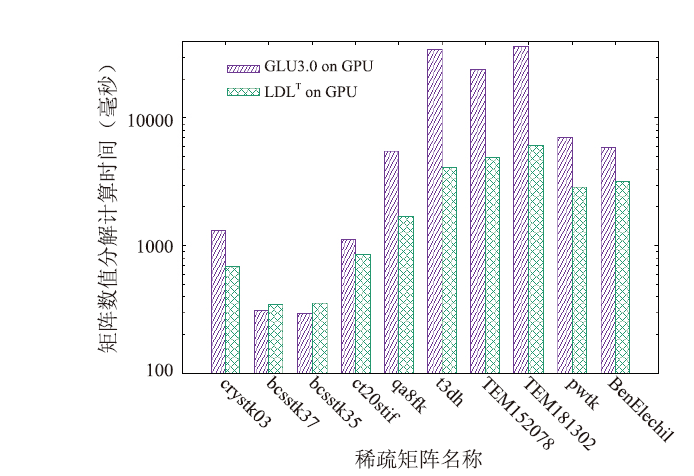
从图5、图6可以看出,GPU上的LDL^T求解器性能优于UMFPACK、MA57和cuSolver求解器,虽然对少数矩阵（如bcsstk37、bcsstk35）,LDL^T数值分解部分与MA57相比没有加速,但求解总时间是最快的,因为其符号分解策略更佳。从图7和表2可以看出,和UMFPACK相比,LDL^T求解器数值分解阶段最高可加速46.2倍,分解和求解总时间最高加速25.2倍。我们将LDL^T与GLU 3.0的LU分解进行对比, GPU上的数值分解部分运行时间见图8。从图中可以看出,对于大多数算例,LDL^T比GLU快2-8倍,仅对bcsstk37、bcsstk35两个矩阵慢了10%。LDL^T比GLU 3.0快的原因是采用了层次划分和动态并行技术,且LDL^T针对的是对称矩阵,GLU3.0针对普通稀疏矩阵（对称矩阵还要补齐另一半非零元数据）。但GLU在CPU端的符号分解部分的性能比2.2节的策略慢10倍以上,因此LDL^T整体矩阵分解时间更快。

图8

新窗口打开|下载原图ZIP|生成PPT
图8LDL^T和GLU3.0在GPU上运行时间（毫秒）

Fig.8Runtime of LDLT and GLU 3.0 on GPU (in ms)

4 结论与展望

本文设计并实现了一种基于GPU的稀疏对称矩阵的LDL^T求解器,该求解器采用Cholesky符号分解和右视算法的LDL^T数值分解,并且该数值分解可以对右视分解算法的三层循环进行完全线程级并行计算,并采用依赖图的层次划分策略和CUDA的动态并行技术,这非常有利于LDL^T数值分解在GPU上的加速。实验结果表明,针对稀疏对称矩阵测试集,GPU上实现的LDL^T数值分解计算速度相对于CPU上的UMFPACK最高加速46.2倍,直接求解整体最高加速25.2倍。而且矩阵分解速度也快于加州大学Peng等开发的基于GPU的稀疏矩阵LU分解数值软件包GLU3.0。

LDL^T分解在GPU上的实现策略可为其它高性能GPU异构平台上开展稀疏方程组的高性能数值求解器的设计实现提供借鉴,并有望应用于复杂电路仿真与设计、结构力学分析等领域的有限元离散线性方程组在GPU上快速高效求解。

利益冲突声明

所有作者声明不存在利益冲突关系。

参考文献 View Option 原文顺序
文献年度倒序
文中引用次数倒序
被引期刊影响因子

[1] NVIDIA Corporation, CUBLAS library
[CP/OL]. http://developer.nvidia.com/cublas.
URL [本文引用: 1]

[2] Rutherford Appleton Laboratory, the HSL mathematical software library
[CP/OL]. http://www.hsl.rl.ac.uk.
URL [本文引用: 1]

[3] NVIDIA Corporation, CUSPARSE library
[CP/OL]. http://developer.nvidia.com/cusparse.
URL [本文引用: 1]

[4] Peng S, Tan S X. GLU3.0: Fast GPU-based Parallel Sparse LU Factorization for Circuit Simulation
[J]. IEEE Design & Test, 2020, 37(3):78-90.
[本文引用: 1]

[5] Kirk D B, Hwu W W. Programming Massively Parallel Processors: A Hands-on Approach
[M]. 2ed, Elsevier Inc., 2013: 1-40.
[本文引用: 1]

[6] Davis T A. Direct Methods for Sparse Linear Systems
[M]. SIAM, 2006: 38-59.
[本文引用: 3]

[7] Gilbert J R, Peierls T. Sparse partial pivoting in time proportional to arithmetic operations
[J]. SIAM journal on scientific and statistical computing, 1988, 9(5):862-874.
DOI:10.1137/0909058URL [本文引用: 1]

[8] Parter S. The use of linear graphs in Gauss elimination
[J]. SIAM review, 1961, 3(2):119-130.
DOI:10.1137/1003021URL [本文引用: 1]

[9] Liu J W. A compact row storage scheme for Cholesky factors using elimination trees
[J]. ACM Transactions on Mathematical Software (TOMS), 1986, 12(2):127-148.
DOI:10.1145/6497.6499URL [本文引用: 1]

[10] Rose D J, Tarjan R E, Lueker G S. Algorithmic aspects of vertex elimination on graphs
[J]. SIAM Journal on computing, 1976, 5(2):266-283.
DOI:10.1137/0205021URL [本文引用: 1]

[11] Schreiber R. A new implementation of sparse Gaussian elimination
[J]. ACM Trans. Math. Softw., 1982, 8(3):256-276.
DOI:10.1145/356004.356006URL [本文引用: 1]

[12] Amestoy R P, Davis T A, Duff I S. Algorithm 837: AMD, an Approximate Minimum Degree Ordering Algorithm
[J]. ACM Trans. Math. Softw., 2004, 30(3):381-388.
DOI:10.1145/1024074.1024081URL [本文引用: 1]

[13] METIS-Serial Graph Partitioing and Fill-reducing Matrix Ordering
[CP/OL]. http://glaros.dtc.umn.edu/gkhome/METIS.
URL [本文引用: 1]

[14] Lee W, Achar R, Nakhla M S. Dynamic GPU Parallel Sparse LU Factorization for Fast Circuit Simulation
[J]. IEEE Transactions on Very Large Scale Integration, 26(11):2518-2529, 2018.
DOI:10.1109/TVLSI.2018.2858014URL [本文引用: 2]

[15] Li X S, Demmel J. A Scalable Sparse Direct Solver Using Static Pivoting
[C]. Proceedings of the Ninth SIAM Conference on Parallel Processing for Scientific Computing, 22-24, 1999.
[本文引用: 1]

[16] Arioli M, Demmel J W, Duff I S. Solving sparse linear systems with sparse backward error
[J]. SIAM Journal on Matrix Analysis and Applications, 1989, 10(2):165-190.
DOI:10.1137/0610013URL [本文引用: 1]

[17] He K, Tan S, Wang H, Shi G. GPU-accelerated parallel Sparse LU factorization method for fast circuit analysis
[J]. IEEE Transactions on Very Large Scale Integration (VLSI) Systems, 2015, 24(3):1140-1150.
DOI:10.1109/TVLSI.2015.2421287URL [本文引用: 1]

[18] Sanders J, Kandrot E. CUDA by Example: an Introduction to General-Purpose GPU Program- ming
[M]. Addison-Wesley Professional, 2011: 163-184.
[本文引用: 1]

[19] 扶月月, 王武, 王乔. 基于FMM-PM方法的宇宙N体模拟在GPU上的实现和优化
[J]. 数据与计算发展前沿, 2020, 2(2):155-164.
[本文引用: 1]

[20] 张留莹, 王鹏飞, 张峰, 刘海龙, 林鹏飞, 王涛, 韦俊林, 田少博, 姜金荣, 迟学斌. 海洋环流模式LICOM的GPU实现与优化
[J]. 数据与计算发展前沿, 2020, 2(4):92-104.
[本文引用: 2]

[21] 党冠麟, 刘世伟, 胡晓东, 张鉴, 李新亮. 基于CPU/GPU异构系统架构的高超声速湍流直接数值模拟研究
[J]. 数据与计算发展前沿, 2020, 2(1):105-116.
[本文引用: 1]

[22] Cheng J, Grossman M, McKercher T. Professional CUDA C Programming
[M]. John Wiley, 2014: 122-131.
[本文引用: 2]

[23] Davis T. the University of Florida Sparse Matrix Collection
[CP/OL]. http://sparse.tamu.edu.
URL [本文引用: 1]

[24] SuiteSparse[CP/OL]. https://people.engr.tamu.edu/davis/suitesparse.html.
URL [本文引用: 1]