Xiao-Wei Qiang, Hai-Long Dong, Kai-Xin Xiong, Wenbing Zhang^,∗, Zhi-Jie Tan^,∗Department of Physics and Key Laboratory of Artificial Micro & Nano-Structures of Ministry of Education, School of Physics and Technology, Wuhan University, Wuhan 430072, China

First author contact: ∗Authors to whom any correspondence should be addressed.
Received:2021-03-31Revised:2021-04-13Accepted:2021-04-15Online:2021-05-20


Abstract
Structural elasticity of double-strand DNAs is very important for their biological functions such as DNA-ligand binding and DNA-protein recognition. By all-atom molecular dynamics simulations, we investigated the bending elasticity of DNA with three typical sequences including poly(A)-poly(T) (AA-TT), poly(AT)-poly(TA) (AT-TA), and a generic sequence (GENE). Our calculations indicate that, AA-TT has an apparently larger bending persistence length (P ∼63 nm) than GENE (P ∼49 nm) and AT-TA (P ∼48 nm) while the persistence length of AT-TA is only very slightly smaller than that of GENE, which agrees well with those from existing works. Moreover, through extensive electrostatic calculations, we found that the sequence-dependent bending elasticity is attributed to the sequence-dependent electrostatic bending energy for AA-TT, AT-TA and GENE, which is coupled to their backbone structures. Particularly, the apparently stronger bending stiffness of AA-TT is attributed to its narrower minor groove. Interestingly, for the three DNAs, we predicted the non-electrostatic persistence length of ∼17 nm, thus electrostatic interaction makes the major contribution to DNA bending elasticity. The mechanism of electrostatic energy dominating sequence effect in DNA bending elasticity is furtherly illustrated through the electrostatic calculations for a grooved coarse-grained DNA model where minor groove width and other microscopic structural parameters can be artificially adjusted.
Keywords： DNA elasticity;molecular dynamic simulation;persistence length;electrostatic interaction


PDF (1870KB)MetadataMetricsRelated articlesExportEndNote|Ris|BibtexFavorite
Cite this article
Xiao-Wei Qiang, Hai-Long Dong, Kai-Xin Xiong, Wenbing Zhang, Zhi-Jie Tan. Understanding sequence effect in DNA bending elasticity by molecular dynamic simulations. Communications in Theoretical Physics, 2021, 73(7): 075601- doi:10.1088/1572-9494/abf825

1. Introduction

The mechanical elasticity of DNAs plays key roles in various biological processes, such as ligand-DNA binding, protein-DNA recognition, and DNA packaging [1–3]. The elasticities of genomic DNAs in different dimensions have been extensively characterized by single molecule techniques and theories [4–15]. For example, a DNA generally has a bending persistence length of ∼50 nm, a stretch modulus of ∼1000–1500 pN, a torsional persistence length of ∼90±20 nm [9, 16–18], and it would become overwound when stretched [17, 19]. Such elasticity of DNAs can also be influenced by salt conditions due to the polyanionic nature of DNAs [20–24].

Importantly, recent experiments indicate that, base composition of DNAs could significantly influence their structure dynamics and the sequence-dependent conformational variations play a significant role in recognition processes with proteins [25–29]. For example, proteins generally recognize DNA sequences in two ways, including the direct readout mechanism where recognition is mediated by direct contacts between amino acids and bases, and the indirect readout mechanism where proteins recognize DNA sequence through their conformational properties. Thus, it is very important to characterize the sequence-dependence elasticity of DNAs [30].

In recent years, much attention has been focused on the sequence-dependent properties of DNAs [18, 31–36]. Shaban and Peters found that sequence compositions can greatly influence the bending stability of DNAs and the ability to form kinks, which can induce base-pair slide to form non-native contacts during bending [2, 37]. Ortiz and Pablo showed that the kink more likely happened in longer repeated sequence segments through a coarse-grained DNA structural model [38]. Scipioni et al studied the sequence-dependent DNA curvature and found that AT-rich sequences are more flexible than CG-rich sequence [39]. Olson et al performed the statistical analysis on x-ray crystal structures and found that DNAs of different sequences have distinct flexibilities, where the AA-TT step belongs to the rigid class while GG-CC and GC-GC dinucleotide are even more flexible [40]. Moreover, Srivastava et al reported that DNAs of poly(A)-poly(T) sequence condense in the presence of divalent ions but no condensation was observed for DNAs of poly(AT)-poly(TA) and generic sequences [41].

Furthermore, many different methods include experiments and theories were employed to determine the bending persistence lengths for DNAs of different sequences [42–45]. Geggier and Vologodskii quantified the persistence lengths of DNAs of 10 distinct dinucleotide steps through cyclization of short DNA fragments and found the persistence lengths vary from ∼43 to ∼55 nm for different dinucleotide sequences [43]. Recently, Chuang et al have shown that the DNA persistence length increases by almost 20% as the percent GC content increases for long genomic DNAs [46]. A recent coarse-grained simulation work for extensive distinct sequences showed that poly(A)-poly(T) has a high outlier persistence length of ∼73 nm and exhibits exceptionally straight and stiff, while poly(AT) has a lowest persistence length of ∼47 nm and appears tightly coiled and exceptionally soft [42]. However, until now, there is still lack of an energetic understanding on sequence effect in bending elasticity of DNAs.

In order to understand the sequence effect in bending elasticity of DNAs, we employed all-atom molecular dynamic simulations to quantify the persistence lengths for DNAs of typical sequences (namely, poly(A)-poly(T), poly(AT)-poly(TA) and generic one), and made the comparisons with the available experiments and simulations. Furthermore, we explored how sequences affect the DNA bending elasticity through calculating the bending energy and the electrostatic bending energy. Additionally, the role of electrostatic bending energy is furtherly illustrated through the electrostatic calculations for a grooved coarse-grained DNA model where minor groove width and other microscopic parameters can be artificially adjusted.

2. Methods

2.1. All-atom MD simulations

In this work, as shown in table 1, three 20-bp DNAs with two C-G base pairs at each end and central 16-bp poly(AA)-poly(TT), poly(AT)-poly(TA) and generic sequences were used in our all-atom MD simulations [14, 15, 47–50], and the three DNAs are named as AA-TT, AT-TA, and GENE respectively. The three sequences were selected according to previous experiments and simulations, corresponding to the upper value, the bottom value and generic one in persistence length for DNAs with different dinucleotides [41–43, 51, 52]. Here, the three DNAs are all capped by two C-G base pairs at each end to improve the end stability of the DNAs since C-G base pairs have higher thermal stability than A-T base pairs [53, 54]. The initial structures of the three DNAs were built in B-form with the Nucleic Acid Builder of AMBER [55]; see figure 1. The DNAs were immersed in rectangular boxes containing explicit water and ions. The counterions of Na⁺ and the salt of 150 mM NaCl [56] were added with the ion model from Joung and Cheatham [57] to ensure that our simulated systems are fully neutralized and the three DNAs are rather stable at room temperature [53, 58, 59]. The isothermic-isobaric ensemble was used in all MD simulations during the energy minimization, thermalized and equilibrated process. Afterwards, all of our MD simulations were performed for 500 ns at constant temperature (298 K) and constant pressure (1 atm), with the Particle Mesh Ewald method for long-range interactions and the periodic boundary conditions [60]. In each simulation, we used 2 fs as an integration step. The Gromacs 4.6 software package was used in the three simulations and the newly refined AMBER ff99bsc1 force field and TIP3P water model were chosen. As shown in figure 1(b), the systems quickly reach their equilibriums after ∼100 ns. The MD trajectories after 200 ns were used for our analyses. Please see the detailed information about our MD simulations in our previous works [52, 54, 61–63].


Table 1.
Table 1.The DNA sequences used in the work.

Name	Sequencesa	Cell size (nm3)b	Tmc
AA-TT	5′-CGAAAAAAAAAAAAAAAAGC-3′	12×12×10	87.2 °C
	GCTTTTTTTTTTTTTTTTCG
AT-TA	5′-CGATATATATATATATATGC-3′	12×12×10	79.9 °C
	GCTATATATATATATATACG
GENE	5′-CGACTCTACGGCATCTGCGC-3′	12×12×10	104.2 °C
	GCTGAGATGCCGTAGACGCG

^aThe sequences were selected according to the existing experiments [41, 51] and simulations [42].
^bThe cell sizes were used in our molecular dynamic simulations.
^cThe melting temperatures are calculated at 0.15 M NaCl through the nearest-neighbor model with the measured thermodynamic parameters and the salt extension from [53, 59, 73].

New window|CSV

Figure 1.

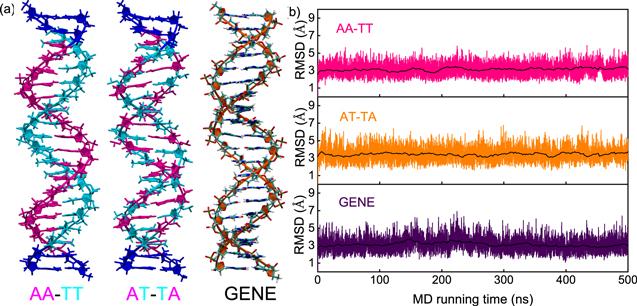New window|Download| PPT slide
Figure 1.(a) The initial three-dimensional DNA structures with typical sequences of poly(A)-poly(T) duplex (AA-TT), poly(AT)-poly(TA) duplex (AT-TA) and generic one (GENE) for our all-atom molecular dynamics simulations, respectively. The three sequences were chosen according to the recent experiments [41, 51] and coarse-grained simulations [42]. (b) The root mean square deviations (RMSD) versus MD running time (500 ns) for the central 14-bp segment of the DNAs with three typical sequences. The black lines represent the RMSD values averaged over every 2 ns. The DNAs are in 150 mM NaCl solutions.

2.2. Helical parameters and persistence length

To avoid the end effect of short duplexes, the three base pairs at each end were removed for all the analyses of the MD trajectories, and consequently the two C-G base pairs at each end have no influence on our calculations and analyses [54]. As shown in figure 1(b), all the MD simulations are nearly converged after ∼100 ns. In this work, helical and geometrical parameters were all obtained using the program Curves+[61, 62, 64]. Helical radius, as one of important helical parameters, is related to the radius of phosphate groups, helical rise and helical twist, and was calculated by [62, 65, 66]:(1)$\begin{eqnarray}{\rm{Helical}}\,{\rm{radius}}=\left\langle \sqrt{\left({d}_{pp}^{2}-{\left({\rm{helical}}{\rm{rise}}\right)}^{2}\right)/2\left(1-\,\cos \left({\rm{helical}}\,{\rm{twist}}\right)\right)}\right\rangle ,\end{eqnarray}$where ⟨…⟩ is an ensemble average over MD simulation time and d_pp is the distance between two adjacent phosphate groups.

In this work, to quantify persistence length P of DNAs, we calculated the probability distribution p(θ, l) based on the MD trajectories, where θ is the bending angle between average vectors of consecutive 10-bp helical repeats and l is the averaged contour length of the 10-bp helical repeats [52, 67]. Afterwards, the persistence length P for a DNA can be given through fitting p(θ, l) to [52, 67](2)$\begin{eqnarray}-\,\mathrm{ln}\left(\displaystyle \frac{p\left(\theta ,l\right)}{\sin \left(\theta \right)}\right)=\displaystyle \frac{P}{2l}{\theta }^{2}-\,\mathrm{ln}\left(\sqrt{\displaystyle \frac{2\pi P}{l}}\right).\end{eqnarray}$

2.3. Electrostatic calculations

To reveal the underlying mechanism for the sequence effect in DNA bending elasticity, we calculated the electrostatic energy E_el for the conformations at different bending angle using the software of APBS, a well-established Poisson–Boltzmann solver for biomolecules [56, 68]. In the calculations, the radii of ions (Na⁺ and Cl^-) were set as 2 Å, and the dielectric constants of the DNAs and solvent were taken as 2 and 78, respectively. For the conformations taken from the MD simulations, all the atom charges including H atoms were included in the electrostatic calculations according to the atom charge distributions from AMBER ff99bsc1 force field. Since hydrogen bond is essentially an electrostatic interaction between positively and negatively charged atoms at a close separation [69, 70], in principle, hydrogen bond opening/closing can be captured in the electrostatic calculations. Therefore, the electrostatic bending energy ΔE_el(θ) is given by ΔE_el(θ)= E_el(θ)− E_el(θ=0)[71].

2.4. A grooved coarse-grained model for DNA

To examine the role of electrostatic bending energy in DNA bending elasticity, we also employed a grooved coarse-grained model for DNA structure where minor groove width and other helical parameters can be artificially adjusted; see appendix and [58, 71–73] for details. The grooved model can be used to minimally mimic a DNA structure [58, 59, 72, 73], and can be easily used to produce bent conformations [71]. In present work, the central six base pairs of a coarse-grained DNA are bent uniformly along the helical axis, and the two end helix parts keep straight (unbent) and are rotated according to the central bent axis, keeping the helical axis continuous; see [71] for details. Corresponding to the 14 central base pairs in all-atom MD simulations, we also calculated the electrostatic bending energy for 14-bp coarse-grained DNAs, with the software of APBS [68].

3. Results and discussion

In the following, firstly, we calculated the bending persistence lengths for AA-TT, AT-TA and GENE sequences based on the MD trajectories and made the comparisons with the available experimental and simulation data. Afterwards, we calculated the bending energy and electrostatic bending energy to explore the underlying energetic mechanism. Moreover, we calculated the non-electrostatic persistence length of DNAs. Finally, we employed a minimal coarse-grained model with artificial adjustment on helical parameters to furtherly illustrate the energetic mechanism.

3.1. Persistence length of AA-TT is apparently larger than those of AT-TA and GENE sequences

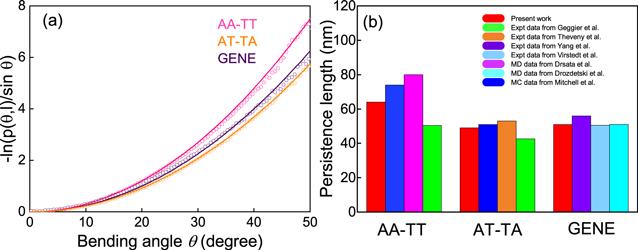
As shown in figure 2(a), the bending angle distribution –ln(p(θ, l)/sin(θ)) of the AA-TT sequence is apparently higher than that of GENE and AT-TA sequences, while that of AT-TA is only very slightly lower than that of GENE, suggesting AA-TT is apparently stiffer in bending than GENE and AT-TA, and AT-TA is only very slightly more bendable than GENE. The bending persistence length P can be calculated by fitting the data of –ln(p(θ, l)/sin(θ)) to equation (2). As shown in figure 2(b), our calculated P is ∼63 nm for AA-TT, which is distinctly larger than that of ∼49 nm for GENE and that of ∼48 nm for AT-TA; see also table 2. Our calculations of P for AA-TT, GENE and AT-TA are in good accordance with the recent experiments and simulations except for small deviations for AA-TT, as shown in figure 2(b). For AA-TT, our value of P=63 nm is smaller than those from an all-atom MD simulation (P∼80 nm) with the parmbsc0 AMBER force field [29] and a MC simulation with coarse-grained force field (P∼74 nm) [42], while is larger than the experimental data (P∼50 nm) from cyclization method [43]. Such deviation from the existing simulations may come from the use of the newly refined parmbsc1 force field and the specific salt condition of 150 mM NaCl in the present work. Therefore, AA-TT is apparently stiffer in bending than those of GENE and AT-TA, and AT-TA has similar while very slightly weaker bending stiffness than GENE.

Figure 2.

New window|Download| PPT slide
Figure 2.(a) The bending angle distributions p(θ, l) versus bending angle θ over 10 base steps for the central 14-bp segments of the DNAs with three sequences of AA-TT, AT-TA and GENE. The bending persistence lengths can be estimated by fitting the shown curves to equation (2). (b) The calculated bending persistence lengths from panel (a) compared with those values from [29, 42, 43, 67].



Table 2.
Table 2.The helical parameters and persistence length for DNAs with different sequences^a.

	AA-TT	AT-TA	GENE
Helical rise (Å)	3.34±0.08	3.29±0.08	3.33±0.09
Helical twist (degree)	34.32±0.83	34.94±0.90	34.62±1.10
Helical radius (Å)	10.17±0.17	10.07±0.16	10.14±0.24
Major groove width (Å)	13.36±0.84	12.34±0.72	11.92±0.64
Minor groove width (Å)	4.91±0.45	5.36±0.46	5.64±0.45
Persistence length (nm)b	63	48	49

^aAll the microscopic parameters were calculated with the software Curves+[61, 62, 64].
^bThe persistence lengths were calculated according to equation (2).

New window|CSV

3.2. Electrostatic energy makes the major contribution to sequence-dependent bending energy

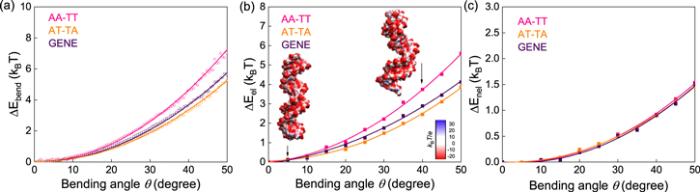
To explore the underlying mechanism why AA-TT is apparently stiffer than GENE and AT-TA, we calculated the bending energy ΔE_bend(θ) over the central 14 base pairs according to the bending angle distributions p(θ, l) and the worm-like chain model [74]:(3)$\begin{eqnarray}{\rm{\Delta }}{E}_{{\rm{bend}}}\,\left(\theta ,l\right)=-{k}_{{\rm{B}}}T\,\mathrm{ln}\left(\displaystyle \frac{p\left(\theta ,l\right)}{\sin \,\theta }\right).\end{eqnarray}$As shown in figure 3(a), the bending energy ΔE_bend(θ) increases quadratically with the bending angle θ for the three sequences, and for the sequence AA-TT, the bending energy ΔE_bend(θ) increases more rapidly than those of GENE and AT-TA. For example, ΔE_bend(θ) of AA-TT is ∼1 k_BT higher than that of GENE and ΔE_bend(θ) of AT-TA is very slightly smaller than that of GENE at bending angle θ∼40°. This is in good correspondence with the persistence lengths discussed above for AA-TT, GENE and AT-TA.

Figure 3.

New window|Download| PPT slide
Figure 3.(a) The bending energy ΔE_bend(θ) versus bending angle θ over the central 14 base pairs, for AA-TT, AT-TA and GENE. (b) The electrostatic bending energy ΔE_el(θ) versus bending angle θ over the central 14 base pairs for AA-TT, AT-TA and GENE. Here, ΔE_el(θ) was calculated directly with the APBS [68]. (c) The non-electrostatic bending energy ΔE_nel(θ) versus bending angle θ over the central 14 base pairs for AA-TT, AT-TA and GENE. The electrostatic energies and the surface potentials in panels (b), (c) were calculated with the APBS [68].


Furthermore, we split bending energy ΔE_bend(θ) into electrostatic contribution ΔE_el(θ) and non-electrostatic one ΔE_nel(θ). Here, electrostatic bending energy ΔE_el(θ) were directly calculated using the software of APBS, a well-established Poisson–Bolztmann solver for calculating electrostatic energy of a biomolecule [68]; see Methods. Specifically, we randomly selected enough (∼100) conformations for each DNA at each bending angle and calculated their electrostatic energies E_el(θ) with the APBS, ensuring the convergence of E_el(θ). As shown in figure 3(b), the calculated ΔE_el(θ) increases quadratically with the increase of bending angle θ and ΔE_el(θ) of AA-TT increases more rapidly than those of GENE and AT-TA, in a very similar trend to the bending energy ΔE_bend(θ). Subsequently, we calculated the non-electrostatic bending energy ΔE_nel(θ) by ΔE_nel(θ)=ΔE_bend(θ)−ΔE_el(θ) for AA-TT, AT-TA, and GENE. As shown in figure 3(c), it is surprising that the relationships of ΔE_nel(θ) with bending angle θ emerge together and are indistinguishable for the three sequences, suggesting that the difference in bending energy is attributed to the difference in electrostatic bending energy for the three sequences. Thus, the apparently larger bending stiffness (persistence length) of AA-TT than those of AT-TA and GENE is attributed to the visibly higher electrostatic bending energy.

Here, it is also interesting to calculate the persistence length P₀ of ‘neutral' DNAs based on the non-electrostatic bending energy ΔE_nel(θ) and electrostatic persistence length P_el based on electrostatic bending energy ΔE_el(θ), through ${\rm{\Delta }}{E}_{{\rm{bend}}}\left(\theta ,l\right)=\tfrac{1}{2}\,{k}_{B}T\tfrac{P}{l}{\theta }^{2}$ [52, 67]. We obtained that P₀=∼17 nm for the three sequences, and P_el=∼46 nm, ∼31 nm and ∼32 nm for AA-TT, AT-TA, and GENE, respectively. Our calculated value of P₀∼17 nm is between that from the counterion condensation-based modeling (P₀∼7 nm) [75] and that from the MD simulations through adding protons to fully neutralize negatively charged phosphate groups (P₀∼30 nm) [75, 76]. We note that our predicted P₀ can be a reasonable value since our simulations involved the newly refined parmbsc1 force field and no artificial effect on DNA structures and the electrostatic calculations with the APBS were explicitly performed for extensive conformations from the MD simulations. In contrast, the treatment of adding protons to neutralize surfacial phosphate groups by Savelyev et al may naturally underestimate the electrostatic contribution to bending stiffness since the DNA interior electrostatic interactions were still reserved [73]. Therefore, for the DNA sequences studied here, our calculations indicate that the electrostatic interaction makes the major contribution to DNA bending stiffness.

3.3. Narrower minor groove width visibly increases electrostatic bending energy of AA-TT

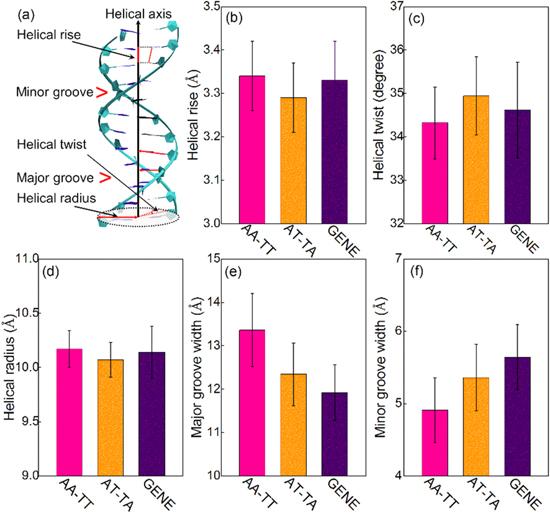
Since AA-TT is exceptionally stiffer than GENE and AT-TA and electrostatic interaction makes the major contribution to the sequence effect, we will emphasize exploring why the electrostatic bending energy is exceptionally high for AA-TT in the following. First, we calculated all helical (structural) parameters for the three DNAs with Curves+[64]. As shown in figure 4 and table 2, almost all parameters of AA-TT are close to those of GENE, including helical rise, helical radius, and helical twist, except for the minor and major groove widths. AA-TT has an apparently narrower minor groove while a wider major groove, compared with GENE and AT-TA. Thus, the apparently narrower minor groove should be the reason that AA-TT has exceptionally higher electrostatic bending energy especially than GENE.

Figure 4.

New window|Download| PPT slide
Figure 4.(a) An illustration for helical rise, helical twist, helical radius, major groove width and minor groove width for a DNA. The helical parameters for the central 14-bp segments of AA-TT, AT-TA and GENE including helical rise (b), helical twist (c), helical radius (d), major groove width (e), minor groove width (f). The error bars are the standard deviations to the respective mean values.


To explore the role of minor groove width in higher electrostatic bending energy for AA-TT, we employed a grooved coarse-grained DNA model where minor groove width (and other helical parameters) can be artificially adjusted; see Method and appendix for the details about the model [71]. First, we calculated the electrostatic energy for straight DNA models with different minor groove widths (i.e. bending angle =0), with the APBS [68]. As shown in figure 5(b), the electrostatic energy of DNA models increases visibly with the decrease of the minor groove width, due to the increased local charge density of DNA backbone. Afterwards, the central six base pairs of the DNA models with different minor groove widths are bent uniformly along the helical axis according to [71], and we calculated the electrostatic bending energy at different bending angle θ with the APBS [68]. As shown in figure 5(c), with the increase of bending angle θ, the electrostatic bending energy increases quadratically, which is in a similar trend with ΔE_el(θ) from our MD simulations. Furthermore, for a DNA model with narrower minor groove, ΔE_el(θ) increases with θ in a more rapid trend than that for a DNA with wider minor groove, suggesting that narrower minor groove causes a higher bending stiffness for a DNA. Thus, the calculations with the groove coarse-grained DNA model clearly illustrate that the exceptional bending stiffness of AA-TT is attributed to its narrower minor groove.

Figure 5.

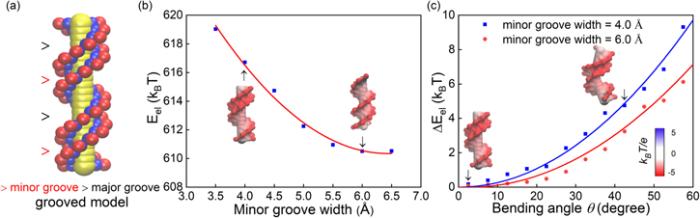New window|Download| PPT slide
Figure 5.(a) A grooved coarse-grained model for DNA structure [71, 72], where every base pair is composed of two phosphate spheres (in red), two sugar spheres (in blue) and one big base sphere (in yellow); see details in the appendix. (b) The electrostatic energy for straight 14-bp DNAs (bending angle θ=0) with different minor groove widths from the grooved DNA model. (c) The electrostatic bending energy ΔE_el(θ) for a 14-bp DNA versus bending angle θ over central 6 base pairs. The electrostatic energies and the surface potentials in panels (b), (c) were calculated with the APBS [68].


We also notice that AT-TA has a slightly narrower minor groove while very slightly electrostatic bending energy than GENE. This is because all the helical parameters between AT-TA and GENE almost differ slightly from each other, and the effects of the helical parameters on electrostatic bending energy can compensate each other. Specifically, as shown in figure 4 and table 2, helical rise (AT-TA)< helical rise (GENE), helical twist (AT-TA)> helical twist (GENE), helical radius (AT-TA)< helical radius (GENE), and major groove width (AT-TA)> major groove width (GENE). Table 3 shows that the different helical twist, helical radius and major groove width of AT-TA from GENE can decrease the electrostatic bending energy, which can certainly compensate (even over compensate) the increased the electrostatic bending energy by slightly narrower minor groove.


Table 3.
Table 3.Effects of helical parameters on electrostatic energy for the grooved DNA model^a.

	Helical rise	Helical twist	Helical radius	Minor groove width
	3.2→3.4 Å	33.0→35.0°	10.0→10.2Å	4.0→6.0 Å
Eel(θ=0°) (kBT)	614 ↓	610 ↓	611 ↓	617 ↓
	609	609	610	610
△Eel(θ=40°) (kBT)	3.7 ↓	3.4 ↓	1.9 ↑	4.6 ↓
	0.8	1.3	4.0	3.2

^aThe bending angle θ is over 14-bp DNA, and the positive and negative effects by the changes of helical parameters are marked with ‘↑'and ‘↓', respectively.

New window|CSV

Therefore, through the extensive electrostatic calculations for the structures from our MD simulations and the groove DNA models with adjustable helical parameters including minor groove width, we found that the sequence effect in bending stiffness of AA-TT, GENE and AT-TA is attributed to the different electrostatic bending energy, which is coupled to the backbone structures of AA-TT, GENE and AT-TA. Particularly, the exceptional bending stiffness of AA-TT is attributed to its narrow minor groove.

4. Conclusions

In this work, we employed all-atom MD simulations to quantify the bending persistence lengths for the DNAs with AA-TT, GENE and AT-TA sequences. Our calculations indicate that AA-TT has an exceptionally larger bending persistence length than AT-TA and GENE while AT-TA is only slightly smaller than that of GENE, which is in good agreement with the existing works. Our calculations on bending energy and electrostatic bending energy show that the sequence-dependent bending stiffness for the three typical sequences is attributed to the sequence-dependent electrostatic bending energy, which is coupled to their backbone structures. Particularly, the apparently stronger bending stiffness of AA-TT is attributed to its obviously narrower minor groove. Interestingly, our calculations predicted the non-electrostatic persistence length of ∼17 nm and consequently the electrostatic interaction makes the major contribution to the persistence length for the three typical sequences. Certainly, the universality of our conclusions is still required to be examined furtherly against more dinucleotide sequences and more generic sequences with different C-G contents. Nevertheless, our findings and analyses for the three typical sequences can be very important in understanding sequence effect in DNA bending elasticity and the ligand/protein recognitions with AT-rich DNAs.

Acknowledgments

We are grateful to Professors Xinghua Zhang (Wuhan University), Xiangyun Qiu (George Washington University), and Shi-Jie Chen (University of Missouri) for helpful communications. This work was supported by grants from the National Science Foundation of China (Grant Nos. 11774272, and 12075171). Parts of the numerical calculations in this work are performed on the super computing system in the Super Computing Center of Wuhan University.

Reference View Option By original order
By published year
By cited within times
By Impact factor

[1]Richmond T J Davey C A 2003 Nature 423 145
DOI:10.1038/nature01595 [Cited within: 1]

[2]Peters J P Maher L J III 2010 Q. Rev. Biophys. 43 23
DOI:10.1017/S0033583510000077 [Cited within: 1]

[3]Raniolo S Limongelli V 2020 Nat. Protocols 15 2837
DOI:10.1038/s41596-020-0342-4 [Cited within: 1]

[4]Zhang X H Chen H Fu H Doyle P S Yan J 2012 Proc. Natl Acad. Sci. USA 109 8103
DOI:10.1073/pnas.1109824109 [Cited within: 1]

[5]Zhang X H Chen H Le S Rouzina I Doyle P S Yan J 2013 Proc. Natl Acad. Sci. USA 110 3865
DOI:10.1073/pnas.1213740110

[6]Yang Y J et al. 2020 J. Am. Chem. Soc. 142 9203
DOI:10.1021/jacs.9b11957

[7]Li W Wang P Y Yan J Li M 2012 Phys. Rev. Lett. 109 218102
DOI:10.1103/PhysRevLett.109.218102

[8]Yan J Marko J F 2004 Phys. Rev. Lett. 93 108108
DOI:10.1103/PhysRevLett.93.108108

[9]Forth S Sheinin M Y Inman J Wang M D 2013 Annu. Rev. Biophys. 42 583
DOI:10.1146/annurev-biophys-083012-130412 [Cited within: 1]

[10]Vladescu I D McCauley M J Nuñez M E Rouzina I Williams M C 2007 Nat. Methods 4 517
DOI:10.1038/nmeth1044

[11]Bustamante C Smith S B Liphardt J Smith D 2000 Curr. Opin. Struct. Biol. 10 279
DOI:10.1016/S0959-440X(00)00085-3

[12]Zhou H J Zhang Y Ou-Yang Z C 2000 Phys. Rev. E 62 1045
DOI:10.1103/PhysRevE.62.1045

[13]Zhou H J Zhang Y Ou-Yang Z C 1999 Phys. Rev. Lett. 82 4560
DOI:10.1103/PhysRevLett.82.4560

[14]Bian Y Tan C Wang J Sheng Y Zhang J Wang W 2014 PLoS Comput. Biol. 10 e1003562
DOI:10.1371/journal.pcbi.1003562 [Cited within: 1]

[15]Gu L Zhou Q Zhou H Gao Q Peng Y Song X Liu Y Zhou X Liu Y H 2018 Physica A 507 489
DOI:10.1016/j.physa.2018.05.011 [Cited within: 2]

[16]Herrero-Galán E Fuentes-Perez M E Carrasco C Valpuesta J M Carrascosa J L Moreno-Herrero F Arias-Gonzalez J R 2013 J. Am. Chem. Soc. 135 122
DOI:10.1021/ja3054755 [Cited within: 1]

[17]Gore J Bryant Z Nöllmann M Le M U Cozzarelli N R Bustamante C 2006 Nature 442 836
DOI:10.1038/nature04974 [Cited within: 1]

[18]Bryant Z Stone M D Gore J Smith S B Cozzarelli N R Bustamante C 2003 Nature 424 338
DOI:10.1038/nature01810 [Cited within: 2]

[19]Lipfert J et al. 2014 Proc. Natl Acad. Sci. USA 111 15408
DOI:10.1073/pnas.1407197111 [Cited within: 1]

[20]Chen S J 2008 Annu. Rev. Biophys. 37 197
DOI:10.1146/annurev.biophys.37.032807.125957 [Cited within: 1]

[21]Manning G S 2015 Biopolymers 103 223
DOI:10.1002/bip.22585

[22]Qiu X Y Rau D C Parsegian V A Fang L T Knobler C M Gelbart W M 2011 Phys. Rev. Lett. 106 028102
DOI:10.1103/PhysRevLett.106.028102

[23]Katz A M Tolokh I S Pabit S A Baker N Onufriev A V Pollack L 2017 Biophys. J. 112 22
DOI:10.1016/j.bpj.2016.11.018

[24]Sun L Z Zhang D Chen S J 2017 Annu. Rev. Biophys. 46 227
DOI:10.1146/annurev-biophys-070816-033920 [Cited within: 1]

[25]Adam S Anteneh H Hornisch M Wagner V Lu J Radde N E Bashtrykov P Song J Jeltsch A 2020 Nat. Commun. 11 1
DOI:10.1038/s41467-020-17531-8 [Cited within: 1]

[26]Li M R Zhang N Xu H T Zhang F S 2020 Chem. Phys. Lett. 748 137344
DOI:10.1016/j.cplett.2020.137344

[27]Regy R M Dignon G L Zheng W Kim Y C Mittal J 2020 Nucleic Acids Res. 48 12593
DOI:10.1093/nar/gkaa1099

[28]Jabbari K Chakraborty M Wiehe T 2019 Sci. Rep. 9 1
DOI:10.1038/s41598-019-51036-9

[29]Dršata T Špačková N Jurečka P Zgarbová M Šponer J Lankaš F 2014 Nucleic Acids Res. 42 7383
DOI:10.1093/nar/gku338 [Cited within: 3]

[30]Sarai A Kono H 2005 Annu. Rev. Biophys. Biomol. Struct. 34 379
DOI:10.1146/annurev.biophys.34.040204.144537 [Cited within: 1]

[31]Lankaš F Šponer J Hobza P Langowski J 2000 J. Mol. Biol. 299 695
DOI:10.1006/jmbi.2000.3781 [Cited within: 1]

[32]Williams L Maher L 2000 Annu. Rev. Biophys. Biomol. Struct 29 497
DOI:10.1146/annurev.biophys.29.1.497

[33]Fujii S Kono H Takenaka S Go N Sarai A 2007 Nucleic Acids Res. 35 6063
DOI:10.1093/nar/gkm627

[34]Vinogradov A Anatskaya O 2017 Mamm. Genome 28 455
DOI:10.1007/s00335-017-9713-8

[35]Chen H Liu Y H Zhou Z Hu L Ou-Yang Z C Yan J 2009 Phys. Rev. E 79 041926
DOI:10.1103/PhysRevE.79.041926

[36]Bao L Zhang X Jin L Tan Z J 2016 Chin. Phys. B 25 018703
DOI:10.1088/1674-1056/25/1/018703 [Cited within: 1]

[37]Shaban N Z Yehia S A Shoueir K R Saleh S R Awad D Shaban S Y 2019 J. Mol. Liq. 287 111002
DOI:10.1016/j.molliq.2019.111002 [Cited within: 1]

[38]Ortiz V de Pablo J J 2011 Phys. Rev. Lett. 106 238107
DOI:10.1103/PhysRevLett.106.238107 [Cited within: 1]

[39]Scipioni A Anselmi C Zuccheri G Samori B De Santis P 2002 Biophys. J. 83 2408
DOI:10.1016/S0006-3495(02)75254-5 [Cited within: 1]

[40]Olson W K Marky N L Jernigan R L Zhurkin V B 1993 J. Mol. Biol. 232 530
DOI:10.1006/jmbi.1993.1409 [Cited within: 1]

[41]Srivastava A Timsina R Heo S Dewage S W Kirmizialtin S Qiu X Y 2020 Nucleic Acids Res. 48 7018
DOI:10.1093/nar/gkaa499 [Cited within: 4]

[42]Mitchell J S Glowacki J Grandchamp A E Manning R S Maddocks J H 2017 J. Chem. Theory Comput. 13 1539
DOI:10.1021/acs.jctc.6b00904 [Cited within: 6]

[43]Geggier S Vologodskii A 2010 Proc. Natl Acad. Sci. USA 107 15421
DOI:10.1073/pnas.1004809107 [Cited within: 4]

[44]Hagerman P J 1990 Annu. Rev. Biochem. 59 755
DOI:10.1146/annurev.bi.59.070190.003543

[45]Bednar J Furrer P Katritch V Stasiak A Dubochet J Stasiak A 1995 J. Mol. Biol. 254 579
DOI:10.1006/jmbi.1995.0640 [Cited within: 1]

[46]Chuang H M Reifenberger J G Cao H Dorfman K D 2017 Phys. Rev. Lett. 119 227802
DOI:10.1103/PhysRevLett.119.227802 [Cited within: 1]

[47]Zhang Y Zhang J Wang W 2011 J. Am. Chem. Soc. 133 6882
DOI:10.1021/ja1109425 [Cited within: 1]

[48]Xu X J Yu T Chen S J 2016 Proc. Natl Acad. Sci. USA 113 116
DOI:10.1073/pnas.1517511113

[49]Wang J Zhao Y Wang J Xiao Y 2015 Phys. Rev. E 92 062705
DOI:10.1103/PhysRevE.92.062705

[50]Bao L Wang J Xiao Y 2019 Phys. Rev. E 99 012420
DOI:10.1103/PhysRevE.99.012420 [Cited within: 1]

[51]Mathew-Fenn R S Das R Harbury P A 2008 Science 322 446
DOI:10.1126/science.1158881 [Cited within: 3]

[52]Fu H Zhang C Qiang X W Yang Y J Dai L Tan Z J Zhang X H 2020 Phys. Rev. Lett. 124 058101
DOI:10.1103/PhysRevLett.124.058101 [Cited within: 5]

[53]Santa Lucia J 1998 Proc. Natl Acad. Sci. USA 95 1460
DOI:10.1073/pnas.95.4.1460 [Cited within: 3]

[54]Wu Y Y Bao L Zhang X Tan Z J 2015 J. Chem. Phys. 142 125103
DOI:10.1063/1.4915539 [Cited within: 3]

[55]Pérez A Marchán I Svozil D Sponer J Cheatham T EIIILaughton C A Orozco M 2007 Biophys. J. 92 3817
DOI:10.1529/biophysj.106.097782 [Cited within: 1]

[56]Xi K Wang F H Xiong G Zhang Z L Tan Z J 2018 Biophys. J. 114 1776
DOI:10.1016/j.bpj.2018.03.001 [Cited within: 2]

[57]Joung I S Cheatham T EIII 2008 J. Phys. Chem. B 112 9020
DOI:10.1021/jp8001614 [Cited within: 1]

[58]Tan Z J Chen S J 2005 J. Chem. Phys. 122 044903
DOI:10.1063/1.1842059 [Cited within: 4]

[59]Tan Z J Chen S J 2006 Biophys. J. 90 1175
DOI:10.1529/biophysj.105.070904 [Cited within: 3]

[60]Darden T York D Pedersen L 1993 J. Chem. Phys. 98 10089
DOI:10.1063/1.464397 [Cited within: 1]

[61]Bao L Zhang X Shi Y Z Wu Y Y Tan Z J 2017 Biophys. J. 112 1094
DOI:10.1016/j.bpj.2017.02.022 [Cited within: 3]

[62]Liu J H Xi K Zhang X Bao L Zhang X H Tan Z J 2019 Biophys. J. 117 74
DOI:10.1016/j.bpj.2019.05.018 [Cited within: 3]

[63]Zhang X Bao L Wu Y Y Zhu X L Tan Z J 2017 J. Chem. Phys. 147 054901
DOI:10.1063/1.4991689 [Cited within: 1]

[64]Lavery R Moakher M Maddocks J H Petkeviciute D Zakrzewska K 2009 Nucleic Acids Res. 37 5917
DOI:10.1093/nar/gkp608 [Cited within: 3]

[65]Rauzan B McMichael E Cave R Sevcik L R Ostrosky K Whitman E Stegemann R Sinclair A L Serra M J Deckert A A 2013 Biochemistry 52 765
DOI:10.1021/bi3013005 [Cited within: 1]

[66]Marin-Gonzalez A Vilhena J Perez R Moreno-Herrero F 2017 Proc. Natl Acad. Sci. USA 114 7049
DOI:10.1073/pnas.1705642114 [Cited within: 1]

[67]Drozdetski A V Tolokh I S Pollack L Baker N Onufriev A V 2016 Phys. Rev. Lett. 117 028101
DOI:10.1103/PhysRevLett.117.028101 [Cited within: 4]

[68]Baker N A Sept D Joseph S Holst M J McCammon J A 2001 Proc. Natl Acad. Sci. USA 98 10037
DOI:10.1073/pnas.181342398 [Cited within: 8]

[69]Emamian S Lu T Kruse H Emamian H 2019 J. Comput. Chem. 40 2868
DOI:10.1002/jcc.26068 [Cited within: 1]

[70]Scheiner S 2020 J. Chem. Phys. 153 140901
DOI:10.1063/5.0026168 [Cited within: 1]

[71]Tan Z J Chen S J 2008 Biophys. J. 94 3137
DOI:10.1529/biophysj.107.122366 [Cited within: 8]

[72]Montoro J G Abascal J 1995 J. Chem. Phys. 103 8273
DOI:10.1063/1.470191 [Cited within: 3]

[73]Tan Z J Chen S J 2007 Biophys. J. 92 3615
DOI:10.1529/biophysj.106.100388 [Cited within: 4]

[74]Mazur A K 2007 Phys. Rev. Lett. 98 218102
DOI:10.1103/PhysRevLett.98.218102 [Cited within: 1]

[75]Manning G S 2006 Biophys. J. 91 3607
DOI:10.1529/biophysj.106.089029 [Cited within: 2]

[76]Savelyev A Materese C K Papoian G A 2011 J. Am. Chem. Soc. 133 19290
DOI:10.1021/ja207984z [Cited within: 1]