,, Wen-Wen Li,, Yu-Chen Guo,, Ji-Chong Yang,∗Department of Physics, First author contact:
Received:2021-04-11Revised:2021-04-30Accepted:2021-05-1Online:2021-06-01
Abstract
Keywords：
PDF (2357KB)MetadataMetricsRelated articlesExportEndNote|Ris|BibtexFavorite
Cite this article
Yu-Jiao Bo, Wen-Wen Li, Yu-Chen Guo, Ji-Chong Yang. The relation between the radii and the densities of magnetic skyrmions. Communications in Theoretical Physics, 2021, 73(7): 075701- doi:10.1088/1572-9494/abfda0
1. Introduction
Skyrmion is a topological soliton originally proposed to describe the baryons [1]. In condensed matter, a particle-like object known as magnetic skyrmion was introduced theoretically in 1989 [2]. It was observed for the first time in 2D magnetic systems [3–6] involving Dzyaloshinskii-Moriya interactions (DMI) [7, 8]. Compared with the traditional magnetic bubble, the skyrmion is smaller, more stable and needs lower power to manipulate, therefore, it has been proposed that the skyrmion is a promising candidate for high density, high stability, high speed, high storage and low energy consumption memory devices [9–11]. As a result, the magnetic skyrmions have drawn a lot of attention and been studied intensively recently [11–15].A prerequisite for the use of skyrmions in devices is the knowledge of the relationship between the size of a skyrmion and parameters such as exchange strength, DMI strength and the strength of external magnetic field. Such a relationship can be investigated by solving the Euler–Lagrange equation of a skyrmion, for example numerically [16] or by using an ansatz [9], or by using the harmonic oscillation expansion [17], or by an asymptotic matching [18]. It has been noticed that the radius of a skyrmion in the skyrmion phase is much smaller than that of an isolated skyrmion [17]. Both the radii of an isolated skyrmion and the skyrmions in the skyrmion lattice were studied quantitatively in [19]. In particular, numerical results were obtained for the equilibrium radii of skyrmion lattices.
However, as a potential candidate for storage, the skyrmion is meant to be manipulated, erased and created. In this case, the number of skyrmions can vary from only just one to filling the entire skyrmion lattice. The transformation of a skyrmion lattice to the saturated state is continuous, in this process, the skyrmion lattice gradually decomposes into isolated skyrmions in the saturated state [15]. In this paper, we study the average radius of skyrmions with the density of skyrmions in the range between a single isolated skyrmion and the skyrmion lattice. While the results have been obtained for a single isolated skyrmion, and for skyrmion lattices, up to our knowledge, the radius of a skyrmion when the density of the skyrmions is between the skyrmion lattice and the single isolated skyrmion is poorly understood at a quantitative level.
The rest of the paper is organized as the following. The analytical and numerical results based on circular cell approximation are established in section
2. Circular cell approximation
The local magnetic moment of a skyrmion can be parameterized asBy using the circular cell approximation, the skyrmions are viewed as sitting in circular cells with radius R, which means the boundary condition θ(0) = π and θ(R) = 0 [19]. In principle, θ(r) can be expanded using any Hilbert space. Since the wave-function of the ground state of the harmonic oscillator and the numerical solution of the Euler–Lagrange equation of a skyrmion are close in shape [17], we use the Hilbert space of harmonic oscillator to expand θ(r). We do not require $\theta ^{\prime} (r)=0$ as in [17] because $\theta ^{\prime} (r)\ne 0$ is allowed by the Euler–Lagrange equation, therefore the eigen-functions of odd energy levels are also included. To impose the boundary conditions θ(0) = π and θ(R) = 0, θ(r) to the next-to-next-to leading order can be written as
We concentrate on the case when the anisotropy is absent, the energy to be minimized is $F=2\pi {\int }_{0}^{R}{\rm{d}}{rr}{ \mathcal F }(r)$ with the energy density
Denoting s ≡ 1/R, F can be expanded as $F=\hat{F}+{ \mathcal O }({s}^{5})$ with
For d = 0.4, b = 0.1, R = 20, in the region that ω ∼ 0.15 and c ∼ − 0.01, we compare F with $\hat{F}$ in figure 1. $\hat{F}$ can approximate F well in the region concerned. Especially, the positions where F and $\hat{F}$ are minimized fit each other very well. To minimize F, we use variational method, so that there are two equations ∂F/∂ω = 0 and ∂F/∂c = 0, by which ω and c can be solved.
Figure 1.
New window|Download| PPT slideFigure 1.Compare F with $\hat{F}$ at d = 0.4, b = 0.1, R = 20. The left panel is F and $\hat{F}$ at ω = 0.15 as functions of c, the right panel is F and $\hat{F}$ at c = − 0.012 as functions of ω.
By setting a threshold h such that the sites with nz < h are determined as inside a skyrmion, the radius of a skyrmion can be obtained by solving the equation $\cos (\theta (r))=h$. Considering the leading order approximation which corresponds to c = s = 0 (denoted as θLO), by solving $\cos ({\theta }_{\mathrm{LO}}(r))=h$, the radius of a skyrmion (denoted as rs) is approximately
With the numerical solutions of ω, we can investigate the change of rs as function of s. For this purpose, we define $\hat{r}={r}_{s}/{r}_{\mathrm{iso}}$ where rs is calculated by ω solved at s, and riso is the radius of a single isolated skyrmion which is calculated by ω solved at s → 0.
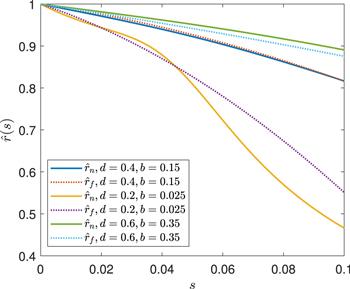
Since the numerical solutions are inconvenient to use, we fit the solutions as bilinear function of s around d ∼ 0.4, with the numerical solution of $\hat{r}$ denoted as ${\hat{r}}_{n}$ and the fitted solution denoted as ${\hat{r}}_{f}$, the result is ${\hat{r}}_{n}\approx {\hat{r}}_{f}$ with
Figure 2.
New window|Download| PPT slideFigure 2.${\hat{r}}_{f}$ Compared with ${\hat{r}}_{n}$.
We define the density of skyrmions as ρ = N/A where N is the number of skyrmions within an area A. R is approximately half of the average distance between the skyrmions, therefore R can be related to ρ. Assuming the skyrmions are distributed homogenously, then N ≈ A/πR2, and $s\approx \sqrt{\pi N/A}$.
It has been found that, by using the leading order ansatz θLO, to minimize F yields ω = w0b2/d2 where w0 = 0.768548 is a constant [17]. By using equation (
For a skyrmion, nz varies from −1 to 1 from the center to the edge, and the radius is determined by the number of sites with nz < 1. But nz only approaches 1, so we need to set a threshold slightly smaller than 1. If the approximate expression for θ(r) is sufficiently precise, the radius of the skyrmion is consistent as long as we choose a same h for theoretical predictions, lattice simulations and experimental measurements, and the verification of the theory is independent of the specific value of h taken. In this paper we choose 0.9 which is close to 1, other choices would lead to small differences, but would not change the conclusion. Then $\sqrt{2\mathrm{log}\left(\pi /{\cos }^{-1}(h)\right)/{w}_{0}}\approx 2.247\,44$, using ${\hat{r}}_{f}$ to approximate $\hat{r}$,
In [19], the equilibrium R is numerically solved by minimize the energy density. Note that R in this case is independent of the density of the skyrmions. In our case, R is a quantity between the case of skyrmion lattice and the case of a single isolated skyrmion, and is determined by the density of the skyrmions, one can calculate rs after R is given.
3. Lattice simulation
The lattice simulation is based on the LLG equation, denoting nr as the local magnetic momentum at site r, the LLG can be written as [20–23]4. Numerical results
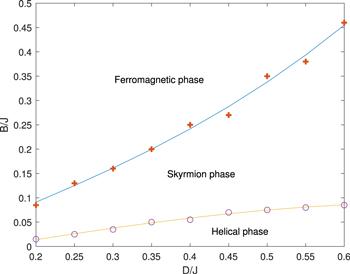
We run the simulation on a 512 × 512 square lattice. In the simulation, we use dimensionless homogeneous J, D and B. J = 1 is used as the definition of the energy unit [25–27], the results are presented with d and b. In the previous works, the Gilbert constant was chose to be α = 0.01 to 1 [21, 23, 26–35]. In this work, we use α = 0.04 which is in the region of commonly used α. The time step is denoted as Δt. We use Δt = 0.01 time unit, and the configurations typically become stable after about 106−107 steps starting with a randomized initial state. The average radius of the skyrmions is measured as rs = As/NA where As is the total area of the skyrmions which is determined by the number of sites in the isoheight nz = h with h = 0.9, A = 5122 and N is the number of skyrmions. The standard errors of the radii of skyrmions are also measured.To investigate the relationship between r, d and b, we simulate with d in the range of 0.2−0.6, and with growing b for each fixed d. We focus on those configurations that are in the skyrmion phase when stable. The phase diagram is shown in figure 3.
Figure 3.
New window|Download| PPT slideFigure 3.The phase diagram obtained by lattice simulation of LLG with randomized initial states.
4.1. The relationship between the average radius and density
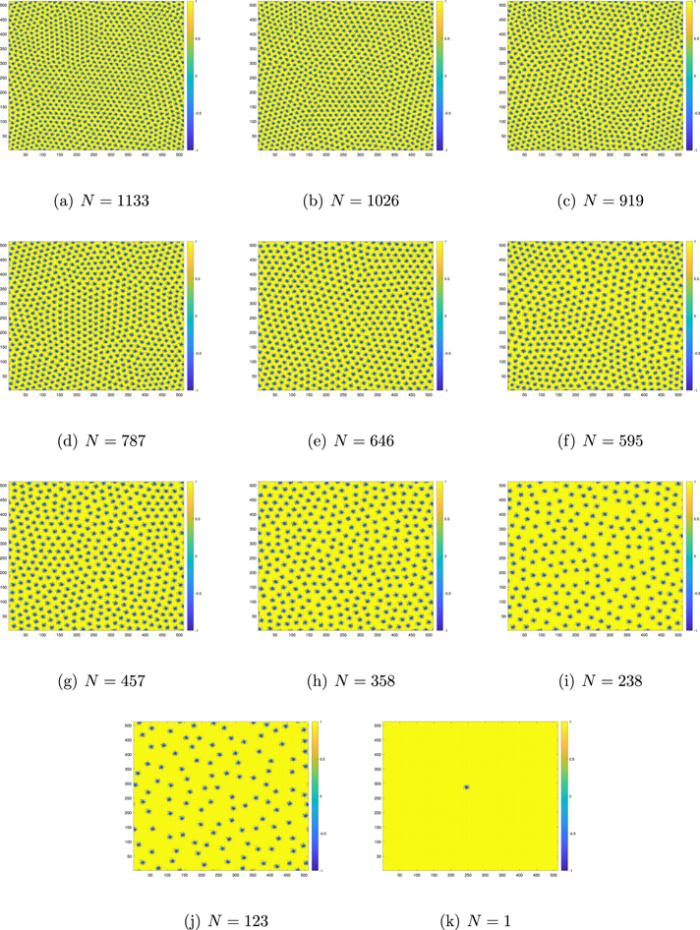
In this subsection, we use the configurations at d = 0.2, b = 0.025, d = 0.35, b = 0.1, d = 0.4, b = 0.1, d = 0.4, b = 0.2, d = 0.45, b = 0.15 and d = 0.6, b = 0.15 to investigate the relationship between the average radius and density. Firstly we calculate the number of skyrmions in each configuration. By repeatedly and randomly erasing about 10% of the total number of skyrmions at a time and performing the simulation sequentially, we obtain the configurations at different N. Taking the case of d = 0.4, b = 0.1 as an example, the resulting configurations are shown in figure 4.Figure 4.
New window|Download| PPT slideFigure 4.The configurations corresponding to different N.
Because the size of the lattice is 512 × 512, $s\approx \sqrt{N\pi /{512}^{2}}\approx 0.003\,46\sqrt{N}$. The ratios of the average radii of skyrmions at different N to the radius of an isolated skyrmion are measured and denoted as ${\hat{r}}_{m}$. We compare ${\hat{r}}_{m}$, ${\hat{r}}_{f}$ and ${\hat{r}}_{n}$ in figure 5. It can be seen that the theocratical results ${\hat{r}}_{n}$ and ${\hat{r}}_{f}$ can approximately predict ${\hat{r}}_{m}$ correctly, the deviations between ${\hat{r}}_{m}$ and ${\hat{r}}_{s,f}$ are generally within about 10%. Besides, for larger skyrmions, the theocratical results are generally better. Especially, for d = 0.4, b = 0.1, ${\hat{r}}_{s}$ can fit ${\hat{r}}_{m}$ very well. For the cases where the sizes of skyrmions are relatively smaller, there are several possible reasons for the deviation. On one hand, when the skyrmions are smaller, they are not homogenously aligned, the distances between the skyrmions become larger, consequently the actual s is smaller for ${\hat{r}}_{m}$, so the points of ${\hat{r}}_{m}$ are biased towards a larger s. Secondly, the lattice simulation is more coarse for smaller skyrmions, which can also lead to differences with the theoretical results. Similarly, if the skyrmions are small and occupy only hundreds of sites, the θ(r) can no longer be treated as a continuous function.
Figure 5.
New window|Download| PPT slideFigure 5.Compare ${\hat{r}}_{m}$ with ${\hat{r}}_{n}$ and ${\hat{r}}_{f}$.
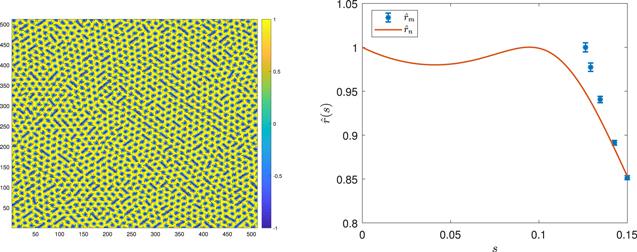
There are also cases that the ${\hat{r}}_{m}$ are not fitted very well by the theocratical predictions. In the case of d = 0.6, b = 0.15, after erasing some skyrmions, the configuration began to enter the helical phase as shown in figure 6(a). In this case, when an isolated skyrmion is created, it is not stable and will grow into stripes. If we choose the average radius near the phase transition as a baseline, that is, we choose the ${\hat{r}}_{m}$ near the phase transition as 1, the results are shown in figure 6(b). It can be seen that the ${\hat{r}}_{m}$ approaches ${\hat{r}}_{n}$.
Figure 6.
New window|Download| PPT slideFigure 6.Compare ${\hat{r}}_{m}$ with ${\hat{r}}_{n}$ for d = 0.6, b = 0.15.
Another case is when d = 0.4, b = 0.2 as shown in figure 7. This is an example that when the skyrmions are small, they are no longer homogenously aligned. It can been found from figure 3 that the configuration is also near the phase transition from the skyrmion phase to the ferromagnetic phase. It is interesting that, the average radius is not always decreasing with s especially when s is small. For N = 51, rs = 4.7003 ± 0.0054, for N = 103, rs = 4.7005 ± 0.0043, which are larger than the case of a signle isolated skyrmion rs = 4.6865. One can see that ${\hat{r}}_{n}$ has a similar behavior.
Figure 7.
New window|Download| PPT slideFigure 7.Compare ${\hat{r}}_{m}$ with ${\hat{r}}_{n}$ for d = 0.4, b = 0.2.
4.2. A formula for the average radius in the skyrmion phase
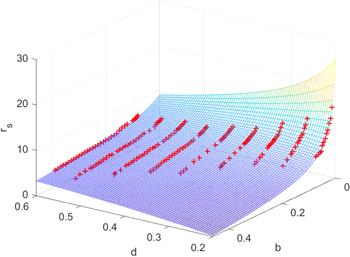
Since we start from the randomized initial state, the obtained configurations are the skyrmion lattices. In this case, the relationship between rs, d and b are fitted by a rational function, the result isFigure 8.
New window|Download| PPT slideFigure 8.rs at different d and b (marked as ‘+') and the fitted rs(d, b), i.e. Equation (
We compare equation (
Figure 9.
New window|Download| PPT slideFigure 9.rs calculated with equation (
4.3. The shape of the skyrmion in the skyrmion phase
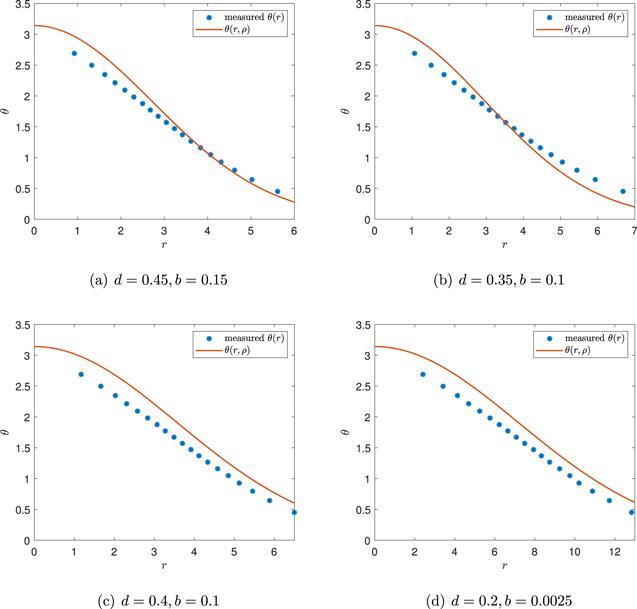
The function θ(r) is often used to describe the shape of a skyrmion [17]. It has been assumed that the higher order corrections to θ(r) are small, which in fact requires that the shape of a skyrmion is not changed significantly in the skyrmion phase. Choosing the configurations at d = 0.2, b = 0.025, d = 0.35, b = 0.1, d = 0.4, b = 0.1 and d = 0.45, b = 0.15 as examples, we measure the average θ(r) with θ in the range ${\cos }^{-1}(0.9)\leqslant \theta \leqslant {\cos }^{-1}(-0.9)$. The results are compared with θLO(r) with r rescaled according to $r\to r/{\hat{r}}_{f}(s)$, for example, in the case of d = 0.4, b = 0.1, one has s ≈ 0.116 165 and θ(r, ρ) = θLO(r/0.783516). The results are shown in figure 10.Figure 10.
New window|Download| PPT slideFigure 10.The shapes of isolated skyrmions in the saturated state.
As shown in figure 10, the shapes of isolated skyrmions in a saturated state are similar to the shape of a single isolated skyrmion with r rescaled. This result indicates that our assumption is valid. Note that θ(r, ρ) is also the function θLO(r) with b rescaled as $b/\hat{r}$. It implies that the skyrmions can be seen as being experiencing an effective magnetic strength $B^{\prime} =B/\hat{r}$ when affected by other skyrmions.
4.4. Matching
In the calculations and lattice simulations, we use dimensionless parameters. The numerical results can be matched to the real material by using the rescaling introduced in [21, 36]. The rescaling factor is denoted as q and $q\,=(D/J)\lambda /(2\pi \sqrt{2}a)$ where λ is helical wavelength and a is the lattice spacing. The helical wavelengthes of real materials can be found in [12]. For example, if we take λ ≈ 60 nm, a = 0.4 nm and D/J = 0.4, then q ≈ 6.75. Then r = 6.2854 corresponds to r = 6.2854 × q × a ≈ 16.97 nm. Meanwhile the time unit is rescaled as $t^{\prime} ={q}^{2}J{\hslash }/J^{\prime} $, where J is the dimensionless exchange strength and $J^{\prime} $ is the exchange strength of a real material. If we choose $J^{\prime} \approx 3\ \mathrm{meV}$, the time unit is $t^{\prime} \approx 0.01\ \mathrm{ns}$. The time step in the simulation is ${\rm{\Delta }}t=0.01t^{\prime} \approx 1\ \mathrm{ps}$.5. Summary
One of the reasons that the skyrmion is proposed as a candidate for the future memory devices is because the size of a skyrmion is small. The radius of a skyrmion when the density of skyrmions is between the skyrmion lattice and the single isolated skyrmion is an important issue which is lack of exploration. In this paper, we study the average radius of skyrmions when the density is between a skyrmion lattice and a single isolated skyrmion. By using the harmonic oscillator expansion, the dependency of the average radius of skyrmions on the parameters of materials, strength of external magnetic field and the density of skyrmions is obtained theoretically. Then, a lattice simulation of LLG equation is performed to verify our results.The theoretical result is presented in equation (
Acknowledgments
This work was partially supported by the National Natural Science Foundation of China under Grant No. 12 047 570 and the Natural Science Foundation of the Liaoning Scientific Committee Grant No. 2019-BS-154.Reference By original order
By published year
By cited within times
By Impact factor
DOI:10.1016/0029-5582(62)90775-7 [Cited within: 1]
[Cited within: 1]
DOI:10.1038/nature05056 [Cited within: 1]
DOI:10.1126/science.1166767
DOI:10.1038/nature09124
DOI:10.1038/nphys2045 [Cited within: 1]
DOI:10.1016/0022-3697(58)90076-3 [Cited within: 1]
DOI:10.1103/PhysRev.120.91 [Cited within: 1]
DOI:10.1038/s42005-018-0029-0 [Cited within: 2]
DOI:10.1038/ncomms2442
DOI:10.1038/natrevmats.2017.31 [Cited within: 2]
DOI:10.1038/nnano.2013.243 [Cited within: 1]
DOI:10.1063/5.0027042
DOI:10.1088/1367-2630/18/6/065003
DOI:10.1038/s42254-020-0203-7 [Cited within: 2]
DOI:10.1002/pssb.2221860223 [Cited within: 1]
DOI:10.1088/1361-648x/ab01ef [Cited within: 6]
DOI:10.1088/1361-6544/ab81eb [Cited within: 1]
DOI:10.1016/0304-8853(94)90046-9 [Cited within: 3]
DOI:10.1142/S0217984919500404 [Cited within: 2]
DOI:10.1088/0953-8984/25/7/076005 [Cited within: 2]
DOI:10.1016/j.physrep.2008.07.003
DOI:10.1088/0953-8984/25/7/076005 [Cited within: 2]
DOI:10.1038/nnano.2013.176 [Cited within: 1]
DOI:10.1103/PhysRevLett.108.017601 [Cited within: 2]
DOI:10.1103/PhysRevB.90.174434 [Cited within: 1]
DOI:10.1038/srep42645 [Cited within: 1]
DOI:10.1103/PhysRevB.96.144432
DOI:10.1063/1.5013620
DOI:10.1038/nnano.2013.210
DOI:10.1038/nphys4000
DOI:10.1038/nphys3883
DOI:10.1088/1361-6463/aa7a98
DOI:10.1038/nnano.2014.324
DOI:10.1103/PhysRevLett.116.147203 [Cited within: 1]
DOI:10.1103/PhysRevB.85.174416 [Cited within: 1]
