Feng-He Ju, Zuo-Yuan Zhang, Jin-Ming Liu^,State Key Laboratory of Precision Spectroscopy, East China Normal University, Shanghai 200062, China

Received:2020-06-8Revised:2020-07-16Accepted:2020-07-29Online:2020-11-23


Abstract
We investigate the quantum-memory-assisted entropic uncertainty relation (QMA-EUR) in a Heisenberg XYZ mixed-spin (1/2, 1) model. Coupling strength, Dzyaloshinskii-Moriya (DM) interaction and inhomogeneous magnetic field, respectively, contributing to QMA-EUR by a thermal entanglement in the hybrid-spin model are studied in detail. Furthermore, we compare the uncertainty of the bipartite hybrid model with those of qubit-qubit and qutrit-qutrit systems. Meanwhile, the effects of local PT-symmetric operation and weak measurement on the steering of entropic uncertainty are analyzed. We find that the local PT-symmetric operation can reduce the entropic uncertainty, and the entropic uncertainty can also be decreased by weak measurement reversal.
Keywords： entropic uncertainty relation;Heisenberg XYZ model;weak measurement;PT-symmetry


PDF (967KB)MetadataMetricsRelated articlesExportEndNote|Ris|BibtexFavorite
Cite this article
Feng-He Ju, Zuo-Yuan Zhang, Jin-Ming Liu. Entropic uncertainty relation of a qubit-qutrit Heisenberg spin model and its steering. Communications in Theoretical Physics, 2020, 72(12): 125102- doi:10.1088/1572-9494/abb7ca

1. Introduction

Quantum entanglement is the most basic physical resource in the field of quantum information science such as quantum key distribution, quantum teleportation and quantum dense coding. Therefore, the research on entanglement including measurement and control are the key problems of quantum information science. Quantum discord and concurrence are two different methods to quantify quantum correlations. Recently, it was pointed out that to some extent, entropic uncertainty relation (EUR) can also be used to witness the degree of quantum correlation [1, 2]. The uncertainty relation originates from the Heisenberg uncertainty principle [3] which indicates momentum and position for a particle cannot be measured accurately at the same time. With the development of quantum theory, the concept of entropy was used to describe the limitation relationship of the arbitrary anti-commutation observables. Subsequently, Berta et al proved that the uncertainty can be reduced in a two-particle entangled system [4] and proposed the quantum-memory-assisted entropic uncertainty relation (QMA-EUR) on the basis of the previous works [5-9], which can be written as(1)$\begin{eqnarray}H(U| B)+H(V| B)\geqslant {{\rm{log}}}_{2}\displaystyle \frac{1}{c}+H(A| B),\end{eqnarray}$where $H(X| B)=H({\rho }_{{XB}})-H({\rho }_{B})$ is the conditional von Neumann entropy with $H(\rho )=-{\rm{Tr}}(\rho {{\rm{log}}}_{2}\rho )$, $c\,={\max }_{{ij}}| \langle {\phi }_{i}| {\varphi }_{j}\rangle | $, where $| {\phi }_{i}\rangle $ and $| {\varphi }_{j}\rangle $ are the eigenstates of two arbitrary anti-commutation observations U and V, respectively, ${\rho }_{{XB}}={{\rm{\Sigma }}}_{i}(| {\phi }_{i}\rangle \langle {\phi }_{i}| \otimes I){\rho }_{{AB}}(| {\phi }_{i}\rangle \langle {\phi }_{i}| \otimes I)$ represents the post-measurement state after system A is measured by the operator X, $X\in (U,V)$.

QMA-EUR can be described as an interesting quantum task [10]: at the beginning, a bipartite quantum state (ρ_AB) consisting of particle A and quantum memory particle B is shared between Alice and Bob. Then Alice measures one of the two incompatible operators U or V. After she informs Bob of her measurement choice, he can minimize the uncertainty of the measured particle based on his memory. It has been demonstrated that inequality (1) can be applicable to the witness of the entanglement [4, 11, 12]. Moreover, in [13-24] QMA-EUR was compared with quantum entanglement, correlations and coherence, respectively. In recent years, the wide application prospects of QMA-EUR in quantum information science have attracted much attention [25-29].

The Heisenberg spin chain model can explain many phenomena in magnetic systems and has been applied to the study of quantum correlations, quantum phase transitions, and so on. Some research of QMA-EUR in Heisenberg XX, XXZ and XYZ spin-1/2 or spin-1 models are carried out in [30-34]. But QMA-EUR is rarely analyzed in the Heisenberg XYZ hybrid-spin (1/2,1) model. This model is an important extension of the two-qubit case or two-qutrit case [35, 36], because it has richer phase diagrams and can explain more complex physical phenomena. Investigations of QMA-EUR on such a hybrid system can provide more universal research significance to a higher dimension.

To offset the partial effects of decoherence and dissipation on quantum entanglement resources, recently people have proposed the weak measurements and the PT-symmetry as two effective methods for increasing the degree of quantum entanglement in some physical systems (i.e. decreasing QMA-EUR) [37-40]. We make a brief comparison between the two methods and give the corresponding physical interpretation of our results. Our studies on the EUR are helpful to quantum cryptography and quantum precision measurement, and also have certain importance to the research on the hybrid high spin system.

This paper is arranged as follows: in section 2, we study the QMA-EUR of the hybrid-spin systems under the condition of external magnetic field and Dzyaloshinskii-Moriya (DM) interaction. In section 3, two different steerings of QMA-EUR with weak measurements and PT-symmetry are examined. Finally, we give a brief conclusion in section 4.

2. (1/2,1) hybrid-spin XYZ model with DM interaction

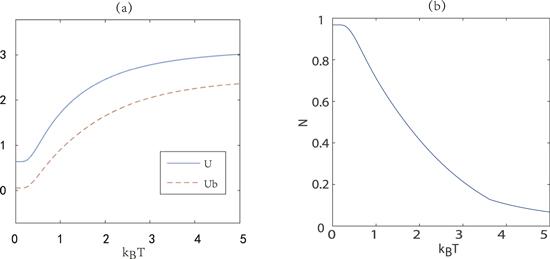
Here, we give the Hamiltonian of a hybrid-spin Heisenberg XYZ chain with DM interaction and external magnetic field being all forced along the z-direction as follows,(2)$\begin{eqnarray}\begin{array}{rcl}H & = & J(1+{\rm{\Delta }}){\sigma }_{1}^{x}{\sigma }_{2}^{x}+J(1-{\rm{\Delta }}){\sigma }_{1}^{y}{\sigma }_{2}^{y}+{J}_{z}{\sigma }_{1}^{z}{\sigma }_{2}^{z}\\ & & +{D}_{z}({\sigma }_{1}^{x}{\sigma }_{2}^{y}-{\sigma }_{1}^{y}{\sigma }_{2}^{x})+\displaystyle \frac{B+b}{2}{\sigma }_{1}^{z}+\displaystyle \frac{B-b}{2}{\sigma }_{2}^{z},\end{array}\end{eqnarray}$where ${\sigma }_{1}^{m}$ (m=x, y, z) is the spin-1 operator of the first qutrit and takes the form(3)$\begin{eqnarray}\begin{array}{rcl}{\sigma }_{1}^{x} & = & \displaystyle \frac{1}{\sqrt{2}}\left(\begin{array}{ccc}0 & 1 & 0\\ 1 & 0 & 1\\ 0 & 1 & 0\end{array}\right),{\sigma }_{1}^{y}=\displaystyle \frac{1}{\sqrt{2}}\left(\begin{array}{ccc}0 & -{\rm{i}} & 0\\ {\rm{i}} & 0 & -{\rm{i}}\\ 0 & {\rm{i}} & 0\end{array}\right),\\ {\sigma }_{1}^{z} & = & \left(\begin{array}{ccc}1 & 0 & 0\\ 0 & 0 & 0\\ 0 & 0 & -1\end{array}\right),\end{array}\end{eqnarray}$and ${\sigma }_{2}^{m}$ is the Pauli matrix of the second qubit. J is the coupling parameter for the spin interaction in the x- and y- directions, J_z denotes the coupling strength in the z-direction of the two spin particles, Δ represents the anisotropic intensity in the XY-plane, D_z is the parameter of the DM interaction, and the parameters B and b are along the z-direction. In this way, the Hamiltonian H can be rewritten in the following matrix form:(4)$\begin{eqnarray}H=\left(\begin{array}{cccccc}{J}_{z}+2B & 0 & 0 & 2{\rm{\Delta }} & 0 & 0\\ 0 & -{J}_{z}+2b & 2J+2D{\rm{i}} & 0 & 0 & 0\\ 0 & 2J-2D{\rm{i}} & B-b & 0 & 0 & 2{\rm{\Delta }}\\ 2{\rm{\Delta }} & 0 & 0 & b-B & 2J+2D{\rm{i}} & 0\\ 0 & 0 & 0 & 2J-2D{\rm{i}} & -{J}_{z}-2b & 0\\ 0 & 0 & 2{\rm{\Delta }} & 0 & 0 & {J}_{z}-2B\end{array}\right).\end{eqnarray}$To investigate the QMA-EUR of the Heisenberg XYZ mixed-spin (1/2,1) model with DM interaction in the thermal equilibrium, the density matrix relying on environment temperature T is adopted here, which is given by $\rho (T)={\rm{\exp }}(-\beta H)/Z(T)$ with $\beta =1/{k}_{{\rm{B}}}T$, here k_B represents the Boltzmann constant and $Z(T)={\rm{Tr}}[{\rm{\exp }}(-\beta H)]$ represents the partition function. We assume $\left|{{\rm{\Psi }}}_{i}\right\rangle $ to be the ith eigenvector versus the eigenvalue E_i of the Hamiltonian H, then the density matrix of the system can be written as(5)$\begin{eqnarray}\rho (T)=\displaystyle \frac{1}{Z(T)}\displaystyle \sum _{i}{{\rm{e}}}_{}^{-\beta {E}_{i}}\left|{{\rm{\Psi }}}_{i}\right\rangle \left\langle {{\rm{\Psi }}}_{i}\right|.\end{eqnarray}$Hereafter, the quantum memory state is assumed to be the qubit state, and the measurement operators σ^x and σ^z are applied to the spin-1 particle. Generally speaking, it is difficult to directly obtain the analytical solution of the above density matrix due to the large number of parameters. Throughout this paper, we only provide the numerical solution. For clarity, U (Ub) is set to be the left- (right)-hand side of the inequality (1).

Obviously, from figure 1(a) we can see that the lower bound Ub of entropic uncertainty based on entanglement is less than entropic uncertainty U and they all increase with the growth of temperature for the thermal equilibrium state. This is because of the fact that the entanglement between the two particles decreases as the temperature increases. In figure 1(b), we plot the behavior of negativity as a contrast. The negativity is defined by(6)$\begin{eqnarray}N(\rho )=\displaystyle \sum _{i}\left|{\lambda }_{i}\left({\rho }^{{T}_{1}}\right)\right|-1,\end{eqnarray}$here, ρ denotes the density matrix of equation (5), ${\rho }^{{T}_{1}}$ is the partial transpose matrix for the measured particle, and λ_i is the ith eigenvalue of ${\rho }^{{T}_{1}}$. Thus according to figure 1, we can find that the variation trend of the entropic uncertainty versus ${k}_{{\rm{B}}}T$ is approximately anti-correlated with that of the entanglement, which is in good agreement with the result obtained in [31].

Figure 1.

New window|Download| PPT slide
Figure 1.Entropic uncertainty U and its lower bound Ub (a) as well as negativity (b) as a function of ${k}_{{\rm{B}}}T$ with J=1, J_z=2, Δ=0.3, B=2, b=1, and D_z=2.


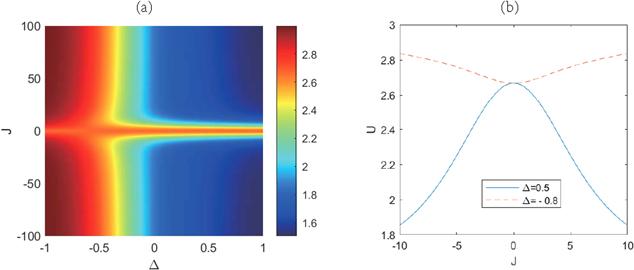
Next we focus on the relationship of QMA-EUR with coupling constant J and the anisotropic intensity Δ in the XY-plane. As can be seen from figure 2(a), the entropic uncertainty is symmetric with respect to J=0. However, the systemic uncertainty goes down as Δ goes up if $J\ne 0$. This may be due to the fact that one of the measurement operators we choose is σ^x. On the other hand, the coupling strength of the term ${\sigma }_{1}^{x}{\sigma }_{2}^{x}$ in the Hamiltonian of the system is proportional to parameter Δ. When Δ=0.5, entropic uncertainty decreases monotonically as the absolute value of J increases. For the case of Δ=−0.8, the evolution trend of the entropic uncertainty with $| J| $ is on the contrary to that of Δ=0.5 as shown in figure 2(b). Especially, when J=0, the Hamiltonian of the system is independent of Δ, thus the uncertainty for Δ=0.5 is equal to that for Δ=−0.8.

Figure 2.

New window|Download| PPT slide
Figure 2.(a) Entropic uncertainty U versus J and Δ. (b) U as a function of J for Δ=0.5 and Δ=−0.8. Here, k_BT=2.5, J_z=8, B=2, b=1, and D_z=2.


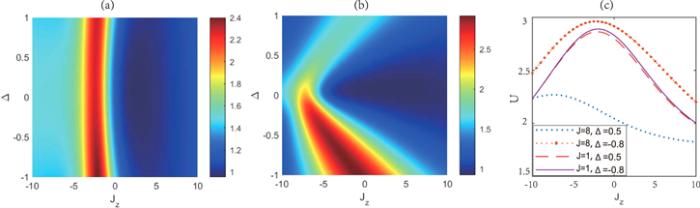
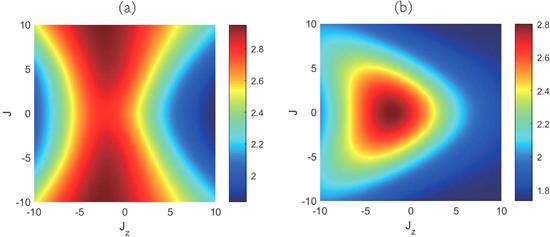
Meanwhile, figure 3 shows that the entropic uncertainty is not symmetrical to J_z=0, the reason is that there exist a DM interaction and inhomogeneous magnetic field the along z-direction. However, with J_z growing the value of the uncertainty increases initially and decreases afterwards for the fixed Δ. For clarity, in figure 3(c) we give a two-dimensional diagram corresponding to figures 3(a) and (b) for several certain parameters Δ and J, which can more obviously reflect the function relationship between J_z and U. Furthermore, we plot a contour map of entropic uncertainty about J and J_z in figure 4. It is found that the uncertainty is also symmetric about J=0 instead of J_z=0 due to the same reason, which coincides with the results of figure 2 and 3.

Figure 3.

New window|Download| PPT slide
Figure 3.Entropic uncertainty U versus J_z and Δ for (a) J=1 and (b) J=8. (c) U versus J_z for several fixed values of J and Δ. Here, k_BT=0.5, B=2, b=1, and D_z=2.

Figure 4.

New window|Download| PPT slide
Figure 4.Entropic uncertainty U as functions of J and J_z with k_BT=2, B=2, b=1, and D_z=2 for (a) Δ=−0.8 and (b) Δ=0.5.


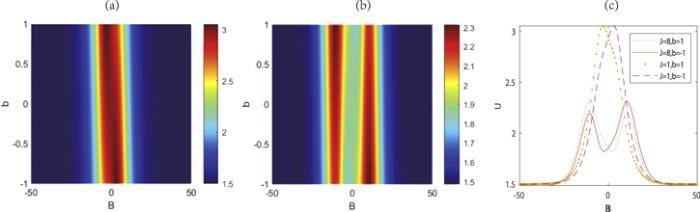
Now, we turn to discuss the effects of the inhomogeneous magnetic field on the entropic uncertainty, as shown in figure 5. Obviously, the value of the entropic uncertainty is very low if the Heisenberg chain locates in the magnetic field with high intensity. From figure 5(c), it can be seen U has two apparent peak values with respect to magnetic field for coupling strength J=8 with b=±1. However, for the situation of J=1, there only is one peak. This means that with the increasing absolute value of magnetic field intensity, the entropic uncertainty is monotonically decreased when the coupling strength J is relatively weak. However, for the large value of J the uncertainty U first gradually increases and then diminishes.

Figure 5.

New window|Download| PPT slide
Figure 5.Entropic uncertainty U versus B and b for (a) J=1 and (b) J=8. (c) U versus B for several fixed values of J and b. Here, k_BT=2, J_z=2, Δ=0.5, and D_z=0.


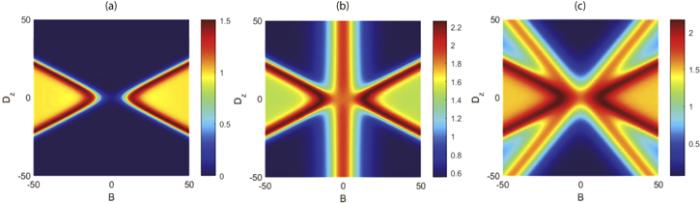
The behavior of entropic uncertainty for the types of qubit-qubit, qubit-qutrit and qutrit-qutrit Heisenberg model about magnetic field B and DM interaction D_z are given in figure 6. This diagram is a good illustration of the progressive relationship between a system with two spins of 1/2, a hybrid system and a system with two spins of 1. There are similarities and differences between them. We can see that as the systemic dimension becomes higher, the area of lower level entropic uncertainty become less under the same condition. Moreover, the complexity degree of the qubit-qutrit system is between those of the qubit-qubit and qutrit-qutrit systems, which means that the hybrid system can be controlled more easily than the spin-1 system, in the meantime it can encode more quantum information than the spin-1/2 system.

Figure 6.

New window|Download| PPT slide
Figure 6.Entropic uncertainty U versus Dz and B with J_z=5, J=8, Δ=0.5, and b=0 for (a) qubit-qubit, (b) qubit-qutrit, (c) qutrit-qutrit.

3. Some ways to improve entanglement

In the above section, we analyze the influence of some parameters on the hybrid-spin model. In what follows we turn to discuss steering of the uncertainty with weak measurement and PT-symmetry.

As we know, the advantage of weak measurement over von Neumann orthogonal measurement is that it has less perturbation to the quantum system. Because of the existence of various noises in the environment, the entanglement degree of a systemic quantum state will be reduced due to decoherence. In general, the quantum state of the system can be restored to the initial state with a probability by means of a proper measurement reversal operation. The weak measurement reversal (WMR) acting on a qutrit particle can be expressed as a non-unitary quantum operation with strength 0≤p<1 and 0≤q<1, which is written as [41](7)$\begin{eqnarray}\begin{array}{rcl}M & = & \sqrt{(1-p)(1-q)}\left|0\right\rangle \left\langle 0\right|\\ & & +\ \sqrt{1-q}\left|1\right\rangle \left\langle 1\right|+\sqrt{1-p}\left|2\right\rangle \left\langle 2\right|.\end{array}\end{eqnarray}$

The WMR has been applied to suppress the decoherence of the quantum system from the external environment [42]. To examine whether the reversal operation is helpful for the reduction of the entropic uncertainty or not, next we apply WMR to the qutrit particle. The post-selection state of the system becomes(8)$\begin{eqnarray}\rho ^{\prime} =\displaystyle \frac{(M\bigotimes I)\rho {\left(M\bigotimes I\right)}^{\dagger }}{{\rm{Tr}}[(M\bigotimes I)\rho {\left(M\bigotimes I\right)}^{\dagger }]}.\end{eqnarray}$Now we explore how different measurement strengths p and q affect the EUR.

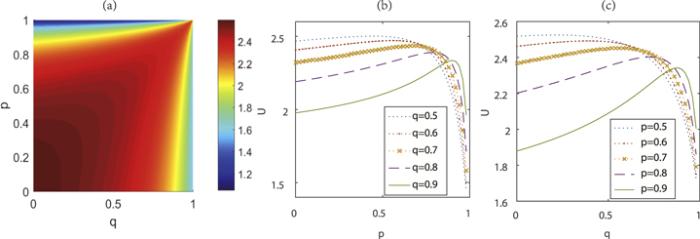
From figure 7(a), we can find when the value of p is small, the entropic uncertainty decreases monotonously with q increasing. If p is large and close to 1, the entropic uncertainty will increase first and then decay with the growth of q, vice versa. It implies that WMR has no effect on the decrease of entropic uncertainty for the small value of the measurement strength. When the measurement strength (p or q) is large enough, the uncertainty will be smaller than the initial value. To clearly describe the evolution behaviors of entropic uncertainty, we plot the two-dimension pictures of figure 7(a), as shown in figures 7(b) and (c).

Figure 7.

New window|Download| PPT slide
Figure 7.(a) Entropic uncertainty U versus measurement strengths p and q. (b) U as a function of p for different q. (c) U as a function of q for different p. Here, k_BT=2.5, J_z=2, J=2, Δ=0.2, B=2, b=1, and D_z=2.


The local PT-symmetric operation is another method for the steering of quantum information processing, which is similar to weak measurement operations. It can protect the quantum entanglement in a noisy environment as well, which can be written as [43](9)$\begin{eqnarray}H^{\prime} =s\left(\begin{array}{cc}{\rm{i}}\;{\rm{\sin }}\alpha & 1\\ 1 & -{\rm{i}}{\rm{\sin }}\alpha \end{array}\right),\end{eqnarray}$where $\alpha \in (-\pi /2,\pi /2)$ denotes the non-Hermiticity of the Hamiltonian and s is a general scaling constant of the matrix. H' can be rewritten as the form of time-evolution operation(10)$\begin{eqnarray}{U}_{t}={{\rm{e}}}^{{\rm{-i}}H^{\prime} t}=\displaystyle \frac{1}{{\rm{\cos }}\alpha }\left(\begin{array}{cc}{\rm{\cos }}(\tilde{t}-\alpha ) & {\rm{-i}}\;{\rm{\sin }}\tilde{t}\\ {\rm{-i}}\;{\rm{\sin }}\tilde{t} & {\rm{\cos }}(\tilde{t}+\alpha )\end{array}\right),\end{eqnarray}$here $\tilde{t}=\tfrac{{\rm{\Delta }}{Et}}{2}$ , ${\rm{\Delta }}E={E}_{+}-{E}_{-}$, ${E}_{\pm }=\pm s{\rm{\cos }}\alpha $ represent the eigenvalues of the Hamiltonian. Then the final state ${\tilde{\rho }}_{t}$ of the system after performing the PT-symmetric operation on the qubit particle can be obtained(11)$\begin{eqnarray}{\tilde{\rho }}_{t}=\displaystyle \frac{(I\bigotimes {U}_{t})\rho {\left(I\bigotimes {U}_{t}\right)}^{\dagger }}{{\rm{Tr}}[(I\bigotimes {U}_{t})\rho {\left(I\bigotimes {U}_{t}\right)}^{\dagger }]}.\end{eqnarray}$

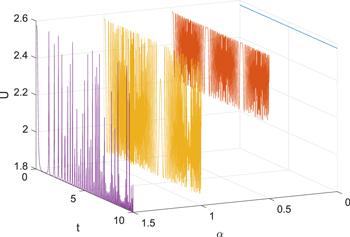
We plot entropic uncertainty dynamics in figure 8 to clearly demonstrate the effectiveness of PT-symmetric operation, where the blue line (α=0) represents the entropic uncertainty of the hybrid system in the thermal equilibrium state without PT-symmetric operation, which has no variation with time. When there exists PT-symmetric operation, i.e. $\alpha \ne 0$, we can see that the operation of PT-symmetry can obviously reduce the entropic uncertainty for a certain time. And the larger the value of α is, the more effective the influence of PT-symmetric operation on U will be. Interestingly, in the condition of α=0.5 it seems that the uncertainty U performs periodic behavior during evolution, which may be similar to the phenomenon of beat frequency.

Figure 8.

New window|Download| PPT slide
Figure 8.Entropic uncertainty U versus t and α with s=1.

4. Conclusions

In summary, we have investigated the QMA-EUR of the Heisenberg mixed-spin (1/2, 1) XYZ model with DM interaction and inhomogeneous magnetic field. The influences of coupling strengths J and J_z, anisotropic intensity Δ, magnetic fields, and DM interaction on the entropic uncertainty are analyzed in detail. Our results show that the increase of temperature can lead to the enhancement of entropic uncertainty, but the uncertainty degree can be decreased by choosing proper values of coupling strength and anisotropic parameters. If the magnetic field is very strong, the uncertainty will stay at a low level. Moreover, by comparing the uncertainty in the mixed-spin (1/2, 1) model with the cases of spin (1/2, 1/2) and spin (1, 1), it is found that the higher the systemic dimension is, the more complex the distribution of the uncertainty is. Additionally, we put forward two schemes of PT-symmetry and WMR for the steering of the entropic uncertainty. It is proved that PT-symmetric operation and WMR can effectively reduce the entropic uncertainty by adjusting proper parameters. Our findings could shed some new light on the quantum precision measurement in the hybrid physical systems.

Acknowledgments

This work was supported by the National Natural Science Foundation of China under Grant Nos. 91950112 and 11174081, and the National Key Research and Development Program of China under Grant No. 2016YFB0501601.

Reference View Option By original order
By published year
By cited within times
By Impact factor

[1]Hu M L Fan H 2012 Phys. Rev. A 86 032338
DOI:10.1103/PhysRevA.86.032338 [Cited within: 1]

[2]Prevedel R Hamel D R Colbeck R Fisher K Resch K J 2011 Nat. Phys. 7 757
DOI:10.1038/nphys2048 [Cited within: 1]

[3]Heisenberg W 1927 Z. Phys. 43 172
DOI:10.1007/BF01397280 [Cited within: 1]

[4]Berta M Christandl M Colbeck R Renes J M Renner R 2010 Nat. Phys. 6 659
DOI:10.1038/nphys1734 [Cited within: 2]

[5]Deutsch D 1983 Phys. Rev. Lett. 50 631
DOI:10.1103/PhysRevLett.50.631 [Cited within: 1]

[6]Kraus K 1987 Phys. Rev. D 35 3070
DOI:10.1103/PhysRevD.35.3070

[7]Maassen H Uffink J B M 1988 Phys. Rev. Lett. 60 1103
DOI:10.1103/PhysRevLett.60.1103

[8]Tomamichel M Renner R 2011 Phys. Rev. Lett. 106 110506
DOI:10.1103/PhysRevLett.106.110506

[9]Renes J M Boileau J C 2009 Phys. Rev. Lett. 103 020402
DOI:10.1103/PhysRevLett.103.020402 [Cited within: 1]

[10]Pati A K 2011 Phys. Rev. A 63 014302
DOI:10.1103/PhysRevA.63.014302 [Cited within: 1]

[11]Shi J Ding Z Wu T He J Yu L Sun W Wang D Ye L 2017 Laser Phys. Lett. 14 125208
DOI:10.1088/1612-202X/aa82a0 [Cited within: 1]

[12]Zou H M Fang M F Yang B Y Guo Y N He W Zhang S Y 2014 Phys. Scr. 89 115101
DOI:10.1088/0031-8949/89/11/115101 [Cited within: 1]

[13]Coles P J Colbeck R Yu L Zwolak M 2012 Phys. Rev. Lett. 108 210405
DOI:10.1103/PhysRevLett.108.210405 [Cited within: 1]

[14]Xu Z Y Yang W Feng M 2012 Phys. Rev. A 86 012113
DOI:10.1103/PhysRevA.86.012113

[15]Liu S Mu L Z Fan H 2015 Phys. Rev. A 91 042133
DOI:10.1103/PhysRevA.91.042133

[16]Pramanik T Chowdhury P Majumdr A S 2013 Phys. Rev. Lett. 110 020402
DOI:10.1103/PhysRevLett.110.020402

[17]Schneeloch J Broadbent C J Walborn S P Cavalcanti E G Howell J C 2013 Phys. Rev. A 87 062103
DOI:10.1103/PhysRevA.87.062103

[18]Hu M L Fan H 2013 Phys. Rev. A 87 022314
DOI:10.1103/PhysRevA.87.022314

[19]Zhang Z Y Liu J M Hu Z F Wang Y Z 2018 Ann. Phys., Berlin 530 180020
DOI:10.1002/andp.201800208

[20]Zhang S Y Fang M F Yu M 2016 Int. J. Theor. Phys. 55 1824
DOI:10.1007/s10773-015-2822-9

[21]Xiao Y Jing N Li-Jost X 2017 Quantum Inf. Process. 16 104
DOI:10.1007/s11128-017-1554-6

[22]Yu M Fang M F 2017 Quantum Inf. Process. 16 213
DOI:10.1007/s11128-017-1666-z

[23]Ming F Wang D Shi W N Huang A J Sun W Y Ye L 2018 Quantum Inf. Process. 17 89
DOI:10.1007/s11128-018-1857-2

[24]Li C F Xu J S Xu X Y Li K Guo G C 2011 Nat. Phys. 7 752
DOI:10.1038/nphys2047 [Cited within: 1]

[25]Haseli S Ahmadi F 2019 Eur. Phys. J. D 73 65
DOI:10.1140/epjd/e2019-90526-1 [Cited within: 1]

[26]Yuan X Bai G Peng T Ma X 2017 Phys. Rev. A 96 032313
DOI:10.1103/PhysRevA.96.032313

[27]Mohammad R P Saeed H 2020 Laser Phys. Lett. 17 025206
DOI:10.1088/1612-202X/ab6a15

[28]Pourkarimi M R 2019 Int. J. Quantum Inf. 17 1950008
DOI:10.1142/S0219749919500084

[29]Wang D Huang A J Hoehn R D Ming F Sun W Y Shi J D Ye L Kais S 2017 Sci. Rep. 7 1066
DOI:10.1038/s41598-017-01094-8 [Cited within: 1]

[30]Wang D Ming F Huang A J Sun W Y Ye L 2017 Laser Phys. Lett. 14 095204
DOI:10.1088/1612-202X/aa7b4e [Cited within: 1]

[31]Zhang Z Y Wei D X Liu J M 2017 Laser Phys. Lett. 15 065207
DOI:10.1088/1612-202X/aabb36 [Cited within: 1]

[32]Zhu Y Y Zhang Y 2013 Commun. Theor. Phys. 59 407 410
DOI:10.1088/0253-6102/59/4/04

[33]Zhao L M Zhang G F 2017 Quantum Inf. Process. 16 216
DOI:10.1007/s11128-017-1665-0

[34]Albayrak E 2011 Opt. Commun. 284 1631
DOI:10.1016/j.optcom.2010.11.034 [Cited within: 1]

[35]Horodecki M Horodecki P Horodecki R 1996 Phys. Lett. A 1 223
DOI:10.1016/0375-9601(95)00904-3 [Cited within: 1]

[36]Mendonca P E M F Marchiolli M A Hedemann S R 2017 Phys. Rev. A 95 022324
DOI:10.1103/PhysRevA.95.022324 [Cited within: 1]

[37]Chen P F Sun W Y Ming F Huang A J Wang D Ye L 2018 Laser Phys. Lett. 15 015206
DOI:10.1088/1612-202X/aa9639 [Cited within: 1]

[38]Zhang Y L Fang M F Kang G D Zhou Q P 2015 Quantum Inf. Process. 13 1550037
DOI:10.1142/S0219749915500379

[39]Haseil S Dolatkhah H Salimi S Khorashad A S 2019 Laser Phys. Lett. 16 045207
DOI:10.1088/1612-202X/ab0a58

[40]Wang Q Yao C M 2014 Commun. Theor. Phys. 61 464
DOI:10.1088/0253-6102/61/4/10 [Cited within: 1]

[41]Xiao X Li Y L 2013 Eur. Phys. J. D 67 204
DOI:10.1140/epjd/e2013-40036-3 [Cited within: 1]

[42]Yang R Y Liu J M 2017 Quantum Inf. Process. 16 125
DOI:10.1007/s11128-017-1575-1 [Cited within: 1]

[43]Gunther U Samsonov B F 2008 Phys. Rev. Lett. 101 230404
DOI:10.1103/PhysRevLett.101.230404 [Cited within: 1]