Jian Li(李剑)^,1,2, Wu-Ji Sun(孙无忌)¹¹College of Physics, Jilin University, Changchun 130012, China
²Department of Physics, Western Michigan University, Kalamazoo, MI 49008, United States of America

Received:2019-12-13Revised:2020-01-20Accepted:2020-01-20Online:2020-04-01


Abstract
The ground-state properties, especially the magnetic moments, of odd-A aluminum isotopes have been studied and well reproduced in covariant density functional theory after considering the rotational coupling. The present calculations support the rotational structure in the ground state of odd-A aluminum isotopes, i.e. the ground state $5/{2}^{+}$ is built on the intrinsic state 5/2[202]. In addition, the contribution from the time-odd fields is also discussed.
Keywords： nuclear magnetic moment;covariant density functional theory;aluminum isotopes;rotational coupling;time-odd fields


PDF (497KB)MetadataMetricsRelated articlesExportEndNote|Ris|BibtexFavorite
Cite this article
Jian Li(李剑), Wu-Ji Sun(孙无忌). Magnetic moments of odd-A aluminum isotopes in covariant density functional theory. Communications in Theoretical Physics, 2020, 72(5): 055301- doi:10.1088/1572-9494/ab7708

1. Introduction

Magnetic moment, as one of the most important observables of atomic nucleus, provides rich information about nuclear structure, has attracted a lot of attentions for decades [1–4] and also challenges the various nuclear models. Among them, the description of the odd-A nuclei is one of the greatest successes of the nuclear shell model by Mayer and Jensen. In this extreme single-particle picture, the even–even core of the odd-A nuclei is regarded as an inert object and the corresponding magnetic moment is from the unpaired valence nucleon (valence-nucleon approximation), which leads to the well-known Schmidt values. Thus the magnetic moment of odd–even nuclei around doubly magic ones can be reproduced well, and the still existing deviations can be further explained by the meson exchange current (MEC, i.e. the exchange of a charged meson) and configuration mixing (CM, or core polarization, i.e. the correlation not included in the mean-field approximation) [2, 3, 5–9]. Recently, by considering the configuration mixing and meson exchange current corrections, the newly measured magnetic moment of ¹³³Sb [10], ⁶⁷Ni, ⁶⁹Cu [11], ⁴⁹Sc [12] and other odd nuclei near magic ones [13] have been well reproduced.

In spherical odd-mass nuclei, the addition of an odd nucleon to an even core generates the configuration mixing, which can be treated in the perturbation theory. For deformed odd-A nuclei, the even–even core is not inert, and the magnetic moment can not be fully understood by the valence-nucleon approximation. Although the spin of the deformed odd-A nuclei is in some way determined by the orbit of the last odd nucleon, the contribution from the core can not be ignored. Therefore the odd nucleon should be coupled to a collective nuclear droplet (the core), i.e. a strong coupling between the collective rotation and intrinsic single particle motion in the well-deformed nuclei [14]. In such a strong coupling approximation, the magnetic moment is determined by the final spin and intrinsic nucleonic motion. Up to now, the magnetic moments of odd-mass nuclei such as carbon and neon isotopes have been investigated by using the deformed Skyrme Hartree–Fock model [15] and deformed axially symmetric Woods–Saxon potential [16].

On the theoretical side, many successful nuclear structure models have been developed in the past few decades. However, the application for nuclear magnetic moments is still not satisfactory and the theoretical description of nuclear magnetic moments has been a long-standing problem [3, 6, 7]. The covariant density functional theory (CDFT), taking Lorentz symmetry into account in a self-consistent way, has received wide attention due to its successful description of many nuclear properties in a large number of stable and exotic nuclei [17–23] and the successful application of its predictions to r-process simulations [24–26]. It includes naturally the nuclear spin–orbit potential in a covariant way. It can well reproduce the isotopic shifts of Pb isotopes [27] and explain naturally the origin of the pseudospin symmetry as the relativistic symmetry [28] and the spin symmetry in the anti-nucleon spectrum [29]. Moreover, it can include the nuclear magnetism self-consistently [30], and provide a consistent description of currents and time-odd fields, which play an important role in nuclear magnetic moments [8, 31–35] and nuclear rotations [36–41].

In particular, by considering the time-odd fields, one-pion exchange current, first-order and second-order configuration mixing effects, the magnetic moments of spherical odd-A nuclei with doubly closed shell core plus or minus one nucleon have been well reproduced [9, 32–35]. However, the present covariant description of nuclear magnetic moment is mainly restricted to the spherical odd-A nuclei near magic shell. Although the magnetic moment of deformed odd-A nucleus ³³Mg has also been described by the CDFT [42], the ground-state spin should be investigated further.

Rotational phenomenon in sd shell of light nuclei has attracted a lot of attentions, including the rotational bands in alpha-cluster nuclei [43]. In the middle of the sd shell, odd-mass nuclei with mass number 19≤A≤25 are strongly deformed [14], and their low-lying states form rotational bands. In particular, the 5/2[202] orbit, the only nilsson orbit with ${K}^{\pi }=5/{2}^{+}$ in the sd shell region, forms the ground-state band in the A=25 mirror nuclei ²⁵Mg and ²⁵Al. The facts that ground state spin of odd-A aluminum isotopes, i.e. ^{23,25,27,29,31,33}Al, is $5/{2}^{+}$, and the ab initio shell-model calculations [44] indicate the odd proton occupying the d_5/2 orbit in the ground state together with corresponding nuclear magnetic moments provides a good opportunity to investigate the rotational structure in those deformed nuclei.

Based on the above considerations, it is necessary to study the ground-state magnetic moment of odd-A aluminum isotopes in deformed CDFT. In section 2, we will briefly introduce the theoretical framework of CDFT and corresponding formulas for calculating the magnetic moments in the strong coupling approximation. The calculations are described and the results are discussed in section 3. Finally, section 4 contains a brief summary and a perspective.

2. Framework

Following the finite-range meson-exchange version of the covariant density functional theory in [22, 45, 46], where nucleons are described as Dirac particles interacting via the exchange of the isoscalar meson σ, isoscalar-vector meson ω and isovector-vector meson ρ as well as photon, the lagrangian density is adopted as follows(1)$\begin{eqnarray}\begin{array}{rcl}{ \mathcal L } & = & \overline{\psi }\left[{\rm{i}}{\gamma }^{\mu }{\partial }_{\mu }-M-{g}_{\sigma }\sigma -{g}_{\omega }{\gamma }^{\mu }{\omega }_{\mu }-{g}_{\rho }{\gamma }^{\mu }\vec{\tau }\cdot {\vec{\rho }}_{\mu }\right.\\ & & \left.-e{\gamma }^{\mu }\displaystyle \frac{1-{\tau }_{3}}{2}{A}_{\mu }\right]\psi +\displaystyle \frac{1}{2}{\partial }^{\mu }\sigma {\partial }_{\mu }\sigma -\displaystyle \frac{1}{2}{m}_{\sigma }^{2}{\sigma }^{2}-\displaystyle \frac{1}{3}{g}_{2}{\sigma }^{3}\\ & & -\displaystyle \frac{1}{4}{g}_{3}{\sigma }^{4}-\displaystyle \frac{1}{4}{{\rm{\Omega }}}^{\mu \nu }{{\rm{\Omega }}}_{\mu \nu }+\displaystyle \frac{1}{2}{m}_{\omega }^{2}{\omega }^{\mu }{\omega }_{\mu }+\displaystyle \frac{1}{4}{c}_{3}{\left({\omega }^{\mu }{\omega }_{\mu }\right)}^{2}\\ & & -\displaystyle \frac{1}{4}{\vec{R}}^{\mu \nu }\cdot {\vec{R}}_{\mu \nu }+\displaystyle \frac{1}{2}{m}_{\rho }^{2}{\vec{\rho }}^{\mu }\cdot {\vec{\rho }}_{\mu }-\displaystyle \frac{1}{4}{F}^{\mu \nu }{F}_{\mu \nu }.\end{array}\end{eqnarray}$

It should be noted that for the even–even nuclei with time-reversal symmetry, the space-like components of vector meson and photon fields, i.e. time-odd fields, vanish and do not contribute to the energy functional. However, in odd-A nuclei, the unpaired odd nucleon breaks the time-reversal invariance, and time-odd fields ${\boldsymbol{V}}({\boldsymbol{r}})$ exist. Then the Dirac equation for nucleon becomes(2)$\begin{eqnarray}\{{\boldsymbol{\alpha }}\cdot [-{\rm{i}}{\boldsymbol{\nabla }}-{\boldsymbol{V}}({\boldsymbol{r}})]+{V}_{0}({\boldsymbol{r}})+\beta [M+S({\boldsymbol{r}})]\}{\psi }_{i}={\varepsilon }_{i}{\psi }_{i},\end{eqnarray}$with $S({\boldsymbol{r}})$ the scalar potential(3)$\begin{eqnarray}S({\boldsymbol{r}})={g}_{\sigma }\sigma ({\boldsymbol{r}}),\end{eqnarray}$${V}_{0}({\boldsymbol{r}})$ the usual vector potential, i.e. the time-like component of vector potential,(4)$\begin{eqnarray}{V}_{0}({\boldsymbol{r}})={g}_{\omega }{\omega }_{0}({\boldsymbol{r}})+{g}_{\rho }{\tau }_{3}{\rho }_{0}({\boldsymbol{r}})+e(1-{\tau }_{3}){A}_{0}({\boldsymbol{r}})/2,\end{eqnarray}$and ${\boldsymbol{V}}({\boldsymbol{r}})$ the space-like component of vector potential(5)$\begin{eqnarray}{\boldsymbol{V}}({\boldsymbol{r}})={g}_{\omega }{\boldsymbol{\omega }}({\boldsymbol{r}}).\end{eqnarray}$${\boldsymbol{\rho }}({\boldsymbol{r}})$ and ${\boldsymbol{A}}({\boldsymbol{r}})$ are often not taken into account as they turn out to be small compared with ${\boldsymbol{\omega }}({\boldsymbol{r}})$ field in light nuclei [47]. In the present paper, the bold types are adopted to indicate space vectors and arrows for the vectors in isospin space.

The Klein–Gordon equations for scalar meson field σ, time-like components of vector mesons fields ω₀, ρ₀ and electromagnetic fields A₀ are the same as in the [45]. The space-like component of vector meson field ${\boldsymbol{\omega }}$ is determined by(6)$\begin{eqnarray}\{-{\rm{\Delta }}+{m}_{\omega }^{2}\}{\boldsymbol{\omega }}={g}_{\omega }{{\boldsymbol{j}}}_{{\rm{B}}}-{c}_{3}{\omega }^{\nu }{\omega }_{\nu }{\boldsymbol{\omega }},\end{eqnarray}$with the baryon current ${{\boldsymbol{j}}}_{{\rm{B}}}={\sum }_{i}{n}_{i}{\bar{\psi }}_{i}{\boldsymbol{\gamma }}{\psi }_{i}$. As the pair correlation is not considered here, the occupation numbers n_i take the value one (zero) for the states below (above) the Fermi surface. For more details, such as the total energy of the nucleus after considering the time-odd fields, can be found in [42] and references therein.

The electromagnetic current operator used to describe the nuclear magnetic moment is written as [31, 42, 48–50](7)$\begin{eqnarray}{\hat{J}}^{\mu }(x)=Q\bar{\psi }(x){\gamma }^{\mu }\psi (x)+\displaystyle \frac{\kappa }{2M}{\partial }_{\nu }[\bar{\psi }(x){\sigma }^{\mu \nu }\psi (x)],\end{eqnarray}$where the nucleon charge is $Q\equiv \displaystyle \frac{e}{2}(1-{\tau }_{3})$, the antisymmetric tensor operator is ${\sigma }^{\mu \nu }=\displaystyle \frac{{\rm{i}}}{2}[{\gamma }^{\mu },{\gamma }^{\nu }]$, and κ is the free anomalous gyromagnetic ratio of the nucleon with κ_p=1.793 and κ_n=−1.913 for proton and neutron respectively.

In equation (7), the first term gives the Dirac current and the second term is the so-called anomalous current. The nuclear dipole magnetic moment, in unit of the nuclear magneton ${\mu }_{{\rm{N}}}=e{\hslash }/2{Mc}$, is given by [35](8a)$\begin{eqnarray}{\boldsymbol{\mu }}=\displaystyle \frac{1}{2{\mu }_{{\rm{N}}}}\int {\rm{d}}{\boldsymbol{r}}{\boldsymbol{r}}\times \langle g.s.| \hat{{\boldsymbol{j}}}({\boldsymbol{r}})| g.s.\rangle \end{eqnarray}$(8b)$\begin{eqnarray}=\int {\rm{d}}{\boldsymbol{r}}\,\left[\displaystyle \frac{{{Mc}}^{2}}{{\hslash }c}Q{\psi }^{+}({\boldsymbol{r}}){\boldsymbol{r}}\times {\boldsymbol{\alpha }}\psi ({\boldsymbol{r}})+\kappa {\psi }^{+}({\boldsymbol{r}})\beta {\boldsymbol{\Sigma }}\psi ({\boldsymbol{r}})\right],\end{eqnarray}$where $\hat{{\boldsymbol{j}}}({\boldsymbol{r}})$ is the operator of space-like components of the electromagnetic current in equation (7). The first term in above equation gives the Dirac magnetic moment, and the second term gives the anomalous magnetic moment.

Therefore, the nuclear magnetic moment vector operator in the covariant density functional theory, in unit of μ_N, is given by(9)$\begin{eqnarray}\hat{{\boldsymbol{\mu }}}=\displaystyle \frac{{{Mc}}^{2}}{{\hslash }c}Q{\boldsymbol{r}}\times {\boldsymbol{\alpha }}+\kappa \beta {\boldsymbol{\Sigma }}.\end{eqnarray}$

For deformed odd-A nuclei, the valence nucleon approximation is invalid and there is a strong coupling between the core and the valence nucleon. Therefore, the total magnetic moment consists of two parts, i.e. the intrinsic nucleonic motion and the collective rotational motion. In the axially deformed case with the projection of the momentum on the nuclear symmetry axis K (contribution from the intrinsic nucleonic motion) and spin I, the nuclear magnetic moment can be written as [14](10)$\begin{eqnarray}\mu ={g}_{R}I+({g}_{K}-{g}_{R})\displaystyle \frac{{K}^{2}}{I+1},\quad \quad ({\rm{for}}\ K\gt 1/2).\end{eqnarray}$g_R is the corresponding effective rotational gyromagnetic factor, with ${g}_{R}\sim Z/A$. The intrinsic gyromagnetic factor reads ${g}_{K}={\mu }_{\mathrm{intri}.}/K$ and intrinsic magnetic moment ${\mu }_{\mathrm{intri}.}$ is obtained from self-consistent CDFT calculations in equation (8a).

3. Results and discussion

In the present CDFT calculations, both the Dirac equation for nucleons and the Klein–Gordon equations for mesons are solved in a isotropic harmonic oscillator basis [51, 52] and a basis of 14 major oscillator shells is adopted. The oscillator frequency is given by ${\hslash }{\omega }_{0}=41{A}^{-1/3}$ MeV. The effective meson-exchange interaction parameter PK1 [46] is used throughout the calculation.

The energy curve, i.e. the total energies as a function of quadrupole deformation, is obtained through the quadrupole deformation constrained calculation by constraining the mass quadrupole moment $\langle {\hat{Q}}_{2}\rangle $ to a given value q [53],(11)$\begin{eqnarray}\langle H^{\prime} \rangle =\langle H\rangle +\displaystyle \frac{1}{2}C{\left(\langle {\hat{Q}}_{2}\rangle -q\right)}^{2},\end{eqnarray}$where $\langle H\rangle $ is the total energy and C is the stiffness constant. The quadrupole deformation parameter β₂ is obtained from the calculated $\langle {\hat{Q}}_{2}\rangle $ through(12)$\begin{eqnarray}\langle {\hat{Q}}_{2}\rangle =\langle {\hat{Q}}_{2}{\rangle }_{p}+\langle {\hat{Q}}_{2}{\rangle }_{n}=\displaystyle \frac{3}{\sqrt{5\pi }}{{AR}}_{0}^{2}{\beta }_{2},\end{eqnarray}$with ${R}_{0}=1.2{A}^{1/3}$. Both the adiabatic and the configuration-fixed deformation constrained calculations [45, 54, 55] will be adopted in the following.

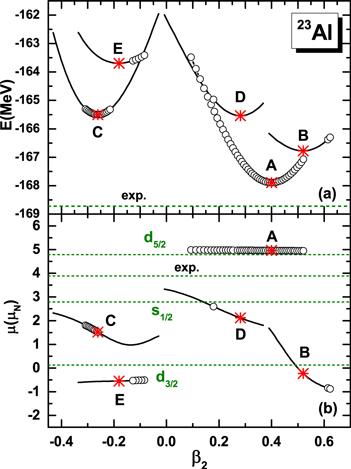
In figure 1(a), the energy curves for ²³Al, i.e. the total energies as a function of the quadrupole deformation parameter β₂ calculated by adiabatic (shown as open circles) and configuration-fixed (shown as solid lines) deformation constrained CDFT approach with time-odd fields, are presented. The local minima in the energy curves for each configuration are represented by stars and labeled as A, B, C, D and E. A is the ground state and found to be prolate deformed, β₂=0.40, with the total energy of −167.89 MeV, in comparison with the corresponding data of −168.72 MeV [56]. The deviation between experimental and theoretical energy is 0.83 MeV, which could be caused by rotational energy correction [58]. It should be noted that the ${\beta }_{2}$ values obtained by Hartree–Fock–Bogoliubov calculations based on the D1S Gongy effective nucleon–nucleon interaction is also around 0.4 [59], further supporting the large deformation in ²³Al.

Figure 1.

New window|Download| PPT slide
Figure 1.The total energies (a) and magnetic moments (b) for ²³Al as functions of quadrupole deformation β₂ by adiabatic and configuration-fixed (indicated by open circles and solid lines respectively) deformation constrained CDFT approach with time-odd fields using PK1 parameter set. The minima in the energy curves for different configurations are indicated by stars and marked as A, B, C, D, and E respectively. In panel (a), the experimental energy −168.72 MeV [56] (dotted line) is shown for comparison with A. In panel (b), the experimental magnetic moment μ=3.889μ_N [57] (dotted line in (b)) and the Schmidt magnetic moments of $\pi 2{s}_{1/2},\pi 1{d}_{3/2}$, and $\pi 1{d}_{5/2}$ orbitals (dashed lines) are also shown for comparison.


Using equation (8a), the effective electromagnetic current gives the intrinsic magnetic moment of valence nucleons with assigned configurations in figure 1(b). The calculated magnetic moment for the ground state is 4.96 μ_N, larger than the data μ=3.889 μ_N [57]. It could be seen that the intrinsic magnetic moment is sensitive to configuration, but to β₂, it is not sensitive for the configurations A and E, and sensitive for B, C and D. This can be understood by the configuration mixing of single particle components. For example, the magnetic moment of configuration A does not change much with β₂, as the odd proton occupies the orbital $\pi 5/2$[202+] with third component K = 5/2 and the configuration mixing is very weak. In comparison, the third component in configuration B, i.e. π1/2[211+], is K=1/2, which has a strong mixing for configurations πd_3/2, s_1/2 and d_5/2, thus the magnetic moment varies quickly with β₂.

The calculated total energies (E_tot), excitation energies (E_x), quadrupole deformation (β_cal), valence nucleon configuration and intrinsic magnetic moments (μ_intri.) of ²³Al for different configurations are listed in table 1. For ground state A, it has prolate deformation, and main component of corresponding valence nucleon wave function $\pi \tfrac{5}{2}$[202+] belongs to $\pi \,1{d}_{5/2}$, while the intrinsic magnetic moment $\,4.96\,{\mu }_{{\rm{N}}}$ is close to the Schmidt value $\,4.79\,{\mu }_{{\rm{N}}}$ of $\pi \,1{d}_{5/2}$. For state B, the unpaired valence nucleon configuration is $\pi \tfrac{1}{2}$[211+] with the main component belonging to $\pi \,2{s}_{1/2}$, and the calculated excitation energy 1.12 MeV is also in reasonable agreement with the corresponding experimental data 0.550 MeV of $1/{2}^{+}$ in [60]. For states C, and E, they have negative quadrupole deformation, and corresponding configurations are $\pi \tfrac{1}{2}$[220+] and $\pi \tfrac{3}{2}$[211+]. It could be seen one pair of neutrons have been broken in state D. In fact, Both the main components of state C and E are belonging to $\pi \,1{d}_{5/2}$ but with different third components, and the corresponding excitation energies of states C and E are 2.39 and 4.20 MeV, close to the experimental values 2.575 and 3.197 MeV.


Table 1.
Table 1.The calculated total energies (E_tot), the excitation energies (E_x), the quadrupole deformation parameters (β₂), the valence nucleon configuration, and the intrinsic magnetic moments (μ_intri.) of ²³Al for states A, B, C, D and E, in comparison with the experimental energies E_x(exp.) [60], and ground-state magnetic moment (μ_exp.) [57]. The energy is in unit of MeV and the magnetic moment is in μ_N.

State	$\,\,{E}_{x}({E}_{{\rm{tot}}})$	β2	Valence nucleon configuration	μintri.(μexp.)	Ex(exp.)
A	(−167.89)	0.40	$\pi \tfrac{5}{2}$[202+] $\left(1{d}_{5/2}\tfrac{5}{2}\right)$	4.96 (3.889)
B	1.12(−166.77)	0.52	$\pi \tfrac{1}{2}$[211+] $\left(2{s}_{1/2}\tfrac{1}{2}\right)$	−0.23	0.550
C	2.39(−165.50)	−0.26	$\pi \tfrac{1}{2}$[220+] $\left(1{d}_{5/2}\tfrac{1}{2}\right)$	1.52	(2.575)
D	2.35(−165.54)	0.28	$\pi \tfrac{5}{2}[202+]\otimes \nu \left\{\tfrac{1}{2}[220+]\tfrac{3}{2}[211+]\right\}$	2.11
			$\left(\pi \ 1{d}_{5/2}\tfrac{5}{2}\otimes \nu \ 1{d}_{5/2}\tfrac{1}{2}\ 1{d}_{5/2}\tfrac{3}{2}\right)$
E	4.20(−163.69)	−0.18	$\pi \tfrac{3}{2}$[211+] $\left(1{d}_{5/2}\tfrac{3}{2}\right)$	−0.55	(3.197)

New window|CSV

In order to inspect the evolution of the single-proton level and corresponding configuration for ²³Al, proton single-particle energies as a function of β₂ for the configuration A and C are shown in figure 2. The states with positive (negative) parity are marked by solid (dashed) lines, and the occupied orbitals are labeled by filled circles. The self-consistent CDFT calculation indicates the odd proton is in 5/2[202] orbital with β₂=0.40 for the ground state.

Figure 2.

New window|Download| PPT slide
Figure 2.Single-proton energy levels of the ground-state configuration A and C in ²³Al obtained from configuration-fixed deformation constrained calculations. Each pair of time reversal conjugate states are split up into two levels with the opposite third component of angular momentum Ω>0 and $\bar{{\rm{\Omega }}}\lt 0$, denoted by black and red lines respectively. The filled circles indicate the corresponding occupations in the ground state A and state C.


As presented in figure 2, each pair of time reversal conjugate states is split up into two levels with opposite third component of angular momentum Ω>0 and $\bar{{\rm{\Omega }}}\lt 0$, due to the broken time reversal invariance by the time-odd fields. The energy splitting for time reversal conjugate states ranges from 0.01 to 0.6 MeV, and the larger splitting occurs at the orbital with larger third component. At β₂≈0.48, the level crossing happens between the 5/2[202] and 1/2[211] orbital.

In table 2, the calculated energy (E_cal), quadrupole deformation (β₂), valence nucleon configuration, intrinsic magnetic moment (μ_intri.), and the final magnetic moment (μ_tot.) of odd-A Al isotopes in CDFT approach are presented, in comparison with the corresponding experimental spin, parity and magnetic moment. Generally speaking, the quadrupole deformation of Al isotopes is decreasing as the neutron number increases except for ²⁹Al. The quadrupole deformation β₂ of ³³Al in CDFT calculation is 0.06 and indicates a good magic shell for N=20. The obtained β₂ is also in agreement with the Hartree–Fock–Bogoliubov calculations based on the D1S Gongy effective nucleon–nucleon interaction [59]. In fact, the region of deformation around the classic magic number N=20 is a hot topic, while ³³Al located at the edge of the island of inversion has a transitional character and is thought to be a key isotope as the transition into the island of inversion [61] is particularly rapid in the N=20 isotones. Recently, the measurement of electric quadrupole moment and corresponding shell model calculation show that a component of intruder configuration, i.e. two-particle-two-hole (2p–2h) neutron excitation across N=20, from the sd orbitals to the fp orbitals, exists in the ground state wave function [62]. However, the ab initio shell-model calculations together with phenomenological USDB interaction [63] present that the sd model space is able to reproduce correctly the electromagnetic moments of Al isotopes, including ³³Al [44]. Thus the shell structure in ³³Al needs more investigation. In addition, the ab initio shell-model calculations also support the occupancy of d_5/2 proton orbital is approaching 5 [44], in agreement with the present CDFT calculation as well as the last unpaired proton occupying the $5/{2}^{+}[202]$ orbital. It should be pointed out that the calculated total energies within CDFT in ^{23,25,27,29,31}Al are close and also slightly larger than the experimental values except for ³³Al. The case that the CDFT energies of Al isotopes with N≥20 are smaller than the data is also observed in relativistic continuum Hartree-Bogoliubov (RCHB) calculations [64].


Table 2.
Table 2.The calculated energy $\left({E}_{{\rm{cal}}}\right)$, the quadrupole deformation (β₂), valence nucleon configuration, intrinsic magnetic moment (μ_intri.), and final magnetic moments (μ_tot.) of odd-A Al isotopes in CDFT approach, in comparison with the corresponding experimental spin, parity, energy and magnetic moment.

	CDFT					Exp.
Nuclei	β2	Etot(MeV)	Configuration	μintri.(μN)	μtot.(μN)	Iπ	Eexp.	μexp.
23Al	0.40	−167.89	$\pi 5/{2}^{+}[202]$	4.96	3.92	5/2+	−168.72	3.889(5)
25Al	0.39	−198.01	$\pi 5/{2}^{+}[202]$	5.00	3.91	5/2+	−200.52	3.6455(12)
27Al	0.18	−221.26	$\pi 5/{2}^{+}[202]$	5.10	3.96	5/2+	−224.95	3.6415069(7)
29Al	0.27	−239.65	$\pi 5/{2}^{+}[202]$	5.12	3.96	5/2+	−242.10
31Al	0.17	−253.63	$\pi 5/{2}^{+}[202]$	5.16	3.96	5/2+	−255.00	3.830(5)
33Al	0.06	−267.43	$\pi 5/{2}^{+}[202]$	5.22	3.99	5/2+	−264.65	4.088(5)

New window|CSV

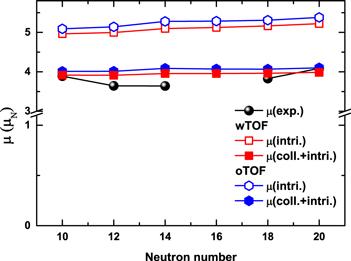
In figure 3, the magnetic moments of odd-A Al isotopes in CDFT approach with and without considering the collective coupling are presented, in comparison with the corresponding experimental data [57]. The intrinsic magnetic moments are obtained from the CDFT calculations based on the valence nucleon configuration $\pi 1{d}_{5/2}$ for ^{23,25,27,29,31,33}Al. It is easy to see that the intrinsic magnetic moments for Al isotopes are around 5μ_N, close to the Schmidt value 4.79 μ_N of $\pi 1{d}_{5/2}$. After including the coupling of collective rotation and intrinsic single particle motion within equation (10), the calculation is greatly improved and the magnetic moments of Al isotopes are well reproduced, with relative deviation from the available data of five nuclei is about 5%. Taking ²³Al as an example, the intrinsic magnetic moment is 4.96 μ_N and the final magnetic moment with collective motion is 3.92 μ_N, excellently reproducing the experimental value 3.889 μ_N. The calculated magnetic moments of ²⁵Al and ²⁷Al are 3.91 and 3.96 μ_N, close to the data 3.646 and 3.642 μ_N, respectively. For ³¹Al and ³³Al, the calculated magnetic moment in CDFT are 3.96 and 3.99 μ_N, also well reproducing the corresponding data 3.830 and 4.088 μ_N, respectively.

Figure 3.

New window|Download| PPT slide
Figure 3.Magnetic moments of odd-A Al isotopes in CDFT approaches with and without considering the collective motion, in comparison with the corresponding experimental data [57]. The results with (red) and without (blue) time-odd fields (TOF) are also shown.


Comparing the CDFT results with and without considering the time-odd fields shown in figure 3, it is found that the theoretical descriptions are improved after including the time-odd fields, i.e. the relative deviation from the data of five nuclei is reduced from 7.6% to 5%. It can be understood that the self-consistent polarization currents in core will slightly reduce the intrinsic magnetic moment here and finally bring the total magnetic moment closer to the data, while the importance of time-odd fields on nuclear magnetic moments has been discussed in [31, 47].

In the CDFT calculations, the empirical value ${g}_{R}=Z/A$ of rigid rotor is adopted and it varies from 0.39 to 0.57 for ^23–33Al. Moreover, the collective gyromagnetic factors g_R for ²⁵Al and ²⁷Al are 0.52 and 0.48, respectively, close to the available experimental gyromagnetic factor for even–even core ²⁴Mg (0.54) and ²⁶Mg (0.50). In [65], the self-consistent CDFT calculations for the gyromagnetic factor of low-lying excited states in ²⁴Mg were carried out, and the available experimental gyromagnetic factor has been reproduced quite well. Furthermore, the calculated gyromagnetic factors have been found to be almost the same for the low-lying excited states with different angular momenta and close to the empirical value. In fact, even when the collective gyromagnetic factor g_R is increased or decreased by 20%, the final magnetic moments change slightly. It can be understood that the collective gyromagnetic factor Z/A is far less than the intrinsic magnetic moment μ_intri. as shown in equation (10).

4. Summary and prospective

In summary, the ground-state properties, especially the magnetic moments of ^{23,25,27,29,31,33}Al have been studied in CDFT. At first, using the configuration-fixed deformation constrained calculation, the potential energy, intrinsic magnetic moment and single proton energy levels as a function of quadrupole deformation for ²³Al are given. The ground state of ²³Al has been found to be prolate deformed, β₂=0.40, with the odd proton in 5/2[202] orbital and intrinsic magnetic moment 4.96 μ_N, which is close to the Schmidt value of πd_5/2. After including the strong coupling of collective rotation and intrinsic single particle motion, the ground-state spin and parity $5/{2}^{+}$ of odd-A Al isotopes can be understood and the corresponding magnetic moments are well reproduced, with relative deviation from the data of five nuclei about 5%. In addition, it is found that the theoretical descriptions are improved after considering the time-odd fields, i.e. the relative deviation from the data of five nuclei is reduced from 7.6% to 5%. The above calculations support that the ground state $5/{2}^{+}$ is built on the intrinsic state 5/2[202] and a rotational structure exists in the ground state of the odd mass Al isotopes. A further investigation with angular momentum projection based on our deformed CDFT solution is to be done in the future, and other forms of energy functionals such as PC-PK1 [66], one of the most accurate density functionals at present, should be adopted to check whether the present conclusion depends on the functionals.

Acknowledgments

This work is supported by the National Natural Science Foundation of China under Grants No. 11675063, No. 11205068, No. 11475072, and No. 11847310.

Reference View Option By original order
By published year
By cited within times
By Impact factor

[1]Blin-Stoyle R J 1956 Rev. Mod. Phys. 28 75
DOI:10.1103/RevModPhys.28.75 [Cited within: 1]

[2]Arima A 1984 Prog. Part. Nucl. Phys. 11 53
DOI:10.1016/0146-6410(84)90012-7 [Cited within: 1]

[3]Castel B Towner I S 1990 Modern Theories of Nuclear Moments Oxford Oxford University Press
[Cited within: 2]

[4]Talmi I 2005 Int. J. Mod. Phys. E 14 821
DOI:10.1142/S0218301305003570 [Cited within: 1]

[5]Arima A 1978 Prog. Part. Nucl. Phys. 1 41
DOI:10.1016/0146-6410(78)90005-4 [Cited within: 1]

[6]Towner I S 1987 Phys. Rep. 155 263
DOI:10.1016/0370-1573(87)90138-4 [Cited within: 1]

[7]Arima A Shimizu K Bentz W Hyuga H 1987 Adv. Nucl. Phys. 18 1
[Cited within: 1]

[8]Arima A 2011 Sci. China Phys. Mech. Astron. 54 188
DOI:10.1007/s11433-010-4224-6 [Cited within: 1]

[9]Li J Meng J 2018 Front. Phys. 13 132109
DOI:10.1007/s11467-018-0842-7 [Cited within: 2]

[10]Stone N J et al. 1997 Phys. Rev. Lett. 78 820
DOI:10.1103/PhysRevLett.78.820 [Cited within: 1]

[11]Rikovska J et al. 2000 Phys. Rev. Lett. 85 1392
DOI:10.1103/PhysRevLett.85.1392 [Cited within: 1]

[12]Ohtsubo T et al. 2012 Phys. Rev. Lett. 109 032504
DOI:10.1103/PhysRevLett.109.032504 [Cited within: 1]

[13]Co’ G De Donno V Anguiano M Bernard R N Lallena A M 2015 Phys. Rev. C 92 024314
DOI:10.1103/PhysRevC.92.024314 [Cited within: 1]

[14]Bohr A Mottelson B R 1975 Nuclear Structure Vol II: Nuclear Deformation New York Benjamin
[Cited within: 3]

[15]Sagawa H Zhou X R Zhang X Z Suzuki T 2004 Phys. Rev. C 70 054316
DOI:10.1103/PhysRevC.70.054316 [Cited within: 1]

[16]Yakut H Tabra E Akbra K A Zenginerler Z Kaplan P 2013 Int. J. Mod. Phys. E 22 1350076
DOI:10.1142/S0218301313500766 [Cited within: 1]

[17]Ring P 1996 Prog. Part. Nucl. Phys. 37 193
DOI:10.1016/0146-6410(96)00054-3 [Cited within: 1]

[18]Vretenar D Afanasjev A V Lalazissis G A Ring P 2005 Phys. Rep. 409 101
DOI:10.1016/j.physrep.2004.10.001

[19]Meng J Toki H Zhou S G Zhang S Q Long W H Geng L S 2006 Prog. Part. Nucl. Phys. 57 470
DOI:10.1016/j.ppnp.2005.06.001

[20]Meng J et al. 2011 Prog. Phys. 31 199 (in Chinese)


[21]Nikšić T Vretenar D Ring P 2011 Prog. Part. Nucl. Phys. 66 519
DOI:10.1016/j.ppnp.2011.01.055

[22]Meng J 2015 Relativistic Density Functional for Nuclear Structure Singapore World Scientific
[Cited within: 1]

[23]Niu Z M Niu Y F Liang H Z Long W H Meng J 2017 Phys. Rev. C 95 044301
DOI:10.1103/PhysRevC.95.044301 [Cited within: 1]

[24]Niu Y Paar N Vretenar D Meng J 2009 Phys. Lett. B 681 315
DOI:10.1016/j.physletb.2009.10.046 [Cited within: 1]

[25]Niu Z Niu Y Liang H Long W Nikšić T Vretenar D Meng J 2013 Phys. Lett. B 723 172
DOI:10.1016/j.physletb.2013.04.048

[26]Li Z Niu Z M Sun B H 2019 Sci. China Phys. Mech. Astron. 62 982011
DOI:10.1007/s11433-018-9355-y [Cited within: 1]

[27]Sharma M M Lalazissis G A Ring P 1993 Phys. Lett. B 317 9
DOI:10.1016/0370-2693(93)91561-Z [Cited within: 1]

[28]Liang H Meng J Zhou S-G 2015 Phys. Rep. 570 1
DOI:10.1016/j.physrep.2014.12.005 [Cited within: 1]

[29]Zhou S-G Meng J Ring P 2003 Phys. Rev. Lett. 91 262501
DOI:10.1103/PhysRevLett.91.262501 [Cited within: 1]

[30]Koepf W Ring P 1989 Nucl. Phys. A 493 61
DOI:10.1016/0375-9474(89)90532-0 [Cited within: 1]

[31]Yao J M Chen H Meng J 2006 Phys. Rev. C 74 024307
DOI:10.1103/PhysRevC.74.024307 [Cited within: 3]

[32]Li J Meng J Ring P Yao J M Arima A 2011 Sci. China Phys. Mech. Astron. 54 204
DOI:10.1007/s11433-010-4215-7 [Cited within: 1]

[33]Li J Yao J M Meng J Arima A 2011 Prog. Theor. Phys. 125 1185
DOI:10.1143/PTP.125.1185

[34]Wei J Li J Meng J 2012 Prog. Theor. Phys. Suppl. 196 400
DOI:10.1143/PTPS.196.400

[35]Li J Wei J X Hu J N Ring P Meng J 2013 Phys. Rev. C 88 064307
DOI:10.1103/PhysRevC.88.064307 [Cited within: 3]

[36]König J Ring P 1993 Phys. Rev. Lett. 71 3079
DOI:10.1103/PhysRevLett.71.3079 [Cited within: 1]

[37]Afanasjev A V Ring P 2000 Phys. Rev. C 62 031302
DOI:10.1103/PhysRevC.62.031302

[38]Afanasjev A V Abusara H 2010 Phys. Rev. C 82 034329
DOI:10.1103/PhysRevC.82.034329

[39]Zhao P W Zhang S Q Peng J Liang H Z Ring P Meng J 2011 Phys. Lett. B 699 181
DOI:10.1016/j.physletb.2011.03.068

[40]Zhao P W Peng J Liang H Z Ring P Meng J 2011 Phys. Rev. Lett. 107 122501
DOI:10.1103/PhysRevLett.107.122501

[41]Meng J Peng J Zhang S-Q Zhao P-W 2013 Front. Phys. 8 55
DOI:10.1007/s11467-013-0287-y [Cited within: 1]

[42]Li J Zhang Y Yao J M Meng J 2009 Sci. China G 52 1586
DOI:10.1007/s11433-009-0194-y [Cited within: 3]

[43]Roshanbakht N Shojaei M R 2018 Commun. Theor. Phys. 70 67
DOI:10.1088/0253-6102/70/1/67 [Cited within: 1]

[44]Saxena A Srivastava P C 2017 Phys. Rev. C 96 024316
DOI:10.1103/PhysRevC.96.024316 [Cited within: 3]

[45]Meng J Peng J Zhang S Q Zhou S-G 2006 Phys. Rev. C 73 037303
DOI:10.1103/PhysRevC.73.037303 [Cited within: 3]

[46]Long W H Meng J Van Giai N Zhou S-G 2004 Phys. Rev. C 69 034319
DOI:10.1103/PhysRevC.69.034319 [Cited within: 2]

[47]Hofmann U Ring P 1988 Phys. Lett. B 214 307
DOI:10.1016/0370-2693(88)91367-6 [Cited within: 2]

[48]Furnstahl R J Brian D S 1987 Nucl. Phys. A 468 539
DOI:10.1016/0375-9474(87)90182-5 [Cited within: 1]

[49]Furnstahl R J Price C E 1989 Phys. Rev. C 40 1398
DOI:10.1103/PhysRevC.40.1398

[50]Morse T M Price C E Shepard J R 1990 Phys. Lett. B 251 241
DOI:10.1016/0370-2693(90)90929-Z [Cited within: 1]

[51]Gambhir Y K Ring P Thimet A 1990 Ann. Phys. 198 132
DOI:10.1016/0003-4916(90)90330-Q [Cited within: 1]

[52]Ring P Gambhir Y K Lalazissis G A 1997 Comput. Phys. Commun. 105 77
DOI:10.1016/S0010-4655(97)00022-2 [Cited within: 1]

[53]Ring P Schuck P 1980 The Nuclear Many-Body Problem New York Springer
[Cited within: 1]

[54]Guo L Sakata F Zhao E-G 2004 Nucl. Phys. A 740 59
DOI:10.1016/j.nuclphysa.2004.04.117 [Cited within: 1]

[55]Lü H Geng L S Meng J 2007 Eur. Phys. J. A 31 273
DOI:10.1140/epja/i2006-10224-4 [Cited within: 1]

[56]Wang M Audi G Kondev F Huang W Naimi S Xu X 2017 Chin. Phys. C 41 030003
DOI:10.1088/1674-1137/41/3/030003 [Cited within: 2]

[57]Stone N J 2014 Table of nuclear magnetic dipole and electric quadrupole moments International Atomic Energy Agency, International Nuclear Data Committee Report INDC(NDS)-0658, Vienna, Austria
[Cited within: 5]

[58]Wang Y Li J Bin Lu J Ming Yao J 2014 Prog. Theor. Exp. Phys. 2014 113D03
DOI:10.1093/ptep/ptu155 [Cited within: 1]

[59]Hilaire S Girod M 2007 Eur. Phys. J. A 33 237
DOI:10.1140/epja/i2007-10450-2 [Cited within: 2]

[60]Firestone R 2007 Nucl. Data Sheets 108 1
DOI:10.1016/j.nds.2007.01.002 [Cited within: 2]

[61]Warburton E K Becker J A Brown B A 1990 Phys. Rev. C 41 1147
DOI:10.1103/PhysRevC.41.1147 [Cited within: 1]

[62]Heylen H et al. 2016 Phys. Rev. C 94 034312
DOI:10.1103/PhysRevC.94.034312 [Cited within: 1]

[63]Brown B A Richter W A 2006 Phys. Rev. C 74 034315
DOI:10.1103/PhysRevC.74.034315 [Cited within: 1]

[64]Xia X et al. 2018 At. Data Nucl. Data Tables 121–122 1
DOI:10.1016/j.adt.2017.09.001 [Cited within: 1]

[65]Yao J M Peng J Meng J Ring P 2011 Sci. China Phys. Mech. Astron. 54 204
DOI:10.1007/s11433-010-4215-7 [Cited within: 1]

[66]Zhao P W Li Z P Yao J M Meng J 2010 Phys. Rev. C 82 054319
DOI:10.1103/PhysRevC.82.054319 [Cited within: 1]