Dan Wu¹, Fu-Ming Guo¹, Jun Wang¹, Ji-Gen Chen², Yu-Jun Yang^,11Institute of Atomic and Molecular Physics, Jilin University, Changchun 130012, China
²Department of Materials Engineering, Taizhou University, Taizhou 318000, China

Received:2019-11-25Revised:2020-03-9Accepted:2020-03-10Online:2020-04-22


Abstract
Double ionization of H₂ in a co-rotating two-color circularly polarized (TCCP) laser field is theoretically investigated. By changing the ratio of electric field peak amplitudes of the TCCP laser pulses, the double ionization probability as a function of the laser intensity shows a clear knee structure, which is suppressed significantly in the case of the atom. Due to the large spatial range of the electronic initial distribution, with the analysis of classical trajectories of ionized electrons, it is found that the ionization of the electron in the farther distance increases the probability of recollision. Furthermore, the yield of nonsequential double ionization created by the recollision can be enhanced by controlling the amplitude ratio of the TCCP laser field.
Keywords： circularly polarized laser field;knee structure;H₂


PDF (1204KB)MetadataMetricsRelated articlesExportEndNote|Ris|BibtexFavorite
Cite this article
Dan Wu, Fu-Ming Guo, Jun Wang, Ji-Gen Chen, Yu-Jun Yang. Dynamics of strong-field double ionization of H₂ in co-rotating two-color circularly polarized laser fields. Communications in Theoretical Physics, 2020, 72(5): 055503- doi:10.1088/1572-9494/ab7eca

1. Introduction

When intense laser pulses interact with atoms or molecules, many nonlinear phenomena can be observed, such as high-order harmonic generation (HHG) [1–8], above-threshold ionization (ATI) [9–12] and nonsequential double ionization (NSDI) [13–16], etc. Among these nonperturbative phenomena, NSDI has been extensively investigated because it can observe the electron momentum distribution, which intuitively reflects the electron correlation effect caused by the recollision process. Generally, NSDI of an atom or a molecule in a linearly polarized laser field can be understood by the rescattering model [17–19]: an electron in the bound state can be liberated via tunnel ionization or ATI, then accelerated in the laser field and driven back to the parent ion as the oscillating electric field reverses its direction, finally recolliding with the parent ion and transferring a part of the energy to the second electron, the ionization of which can be occurred [20, 21]. In the case of the driving laser pulse with higher intensity, the returning electron can obtain enough energy to directly kick out the other, which is called recollision-impact ionization (RII) [22, 23]. For the laser pulse with lower intensity, the second electron can be induced to the excited state by the returning electron with lower energy, then ionized by the electric field, which is called recollision-induced excitation with subsequent ionization (RESI) [24–26].

Electronic motions in linearly polarized laser fields are mainly limited to one-dimension space, thus spatial structure characteristics of atoms and molecules cannot be reflected by the electronic correlation information. Recently, owing to the progress in experimental techniques, the waveform of the laser pulse can be effectively modulated in space and time domains. By using the modulated laser pulse to irradiate atoms or molecules, more spatio-temporal changes of the system structure can be detected by the electronic correlation information. A common scheme for modulating the laser field is to synchronize the fundamental frequency laser pulse and the second-harmonic field. Recently, the counter-rotating two-color circularly polarized (TCCP) laser field has been successfully used to generate circularly polarized HHG [27], and a bright source from the circularly polarized high frequency radiation can be utilized to probe magnetic materials and chiral molecules [28, 29]. Therefore, the study of the TCCP laser pulse interacting with atoms or molecules has become a research hotspot. Correspondingly, the NSDI process of atoms and molecules in the counter-rotating TCCP laser field has also attracted people’s interest in research. Chaloupka et al theoretically studied the double ionization of helium in counter-rotating TCCP laser fields [30]. In the subsequent experiments for Ar in counter-rotating TCCP laser fields, the enhancement of the double ionization yields can be achieved by adjusting the amplitude ratio of the TCCP laser field [31, 32]. Recently, Mancuso et al studied the double ionization process in the counter-rotating and co-rotating TCCP laser fields, and they found that the yield of NSDI is suppressed significantly in the co-rotating TCCP laser field [33].

Compared with the counter-rotating TCCP laser pulse, the probability of recollision in the co-rotating TCCP laser field is extremely low [34, 35], usually its double ionization yield as a function of the laser intensity does not present the knee structure. However, by changing the amplitude ratio of co-rotating TCCP laser fields, recent theoretical studies have demonstrated that the double ionization probability of Ar as a function of the laser intensity shows a knee structure at some certain amplitude ratios [36]. NSDI is the main double ionization mechanism in these amplitude ratios and the electronic momentum distribution can be used to map the recollision instants of rescattered electrons.

Compared with atoms, the molecular structures are more complicated, and double ionizations of molecules in co-rotating TCCP fields need further study. In this paper, we investigated the double ionization of H₂ in a co-rotating TCCP laser pulse by a three-dimensional classical ensemble method. Our numerical simulation indicates that the double ionization probability of H₂ as a function of the laser intensity depends strongly on the amplitude ratio of the co-rotating TCCP laser pulse, and shows a distinct knee structure in a wide range of the amplitude ratio. Through tracing ionized electron trajectories, it is found that, with the increase of the amplitude ratio, the proportion of NSDI in the double ionization is increasing step by step, and becomes maximum as the amplitude ratio is equal to 3, then decreased gradually. This result can be attributed to the change of the ionization probability of the recollision electron and the depletion effect of the initial state based on the analysis of the electron trajectories and the laser fields.

2. Model and method

In order to investigate the molecular double ionization, a full classical ensemble model is used here [37–39]. With this scheme, double ionizations of atoms and molecules in linearly polarized laser fields or modulated laser pulses have been widely studied [40–45]. It has been proved that the classical ensemble model is very successful in reproducing experimental features and predicting new phenomena [46, 47]. In the co-rotating TCCP laser field, the evolution of the two-electron system in the three-dimension space is described by the classical Newtonian equation (atomic units are used throughout this paper):(1)$\begin{eqnarray}\displaystyle \frac{{\partial }^{2}{{\boldsymbol{r}}}_{i}}{\partial {t}^{2}}=-{\rm{\nabla }}[{V}_{{ne}}\left({{\boldsymbol{r}}}_{i}\right)+{V}_{{ee}}({{\boldsymbol{r}}}_{1},{{\boldsymbol{r}}}_{2})]-{\boldsymbol{E}}\left(t\right).\end{eqnarray}$In this work, the Runge–Kutta method is adopted to solve the classical Newtonian equation, where subscripts i=1, 2 are the label of two electrons, r_i is the coordinate of the electron. The potentials of ion-electron and electron-electron Coulomb interactions are ${V}_{{ne}}({{\boldsymbol{r}}}_{i})=-1/\sqrt{| {{\boldsymbol{r}}}_{i}-{\boldsymbol{R}}/2{| }^{2}+{a}^{2}}\,-1/\sqrt{| {{\boldsymbol{r}}}_{i}+{\boldsymbol{R}}/2{| }^{2}+{a}^{2}}$ and ${V}_{{ee}}({{\boldsymbol{r}}}_{1},{{\boldsymbol{r}}}_{2})$ =$\,1/\sqrt{| {{\boldsymbol{r}}}_{1}-{{\boldsymbol{r}}}_{2}{| }^{2}\,+\,{b}^{2}}$, respectively. In the calculation, the two nuclei are fixed along the x axis. In order to avoid autoionization and obtain a stable initial state, we set ion-electron and electron-electron softening parameters a=1.25 a.u. and b=0.05 a.u.. Softening parameter b is applied to remove the numerical singularity. In this paper, the internuclear distance R is chosen as 2 a.u., and the corresponding total energy of E_g=−1.63 a.u.. The electric fields of the co-rotating TCCP laser pulse are given by:(2)$\begin{eqnarray}{{\boldsymbol{E}}}_{\omega }t=\displaystyle \frac{{E}_{0}}{1+{\gamma }_{{\rm{E}}}}f(t)[\cos (\omega t+{\varphi }_{0})\hat{{\boldsymbol{x}}}+\sin (\omega t+{\varphi }_{0})\hat{{\boldsymbol{y}}}],\end{eqnarray}$(3)$\begin{eqnarray}{{\boldsymbol{E}}}_{2\omega t}=\displaystyle \frac{{\gamma }_{{\rm{E}}}{E}_{0}}{1+{\gamma }_{{\rm{E}}}}f(t)[\cos (2\omega t+{\varphi }_{0})\hat{{\boldsymbol{x}}}+\sin (2\omega t+{\varphi }_{0})\hat{{\boldsymbol{y}}}],\end{eqnarray}$where $\hat{{\boldsymbol{x}}}$ and $\hat{{\boldsymbol{y}}}$ are the unit vectors along x and y directions, respectively. E₀ is the maximum amplitude of the combined laser field, γ_E is the amplitude ratio between the fundamental frequency laser pulse and the second harmonic one. The frequency of the fundamental laser pulse ω=0.0584 a.u., and the carrier-envelope phase φ₀=0, f(t) is a trapezoidal pulse envelope with a two-cycle turn on, six cycles at full strength, and two-cycle turn off.

To obtain the initial condition of equation (1), we first randomly selected positions of two electrons to determine the total potential energy of the system. The kinetic energy of two electrons is calculated in terms of the conservation of energy, and the total kinetic energy is randomly assigned to the two electrons. Then two-electron system is allowed to evolve a sufficient long time in the absence of the laser field to reach a stable initial distribution. Once the initial ensemble is obtained, the laser field is turned on and all trajectories are evolved in the combined potential formed by the Coulomb interaction and the laser field.

At the end of the laser field, the double ionization, the sequential double ionization (SDI) and the NSDI of the ensemble are calculated based on positions and momenta of two electrons. Here, we set the criterion of the molecular ionization. The double ionization of the molecule occurs when energies of both electrons are greater than zero. If the energy of any of two electrons is greater than zero for the first time, the single ionization of the molecule is considered. After the single ionization, if the distance between two electrons is less than 5 a.u. at a certain time, then a recollision process exists (for the standard of the recollision, statistical results change very little when the distance ranges from 4 a.u. to 7 a.u, which is consistent with that from the literature [47]). According to the recollision in the double ionization process, the double ionization is further divided into NSDI and SDI. If the recollision occurs, double ionization is classified into NSDI. Otherwise double ionization is classified into SDI. In this work, an ensemble consisting of 10⁸ two-electron ‘trajectories’ is adopted.

3. Results and discussions

We first studied the double ionization probability of H₂ as a function of the laser intensity by co-rotating TCCP laser fields, as shown in figure 1. When the amplitude ratio γ_E equals to zero, the combined field becomes the circularly polarized laser pulse. It can be seen from figure 1 that the double ionization probability of H₂ is enhanced with the laser intensity. In the co-rotating TCCP pulse, the double ionization yield of H₂ is much larger than that in the monochromatic circularly polarized laser, although the maximum amplitude of the combined laser field is the same. If driving laser pulses have the same intensity and duration, then the higher the frequency, the larger the sequence ionization. So, it can be observed from figure 1 that the ionization of the co-rotating TCCP laser field is two orders of magnitude higher than that of the circularly polarized laser, and the increase of the amplitude ratio of the co-rotating TCCP pulse not only improves the number of sequence double ionization but also changes the proportion of nonsequential double ionization. Thus, in low intensity regions, there is no contribution of non-sequential double ionization, and the enhancement in sequential double ionization in the TCCP field also contributes to the increase of the double ionization yield. Simultaneously, with the increase of the amplitude ratio, the curves of the double ionization probability as a function of the laser intensity exhibit a clear knee structure, the most obvious one of which appears at γ_E=3 , and this structure disappears gradually with the further increase of the amplitude ratio.

Figure 1.

New window|Download| PPT slide
Figure 1.Double ionization probability of H₂ as a function of the laser intensity for different γ_E.


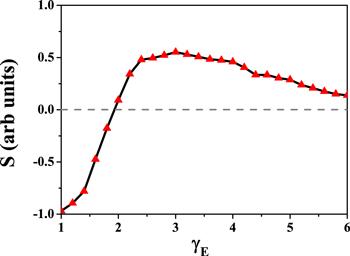
In order to understand how the amplitude ratio γ_E affects the double ionization probability, an asymmetry parameter $S=({N}_{\mathrm{NSDI}}-{N}_{\mathrm{SDI}})/({N}_{\mathrm{NSDI}}+{N}_{\mathrm{SDI}})$ is introduced, where ${N}_{\mathrm{NSDI}}$ and ${N}_{\mathrm{SDI}}$ are yields of NSDI and SDI, respectively. Here, the intensity of the co-rotating TCCP laser pulse is chosen as 0.3 PW cm⁻², and the corresponding double ionization probability shows a prominent knee structure. In terms of the definition of S, NSDI becomes the main ionization mechanism when S is positive, and SDI dominates the double ionization process when S is negative. Figure 2 shows the dependence of the asymmetry parameter on the amplitude ratio γ_E. When γ_E is altered from 1 to 2, the asymmetry parameter S improves gradually from −1 to 0, which indicates that the main mechanism of the double ionization is SDI in this parameter range. With the further increase of γ_E, S is greater than zero and gets a maximum value at about γ_E, then decreases step by step. This change means that the double ionization is dominated by NSDI when γ_E is larger than 2, and the proportion of NSDI reaches a maximum and then decreases gradually with the increase of γ_E.

Figure 2.

New window|Download| PPT slide
Figure 2.Double ionization asymmetry parameter as a function of the laser amplitude ratio γ_E.


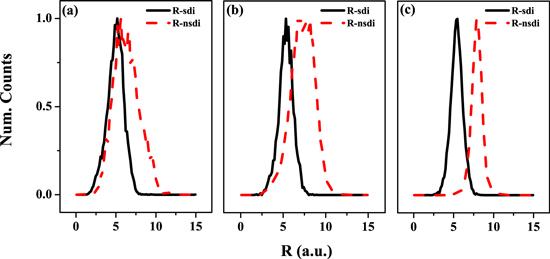
Based on the above analysis, in a wide range of the amplitude ratio, it is NSDI rather than SDI that dominates the double ionization of the molecule in the co-rotating TCCP laser pulse. Whether the electron returns to the parent ion or not, which is closely related to their positions and velocities at the ionization moment, therefore we analyzed the distance between the ionized electron and the closer one of two nuclei at the ionization moment of the first ionized electron in the double ionization. Figure 3 presents distances for SDI (black solid line) and NSDI (red dotted line) with γ_E=1.8, 3 and 6, respectively. It can be noticed that, for different amplitude ratios γ_E, distances of SDI are similar and peaks of distance distributions are mainly located at about 5 a.u., however, distances of NSDI are enhanced gradually with the increase of γ_E, and peak positions of distance distributions for γ_E=1.8, 3 and 6 are at about 6 a.u., 7.5 a.u., and 8.5 a.u, respectively. For the atomic case, the electron ionization occurs near the nuclear region, and the subsequent motion behavior is mainly away from the nuclear region. But for the molecular case, the more electronic positions at the ionization instant are far from the parent ion. With the increase of γ_E, the shape of the electric field becomes more circular and the first ionized electron needs to be farther away from the nucleus for having a chance to recollide with the parent ion.

Figure 3.

New window|Download| PPT slide
Figure 3.Distances between the ionized electron and the closer one of two nuclei at the moment of the single ionization in SDI (black solid curve) and NSDI (red dotted curve) with the amplitude ratio (a) γ_E=1.8, (b) γ_E=3 and (c) γ_E=6, respectively.


For intuitively observing the dynamics of the electronic recollision process in the co-rotating TCCP laser pulse, we investigated trajectories of firstly ionized electrons in the NSDI process with γ_E=3. According to the travelling time of the ionized electron, shorter or longer than one optical cycle of the fundamental laser pulse, the recollision trajectory is divided into a short recollision trajectory (SRT) or a long recollision trajectory (LRT), respectively. Figures 4(a) and (b) show SRT and LRT of firstly ionized electrons, respectively. A typical trajectory (solid red line) is also presented in figures 4(a) and (b), and the red arrow marks the motion direction of the ionized electron. Unlike the case of the linear polarization laser field, the first ionized electron can recollide with the parent ion, which results in the ionization of the second electron. In the co-rotating TCCP laser field, ionized electrons mainly rotate around the parent ion, and some of ionized electrons have a chance to recollide with the parent ion, as shown in figure 4(a). This ionization behavior is similar to the atom in the co-rotating TCCP. Compared with the case of the atom, the initial distribution of the molecule is larger, the electron is farther away from the parent ion at the ionization time, and it has a greater chance to return to the nuclear region in a shorter time. Therefore, compared with the case of the atom, the molecular double ionization curve exhibits a distinct knee structure over a large amplitude ratio range. Similarly, the angle distribution between the initial velocity and the laser field force is the other factor that determines whether electrons can return to the parent ion in a relatively short period or not, as shown in figure 4(c). In the case of the SRT, the ionized electron is farther away from the nucleus (figure 4(d)) and the angle distribution is larger than the LRT process, thereby it can recollide with the parent ion in a shorter time.

Figure 4.

New window|Download| PPT slide
Figure 4.Classical trajectories of NSDI with γ_E=3. (a) Short recollision trajectory(SRT); (b) long recollision trajectory (LRT); (c) angle distribution between the initial velocity and the force of the laser field at the ionization moment; (d) distance from the ionized electron to the nucleus at the ionization moment for LRT and SRT processes.


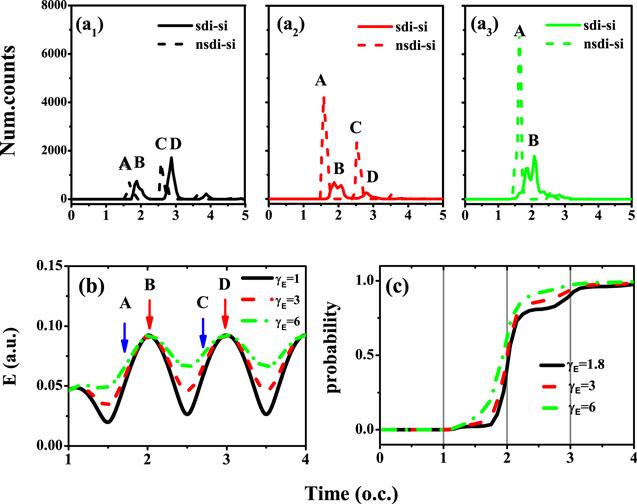
For the case of the usual linear polarization laser field, the first ionized electron carries higher energy back to recollide with the parent ion, which leads to the ionization of the second electron. However, ionized electrons in the co-rotating TCCP laser field will be far away from the parent ion, and the chance of electrons returning to the nucleus is small. The probability of the direct ionization of molecular ions in the co-rotating TCCP field is also small. Thereby, for different amplitude ratios of the co-rotating TCCP laser, the single ionization probability is close to 1, but the probability of the double ionization is only 10⁻³. The ionization probability of the first ionized electron in the double ionization has an important influence on the probability of the subsequent double ionization. So, we calculated the probability of the ionization time of the first ionized electron in NSDI and SDI for three amplitude ratios γ_E=1.8, 3 and 6. In figure 5(a₁) γ_E=1.8, 5(a₂) γ_E=3, 5(a₃) γ_E=6, the solid and dashed lines are the probability of the ionization time of the first ionized electron in SDI and NSDI, respectively. It can be seen from figure 5(a) that the probability of the ionization time of the first ionized electron is quite different for three amplitude ratios in the case of SDI. For peak B, the ionization probability enhances with the increase of the amplitude ratio. But peak D is just the opposite, it decreases with the increase of the amplitude ratio, when the amplitude ratio γ_E=6, the ionization only occurs at peak B. For the case of NSDI, the probability of the ionization time of the first ionized electron is mainly located at peaks A and C. For peak A, the ionization probability also increases with the amplitude ratio. But for peak C, with the increase of the amplitude ratio, the ionization probability is small at γ_E=1.8, and increases at γ_E=3, finally disappears at γ_E=6. In addition, the single ionization yield in SDI and NSDI has a strong dependence on the laser field amplitude. Figure 5(b) presents laser field amplitudes for three amplitude ratios γ_E=1.8, 3 and 6. It can be seen that the amplitudes of co-rotating TCCP lasers are the same at integer optical cycles for different amplitude ratios; however, at non-integer optical cycles, the amplitude is gradually enhanced with the increase of γ_E. We marked the corresponding peaks A, B, C, and D in figure 5(b) and found that the variation of the peaks A and B with the amplitude ratio is consistent with the change of the laser amplitude, but the variation of peaks C and D with the amplitude ratio is different from the change of the laser amplitude. When bound electrons of the system are not exhausted, the field strength at the first electron ionization time increases with the amplitude ratio and the ionization yield should be increased with the amplitude ratio. Figure 5(c) shows total single ionization probabilities in the three amplitude ratios. For the case of γ_E=1.8, bound electrons of the system are almost ionized when the ionization time is larger than 3 o.c.. With the amplitude ratio increases (γ_E=3), bound electrons of the system are exhausted rapidly, and the ionization probability of the SDI decreases (peak D), thus the proportion of the nonsequential ionization in the total double ionization increases (γ_E=3). With the amplitude ratio further increasing (γ_E=6), the ground state of the system is depleted at about ionization time C, and peak C contributes to NSDI. Thereby, the proportion of NSDI decreases by raising the amplitude ratio. According to the above analysis, due to the difference of laser amplitudes at the ionization time of the first ionized electrons in SDI and NSDI and the single ionization saturation effect, yields of NSDI and SDI can be effectively controlled by changing the amplitude ratio of the co-rotating TCCP laser field.

Figure 5.

New window|Download| PPT slide
Figure 5.(a₁) γ_E=1.8, (a₂) γ_E=3, (a₃) γ_E=6 ionization time statistics of the first ionized electron of SDI (solid line) and NSDI (dashed line). (b) Laser fields for three amplitude ratios at the duration from 1 o.c.to 4 o.c., the blue and red arrows show the ionization instant of the first ionized electron of NSDI and SDI, respectively; (c) total single ionization probabilities in the three amplitude ratios.

4. Conclusions

In conclusion, we investigated the dynamics of the strong-field double ionization of the hydrogen molecule in the co-rotating two-color circularly polarized laser pulse. It is found that a large yield of NSDI exists in the double ionization process. By controlling the amplitude ratio of the co-rotating TCCP laser field, the double ionization probability as a function of the laser intensity shows an obvious knee structure, which is apparently different with the double ionization from the atom. Because the electronic initial distribution of H₂ in the co-rotating TCCP laser pulse is extended at a wide spatial region, and the ionization of electrons in farther distances can increase the probability of the recollision, thus the yield of NSDI can be effectively enhanced and the double ionization probability appears in the knee structure.

Acknowledgments

This project was supported by the National Key Research and Development Program of China (Grant No. 2019YFA0307700 and No. 2017YFA0403300), National Natural Science Foundation of China (NSFC) (Grants No. 11627807, No. 11774175, No. 11534004, No. 11774129 and No. 11975012), the Jilin Provincial Research Foundation for Basic Research, China (Grant No. 20170101153JC), and the Science and Technology project of the Jilin Provincial Education Department (Grant No. JJKH20190183KJ), and , the outstanding Youth project of Taizhou University (Grant No. 2019JQ002). We acknowledge the High Performance Computing Center of Jilin University for supercomputer time.

Reference View Option By original order
By published year
By cited within times
By Impact factor

[1]Chen M-C et al. 2014 Proc. of the National Academy of Sciences 201407421
[Cited within: 1]

[2]Ferray M L’Huillier A Li X Lompre L Mainfray G Manus C 1988 J. Phys. B: At. Mol. Opt. Phys. 21 L31
DOI:10.1088/0953-4075/21/3/001

[3]Krause J L Schafer K J Kulander K C 1992 Phys. Rev. Lett. 68 3535
DOI:10.1103/PhysRevLett.68.3535

[4]Kuchiev M Y 1987 JETP Lett 45 404


[5]Popmintchev D et al. 2015 Science 350 1225
DOI:10.1126/science.aac9755

[6]Wang J Chen G Li S-Y Ding D-J Chen J-G Guo F-M Yang Y-J 2015 Phys. Rev. A 92 033848
DOI:10.1103/PhysRevA.92.033848

[7]Chen J Yang Y Chen J Wang B 2015 Phys. Rev. A 91 043403
DOI:10.1103/PhysRevA.91.043403

[8]Zhao Y-T Ma S-Y Jiang S-C Yang Y-J Zhao X Chen J-G 2019 Opt. Express 27 34392
DOI:10.1364/OE.27.034392 [Cited within: 1]

[9]Agostini P Fabre F Mainfray G Petite G Rahman N K 1979 Phys. Rev. Lett. 42 1127
DOI:10.1103/PhysRevLett.42.1127 [Cited within: 1]

[10]Kruit P Kimman J Muller H G Van der Wiel M 1983 Phys. Rev. A 28 248
DOI:10.1103/PhysRevA.28.248

[11]Paulus G Nicklich W Xu H Lambropoulos P Walther H 1994 Phys. Rev. Lett. 72 2851
DOI:10.1103/PhysRevLett.72.2851

[12]Yuan H-Y Guo F-M Zhang D-Y Wang J Chen J-G Yang Y-J 2018 Chin. Phys. B 27 103201
DOI:10.1088/1674-1056/27/10/103201 [Cited within: 1]

[13]Zhou Y Huang C Lu P 2011 Phys. Rev. A 84 023405
DOI:10.1103/PhysRevA.84.023405 [Cited within: 1]

[14]Zhou Y Liao Q Lu P 2009 Phys. Rev. A 80 023412
DOI:10.1103/PhysRevA.80.023412

[15]Ho P J 2005 Phys. Rev. A 72 045401
DOI:10.1103/PhysRevA.72.045401

[16]Emmanouilidou A Staudte A 2009 Phys. Rev. A 80 053415
DOI:10.1103/PhysRevA.80.053415 [Cited within: 1]

[17]Rudenko A De Jesus V Ergler T Zrost K Feuerstein B Schröter C Moshammer R Ullrich J 2007 Phys. Rev. Lett. 99 263003
DOI:10.1103/PhysRevLett.99.263003 [Cited within: 1]

[18]Staudte A et al. 2007 Phys. Rev. Lett. 99 263002
DOI:10.1103/PhysRevLett.99.263002

[19]Lein M Gross E K Engel V 2000 Phys. Rev. Lett. 85 4707
DOI:10.1103/PhysRevLett.85.4707 [Cited within: 1]

[20]Kulander K C Cooper J Schafer K J 1995 Phys. Rev. A 51 561
DOI:10.1103/PhysRevA.51.561 [Cited within: 1]

[21]Corkum P B 1993 Phys. Rev. Lett. 71 1994
DOI:10.1103/PhysRevLett.71.1994 [Cited within: 1]

[22]Weber T et al. 2000 Nature 405 658
DOI:10.1038/35015033 [Cited within: 1]

[23]Feuerstein B et al. 2001 Phys. Rev. Lett. 87 043003
DOI:10.1103/PhysRevLett.87.043003 [Cited within: 1]

[24]Camus N et al. 2012 Phys. Rev. Lett. 108 073003
DOI:10.1103/PhysRevLett.108.073003 [Cited within: 1]

[25]Chen Y Zhou Y Li Y Li M Lan P Lu P 2018 Phys. Rev. A 97 013428
DOI:10.1103/PhysRevA.97.013428

[26]Liu Y Fu L Ye D Liu J Li M Wu C Gong Q Moshammer R Ullrich J 2014 Phys. Rev. Lett. 112 013003
DOI:10.1103/PhysRevLett.112.013003 [Cited within: 1]

[27]Fleischer A Kfir O Diskin T Sidorenko P Cohen O 2014 Nat. Photonics 8 543
DOI:10.1038/nphoton.2014.108 [Cited within: 1]

[28]Milos̆ević D 2015 Phys. Rev. A 92 043827
DOI:10.1103/PhysRevA.92.043827 [Cited within: 1]

[29]Smirnova O Mairesse Y Patchkovskii S 2015 J. Phys. B: At. Mol. Opt. Phys. 48 234005
DOI:10.1088/0953-4075/48/23/234005 [Cited within: 1]

[30]Chaloupka J L Hickstein D D 2016 Phys. Rev. Lett. 116 143005
DOI:10.1103/PhysRevLett.116.143005 [Cited within: 1]

[31]Mancuso C A et al. 2016 Phys. Rev. Lett. 117 133201
DOI:10.1103/PhysRevLett.117.133201 [Cited within: 1]

[32]Eckart S et al. 2016 Phys. Rev. Lett. 117 133202
DOI:10.1103/PhysRevLett.117.133202 [Cited within: 1]

[33]Mancuso C A et al. 2015 Phys. Rev. A 91 031402
DOI:10.1103/PhysRevA.91.031402 [Cited within: 1]

[34]Huang C Zhong M Wu Z 2018 Opt. Express 26 26045
DOI:10.1364/OE.26.026045 [Cited within: 1]

[35]Lin K et al. 2017 Phys. Rev. Lett. 119 203202
DOI:10.1103/PhysRevLett.119.203202 [Cited within: 1]

[36]Huang C Zhong M Wu Z 2019 Opt. Express 27 7616
DOI:10.1364/OE.27.007616 [Cited within: 1]

[37]Panfili R Eberly J H Haan S L 2001 Opt. Express 8 431
DOI:10.1364/OE.8.000431 [Cited within: 1]

[38]Prauzner-Bechcicki J S Sacha K Eckhardt B Zakrzewski J 2008 Phys. Rev. A 78 013419
DOI:10.1103/PhysRevA.78.013419

[39]Panfili R Haan S L Eberly J H 2002 Phys. Rev. Lett. 89 113001
DOI:10.1103/PhysRevLett.89.113001 [Cited within: 1]

[40]Ho P J Panfili R Haan S Eberly J 2005 Phys. Rev. Lett. 94 093002
DOI:10.1103/PhysRevLett.94.093002 [Cited within: 1]

[41]Haan S Breen L Karim A Eberly J 2006 Phys. Rev. Lett. 97 103008
DOI:10.1103/PhysRevLett.97.103008

[42]Haan S Van Dyke J Smith Z 2008 Phys. Rev. Lett. 101 113001
DOI:10.1103/PhysRevLett.101.113001

[43]Tang Q Zhou Y Huang C Liao Q Lu P 2012 Opt. Express 20 19580
DOI:10.1364/OE.20.019580

[44]Tong A Li Q Ma X Zhou Y Lu P 2019 Opt. Express 27 6415
DOI:10.1364/OE.27.006415

[45]Fu L-B Liu J Chen J Chen S-G 2001 Phys. Rev. A 636 043416
DOI:10.1103/PhysRevA.63.043416 [Cited within: 1]

[46]Zhang L et al. 2014 Phys. Rev. Lett. 112 193002
DOI:10.1103/PhysRevLett.112.193002 [Cited within: 1]

[47]Tong A Liao Q Zhou Y Lu P 2010 Opt. Express 18 9064
DOI:10.1364/OE.18.009064 [Cited within: 2]