Ya-Dong Song^,1,2,?, Sachin Barthwal^1,31 State Key Laboratory of Magnetic Resonance and Atomic and Molecular Physics, Wuhan Institute of Physics and Mathematics, Chinese Academy of Sciences, Wuhan 430071, China
2 School of Physical Sciences, University of Chinese Academy of Sciences, Beijing 100049, China
3 Center for Cold Atom Physics, Chinese Academy of Sciences, Wuhan 430071, China

Corresponding authors: ^?E-mail:yadong.s@yahoo.com

Received:2018-12-5Online:2019-05-1

Fund supported:

National Natural Science Foundation of China under Grant.11374331 National Natural Science Foundation of China under Grant.11304364 National Natural Science Foundation of China under Grant.11534014

Abstract
Using the variational method, we study the properties of a spin-down impurity immersed in a one-dimensional (1D) spin-up Fermi sea. With repulsive interactions between them, the impurity is dressed up by surrounding particles in Fermi sea and forms a polaron. We clearly calculate the binding energy, effective mass, momentum distribution, Tan contact, and pair correlation. Even in strong repulsive regimes, the results can agree with the exact Bethe Ansatz results. The repulsive polaron energy $E_+$ is below Fermi energy $E_F$ and no negative effective masses are found in whole interaction regimes, unequal masses polarons are also calculated. We show a clear momentum distribution and calculate the Tan contact from three different aspects. Furthermore, we explore the particle-hole excitation and find that the hole terms in Fermi sea have a great influence on the polaron energy and contact in repulsive regime. These results show that the variational method can still be used effectively in 1D repulsive polaron system.
Keywords： polaron;variational method;Tan contact;cold atom


PDF (478KB)MetadataMetricsRelated articlesExportEndNote|Ris|BibtexFavorite
Cite this article
Ya-Dong Song, Sachin Barthwal. Repulsive Polarons in One-Dimensional Fermi Gases. [J], 2019, 71(5): 617-622 doi:10.1088/0253-6102/71/5/617

1 Introduction

Impurity problems are essential in determining low-temperature properties of many-body physics.^[1-3] With a high degree of control and tunability by Feshbach resonance,^[4-6] the impurity problem and the realization of associated polaron physics has attracted great attentions over the past years.^[7-11] In these systems, polarons are realized by means of population-imbalanced atomic gas, the minority playing the role of impurity, and majority atoms playing the role of bath.^[12] The system depends strongly on the quantum nature of the bath and the mass of impurity. Properties of polaron are fundamentally relevant for understanding more complex scenario of partially and balanced Fermi mixtures.^[13]

Initiated with the investigation of Fermi gases in BEC-BCS crossover, the study of polaron physics has extended to unequal masses fermionic systems and bosonic environments.^[14-15] On one hand, this many-body system is appealing because it can be described almost exactly with simple diagrammatic and/or variational theoretical approaches. On the other, it provides a quantitatively reliable insight into the phase diagram of strongly interacting population-imbalanced quantum mixtures. Experimentally, polaron systems have been realized with a medium composed either of bosonic or fermionic atoms.^[16-19] In a low-temperature fermionic gas medium, results instead in excitations named Fermi polarons, which are a paradigmatic realization of Landau's fundamental concept of a quasi-particle. In this paper the variational approach presents a whole energy spectrum and momentum distribution clearly. In the polaron system with repulsive interactions, there is another complex topic about the itinerant ferromagnetic (IFM) phase argued for a long time.^[20-22] Recent research found that polaron energy can exceed the Fermi energy and the effective mass $m^*$ could be negative in three-dimensional case.^[21] but the IFM phase is still a controversial topic. The repulsive polaron system is stable in 1D, and IFM phase can be rigorously excluded by exact Bethe Ansatz (BA) method.^[23] In whole 1D repulsive regime, it is interesting to see polaron properties calculated by variational method, which can be compared with results by BA method.

On the other side, in recent years a remarkable development has been made in many-body physics by studying strongly interacting Fermi gases with a large scattering length, which was started in a series of papers by Tan.^[24-26] The Tan contact is a central property in many-body system, and it determines both the thermodynamics and the tail of momentum distribution.^[27] The Tan relations can also hold for Fermi gases in 1D case, and the analog was first presented by Barth.^[28] A T-matrix approach was used to calculate the Tan contact in 1D polaron system, without a good treatment of momentum distribution.^[29]

In this paper, we calculate the properties of repulsive polaron with a spin-$\downarrow$ impurity immersed in a spin-$\uparrow$ Fermi sea by variational method. We show that, the polaron energy $E_+$ is below Fermi energy, and effect mass becomes infinite in strong repulsive interaction regime. Good agreements with exact results is existent even in strong repulsive regime for equal masses case,^[30-32] which indicate no IFM phases clearly. We also investigate the heavy and light polaron systems. On the other side, unlike treating the momentum of major particles as ideal Fermi-Dirac distribution by T-matrix approach, here we present the momentum distribution clearly. We investigate the Tan contact from three different aspects and calculate the pair correlation. Moreover, we study the influence of the particle-hole in repulsive polaron system. We find that the hole term in Fermi sea excited by the impurity has a great influence both on the polaron energy and Tan contact.

The rest of paper is organized as follows. In Sec. 2, we introduce the Fermi polaron model, the variational method. In Sec. 3, we calculate the repulsive polaron energy and effective mass. Properties of heavy and light polarons are also calculated. In Sec. 4, we exhibit the momentum distribution, calculate the pair correlations and Tan contact. The importance of hole momentum in Fermi sea is illustrated. Finally, a summary is given in Sec. 5.

2 Model and Methods

In the following, we consider a 1D Fermi polaron system with short-range repulsive interaction, described by the Hamiltonian

(1)$ H = \sum_{k \sigma} \epsilon(k,\sigma) c_{k \sigma}^\dagger c_{k \sigma} + g \sum_{kk'q} c^\dagger_{k \uparrow} c^\dagger_{k' \downarrow} c_{q \downarrow} c_{k+k'-q, \uparrow} ,$
with the single-particle spectrum $\epsilon(k,\sigma) = k_{\sigma}^2/2$ and $\hbar=1$. $c_{k\sigma}^\dagger$ ($c_{k \sigma}$) is the creation (annihilation) operator of a fermion with spin $\sigma$ in momentum space. We denote the density of spin-$\uparrow$ fermion as $n_{\uparrow} = k_{F} / \pi$, where $k_{F}$ is the Fermi momentum. The interaction between impurity and particles in the Fermi sea is a contact interaction and in this paper we mainly consider repulsive interactions with positive $g$. In order to study the Tan contact, the coupling constant $g$ is expressed in terms of the 1D scattering length $a$ with $g = -1/a$.^[28] The scattering length $a$, can be tuned accurately by Feshbach Resonance.^[5] A trial wave function for the ground-state of an impurity system can be expressed as

(2)$ |\Psi\rangle=\alpha_0c_{p \downarrow}^\dagger|0 \rangle +\sum_{k_1q_1}\alpha_{k_1q_1}c^\dagger_{p + q_1 - k_1\downarrow}c_{k_1 \uparrow}^\dagger c_{q_1 \uparrow}|0\rangle+\cdots $
It is well known that the dressed impurity can excite particle-hole pairs in the spin up Fermi sea. Here and below, the term $k_1$ or $k_2$ represents momentum out of Fermi sea excited by the impurity is with $|k_{1(2)}|>k_{F}$, and the term $q_1$ represents hole momentum in Fermi sea excited by the impurity restricted with $|q_{1}|\leq k_{F}$. The vacuum $|0\rangle$ is defined as a tensor state of the true vacuum state for spin-$\downarrow$ fermion and the Fermi sea for spin-$\uparrow$ fermions. $p$ denotes the momentum of polaron or the whole system. Using the above trial wave function and minimizing the functional $\langle\Psi |(H - E)|\Psi\rangle$, one can get following two coupled equations:^[8]

(3)$ -g^{-1}|E|\alpha_0=\sum_{k_1q_1}\alpha_{k_1q_1} , \\ -g^{-1}E^1_{k_1q_1}\alpha_{k_1q_1}=\alpha_0 +\sum_{k_2} \alpha_{k_2q_1}-\sum_{q_2} \alpha_{k_1q_2} ,$
with $E^1 = -E +gn_{\uparrow} +\epsilon(p+q_1-k_1,\uparrow)+ \epsilon(k_1,\uparrow)-\epsilon (q_1,\uparrow)$. $E$ is the ground-state energy, which is also defined as the energy of polaron.

Considering the fluctuation and no ultra-violet divergence in 1D polaron system, the excited momentum $k$ needing to be taken into account is much larger than $10k_{F}$. The last term on the right side of Eq. (3) is derived from the hole momentum term $q$ in the wave function in Eq. (2). Although hole term $q$ is small compared with momentum $k$, but it can not be neglected in repulsive regime. Under the quasiparticle picture and when $p\ll k_{F}$, the energy of polaron can be written as

(4)$ E(p)= E_++\frac{p^2}{2 m^*} . $
Here the energy $E_+$ is the ground-state energy for a system with the impurity at zero-momentum, and $m^*$ is the effective mass of polaron. The energy and effective mass results in equal masses polaron system can also be calculated by exact BA method, given by McGuire^[31] and Guan^[32-33]

(5)$ \frac{E}{E_{F}}=\frac{2}{\pi}\Big[-\frac{1}{2ak_{F}}-\frac{\pi}{8a^2k^2_{F}}+ \Big(1+\frac{1}{4a^2k^2_{F}}\Big)\arctan \Big(-\frac{1}{2ak_{F}}\Big)\Big] ,$
(6)$ m^{\ast}=\frac{(1-({2}/{\pi})\arctan(-{1}/{2ak_{F}}))^2}{1-({2}/{\pi})[\arctan (-{1}/{2ak_{F}}) -({2ak_{F}}/({4a^2(k_{F})^2+1}))]} . $
With all the above equations, we can study the universal properties of repulsive polaron in 1D.

3 Energy and Effective Mass

The polaron energy in 1D can also be calculated by T-matrix approach method, but it can not exhibit a valid energy value in the weak attractive regime.^[29] Here we can present the energy spectrum in whole interaction regime. In equal masses repulsive polaron system, the energy $E_+$ is below Fermi energy $E_F$, and effective mass becomes infinite in strong interactions by considering the excited hole term $q$ completely. In Fig. 1, we show energy of repulsive polaron as a function of the scaled interaction strength $g/2k_{F}$ for different mass ratios. First of all, one can see that the polaron energy is $0.95E_F$ in strong repulsive interaction regime for equal masses. The result is much closer to the exact BA result $0.9E_F$, while the energy value is $1.24E_F$ calculated by T-matrix approach.^[29] The light polaron with $m_\downarrow/m_\uparrow=6/40$, has a larger polaron energy, while the heavy polaron has a smaller energy. This phenomenon just accords with the case of three-dimensional repulsive polaron.^[20]

Fig. 1

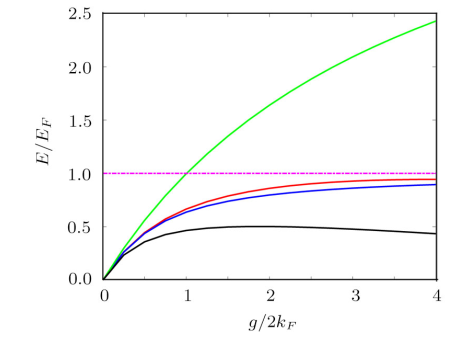New window|Download| PPT slide
Fig. 1(Color online) Energy of repulsive polaron vs. the scaled interaction strength $g/2k_{F}$ calculated by the variational method for different mass ratios: solid lines from top to bottom, $m_\downarrow/m_\uparrow=6/40,1,40/6$. The red dot-dashed line is exact BA results for equal masses, the dot transverse line is $E_F$.



In Fig. 2(a), the polaron energy for equal masses are presented clearly in whole interaction regime. The hole momentum term $q$ which represents the last term on the right side of Eq. (3), is usually ignored in energy calculating. We show the relative deviation of polaron energy caused by hole term $q$ in Fig. 2(b). $q$ is small compared with $k$ outside Fermi sea, and has a small influence on attractive polaron energy. But in repulsive regime, the relative deviation between polaron energy $E_a$ calculated without term $q$ and $E$ with term $q$ can be $(E_a-E)/E=0.2$ at $g/2k_{F}=0.87$. The deviation increases almost linearly to $E_a=2E$ in strong repulsive regime. For the term $E^1 = -E +gn_{\uparrow} +\epsilon(p+q_1-k_1,\uparrow)+ \epsilon(k_1,\uparrow)-\epsilon (q_1,\uparrow)$, repulsive polaron energy $E$ is too close to Fermi energy $E_F$ to ignore any term of $q$ in Eq. (3). But the attractive polaron energy can be almost $50E_F$. The spin-down impurity is much more sensitive to the hole term $q$ in spin-up Fermi sea in repulsive interaction regime.

By calculating the ground-state energy with finite $p$, one can get the effective mass of a polaron after linearly fitting the energy vs. $p^2$. In Fig. 3 we show the effective mass vs. the scaled interaction strength for different mass ratios. The hole term $q$ is very important in the 1D polaron system and can not be ignored as a small quantity. By considering the excited hole term $q$ completely, one can see that the variational method results are consistent with the BA values for equal masses.^[31] The effective mass becomes infinite for $g\to+\infty$ as the polaron gets increasingly dressed by particle-hole pairs. Just as three-dimensional case, the light impurity has a heavier effective mass^[20] and approaches infinite more quickly than equal mass system. The negative effective mass can not be found even in a very strong repulsive strength $mg/2K_F=5$, which corresponds to the interaction dimensionless parameter $\gamma=10*pi$ in exact BA method.^[32]

Fig. 2

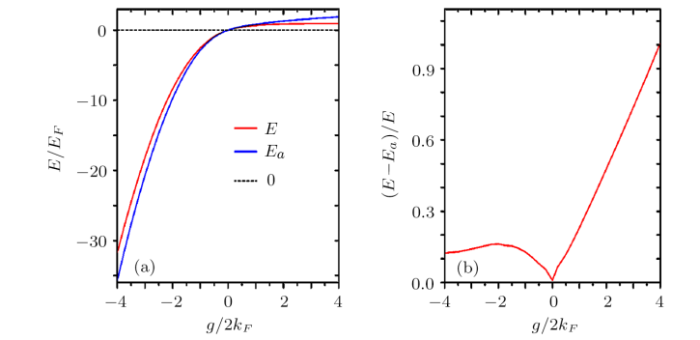New window|Download| PPT slide
Fig. 2(Color online) (a) Red line represents polaron energy $E$ calculated with $q$ by variational method, blue line represents polaron energy $E_a$ calculated without $q$, which are calculated in equal mass systems of whole energy spectrum. (b) The line represents relative deviation of polaron energy $(E-E_a)/E$ by hole term $q$.



In strong repulsive interaction regimes, Stoner argues that two-component Fermi gases undergo a transition to a state characterized by spin polarized domains about the IFM phase. Many theories and experiments have been discussed about the controversial IFM phase^[21-22] in polaron systems. In three-dimensional case, the repulsive polaron energy can exceed $E_F$ and not completely precise negative effective masses are found in recent experiment.^[21] However, the IFM phase of 1D repulsive system has been proved to be nonexistent by exact BA method.^[23] Here we can see that the variational approach gives a same good result. For equal masses case, the polaron energy $E$ is below $E_F$ and the effective mass becomes infinite without being negative in strong repulsive regime. The variational method in whole repulsive interaction regime is valid and indicates the inexistence of IFM phase in 1D.

Fig. 3

New window|Download| PPT slide
Fig. 3(Color online) The effective mass of a polaron for different mass ratios: from top to bottom, $m_\downarrow/m_\uparrow=6/40,1,40/6$. The red dot-dashed line is exact BA results for equal masses.

4 Momentum Distribution, Tan Contact and Pair Correlation

After calculating the ground-state energy, one can use Eqs. (2) and (3) to get the variational wave function. In 1D polaron system by T-matrix approach, the momentums of major component in Fermi sea are directly treated as the Fermi-Dirac distribution.^[29] This treatment is not exact and suitable. The impurity can affect momentum distribution in Fermi sea greatly in strong interaction regime, and Tan contact can not be calculated without the large momentum tail.

Here we use the wave function to calculate and analyze the momentum distributions. We study the momentum distribution for the major component, which is defined as $n_\uparrow(k)=\langle\Psi|c^\dagger_{k\uparrow}c_{k\uparrow }|\Psi\rangle$. In Fig. 4 we show momentum distributions of the major component for systems with $p=0$ by different repulsive interactions. With $p=0$ the distributions are symmetric about $k=0$, and we only show the right half. For systems with $p\neq0$ the momentum distributions are asymmetric, however, as the interaction strength $|g/2k_{F}|$ increases they have the same behavior. With a very weak repulsive interaction, the momentum vitality is small and particle-hole excitations concentrate on the Fermi surface. As the interaction strength increases, particles in Fermi sea are more entangled with the impurity, and more inner particles are excited to higher momentum states. One can see that the momentum excitation has a relative large value below $2k_{F}$ in repulsive regime without a tightly bound dimer. This phenomenon also reflects that the hole term $q<k_{F}$ in Fermi sea plays an important role in repulsive polaron system.

Fig. 4

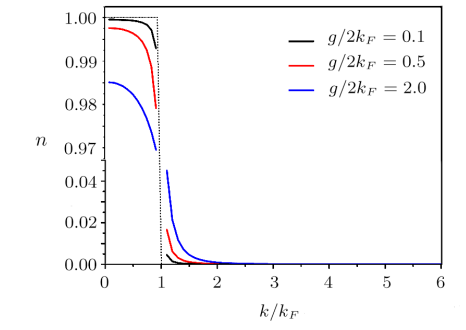New window|Download| PPT slide
Fig. 4(Color online) Momentum distributions of the major component for systems with different interactions in equal mass systems.



With the momentum distributions at hand, now we can study the Tan contact. Tan contact is a central universal quantity in many-body physics, which is highly related to the thermodynamics, asymptotic behavior of the momentum distribution tails and on-site density-density correlation.^[24-28] The Tan relations were first derived by Shina Tan, it measures the probability of finding two particles with different spins at the same place with short range interactions. Tan contact can also hold for Fermi gases in 1D case and was firstly expounded explicitly by Barth.^[28] In 1D polaron it was calculated by treating momentum as ideal Fermi-Dirac distribution without the momentum tail by T-matrix,^[29] which is imprecise as mentioned above. The Tan contact in 1D Fermi system is defined as^[28]

(7)$ C = g^2\int \mathrm{d}x\langle\Psi|\phi^\dagger_{\uparrow}(x)\phi^\dagger_{\downarrow}(x) \phi_{\downarrow}(x)\phi_{\uparrow}(x)|\Psi\rangle .$
Comparing to Hamiltonian of the system, one can find out that the Tan contact is highly related to the interaction energy term in Eq. (1). Firstly we calculate the Tan contact directly with the above definition from the view of correlation. A complicated Fourier transform is needed to transform Eq. (7) into momentum space with the wave function Eq. (2), which has been shown in Fig. 5. On the other hand, the contact can be calculated from the momentum tail clearly by one of Tan's universal relations

(8)$ n_{\downarrow}(k\gg k_{F})=n_{\uparrow}(k\gg k_{F}) = \frac{C}{k^4} , $
with $C$ the Tan contact. There is a linear relation between $n_\sigma(k)$ and $k^4$ for $k\gg k_{F}$, and we show an example in the inset of Fig. 5. After linearly fitting this, one can extract the Tan contact. Besides, from Tan's relation between adiabatic energy and the scattering length, the Tan contact can also be calculated by^[25]

(9)$ C=\frac{\mathrm{d}E}{\mathrm{d}a} , $
with $E$ the paloron energy and $a$ the 1D scattering length between two particles with different spins. The scattering length is related to the interaction strength with $g=-1/a$.^[28] Then with exact BA results in Eq. (6), one can get the exact Tan contact expression in 1D

(10)$ \frac{C}{k_{F}E_{F}}=\frac{2}{\pi a^2k^2_{F}}+\frac{1}{2a^3k^3_{F}}-\frac{1}{\pi a^3 k^3_{F}}\mathrm{arctan}\Big(\frac{-1}{ak_{F}}\Big) . $
Equation~(9) also suggests that given the Tan contact one can get the free energy and then any thermodynamic quantity at zero temperature. It means the Tan contact plays a very central role in the thermodynamics of the system. In Fig. 5 we show the Tan contact vs. the scaled interaction strength calculated from three different aspects: the correlation, large momentum distribution, and adiabatic energy relation. One can see that all results from different aspects are almost the same in whole attractive regime, in repulsive regimes where the interaction strength is below $g/2k_{F}=1$, the results can still agree with each other very well. In extreme strong repulsive regime $g/2k_{F}>2$ which corresponds to $\gamma>4/pi$ in BA equations,^[23,33] the contact from large momentum tail can still show a good trend. The contact of correlation value from Eq. (7) goes down, which indicates more complicated excitations happen and more particle-hole pairs need to be considered.

Fig. 5

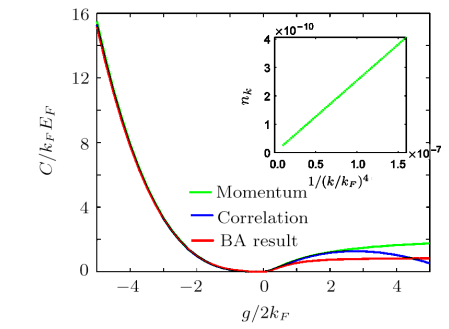New window|Download| PPT slide
Fig. 5(Color online) The Tan contact vs. the scaled interaction strength calculated from different methods. The green line is from fitting the momentum distribution tail, the blue line is from correlation with Eq. (7), the red line is exact BA results with Eq. (10). The left side of zero is attractive regime where three lines are almost the same, right side of zero is repulsive regime. Inset: the plot of momentum distribution of the major component for a system with $g/2k_{F}=0.5$. The straight line is a fitting function in form $\propto1/k^4$ with the regime $50k_{F}<k<100k_{F}$.



On the other side, we study the influence of hole momentum term $q$ on Tan contact. From Fig. 6 one can see, the hole term $q$ has a large influence on the Tan contact even in the attractive regime. Tan contact from fitting momentum tails without hole term $q$ goes up linearly as interaction increases. The influence of excited hole term $q$ on Tan contact is greater when compared with results in Fig. 2. So we declare that the hole term $q$ in Eq. (3) can not be ignored completely in the whole interaction regime of 1D polaron system.

Fig. 6

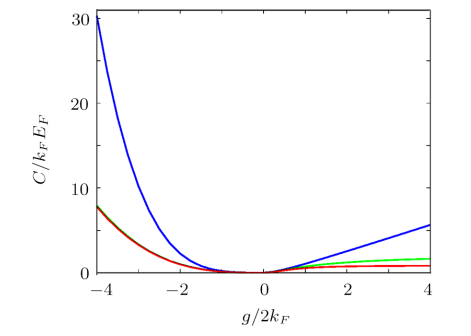New window|Download| PPT slide
Fig. 6(Color online) The Tan contact vs. the scaled interaction strength calculated by the influence of hole term $q$. The dash-dotted green line is from fitting the momentum distribution tail without considering hole term $q$, the solid green line is from fitting the momentum distribution tail completely with $q$, the red line is exact BA results with Eq. (10).



At last, we use the variational method to study pair functions. It is interesting to see how the spin-up and spin-down Fermi pairs behave with different repulsive interactions in 1D polaron. The definition of pair-pair correlation is $C_{P}(r)=\langle\Psi|c_{\uparrow}^\dagger(r)c_{\uparrow}^\dagger(r)c_{\downarrow}(0)c_{\uparrow(0)}|\Psi\rangle$. Translation invariance has been used and only the relative coordinate matters. After transforming it into momentum space, the correlation can be calculated. In Fig. 7 we show pair-pair correlation for systems with different repulsive interactions. The correlation is symmetric about $r=0$ and we only show half of it. When repulsive interaction is small, the correlation has a relative large value at the center ($r=0$). As repulsive interaction increases, correlation becomes small at $r=0$, but the value is still not zero. This signature indicates the incomplete separation of spin-up and spin-down Fermions in strong repulsive regime. From the decay rate of the correlations, we also know that the impurity mainly has significant correlations with nearby spin-$\uparrow$ particles.

Fig. 7

New window|Download| PPT slide
Fig. 7Pair-pair correlations for systems with different repulsive interactions.

5 Summary

We studied the 1D Fermi polaron problem for an impurity immersed in Fermi sea with repulsive interactions between them, the impurity is dressed up by surrounding particles in Fermi sea to form a polaron. Here we used the variational method, and filled up the deficiency in calculating energy and momentum distribution by T-matrix approach. We studied the binding energy, effective mass, momentum distributions, Tan contact and pair correlation for systems of repulsive polaron. We found that the polaron energy $E$ is below $E_F$ for equal masses system, and effective masses become infinite in strong repulsive regime which is consistent with the exact BA results. All results indicate the nonexistence of IFM phase in 1D polaron system. We get the Tan contact from three different aspects, which give almost the same results in whole attractive and relatively weak repulsive regimes. Furthermore, we illustrate the great importance of the hole momentum term $q$ excited by the impurity in repulsive polaron. We find that the hole term has a large influence on the polaron energy and the Tan contact.

Reference View Option By original order
By published year
By cited within times
By Impact factor

[1] L. D. Landau and S. I. Pekar , J. Exp. Theor. Phys. 18 (1948)419.
[Cited within: 1]

[2] J. M. D. Teresa, M. R. Ibarra, P. A. Algarabel , et al., Nature(London) 386 (1997)256.


[3] A. J. Millis , Nature(London) 392 (1998)147.
[Cited within: 1]

[4] I. Bloch, J. Dalibard, and W. Zwerger , Rev. Mod. Phys. 80 (2008)885.
[Cited within: 1]

[5] S. Giorgini, L. P. Pitaevskii, and S. Stringari , Rev. Mod. Phys. 80 (2008)1215.
[Cited within: 1]

[6] M. Lewenstein, A. Sanpera, V. Ahufinger , et al., Adv. Phys. 56 (2007)243.
[Cited within: 1]

[7] R. Schmidt, H. R. Sadeghpour, and E. Demler , Phys. Rev. Lett. 116 (2016)105302.
[Cited within: 1]

[8] R. Combescot, A. Recati, C. Lobo, and F. Chevy , Phys. Rev. Lett. 98 (2007)180402.
[Cited within: 1]

[9] S. Giraud and R. Combescot , Phys. Rev. A 79 (2009)043615.


[10] M. Koschorreck, D. Pertot, E. Vogt , et al., Nature(London) 485 (2012)619.


[11] Y. D. Song and X. M. Cai , Chin. Phys. Lett. 35 (2018)110301.
[Cited within: 1]

[12] P. Massignan, M. Zaccanti, and G. M. Bruun , Rep. Prog. Phys. 77 (2014)034401.
[Cited within: 1]

[13] Y. A. Liao, A. S. C. Rittner, T. Paprotta , et al., Nature(London) 467 (2010)567.
[Cited within: 1]

[14] N. B. Jrgensen, L. Wacker, K. T. Skalmstang , et al., Phys. Rev. Lett. 117 (2016)055302.
[Cited within: 1]

[15] F. Grusdt and M. Fleischhauer , Phys. Rev. Lett. 116 (2016)053602.
[Cited within: 1]

[16] J. Catani, G. Lamporesi, D. Naik , et al., Phys. Rev. A 85 (2012)023623.
[Cited within: 1]

[17] F. Chevy , Phys. Rev. A 74 (2006)063628.


[18] V. Ngampruetikorn, J. Levinsen, and M. M. Parish , Europhys. Lett. 98 (2012)30005.


[19] A. Schirotzek, C. H. Wu, A. Sommer, and M. W. Zwierlein , Phys. Rev. Lett. 102 (2009)230402.
[Cited within: 1]

[20] P. Massignan and G. M. Bruun , Eur. Phys. J. D 65 (2011)83.
[Cited within: 3]

[21] F. Scazza, G. Valtolina, P. Massignan , et al., Phys. Rev. Lett. 118 (2017)083602.
[Cited within: 3]

[22] W. L. Li and X. Cui , Phys. Rev. A 96 (2017)053609.
[Cited within: 2]

[23] E. Lieb and D. Mattis , Phys. Rev. 125 (1962)16472.
[Cited within: 3]

[24] S. Tan , Ann. Phys. 323 (2008)2952A.
[Cited within: 2]

[25] S. Tan , Ann. Phys. 323 (2008)2971A.
[Cited within: 1]

[26] S. Tan , Ann. Phys. 323 (2008)2987A.
[Cited within: 1]

[27] E. Braaten , arXiv: cond-mat.quant-gas/1008.2922.
[Cited within: 1]

[28] M. Barth and W. Zwerger , Ann. Phys. 326 (2011)2544.
[Cited within: 6]

[29] E. V. H. Doggen and J. J. Kinnunen , Phys. Rev. Lett. 111 (2013)025302.
[Cited within: 5]

[30] J. B. McGuire , J. Math. Phys. 6 (1965)432.
[Cited within: 1]

[31] J. B. McGuire , J. Math. Phys. 7 (1966)123.
[Cited within: 2]

[32] X. W. Guan , Front. Phys. 7 (2012)8.
[Cited within: 3]

[33] R. X. Mao, X. W. Guan, and B. Wu , Phys. Rev. A 94 (2016)043645.
[Cited within: 2]