Zheng-Mao Xu, Hong-Wei Li^,?Zhengzhou Information Science and Technology Institute, Zhengzhou 450004, China

Corresponding authors: ? E-mail:lihow@ustc.edu.cn

Received:2018-11-23Online:2019-04-1

Fund supported:

*Supported by National Natural Science Foundation of China under Grant.61675235 Supported by National Natural Science Foundation of China under Grant.11304397 National Key Research and Development Program of China under Grant.2016YFA0302600

Abstract
Bell inequality is an important resource in the quantum information theory, which can be applied to guarantee security of the device independent quantum information protocols. By utilizing the quantum weak measurement technology, we propose the Chain inequality violation with three parties, and the analysis result demonstrates that double Chain inequality violation can be observed in the case of Alice and Bob have two different measurement bases. Since the weak measurement model can be assumed to be an eavesdropping model, our analysis model may be applied to analyze security of the device independent quantum information protocols.
Keywords： chain inequality;weak measurement


PDF (292KB)MetadataMetricsRelated articlesExportEndNote|Ris|BibtexFavorite
Cite this article
Zheng-Mao Xu, Hong-Wei Li. Chain Inequality Violation with Quantum Weak Measurement Technology ^*. [J], 2019, 71(4): 393-396 doi:10.1088/0253-6102/71/4/393

1 Introduction

Based on Einstein's local realism and hidden variable model, Bell proposed the famous Bell inequality,^[1] which is an important resource in the quantum information theory. Chain inequality is an important kind of Bell inequality, which has $n$ ($n\geq2$) measurement bases, and the Clauser-Horne-Shimony-Holt (universally known as CHSH inequality^[2]) inequality can be assumed to be a special Chain inequality with $n=2$. More precisely, Chain inequality can be applied to propose device independent quantum information protocols,^[3-4] where security of the protocols can be guaranteed by the Chain inequality violation, not based on the perfect quantum states preparation and measurement assumption. More recently, Colbeck et al.^[5-10] have proved that the imperfect randomness could be amplified via Chain inequality.

The Bell inequality violation is usually based on the entanglement states preparation and the projective measurement assumption, which will lead to the states collapse after the projective measurement. However, by applying the weak measurement technology, an observer can extract less information about a system with the smaller disturbance.^[11-12] The weak measurement technology has been proved to propose double CHSH inequality violation,^[13-15] and double classical dimension witness violation^[16-17] respectively. Inspired by the double classical dimension witness violation with the weak measurement technology, we propose the double Chain inequality violation with three parties. More precisely, we propose the weak measurement model in the Chain inequality with different measurement setups ($n\geq2$), and the result demonstrates that double Chain inequality violation can be realized in the case of $n=2$. Since our analysis model is based on three parties, the analysis result may be applied to propose device independent protocols based on the network environment. On the other side, the weak measurement model can be assumed to be controlled by the eavesdropper, thus our analysis model may be applied to analyze security of the device independent quantum information protocols.

2 Chain Inequality

Bell inequality was proposed to study the local reality theory, which demonstrates that the entanglement state measurement outcomes cannot be reproduced by the local hidden variable theory. Chain inequality is one significant type of the Bell inequality, which was proposed by Braunstein and Caves in 1988,^[18] and it can be applied to propose the device independent quantum information protocols.

Chain inequality has two cooperate parties Alice and Bob, which links $n-$1 CHSH inequalities. More precisely, Alice and Bob have $n$ different measurement bases, which should be selected with true random numbers. The detailed Chain inequality can be given by

(1)$ C(x_{1},y_{2})+C(y_{2},x_{3})+C(x_{3},y_{4})+\cdots +C(x_{N-1},y_{N}) \quad -C(y_{N},x_{1})\leq N-2\,, $

where $N=2n$, $x_{i}$, $y_{i}$, $i=1,2,\ldots,N$ are the measurement bases selected by Alice and Bob respectively. $$ C(x_i,y_j)=\langle a_ib_j\rangle=\sum\limits_{a_i,b_j} a_ib_jP(a_i,b_j)=\cos(2\theta), $$ where $a_i,b_j$ demonstrate Alice's and Bob's measurement outcomes respectively, $\theta$ is the included angle between $x_i$ and $y_i$. In this formulation, $\langle a_ib_j\rangle$ and $P(a_i,b_j)$ demonstrate the expectation value of $a_i,b_j$ and the probability when Alice measures $a_i$ and Bob measures $b_j$. By utilizing this inequality, the classical upper bound of Chain inequality is $N-2$, while the quantum bound is $N\cos({\pi}/{N})$. To analyze the Chain inequality violation, the $n$ measurement operators applied by Alice and Bob have the following type

(2)

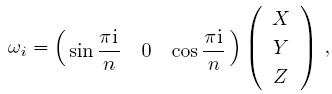
where $\omega_{i}$, $i=1,3,\ldots, N-1$ are Alice's measurement operators when Alice's measurement bases selection are $x_i$, and Alice's measurement operators can be represented by $A_{x_i}^{a_i}$. Similarly, $i=2,4, \ldots, N$ are Bob's measurement operators when Bob's measurement bases selection are $y_i$, and Bob's measurement operators can be represented by $B_{y_i}^{b_i}$. Here $X=\sigma_{x}=$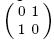, $Y=\sigma_{y}=$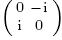, and $Z=\sigma_{z}=$ 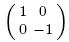are Pauli operators. Specifically, if there are only four measurement bases (i.e. $N=2n=4$), Chain inequality is equal to the CHSH inequality.

3 Weak Measurement

Quantum weak measurement was proposed by Aharonov, Albert, and Vaidamn in 1988,^[19] which was proven to be useful for signal amplification, state tomography, and solving quantum paradoxes.^[20-24] Comparing with the projective measurement, quantum weak measurement only introduces small disturbance to quantum system and will not make quantum states collapse entirely. The detailed weak measurement model is demonstrated in Fig. 1.

Fig. 1

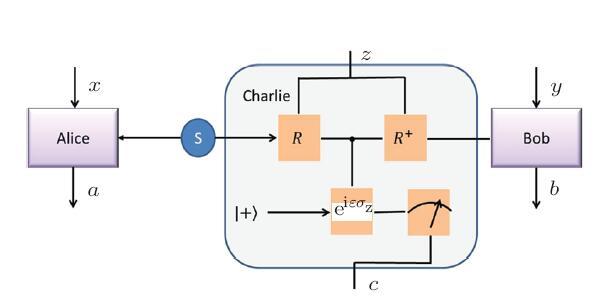New window|Download| PPT slide
Fig. 1(Color online) Operating procedure of weak measurement.



In the weak measurement model, $S$ generates the maximal entanglement state $\Psi_{AB}={(|01\rangle-|10\rangle)}/{\sqrt{2}}$ and sends the two particles to Alice and Bob respectively. After receiving the quantum state, Alice (Bob) selects measurement basis with the random number $x$ ($y$). The weak measurement model Charlie receives the quantum state and applies the operation $R_{z}|0\rangle=|\omega_{z}\rangle$, $R_{z}|1\rangle=|\omega_{z}^{\bot}\rangle$, where $|\omega_{z}\rangle$ and $|\omega_{z}^{\bot}\rangle$ are a new basis in the two-dimensional Hilbert space.

After receiving the quantum state $|1\rangle$, Charlie applies the following control operation $e^{i\varepsilon\sigma_{z}}$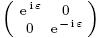, where $\varepsilon$ is the weak measurement parameter. This process is equal to the operation that carries out collective measurement on the particle sent to Bob and Charlie's state $|+\rangle$, then Alice, Bob, and Charlie measure their quantum states to get the measurement outcomes. By considering Alice, Bob and Charlie as an integer system, the previous $R$ operation can be represented as

(3)$ U_{1}=I\otimes R_{z}\otimes I\,. $

After the $R$ operation, the weak measurement operation $e^{i\varepsilon\sigma_{z}}$ can be represented as

(4)$ U_{2}=I\otimes |0\rangle \langle0| \otimes I +I\otimes |1\rangle \langle1| \otimes e^{i\varepsilon\sigma_{z}}\,. $

Finally, the last operation can be represented as

(5)$ U_{3}=I\otimes R_{z}^{+}\otimes I\,. $

Combining these three steps, we can get

(6)$ \qquad U=U_{3}U_{2}U_{1} =I\otimes \pi_{B}^{+Z}\otimes I +I\otimes \pi_{B}^{-Z}\otimes e^{i \varepsilon \sigma_{z}}\,, $

where $\pi_{B}^{+Z}=|\omega_{z}\rangle\langle\omega_{z}|$ and $ \pi_{B}^{-Z}=|\omega_{z}^{\bot}\rangle\langle\omega_{z}^{\bot}|$.

The density matrix of the initial state about Alice, Bob and Charlie's quantum system can be given by $\rho_{ABC}=\rho_{AB}\otimes |+\rangle\langle+|_{C}$, where Alice and Bob's systems have no correlation with Charlie's system. The density matrix of Alice and Bob's system is $\rho_{AB}=({1}/{2})P(|0\rangle|1\rangle-|1\rangle|0\rangle)=({1}/{2})P(|\omega_{z}\rangle |\omega_{z}^{\bot}\rangle-|\omega_{z}^{\bot}\rangle|\omega_{z}\rangle)$ where $P|x\rangle=|x\rangle\langle x|$. After the corresponding quantum state evolution, the density matrix of Alice, Bob and Charlie's quantum system can be given by

(7)$ \rho_{ABC}^{'}=U\rho_{ABC}U^{\dagger} =(I\otimes \pi_{B}^{+Z}\otimes I+I\otimes \pi_{B}^{-Z}\otimes e^{i \varepsilon \sigma_{z}})\rho_{ABC}(I\otimes \pi_{B}^{+Z} \otimes I+I\otimes \pi_{B}^{-Z}\otimes e^{i \varepsilon \sigma_{z}})^{\dagger}\,. $

4 Chain Inequality with Weak Measurement

After receiving the quantum state $\rho_{AB}$, Alice and Bob firstly calculate their own Bell inequality according to their measurement outcomes. Similarly, Alice and Charlie also can calculate their Bell inequality by receiving the quantum state $\rho_{AC}$. If the two Bell inequality values both violate classical upper bound, we can realize the double Bell inequality violation.

The number of measurement bases $N$ is determined by Alice and Bob, which have different Bell inequality values. Note that, the measurement bases selected by Charlie are equal to Bob's measurement bases selection, which can be represented by $C^{c}$, $c$ is Charlie's measurement outcome.

When applying the weak measurement model with the Chain inequality, we calculate the Chain inequality about Alice and Bob's systems to get the inequality value $I_{AB}$. Similarly, we can calculate the Chain inequality about Alice and Charlie's systems to get the inequality value $I_{AC}$. To calculate the Chain inequality value, we apply the following equation

$$ I _{AB}=C(x_{1},y_{2})+C(y_{2},x_{3})+C(x_{3},y_{4})+\cdots +C(x_{N-1},y_{N}) -C(y_{N},x_{1}) (C(x_i,y_j)=\sum\limits_{a_i,b_j} a_ib_jP(a_i,b_j|x_i,y_j)) $$

represents the Chain inequality value about Alice and Bob's quantum systems with input random number $x_i$ and $y_j$ and measurement outcomes $a_i$ and $b_j$.

$$ I _{AC}=C(x_{1},z_{2})+C(z_{2},x_{3})+C(x_{3},z_{4}) +\cdots+C(x_{N-1},z_{N}) -C(z_{N},x_{1}) (C(x_i,z_k)=\sum\limits_{a_i,c_k} a_ic_kP(a_i,c_k|x_i,z_k)) $$

represents the Chain inequality value about Alice and Charlie's quantum systems with input random number $x_i$ and $z_k$ and measurement outcomes $a_i$ and $c_k$.

To calculate the Chain inequality value, the conditional probabilities between Alice and Bob can be given by

(8)$ \qquad P(a_ib_j|x_iy_j)=\sum\limits_{z_k}P(z_k) {\rm tr}(A_{x_i}^{a_i}B_{y_j}^{b_j}\rho_{AB}^{'}(z_k))\,. $

Correspondingly, the conditional probabilities between Alice and Charlie can be given by

(9)$ P(a_ic_k|x_iz_k)={\rm tr}(A_{x_i}^{a_i}C^{c_k}\rho_{AC}^{'}(z_k))\,. $

The corresponding density matrices are $\rho_{AB}^{'}(z_k)={\rm tr}_{C}(\rho_{ABC}^{'})$ and $\rho_{AC}^{'}(z_k)={\rm tr}_{B}(\rho_{ABC}^{'})$. The main difficulty to estimate the Chain inequality is to calculate the conditional probabilities $P(a_ib_j|x_iy_j)$ and $P(a_ic_k|x_iz_k)$. The precise density matrix can be respectively given by

(10)$ \rho_{ABC}^{'}=\pi_{B}^{+Z}\rho_{ABC}\pi_{B}^{+Z}+ \pi_{B}^{+Z}\rho_{ABC}\pi_{B}^{-Z}(e^{-i\varepsilon\sigma_{z}})_{C} +\pi_{B}^{-Z}(e^{i\varepsilon\sigma_{z}})\rho_{ABC}\pi_{B}^{+Z} +\pi_{B}^{-Z}(e^{i\varepsilon\sigma_{z}})\rho_{ABC}\pi_{B}^{-Z} \times(e^{-i\varepsilon\sigma_{z}})\,, $

then

(11)$ \rho_{AB}^{'}(z_k)={\rm tr}_{C}(\rho_{ABC}^{'}) =\pi_{B}^{+Z}\rho_{AB}\pi_{B}^{+Z}+\pi_{B}^{+Z}\rho_{AB} \pi_{B}^{-Z}\cos \varepsilon +\pi_{B}^{-Z}\rho_{AB}\pi_{B}^{+Z}\cos \varepsilon +\pi_{B}^{-Z}\rho_{AB}\pi_{B}^{-Z} =\rho_{AB}\cos\varepsilon+(1-\cos\varepsilon)(\pi_{B}^{+Z} \rho_{AB}\pi_{B}^{+Z} +\pi_{B}^{-Z}\rho_{AB}\pi_{B}^{-Z})\,. $

Substituting Eq. (11) into Eq. (8),

(12)$ P(a_ib_j|x_iy_j) =\sum\limits_{z_k}P(z_k){\rm tr}(A_{x_i}^{a_i}B_{y_j}^{b_j}\rho_{AB}^{'}(z_k)) =\sum\limits_{z_k}P(z_k){\rm tr}(|\mu_{x_i}^{a_i} \rangle\langle\mu_{x_i}^{a_i}||\theta_{y_j}^{b_j}\rangle\langle \theta_{y_j}^{b_j}|(\rho_{AB}\cos\varepsilon +(1-\cos\varepsilon)(\pi_{B}^{+Z}\rho_{AB}\pi_{B}^{+Z} +\pi_{B}^{-Z}\rho_{AB}\pi_{B}^{-Z}))) =\frac{1}{4}\sum\limits_{z_k}P(z_k)(\cos\varepsilon(1-a_ib_j (\mu_{x_i}\cdot\theta_{y_j})) +(1-\cos\varepsilon) (1-a_ib_j(\mu_{x_i}\cdot\eta_{z_k})(\theta_{y_j}\cdot\eta_{z_k})))\,. $

We assume that Alice, Bob and Charlie apply the optimal measurement to reach the upper bound value of the Chain inequality, the corresponding Pauli operators can be given by $\mu_{x_i}$, $\theta_{y_j}$, and $\eta_{z_k}$.

Then we have the Chain inequality value between Alice and Bob is

(13)$ I_{AB}=\cos\frac{\pi}{N}((N-2)\cos\varepsilon+2)\,. $

Similarly, the Chain inequality value between Alice and Charlie is given by

(14)$ I_{AC}=N\cos\frac{\pi}{N}\sin^{2}\varepsilon\,. $

Note that $\varepsilon=0$ indicates $I_{AB}=N\cos({\pi}/{N})$ and $I_{AC}=0$, which demonstrates that Charlie's quantum state has no interaction with Bob's system. In this case, only $I_{AB}$ violates the classical upper bound $N-2$. In the case of $\varepsilon={\pi}/{2}$, we can get $I_{AB}=2\cos{\pi}/{N}$ and $I_{AC}=N\cos{\pi}/{N}$, which demonstrates that only Charlie and Bob's system can violate the classical upper bound.

Figures 2, 3, and 4 illustrate the Chain inequality values $I_{AB}$ and $I_{AC}$ with different weak measurement parameters $\varepsilon$, where the blue line represents the Chain inequality value $I_{AB}$, the red line represents the Chain inequality value $I_{AC}$, the green curve represents the classical upper bound of different Chain inequalities.

Fig. 2

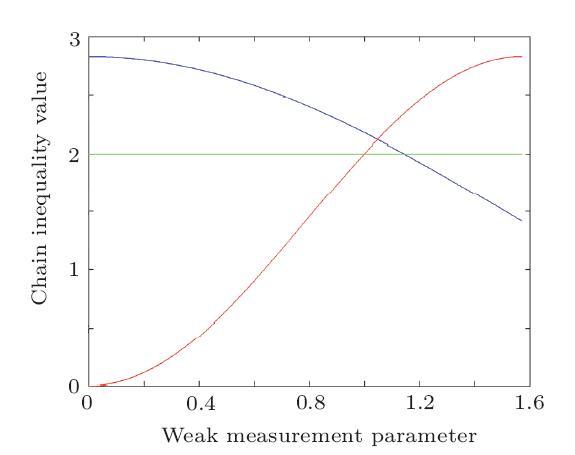New window|Download| PPT slide
Fig. 2(Color online) Two measurement basis with $n$=2. The blue line represents the Chain inequality value $I_{AB}$, the red line represents the Chain inequality value $I_{AC}$, the green curve represents the classical upper bound of Chain inequalities.

Fig. 3

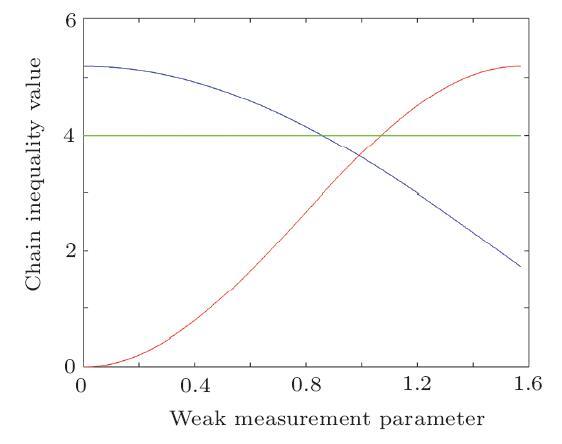New window|Download| PPT slide
Fig. 3(Color online) Two measurement basis with $n$=3. The blue line represents the Chain inequality value $I_{AB}$, the red line represents the Chain inequality value $I_{AC}$, the green curve represents the classical upper bound of Chain inequalities.

Fig. 4

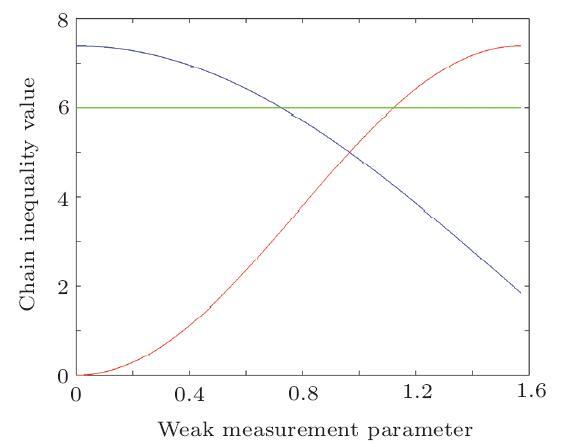New window|Download| PPT slide
Fig. 4(Color online) Two measurement basis with $n$=4. The blue line represents the Chain inequality value $I_{AB}$, the red line represents the Chain inequality value $I_{AC}$, the green curve represents the classical upper bound of Chain inequalities.



We can figure out that the inequality values $I_{AB}$ and $I_{AC}$ can both violate the classical upper bound value in the case of $n=2$ with the appropriate weak measurement parameter. In the case of $n\geq3$, the Chain inequality can not realize the double classical upper bound violation. However, we can realize the inequality value $I_{AB}$ or $I_{AC}$ violate the classical upper bound with different weak measurement parameters. Thus our analysis model may be applied to analyze the device independent protocols with the network environment.

5 Conclusion

In conclusion, we propose the weak measurement model to analyze the Chain inequality, and the double inequality violation can be observed in the case of $n=2$. In the case of $n\geq3$, two different parties can respectively realize the Chain inequality violation with different weak measurement parameters. The analysis results demonstrate that weak measurement may have significant applications in multi observer quantum information theory. More precisely, our analysis model may be applied to analyze the device independent quantum information protocols in the network environment, which can be utilized to generate high efficiency device independent random numbers. On the other side, our analysis result also provides tremendous motivation for further experimental research.

The authors have declared that no competing interests exist.

Reference View Option By original order
By published year
By cited within times
By Impact factor

[1] J. S. Bell , Physics (New York) 1(1964) 195.
[Cited within: 1]

[2] J. F. Clauser, M. A. Horne, A. Shinomy, R. A. Holt , Phys. Rev. Lett. 23(1969) 880.
DOI:10.1103/PhysRevLett.23.880URL [Cited within: 1]

[3] S. Pironio, A. Acín, S. Massar , et al., Nature (London) 464(2010) 1021.
DOI:10.1038/nature09008 [Cited within: 1]

[4] A. Acín, N. Brunner , N. Gisin, et al., Phy. Rev. Lett. 98(2007) 230501.
DOI:10.1103/PhysRevLett.98.230501URLPMID:17677888 [Cited within: 1]
We present the optimal collective attack on a quantum key distribution protocol in the "device-independent" security scenario, where no assumptions are made about the way the quantum key distribution devices work or on what quantum system they operate. Our main result is a tight bound on the Holevo information between one of the authorized parties and the eavesdropper, as a function of the amount of violation of a Bell-type inequality.

[5] R. Colbeck and R. Renner, Nature Phys. 10(2012) 1038.
[Cited within: 1]

[6] R. Gallego, L. Masanes , G. De La Torre, et al., Nature Commun. 4(2012) 2654.


[7] M. Herrero-Collantes and J.C. Garcia-Escartin, Rev. Mod. Phys. 89(2017) 015004.
DOI:10.1103/RevModPhys.89.015004URL

[8] J. D. Bancal, L. Sheridan, V. Scarani , New J. Phys. 16(2014) 258.


[9] M. J. W. Hall , Phys. Rev. A 84 (2011) 022102.
DOI:10.1103/PhysRevA.84.022102URL

[10] R. Colbeck and R. Renner, Nature Commun. 2(2011) 411.
[Cited within: 1]

[11] O. Hosten and P. Kwiat , Science 319 (2008) 787.
[Cited within: 1]

[12] P. B. Dixon, D. J. Starling, A. N. Jordan, J. C. Howell , Phys. Rev. Lett. 102(2009) 173601.
DOI:10.1103/PhysRevLett.102.173601URL [Cited within: 1]

[13] M. J. Hu, Z. Y. Zhou, X. M. Hu , et al., arXiv:quant-ph/1609.01863, ( 2016).
[Cited within: 1]

[14] M. Schiavon, L. Calderaro, M. Pittaluga , et al., Quant. Sci.Technol. 2(2017) 015010.
DOI:10.1088/2058-9565/aa62beURL
Bipartite Bell inequalities can be simultaneously violated by two different pairs of observers when weak measurements and signaling is employed. Here we experimentally demonstrate the violation of two simultaneous CHSH inequalities by exploiting a two-photon polarization maximally entangled state. Our results demonstrate that large double violation is experimentally achievable. Our demonstration may have impact for Quantum Key Distribution or certification of Quantum Random Number generators based on weak measurements.

[15] R. Silva, N. Gisin, Y. Guryanova, S. Popescu , Phys. Rev. Lett. 114(2015) 250401.
DOI:10.1103/PhysRevLett.114.250401URL [Cited within: 1]
We investigate the trade-off between information gain and disturbance for von Neumann measurements on spin-1/2 particles, and derive the measurement pointer state that saturates this trade-off, which turns out to be highly unusual. We apply this result to the question of whether the nonlocality of a single particle from an entangled pair can be shared among multiple observers that act sequentially and independently of each other, and show that an arbitrarily long sequence of such observers can all violate the Clauser-Horne-Shimony-Holt-Bell inequality.

[16] H. W. Li, Y. S. Zhang, X. B. An , et al., Commun. Phys. 1(2018) 10.
DOI:10.1038/s42005-018-0011-xURL [Cited within: 1]

[17] X. B. An, H. W. Li, M. J. Hu , et al., Opt. Lett. 43(2018) 14.
[Cited within: 1]

[18] S. L . Braunstein and C. M.Caves, Phys. Rev. Lett. 61(1988) 662.
DOI:10.1103/PhysRevLett.61.662URL [Cited within: 1]

[19] Y. Aharonov, D. Z. Albert, L. Vaidman , Phys. Rev. Lett. 60(1988) 1351.
DOI:10.1103/PhysRevLett.60.1351URL [Cited within: 1]

[20] P. B. Dixon, D. J. Starling, A. N. Jordan, J. C. Howell , Phys. Rev. Lett. 102(2009) 173601.
DOI:10.1103/PhysRevLett.102.173601URL [Cited within: 1]

[21] X. Y. Xu, Y. Kedem, K. Sun , et al., Phys. Rev.Lett. 111(2013) 033604.
DOI:10.1103/PhysRevLett.111.033604URLPMID:23909319
We report results of a high precision phase estimation based on a weak measurements scheme using commercial light-emitting diode. The method is based on a measurement of the imaginary part of the weak value of a polarization operator. The imaginary part of the weak value appeared due to the measurement interaction itself. The sensitivity of our method is equivalent to resolving light pulses of order of attosecond and it is robust against chromatic dispersion.

[22] J. S. Lundeen, B. Sutherland, A. Patel , et al., Nature (London) 474(2011) 188.
DOI:10.1038/nature10120URLPMID:21654800
Abstract: Central to quantum theory, the wavefunction is the complex distribution used to completely describe a quantum system. Despite its fundamental role, it is typically introduced as an abstract element of the theory with no explicit definition. Rather, physicists come to a working understanding of the wavefunction through its use to calculate measurement outcome probabilities via the Born Rule. Presently, scientists determine the wavefunction through tomographic methods, which estimate the wavefunction that is most consistent with a diverse collection of measurements. The indirectness of these methods compounds the problem of defining the wavefunction. Here we show that the wavefunction can be measured directly by the sequential measurement of two complementary variables of the system. The crux of our method is that the first measurement is performed in a gentle way (i.e. weak measurement) so as not to invalidate the second. The result is that the real and imaginary components of the wavefunction appear directly on our measurement apparatus. We give an experimental example by directly measuring the transverse spatial wavefunction of a single photon, a task not previously realized by any method. We show that the concept is universal, being applicable both to other degrees of freedom of the photon (e.g. polarization, frequency, etc.) and to other quantum systems (e.g. electron spin-z quantum state, SQUIDs, trapped ions, etc.). Consequently, this method gives the wavefunction a straightforward and general definition in terms of a specific set of experimental operations. We expect it to expand the range of quantum systems scientists are able to characterize and initiate new avenues to understand fundamental quantum theory.

[23] J. S . Lundeen and C. Bamber, Phys.Rev. Lett. 108(2012) 070402.
DOI:10.1103/PhysRevLett.108.070402URLPMID:22401180
Abstract Recent work by Lundeen et al. [Nature (London) 474, 188 (2011)] directly measured the wave function by weakly measuring a variable followed by a normal (i.e., "strong") measurement of the complementary variable. We generalize this method to mixed states by considering the weak measurement of various products of these observables, thereby providing the density matrix an operational definition in terms of a procedure for its direct measurement. The method only requires measurements in two bases and can be performed in situ, determining the quantum state without destroying it.

[24] Y. Aharonov, A. Botero, S. Popescu , et al., Phys. Lett. A 301 (2002) 130.
DOI:10.1016/S0375-9601(02)00986-6URL [Cited within: 1]
Hardy's paradox is revisited. Usually the paradox is dismissed on grounds of counterfactuality, i.e., because the paradoxical effects appear only when one considers results of experiments which do not actually take place. We suggest a new set of measurements in connection with Hardy's scheme, and show that when they are actually performed, they yield strange and surprising outcomes. More generally, we claim that counterfactual paradoxes point to a deeper structure inherent to quantum mechanics.