 ,1,?, Yun-Song Piao1,2
,1,?, Yun-Song Piao1,2Corresponding authors: ? E-mail:yegen14@mails.ucas.ac.cn
Received:2019-01-18Online:2019-04-1
| Fund supported: |

Abstract
Keywords:
PDF (360KB)MetadataMetricsRelated articlesExportEndNote|Ris|BibtexFavorite
Cite this article
Gen Ye, Yun-Song Piao. Implication of GW170817 for Cosmological Bounces *. [J], 2019, 71(4): 427-434 doi:10.1088/0253-6102/71/4/427
1 Introduction
Inflation is a successful scenario of the early universe[1-4] However, it is well-known that inflation suffered from the singularity problem.[5-6] This suggests that our understanding about the gravity and the early universe is incomplete. Instead of going to the quantum regime and studying the physics of the "singularity", one might construct classical nonsingular cosmological models alternative or complementary to the inflation scenario. Bouncing cosmology is a class of such models with different applications, see e.g. Refs. [7-9] for earlier studies, Refs. [10-12] for recent reviews.Building nonsingular cosmological models in the scalar field theories has been still one of the endeavors. It has been observed that the spatially flat bounce models constructed in Horndeski theories[13] inevitably encounter instabilities (or else the singularity in Lagrangian),[14-15] the so-called No-go Theorem, see also Refs. [16-18] for the attempts in the Horndeski theory. Recently, based on the effective field theory (EFT) of cosmological perturbations, it has been found that the solutions of fully stable (without ghosts, gradient instabilities, etc., throughout the whole evolution) cosmological bounce do exist if one goes beyond Horndeski,[19-20] see Refs. [21-23] for the corresponding bounce models performed in full covariant Lagrangians (of the beyond Horndeski theory[24]). The progress caused by "No-go" have also stimulated lots of studies, e.g. Refs. [25-32].
Beyond Horndeski theories are a subclass of the degenerate higher-order scalar-tensor (DHOST) theory.[33-36] Unlike in general relativity (GR), the propagating speed $c_{T}$ of gravitational waves (GW) in the DHOST theory might deviate considerably from the speed of light. Recently, the detection of GW170817[37] and its electromagnetic counterpart has provided a precise measurement for the speed of GWs: it coincides with the speed of light with deviations smaller than a few $\times 10^{-15}$, i.e.\ $c_{T}=1$. This measurement strictly constrained the scalar-tensor theories responsible for the acceleration of the current universe.[38-43] Though the physics implied by GW170817 seems not straightly related with that for the primordial universe, undeniably, such potential relevance will be interesting.
In this paper, inspired by the implication of GW 170817, we will construct the stable cosmological bounce models with $c_{T}=1$. Using the ADM metric, we replace the covariant $c_{T}=1$ DHOST Lagrangian with its ADM form (Sec. 2), and perform the perturbation calculations with it. We construct fully stable bounce models in the beyond Horndeski theory with $c_{T}=1$ (SubSec. 3.1), which is a special subclass of the DHOST theory, and in the full $c_{T}=1$ DHOST theory (SubSec. 3.2), respectively.
2 DHOST Theory with $c_{T}=1$
2.1 The Lagrangians
We begin with the covariant Lagrangian of the beyond Horndeski theory with $c_{T}=1$[38]where $\nabla_\mu\phi\equiv \phi_\mu$, $\nabla_\nu\nabla_\mu\phi\equiv\phi_{\mu\nu}$, and $X\equiv\phi_\mu\phi^\mu$.
We adopt the ADM metric
where $N$ is the lapse, $N_i$ is the shift, $h_{ij}$ is the spatial metric. We will use $\eta =\phi$ as the time coordinate in the FRW metric, $d s^2=-N(\eta )^2d\eta ^2+a^2|d\vec{x}|^2$. Dynamics of $\phi$ has been absorbed into $N(\eta )$, since $\phi'\equiv{d\phi}/{d\eta }=1$.
In the unitary gauge $\delta\phi=0$, the covariant Lagrangian $L_{c_{T}=1}^{bH}$ (1) may be rewritten in the ADM form[24]
where $R\equiv h^{ij}R_{ij}$ is the Ricci scalar on the spacelike hypersurface, $K\equiv h^{ij}K_{ij}$ is the extrinsic curvature on the spacelike hypersurface and $K_2\equiv K^2-K_{ij}K^{ij}$. The coefficients $P(N,\eta )$, $Q(N,\eta )$ and $A(N,\eta )$ are related with $G_2$, $G_3$, and $B_4$ in Eq. (1) by
The covariant Lagrangian $L^{\rm DHOST}_{c_{T}=1}$ of the DHOST theory with $c_{T}=1$ has been identified in Ref. [43]. As pointed out in Ref. [38], $L^{\rm DHOST}_{c_{T}=1}$ may be obtained by performing a conformal rescaling $g_{\mu\nu}\to C(\phi,X)g_{\mu\nu}$ to $L^{bH}_{c_{T}=1}$. Since the light cone is not altered, the corresponding DHOST theory will maintain $c_{T}=1$. Therefore, the ADM Lagrangian of DHOST theories with $c_{T}=1$ may be straightly calculated by rescaling $N\to\sqrt{C}N$, $h_{ij}\to Ch_{ij}$, $h^{ij}\to C^{-1}h^{ij}$, where $C=C(N,\eta)$. Here, without loss of generality, we will set $N_i=0$ in the calculation. Considering $K_{ij}=({1}/{2N})(h_{ij}'-\nabla_i N_j-\nabla_j N_i)$, after some integrations by parts and the redefinition of coefficients, we have
where $B(N,\eta)=\partial_N(\log C)$. It can be checked that this ADM Lagrangian is equivalent to the covariant $L^{\rm DHOST}_{c_{T}=1}$ showed in Ref. [43]. When $B=0$ (or $C=$ const.), ${L}^{\rm DHOST}_{c_{T}=1}$ reduces to the beyond Horndeski Lagrangian $L^{bH}_{c_{T}=1}$ in Eq. (3). In order to write out Eq. (5), we have absorbed the term linear in $N'$ into $P+QK$ by
$$ \frac{f(N,\eta)}{N}N'=n^{\mu}\nabla_\mu F-\frac{1}{N} \partial_\eta F \\ =-F K-\frac{1}{N}\partial_\eta F\,, $$
where $F\equiv\int f d N$.
2.2 The EFT of Scalar Perturbation
The quadratic order EFT of the DHOST theory is[35]Contracting Eq. (5) with Eq. (6), we can directly read off the effective coefficients in EFT (6),
where $\mathcal{H}/N\equiv ({d a/d\eta})/{aN}=H$, and ${L}^{\rm DHOST}_{c_{T}=1}=L$ is set for simplicity. Degenerate conditions have been checked
Compared with that in Ref. [35], the condition (9) has been slightly modified, since we have not necessarily $N(\eta)=1$ here.
Use the scalar perturbation
to expand (5) or EFT (6). When $N_i\ne0$, $N'$ in $\mathcal{L}^{\rm DHOST}_{c_{T}=1}$ (5) should be promoted to $N'-N^i\partial_i N$. In the corresponding result, $\delta N'\zeta'$ is absorbed into $\tilde{\zeta}^{\prime2}$ by replacing $\zeta$ with a new variable $\tilde{\zeta}=\tilde{\zeta}(\zeta,\delta N)$. Using $\delta L/\delta\psi=0$, and after some integrations by parts, we get the quadratic order Lagrangian of $\zeta$,
with coefficients
where
The $\gamma$ in Eq. (14) is related to the $\gamma$ in Refs. [16, 44] by $2A\gamma\to \gamma$.
The absence of ghost suggests $U>0$. The sound speed of scalar perturbation is $c_{ S}^2=V/U$. Gradient stability suggests $c^2_{ S}>0$.
3 Stable Bounce Models
We will construct the fully stable (pathology-free) bounce models in the beyond Horndeski theory (3) and DHOST theory (5) with $c_{T}=1$, respectively. Both actually belong to the subclasses of the full DHOST theory. We will follow the method in Refs. [22-23].We first set the evolutions of background (the Hubble parameter $H$ and $N$). In our model, $H={\mathcal{H}}/{N}$ follows
with
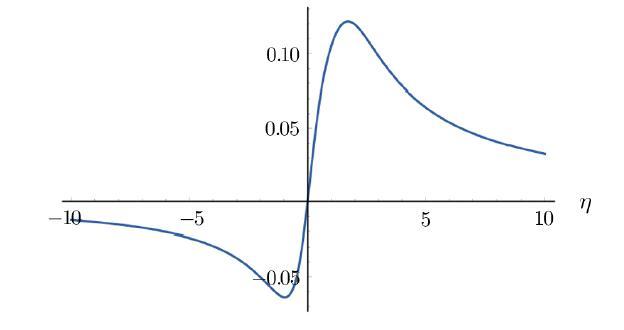
where $p_f$, $p_i$, $\eta_p$, and $\tau_p=$ const. Initially $\eta\ll -1$, ${\cal H}<0$, the universe contracts with $p(\eta)=p_i$ ($p_i\gg 1$ corresponds to the ekpyrotic contraction[7]). Cosmological bounce occurs at $\eta=0$. Hereafter, the universe expands, and ${\cal H}>0$ has the desired asymptotic form $\sim 1/(p_f\eta)$, see Fig. 1. Meanwhile $N$ follows
Fig. 1
 New window|Download| PPT slide
New window|Download| PPT slideFig. 1The evolution of $H$ with $p_i=8$ and $p_f=3$.
where $x_f$, $x_i$, $\eta_x$, and $\tau_x=$ const. The choice of Refs. [22-23] is equivalent to setting $p_i=p_f=3$ and $x_i=x_f=1$ (equivalently ${\dot \phi}=1$) in Eqs. (18) and (19), respectively.
3.1 In Beyond Horndeski Theory
We set $M_p^2=(8\pi G)^{-1}=1$, and write $P(N,\eta)$, $Q(N,\eta)$ and $A(N,\eta)$ in Eq. (3) aswhere the $N$-dependent part of $A(N,\eta)$ sets the coefficient $\sim B_{4,X}(\phi, X)\neq 0$ in $L_{c_{T}=1}^{bH}$ (1), and is required for the fully stable bounce.[19-22] $Q(N,\eta)$ is related with the cubic Galileon $G_3(\phi,X)\Box\phi$ in $L_{c_{T}=1}^{bH}$ (1), see Refs. [45-48] for the so-called G-bounce and Ref. [49] for super-bounce. However, $G_3(\phi,X)\Box\phi$ only moves the period of $c_{ S}^2<0$ to the outside of the bounce phase, but cannot dispel it completely, as pointed out in Refs. [16, 46]. Thus we set $Q(N,\eta)=0$ for simplicity.
Since $Q(N,\eta)=0$, Eq. (14) is simplified as
noting $\beta_1=0$ in the beyond Horndeski theory (1). To avoid possible divergence of $U$ induced by $\gamma=0$ (usually called $\gamma$-crossing,[16-17,44] we choose $\Sigma$ in Eq. (15) as
$U>0$ (avoiding the ghost instability) can be insured by adjusting $c_1(\eta)$. $\gamma$-crossing will bring a singularity in unitary gauge.[44] However, as pointed out in Ref. [23], this singularity does not affect the proof of the No-go Theorem.[14-15]
According to Eq. (3), we have the equations of ${\cal H}$ and $N$ as follows,
One can solve out $g_1(\eta)$, $g_2(\eta)$, and $g_3(\eta)$ in $P(N,\eta)$ algebraically by considering Eqs. (22) and (23), which are showed in Appendix A.
Substituting the corresponding solutions into Eq. (16), we have
$$ \mathcal{M}=\frac{1-4f_1^2x^4}{2\mathcal{H}(1+6f_1x^2)}\,. $$
We choose $f_1(\eta)$ as
to make $\mathcal{M}$ not divergent at ${\cal H}=0$. $V>0$ (avoiding the gradient instability) can be insured by adjusting $c_2(\eta)$ and $c_3(\eta)$, noting $1-4f_1^2x^4=0$ at ${\cal H}=0$.
Therefor, with $c_1(\eta)$, $c_2(\eta)$, and $c_3(\eta)$ satisfying certain conditions, we will have a fully stable bounce model. As a concrete example, setting
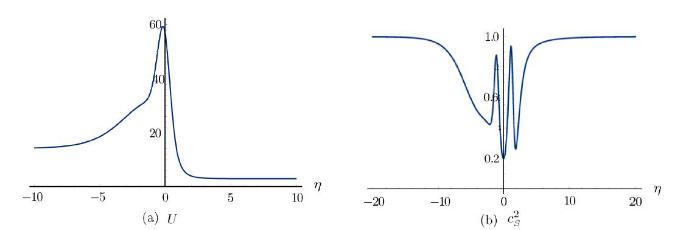
we plot Figs. 2 adn 3 with the parameters $p_i=8$, $p_f=3$, $\tau_p=1$, $\eta_p=0.7$, and $-\eta_x=\tau_x=3$ in Eqs. (17) and (19), as well as $k_1=0.06$, $k_2=2$, $\tau_1=2$, and $\tau^2_2=0.6$ in Eq. (25). Figure 2 shows that the coefficients $g_1(\eta)$, $g_2(\eta)$, $g_3(\eta),$ and $f_1(\eta)$ in Eq. (20) have been fixed. Figure 3 shows that the model is indeed gradient-stable and ghost-free.
Fig. 2
 New window|Download| PPT slide
New window|Download| PPT slideFig. 2Coefficients of the beyond Horndeski Lagrangian (20) in our bounce model.
Fig. 3
 New window|Download| PPT slide
New window|Download| PPT slideFig. 3The model is ghost-free and gradient-stable since $U>0$ and $c_{ S}^2>0$. During the expansion and contraction far from the bounce phase, $c_{ S}^2=1$.
That the gravity should asymptotically approach GR requires $f_1\to 0$ in the asymptotic future. The asymptotic behavior of $f_1$ is controlled by $c_2(\eta)$. As a result, the sound speed squared $c^2_{ S}(+\infty)$ is (assume $c_1(+\infty)$ vanishes)
$$ c^2_{ S}(+\infty)=\frac{-xH'+Hx'}{3H^2x^2}\,. $$
Require $c_{ S}^2(+\infty)=1$ and insert background (19), one finds
Similarly, $x_i$ is related to $p_i$ by requiring $c_{ S}^2(-\infty)=1$.
3.2 In DHOST Theory
The procedure is similar to that in SubSec. 3.1. We write $P(N,\eta)$, $Q(N,\eta)$, $A(N,\eta)$, and $B(N,\eta)$ in Eq. (5) aswith $b_0\neq 0$ constant. So $\beta_1$, $\beta_2$, $\beta_3\neq 0$ in the quadratic order EFT of the DHOST theory (6).
Substituting Eq. (27) into Eq. (14), we have $\gamma\sim 2\mathcal{H}+b_0N'$. Considering (19), we have $N'(\pm\infty)=0$. This suggests $\gamma(-\infty)\sim {\cal H}<0$ and $\gamma(+\infty)>0$. In other words, the existence of $b_0$ only shifts the $\gamma$-crossing point to $\eta_0\neq 0$ instead of eliminating it. Therefore, the condition (22) is still needed. To make $\mathcal{M}$ not divergent at $\eta_0$, we might choose $g_4(\eta)$ as
Thus with $c_1(\eta)$ required in Eq. (22), $c_2(\eta)$ and $c_3(\eta)$ in Eq. (28), we could have a fully stable bounce model based on the DHOST theory (5).
As a concrete example, setting
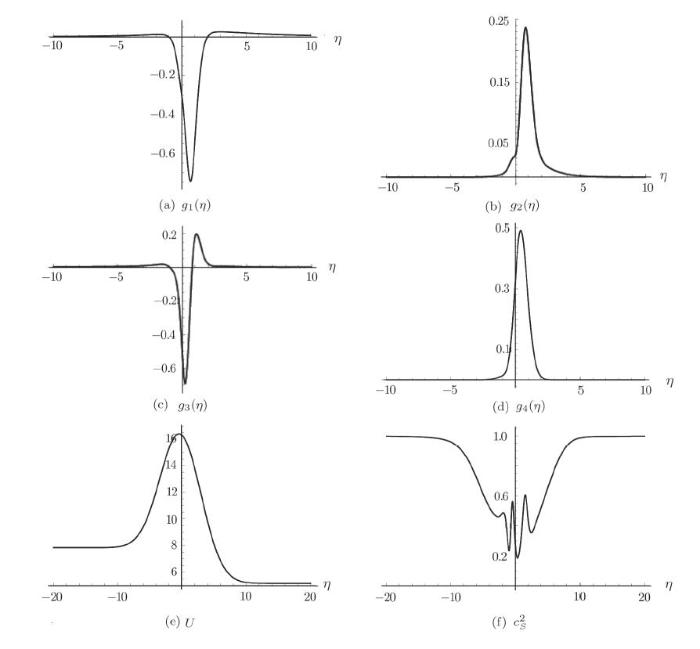
we plot Fig. 4 with the parameters $p_i=8$, $p_f=3$, $\eta_p=\eta_x=0$, $\tau_p=1$, and $\tau_x=3$ in Eqs. (17) and (19), as well as $\tau_1=20$ and $k_1=40$ in Eq. (29), and $b_0=0.5$. Figure 4 shows that the model is indeed gradient-stable and ghost-free.
Fig. 4
 New window|Download| PPT slide
New window|Download| PPT slideFig. 4An example of the fully stable bounce model with a constant DHOST term $b_0= 0.5$.
4 Discussion
We have constructed the spatially flat stable cosmological bounce models with GR asymptotics in the $c_{T}=1$ beyond Horndeski theory and in the full $c_{T}=1$ DHOST theory, respectively. In Ref. [23], the stable bouncing solution with $c_{T}=1$ has also been built in the beyond Horndeski theory (but not in the full DHOST theory). Here, since we start straightly from the Lagrangians with the constraint $c_{T}=1$, the procedure of building models (even in full DHOST theory) is simpler.It is well-known that the solutions of fully stable cosmological bounce do exist in theories beyond Horndeski. Though the simplest implementing is to work in the beyond Horndeski theory,[21-22] the stable bounce in a full DHOST theory is still interesting for study, which might bring unexpected results. In our implementing, we set the parameter $B(\phi,X)=$ const. in the full $c_{T}=1$ DHOST theory (5), see Eq. (27). Generally, it is not this case. The relevant issue will be studied elsewhere.
The singularity of inflation implies that a bounce preceding inflation might occur,[8] see also Refs. [50-54]. Recently, it has been showed in Ref. [55] that the bounce inflation scenario can explain the power deficit of CMB TT-spectrum at low multipoles, specially the dip at multipole $l\sim 20$. Thus it is interesting to embed the bounce models built here into the corresponding scenario, which might bring distinct imprint of DHOST terms in the CMB spectrum.
Appendix A On $g_1$, $g_2$, $g_3$
We give the explicit algebraic solutions of $g_1$, $g_2$, $g_3$ here.(i) The Beyond Horndeski Model
Recall that $x\equiv1/N$ and $H=h/N$.
$$ g_1=\frac{1}{2 x^2}\big(288 c_1 f_1^2 H^2 x^6+96 c_1 f_1 H^2 x^4+8 c_1 H^2 x^2+12 H x^3 f_1' \\ +36 f_1 H^2 x^2+12 f_1 x^3 H'+24 f_1 H x^2 x'+6 H^2+6 x H'\big)\,, \\ g_2=\frac{1}{8 x^4}\big(-288 c_1 f_1^2 H^2 x^6-96 c_1 f_1 H^2 x^4-8 c_1 H^2 x^2-4 H x^3 f_1' \\ -60 f_1 H^2 x^2-4 f_1 x^3 H'-8 f_1 H x^2 x'-6 H^2-2 x H'\big)\,, \\ g_3=\frac{1}{8} (-18 H^2 + 8 c_1 H^2 x^2 - 36 f_1 H^2 x^2 + 96 c_1 f_1 H^2 x^4 + 288 c_1 f_1^2 H^2 x^6 \\ - 12 H x^3 f_1' - 6 x H' - 12 f_1 x^3 H' - 24 f_1 H x^2 x')\,. $$
(ii) The DHOST Model
$$ g_1= \frac{1}{8 N^3 (2 g_4+N^2)} \big(-36 b_0^2 c_1 g_4^2 N^3 (N')^2-12 b_0^2 c_1 g_4 N^5 (N')^2-b_0^2 c_1 N^7 (N')^2+432 b_0^2 g_4^2 H N^2 N' \\ +144 b_0^2 g_4^2 N^2 N^{\prime\prime}-504 b_0^2 g_4^2 N (N')^2+72 b_0^2 N^4 g_4' N'+144 b_0^2 g_4 N^2 g_4' N' \\ +360 b_0^2 g_4 H N^4 N'+120 b_0^2 g_4 N^4 N^{\prime\prime}-288 b_0^2 g_4 N^3 (N')^2+72 b_0^2 H N^6 N' \\ +24 b_0^2 N^6 N^{\prime\prime}-18 b_0^2 N^5 (N')^2-144 b_0 c_1 g_4^2 H N^3 N'-48 b_0 c_1 g_4 H N^5 N' \\ -4 b_0 c_1 H N^7 N'+720 b_0 g_4^2 H^2 N^2+96 b_0 g_4^2 N^2 H'-816 b_0 g_4^2 H N N' \\ -48 b_0 g_4^2 N N^{\prime\prime}+144 b_0 g_4^2 (N')^2+120 b_0 H N^4 g_4'+240 b_0 g_4 H N^2 g_4' \\ -48 b_0 g_4 N g_4' N'-24 b_0 N^3 g_4' N'+576 b_0 g_4 H^2 N^4+120 b_0 g_4 N^4 H'-456 b_0 g_4 H N^3 N' \\ -48 b_0 g_4 N^3 N^{\prime\prime}+96 b_0 g_4 N^2 (N')^2+108 b_0 H^2 N^6+36 b_0 N^6 H'-24 b_0 H N^5 N' \\ -12 b_0 N^5 N^{\prime\prime}+12 b_0 N^4 (N')^2-144 c_1 g_4^2 H^2 N^3-48 c_1 g_4 H^2 N^5-4 c_1 H^2 N^7 \\ -288 g_4^2 H^2 N-96 g_4^2 N H'+288 g_4^2 H N'-48 H N^3 g_4'-96 g_4 H N g_4'-192 g_4 H^2 N^3 \\ -96 g_4 N^3 H'+192 g_4 H N^2 N'-24 H^2 N^5-24 N^5 H'+24 H N^4 N'\big)\,, \\\ g_2=\frac{1}{32 N (2 g_4+N^2)}\big(36 b_0^2 c_1 g_4^2 N^3 (N')^2+12 b_0^2 c_1 g_4 N^5 (N')^2+b_0^2 c_1 N^7 (N')^2-288 b_0^2 g_4^2 H N^2 N'-96 b_0^2 g_4^2 N^2 N^{\prime\prime} \\ +456 b_0^2 g_4^2 N (N')^2-48 b_0^2 N^4 g_4' N'-96 b_0^2 g_4 N^2 g_4' N'-216 b_0^2 g_4 H N^4 N'-72 b_0^2 g_4 N^4 N^{\prime\prime} \\ +264 b_0^2 g_4 N^3 (N')^2-36 b_0^2 H N^6 N'-12 b_0^2 N^6 N^{\prime\prime}+18 b_0^2 N^5 (N')^2+144 b_0 c_1 g_4^2 H N^3 N' \\ +48 b_0 c_1 g_4 H N^5 N'+4 b_0 c_1 H N^7 N'-432 b_0 g_4^2 H^2 N^2+816 b_0 g_4^2 H N N'+16 b_0 g_4^2 N N^{\prime\prime} \\ -48 b_0 g_4^2 (N')^2-72 b_0 H N^4 g_4'-144 b_0 g_4 H N^2 g_4'+16 b_0 g_4 N g_4' N'+8 b_0 N^3 g_4' N' \\ -288 b_0 g_4 H^2 N^4-24 b_0 g_4 N^4 H'+456 b_0 g_4 H N^3 N'+16 b_0 g_4 N^3 N^{\prime\prime}-32 b_0 g_4 N^2 (N')^2 \\ -36 b_0 H^2 N^6-12 b_0 N^6 H'+24 b_0 H N^5 N'+4 b_0 N^5 N^{\prime\prime}-4 b_0 N^4 (N')^2+144 c_1 g_4^2 H^2 N^3 \\ +48 c_1 g_4 H^2 N^5+4 c_1 H^2 N^7+480 g_4^2 H^2 N+32 g_4^2 N H'-96 g_4^2 H N'+16 H N^3 g_4' \\ +32 g_4 H N g_4'+288 g_4 H^2 N^3+32 g_4 N^3 H'-64 g_4 H N^2 N'+24 H^2 N^5+8 N^5 H' -8 H N^4 N'\big) \,, \\\ g_3= \frac{1}{32 N^5 (2 g_4+N^2)}\big(36 b_0^2 c_1 g_4^2 N^3 (N')^2+12 b_0^2 c_1 g_4 N^5 (N')^2+b_0^2 c_1 N^7 (N')^2-576 b_0^2 g_4^2 H N^2 N'-192 b_0^2 g_4^2 N^2 N^{\prime\prime} \\ +648 b_0^2 g_4^2 N (N')^2-96 b_0^2 N^4 g_4' N'-192 b_0^2 g_4 N^2 g_4' N'-504 b_0^2 g_4 H N^4 N'-168 b_0^2 g_4 N^4 N^{\prime\prime} \\ +408 b_0^2 g_4 N^3 (N')^2-108 b_0^2 H N^6 N'-36 b_0^2 N^6 N^{\prime\prime}+42 b_0^2 N^5 (N')^2+144 b_0 c_1 g_4^2 H N^3 N' \\ +48 b_0 c_1 g_4 H N^5 N'+4 b_0 c_1 H N^7 N'-1008 b_0 g_4^2 H^2 N^2-192 b_0 g_4^2 N^2 H'+816 b_0 g_4^2 H N N' \\ -48 b_0 g_4^2 N N^{\prime\prime}+144 b_0 g_4^2 (N')^2-168 b_0 H N^4 g_4'-336 b_0 g_4 H N^2 g_4'-48 b_0 g_4 N g_4' N' \\ -24 b_0 N^3 g_4' N'-864 b_0 g_4 H^2 N^4-216 b_0 g_4 N^4 H'+456 b_0 g_4 H N^3 N'-48 b_0 g_4 N^3 N^{\prime\prime} \\ +96 b_0 g_4 N^2 (N')^2-180 b_0 H^2 N^6-60 b_0 N^6 H'+24 b_0 H N^5 N'-12 b_0 N^5 N^{\prime\prime}+12 b_0 N^4 (N')^2 \\ +144 c_1 g_4^2 H^2 N^3+48 c_1 g_4 H^2 N^5+4 c_1 H^2 N^7-288 g_4^2 H^2 N-96 g_4^2 N H' +288 g_4^2 H N'-48 H N^3 g_4' \\ -96 g_4 H N g_4'-288 g_4 H^2 N^3-96 g_4 N^3 H'+192 g_4 H N^2 N' -72 H^2 N^5-24 N^5 H'+24 H N^4 N'\big) \,. $$
Acknowledgments
We thank Yong Cai for helpful discussions.Reference By original order
By published year
By cited within times
By Impact factor
DOI:10.1103/PhysRevD.23.347URL [Cited within: 1]
DOI:10.1103/PhysRevLett.48.1220URL [Cited within: 1]

The treatment of first-order phase transitions for standard grand unified theories is shown to break down for models with radiatively induced spontaneous symmetry breaking. It is argued that proper analysis of these transitions which would take place in the early history of the universe can lead to an explanation of the cosmological homogeneity, flatness, and monopole puzzles.
DOI:10.1098/rspa.1970.0021URL [Cited within: 1]
[Cited within: 1]
[Cited within: 2]
[Cited within: 1]
[Cited within: 1]
[Cited within: 1]
[Cited within: 1]
[Cited within: 1]
[Cited within: 2]
[Cited within: 2]
[Cited within: 3]
[Cited within: 1]
[Cited within: 1]
[Cited within: 2]
[Cited within: 1]
[Cited within: 2]
[Cited within: 4]
[Cited within: 5]
[Cited within: 2]
[Cited within: 1]
[Cited within: 1]
URL [Cited within: 1]

It is known that any nondegenerate Lagrangian containing time derivative terms higher than first order suffers from the Ostrogradsky instability, pathological excitation of positive and negative energy degrees of freedom. We show that, within the framework of analytical mechanics of point particles, any Lagrangian for third-order equations of motion, which evades the nondegeneracy condition, still leads to the Ostrogradsky instability. Extension to the case of higher odd order equations of motion is also discussed.
[Cited within: 2]
[Cited within: 1]
[Cited within: 1]
[Cited within: 3]
URLPMID:29303345

Abstract: The LIGO/VIRGO collaboration has recently announced the detection of gravitational waves from a neutron star-neutron star merger (GW170817) and the simultaneous measurement of an optical counterpart (the gamma-ray burst GRB 170817A). The close arrival time of the gravitational and electromagnetic waves limits the difference in speed of photons and gravitons to be less than about one part in $10^{15}$. This has three important implications for cosmological scalar-tensor gravity theories that are often touted as dark energy candidates and alternatives to $\Lambda$CDM. First, for the most general scalar-tensor theories---beyond Horndeski models---three of the five parameters appearing in the effective theory of dark energy can now be severely constrained on astrophysical scales; we present the results of combining the new gravity wave results with galaxy cluster observations. Second, the combination with the lack of strong equivalence principle violations exhibited by the supermassive black hole in M87, constrains the quartic galileon model to be cosmologically irrelevant. Finally, we derive a new bound on the disformal coupling to photons that implies that such couplings are irrelevant for the cosmic evolution of the field.
URL

On August 17, 2017 the LIGO interferometers detected the gravitational wave (GW) signal (GW170817) from the coalescence of binary neutron stars. This signal was also simultaneously seen throughout the electromagnetic (EM) spectrum from radio waves to gamma-rays. We point out that this simultaneous detection of GW and EM signals rules out a class of modified gravity theories, which dispense with the need for dark matter. This simultaneous observation also provides the first ever test of Einstein's Weak Equivalence Principle (WEP) between gravitons and photons. We calculate the Shapiro time delay due to the gravitational potential of the total dark matter distribution along the line of sight (complementary to the calculation in ) to be about 1000 days. Using this estimate for the Shapiro delay and from the time difference of 1.7 seconds between the GW signal and gamma-rays, we can constrain violations of WEP using the parameterized post-Newtonian (PPN) parameter $\gamma$, and is given by $|\gamma_{\rm {GW}}-\gamma_{\rm{EM}}|<3.9 \times 10^{-8}$.
[Cited within: 3]
[Cited within: 2]
[Cited within: 1]
[Cited within: 1]
[Cited within: 1]
[Cited within: 1]
[Cited within: 1]
[Cited within: 1]
[Cited within: 1]
