摘要:神经元放电率自稳态是指大脑神经网络的放电率维持在相对稳定的状态. 大量实验研究发现神经元放电率自稳态是神经电活动的重要特征, 并且放电率自稳态是实现神经信息处理及维持正常脑功能的基础, 因此放电率自稳态的研究是神经科学领域的重要科学问题. 脑神经网络是一个高度复杂的动态系统, 存在大量输入扰动信号及由于动态链接导致的参数摄动, 因此如何建立并维持神经元放电率自稳态及其鲁棒性仍有待深入研究. 反馈神经回路是皮层神经网络的典型连接模式, 抑制性突触可塑性对神经元放电率自稳态具有重要的调控作用. 本文通过构建包含抑制性突触可塑性的反馈神经回路模型对神经元放电率自稳态及其鲁棒性进行计算研究. 结果表明: 在抑制性突触可塑性的作用下, 神经元放电率可自适应地跟踪目标放电率, 从而取得放电率自稳态; 在有外部输入干扰和参数摄动的情况下, 神经元放电率具有良好的抗扰动性能, 表明放电率自稳态具有很强的鲁棒性; 理论分析揭示了抑制性突触可塑性学习规则是神经元放电率自稳态的神经机制; 仿真分析进一步揭示了学习率及目标放电率对放电率自稳态建立过程具有重要影响.
关键词: 抑制性突触可塑性/
放电率自稳态/
鲁棒性

English Abstract

全文HTML

--> --> -->

神经元放电率自稳态是指神经元的放电率维持在相对稳定的状态, 放电率自稳态是神经电活动的重要特征^[1,2]. 1990年到1996年期间, Ramakers等^[3-6]通过培养皮质细胞形成由兴奋性锥体神经元和抑制中间神经元构成的神经网络, 然后用药物改变突触输入使神经元放电发生紊乱, 结果发现在去药后神经元的放电率可通过自身调节恢复到目标放电率水平. 1998年, Turrigiano等^[7,8]的实验研究分析表明α-氨基-3-羟基-5-甲基-4-异恶唑丙酸(AMPA)介导的突触可塑性可有效控制神经元活动, 使神经元放电率维持在稳态水平. 2002年, Burrone等^[9]通过对单个海马神经元钾通道进行观察研究, 发现抑制神经元的活动导致突触输入的稳定增加, 进而使神经元活动恢复至目标水平. 2004年, Turrigiano 和Nelson ^[10]通过实验发现稳态突触可塑性在神经元的实际放电率从初始放电率到目标放电率的过程中起到了至关重要的作用. 2012年, Turrigiano等^[5,11]的实验研究发现当神经元受到刺激后放电率减小或者增大, 但是最终神经元的放电率会恢复到稳定状态.
上述生理实验研究表明在生物体中存在放电率自稳态这一现象, 为了进一步对神经元放电率进行研究, 研究者们在生理实验的基础上进行了相关的建模仿真. 2011年, Gl?ser和Joublin^[1]通过构建递归神经网络进行的仿真研究表明神经网络可以通过自组织使放电活动维持在稳定水平, 并且可以适应输入强度和输入分布的变化. 2016和2017年, Cannon和Miller^[12,13]的研究表明, 对于单个神经元而言, 在系统内部和突触双重稳态机制作用下, 神经元放电率可以维持在特定水平且在受到干扰时仍能恢复至原水平. 2018年, Miller和Cannon^[14]通过仿真分别研究了在双重积分反馈控制器和双重继电式控制器作用下的神经元放电率自稳态机制.
突触可塑性是学习和记忆的基础^[15-18], 长期以来, 兴奋性突触可塑性的研究得到了广泛的关注^[19,20]. 近年来, 越来越多的研究表明抑制性突触可塑性对神经电活动具有重要的调控作用^[21-24]. 2001年, Stephen和James ^[25]的研究表明在抑制性突触可塑性的调控下, 视觉皮层结构中的兴奋性与抑制性突触连接不断发育并趋于成熟. 2006年, Haas等^[21]对嗅觉皮层抑制性放电时刻依赖的突触可塑性(spike-timing-dependent plasticity, STDP)进行了研究, 结果表明抑制性STDP可对网络活动进行有效的调控, 并且具有很强的灵活性. 2012年, Luz和Shamir ^[26]的研究表明抑制性突触可塑性是神经元实现兴奋性与抑制性瞬态平衡的有效机制. 2015年, D’amour和Froemke ^[22]对听觉皮层中的兴奋性STDP和抑制性STDP进行了实验研究, 研究结果表明即使存在兴奋性突触可塑性的作用, 抑制性突触可塑性仍能使神经网络达到兴奋性和抑制性平衡. 2017年, Hennequin等^[27]的研究证明抑制性突触可塑性是实现网络平衡和调控复杂信息通路与记忆的理想机制.
神经元放电率自稳态是神经元放电活动的典型特征, 是衡量神经电活动水平的重要指标, 对于神经网络实现神经信息处理及维持正常功能具有重要的意义. 尽管已有大量实验研究发现神经元放电率自稳态是大脑电活动的普遍现象, 但是放电率自稳态机制仍有待进一步研究; 同时, 大脑神经网络是一个高度复杂的动态系统, 存在大量输入扰动信号, 以及由于动态链接导致的参数摄动, 因此如何维持神经元放电率自稳态的鲁棒性仍有待探索. STDP型抑制性突触可塑性是突触可塑性的典型形式, 其对神经电活动具有重要的调控作用, 本文构建包含STDP型抑制性突触可塑性的神经反馈回路模型, 研究基于抑制性突触可塑性的神经元放电率自稳态及其鲁棒性机制.

2

-->

2.1.模型结构

脑神经网络是由大量兴奋性和抑制性神经元依靠突触连接形成的具有复杂拓扑结构的复杂网络^[28]. 反馈结构是神经网络中的典型连接模式^[29,30], 主要包括抑制性反馈回路和兴奋性反馈回路两种形式^[31], 本文构建同时具有兴奋性和抑制性反馈回路的神经反馈回路模型, 结构如图1所示, 其中前向通路的神经元为目标神经元, E和I分别代表兴奋性和抑制性反馈回路的神经元网络模型, 目标神经元的放电率同时受兴奋性和抑制性反馈回路调控. 模型中兴奋性和抑制性神经元个数之比N_E:N_I取4:1^[32,33], 反馈回路的兴奋性和抑制性神经网络分别是由800个兴奋性神经元和200个抑制性神经元构成的随机连接神经网络模型^[34], 神经元之间通过不同突触类型按照设定的概率P_EE, P_EI, P_IE, P_II进行连接, 连接概率的取值如表1所列. P_i(t)和P_e(t)分别表示抑制性和兴奋性反馈回路信号; I_b(t)表示目标神经元的外部输入信号; Y(t)表示目标神经元的输出^[35].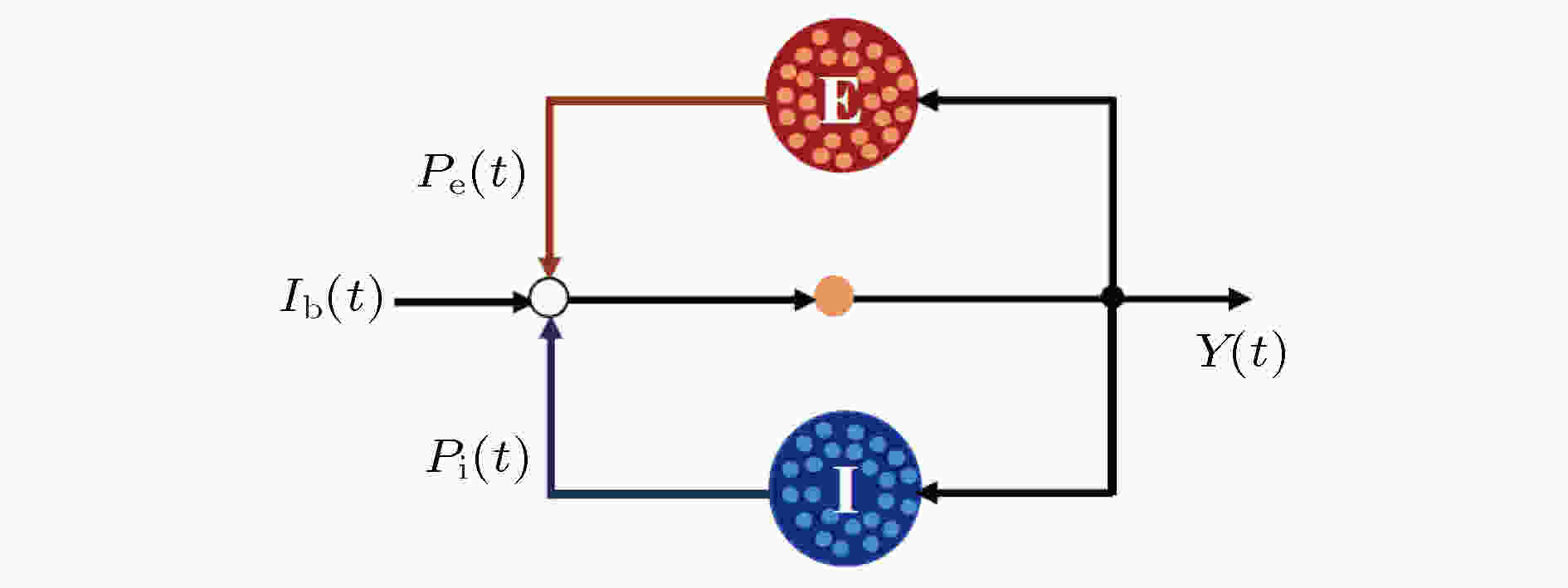
图 1 反馈神经回路模型结构
Figure1. Structure of the feedback neural network.

参数	描述	取值
NE	兴奋性神经元规模	800
NI	抑制性神经元规模	200
PEE	E-E的连接概率	0.2
PEI	E-I的连接概率	0.4
PIE	I-E的连接概率	0.4
PII	I-I的连接概率	0.4

表1神经网络结构相关参数取值
Table1.Parameters values of the neural feedback model structure.

模型中主要包括神经元模型、兴奋性与抑制性突触模型及抑制性突触可塑性模型, 三种模型的数学表达如下.
2 -->

2.2.神经元模型

Leaky integrate-and-fire(LIF)神经元模型^[35-37]计算简单且能准确描述神经元的电生理特性, 被广泛应用于神经系统的建模与仿真, 因此本文采用LIF神经元模型进行建模. LIF神经元$i$的阈下膜电位${V_i}$的表达为:

$ \begin{split} {\tau _{\rm{m}}}\frac{{{\rm{d}}{V_i}}}{{{\rm{d}}t}} = & \left( {{V^{{\rm{rest}}}} - {V_i}} \right) +\\ & \left( {g_i^{\rm{E}}\left( {{V^{\rm{E}}} - {V_i}} \right) + g_i^{\rm{I}}\left( {{V^{\rm{I}}} - {V_i}} \right) + {I_{\rm{b}}}} \right)\frac{1}{{{g^{{\rm{leak}}}}}},\\ & \;\;\;\;\;\;\;\;{\rm{if}}\;{V_i} > {V_{{\rm{th}}}},\;{\rm{then}}\;{V_i} = {V^{{\rm{rest}}}}, \end{split} $

其中, ${V_i}$表示神经元$i$的阈下膜电位; ${\tau _{\rm{m}}}$表示膜时间常数; ${V^{{\rm{rest}}}}$表示神经元的静息态电位; ${V_{{\rm{th}}}}$表示神经元放电的膜电位阈值; ${g^{{\rm{leak}}}}$表示漏电导; ${V^{\rm{E}}}$和${V^{\rm{I}}}$分别表示兴奋性反转电位和抑制性反转电位; $g_i^{\rm{E}}$和$g_i^{\rm{I}}$分别表示神经元$i$的兴奋性电导和抑制性电导; ${I_{\rm{b}}}$表示神经元的背景噪声电流输入. 在本研究中, 采用泊松信号作为神经元的外部输入. 神经元模型的参数取值如表2所列.

参数	取值	单位
${\tau _{\rm{m}}}$	20	ms
${V^{{\rm{rest}}}}$	–60	mV
${V_{{\rm{th}}}}$	–50	mV
${V^{\rm{E}}}$	0	mV
${V^{\rm{I}}}$	–70	mV
${g^{{\rm{leak}}}}$	10	nS

表2神经元模型各参数取值
Table2.Parameters values of LIF neuron model.

2 -->

2.3.突触模型

神经元之间通过不同类型的突触相连接, 突触连接共有以下四种: 兴奋性神经元到兴奋性神经元(E-E)、兴奋性神经元到抑制性神经元(E-I)、抑制性神经元到兴奋性神经元(I-E)、抑制性神经元到抑制性神经元(I-I), 其中E-E, E-I属于兴奋性突触, I-E, I-I属于抑制性突触.
在本研究中, 采用电导型突触模型, 根据突触性质的不同, 突触电导模型可分为兴奋性和抑制性突触电导模型两种形式, 其数学表达式分别如下:

$ \normalsize {\tau _{\rm{E}}}\frac{{{\rm{d}}g_i^{\rm{E}}}}{{{\rm{d}}t}} = - g_i^{\rm{E}} + {\bar g^{\rm{E}}}{W_{ij}}\sum\limits_k {\delta \left( {t - t_j^k} \right)},\tag{2a} $

$ \normalsize {\tau _{\rm{I}}}\frac{{{\rm{d}}g_i^{\rm{I}}}}{{{\rm{d}}t}} = - g_i^{\rm{I}} + {\bar g^{\rm{I}}}{W_{ij}}\sum\limits_k {\delta \left( {t - t_j^k} \right)},\tag{2b} $

其中, 神经元$i$为目标神经元, 当兴奋性突触前神经元$j$放电时, 兴奋性突触电导增加, 反之衰减. 同理, 当抑制性突触前神经元$j$放电时, 抑制性突触电导增加, 反之衰减. ${\tau _{\rm{E}}}$表示兴奋性突触时间常数; ${\tau _{\rm{I}}}$表示抑制性突触时间常数; 公式右侧求和符号表示突触前神经元$j$的放电序列之和; ${W_{ij}}$表示从神经元$j$到神经元$i$的突触权重; ${\bar g^{\rm{E}}}$表示单位兴奋性电导; ${\bar g^{\rm{I}}}$表示单位抑制性电导. 兴奋性与抑制性突触模型的参数取值如表3所列.

参数	取值	单位
${\tau _{\rm{E}}}$	5	ms
${\tau _{\rm{I}}}$	10	ms
${\bar g^{\rm{E}}}$	140	pS
${\bar g^{\rm{I}}}\normalsize$	350	pS

表3突触模型参数取值
Table3.Parameters values of synapse model.

2 -->

2.4.抑制性突触可塑性模型

在图1所示的模型中, 只在抑制性神经元到兴奋性神经元(I-E)的抑制性突触引入可塑性, I-E抑制性突触权重${W_{ij}}^{}$随着突触前后神经元的放电活动而调节, E-E, E-I及I-I连接的突触权重保持不变. 抑制性突触可塑性模型采用STDP型可塑性模型^[38], 如图2所示, 突触前后两个神经元放电时刻间隔越小突触权重增加幅度越大.
在仿真实现时, 给每个神经元$i$建立一个突触踪迹, 随着神经元$i$的放电情况其变化如(3)和(4)式所示:
神经元$i$放电

${x_i} \to {x_i} + 1,$

神经元$i$不放电

${\tau _{{\rm{STDP}}}}\frac{{{\rm{d}}{x_i}}}{{{\rm{d}}t}} = - {x_i},$

其中${\tau _{{\rm{STDP}}}}$表示突触可塑性的时间常数.
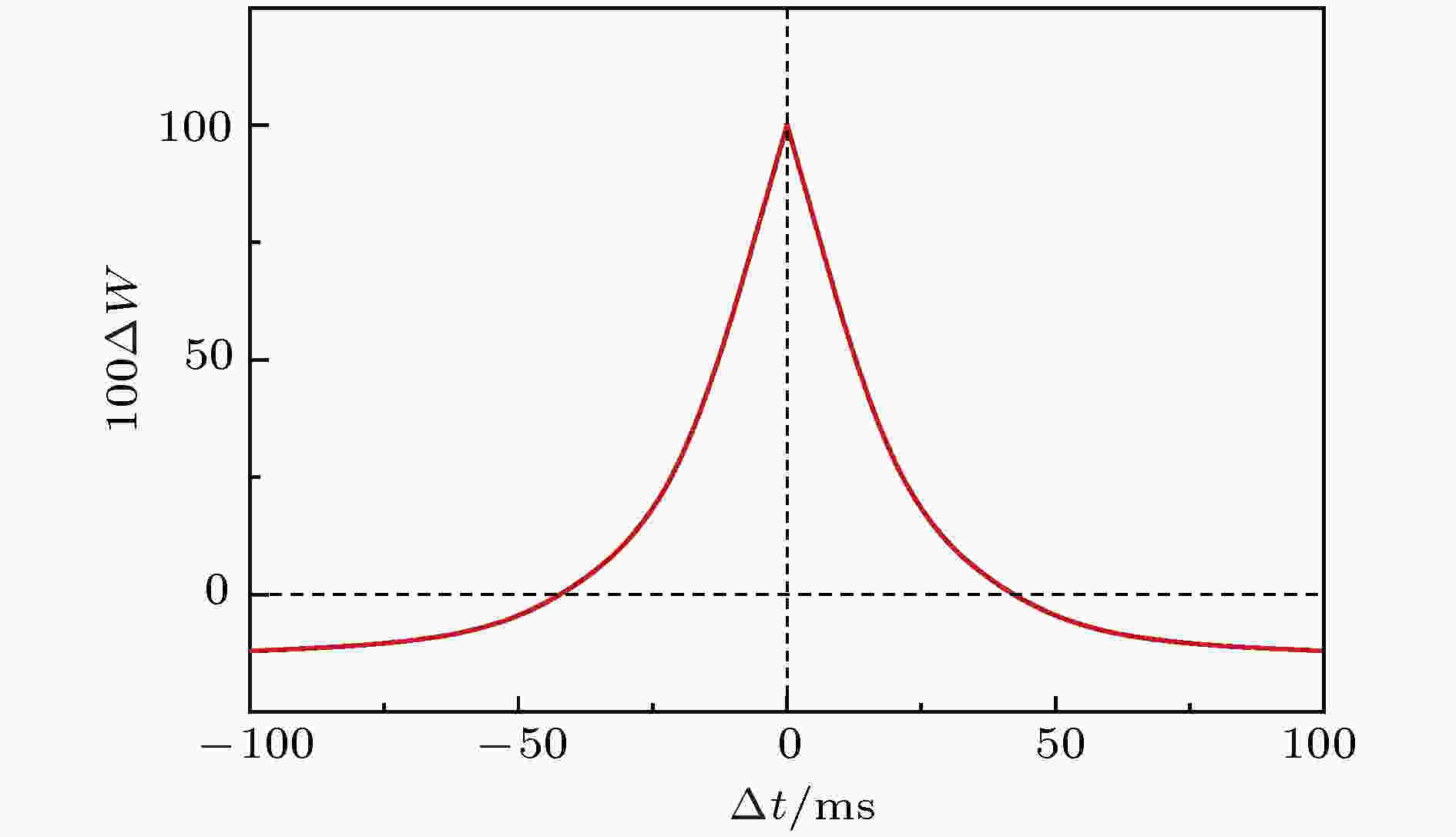图 2 抑制性突触可塑性(STDP)调节规则示意图
Figure2. The regulation rule of inhibitory synaptic plasticity (STDP).

从抑制性神经元$j$到兴奋性神经元$i$的抑制性突触权重${W_{ij}}$跟随每一个突触前或突触后神经元的踪迹而变化, 如(5)和(6)式所示:
突触前神经元在$t_j^f$时刻放电

${W_{ij}} \to {W_{ij}} + \eta \left( {{x_i} - \alpha } \right),$

突触后神经元在$t_i^f$时刻放电

${W_{ij}} \to {W_{ij}} + \eta {x_j},$

其中${x_i}$与${x_j}$分别表示神经元$i$与$j$的突触踪迹; $\eta $表示学习率; $\alpha = 2{\rho _0}{\tau _{{\rm{STDP}}}}$表示衰减因子; ${\rho _0}$表示目标放电率. 抑制性突触可塑性的参数意义与取值如表4所列.

参数	描述	取值
${W_{ij}}^{}$	抑制性突触权重	0
${\tau _{{\rm{STDP}}}}$	可塑性时间常数	20
$\eta $	学习率	0.005
$\alpha $	抑制因子	0.12
${\rho _0}\normalsize$	目标放电率

表4抑制性突触可塑性的参数取值
Table4.Parameters values of inhibitory synaptic plasticity.

基于包含抑制性突触可塑性的反馈神经回路模型, 分别从不同目标放电率下的放电率自稳态特性、放电率自稳态的鲁棒性、抑制性突触可塑性的作用以及放电率自稳态机制四个方面对放电率自稳态进行研究.
2

-->

3.1.放电率自稳态

神经元目标放电率为5, 10, 20, 50 Hz四种不同取值时的神经元膜电位及平均放电率分别如图3—图6所示. 在这四种不同情况下, 图(a)为目标神经元膜电位图; 图(b)为采用滑动平均窗方法确定的神经元平均放电率, 其中滑动时间窗取10 ms; 图(c)为随机取一个突触前神经元, 其与目标神经元之间抑制性突触权重(下文简称抑制性突触权重)的变化曲线.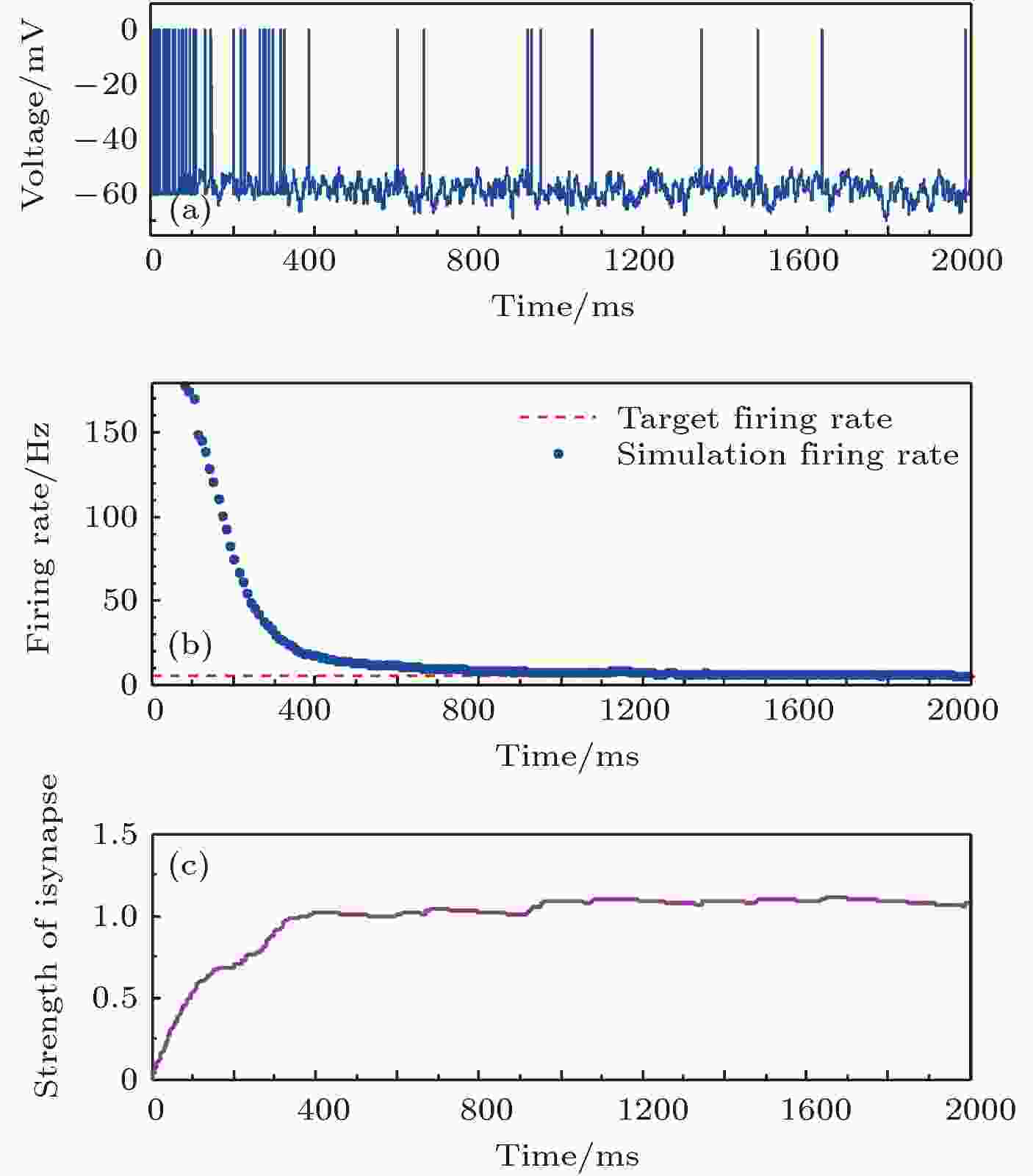
图 3 目标放电率为5 Hz时的神经元放电率自稳态分析图　(a)神经元膜电位; (b)神经元平均放电率曲线; (c)抑制性突触权重变化曲线
Figure3. Firing rate homeostasis with the target firing rate equal to 5 Hz: (a) Neural membrane potential; (b) the average firing rate; (c) the strength of inhibitory synapse.

图 4 目标放电率为10 Hz时的神经元放电率自稳态分析图　(a)神经元膜电位; (b)神经元平均放电率曲线; (c)抑制性突触权重变化曲线
Figure4. Firing rate homeostasis with the target firing rate equal to 10 Hz: (a) Neuronal membrane potential; (b) the average firing rate; (c) the strength of inhibitory synapse.

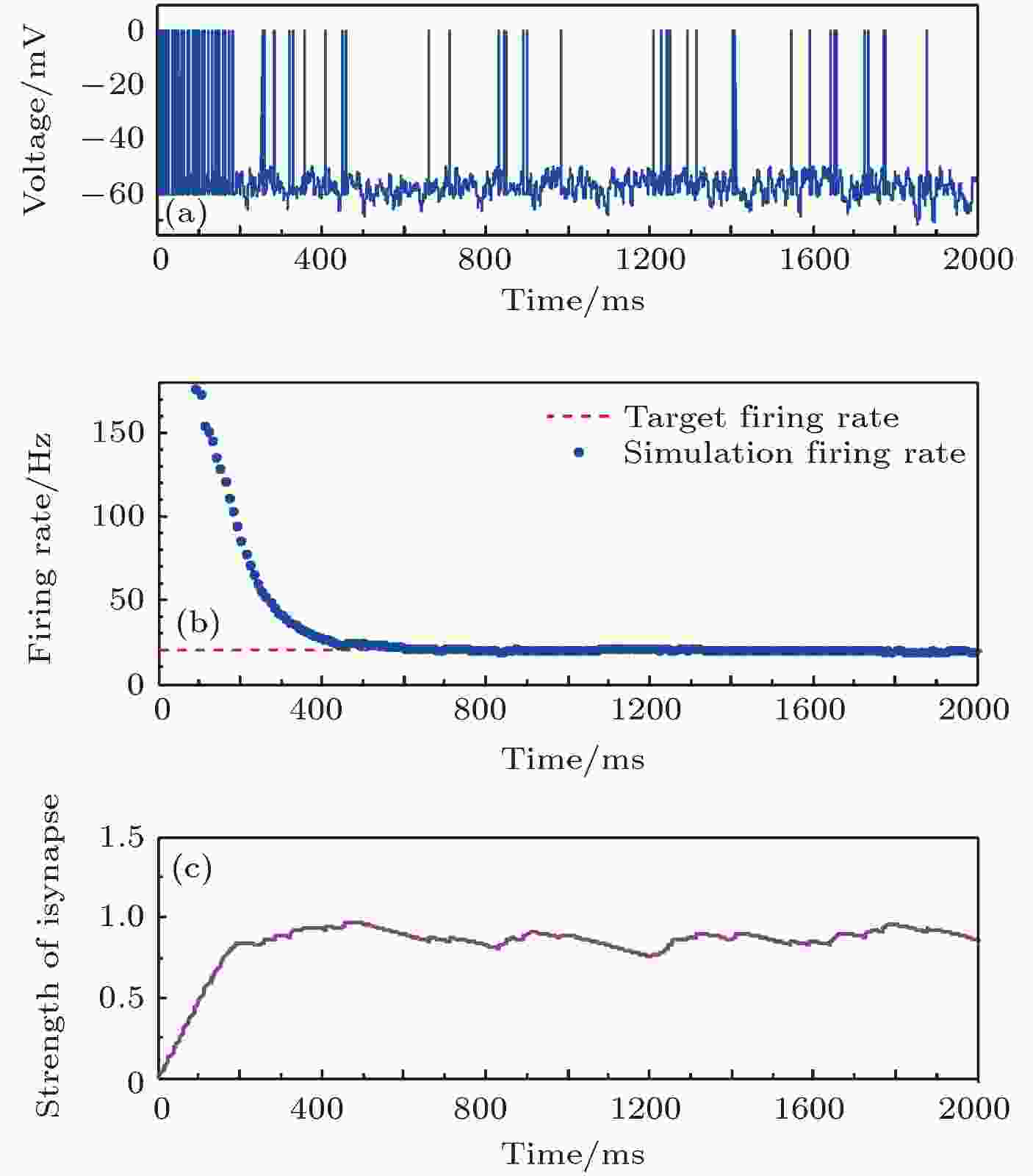图 5 目标放电率为20 Hz时的神经元放电率自稳态分析图　(a)神经元膜电位; (b)神经元平均放电率曲线; (c)抑制性突触权重变化曲线
Figure5. Firing rate homeostasis with the target firing rate equal to 20 Hz: (a) Neuronal membrane potential; (b) the average firing rate; (c) the strength of inhibitory synapse.

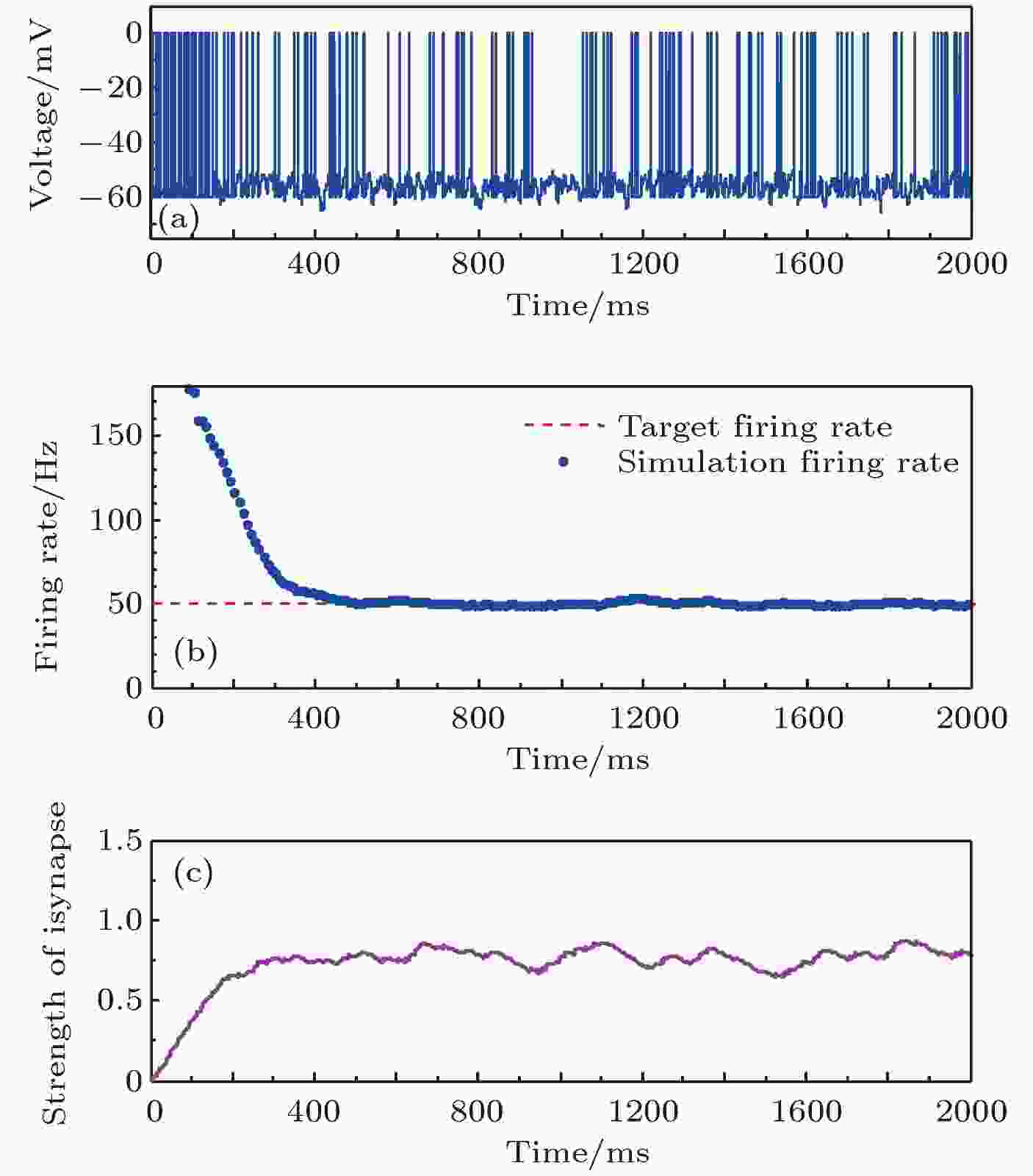图 6 目标放电率为50 Hz时的神经元放电率自稳态分析图　(a)神经元膜电位; (b)神经元平均放电率曲线; (c)抑制性突触权重变化曲线
Figure6. Firing rate homeostasis with the target firing rate equal to 50 Hz: (a) Neuronal membrane potential; (b) the average firing rate; (c) the strength of inhibitory synapse.

由以上四种不同目标放电率的仿真结果可以看出, 在仿真初期由于抑制性突触可塑性的调节作用尚小, 神经元的放电较密集, 神经元的平均放电率较大, 随着时间的推移, 在抑制性突触可塑性的作用下, 抑制性突触权重逐渐增大, 导致神经元放电率逐渐减小, 最后趋近并稳定在目标放电率水平, 神经元放电率取得自稳态, 抑制性突触权重维持在相对稳定的水平.
此外,进一步改变目标放电率的值, 通过多次仿真, 得到实际放电率跟踪目标放电率的总体示意图, 如图7所示. 在抑制性突触可塑性的调控下, 反馈神经回路模型前向通路目标神经元的放电率可以准确地逼近目标放电率, 实现放电率自稳态.
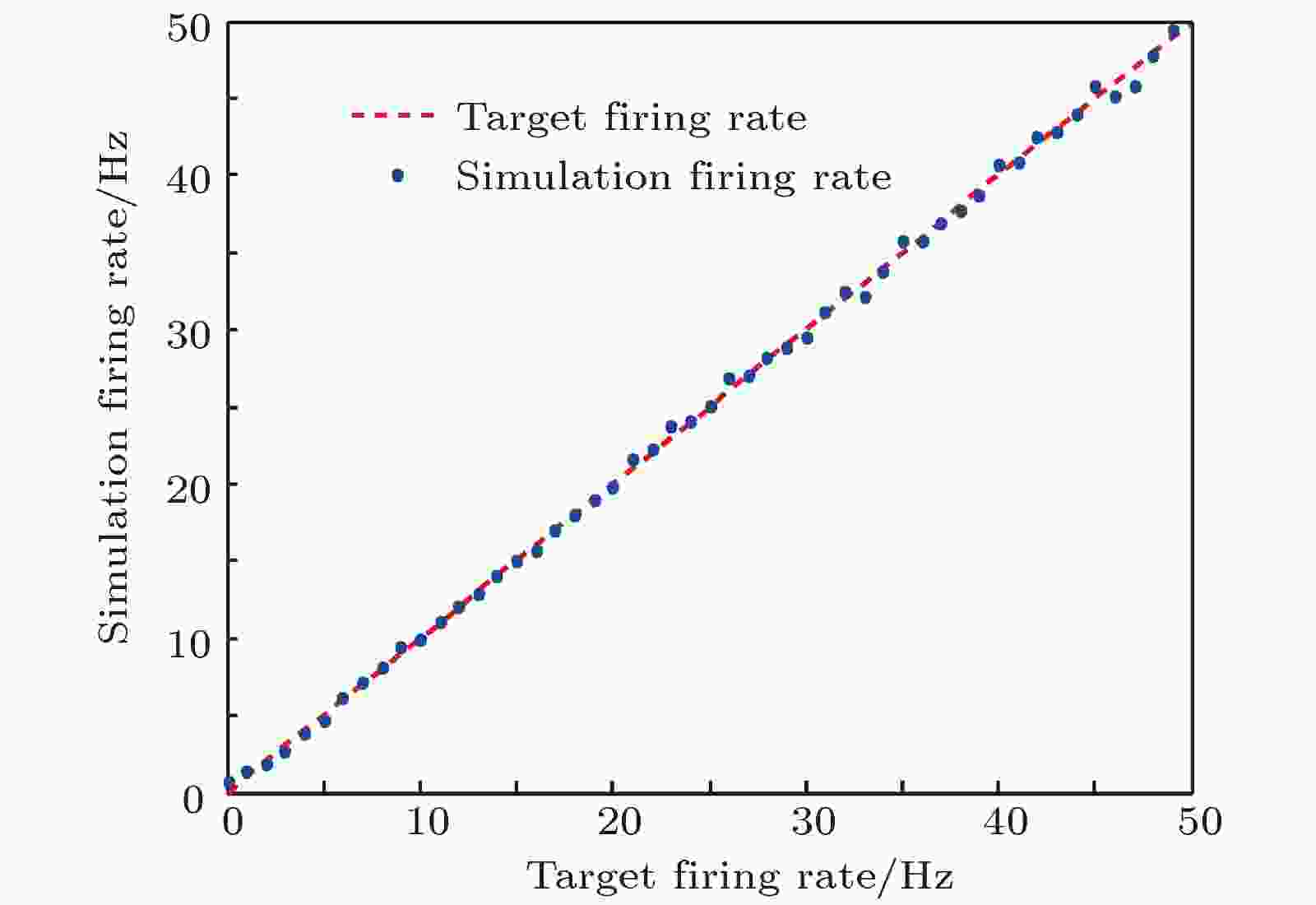图 7 神经元实际放电率跟踪目标放电率的总体情况
Figure7. The simulation firing rate and target firing rate.

2 -->

3.2.放电率自稳态的鲁棒性分析

脑神经网络是一个高度复杂的动态系统, 对神经元而言, 存在大量类似于噪声的外界输入, 同时来自与之连接的其他神经元的输入也存在很强的波动性^[39-42]. 另外, 神经元之间的连接动态变化等因素导致模型存在参数摄动. 神经元的噪声输入及参数摄动对神经元放电率有直接影响, 本小节主要研究在噪声扰动及参数摄动作用下神经元如何维持放电率自稳态、实现放电率自稳态的鲁棒性.
3 -->

3.2.1.输入扰动时的鲁棒性分析

在仿真中, 神经元输入噪声叠加于神经元背景噪声电流${I_{\rm{b}}}$, 干扰信号的数学表达如(7)式所示:

${I_{\rm{b}}} = N(200,30),$

从1500 ms开始施加噪声扰动信号, 相应的放电率自稳态鲁棒性分析结果如图8所示. 图8(a)为外部输入干扰信号; 图8(b)为目标神经元膜电位变化情况, 可以观察到在1500 ms加入外部输入噪声后神经元放电率增加, 经过抑制性突触可塑性的调控神经元放电率逐渐减小, 最后恢复到稳定状态; 图8(c)为神经元平均放电率曲线, 从图形中可以观察到神经元在仿真初期具有较高的放电率, 在抑制性突触可塑性的调控作用下神经元平均放电率维持在目标放电率5 Hz附近, 取得放电率自稳态. 在1500 ms加入噪声后, 神经元放电率快速增加, 神经放电率自稳态被打破; 随后由于抑制性突触可塑性的作用使得抑制性突触连接强度增加, 神经放电率降低, 最终神经元放电率又恢复到目标放电率5 Hz附近, 重新取得了放电率自稳态, 表明放电率自稳态对噪声扰动具有很强的鲁棒性. 在此过程中, 神经元抑制性突触权重变化曲线如图8(d)所示, 在0—1500 ms期间由于网络已逐步进入稳态, 抑制突触权重不再改变并稳定在1附近; 在1500 ms加入噪声干扰信号后, 抑制性突触权重的调节机制再次启动并最终稳定在1.5附近.
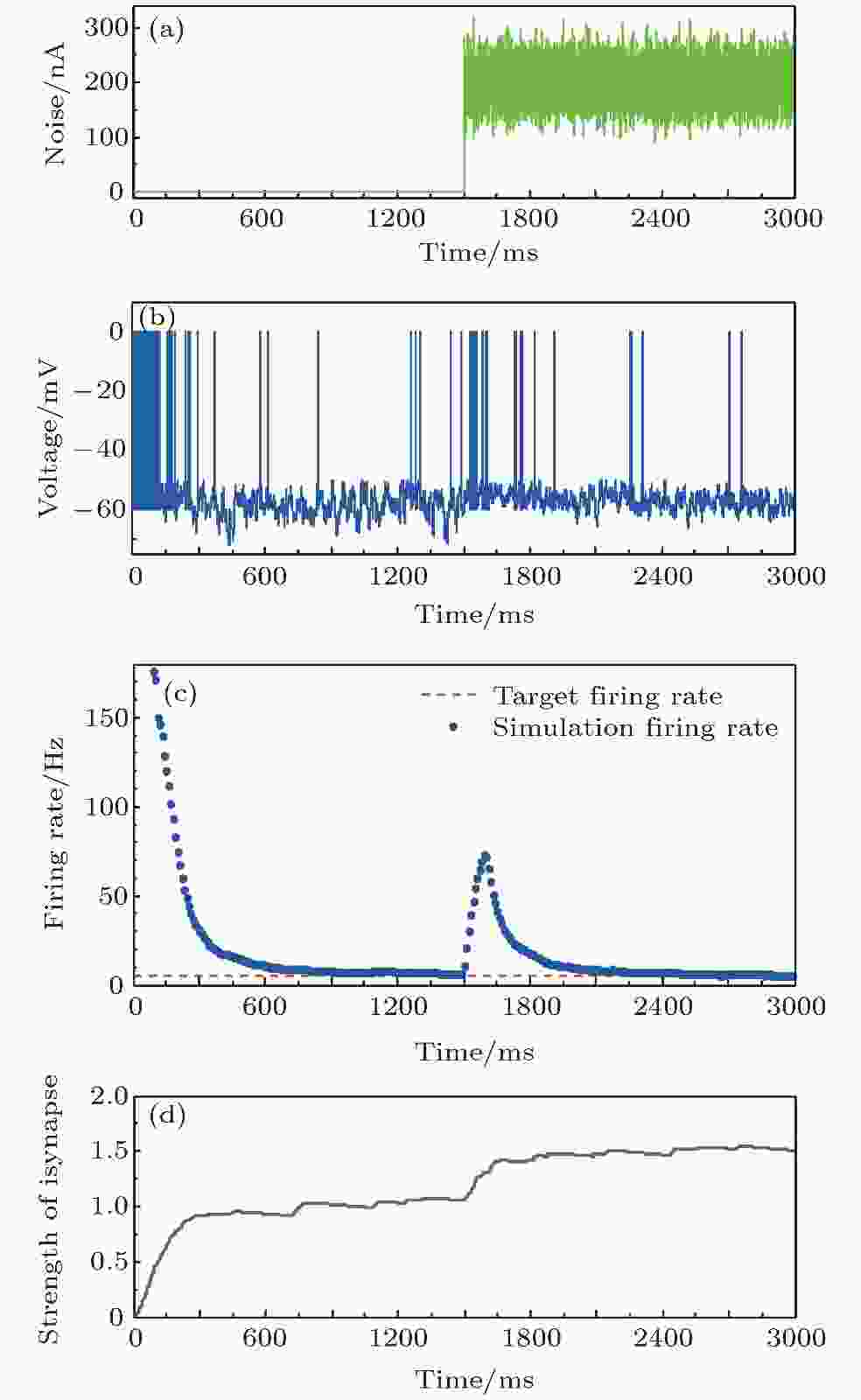图 8 噪声干扰下的神经元放电率鲁棒性　(a)噪声干扰信号; (b)神经元膜电位; (c)神经元平均放电率曲线; (d)抑制性突触权重变化曲线
Figure8. The robustness of neural firing rate homeostasis under noise disturbances: (a) The noise signal; (b) neuronal membrane potential; (c) the average firing rate; (d) the strength of inhibitory synapse.

3 -->

3.2.2.参数摄动时的鲁棒性分析

神经元之间的连接是动态变化的, 采用兴奋性突触电导的参数摄动模拟动态连接对放电率自稳态的影响. 本研究采用阶跃形式的兴奋性突触电导参数摄动, 其中参数摄动的数学表达如下:

$\begin{aligned}Dt = \left\{ \begin{aligned}& 0,t - {t_1} < 0\\& 1,t - {t_1} > 0\end{aligned} \right.,\\\;{t_1} = 1500\;{\rm{ms}}.\end{aligned}$

在1500 ms后引入参数摄动来增大兴奋性突触电导的数值, 参数摄动时的鲁棒性分析结果如图9所示. 图9(a)为阶跃型参数摄动信号; 9(b)为目标神经元膜电位图; 图9(c)为神经元平均放电率曲线; 图9(d)为神经元抑制性突触权重变化曲线. 从图9可以观察到在1500 ms对兴奋性突触电导施加阶跃参数摄动后, 神经元放电率迅速增加, 已经建立的神经元放电率自稳态被打破; 在抑制性突触可塑性的调节下抑制性突触连接强度增加, 进而导致神经元放电率降低, 最终神经元平均放电率再次恢复到目标放电率5 Hz, 实现神经元放电率自稳态. 在0—1500 ms期间由于放电率逐步进入到稳态, 抑制性突触权重稳定在1附近; 在1500 ms加入阶跃参数摄动后, 抑制性突触权重调节机制再次启动, 最终稳定在1.75附近.
以上结果表明, 无论是在外界干扰还是在神经网络内部参数摄动下, 神经元都可以通过抑制性突触可塑性的调节快速恢复至目标放电率, 表明放电率自稳态具有很强的鲁棒性.
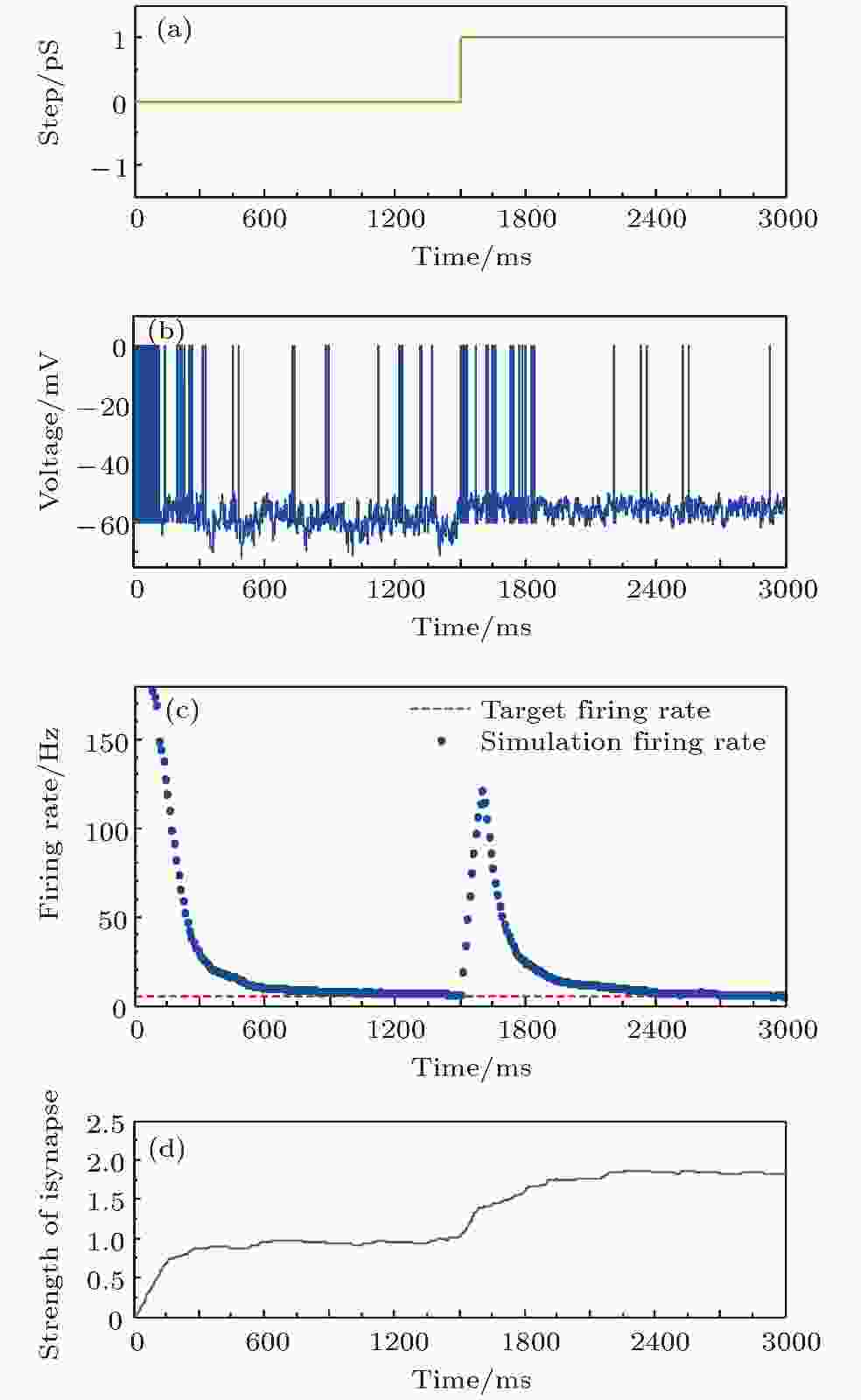图 9 参数摄动下的放电率自稳态鲁棒性　(a)参数摄动信号; (b)神经元膜电位; (c)神经元平均放电率曲线; (d)抑制性突触权重变化曲线
Figure9. The robustness of neural firing rate homeostasis under parameter perturbation: (a) The parameter perturbation signal; (b) neuronal membrane potential; (c) the average firing rate; (d) the strength of inhibitory synapse.

2 -->

3.3.抑制性突触可塑性的作用

为了进一步验证抑制性突触可塑性在神经元放电率自稳态中的重要作用, 研究中进行了新的仿真分析, 用于对比在有、无抑制性突触可塑性两种情况下神经元放电率自稳态及鲁棒性. 在仿真中参数摄动信号的数学表达为:

$ Dt = \left\{ \begin{aligned} & 0,\;t - {t_1} < 0\\& 1,\;t - {t_1} > 0{\text{且}}t - {t_2} < 0,\\ & 1.5,\;t - {t_2} > 0 \end{aligned} \right. $

其中${t_1} = 2000 \;{\rm{ms}} $、${t_2} = 3000\; {\rm{ms}} $. 仿真结果如图10所示, 其中图10(a)为阶跃型参数摄动信号; 图10(b)和图10(c)分别为神经元膜电位图和平均放电率曲线图. 由图10的结果可以看出, 在2000 ms加入第一个阶跃型参数摄动后, 在抑制性突触可塑性的调节下, 神经元重新恢复至放电率稳定状态; 在3000 ms施加第二个阶跃型参数摄动并去掉抑制性突触可塑性, 此时神经元在参数摄动的影响下偏离目标放电率并且无法恢复到目标放电率; 在4000 ms重新加入抑制性突触可塑性后, 神经元放电率再次恢复至目标放电率, 再次取得放电率自稳态. 本小节的结果充分表明了抑制性突触可塑性在神经元实现放电率自稳态及其鲁棒性方面具有重要的调节作用.
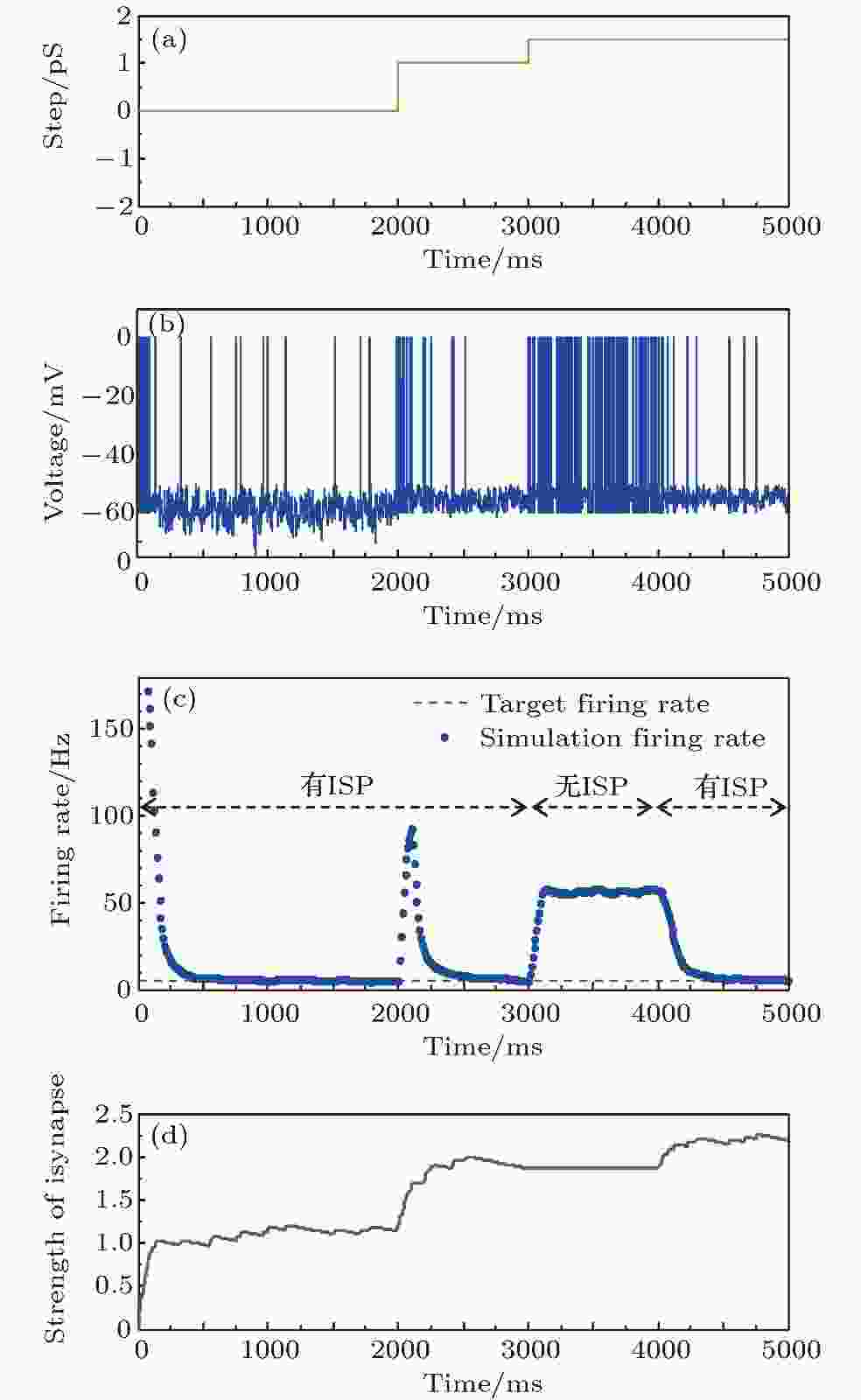图 10 参数干扰时有无抑制性突触可塑性两种情况下的神经元平均放电率自稳态特性　(a)参数摄动信号; (b)神经元膜电位; (c)神经元平均放电率曲线; (d)抑制性突触权重变化曲线
Figure10. The firing rate characteristics with and without inhibitory synaptic plasticity under parameter perturbation: (a) The parameter perturbation signal; (b) neural membrane potential; (c) the average firing rate; (d) the strength of inhibitory synapse.

2 -->

3.4.放电率自稳态机制分析

神经元放电率自稳态是指神经系统的放电率维持在相对稳定的状态, 即使在各种干扰作用下仍能维持在目标放电率. 上述仿真研究表明抑制性突触可塑性在神经元放电率自稳态调节中发挥了关键作用, 本小节将从抑制性突触可塑性原理方面进一步给出放电率自稳态机制的理论解释.
抑制性突触可塑性的权重调节规则可表示为:

${\text{Δ}}w = \eta \left( {pre \times post - {\rho _0} \times pre} \right),$

$W_{{\rm{new}}}^{} = W_{{\rm{old}}}^{} + {\text{Δ}}w,$

其中${\text{Δ}}w$表示抑制性突触权重的变化量; $\eta $表示学习率; $pre$表示突触前神经元的放电率; $post$表示突触后神经元的放电率; ${\rho _0}$表示突触后神经元的目标放电率; ${W^{}}$表示抑制性突触权重.
仿真初期由于抑制性突触权重${W^{}}$较小, 因此抑制性突触电导相对于兴奋性突触电导较弱, 此时突触后神经元放电率$post$较高, 由(10)式所示的抑制性突触可塑性规则可知, 此时${\text{Δ}}w$的值较大, 抑制性突触权重$W_{{\rm{new}}}^{}$快速增大, 导致突触后神经元放电率$post$减小, 随着突触后神经元实际放电率$post$逐渐逼近目标放电率${\rho _0}$, ${\text{Δ}}w$逐渐减小并最终趋近于0, 此时抑制性突触权重$W_{{\rm{new}}}^{}$增速减缓, 当${\text{Δ}}w$为0时突触后神经元实际放电率$post$等于目标放电率${\rho _0}$, 表明神经元在抑制性突触可塑性的调节下取得放电率自稳态.
当突触后神经元放电率$post$受到外界输入及参数摄动的扰动而偏离目标放电率${\rho _0}$时, 分$post < {\rho _0}$与$post > {\rho _0}$两种情况分别讨论. 当$post < {\rho _0}$时, 由(10)式可知${\text{Δ}}w < 0$为负, 即抑制性突触权重$W_{{\rm{new}}}^{}$减小, 导致突触后神经元放电率$post$增大, 只要$post < {\rho _0}$, 抑制性突触权重$W_{{\rm{new}}}^{}$就不断减小, 神经元放电率$post$不断增大, 最终$post$逼近${\rho _0}$, 此时${\text{Δ}}w$接近于0, 抑制性突触权重${W^{}}$基本保持不变, 进入稳定状态. 当$post > {\rho _0}$时, ${\text{Δ}}w > 0$, 抑制性突触权重$W_{{\rm{new}}}^{}$增大, 导致神经元放电率$post$减小, 最终突触后神经元实际放电率$post$稳定在目标放电率${\rho _0}$附近.

2

-->

4.1.学习率的影响

由以上仿真结果可以看出, 神经元在抑制性突触可塑性的调节下实际放电率稳定在设定的目标放电率, 实现放电率自稳态. 本小节进一步定量分析抑制性突触可塑性中的学习率对神经元放电率自稳态的影响.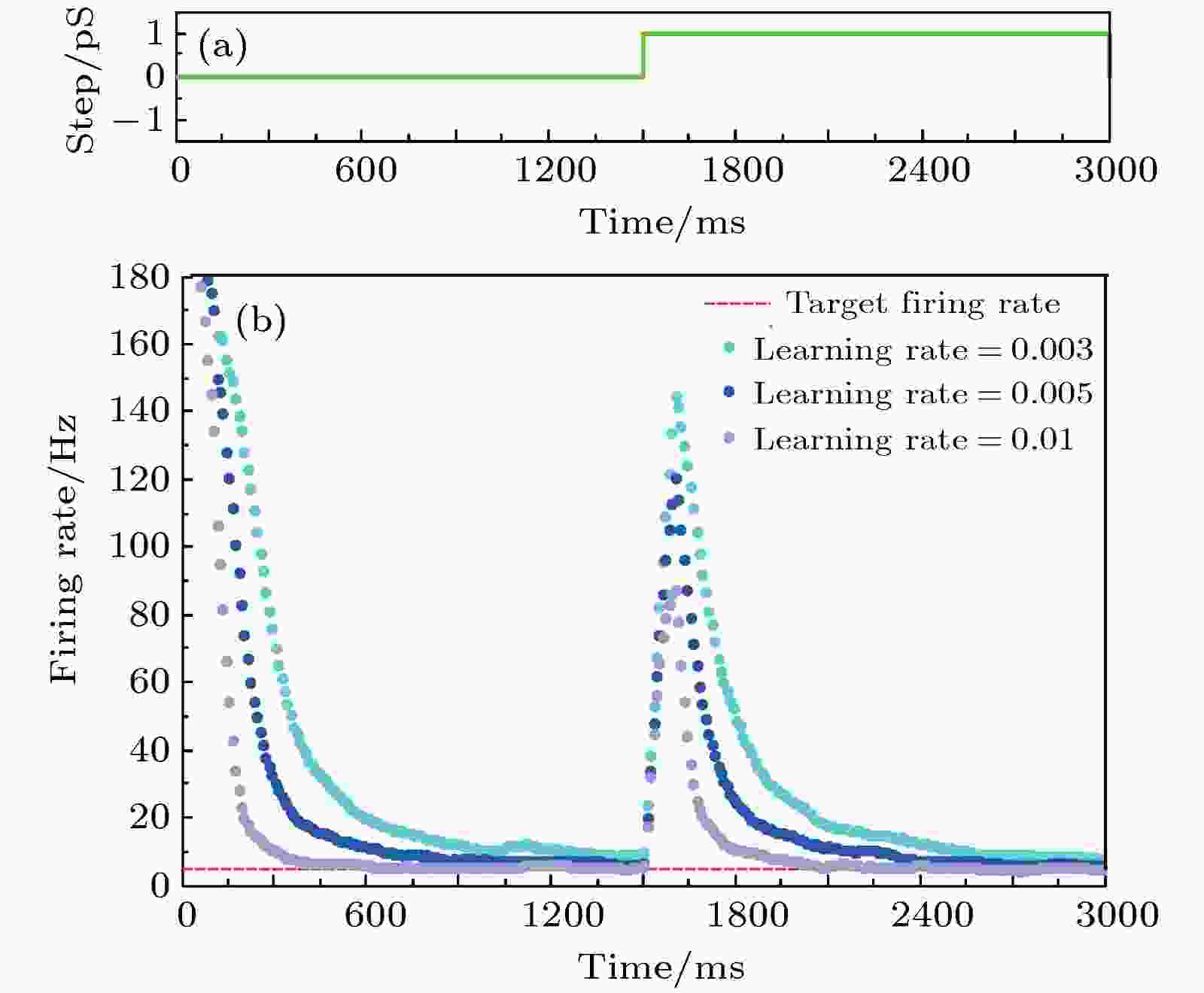
图 11 学习率对放电率自稳态的影响　(a)参数摄动信号; (b)不同学习率时的神经元平均放电率曲线
Figure11. The effect of learning rate on neural firing rate homeostasis: (a) The parameter perturbation signal; (b) the firing rate with different learning rates.

分别取抑制性突触可塑性中学习率的值为0.003, 0.005, 0.01, 仿真结果如图11所示. 图11表明, 学习率取值越大, 神经元取得放电率自稳态以及受干扰后恢复至放电率自稳态所需要的时间越短.
2 -->

4.2.目标放电率的影响

由于神经元存在不应期, 因此神经元实际放电率存在上限. 神经元的绝对不应期为5 ms, 神经元的实际放电率极限值和不应期之间存在以下关系:

${y_{\rm{d}}} \approx {1}/{{{\tau _{{\rm{ref}}}}}},$

其中${y_d}$表示实际放电率; ${\tau _{\rm ref}}$表示绝对不应期,取值为5 ms.
在仿真中, 当目标放电率从0 Hz增至250 Hz时, 神经元的实际放电率如图12所示, 图中红色虚线表示目标放电率, 蓝色散点代表在仿真中得到的实际放电率. 由图可以看出, 当目标放电率大于180 Hz后实际放电率受不应期影响不再增加, 表明只要目标放电率在这个范围内, 实际放电率就可以很精确地跟踪目标放电率, 实现神经元放电率自稳态. 在实际中神经元的放电率不会过大, 所以神经元放电率自稳态具有普遍性.
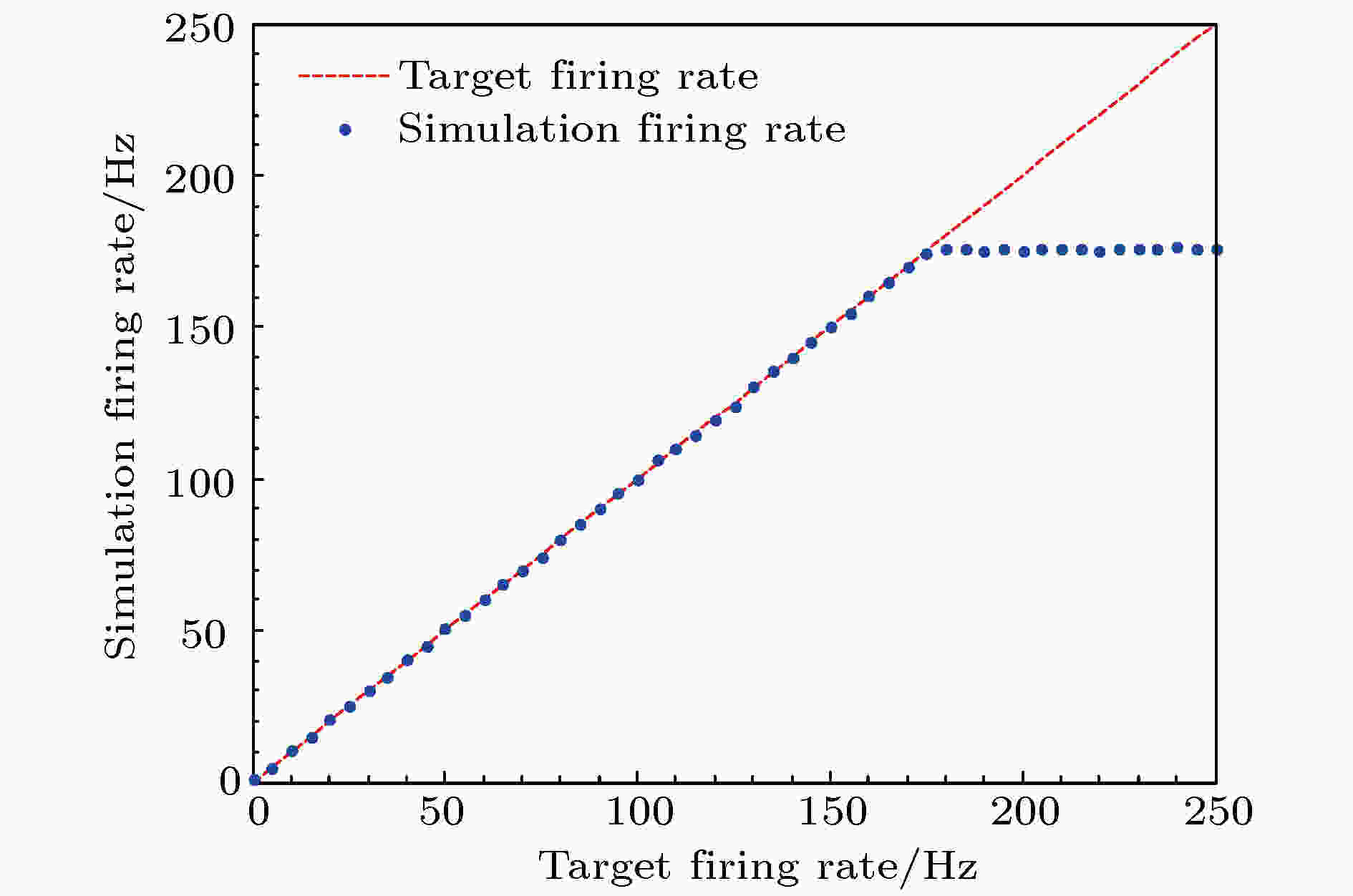图 12 神经元实际放电率极限值
Figure12. The limitation value of neural firing rate.

在抑制性突触可塑性调节规则中, 目标放电率${\rho _0}$的取值是需要预先设定的, 关于如何设定目标放电率尚存在不同的观点. 一种观点认为神经元目标放电率的设定主要受钙离子感受器灵敏度的控制, 当系统内部偏离目标钙值时钙离子感受器产生稳定补偿^[43]; 另一种观点认为神经元目标放电率的设定是由具有相反作用的受体之间的平衡点决定的, 其原理如图13所示^[43], 其中Factor⁺和Factor^－表示随放电率具有相反变化趋势的两种因素, 这两种趋势的平衡点对应的放电率即为目标放电率. 除上述观点外, Marder和Tang^[44]以及Davis等^[45]从脑结构特征的角度给出了另外的解释, 因为大脑是一个层级系统, 下级的放电率期望值由上级设定, 相当于上级的输出. 综上, 我们认为关于放电率期望值的设定问题仍然是一个开放式的问题, 有待后续研究的进一步探索.
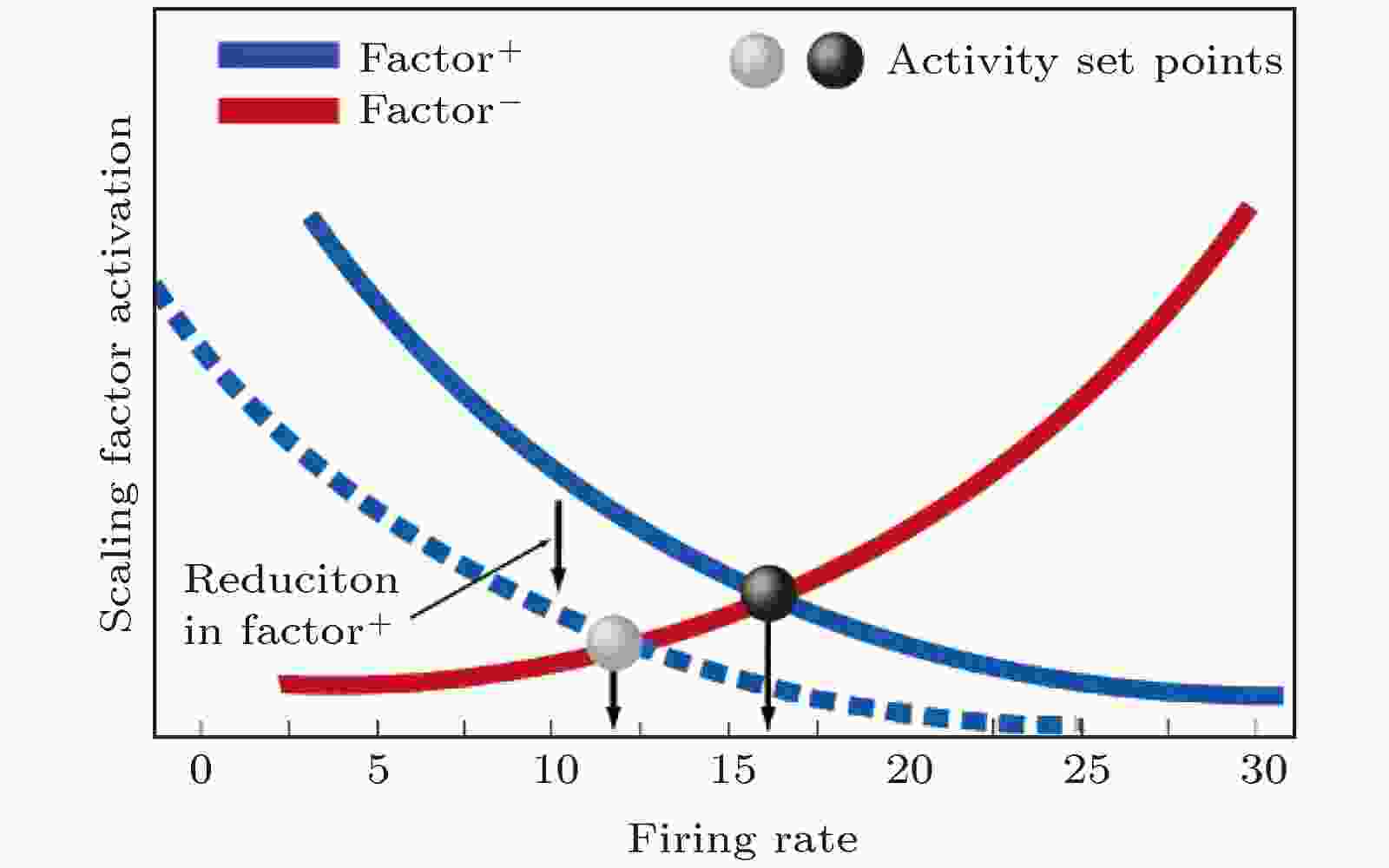图 13 目标放电率的确定^[43]
Figure13. Establishing a set point for the neuronal firing rate^[43].

关于目标放电率的含义, 仿真及理论分析结果已经表明, 在抑制性突触可塑性的调节下, 神经元的实际放电率最终会趋于目标放电率的设定值, 因此目标放电率的取值决定了神经元的放电水平, 即放电活动的强弱, 这和神经元不同的认知任务和功能相对应^[2].

神经元放电率自稳态是神经电活动的普遍现象, 是脑神经网络实现信息处理和维持正常脑功能的基础. 本文通过构建具有抑制性突触可塑性的反馈神经回路模型, 研究了基于抑制性突触可塑性的神经元放电率自稳态机制. 研究结果表明, 在抑制性突触可塑性的调节下, 神经元放电率可以自适应地准确跟踪目标放电率, 实现神经元放电率自稳态. 当神经元受到外界噪声和参数摄动干扰时, 神经元放电率会偏离目标放电率, 但是在抑制性突触可塑性的调节下, 神经元可以克服上述扰动的影响, 放电率仍能恢复并稳定至目标放电率, 表明基于抑制性突触可塑性的放电率自稳态具有很强的鲁棒性. 本文主要为计算研究, 根据本文的研究结果设计神经生物学实验是值得进一步探索的方向.