摘要: 能够长时间储存量子信息的量子存储设备是实现大规模量子计算和量子通信的基本要素. 与其他量子计算平台相比, 囚禁离子系统的优势之一在于具有很长的相干时间. 此前, 基于囚禁离子的单量子比特相干时间不到1 min. 研究发现, 在囚禁离子系统中, 限制量子比特相干时间的主要因素是运动能级加热和环境噪声, 其中后者包含环境磁场涨落和微波相位噪声. 在同时囚禁
171 Yb
+ 离子和
138 Ba
+ 离子的混合囚禁系统中, 通过实施协同冷却和动力学解耦, 可以实现相干时间超过10 min的单离子量子比特. 这一技术有望用于实现量子密码学和搭建混合量子计算平台.
关键词: 量子存储 /
囚禁离子 /
协同冷却 /
动力学解耦 English Abstract Single-ion qubit with coherence time exceeding 10 minutes Wang Ye Zhang Jing-Ning Kim Kihwan Center for Quantum Information, Institute for Interdisciplinary Information Sciences, Tsinghua University, Beijing 100084, China Fund Project: Project supported by the National Key Research and Development Program of China (Grant No. 2016YFA0301901) and the National Natural Science Foundation of China (Grant Nos. 11374178, 11574002, 11504197).Received Date: 19 September 2018Accepted Date: 18 October 2018Available Online: 01 February 2019Published Online: 05 February 2019Abstract: Quantum memory device capable of storing quantum information for a long period of time is one of the fundamental ingredients to realize large-scale quantum computation and quantum communication. Comparing with other quantum computation platforms, one of the advantages of the trapped-ion system is the long intrinsic coherence time. Before our work, the longest single-qubit coherence time in trapped-ion systems has been achieved to be less than 1 minute. It is discovered that the main limitation for the coherence time is the motional mode heating and the environment noise that includes the contributions from the magnetic field fluctuation and the phase noise of the microwaves. In a hybrid trapping system simultaneously trapping 171 Yb+ and 138 Ba+ ions, single-qubit quantum memories with coherence time longer than 10 minutes can be realized by applying sympathetic cooling and dynamical decoupling. This technique may have some value as the building blocks for quantum cryptography protocols and hybrid quantum computation platforms.Keywords: quantum memory /trapped ions /sympathetic cooling /dynamical decoupling 全文HTML --> --> --> 1.引 言 量子计算和量子模拟[1 ] 是近年来飞速发展的理论与实验并重的热点研究领域之一. 它以量子力学和量子信息学为理论基础, 以囚禁离子、超导电路等实验技术的进步为前提, 致力于实现实用的量子计算和量子通信[2 ,3 ] , 具有广阔的应用前景. 量子计算平台的基本元素是量子比特, 它是完全可控的量子二能级系统, 人们可以对其进行初始化、量子逻辑门和测量等基本操作. 量子力学中的不可克隆原理告诉我们, 储存在量子比特上的未知量子信息不能被精确地复制[4 ,5 ] . 这项量子信息独有的性质只能够通过对单个量子比特的相干操作和探测来验证. 如果不能完全控制单个量子比特, 量子信息的储存、操作和读出从根本上是难以令人信服的. 长期以来, 人们一直致力于发展在单量子比特层面的相干操作和探测技术.[6 ] 包括光子链接[3 ] 和离子穿梭[7 ] . 光子链接方案结合了远程量子通信和局域量子计算, 为实现量子网络提供了一个竞争性很强的物理平台. 人们已经演示了离子光子纠缠[8 ] 以及以光子为媒介的远距离离子纠缠[9 ] , 这是构建离子-光子网络的基本单元. 离子穿梭方案是将囚禁离子系统划分为操作区域和存储区域, 通过离子穿梭技术在区域间移动离子. 在这一架构下, 人们已通过实验演示了操作区域的基本结构和操作[10 ] . 随着系统规模的增大, 对存储区域量子比特储存时间的需求将相应增加. 为了将量子比特误码率保持在容错量子计算的阈值之下, 延长量子比特的相干时间是十分关键的. 随着系统规模的增大, 这两种方案对量子比特的相干时间的要求都会相应地提高.[11 ,12 ] . 然而, 经过十多年的发展后, 单量子比特系统的相干时间仍然远低于系综相干时间, 只有不到1 min[13 -15 ] . 对于囚禁离子量子比特, 特别是基于超精细能级的量子比特, 由自发辐射导致的固有弛豫时间T 1 远长于由磁场涨落和本振源的相位噪声导致的退相干时间T 2 * . 目前在离子阱系统中限制相干时间的主要是环境磁场涨落和本振源相位噪声导致的非相干演化, 同时我们还注意到, 加热导致的测量效率降低也极大地限制了离子阱系统中相干时间的测量[16 ,17 ] . 具体来说, 由于运动能级加热, 离子的波包随时间不断弥散, 收集到的荧光光子数减少, 这使得区分离子内态的测量效率低下. 在硬件方面, 通过清洁离子阱表面[18 ] 或将离子阱置入低温环境中[19 ] 可以显著地抑制运动能级加热效应. 在同时囚禁不同种类离子的混合囚禁系统中, 还可以通过协同冷却来消除运动能级加热, 从而保证在整个实验过程中探测效率不降低. 此外, 动力学解耦技术能够消除来自环境磁场和本振源的噪声, 从而延长量子系统的相干时间[20 -22 ] . 最近有文献报道, 在离子化供体的核自旋系综中实现了小时量级的相干时间[23 ,24 ] .2.协同冷却 令人奇怪的是, 二十年前关于离子系综的实验中[11 ,12 ] 测得的相干时间远比在最近的单离子实验中测得的相干时间来得长, 前者大约是10 min, 而后者最长不超过1 min[13 -15 ] . 现在已弄清了导致这一现象的原因. 原因之一是能够操作单量子比特的离子阱系统复杂度远高于之前的离子阱系综系统, 导致很难在系统上实施磁屏蔽以降低磁场噪声; 原因之二是离子阱系统的背景加热使得同种离子的探测效率随着时间的增加而大量降低. 之前离子阱系综的系统使用了非常大型的离子阱结构, 这种结构的电极与离子云距离较远, 背景加热较低. 但是为了能够实现速度较为理想的量子比特门, 量子信息领域中使用的离子阱结构都更加微小, 导致背景加热效应更加显著. 因此我们相信, 只要找到合适的方法, 能够在激光冷却停止后减轻运动加热效应, 单离子实验应该可以展示出和离子系综可比拟的长相干时间.$ ^{171}{\rm Yb}^+ $ 和$ ^{138}{\rm Ba}^+ $ , 我们可以实施协同冷却. 其中, 单个$ ^{171}{\rm Yb}^+ $ 离子作为量子比特, 单个$ ^{138}{\rm Ba}^+ $ 作为制冷离子. $ ^{171}{\rm Yb}^+ $ 离子具有的基态电子组态具有两个磁场不敏感的超精细能级, 这使得编码于其上的量子比特本身具有较长的内禀相干时间. 同时, 选用$ ^{138}{\rm Ba}^+ $ 离子是因为这两种离子的质量相对接近, 使得协同冷却效率更高.2.1.实验装置 2.1.实验装置 协同冷却的原理是通过对一种离子施加冷却激光, 从而冷却由两种离子组成的混合离子链的运动模式, 因此需要在离子阱中同时囚禁两种类型的离子. 图1(a) 所示为一个标准的Paul离子阱同时囚禁了$ ^{171}{\rm Yb}^+ $ 离子和$ ^{138}{\rm Ba}^+ $ 离子. 图中, 两种离子所对应的操作激光均覆盖整个离子链, 这是因为离子链中的离子会在热噪声的作用下交换位置. 同时, 由$ ^{171}{\rm Yb}^+ $ 离子和$ ^{138}{\rm Ba}^+ $ 离子的能级图可知, 两种离子的光学特性差异很大, 对$ ^{138}{\rm Ba}^+ $ 离子进行激光冷却不会影响编码在$ ^{171}{\rm Yb}^+ $ 离子上的量子比特的相干性.图 1 实验装置和控制系统 (a) 同时囚禁${{}^{171}{\rm Yb}^+ }$ 离子和$ ^{138}{\rm Ba}^+ $ 离子的混合囚禁系统及相关能谱图; (b) 微波和激光信号的控制系统Figure1. Experimental setup and control system: (a) Hybrid trapping system that traps $ ^{171}{\rm Yb}^+ $ and $ ^{138}{\rm Ba}^+ $ simultaneously; (b) control system for generating laser and microwave signals.$ ^{171}{\rm Yb}^+ $ 离子$ ^2{\rm S}_{1/2} $ 电子组态的两个超精细能级 $ \left|\downarrow\right\rangle\equiv\left|F=0, m_F=0\right\rangle $ 和$ \left|\uparrow\right\rangle\equiv\left|F=1, m_F=0\right\rangle $ , 被定义为量子比特的两个能级. 这两个能级的特征频率之差为$ 12642812118+310.8B^2 $ Hz, 其中$ B $ 是以高斯为单位的磁场强度的数值. 在实验中, 可以通过标准的光泵技术将量子比特制备到$ \left|\downarrow\right\rangle $ 态, 并通过荧光测量技术来区分量子比特的两个能级.图1(b) 是用于产生激光和微波信号的控制系统的示意图. 其中微波信号由微波振荡器的信号和直接数字合成器的信号混合而成, 并受到可编程逻辑门阵列的控制. 该控制系统能够在$ 100\;{\rm ns} $ 内改变微波信号的相位. 所有微波源相位均以铷原子钟为标准. 为了处理波长为369 nm的激光的泄漏问题, 设计了由声光调制器、电光脉冲选择器和机械快门组成的三段开关. 该激光用于$ ^{171}{\rm Yb}^+ $ 离子的多普勒冷却、荧光探测和光泵操作. 因为该激光频率与量子比特的跃迁频率接近, 稍有泄漏即会导致巨大的退相干效应.2.2.冷却效果 -->2.2.冷却效果 衡量协同冷却效果的直接途径是测量$ ^{171}{\rm Yb}^+ $ 离子在协同冷却过程中达到的平衡态温度. 为测量平衡态温度, 需要利用双光子拉曼跃迁来耦合内态与运动能级, 从而测量运动能级布居数分布. 然而, 这需要在实验系统中增加额外的激光和相应控制系统.3.动力学解耦 在利用协同冷却技术抑制了运动能级加热效应后, 剩下的退相干的主要因素是磁场涨落和用于操作量子比特的微波的相位涨落, 它们将导致量子比特的相位随机化. 利用动力学解耦技术, 可以抑制来自环境磁场涨落的外界噪声和本振源的相位噪声[20 ,25 -29 ] .$ \hat\sigma_z $ 是泡利自旋算符的$ z $ 分量, $ \omega_0 $ 是两个能级的频率差, $ \beta(t)=\beta_{\rm B}(t)+\beta_{\rm LO}(t) $ 是随机相位噪声, $ \beta_{\rm B} $ 和$ \beta_{\rm LO} $ 分别代表环境磁场涨落和操作微波相位涨落的影响. $ \beta(t) $ 满足$ \left\langle\beta(t)\right\rangle = 0 $ 和$ \left\langle\beta(t)\beta(t')\right\rangle= $ $ g(t-t')$ .[30 ] 在量子信息领域被广泛应用, 是用来消除随机相位噪声影响的一项标准技术. 动力学解耦最简单的实施方案是Hanh回波[31 ] , 又被称作自旋回波. 在经过一段时间$ \tau $ 的退相干后, 该技术通过一个翻转脉冲($ {\text{π}} $ 脉冲)来实现自旋系统的重对焦, 从而在时间为$ 2\tau $ 时得到增强的回波信号. 然而, Hahn回波无法消除时间尺度比$ \tau $ 更小的系统-环境相互作用扰动. 为解决这一问题, 人们试图使用一系列等距$ {\text{π}} $ 脉冲来消除高频扰动, 即Carr-Purcell (CP)序列[32 ] 和Carr-Purcell-Meiboom-Gill (CPMG)序列[33 ] . 可以形象地把这一类型的动力学解耦序列对系统的作用理解为将不需要的相位涨落通过时间平均的方式消除掉. 这类方案原则上要求$ {\text{π}} $ 脉冲之间的间隔$ \tau $ 尽可能小, 然而在实际实验中$ \tau $ 的取值受到硬件和系统最大可承受功率的限制.$ 2{\text{π}}/\tau $ 的高通滤波器. 因此, 如果环境噪声谱已知, 可以设计合适的滤波函数来得到最优的衰减率, 这就是基于非等距脉冲序列的动力学解耦方案[34 ] 的核心思想.[35 ] 可以将系统误差减少到$ O(\varepsilon^n) $ , 其中$ \varepsilon $ 是裸的系统误差率. 完全补偿的组合脉冲可以用于任意初态, 替换任意单个脉冲而不影响其他脉冲. 将组合脉冲与动力学解耦结合起来的方案是KDD$ _{\phi} $ 方案[21 ] , 其中下标$ \phi $ 是Knill组合脉冲[36 ] 的参数, 决定了$ {\text{π}} $ 脉冲在x-y 平面上的角度.$ {\rm KDD}_{ xy} $ 方案来延长量子比特的相干时间, 图2 所示即CPMG方案及$ {\rm KDD}_{xy} $ 方案对应的脉冲序列.图 2 动力学解耦脉冲序列 (a) CPMG方案; (b) $ {\rm KDD}_{xy} $ 方案Figure2. Pulse sequence for dyanmical decoupling: (a) CPMG protocol; (b) ${\rm{KD}}{{\rm{D}}_{{xy}}}$ protocol.3.1.滤波函数 3.1.滤波函数 为了刻画动力学解耦序列对量子态演化的影响, 需要计算动力学解耦序列对应的滤波函数. 任意动力学解耦序列可以看作在$ T $ 时间内执行$ n $ 个$ {\text{π}} $ 脉冲操作, 第$ i $ 个$ {\text{π}} $ 脉冲对应的方位角和时刻分别为$ \phi_i $ 和$ \tau_i $ , 并约定$ \tau_0=0 $ , $ \tau_{n+1}=T $ .$ \left|\psi(0)\right\rangle=\left|\downarrow\right\rangle $ 出发, 首先施加一个$ {\text{π}}/2 $ 脉冲将态矢量旋转到x-y 平面, 然后执行动力学解耦序列, 最后再次施加$ {\text{π}}/2 $ 脉冲并测量Ramsey条纹的对比度. 同时, 态矢量的演化受到噪声的影响. 系统的末态可以写作$ \left|\psi(T)\right\rangle =$ $ D^?_x({\text{π}}/2)\tilde R(T)D_x({\text{π}}/2)\left|\psi(0)\right\rangle $ ,$ \gamma_i={\text{π}} $ , 上述演化算符可化简为$ \tilde R(T)=\exp\left[{\rm{i}} F_n(T)\hat\sigma_z\right] $ ,$ F_n(T) $ 可写为$\sum\limits_{i = 1}^n {{{( - 1)}^{i + 1}}} {\phi _i} = k{\text{π}} $ , k 是整数, 因此(3 )式中的第二项可省略. 定义$ F_n(T) \equiv \int _{-\infty}^{\infty} s_n(t')\beta(t'){\rm{d}} t' $ , 其中时域滤波函数$ s_n(t) $ 定义如下:$ \varTheta(\cdot) $ 是Heaviside阶梯函数.$ z $ 分量的期待值, 即5 )式时, 使用了对高斯型随机变量$ X $ 成立的等式$\left\langle {\exp {\rm{i}}X} \right\rangle = \exp \left( {{\rm{i}}\left\langle X \right\rangle - {{\left\langle {{X^2}} \right\rangle }}/2} \right)$ 和$\left\langle {{F_n}(T)} \right\rangle = 0. $ 定义时域滤波函数的傅里叶变换$ \chi(T) $ 可写成如下形式:7 )式可见, $ \left|\tilde y_n(\omega, T)\right|^2 $ 的作用相当于环境噪声谱$ S_\beta(\omega) $ 在频域的滤波器, 因此被定义为滤波函数.3.2.环境噪声 -->3.2.环境噪声 如前所述, 系统的随机相位噪声$ \beta(t) $ 包含来自随机磁场涨落和操作微波相位涨落两方面的影响, 分别用$ \beta_{\rm B}(t) $ 和$ \beta_{\rm LO}(t) $ 表示. 操作微波相位涨落$ \beta_{\rm LO} $ 与本地振荡器的品质有关, 在使用高品质本地振荡器、铷原子钟和直接数字合成器等设备后, 由频谱分析仪测得的典型相位涨落如图3 所示.图 3 频谱分析仪测得的典型相位涨落噪声谱Figure3. Typical phase noise measured by spectrum analyzer.$ \beta_{\rm LO}(t) $ 业已固定, 无法调整. 而来自于环境磁场涨落的噪声$ \beta_{\rm B}(t) $ 则可以很容易地调整. $ ^{171}{\rm Yb}^+ $ 的二阶塞曼效应为$ \Delta f_{\rm Z2}=KB^2 $ Hz, 其中$ K=310.8\;{\rm Hz}/{\rm G}^2 $ .在(1 )式的哈密顿量中, 量子比特的频率差$ \omega_0 $ 和来自环境磁场涨落的噪声$ \beta_{\rm B}(t) $ 分别为$ \omega_{\rm HF} $ 是超精细能级劈裂, $ B_i $ 是磁场在$ i $ 方向的平均值, $ b_i(t) $ 是$ i $ 方向的磁场涨落, $ i={x, y, z} $ . 假设降低磁场平均值不影响涨落的大小, 则可以通过减小磁场的方式来压制$ \beta_{\rm B}(t) $ , 从而得到更长的相干时间. 由通量计测得$ b_{x}(t)\ll b_{ y, z}(t) $ , 因此使磁场沿$ {x} $ 方向. 在研究系统噪声谱时, 采用$B_{x}=$ $ 8.8\;{\rm G} $ ; 在实现长相干时间量子存储时, 采用$ B_{x} = 3.5\;{\rm G} $ , 这是能够对离子的内态进行有效荧光测量的最小磁场.$ 50\;{\rm Hz} $ 振荡及其谐波, 因此频域噪声谱可以用分立模型来模拟[37 ,38 ] , $ \tilde\beta(\omega)=\sum_{k=1}^d\beta_k\delta(\omega-\omega_k) $ , 其中$ \delta(\cdot) $ 代表狄拉克$ \delta $ 函数. 将$ \tilde\beta(\omega) $ 代入(5 )式, 得到最终信号为$ {\rm J}_0(\cdot) $ 是0阶Bessel函数. 实验上测得末态$ \hat\sigma_z $ 平均值的平均脉冲间距变化的数据后, 可通过数值拟合得到分立噪声谱强度$ \beta_k $ .$ S_\beta(\omega) $ , 拉姆齐条纹的对比度可表示为$ {\rm{e}}^{-\chi(T)} $ , 其中$ \left|\tilde y(\omega, T)\right|^2 $ 可看作中心频率为$ \dfrac{1}{2\tau} $ , 带宽正比于$ \dfrac{1}{2{\text{π}} T} $ 的带通滤波函数. 基于Plancherel定理可以得到$ \left|\tilde y(\omega, T)\right|^2 $ 的带宽很窄, 那么$ S_\beta(\omega) $ 在中心频率附近可看作常数, 即$ S_\beta\left(1/(2\tau)\right)\simeq $ $\chi(T)/(4T) $ . 因此, 可以通过测量$ \chi(T) $ 来估算$ S_\beta(\omega) $ . 图4(a) 为执行包含不同脉冲数量的动力学解耦序列, 测量得到的系统在演化时间$ T $ 后的拉姆齐条纹对比度. 图4(b) 为计算得到的环境噪声谱$ S_\beta(\omega) $ .图 4 (a) 执行包含$ N $ 个脉冲的动力学解耦序列, 不同的总演化时间$ T $ 对应的条纹对比度; (b) 通过分析图(a)中的数据得到的环境噪声谱Figure4. (a) Ramsey contrasts depending on the total evolution time T for various numbers of pulses N in the dynamical decoupling sequence; (b) the noise spectra analized from the measured data in Fig. (a).4.基于微波的量子门操作 量子比特跃迁可通过微波来驱动, 微波信号是通过混合来自安捷伦微波振荡器的$ 12.442812\;{\rm GHz} $ 的信号和来自直接数字合成器的$ 200\;{\rm MHz} $ 的信号产生的. 经过一次放大, 微波信号通过放置在视窗附近的微波喇叭施加于系统. 由于动力学解耦序列通常包含数千乃至数万个单比特逻辑门, 逻辑门误差的累积会导致量子比特退相干. 因此, 微波驱动的单比特量子逻辑门的保真度是实现长相干时间量子存储的最重要的因素之一.4.1.随机化基准测试 4.1.随机化基准测试 随机化基准测试[39 ] 是用来测量极低的单比特量子逻辑门的保真度的一种标准方法. 传统上, 量子操作的误差行为可以通过量子过程层析来标定. 然而, 虽然量子过程层析可以提供关于量子操作的许多信息, 但却无法保证该量子操作嵌入一长串其他量子操作中的表现. 另一方面, 规模化量子计算要求单个量子操作的误差率在$ 10^{-4} $ 量级或更低. 通过传统的量子过程层析在实验上测定这样低的误差率是很困难的. 此外, 量子过程层析无法排除初态制备和测量过程引入的误差. 因此, 人们提出了一种可以克服以上问题的对量子操作的误差行为进行实验研究的新方法, 即随机化基准方法.$ \hat U $ 及其逆操作$ \hat U^{-1} $ . 假如噪声模型可表示为施加在$ \hat U $ 和$ \hat U^{-1} $ 之间的独立的量子操作, 保真度的下降程度即代表了系统的噪声强度. 随机化基准方法是随机化方法的简化版本, 表现在前者将随机幺正操作限制为Clifford门操作.$ {\rm{e}}^{-\rm{i}\sigma{\text{π}}/4} $ 的$ {\text{π}}/2 $ 旋转生成的, 其中$ \sigma $ 是作用于不同量子比特的泡利算符的直积.${{\rm{e}}^{ \pm {\rm{i}}{{\hat \sigma }_{\rm{b}}}{\text{π}} {\rm{/2}}}}$ 形式的幺正操作, 其中随机变量$ b\in\left\{0, { x, y, z}\right\} $ , $\hat\sigma_0=\hat{\mathbb I} $ 是恒等算符. 门计算执行形式为${{\rm{e}}^{ \pm {\rm{i}}{{\hat \sigma }_{\rm{b}}}{\text{π}} {\rm{/4}}}}$ 的幺正操作, $ u\in\left\{{x}, {y}\right\} $ . 除了最后一个$ {\text{π}}/2 $ 脉冲, 上述符号、随机变量$ b $ 和$ \mu $ 都由均匀随机采样得到. 选择系统初态为$ \left|0\right\rangle $ , 是由于序列中的操作均出自Clifford 群, 理想情况下系统的状态总是泡利算符的本征态. 最后一个$ {\text{π}}/2 $ 脉冲将系统状态旋转为$ \hat\sigma_z $ 的本征态, 最终测量是关于$ \hat\sigma_z $ 的冯诺依曼测量. 在理想情况下, 最终测量的结果是已知的. 在误差环境下, 由于随机化, 序列的误差与组成序列的单个或数个操作无关. 序列的长度$ l $ 是序列中$ {\text{π}}/2 $ 脉冲的个数. 可以测量不同长度$ l $ 的序列对应的误差率$ p_l $ , 由$ p_l $ 与$ l $ 的关系可以估算门脉冲的平均误差率,$ p_l=\left[1-(1-d_{\rm if})(1-d)^l\right] $ ,$ d $ 是随机化计算门(一个$ {\text{π}}/2 $ 脉冲和一个泡利脉冲的随机组合)的平均误差率, $ d_{\rm if} $ 为包含初态制备和测量过程的误差率.$ N = N_lN_{\rm G}N_{\rm P}N_{\rm e} $ 次实验的末态测量结果的统计分析, 其中$ N_l $ 是序列长度$ l $ 的不同取值的个数, $ N_{\rm G} $ 是每个长度$ l $ 所对应的随机计算门序列的个数, $ N_{\rm P} $ 是每一计算门序列对应的泡利随机化序列的个数, $ N_{\rm e} $ 是每一序列对应的实验次数. 在实验中, 选取图5 展示了不同序列的保真度, 对于序列长度$ l $ 的每一个不同取值都存在32个数据点, 由此可以估算单量子比特逻辑门保真度为99.994%±0.002%.图 5 序列保真度随序列长度的变化Figure5. Sequence fidelity pl as a function of the sequence length l .5.测量单量子比特相干时间 结合协同冷却和动力学解耦, 最近我们实现了具有超长相干时间的单比特量子存储, 并测得超过10 min的相干时间[40 ] . 我们在标准的Paul阱中同时囚禁$ ^{171}{\rm Yb}^+ $ 和$ ^{138}{\rm Ba}^+ $ 两种离子, 其中$ ^{171}{\rm Yb}^+ $ 离子$ ^2{\rm S}_{1/2} $ 电子组态中的两个超精细能级被定义为量子比特, $\left| \downarrow \right\rangle \equiv \left| {F = 0,{m_F} = 0} \right\rangle $ 和$\left| \uparrow \right\rangle \equiv \left| {F = 1,} \right.$ $ \left. {{m_F} = 0} \right\rangle $ . 在实验过程中, 持续对$ ^{138}{\rm Ba}^+ $ 离子进行激光冷却. 在测量了系统的环境噪声谱后, 通过合适的动力学解耦方案, 即脉冲平均间隔$ \tau=200\;{\rm ms} $ 的$ {\rm KDD}_{xy} $ 方案, 将环境噪声涨落对编码于$ ^{138}{\rm Yb}^+ $ 离子之上的量子比特的影响降到最低.$ 3.5\;{\rm G} $ 来最大限度地减小磁场涨落的影响. 选取六个不同的初态, 分别是$\left| \uparrow \right\rangle $ , $\left| \downarrow \right\rangle $ , $\displaystyle\frac{1}{{\sqrt 2 }}\left( {\left| \uparrow \right\rangle + \left| \downarrow \right\rangle } \right)$ ,$\displaystyle\frac{1}{{\sqrt 2 }}\left( {\left| \uparrow \right\rangle + {\rm{i}}\left| \downarrow \right\rangle } \right)$ , $\displaystyle\frac{1}{{\sqrt 2 }}\left( {\left| \uparrow \right\rangle - \left| \downarrow \right\rangle } \right)$ , $ {\displaystyle\frac{1}{{\sqrt 2 }}( {\left|\uparrow\right\rangle } } - $ $\left. {{\rm{i}}\left|\downarrow \right\rangle } \right)$ . 对于每一个初态执行动力学解耦序列, 并测量拉姆齐条纹的对比度. 以$\displaystyle\frac{1}{{\sqrt 2 }}\left( {\left| \uparrow \right\rangle + \left| \downarrow \right\rangle } \right)$ 为例, 实验的脉冲序列如图6 所示. 其中初始化包括多普勒冷却、激光抽运和$ {\text{π}}/2 $ 脉冲. 随后, 执行一定时间的$ {\rm KDD}_{xy} $ 序列, 再执行$ {\text{π}}/2 $ 脉冲. 在理想情况下, 最后一个$ {\text{π}}/2 $ 脉冲将系统状态旋转到$\left| \uparrow \right\rangle $ . 最后, 测量$ \hat\sigma_{z} $ , 结果为0或1. 为得到代表拉姆齐条纹对比度的$\left\langle {{{\hat \sigma }_{\rm{z}}}} \right\rangle $ , 每个实验被重复30—50次.图 6 测量单量子比特相干时间的脉冲序列Figure6. Pulse sequences for measuring the single-qubit coherent time.$ T $ 后的拉姆齐条纹对比度, 其中$T \in \{ 16\;{\rm{s}},64\;{\rm{s}},128\;{\rm{s}},360\;{\rm{s}},480\;{\rm{s}},$ $600\;{\rm{s}}\}. $ 图7 展示了实验上测得的六个不同初态在演化时间$ T $ 后的拉姆齐条纹对比度. 其中, $\left| \uparrow \right\rangle $ 和$\left| \downarrow \right\rangle $ 的条纹对比度在测量时间内有略微下降, 导致该下降的主要原因是量子逻辑门操作误差的累积, 对应的相干时间是$ (4740\pm1760)\;{\rm s} $ . 其余四个初态对应的相干时间是$ (667\pm17)\;{\rm s} $ , 导致退相干的主要原因是动力学解耦的带通滤波函数中心频率附近的残留噪声谱强度. 上述相干时间是通过对拉姆齐条纹对比度的数据进行指数拟合得到的.图 7 单量子比特六个不同初态的相干时间, 其中$\left| \uparrow \right\rangle $ 和$\left| \downarrow \right\rangle $ , 对应的相干时间是(4740$ \pm $ 1760) s; 其他四个初态对应的相干时间为(667$ \pm $ 17) s; 图中的误差线代表标准差Figure7. Single-qubit coherece time for six different initial states. For $\left| \uparrow \right\rangle $ and $\left| \downarrow \right\rangle $ , the coherence time is (4740$ \pm $ 1760) s. For the other four initial states, the coherence time is (667$ \pm $ 17) s. The error bars are the standard deviation.6.总结与展望 在同时囚禁$ ^{171}{\rm Yb}^+ $ 离子和$ ^{138}{\rm Ba}^+ $ 离子的混合囚禁离子系统中, 结合协同冷却和动力学解耦, 本文实现了相干时间超过10 min的单离子量子比特. 虽然超过10 min的单量子比特相干时间已经刷新了此前该领域的世界纪录, 但我们注意到该相干时间仍然可以进一步延长, 即实现更长的单比特相干时间并没有基础原理上的限制. 具体来说, 可以通过以下几种方式来进一步延长量子比特相干时间: 1) 安装磁场屏蔽; 2) 使用磁场不敏感的量子比特; 3) 使用相干性更好、相位更稳定的微波源.[5 ] 等. 本文所实现的具有超长相干时间的量子存储将刺激混合量子计算系统[41 ,42 ] 的发展, 比如将具有有限相干时间的量子系统中的量子信息映射并储存到囚禁离子量子比特中. 



































 图 1 实验装置和控制系统 (a) 同时囚禁
图 1 实验装置和控制系统 (a) 同时囚禁

























































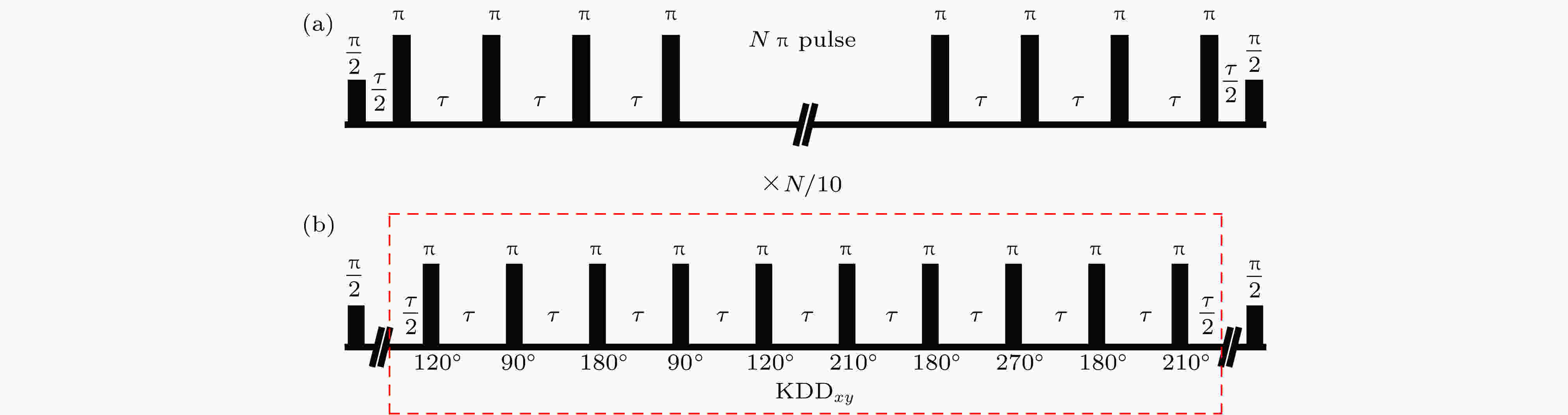 图 2 动力学解耦脉冲序列 (a) CPMG方案; (b)
图 2 动力学解耦脉冲序列 (a) CPMG方案; (b) 





































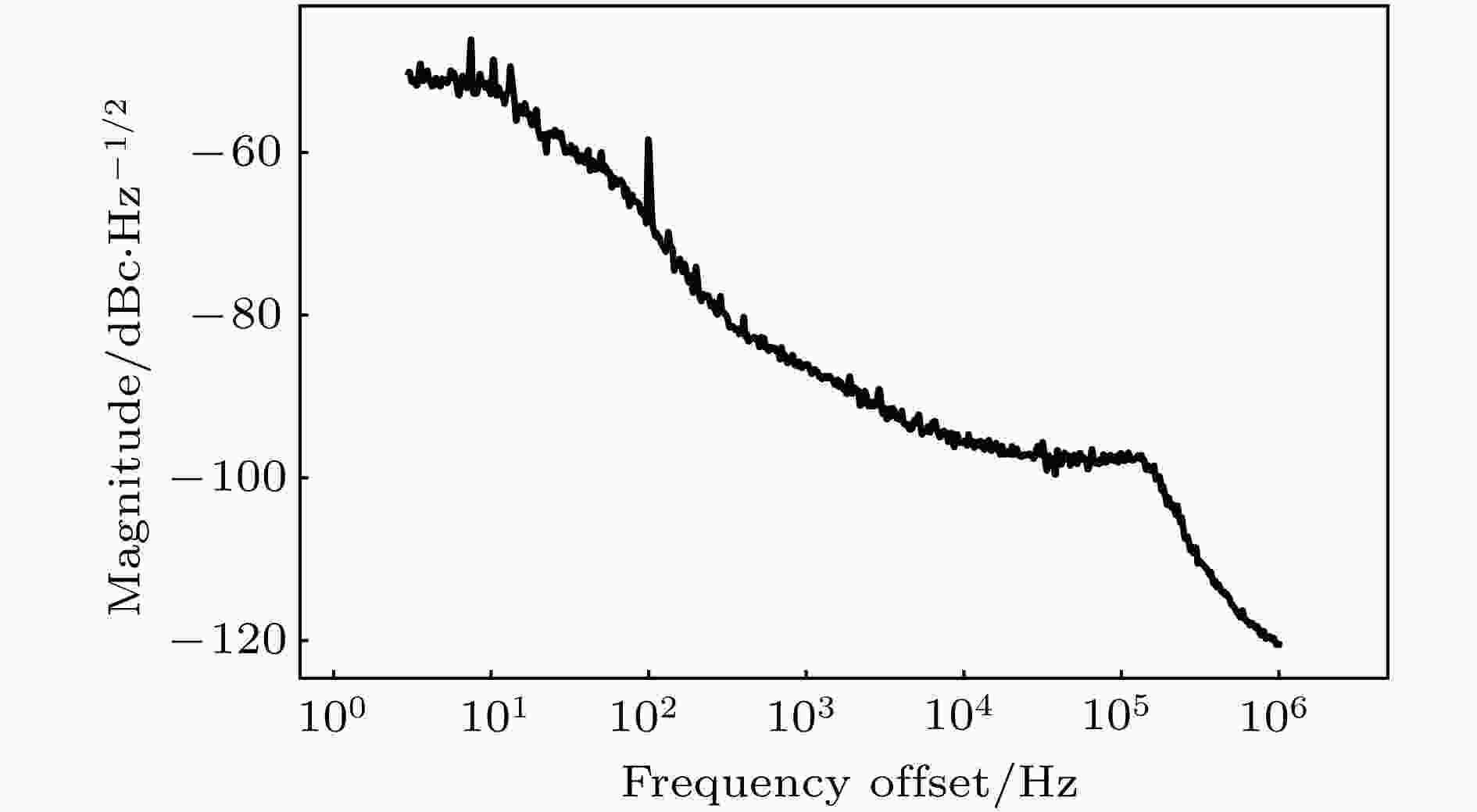 图 3 频谱分析仪测得的典型相位涨落噪声谱
图 3 频谱分析仪测得的典型相位涨落噪声谱

















































 图 4 (a) 执行包含
图 4 (a) 执行包含































































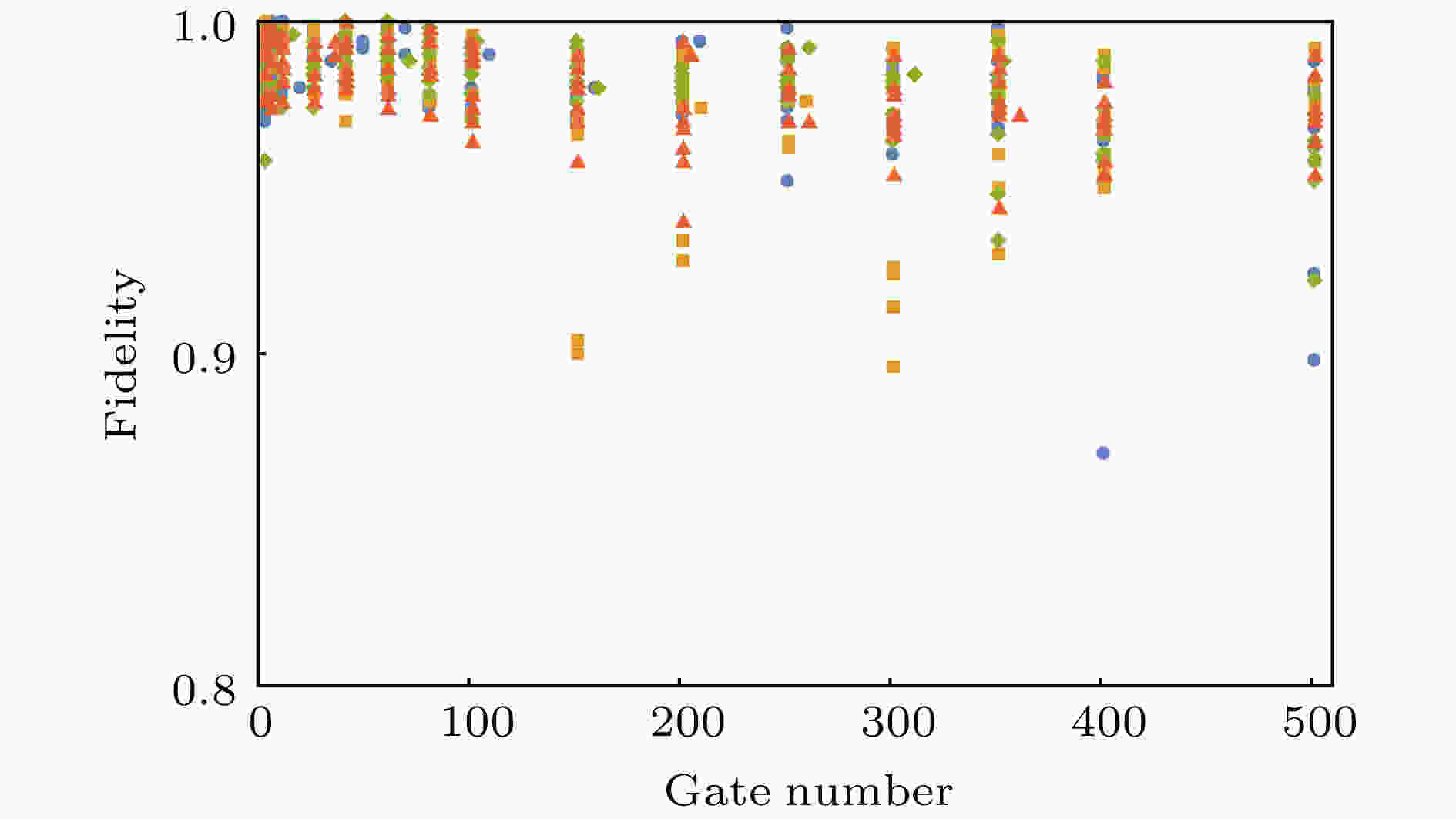 图 5 序列保真度随序列长度的变化
图 5 序列保真度随序列长度的变化








































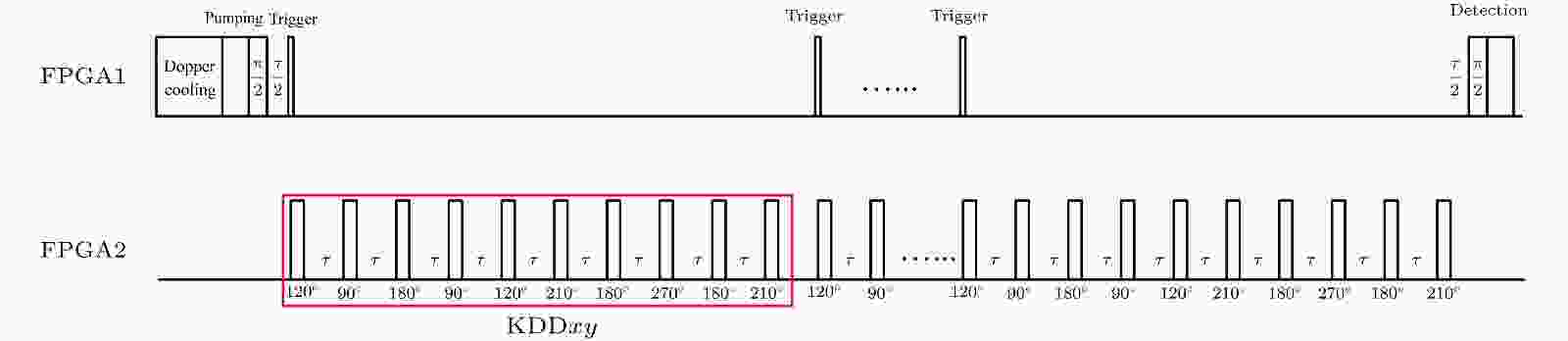 图 6 测量单量子比特相干时间的脉冲序列
图 6 测量单量子比特相干时间的脉冲序列









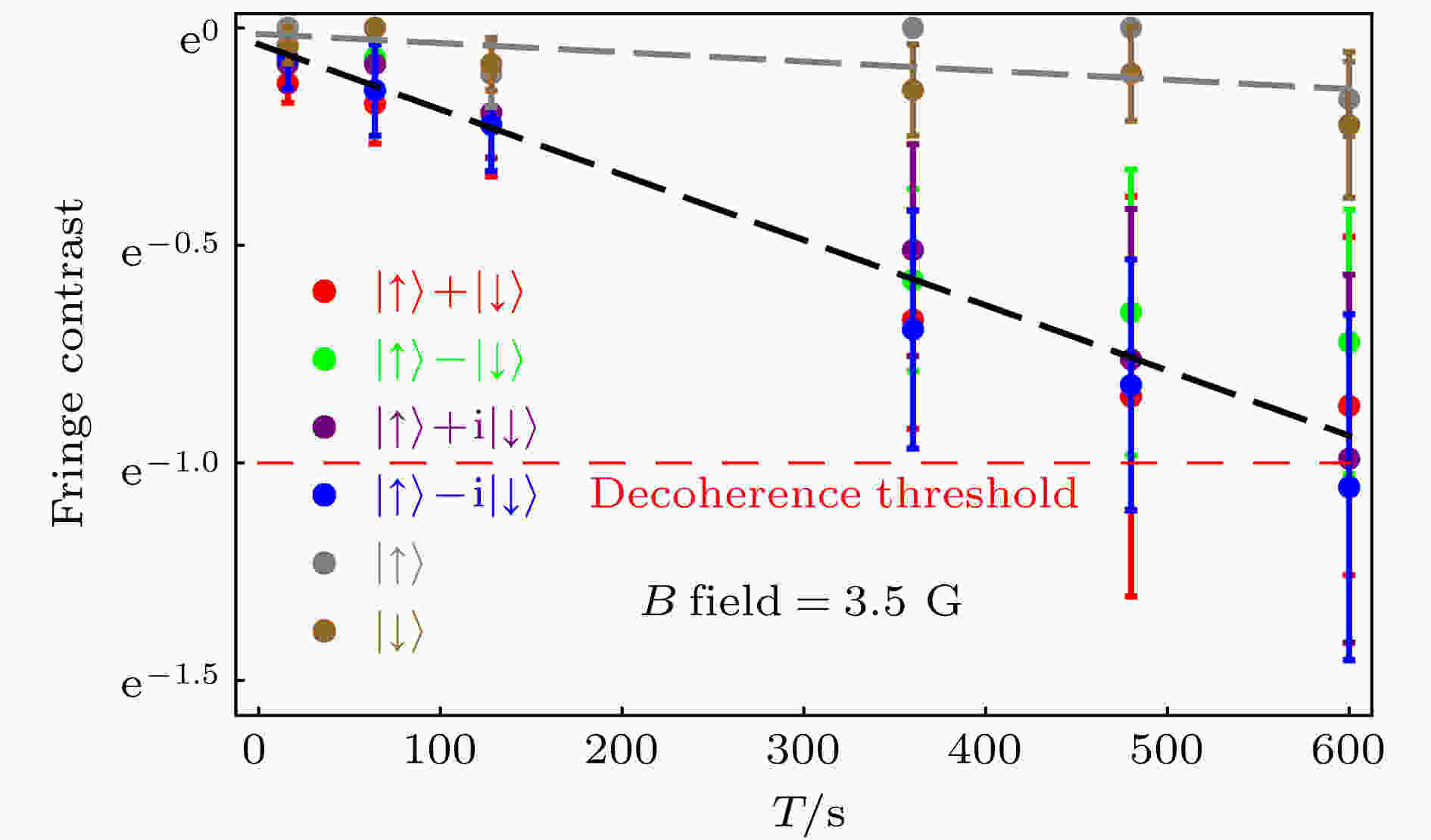 图 7 单量子比特六个不同初态的相干时间, 其中
图 7 单量子比特六个不同初态的相干时间, 其中













