删除或更新信息，请邮件至freekaoyan#163.com(#换成@)

等离子体屏蔽效应对Ar<sup>16+</sup>基态和激发态能级的影响

本站小编 Free考研考试/2021-12-29
摘要:基于Rayleigh-Ritz变分原理, 发展了一套处理弱耦合等离子体环境中多电子原子(离子)非相对论能量及其相对论修正的解析方法. 通过考虑电子间交换相互作用以及内外壳层电子的屏蔽效应, 计算了Ar16+基态1s2 1S、单激发态1sns 1,3S (n = 2—5), 1snp 1,3P (n = 2—5) 和双激发态2snp 1P (n = 2—5)非相对论能量及其相对论修正值(包括质量修正、单体和双体达尔文修正以及自旋-自旋接触相互作用项), 讨论了等离子体屏蔽效应对能级的影响. 结果表明: 相对论质量修正和第一类达尔文修正占主导, 比其他相对论修正项高出三个数量级. 此外, 等离子体屏蔽效应具有明显的态选择性, 屏蔽效应对外壳层电子的影响大于内壳层电子, 随着等离子体屏蔽参数的增加, 外壳层电子轨道向外延展, 激发态越高, 延展程度越大.
关键词: 等离子体/
能级/
相对论修正

English Abstract


全文HTML

--> --> -->
1.引　言
等离子体是指由原子或原子团的部分电子被剥夺后产生的正负离子形成的离子化气体状物质, 其广泛存在于宇宙环境中. 在等离子体环境下, 核外电子所感受到的势发生变化, 导致能级、跃迁光谱和碰撞动力学等原子参数发生改变. 这些原子数据对解释和诊断聚变等离子体中的温度和密度等状态具有重要的参考价值. 近年来, 随着聚变等离子体实验的开展, 以及先导聚变实验项目(如国际热核聚变实验堆(ITER)等)的推进, 人们越来越关注等离子体环境中辐射光谱和动力学参数. 等离子体中粒子之间相互作用与等离子体的温度和密度等状态参数有关. 人们常使用一些参数来表征等离子体的性质, 如等离子体耦合参数$\varGamma = {e^2}/(a{k_{\rm{B}}}{T_{\rm{e}}})$, 其中$a = {(3/4{\text{π}}{n_{\rm{e}}})^{1/3}}$, ${k_{\rm{B}}}$为玻尔兹曼常数, ${T_{\rm{e}}}$为等离子体电子温度, ${n_{\rm{e}}}$为电子密度, e为电荷电量. 当$\varGamma \ll 1$时, 等离子体称为弱耦合等离子体, 其广泛存在于宇宙大气、太阳等恒星表面以及实验室中的气体放电和托克马克等离子体中. 当$\varGamma \geqslant 1$时, 等离子体称为强耦合等离子体. 由于物理模型的局限性, 人们构造了多种计算模型描述不同温度和密度条件下的等离子体. 例如, 对于高温低密弱耦合等离子体, Debye和Hückel[1]提出了Debye-Hückel势代替传统的库仑势, 即将两个带电量分别为$q$和$q'$的点电荷之间相互作用库仑势改写成为$V(r) =$$ - \dfrac{{qq'}}{r}{{\rm{e}}^{ - ur}}$, 其中$u = 1/{r_{\rm{D}}}$, ${r_{\rm{D}} } = \sqrt {{k_{\rm{B}}}{T_{\rm{e}}}/(4{\text{π}}{e^2}{n_{\rm{e}}})} $为等离子屏蔽长度. 对于高密度量子等离子体, 引入余弦指数函数对Debye-Hückel势进行了修正, 以描述较强耦合效应, 该模型广泛应用于凝聚态物理领域[2]. 此外, 人们还采用离子球(IS)模型描述强耦合等离子体中的屏蔽效应. IS模型将离子包围在一个元包中, 元包所含电子的个数与离子的电荷态相等以保证整个元包呈电中性[3-9]. 这些工作的开展, 为人们获取等离子体内部信息提供了重要的帮助.
氩(Ar)作为宇宙丰度元素之一, 其各种离化度离子广泛存在于太阳耀斑、超行星和黑洞的吸积盘等天体等离子体环境中. 早期的光学不透明度工程, 对Ar16+和Ar17+光电离截面作了系统的计算研究, 给出了大量可供分析天体辐射光谱的参考数据[10-12]. 2000年, 钱德拉空间观察站在塞弗特星系NGC 3783中观察到Ar16+的辐射谱线, 这些谱线的分析需要理论数据作为依据[13]. 由此可见, 研究等离子环境中Ar16+能级和辐射光谱的理论, 不仅对天体等离子体的状态诊断和光谱分析起着重要的作用, 而且由于其核外有两个电子, 是考察电子与原子核、电子与电子间相互作用和相对论效应的理想体系[14-22]. 目前对Ar16+能级的研究主要集中在非屏蔽下能级结构和跃迁数据的计算. 如Saha等[14]在非相对论变分框架, 提出了一种新的试探性波函数, 在包含径向和角向关联效应下, 计算了Ar16+基态能量, 获得了较高精度的结果; Costa等[15]在Dirac-Fock近似下计算了Ar16+高激发态到基态的跃迁能、辐射跃迁几率和非辐射跃迁几率; Goryaev等[16]基于Z展开方法的MZ代码计算了Ar16+共振态到基态和低激发态之间的跃迁能和跃迁几率, 为了提高计算精度, 文中的相对论效应包含了Breit作用. Saha等[17]在非相对论框架下计算了弱耦合等离子体环境中2pnd (n = 3—6)以及2pnp (n = 3—6)双电子原子的能级结构, 他们发现随着等离子体耦合强度的增加, 原子趋于不稳定, 且束缚态电子的个数逐渐减少. Fang等[18]研究了等离子环境对${\rm{H}}{{\rm{e}}_\alpha }$线移动的影响, 结果表明等离子体环境下的跃迁谱线存在红移现象, 同时指出红移与德拜长度之间的规律可以作为一种重要的诊断等离子体状态工具. Kar和Ho[19]采用了高度关联的Hylleraas-type基对氦原子双激共振态2s2 1S的共振能和共振宽度进行了计算. Xie等[20]在多组态Dirac-Fock方法的基础上, 将Debye-Hückel势引入能量及跃迁哈密顿量中, 并对C4+ 1s2, 1s2l (l = s, p)以及1s3l (l = s, p, d)组态间的电偶极、磁偶极和磁四极跃迁几率、振子强度等原子参数进行了计算, 分析了电子与电子、电子与原子核相互作用对激发态和跃迁能的影响. 计算表明, 等离子体屏蔽导致原子激发能降低.
尽管目前已开展了大量研究工作, 但对等离子屏蔽下Ar16+能级结构的研究结果匮乏, 有关相对论效应对等离子体中原子能级和跃迁性质影响的报道更少. Chaudhuri等[23]分别利用标准的屏蔽库仑势和余弦屏蔽库仑势对等离子体环境效应下类氢离子基态和最低的两个激发态能级结构进行了计算, 讨论了相对论修正项中的质量修正项、达尔文修正项以及自旋-轨道相互作用项在等离子体环境下的行为. Hu等[24]在库仑屏蔽势下对类氢离子的激发能和跃迁几率进行了计算, 分析了相对论效应对束缚态能级的影响, 结果表明, 库仑屏蔽势可以很好地描述弱耦合等离子体环境对原子结构和跃迁线的影响, 屏蔽势减小原子能级间的跃迁能, 同时指出相对论能量对低电荷类氢离子束缚态能级的影响可以忽略不计. 然而, 以上的解析方法对单电子体系是适用的, 很难推广到多电子体系.
本文基于变分理论, 发展了一套处理弱耦合等离子体环境中多电子原子(离子)基态和激发态非相对论能量及其相对论修正能量的解析计算方法. 为了包括内外壳层电子的不同屏蔽效应以及交换效应, 组态波函数采用了反对称性的Hartree-Fock波函数, 同时将内外层电子径向轨道的变分参数取为独立的值. 我们以类氦氩离子为例, 计算了等离子体环境下基态、单激发态和双激发态的非相对论能级, 给出了质量修正、单体和双体达尔文修正、自旋-自旋接触相互作用和轨道-轨道相互作用等相对论修正项的能量值, 并讨论离子体屏蔽效应对能级和波函数的影响.
2.理论方法
2
2.1.非相对论能量
-->

2.1.非相对论能量

对于孤立双电子原子, 非相对论哈密顿量可以表示为
${H_{{\rm{NR}}}} = - \frac{1}{2}\nabla _1^2 - \frac{1}{2}\nabla _2^2 - \frac{Z}{{{r_1}}} - \frac{Z}{{{r_2}}} + \frac{1}{{{r_{12}}}},$
式中Z为核电荷数. 在弱耦合等离子体中, 原子的非相对论哈密顿可以改写为
${H_{{\rm{NR}}}} = - \frac{1}{2}\nabla _1^2 - \frac{1}{2}\nabla _2^2 - \frac{Z}{{{r_1}}}{{\rm{e}}^{ - u{r_1}}} - \frac{Z}{{{r_2}}}{{\rm{e}}^{ - u{r_2}}} + \frac{1}{{{r_{12}}}}{{\rm{e}}^{ - u{r_{12}}}}.$
需要说明的是, 本文仅考虑电子与原子核之间势的修正, 没有包括电子与电子之间相互作用势的修正. 事实上, 文献[22]的研究表明, 对于高Z高电荷态离子电子-电子相互作用势的修正对结果影响不大, 可以忽略不计. 依据Rayleigh-Ritz变分法, 在Racah表象下的多电子原子非相对论本征能量可以由(3)式得到:
${E_{{\rm{NR}}}} = \min \left\langle {\gamma LS{M_L}{M_S}} \right|{H_{{\rm{NR}}}}\left| {\gamma LS{M_L}{M_S}} \right\rangle ,$
式中$\left| {\gamma LS{M_L}{M_S}} \right\rangle $表示多电子原子的Racah波函数; $L$和$S$分别为原子的总轨道和总自旋角动量; ${M_L}$和${M_S}$分别为总轨道和总自旋角动量在量子轴方向的投影; $\gamma $为其他量子数. $\left| {\gamma LS{M_L}{M_S}} \right\rangle $由Slater行列式线性展开得到, 即
$\left| {\gamma LS{M_L}{M_S}} \right\rangle = \sum\limits_\beta {{C_\beta }{\varPhi _\beta }(\gamma {M_L}{M_S})} ,$
其中${C_\beta }$为组合系数; ${\varPhi _\beta }(\gamma {M_L}{M_S})$为将单电子波函数${\psi _{{n_i}{\ell _i}{m_{\ell i}}{m_{si}}}}({{{x}}_i})$反对称化后得到的Slater行列式波函数, $n,\ell ,{m_\ell },{m_s}$分别为单电子主量子数、轨道量子数、轨道量子数投影和自旋量子数投影. ${\psi _{{n_i}{\ell _i}{m_{\ell i}}{m_{si}}}}({{{x}}_i})$可以进一步写成单电子径向、角向和自旋波函数的乘积形式, 即
${\psi _{{n_i}{\ell _i}{m_{\ell i}}{m_{si}}}}({{{x}}_i}) = {R_{{n_i}{\ell _i}}}({r_i}){{\rm{Y}}_{{\ell _i}{m_{\ell i}}}}({\theta _i}{\phi _i}){\chi _{{m_{si}}}}({s_i}),$
式中的单电子角向波函数${{\rm{Y}}_{{\ell _i}{m_{\ell i}}}}({\theta _i}{\phi _i})$和自旋波函数${\chi _{{m_{si}}}}({s_i})$是已知的, 本文的单电子径向波函数${R_{{n_i}{\ell _i}}}({r_i})$选取Slater型径向波函数, 即
$\begin{split}{R_{n\ell }}(r) = & {N_{n\ell }}\exp \left( { - \frac{{{\alpha _{n\ell }}r}}{n}} \right) \\ &\times\sum\limits_{\nu = 0}^{n - 1} {\frac{{n!}}{{\nu !(n - \nu - 1)!(\nu + 1)!}}{{\left( { - \frac{{2{\alpha _{n\ell }}r}}{n}} \right)}^\nu }},\end{split}$
式中${\alpha _{{n_i}{\ell _i}}}$为变分参数, 通过对非相对论能量变分得到. ${N_{n\ell }}$为归一化系数, 通过使径向波函数满足归一化条件得到, 即
$\int\limits_0^\infty {R_{n\ell }^ * (r){R_{n\ell }}(r){r^2}{\rm{d}}r} = 1.$
将(4)式代入(3)式, 完成角向和自旋部分积分后, 非相对论能量表达式只剩下径向部分的单电子直接积分和双电子积分, 即

$I(n\ell ) = \frac{1}{2}\int_0^\infty r{R_{n\ell }}(r)\left[ - \frac{{{{\rm{d}}^2}}}{{{\rm{d}}{r^2}}} + \frac{{\ell (\ell + 1)}}{{{r^2}}} - \frac{{2Z}}{r}\right] r{R_{n\ell }}(r){\rm{d}}r \tag{8a}, $
${R^{(k)}}\left( {{n_i}{\ell _i}{n_j}{\ell _j},{n_{i'}}{\ell _{i'}}{n_{j'}}{\ell _{j'}}} \right) = \int_0^\infty {\int_0^\infty {{R_{{n_i}{\ell _i}}}({r_1}){R_{{n_i}{\ell _i}}}({r_1}){R_{{n_{i'}}{\ell _{i'}}}}({r_2}){R_{{n_{j'}}{\ell _{j'}}}}({r_2})\frac{{r_ < ^k}}{{r_ > ^{k + 1}}}r_1^2r_2^2{\rm{d}} {r_1}{\rm{d}}{r_2}} }.\tag{8b}$

2
2.2.相对论修正
-->

2.2.相对论修正

非相对论能量的相对论修正哈密顿量可以写成
${H_{{\rm{RS}}}} = {H_{{\rm{MC}}}} + {H_{\rm{D}}} + {H_{{\rm{SSC}}}} + {H_{{\rm{OO}}}},$
式中${H_{{\rm{MC}}}}$为相对论质量修正项; ${H_{\rm{D}}} = {H_{{\rm{D}}1}} + {H_{{\rm{D}}2}}$为达尔文修正项, ${H_{{\rm{D}}1}}$为单体达尔文修正项, ${H_{{\rm{D}}2}}$为双体达尔文修正项; ${H_{{\rm{SSC}}}}$为自旋-自旋接触相互作用项; ${H_{{\rm{OO}}}}$为轨道-轨道相互作用项. 表达式分别为
${H_{{\rm{MC}}}} = - \frac{{{\alpha ^2}}}{8}\sum\limits_i {\nabla _i^4} ,$
${H_{\rm{D}}} = {H_{{\rm{D}}1}} + {H_{{\rm{D}}2}} = \frac{{Z{\text{π}}{\alpha ^2}}}{2}\sum\limits_i {\delta ({{{r}}_i})} - {\text{π}}{\alpha ^2}\sum\limits_{j > i} {\delta ({{{r}}_{ij}})} ,$
${H_{{\rm{SSC}}}} = - \frac{8}{3}{\text{π}}{\alpha ^2}\sum\limits_{j > i} {\left( {{s_i} \cdot {s_j}} \right)\delta ({{{r}}_{ij}})} ,$
${H_{{\rm{OO}}}} = - \frac{{{\alpha ^2}}}{2}\sum\limits_{j > i} {\left[ {\frac{{{{{p}}_i} \cdot {{{p}}_j}}}{{{r_{ij}}}} + \frac{{{{{r}}_{ij}} \cdot ({{{r}}_{ij}} \cdot {{{p}}_i}){{{p}}_j}}}{{r_{ij}^3}}} \right]}. $
在Racah表象下, 各相对论修正项的能量可以分别写为
$\Delta {E_{{\rm{MC}}}} = \left\langle {\gamma LS{M_L}{M_S}} \right|{H_{{\rm{MC}}}}\left| {\gamma LS{M_L}{M_S}} \right\rangle \tag{14a}, $
$\Delta {E_{{\rm{D}}1}} = \left\langle {\gamma LS{M_L}{M_S}} \right|{H_{{\rm{D}}1}}\left| {\gamma LS{M_L}{M_S}} \right\rangle \tag{14b},$
$\Delta {E_{{\rm{D}}2}} = \left\langle {\gamma LS{M_L}{M_S}} \right|{H_{{\rm{D}}2}}\left| {\gamma LS{M_L}{M_S}} \right\rangle \tag{14c},$
$\Delta {E_{{\rm{SSC}}}} = \left\langle {\gamma LS{M_L}{M_S}} \right|{H_{{\rm{SSC}}}}\left| {\gamma LS{M_L}{M_S}} \right\rangle . \tag{14d}$
最后得到总相对论修正能量为
$\begin{split}\Delta {E_{{\rm{RS}}}}(\gamma LS) = & \Delta {E_{{\rm{MC}}}}(\gamma LS) + \Delta {E_{{\rm{D}}1}}(\gamma LS) \\ & + \Delta {E_{{\rm{D}}2}}(\gamma LS) +\Delta {E_{{\rm{OO}}}}(\gamma LS) \\ & + \Delta {E_{{\rm{SSC}}}}(\gamma LS).\end{split}$

3.计算与讨论
基于上述解析推导, 我们编写了处理等离子体环境中原子非相对论能量和相对论修正能量的计算程序. 为了验证计算方法和代码的可靠性, 首先对C4+基态的非相对论能量及其相对论修正能量进行了计算, 并将计算结果与文献进行了比较, 结果如表1 中所列, 其中, $u$为德拜半径的倒数, ${\alpha _{1{\rm s}}}$为轨道变分参数, ENR为非相对论能量, EMC和ED1分别为质量修正和单体达尔文修正, $\Delta \!\, {E_{{\rm{RS}}}}$为总相对论修正能量, ET为总能量. 可以看到, 考虑相对论效应之后, 我们的计算结果与文献[20, 25, 26]符合得非常好, 误差小于0.4%. 需要说明的是, 由于基态的两个电子均处于s轨道, 双体达尔文修正项、自旋-自旋接触作用项和轨道-轨道相互作用项为零.
u${\alpha _{1{\rm{s}}}}$ENREMCED1ΔERSETRef.[20]Ref.[25,26]
05.6875?32.3477?0.06965080.0587822?0.01087?32.35857?32.4176?32.3612
0.15.68614?31.1633?0.06958430.0587401?0.01084?31.17414?31.2324?31.177
0.25.68218?30.0095?0.06939050.0586174?0.01077?30.02027?30.079?30.0237
0.35.67577?28.8854?0.06907810.0584193?0.01066?28.89606?28.9557—
0.45.66706?27.7899?0.06865490.0581507?0.01050?27.80040?27.8614—
0.55.65616?26.7223?0.06812820.0578158?0.01031?26.73261?26.7963?26.7395
0.65.64318?25.6817?0.0675050.0574187?0.01009?25.69179?25.7576—
0.75.62821?24.6674?0.06679160.0569630?0.00983?24.67723?24.7457—
0.85.61134?23.6788?0.06599420.0564522?0.00954?23.68834?23.7006?23.7594
0.95.59263?22.7151?0.06511860.0558895?0.00923?22.72433?22.7986—
1.05.57215?21.7758?0.06417010.0552778?0.00889?21.78469?21.8629—


表1相对论修正对C4+基态1s2 1S能级的影响(单位: a.u.)
Table1.Effects of relativistic correction on ground state 1s2 1S energies level in C4+ (unit: a.u.).

2
3.1.Ar16+非相对论能量
-->

3.1.Ar16+非相对论能量

为了研究相对论修正对原子能级结构的影响, 我们对弱耦合等离子环境下类氦Ar16+基态1s2 1S、单激发态1sns (n = 2—5) 1,3S, 1snp (n = 2—5) 1,3P和双激发态2snp (n = 2—5) 1,3P的非相对论能量及其相对论修正能量值进行了系统的计算.
对于双电子体系单重态, 其原子态的Racah波函数可以展开为
$\left| {(n\ell n'\ell '){}^1L,0,0} \right\rangle = \frac{1}{{\sqrt 2 }}({\varPhi_\alpha } - {\varPhi _\beta }),$
式中
${\varPhi_\alpha } = \frac{1}{{\sqrt {2!} }}\left\| {\begin{array}{*{20}{c}}{{\psi _{n\ell {0^ + }}}({{ x}_1})} & {{\psi _{n\ell {0^ + }}}({{ x}_2})}\\{{\psi _{n'\ell '{0^ - }}}({{ x}_1})} & {{\psi _{n'\ell '{0^ - }}}({{ x}_2})}\end{array}} \right\|\tag{17a},$
${\varPhi _\beta } = \frac{1}{{\sqrt {2!} }}\left\| {\begin{array}{*{20}{c}}{{\psi _{n\ell {0^ - }}}({{ x}_1})} & {{\psi _{n\ell {0^ - }}}({{ x}_2})}\\{{\psi _{n'\ell '{0^ + }}}({{ x}_1})} & {{\psi _{n'\ell '{0^ + }}}({{ x}_2})}\end{array}} \right\|.\tag{17b}$
将(16)式的Racah波函数代入(3)式, 完成角向和自旋部分积分, 可得径向积分部分的非相对论能量表达式, 以1s2s组态为例, 其表达式为
$\begin{split}{E_{{\rm{NR}}}}(1{\rm{s2s,}}{}^{\rm{1}}{\rm{S}}) = & I(1{\rm{s}}) + I(2{\rm{s}}) + {R^{(0)}}(1{\rm{s2s,1s2s}}) \\ &+ {R^{(0)}}(1{\rm{s2s,2s1s}}).\end{split}$
将径向波函数代入(18)式, 完成径向积分, 可得关于变分参数的非相对论能量解析表达式, 即
$\begin{align} &{E_{{\rm{NR}}}}{\rm{(1s2s,}}{}^{\rm{1}}{\rm{S}}) \\ = & \dfrac{{\alpha _{{\rm{1s}}}^{\rm{2}}}}{2} + \dfrac{{\alpha _{{\rm{2s}}}^{\rm{2}}}}{8} + \dfrac{{320\alpha _{{\rm{1s}}}^{\rm{5}}\alpha _{{\rm{2s}}}^{\rm{3}} - 480\alpha _{{\rm{1s}}}^{\rm{4}}\alpha _{{\rm{2s}}}^4 + 208\alpha _{{\rm{1s}}}^{\rm{3}}\alpha _{{\rm{2s}}}^{\rm{5}}}}{{{{(2{\alpha _{{\rm{1s}}}} + {\alpha _{{\rm{2s}}}})}^7}}}\\&+\dfrac{{8\alpha _{{\rm{1s}}}^5{\alpha _{{\rm{2s}}}} \!+\! 20\alpha _{{\rm{1s}}}^{\rm{4}}\alpha _{2{\rm{s}}}^2 \!+\! 12\alpha _{{\rm{1s}}}^{\rm{3}}\alpha _{{\rm{2s}}}^{\rm{3}} \!+\! 10\alpha _{{\rm{1s}}}^2\alpha _{{\rm{2s}}}^{\rm{4}} \!+\! {\alpha _{{\rm{1s}}}}\alpha _{{\rm{2s}}}^5}}{{{{(2{\alpha _{1s}} + {\alpha _{2s}})}^5}}} \\ & - \dfrac{{4\alpha _{{\rm{1s}}}^{\rm{3}}Z}}{{{{(2{\alpha _{{\rm{1s}}}} + \mu )}^2}}} - \dfrac{{\alpha _{2s}^3Z(\alpha _{{\rm{2s}}}^{\rm{2}} + 2{\mu ^2})}}{{4{{({\alpha _{{\rm{2s}}}} + \mu )}^4}}}.\quad\quad\quad\quad\;\;\;{(19)}\end{align}$
对(19)式取极值, 可以得到各轨道的变分参数, 具体数据在表2中给出. 可以看到, 电荷亏损($\delta = |Z - {\alpha _{n\ell }}|$)随着电子轨道的增高逐渐减小, 这是由于电子轨道越高, 电子贯穿和屏蔽效应越来越弱.
2S+1n1sns 2S+1S1snp 2S+1P2snp 2S+1P
${\alpha _{1{\rm{s}}}}$${\alpha _{n{\rm{s}}}}$ENR${\alpha _{1{\rm{s}}}}$${\alpha _{n{\rm{p}}}}$ENR${\alpha _{2{\rm{s}}}}$${\alpha _{n{\rm{p}}}}$ENR
1117.6875—?312.848——————
217.932417.3433?198.38418.010716.9176?197.96917.411317.8229?77.601
317.981517.2194?178.1418.000816.9725?178.01817.942817.2934?56.8575
417.992417.1623?171.06818.000116.9852?171.01717.976617.2143?49.655
517.996117.129?167.7991816.9901?167.77317.988217.1692?46.3425
3218.013717.1931?199.19617.957717.266?198.504———
318.003117.1286?178.35517.9917.1509?178.162———
418.001217.0962?171.15517.996117.1079?171.076———
518.000617.0768?167.84317.998117.0845?167.803———


表2Ar16+ 1sns, 1snp和2s2p组态变分参数
Table2.Variation parameters of 1sns, 1snp and 2snp configurations in Ar16+.

2
3.2.等离子环境中Ar16+基态和激发态相对论能级
-->

3.2.等离子环境中Ar16+基态和激发态相对论能级

在球张量的形式下, 将(10)—(13)式代入各相对论修正项(14)式, 利用不可约张量理论完成径向、角向和自旋部分的积分, 最终可以得到各原子态解析的相对论能量参数表达式. 以基态1s2 (1S)态和激发态1s2s (1S)态为例, 基态1s2 (1S)各相对论修正项的解析参数表达式为
${E_{{\rm{MC}}}}(1{{\rm{s}}^{\rm{2}}}{\rm{,}}{}^{\rm{1}}{\rm{S}}) = - \frac{5}{4}\alpha _{{\rm{1s}}}^{\rm{4}}{\alpha ^2}\tag{20a},$
${E_{{\rm{D}}1}}(1{{\rm{s}}^{\rm{2}}}{\rm{,}}{}^{\rm{1}}{\rm{S}}) = \alpha _{1{\rm{s}}}^3Z{\alpha ^2}\tag{20b},$
${E_{{\rm{D}}2}}(1{{\rm{s}}^{\rm{2}}}{\rm{,}}{}^{\rm{1}}{\rm{S}}) = {E_{{\rm{SSC}}}}(1{{\rm{s}}^{\rm{2}}}{\rm{,}}{}^{\rm{1}}{\rm{S}}) = {E_{{\rm{OO}}}}{\rm{(1}}{{\rm{s}}^{\rm{2}}}{\rm{,}}{}^{\rm{1}}{\rm{S}}) = 0.\tag{20c}$
激发态1s2s (1S)各项相对论修正项的解析参数表达式为
${E_{{\rm{MC}}}}(1{\rm{s2s,}}{}^{\rm{1}}{\rm{S}}) = - \frac{1}{8}\left( {5\alpha _{{\rm{1s}}}^{\rm{4}} + \frac{{13\alpha _{{\rm{2s}}}^4}}{{16}}} \right){\alpha ^2}\tag{21a},$
${E_{{\rm{D1}}}}{\rm{(1s2s,}}{}^{\rm{1}}{\rm{S}}) = \frac{1}{8}\left( {4\alpha _{{\rm{1s}}}^{\rm{3}} + \frac{{\alpha _{{\rm{2s}}}^3}}{2}} \right)Z{\alpha ^2}\tag{21b},$
$\begin{split}& {E_{{\rm{SSC}}}}{\rm{(1s2s,}}{}^{\rm{1}}{\rm{S}}) = - 2{E_{{\rm{D2}}}}{\rm{(1s2s,}}{}^{\rm{1}}{\rm{S}}) \\ =& \frac{{ - 2\alpha _{{\rm{1s}}}^{\rm{3}}\alpha _{2s}^3(4\alpha _{{\rm{1s}}}^{\rm{2}} - {\alpha _{{\rm{1s}}}}{\alpha _{{\rm{2s}}}} + \alpha _{{\rm{2s}}}^{\rm{2}})}}{{{{(2{\alpha _{{\rm{1s}}}} + {\alpha _{{\rm{2s}}}})}^5}}}{\alpha ^2}\end{split} \tag{21c},$
${E_{{\rm{OO}}}}{\rm{(1s2s,}}{}^{\rm{1}}{\rm{S}}) = 0.\tag{21d}$
将非相对论能量计算时得到的变分参数代入以上的解析式中, 即可得到各相对论修正项的能量值. 表3—表8分别给出了基态1s2 (1S)和激发态1sns (1,3S, n = 2—5), 1snp (1,3P, n = 2—5), 2snp (1P, n = 2—5)的相对论性能量. 需要说明的是, 因为双电子原子单重态的两个电子自旋方向相反, 所以双体达尔文修正和自旋-自旋接触相互作用修正项对应的相对论能量为零; 1sns组态两电子轨道量子数相同, 轨道-轨道相互作用项的贡献为零.
u${\alpha _{1{\rm{s}}}}$ENREMCED1ΔERSET
017.6875?312.848?6.514885.30399?1.21089?314.05889
0.117.6871?309.263?6.514255.30360?1.21065?310.47365
0.217.6858?305.708?6.512385.30246?1.20992?306.91792
0.317.6837?302.184?6.509295.30057?1.20872?303.39272
0.417.6808?298.688?6.505015.29796?1.20705?299.89505
0.517.6771?295.222?6.499575.29463?1.20494?296.42694
0.617.6726?291.785?6.492995.29061?1.20238?292.98738
0.717.6674?288.377?6.485305.28591?1.19939?289.57639
0.817.6614?284.997?6.476525.28055?1.19597?286.19297
0.917.6547?281.645?6.466685.27453?1.19215?282.83715
1.017.6473?278.32?6.455805.26787?1.18793?279.50793


表3Ar16+基态1s2 1S相对论性能量(单位: a.u.)
Table3.Relativistic correction on ground state 1s2 1S energies level in Ar16+ (unit: a.u.).

u${\alpha _{2{\rm{s}}}}$${\alpha _{2{\rm{p}}}}$ENREMCED1ED2ESSCEOOΔERSET
017.411317.8229?77.6010?0.594990.31621?8.39310 × 10?41.67862 × 10?3?0.0006009?0.27854?77.87954
0.117.404317.8174?74.0566?0.594060.31583?8.38360 × 10?41.67672 × 10?3?6.00393 × 10?4?0.27800?74.33460
0.217.383917.8014?70.6207?0.591390.31472?8.35602 × 10?41.67120 × 10?3?5.98927 × 10?4?0.27644?70.89714
0.317.35117.7755?67.2898?0.587110.31294?8.31163 × 10?41.66233 × 10?3?5.96551 × 10?4?0.27393?67.56373
0.417.306417.7402?64.0605?0.581320.31053?8.25157 × 10?41.65031 × 10?3?5.93313 × 10?4?0.27055?64.33105
0.517.250817.6959?60.9298?0.574150.30754?8.17686 × 10?41.63537 × 10?3?5.89259 × 10?4?0.26637?61.19617
0.617.184517.6429?57.8948?0.565690.30401?8.08845 × 10?41.61769 × 10?3?5.84432 × 10?4?0.26146?58.15626
0.717.108117.5816?54.9531?0.556060.29998?7.98720 × 10?41.59744 × 10?3?5.78871 × 10?4?0.25586?55.20896
0.817.021917.5122?52.1022?0.545340.29546?7.87391 × 10?41.57478 × 10?3?5.72611 × 10?4?0.24966?52.35186
0.916.926217.4349?49.3398?0.533610.29051?7.74933 × 10?41.54987 × 10?3?5.65688 × 10?4?0.24289?49.58269
1.016.821317.3499?46.6639?0.520980.28514?7.61414 × 10?41.52283 × 10?3?5.58134 × 10?4?0.23563?46.89953


表8Ar16+基态2s2p 1P相对论性能量(单位: a.u.)
Table8.Relativistic correction on excited state 2s2p 1P energies level in Ar16+ (unit: a.u.).

从表3—表8可以看出, 电荷亏损$\delta = |Z - {\alpha _{n\ell }}|$随着等离子体参数u增大而增大, 这表明等离子体对电子轨道的屏蔽作用越来越明显, 这将导致非相对论能级向高能端移动. 图1给出了不同电子组态的相对论修正项能量与等离子体屏蔽参数的关系. 从图中可以看出, 各相对论修正项的能量值对电子组态具有较强的依赖性, 而对等离子体屏蔽参数的依赖性较弱. 如基态1s2的质量修正能量值在u = 0时为?6.51488 a.u.; 当u = 1时, 其值为?6.45580 a.u., 相差仅为0.9%. 而激发态2s2p的质量修正能量值在u = 0时为?0.59499 a.u.; 当u = 1时, 其值为?0.52098, 相差约为14%. 此外, 我们发现, 在各相对论修正项中质量修正值和第一类达尔文修正值占主导, 其数值比双体达尔文修正项、自旋-自旋接触相互作用修正项和轨道-轨道相互作用修正项高3个量级.
u${\alpha _{1{\rm{s}}}}$${\alpha _{2{\rm{s}}}}$ENREMCED1ED2ESSCΔERSET
017.932417.3433?198.384?3.930943.07620?7.249983 × 10?31.450003 × 10?2?0.84749?199.23149
0.117.931917.3364?194.822?3.929823.07562?7.245793 × 10?31.44916 × 10?2?0.84695?195.66895
0.217.930617.3164?191.335?3.926573.07394?7.233613 × 10?31.44672 × 10?2?0.84540?192.18040
0.317.928517.284?187.921?3.921303.07121?7.213953 × 10?31.44279 × 10?2?0.84288?188.76388
0.417.925617.2401?184.577?3.914153.06749?7.187233 × 10?31.43745 × 10?2?0.83947?185.41647
0.517.921817.1852?181.301?3.905223.06284?7.153833 × 10?31.43077 × 10?2?0.83523?182.13623
0.617.917317.1198?178.092?3.894623.05729?7.114063 × 10?31.42281 × 10?2?0.83022?178.92222
0.717.91217.0445?174.947?3.882453.05090?7.068203 × 10?31.41364 × 10?2?0.82448?175.77148
0.817.90616.9594?171.866?3.868803.04371?7.016463 × 10?31.40329 × 10?2?0.81807?172.68407
0.917.899216.865?168.847?3.853773.03575?6.959053 × 10?31.39181 × 10?2?0.81106?169.65806
1.017.891816.7615?165.889?3.837453.02706?6.896133 × 10?31.37923 × 10?2?0.80349?166.69249


表4Ar16+激发态1s2s 1S相对论性能量(单位: a.u.)
Table4.Relativistic correction on excited state 1s2s 1S energies level in Ar16+ (unit: a.u.).

u${\alpha _{1{\rm{s}}}}$${\alpha _{2{\rm{s}}}}$ENREMCED1ΔERSET
018.013717.1931?199.196?3.977033.10590?0.87113?200.06713
0.118.013317.1858?195.635?3.975943.10534?0.87060?196.50560
0.218.012217.1646?192.149?3.972763.10370?0.86906?193.01806
0.318.010417.1305?188.735?3.967613.10104?0.86657?189.60157
0.418.007817.0841?185.392?3.960623.09742?0.86320?186.25520
0.518.004617.0263?182.119?3.951893.09289?0.85900?182.97800
0.618.000616.9574?178.912?3.941523.08748?0.85404?179.76604
0.717.99616.878?175.77?3.929623.08124?0.84838?176.61838
0.817.990716.7885?172.692?3.916273.07421?0.84206?173.53406
0.917.984716.6891?169.676?3.901563.06643?0.83513?170.51113
1.017.978116.5803?166.721?3.885573.05792?0.82765?167.54865


表5Ar16+激发态1s2s 3S相对论性能量(单位: a.u.)
Table5.Relativistic correction on excited state 1s2s 3S energies level in Ar16+ (unit: a.u.).

u${\alpha _{1{\rm{s}}}}$${\alpha _{2{\rm{p}}}}$ENREMCED1ED2ESSCEOOΔERSET
018.010716.9176?197.969?3.581672.80005?2.073823 × 10?34.147643 × 10?3?0.0064010?0.78595?198.75495
0.118.010316.9115?194.403?3.581232.79986?2.071283 × 10?34.142563 × 10?3?6.394563 × 10?3?0.78569?195.18869
0.218.009116.8936?190.903?3.579942.79929?2.063883 × 10?34.127763 × 10?3?6.375753 × 10?3?0.78496?191.68796
0.318.00716.8646?187.467?3.577822.79834?2.051933 × 10?34.103873 × 10?3?6.345353 × 10?3?0.78377?188.25077
0.418.004216.8251?184.094?3.574902.79703?2.035733 × 10?34.071453 × 10?3?6.304033 × 10?3?0.78214?184.87614
0.518.000716.7755?180.783?3.571212.79536?2.015513 × 10?34.031023 × 10?3?6.252373 × 10?3?0.78009?181.56309
0.617.996316.7162?177.532?3.566772.79335?1.991533 × 10?33.983063 × 10?3?6.190923 × 10?3?0.77762?178.30962
0.717.991316.6477?174.339?3.561612.79099?1.963993 × 10?33.927983 × 10?3?6.120133 × 10?3?0.77478?175.11378
0.817.985516.57?171.203?3.555742.78830?1.933093 × 10?33.866193 × 10?3?6.040453 × 10?3?0.77155?171.97455
0.917.97916.4835?168.124?3.549192.78527?1.899033 × 10?33.798063 × 10?3?5.952253 × 10?3?0.76797?168.89197
1.017.971816.3883?165.101?3.541982.78193?1.861983 × 10?33.723953 × 10?3?5.855883 × 10?3?0.76404?165.86504


表6Ar16+激发态1s2p 1P相对论性能量(单位: a.u.)
Table6.Relativistic correction on excited state 1s2p 1P energies level in Ar16+ (unit: a.u.).

u${\alpha _{1{\rm{s}}}}$${\alpha _{2{\rm{p}}}}$ENREMCED1EOOΔERSET
017.957717.266?198.504?3.547362.775396.7643 × 10?3?0.76521?199.26921
0.117.957317.26?194.937?3.546942.775226.75783 × 10?3?0.76496?195.70196
0.217.956217.2424?191.436?3.545712.774696.738923 × 10?3?0.76428?192.20028
0.317.954317.2138?187.998?3.543692.773816.70833 × 10?3?0.76317?188.76117
0.417.951717.1749?184.622?3.540912.772606.66673 × 10?3?0.76164?185.38364
0.517.948317.1261?181.306?3.537392.771066.61473 × 10?3?0.75972?182.06572
0.617.944317.0678?178.05?3.533152.769196.55273 × 10?3?0.75741?178.80741
0.717.939617.0002?174.852?3.528222.767006.48123 × 10?3?0.75474?175.60674
0.817.934216.9237?171.71?3.522622.764506.40083 × 10?3?0.75172?172.46172
0.917.928116.8384?168.624?3.5163702.761706.31163 × 10?3?0.74836?169.37236
1.017.921416.7445?165.593?3.5094902.758596.21423 × 10?3?0.74469?166.33769


表7Ar16+基态1s2p 3P相对论性能量(单位: a.u.)
Table7.Relativistic correction on excited state 1s2p 3P energies level in Ar16+ (unit: a.u.).

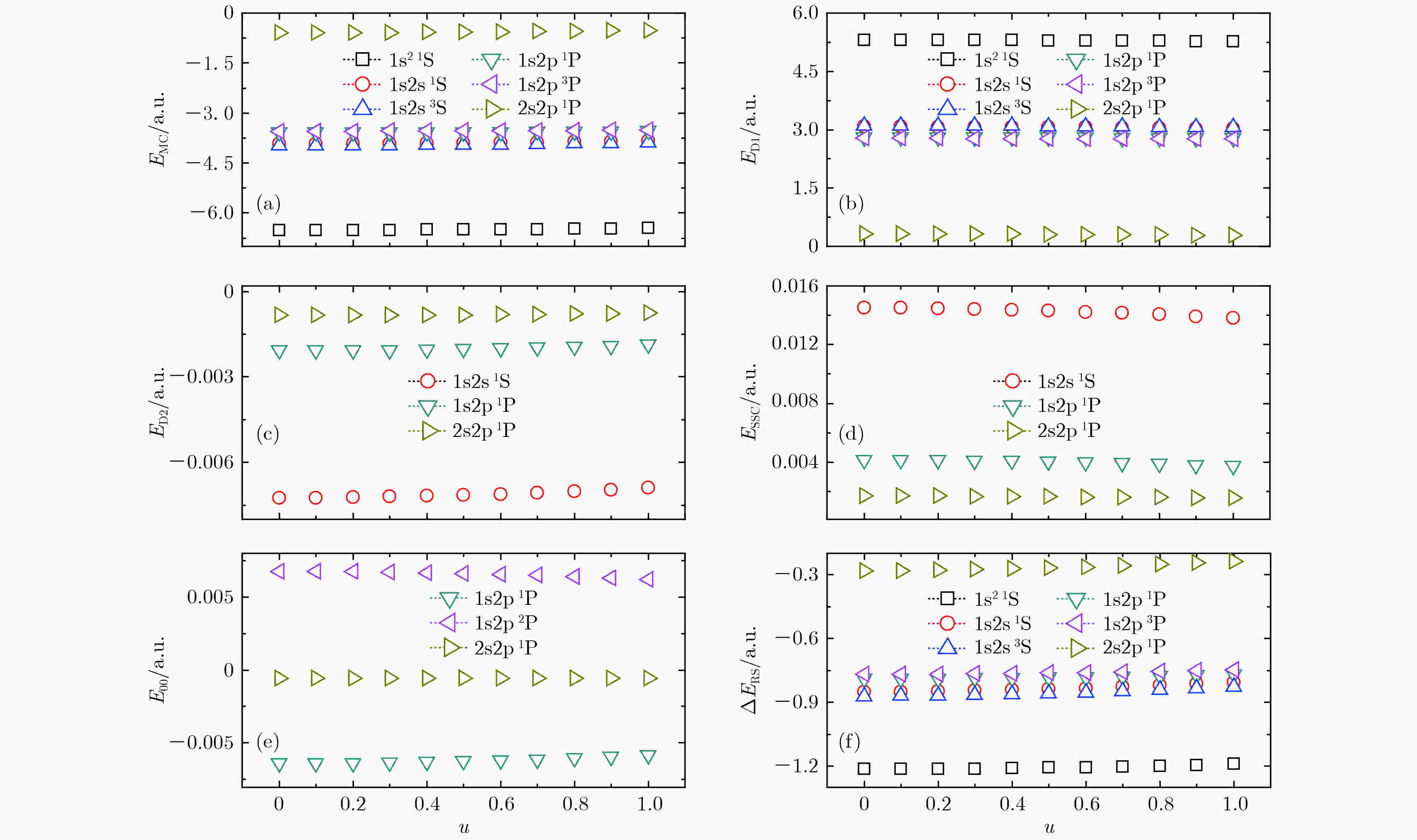图 1 A16+ 1s2 1S, 1s2s 1,3S, 1s2p 1,3P和2s2p 1P 的相对论修正能量随参数u的变化
Figure1. Relativistic corrections against parameter u for 1s2 1S, 1s2s 1,3S, 1s2p 1,3P and 2s2p 1P of Ar16+.

等离子体效应导致的原子能级移动是反映等离子体内部性质的重要参量. 通过计算, 我们发现等离子体环境导致电荷亏损减小, 即核外电子感受到的原子核的影响减弱, 能级位置发生偏移. 此外我们发现, 由等离子效应导致的非相对论能量偏移量大于相对论修正部分的偏移量. 图2以单激发态1sns 和双激发态2s2p的单重态为例, 分别给出了等离子体效应产生的总能量(非相对论能量+相对论修正能量)偏移与等离子体屏蔽参数之间的关系, 其中纵坐标${\rm{\delta }}E = E(u) - E(u = 0)$. 可以看出, 等离子体屏蔽效应导致能级向高能移动, 且随着屏蔽参数的增加, 能移值越大. 这主要由于参数u越大, 等离子体对原子核的屏蔽越明显, 核外电子感受到原子核的吸引势减弱, 从而导致能级向高能移动. 此外, 随着激发态的增高, 核外电子的距离原子核越远, 等离子屏蔽效应对其影响也越小, 三重态也具有类似规律, 图中没有给出.
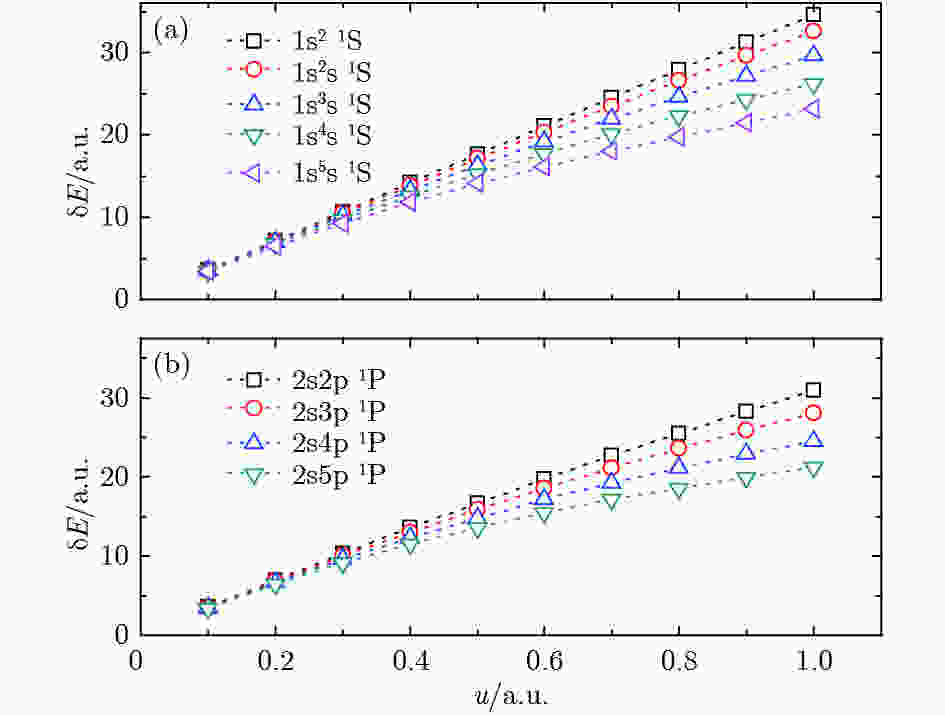图 2 等离子能级偏移与参数u之间的关系
Figure2. Plasma energy shifts against parameter u.

2
3.3.等离子效应对波函数的影响
-->

3.3.等离子效应对波函数的影响

由于等离子屏蔽效应改变核外电子感受到原子核的势场, 从而导致核外电子的波函数形状发生改变, 并进一步导致原子能级位置、跃迁谱线以及碰撞动力学参数的改变. 下面我们将借助(6)式和变分参数的数值展示等离子体屏蔽对不同原子态电子轨道波函数的影响. 图3分别给出了屏蔽参数u = 0, 0.5和1时, 1sns单重态s轨道径向波函数模方. 图3(a)和图3(b)分别给出了基态1s2和激发态1s4s单重态内壳层1s轨道径向波函数模方|R1s|2. 可以看到, 基态1s2和高激发态1s4s内壳层1s电子轨道的波函数几乎一样, 且等离子体屏蔽效应对其影响可以忽略不计; 图3(c)和图3(d)分别给出了1s2s 1S, 1s4s 1S单重态外壳层2s和4s轨道径向波函数模方|R2s|2和|R4s|2. 可以看到, 屏蔽参数越大, 电子轨道越往外侧延展, 且4s轨道比2s轨道延展的明显. 这表明等离子体屏蔽效应使得原子外壳层电子远离原子核, 且激发态越高, 电子轨道感受到等离子体屏蔽效应越明显.
图 3 内外壳层电子径向波函数模方
Figure3. Module of radial wave functions for inner and outer shell electron.

4.结　论
基于Rayleigh-Ritz变分法, 我们发展了一套计算等离子体环境中原子或离子非相对论能量及其相对论能量的计算程序, 该方法可以逐项解析的给出质量修正、第一类和第二类达尔文修正、自旋-自旋接触相互作用以及轨道-轨道相互作用等相对论修正项, 且便于推广到任意多电子原子体系. 为充分考虑了内外壳层电子所感受到不同的屏蔽效应以及电子之间的交换效应, 本文在实际计算时内外壳层电子采用了不同的屏蔽参数, 且原子态波函数采取了Hartree-Fock反对称化性质. 通过对等离子体环境中的C4+基态非相对论能量及其相对论修正能量进行的计算, 验证了程序和计算方法的正确性. 利用该程序进一步系统计算了弱耦合等离子体环境下Ar16+基态1s2和激发态1sns, 1snp, 2snp的非相对论能量及其相对论修正能量, 计算结果表明等离子体屏蔽改变核外电子的势场, 导致外壳层电子轨道向外延展, 且电子轨道越高, 感受到等离子体屏蔽效应越明显. 此外, 计算表明等离子体屏蔽效应对非相对论能量影响较大, 对相对论修正部分的能量影响较小.
相关话题/电子 计算 环境 质量 相对论
  • 领限时大额优惠券,享本站正版考研考试资料!
    大额优惠券
    优惠券领取后72小时内有效，10万种最新考研考试考证类电子打印资料任你选。涵盖全国500余所院校考研专业课、200多种职业资格考试、1100多种经典教材，产品类型包含电子书、题库、全套资料以及视频，无论您是考研复习、考证刷题，还是考前冲刺等，不同类型的产品可满足您学习上的不同需求。 ...
    考试优惠券 本站小编 Free壹佰分学习网 2022-09-19
  • 二维应变作用下超导薄膜LiFeAs的磁性和电子性质
    摘要:基于密度泛函理论的第一性原理计算,研究了二维应变作用下LiFeAs超导薄膜的磁性结构、电子能带和态密度变化,分析了应变对其超导电性的作用.结果显示,对体系施加1%—6%的二维平面张、压应变均不改变其基态条形反铁磁性结构,费米面附近的电子态密度主要来自于Fe-3d轨道电子以及少量的As-4p电子 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 太赫兹量子级联激光器中有源区上激发态电子向高能级泄漏的研究
    摘要:利用热力学统计理论和激光器输出特性理论,建立了太赫兹量子级联激光器(THzQCL)有源区中上激发态电子往更高能级电子态泄漏的计算模型,以输出功率度量电子泄漏程度研究分析了晶格温度和量子阱势垒高度对电子泄漏的影响.数值仿真结果表明,晶格温度上升会加剧电子泄漏,并且电子从上激发态泄漏到束缚态的数量 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 硼或氮掺杂的锯齿型石墨烯纳米带的非共线磁序与电子输运性质
    摘要:基于非共线磁序密度泛函/非平衡格林函数方法,研究了硼或氮掺杂的锯齿型石墨烯纳米带的非共线磁序与电子透射系数.未掺杂的石墨烯纳米带的计算结果表明磁化分布主要遵循类似于Neel磁畴壁的螺旋式磁化分布.相比于未掺杂的情况,硼/氮掺杂的石墨烯纳米带的磁化分布出现了双区域的特征,即杂质原子附近的磁化较小 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 水合物研制、结构与性能及其在能源环境中的应用
    摘要:天然气水合物是与能源和环境相关的物质，可以进行甲烷等能源气体的存储和提取，也可以用于对二氧化碳等废气的封存.天然气水合物主要分为三种结构：sI，sⅡ和sH，在本文中对其稳定性、水笼类型和大小以及可俘获气体进行了论述.中子衍射技术是研究水合物的重要手段之一，有着独特的优势.如中子的穿透性可以研究 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 基于加气水滴灌的土壤环境调节机理研究
    摘要:土壤是粮食安全、水安全和更广泛的生态系统安全的基础.我国水资源贫乏，且分布不均.传统农业采用的大水漫灌方式用水量大，还会破坏土壤团粒结构，造成土壤板结、土地盐碱化等土壤退化现象.地下滴灌技术节水效果明显，水的有效利用率超过95%；但也会在一定程度上破坏土壤结构.研究表明，使用加气水滴灌不但能增 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 光子与相对论麦克斯韦分布电子散射的能谱角度谱研究
    摘要:光子与相对论麦克斯韦分布电子散射的描述及能谱角度谱计算非常复杂且费时.本文提出了一种光子与相对论麦克斯韦速度分布电子散射的蒙特卡罗（MC）模拟方法，该方法能够细致模拟高温等离子体中任意能量光子与任意温度电子的Compton和逆Compton散射问题.对于散射后光子的能谱和角度谱参数，可以根据电 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 第一性原理方法研究N-Pr共掺杂ZnO的电子结构和光学性质
    摘要:作为一种稳定性好、抗辐射能力强、原材料丰富的宽禁带半导体，ZnO在光催化的研究领域中成为热点材料，但是其仅能吸收可见光中的紫光，因此如何扩大ZnO对可见光的响应范围是一个值得研究的问题.掺杂改性是解决这个问题的常用方法.基于以上考量，本文应用第一性原理计算方法研究了N与Pr掺杂对ZnO的电子结 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • Na<sub>2</sub><sup>+</sup>离子较低电子态势能曲线和光谱常数的理论研究
    摘要:通过多组态相互作用方法，结合原子有效芯势与极化势，利用非收缩的高斯基函数，计算了Na2+分子对应最低9个解离限的36个电子态的势能曲线.基于计算获得的束缚态势能曲线，拟合给出了相应的光谱常数，并与已有的实验和理论结果进行了比较.同时，给出了部分电子态的振动-转动能级和一些同类态避免交叉点的信息 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • (Cu,N)共掺杂TiO<sub>2</sub>/MoS<sub>2</sub>异质结的电子和光学性能:杂化泛函HSE06
    摘要:在密度泛函理论的基础上，系统地研究了Cu/N（共）掺杂的TiO2/MoS2异质结体系的几何结构、电子结构和光学性质.计算发现，TiO2/MoS2异质结的带隙相比于纯的TiO2（101）表面明显变小，Cu/N（共）掺杂TiO2/MoS2异质结体系的禁带宽度也明显地减小，这导致光子激发能量的降低和 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 外场作用下C12H4Cl4O2的分子结构和电子光谱研究
    摘要:各种环境毒物危害着人类的生产生活，二噁英更是严重危害人类的健康.C12H4Cl4O2（2，3，7，8-tetrachlorodibenzo-p-dioxin，TCDD）是二噁英中毒性最强的化合物，也是目前已知毒性最强的污染物.为研究TCDD外场效应，采用密度泛函理论方法优化了不同静电场00.0 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29

Free考研考试FreeKaoYan.Com
欢迎来到Free考研考试，"为实现人生的Free而奋斗"

© 2020 FreeKaoYan! . All rights reserved.