摘要: 基于量子理论获取相位参数的导航机制, 理论上可以突破经典物理极限对导航精度的限制. 利用量子零拍探测对相干态光场相位进行测量时, 通常需要相位与之正交的本振光才能使测量精度达到量子标准极限. 由于导航信号相位的高非线性特点, 想要利用传统的线性锁相环获取完全满足条件的本振光具有一定的难度. 为此, 本文设计了一种基于容积准则的非线性锁相环, 实现了在非正交本振光的条件下对相干态相位进行精确测量的功能. 首先, 利用相干态的Wigner函数推导了其相位在量子零拍探测的输出结果, 设计了量子相位估计的非线性数字锁相环框架. 然后基于正交单纯形容积准则设计了非线性滤波算法实现锁相环功能, 该锁相环通过对本振相位进行多次状态更新, 最终实现非线性迭代估计. 实验结果表明, 本文方法突破了本振光相位需与相干态相位正交的局限性, 避免了传统量子锁相环方法引入的线性化误差, 实现了对相干态相位的准确、稳定估计.
关键词: 相干态相位估计 /
量子零拍探测 /
非线性锁相环 /
正交单纯形容积卡尔曼滤波 English Abstract Coherent state phase estimation based on digital nonlinear phase-locked loop Xu Han Chen Shu-Xin Wu Hao Chen Kun Hong Lei Information and Navigation College, Air Force Engineering University, Xi'an 710077, China Fund Project: Project supported by the Young Scientists Fund of the National Natural Science Foundation of China (Grant No. 61703420) and the National Natural Science Foundation of China (Grant No. 61673392).Received Date: 28 August 2018Accepted Date: 29 September 2018Available Online: 01 January 2019Published Online: 20 January 2019Abstract: The navigation mechanism of obtaining phase parameters based on quantum theory can break through the limitation of classical physical limit to navigation accuracy. In order to achieve the accurate estimation of the coherent state phase, it is usually assumed that the local oscillator phase must be orthogonal to the coherent state phase in the method of quantum homodyne detection. However, the coherent state phase is unknown and the hypothesis cannot be guaranteed to be correct in practice. In this paper we design a nonlinear phase-locked loop to solve the problem. Firstly, in order to obtain the Wigner distribution for a coherent state, we start with the Wigner distribution for the vacuum state and analyze the noise characteristics according to Wigner distribution of coherent state, then the output of homodyne detection is derived. Secondly, in order to avoid introducing errors in theory, caused by linearization and cope with the limiting requirement between local oscillator phase and coherent state phase in the phase tracking of coherent state, we design an orthogonal simplex cubature Kalman filter (OSCKF) algorithm to achieve the function of the nonlinear phase-locked loop. The algorithm converges by updating the state of the local oscillator phase multiple times, and then, the accurate coherent phase is obtained. Finally, according to the design of the phase-locked loop, we observe the data of homodyne detection and then verify the correctness of the OSCKF algorithm. The simulation results show that the OSCKF can converge to the real phase after observing 200 sampled data and the accuracy is higher than extended Kalmn filter (EKF) and cubature Kalman filter (CKF), and the real phase can be obtained under different local oscillator phase. In conclusion, the nonlinear phase-locked loop based on OSCKF algorithm breaks the limitation of traditional way in which the initial local oscillator phase is required to be orthogonal to the coherent state phase, and effectively avoid the linearization error and improve the anti-nonlinear ability. It is very significant in theory and application .Keywords: coherent state phase estimation /quantum homodyne detection /nonlinear phase-locked loop /orthogonal simplex cubature Kalman filter 全文HTML --> --> --> 1.引 言 相位估计是导航控制、图像处理、大气波导、混沌通信等领域的关键问题之一[1 ?4 ] . 例如, 在测角定位系统中, 对相位信息估计的精确度直接决定了波达角等参数获取的精度. 然而, 经典相位的精度在理论上有不可逾越的界限, 成为制约各类参数获取精度的瓶颈.[5 ?7 ] . 目前, 已有研究通常是将相干态通过量子零拍探测器, 并建立基于相干态光场强度与其相位相关统计量的函数关系来进行相位估计[8 ,9 ] , 这能够有效提高相位估计精度[10 ,11 ] . Wiseman[12 ] 提出量子反馈测量方案, 即对量子零拍探测器的本振相位进行反馈控制, 从而实现近似正则测量, 并得到了验证[13 ] . 随后, Berry等[14 ] 提出了相干态光场和压缩态光场连续变化相位的自适应测量跟踪方法, 证明了在相位跟踪中反馈测量优于非反馈测量. Tsang等[15 ] 设计了自适应零拍线性锁相环对实时相位和瞬时频率进行测量, 并且在此基础上将非线性方程进行一阶泰勒展开, 利用卡尔曼-布什滤波实现了相位的实时跟踪[16 ,17 ] . 上述方法均是在本振光相位与待测光场相位正交的前提下能够达到标准量子极限, 如果信号为相位压缩态光场, 其相位测试精度能够突破标准量子极限. 然而对于导航信号来说, 相干态相位是未知的, 即使利用自适应锁相环对本振相位进行调整, 也并不能保证本振相位与相干态相位完全正交, 因此利用上述方法进行线性化处理时, 虽然能简化相位估计过程, 但也会不可避免地引入线性化误差, 并且在调整本振相位时带来了时延, 难以保证波达角等参数的实时获取, 这对于导航系统来说显然不合理.[18 ,19 ] 的非线性滤波算法. 在标准容积准则的基础上, 利用正则单纯形[20 ] 来构建容积公式, 提高后验密度的数值积分精度; 然后根据考虑非线性对滤波的影响, 进一步利用正交矩阵将单纯形容积点进行变换, 调整非线性高阶项的影响, 从而避免局部采样效应, 得到正交单纯形容积卡尔曼滤波(OSCKF). 一方面, 上述方法避免了因本振光相位与信号相位无法完全正交引起的误差, 更易于处理且稳定性更好; 另一方面, OSCKF能够有效避免各类误差, 提高量子相位估计精度.2.非线性量子锁相环设计 22.1.量子零拍测相 2.1.量子零拍测相 本文利用Wigner函数推导相干态相位在量子零拍探测的输出模型. 为了得到相干态的Wigner函数, 先分析真空态的Wigner函数. 定义正交分量场$x \equiv \dfrac{1}{2}\left( {a + {a^ + }} \right)$ , $y \equiv \dfrac{1}{{2{\rm{i}}}}\left( {a - {a^ + }} \right)$ , 式中, $a$ 与${a^ + }$ 分别是光子湮灭算符与光子产生算符. 由不确定度原理知, $x$ 和$y$ 的标准偏差满足$\Delta x\Delta y \geqslant \displaystyle\frac{1}{4}$ .${x_0}$ 和${y_0}$ , 则其Wigner函数可表示为1 )式可以看出, ${x_0}$ 和${y_0}$ 的方差均为$\dfrac{1}{4}$ , 标准偏差$\Delta {x_0}\Delta {y_0} = \dfrac{1}{4}$ , 可见真空态是最小不确定度态. 具有平均相位$\phi $ 的相干态$\left| \alpha \right\rangle $ 在相空间中可通过沿相位调制${x_0}$ 方向平移真空态得到, 其Wigner函数具体可以写为:$\eta = \dfrac{1}{2}\left( {{\rm{e}}^{ - {\rm{i}}\varphi }}a +\right.$ $ \left.{{\rm{e}}^{{\rm{i}}\varphi }}{a^ +} \right)$ , 其中$a$ 是相干态$\left| \alpha \right\rangle $ 的湮灭算符. 用正交分量可表示为$a = x + {\rm{i}}y$ , 根据(1 )式和(2 )式, 可用真空态的正交分量表示为$\eta $ 可写为${z_0} = {x_0}\cos \left( {\phi - \varphi } \right) - {y_0}\sin \left( {\phi - \varphi } \right)$ . 由(1 )式知, 真空态的正交场分量服从零均值的高斯分布, 其统计分布与相位$\phi - \varphi $ 不相关, 则${z_0}$ 的统计特性服从高斯分布.可以看出, 正是${z_0}$ 引入了不确定性, 真空波动被分离到了${z_0}$ 中. 将${z_0}$ 处理成高斯噪声, 则(6 )式变成高斯噪声环境下的参数估计问题, 经典估计技术能够很好地解决该问题. 首先将本振光的相位做${\text{π}/2}$ 偏置, 令$\varphi = {\varphi _{\rm{f}}} + \dfrac{\text{π}}{2}$ , 这里定义${\varphi _{\rm{f}}}$ 为本振相位, 则(6 )式可重写为${z_0}' = {x_0}\sin \left( {\phi - {\varphi _{\rm{f}}}} \right) + {y_0}\cos \left( {\phi - {\varphi _{\rm{f}}}} \right)$ , 与${z_0}$ 具有相同的统计特性. 之后将不再区分${z_0}$ 和${z_0}'$ , 统一记作高斯噪声${z_0}$ . 在文献[16 ,17 ]中, 对(7 )式线性化前均做了一个假设, 即7 )式进行线性近似可以得到${\varphi _{\rm{f}}}$ 与相干态相位$\phi $ 较为接近, 则该假设成立, 利用上述线性化模型进行相位估计能够得到较好的结果. 然而对于导航系统来说, 目标的位置并不确定, 也就是说难以找到相干态相位$\phi $ 的准确大小. 因此无法保证本振相位${\varphi _{\rm{f}}}$ 与相位$\phi $ 满足上述假设条件. 如果本振相位与相干态相位相差过大, 则会引入较大的线性化误差, 甚至导致相位估计失败.2.2.非线性数字锁相环设计 -->2.2.非线性数字锁相环设计 在量子零拍探测基础上, 本节建立非线性锁相环框架, 与传统线性锁相环不同的是, 这里采用AD变换引入非线性数据处理方法. 该锁相环能够突破传统方法中本振相位需要接近相干态相位的限制要求, 并避免线性化带来的误差, 进而实现相位的精确估计.[21 ] . 而离散化处理可以有效地减弱极端值和异常值的影响. 此外, 离散化还有利于数值计算与算法迭代, 增强了物理可实现性.图1 所示. 由真空态进行平移和相位调制得到相干态, 其中${ D}(\left| \alpha \right|)$ 表示位移算符, $\exp ({\rm{i}} \phi )$ 表示相位调制, 然后将相干态通过初始本振相位为$\varphi $ 的量子零拍探测器得到输出$\eta $ , 接着进行AD采样, 将所得数据送入数据处理模块(SP)中, 在数据处理后将更新的本振相位反馈给量子零拍探测器, 再重复此过程, 最终能够得到更为精确的估计结果.图 1 数字零拍锁相环Figure1. Digital homodyne phase-lock loop.3.基于正交单纯形容积准则的量子相位估计算法 得到数字零拍锁相环框架后, 问题就转化为将零拍数据离散化, 进而利用SP模块实现相干态相位估计. 对于离散非线性估计问题, 通常将非线性模型线性化, 并采用扩展卡尔曼滤波(EKF), 然而从(9 )式可知, 量测模型是三角函数, 其非线性程度较高, 因此采用EKF会违背局部线性假设, 从而造成较大的线性化误差, 甚至导致滤波发散. 为此, 这里引入正交单纯形容积卡尔曼滤波(OSCKF)方法, 利用正交单纯形三阶球面径向容积准则, 计算相位信息对应的后验密度, 从而在不进行非线性模型泰勒展开、不引入线性化误差的前提下实现对相位$\phi $ 的精确实时估计.3.1.系统模型和容积卡尔曼滤波框架 3.1.系统模型和容积卡尔曼滤波框架 在SP模块中, 分别建立状态方程和量测方程为${{ \phi} _k}$ 为$k$ 时刻的相位信息, 状态转移矩阵${F} = 1$ , 这里假定不含过程噪声, 即${{ v}_k} = 0$ . 量测方程中, ${\eta _k}$ 是$k$ 时刻量子零拍探测的量测值$h\left( {{{ \phi} _k}} \right) = \left| \alpha \right|\sin \left( {{{ \phi} _k} - {\varphi _{\rm{f}}}} \right)$ , ${w_k}$ 为量测噪声, 服从均值为零的高斯白噪声.[22 ] . 其容积点可表示为${\xi _j} = \sqrt {{n_\phi }} {\left[ {\begin{array}{*{20}{c}} {{{I}_{{n_\phi }}}}&{- {{I}_{{n_\phi }}}} \end{array}} \right]_j}$ , 其中${{I}_{{n_\phi }}}$ 为${n_\phi }$ 维单位矩阵, ${\left[ \cdot \right]_j}$ 代表矩阵$\left[ \cdot \right]$ 的第$j$ 列, $j = 1,2, \cdots ,2{n_\phi }$ . 在本问题中, 滤波过程如下.${\hat \phi _{k\left| {k - 1} \right.}}$ 和预测协方差${{P}_{k\left| {k - 1} \right.}}$ 可直接表示为:${{P}_{k\left| {k - 1} \right.}}$ 进行柯西分解${{P}_{k\left| {k - 1} \right.}} = {{S}_{k\left| {k - 1} \right.}}{S}_{k\left| {k - 1} \right.}^{\rm{T}}$ , 得到容积点${\phi _{j,\left. k \right|k - 1}}$ ${\hat {{\eta }}_{k\left| {k - 1} \right.}}$ , 信息协方差矩阵${P}_{\eta \eta ,\left. k \right|k - 1}^{}$ , 互协方差矩阵${{P}_{\phi \eta ,\left. k \right|k - 1}}$ 和卡尔曼增益${K_k}$ ,3.2.正交单纯形容积卡尔曼滤波 -->3.2.正交单纯形容积卡尔曼滤波 考虑${n_\phi }$ 维正则单纯形, 可建立三阶球面单纯形容积准则[22 ] , 其容积点可表示为${{\alpha }_j} \!=\! {\left(\! {{\alpha _{j,1}},{\alpha _{j,2}}, \!\ldots \!,{\alpha _{j,{n_\phi }}}} \!\right)^{\rm{T}}}$ ($j \!=\! 1,2, \cdots ,$ $ {n_\phi } \!+\! 1$ ), 其中[23 ] , 进而影响滤波精度.${A}$ 为正交矩阵, 则将容积采样点进行正交变换后, 其仍然符合数值积分公式. 也就是说, 可以利用正交变换来调节高阶项对滤波的影响. 于是问题就转化为构建合适的正交矩阵, 使得变换后的单纯形容积点能够有效降低高阶干扰项对滤波的影响.${n_\phi } \times {n_\phi }$ 正交矩阵${B} = \left[ {{{B}_1},{{B}_2}, \cdots ,{{B}_{{n_\phi }}}} \right]$ , ${{B}_j} = {\left( {{\beta _{j,1}},{\beta _{j,2}}, \cdots ,{\beta _{j,{n_\phi }}}} \right)^{\rm T}}$ , 其中$r = 1,2, \cdots ,\max \left\{ {p \in \mathbb{Z}|p \leqslant {n_\phi }/2} \right\}$ , 如果${n_\phi }$ 为奇数, 则${\beta _{j,{n_\phi }}} = {\left( { - 1} \right)^j}/\sqrt {{n_\phi }} $ .${B}$ 进行变换, 得到正交单纯形容积点${\gamma }=\left( {{{\gamma }_1},{{\gamma }_2}, \ldots ,{{\gamma }_{2{n_\phi } + 2}}} \right)$ , ${{\alpha }_j} =\left({\alpha _{j,1}},{\alpha _{j,2}}, \cdots,\right.$ $\left.{\alpha _{j,{n_\phi }}} \right)^{\rm{T}}$ , $j = 1,2, \ldots ,2{n_\phi } + 2$ .25 )式中新的容积点及其权重代入(12 )—(21 )式中, 即可得到OSCKF算法.图1 和(12 )—(21 )式, 得到完整的基于量子相位测量的非线性锁相环结构, 如图2 所示.图 2 基于OSCKF算法的量子非线性数字锁相环Figure2. Digital quantum nonlinear phase-lock loop based on OSCKF algorithm.图2 所示, 首先输入一个本振相位, 通过OSCKF算法迭代解算出相干态相位${\phi _k}$ , 然后将本振相位设为${\phi _k}$ , 再解算相干态相位${\phi _{k + 1}}$ , 不断重复该过程, 本振相位将会逐渐逼近相干态相位, 从而实现锁相环的功能. 需要强调的是, 该方法并没有要求本振相位初始值接近相干态相位, 也能实现相干态相位的精确估计.4.实验验证与分析 由于相干态经过零拍探测后可看作是经典信号加上高斯噪声[16 ] , 且主要考察锁相环的有效性, 为此, 在实验验证过程中, 将采用直接模拟经过零拍后的经典信号, 取代构建真实物理实验平台的方法. 假设系统中相干态平均相位$\phi = {{\rm{\pi }}/3}$ , 量测噪声服从均值为0, 方差${\sigma ^2} = {10^{ - 6}}$ 的高斯分布. 则当初始本振相位$\varphi = 0$ 时, 连续对1000个采样数据进行观察, 由(9 )式可得零拍数据, 如图3 所示, 图中测量值的抖动是由于噪声即真空波动引起的.图 3 零拍数据示意图Figure3. Homodyne data schematic diagram.L 为实验仿真次数, ${\hat \phi _{i,100}}$ 为每次实验第100次迭代后的估计值. 实验结果如图4 所示.图 4 不同初始本振相位下所提方法的性能Figure4. Performance comparison of phase-locked loop in different local oscillator phase.图4 所示, 在其他条件相同的情况下, 不同初始本振相位下的相位估计结果相差并不大, 其中最高平均误差和最低平均误差只相差0.0016, 这说明所提方法的相位估计精度并没有受到初始本振相位设置的影响, 突破了传统自适应反馈量子相位测量需要保证本振相位和真实相位相差不大的限制.${\hat \phi _{k,j}}$ 为第$j$ 次仿真$k$ 次迭代的相位估计值, L 为Monte-Carlo次数.L 和每次实验迭代次数$k$ 设为100次. 令${w_k} \propto N(0,{10^6})$ , 初始协方差$P = 2$ , 本振相位$\varphi = {\rm{0}}$ . 各算法的收敛曲线如图5 所示.图 5 各算法误差收敛曲线Figure5. Convergence curve of various algorithms.图5 可以看出, 随着迭代次数的增加, 所有算法的相位估计误差都趋于收敛. 其中 EKF将非线性模型线性化, 虽然处理方式简单, 但会引入较大的线性化误差, 因此收敛速度和最终精度均低于基于容积准则的方法, 而OSCKF算法由于引入了单纯形容积准则, 且利用正交变换进一步调节了非线性对滤波的影响, 因此比传统CKF算法精度更高. 此外, 从仿真实验发现, 采用EKF进行相位估计结果容易发散, 这说明EKF方法稳定性较差. 本文所提方法稳定性相对更好, 且能更快收敛, 与EKF方法相比, 平均误差降低了60%. 此外, 本文的状态模型是线性的, 而所设计的锁相环对于高非线性状态模型, 尤其是导航中的高非线性运动状态, 有望获得更好的效果. 因此, 设计非线性数字锁相环, 并采用正交单纯形容积准则, 不仅能够突破本振相位需要接近相干态相位的限制要求, 更能有效避免线性化误差, 提高相干态相位估计精度.5.结 论 在利用量子零拍探测对相干态相位进行估计时, 对本振相位和相干态相位有严格限制要求. 如果本振相位不满足接近相干态相位的假设条件, 则非线性测量模型在进行线性化时会造成较大的误差. 针对该问题, 设计了一种数字非线性锁相环, 并提出OSCKF算法实现了锁相功能. OSCKF算法利用球面径向容积准则做数值计算近似高维积分, 可以有效避免模型线性化带来的误差, 同时减小了由于量测模型的高非线性带来的局部采样效应对精度的影响. 从仿真实验结果可以得出该锁相环算法利用不满足假设条件的本振相位也能得到相干态相位, 且数值稳定, 误差更小, 能够实现相干态相位的精确估计, 实用性更好. 下一步, 将在此锁相环精确估计的基础上, 实现对连续变化量子相位的精确跟踪, 并对噪声为非高斯的情况做进一步的研究. 








































































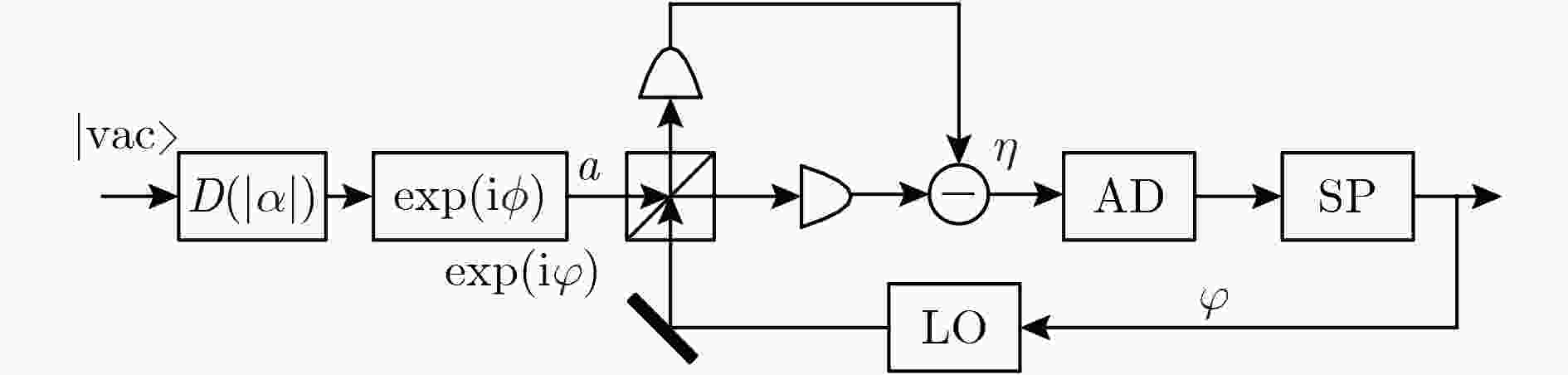 图 1 数字零拍锁相环
图 1 数字零拍锁相环










































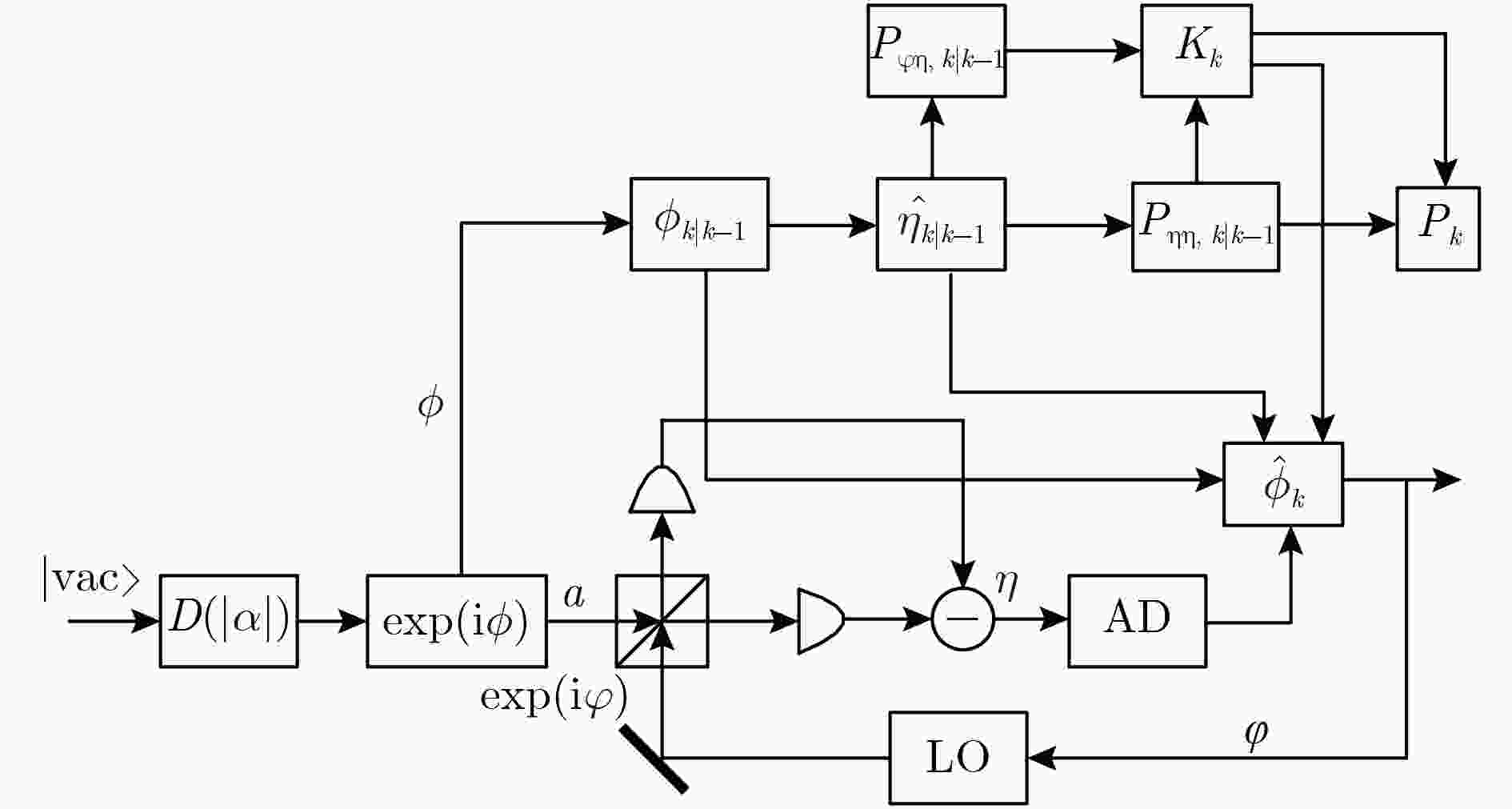 图 2 基于OSCKF算法的量子非线性数字锁相环
图 2 基于OSCKF算法的量子非线性数字锁相环







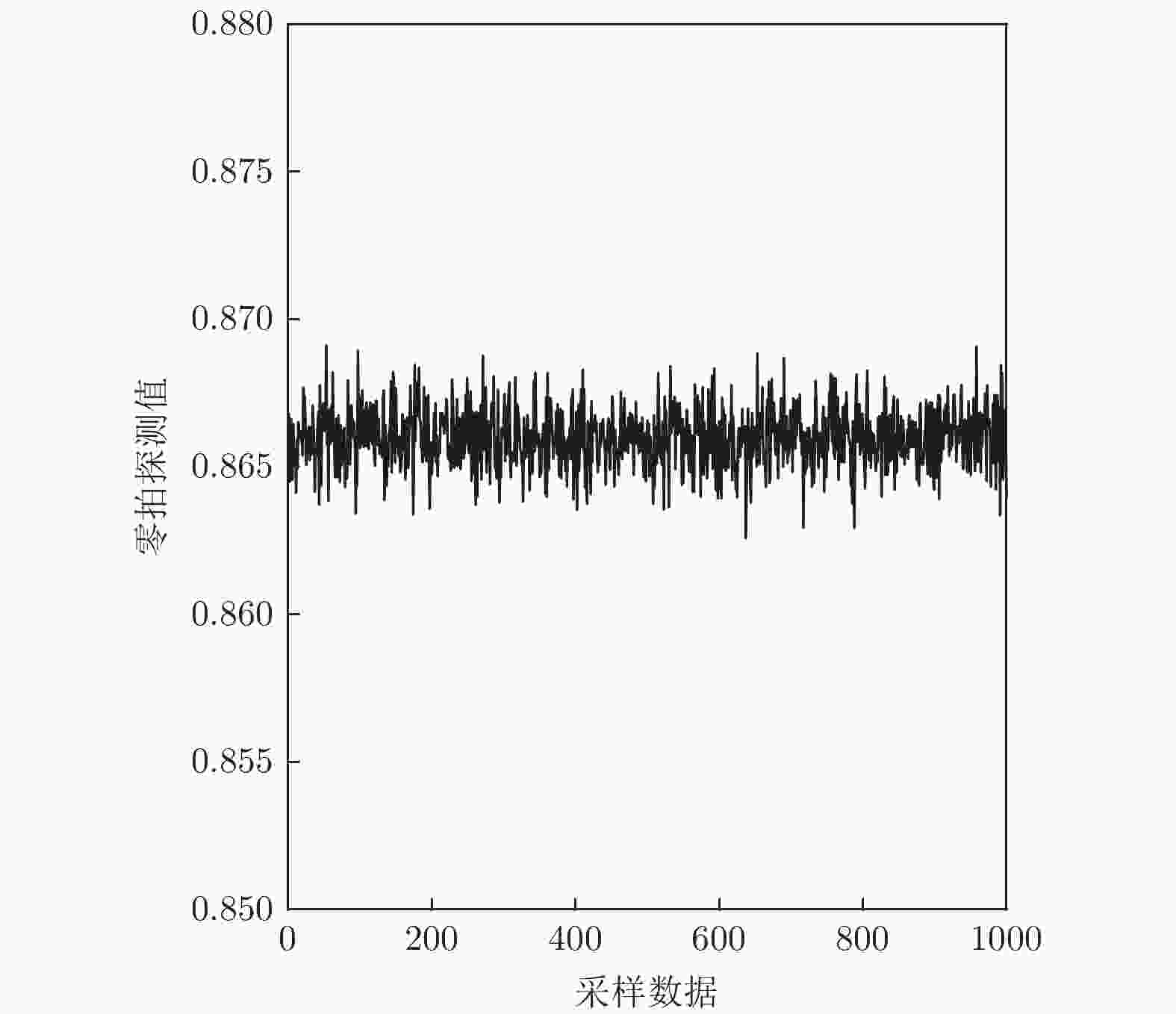 图 3 零拍数据示意图
图 3 零拍数据示意图
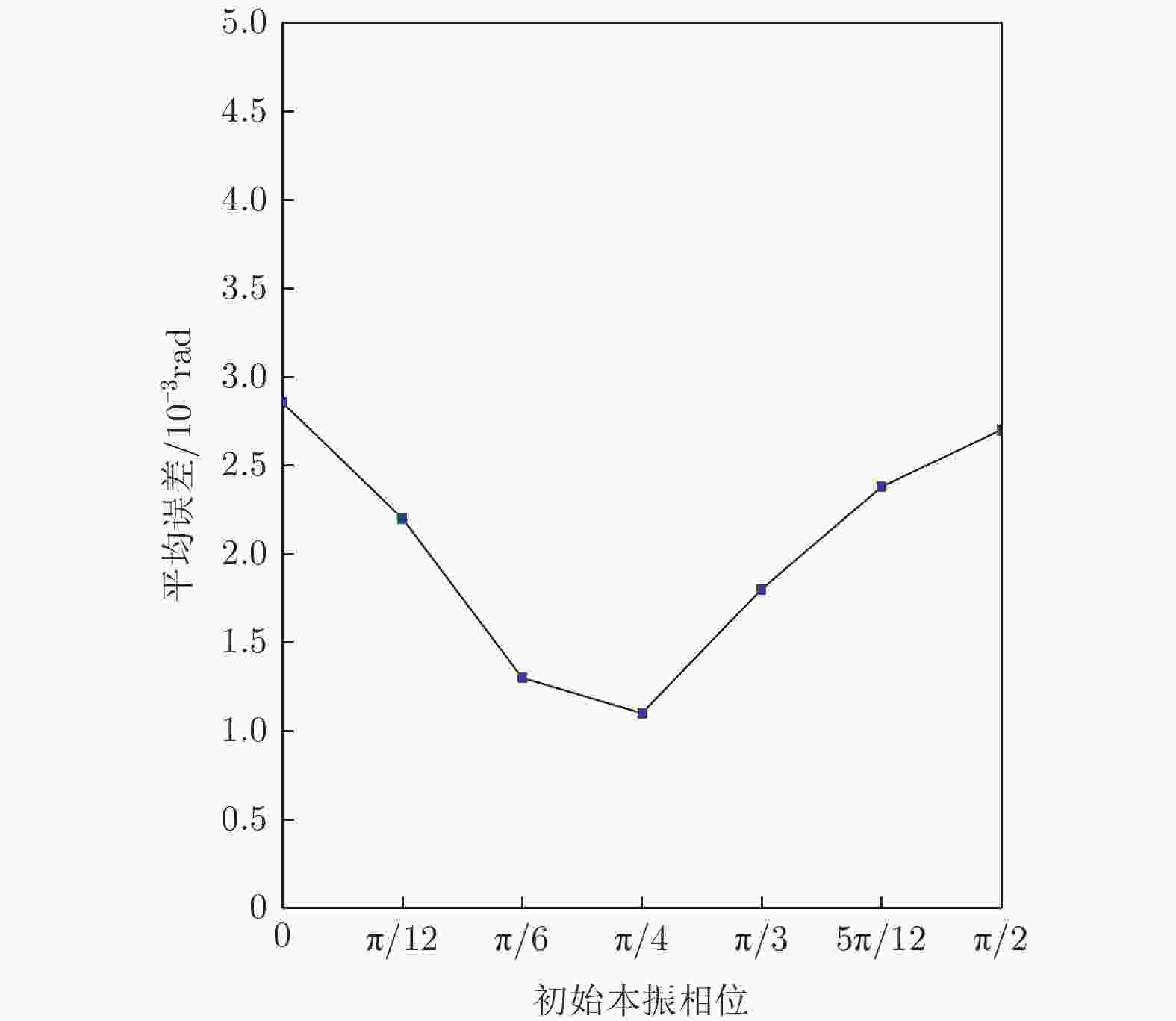 图 4 不同初始本振相位下所提方法的性能
图 4 不同初始本振相位下所提方法的性能






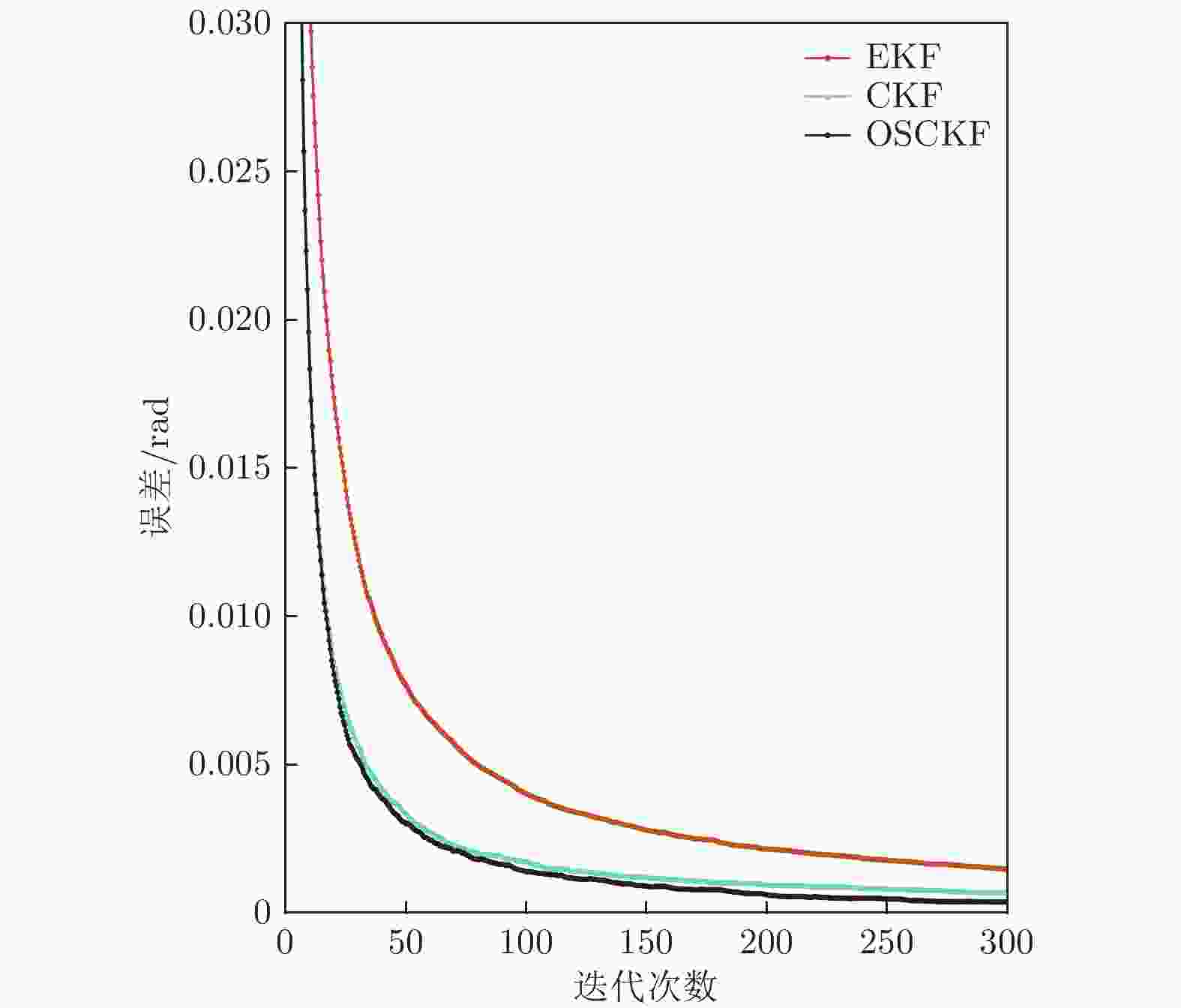 图 5 各算法误差收敛曲线
图 5 各算法误差收敛曲线