在具有强自旋-轨道耦合的半导体纳米线上覆盖超导膜引入超导态,再施加一定磁场后可以使这个体系成为一维拓扑超导体,在两端各形成一个马约拉纳零能模。如果将这个系统在电化学势上与外界隔离,引入库伦充电能,便可精确控制单电子隧穿进出这个拓扑超导系统。若系统是拓扑平庸的超导体,参与隧穿的只能是库珀对,这类器件叫做库珀对晶体管(cooper-pair transistor),它是超导量子比特的核心;如果这个系统是半导体,参与隧穿的是单电子,但是系统并没有超导性,这类器件叫做单电子晶体管(single-electron transistor)或量子点(quantum dot),它是半导体量子点自旋量子比特的核心。虽然半导体量子点中发生的也是单电子隧穿,但它并不保持量子态的相干性;而对于两端各有一个马约拉纳零能模的岛,不论它们之间有多远,电子都可以通过这一对马约拉纳零能模共同构成的准粒子态隧穿过岛并保持量子相干,称之为隐形传输(或遥距传输,teleportation,Phys. Rev. Lett. 104, 056402(2010))。这样的器件称为“马约拉纳岛”。利用岛上电子数的奇偶性可以构建拓扑量子比特的双重简并态|0>态和|1>态,是构建拓扑量子比特最基本和最核心的单元。岛上电子数奇偶性(parity)使得隐形传输的电子有一个π的相移,可以用来测量马约拉纳零能模和拓扑量子比特的量子态。同时用马约拉纳岛构成网络结构,可以利用隐形传输测量量子比特态实现编织(braiding)马约拉纳零能模的功能,避免早期编织方案——在T型结的实空间中编织马约拉纳零能模时影响拓扑保护的问题,已成为国际上广泛认可的编织方案。
拓扑超导体中的单电子隧穿来源于马约拉纳零能模的存在,反映出的拓扑超导基态的二重简并,对应岛上电子数的奇偶性(parity)在偶数态(准粒子态没有被占据,故岛上电子都是库珀对)和奇数态(准粒子态被一个电子占据)之间变化,通过测量岛上电子的奇偶性可以探索马约拉纳零能模。当然,岛上电子数的奇偶性变化也可能由于拓扑平庸的安德列耶夫束缚态引起,这时系统可以看作是超导-正常金属(半导体)复合系统。研究奇偶性随磁场和化学势的变化可以给出这个准粒子态是否是拓扑平庸还是非平庸的依据。奇偶性可以通过库伦振荡电导峰来表征,由库伦峰振荡的间距大小也可以推算出准粒子态所对应的能量。测量奇偶性的前提是在零磁场下岛上库伦振荡的周期是2倍电子电荷(2e),即以库珀对的形式隧穿过岛,说明岛上的诱导超导能隙中没有准粒子态,是硬能隙(hard superconducting gap)。在一定的平行场下,2e周期的库伦振荡会逐渐劈裂成奇偶交替,直到完全等周期的1e周期振荡,这说明有零能模的出现。这个过程称之为2e-1e的转变,转变点发生的磁场B*是零能模出现的临界点,即潜在的拓扑相出现的临界点。值得注意的是,当磁场大于超导临界磁场以后也会出现1e等周期库伦振荡,但这时候施加偏压测量电导不会有超导能隙的出现。关于复合系统的岛最有名的一篇文章是2016年哥本哈根的Marcus组的“马约拉纳岛中零能模的指数保护”(Nature 531, 206 (2016)),他们测量发现InAs-Al体系中不同长度的岛上库伦振荡间距的幅值随磁场振荡,由振荡幅值估算出准粒子态的能量,发现能量随岛长度递增而指数递减,在1微米以上趋向于零能。这个指数关系符合马约拉纳模的特征(PRB 86, 220506 (2012)),提供了电子通过马约拉纳零能模的隐形传输隧穿过岛的有力支持。但这个现象存在与马约拉纳零能模不符合的一点——库伦振荡间距的幅值随磁场减小,而马约拉纳模该增大。之后,各种理论文章应运而生,解释了实际器件中岛的不完美可以带来马约拉纳模的不同现象,比如谢心澄和卢海舟团队提出的在岛的边缘上自旋-轨道耦合的台阶状分布(Phys. Rev. Lett. 122, 147701(2019))。沈洁特聘研究员在代尔夫特做博后期间首次在InSb-Al体系的岛上研究了库伦振荡随磁场和化学势的变化,发现2e-1e的转变磁场B* 会随着化学势而变化,提供了调控奇偶性来构建拓扑量子比特的可能性;同时,也发现库伦振荡的间距随磁场振荡的行为,除了是马约拉纳零能模导致的,也可能是多个安德列耶夫束缚态的叠加效应,给出了一定程度的负面结果。以上结果发表于Nature Communication 9, 4801 (2018)。
为了区别马约拉纳零能模和安德列耶夫束缚态导致的1e周期的库伦振荡的行为,哥本哈根的Flensberg教授提出一个理论预言:由于马约拉纳零能模的粒子-空穴对称性(particle-hole symmetry),库伦振荡间距的幅值随磁场振荡时,库伦振荡电导峰的峰值大小也会随磁场振荡,并且两者有一个锁定关系——前者振荡的极值对应后者振荡的零值,反之亦然(Phys. Rev. B 97, 041411(R)(2018))。这个锁定关系对于安德列耶夫束缚态不成立。这个现象首次被哥本哈根Marcus 和Nichele团队在InAs 二维电子气和铝的复合岛中观察到(Phys. Rev. Lett. 121, 256803 (2018)),但缺乏系统的表征。沈洁特聘研究员在Nature Communication 9, 4801 (2018)中正面和负面结果的基础上全面系统地研究复合岛中所有参数可测量的区间内的库伦振荡,发现2e-1e的转变磁场B* 在可测量的范围内随门电压(化学势)的变化依赖可以分为三个区间,对比理论计算,描绘出了完整的相图。这三个区间的具体性质如下:
在正的门电压的区间(区间Ⅲ),B* 出现在很小的磁场,这个区间以前一直被认为是马约拉纳零能模出现的区间。但现在通过实验和理论对比,发现这个区间的诱导超导能隙很小,由于orbital effect等效应出现拓扑平庸的库伦振荡。
负的门电压对应的区间(区间Ⅰ)由于g因子太小,因此在失超前都很难出现1e周期的库伦振荡。
中间的转变区间(区间Ⅱ)有合适的诱导超导能隙和g因子,是最有可能出现拓扑转变的区间,在这个区间找到了库伦振荡幅值和峰值的锁定关系,这符合马约拉纳零能模的特征,但并不是完全排除其他可能性。要找到更加确切的证据,需要更长的岛、更高的超导临界磁场以及更加快速的高频测量被引入。
在该体系上电导量子化平台文章撤稿(Nature 591, E30 (2021))以后,全面而系统地客观展现参数可测量的所有区间内的数据,给出完整的相图对于研究该体系中的马约拉纳零能模而言尤其重要。该项工作历时两年多,直面复合岛器件中拓扑平庸和非平庸态共存的关键问题,给出完整的相图;并且指出以往认为的拓扑区间很可能是拓扑平庸的,而真正的拓扑态区间在转变区,并给出了该区库伦振荡幅值和峰值关联的明确信息。文章发表在PRB 104, 045422 (2021)。该项工作为未来在该体系中寻找更多的马约拉纳零能模的证据提供了关键信息和工作区间,也为未来构筑拓扑量子比特提供了调控的参数和方式。该项工作得到了国家自然科学基金委(92065203),中国科学院先导专项(XDB33000000)和综合极端条件实验装置(SECUF)的支持。
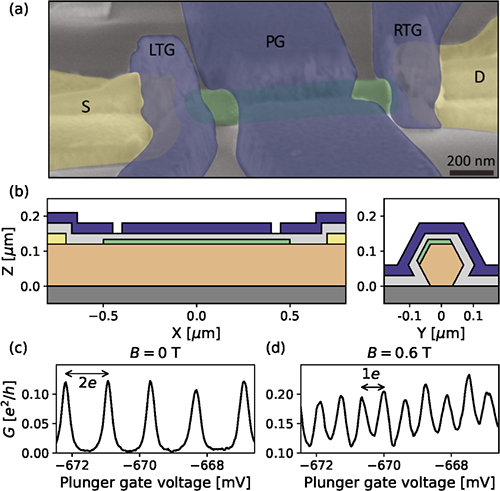
图1. 岛器件的实物图(a)和截面示意图(b纵切面、c横切面)。零场下库伦振荡是2e周期的(c),到0.6T劈裂成1e周期(d)。
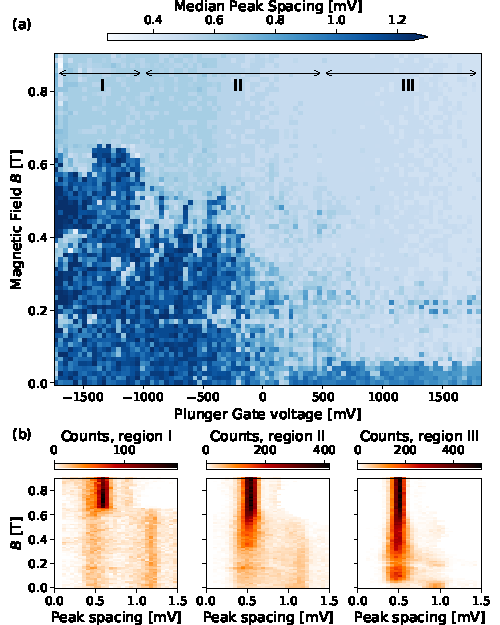
图2. 由20-30个库伦振荡算出的平均周期随门电压(化学势)和磁场变化的相图(a),其中深蓝色表示2e周期,浅蓝色表示1e周期,两者分界线对应2e-1e的转变磁场B*,根据B* 随门电压变化趋势把相图划分为三个区间。第一个区间B*接近于超导临界磁场,是由于准粒子中毒影响超导能隙导致的;第二个区间B*随着门电压变化,是潜在的拓扑态区间;第三个区间B*是稳定的较小的值,是以前认为拓扑转变的区间,但我们发现是由于orbital effect导致的拓扑平庸区间。这三个区间对应的统计周期分布如(b)所示, 更能显示B*的趋势,~0.6mV对应1e,~1.2mV对应2e。
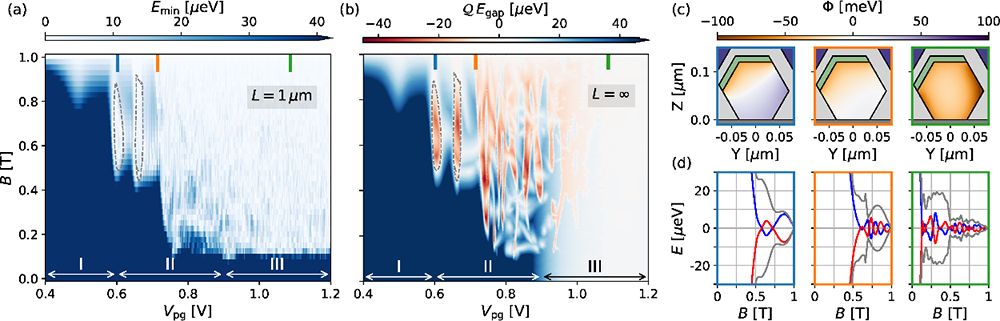
图3. 理论计算的相图(a)和拓扑能隙(b),其中深红色对应好的拓扑态,在对应实验的相图中的转变区间(第二个区间)。(c)给出了三种区间不同门电压(化学势)下横截面内波函数的分布,以及相应的超导能隙内态随磁场的变化。
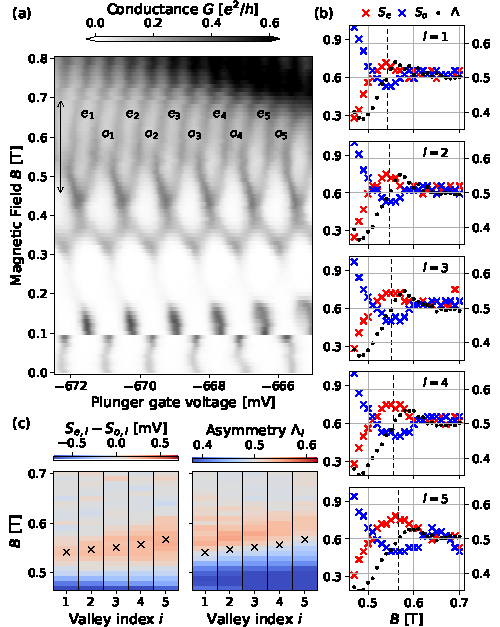
图4. 在第二个区间内具体的库伦振荡电导峰随化学势和磁场而变化的二维图(a)。不同门电压上每一对库伦振荡电导峰的间距和峰值随磁场的变化画在图(b)中,红蓝叉线分别对应奇和偶数电子对应的振荡间距,黑色点线对应奇和偶数电子对应的振荡电导峰的比值。可以看到两者振荡是锁定的,黑色的0.5值对应红蓝线的极值点,这个反应了电子隧穿岛占据的准粒子态的粒子-空穴对称性,与理论预言的马约拉纳零能模的隐形传输符合。图(c)中的“X”指的便是上述的关联点。
文章链接:
Phys. Rev. B 104, 045422 (2021) - Full-parity phase diagram of a proximitized nanowire island (aps.org)
Parity transitions in the superconducting ground state of hybrid InSb–Al Coulomb islands | Nature Communications
PRB 104, 045422 (2021).pdf
