阻挫反铁磁体系丰富的多体效应导致新奇的量子物态与相变，不断吸引着人们在其中探寻凝聚态物理的新效应、新规律、新方法。最近，中国科学院物理研究所/北京凝聚态物理国家研究中心、北京航空航天大学、复旦大学和香港大学的合作研究团队借助张量重正化群与量子蒙特卡洛方法确认阻挫磁体材料TmMgGaO₄ (TMGO)的微观模型为量子伊辛模型，并精准确定了其微观模型参数。据此，研究者预言磁性晶体TMGO在特定的温度范围内会展现出Kosterlitz-Thouless (KT) 相，此项理论工作首次在实际二维磁性晶体中预言了KT物理的存在。相关工作于2020年2月28日以“Kosterlitz-Thouless Melting of Magnetic Order in the Triangular Quantum Ising Material TmMgGaO₄”为题在线发表于综合学术期刊《自然· 通讯》（Nature Communications 11, 1111 (2020)）。
　　如图１所示，该团队通过指数张量重正化群计算，找到了TMGO 材料的一套正确的微观参数，可以完美地拟合实验观测的磁比热、熵曲线、磁化率、磁化曲线等诸多磁热力学性质。

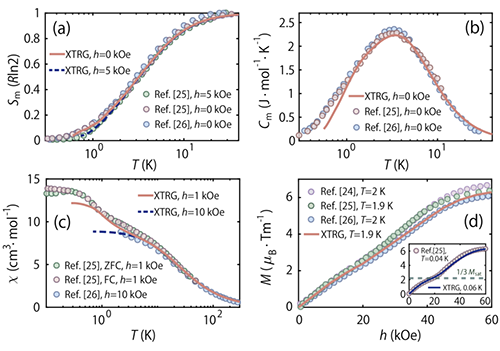图1. 热态张量网络多体计算精确拟合 TMGO磁热力学测量数据。

　　磁性晶体TMGO可以用一个三角格子上的各向异性量子伊辛模型描述。研究发现，在该模型中存在一种基态，名为“钟态序”（clock order，见图2a）。另一种“条纹序态”（stripe order，图2c）虽然在低温下不被相互作用选择，但可以在自旋谱的中段能量区间留下“幽灵”般的痕迹。这些幽灵在比较低的温度下（～1 K）被大量激活，该模型在“上”临界点T_h 进入KT相，在“下”临界点T₁ 转变为钟态序。

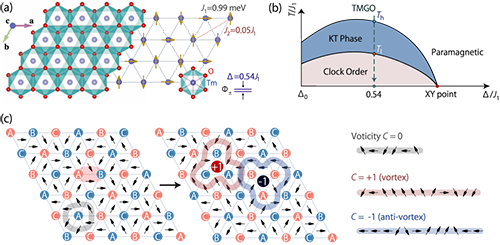图 2. (a) TMGO晶体结构及钟态有序示意图，（b）热力学相图，（c）条纹状有序，赝自旋映射，自旋翻转与涡旋对激发图像。

　　超流体中的旋子（Roton）激发是非常有趣的问题，自朗道的唯象理论提出后 [1]，吸引了诸多著名物理学家来建立旋子的微观量子理论。昂萨格指出旋子代表超流体中涡管的“幽灵”(The Ghost of a Vanished Vortex Ring) [2]；费曼认为旋子对应着量子化的涡旋运动，旋子激发谱的极小点对应着液态结构因子的极大点[3]；较为近代的观点认为超流体旋子激发是与邻近的固体序竞争导致的软模 [4]，并在冷原子实验中被多次观察到。利用大规模量子蒙特卡洛方法辅以随机解析延拓 [5]，该团队研究人员可以精准计算TMGO模型的自旋激发谱。如图３所示，沿着布里渊区高对称性线K-Γ-M-Γ ，在M点附近存在一个平方色散的极小点（ 全局来看，事实上M点是一个鞍点），与超流旋子类似，称为自旋系统的类旋子激发。M旋子可以看成条纹反铁磁序的残存“幽灵”，随温度升高其能隙逐渐减小、软化（图３d）。特别地，M旋子在上KT相变点附近急剧软化，但和通常意义下的软模不同，并不对应某种具体的对称性恢复，所以从这个意义上TMGO中的M旋子的确是一种奇特的“幽灵软模”。

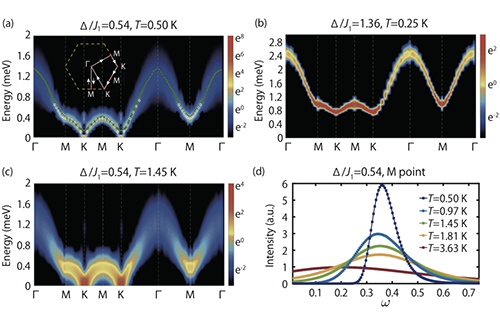图３. 二维自旋阻挫量子磁体 TMGO的量子多体蒙特卡洛动力谱学模拟结果。(a), (c), (d) 运用了正确的微观模型参数。（b） 为之前工作中错误的参数结果，在本团队的研究工作中得到了纠正。

　　该项研究为进一步深入探讨二维量子磁性晶体TMGO提供了坚实的理论基础，证明量子晶体TMGO提供了十分理想的实验平台，供人们研究有着丰富多体物理涌现性质的三角横场伊辛模型 。此外，对TMGO模型的研究也展示了综合平衡态与动力学多体计算开展精确研究关联量子材料的新范式。以上工作的主要参与者为北京航空航天大学博士生李涵（第一作者），中科院物理所博士生廖元达（共同第一作者），复旦大学戚扬教授、中科院物理所孟子杨研究员和北京航空航天大学李伟副教授（并列为论文的通讯作者），北京航空航天大学研究生陈斌斌、曾旭涛和助理教授胜献雷为论文的共同作者。本工作获得科技部重点研发计划（2016YFA0300502），中科院先导专项（XDB28000000），国家自然科学基金委项目（11574359），以及香港特别行政区研究资助局（Grant 17303019，C6026-16W）和北航青年拔尖人才支持计划等的资助。研究工作的大规模量子蒙特卡洛计算，在国家超算天津中心天河１号平台，国家超算广州中心天河２号平台上进行。
参考文献：
　　[1] L. Landau,“On the theory of superfluidity”,Phys.Rev.75,884–885(1949).
　　[2] R. J. Donnelly, “The ghost of a vanished vortex ring” in Quantum Statistical Mechanics in the Natural Sciences: A Volume Dedicated to Lars Onsager on the Occasion of his Seventieth Birthday, edited by S. L. Mintz and S. M. Widmayer (Springer US, Boston, MA, 1974) pp. 359–402.
　　[3] R. P. Feynman, Progress in Low Temperature Physics: Chapter II, Application of Quantum Mechanics to Liquid Helium, edited by C. G. Gorter, Vol. 1 (North Holland, 1955). 　
　　[4] P. Nozieres, “Is the roton in superfluid He4 the ghost of a Bragg spot?” J. Low Temp. Phys. 137, 45–67 (2004). 　
　　[5] Nvsen Ma, Guang-Yu Sun, Yi-Zhuang You, Cenke Xu, Ashvin Vishwanath, Anders W. Sandvik, Zi Yang Meng, “Dynamical Signature of Fractionalization at the Deconfined Quantum Critical Point”, Phys. Rev. B 98, 174421 (2018), Editors' Suggestion.

Nature Comm. 11, 1111 (2020).pdf