手性是指一个物体与其镜像不能重合的现象，就像我们的左手和右手。在相对论物理中，手性是指无质量粒子的自旋和动量方向平行或者反平行。外尔费米子就是一种具有手性的粒子，描述它的哈密顿量 \(H(k)=\vec{\sigma }\cdot \vec{k }\) 其中 \(\vec{\sigma }\) 和 \(\vec{k }\)分别代表自旋和动量。在拓扑能带理论中，当固体中包围能带简并点的费米面具有非零的陈数，该简并点具有手性，被看作动量空间中的磁单极，费米面上的低能准粒子激发是具有磁荷的手性费米子。例如，固体中外尔点的陈数C = ±1，外尔费米子就是磁荷为1的手性费米子。手性的简并点在表面上的投影被螺旋结构的表面态环绕，其等能面就是费米弧，连接手性相反的简并点在表面的投影。
　　在固体中已经实验证实了三种类型的能带简并点，分别是二重简并的外尔点、四重简并的狄拉克点和三重简并点。狄拉克点和三重简并点都可以看成是一对手性相反的外尔点的叠加，手性相互抵消，所以狄拉克费米子和三重简并费米子都没有手性。但可以通过外加条件破缺对称性，比如外加磁场，将它们退简并成手性的外尔费米子。狄拉克半金属和三重简并点半金属中表现出的许多物理性质，例如手性反常导致的负磁阻效应和表面态费米弧，本质上都是来源于手性的外尔费米子。
　　发现外尔费米子之外的新型手性费米子不仅是拓扑半金属领域上的突破，也可以为探索手性费米子相关的物理现象提供更多的途径，具有重要的科学意义和应用价值。近年来，理论上已经预言了多种类型的手性费米子以及相关的材料，但一直未能得到实验证实。在众多关于新型手性费米子的理论预言中，CoSi属于能带结构比较理想的材料，引起了国际上许多研究组的关注。不考虑自旋－轨道耦合的电子能带或声子谱计算显示，在CoSi的体态布里渊区的中心Г和顶角R点分别存在三重和四重能带简并点（图1b）。与之前实验证实的碳化钨结构材料MoP、WC中的三重简并点和Na₃Bi、Cd₃As₂中的四重简并的狄拉克点不同的是，它们是陈数C = ±2的手性的简并点，费米面上的低能准粒子激发是磁荷为2的手性费米子，分别被命名为spin-1和charge-2费米子（图1c）。
　　通过角分辨光电子能谱测量材料的体态和表面态电子结构，可以提供这些手性费米子的直接证据，但实验测量需要原子级平整的样品表面。CoSi是典型的三维材料，通常的解理方法难以得到原子级平整的表面。中国科学院物理研究所/北京凝聚态物理国家研究中心与中国人民大学物理系合作，利用抛光－轰击－退火的方法，经过长时间的不断摸索，终于在CoSi单晶样品上得到原子级平整的表面，并在上海光源“梦之线”观测到清晰的体态和表面态能带。实验结果显示在体布里渊区的中心Г和顶角R点存在体态能带简并点，与理论计算结果高度吻合（图1d-f）。它们在（001）表面的投影被跨越整个布里渊区的超长表面态费米弧连接（图2a,b），在环绕单个简并点投影的闭合路径上存在两条手性的表面态能带，并且这两条闭合路径之间表面态能带的手性相反（图2c,d），标志着这两个能带简并点携带非零的陈数C = ±2，这是CoSi中存在新型手性费米子的确定证据。该实验结果不仅证明了新型手性费米子的存在，而且提供了一个较为理想的平台去探索由手性费米子引起的新奇物理现象。
　　这个工作是在中科院物理所EX7组丁洪研究员、钱天研究员和孙煜杰副研究员组成的研究团队和多个研究组的紧密合作下完成的。中国人民大学物理系博士生田尚杰、硕士生李承贺和雷和畅副教授、物理所EX1组博士生王乐和石友国研究员、物理所N08组博士后李治林提供了高质量的CoSi单晶样品；物理所EX7组博士生饶志成、博士生唐岑瑶和孙煜杰副研究员用抛光－轰击－退火的方法处理出原子级平整的表面，在样品定向过程中得到了物理所EX6组博士生刘哲宏和龙有文研究员的帮助；物理所T03组博士生张田田和翁红明研究员进行了能带计算，方辰研究员和翁红明研究员提供了理论指导；物理所EX7组博士生饶志成、博士生李航、博士生付彬彬和钱天研究员在上海光源“梦之线”进行了ARPES实验测量，实验过程中得到了上海光源黄耀波研究员的全力支持。
　　相关研究成果于2019年3月20日在线发表于Nature杂志。该工作得到了科技部（2016YFA0401000，2015CB921000，2016YFA0300600，2016YFA0300504，2016YFA0302400，2018YFA0305700，2017YFA0302901），国家自然科学基金委（11622435，U1832202，11474340，11822412，11574371，11674369，11574394，11774423，11774399），中国科学院（QYZDB-SSW-SLH04，XDB07000000，XDPB08-1），科学挑战计划（TZ2016004），王宽诚教育基金会（GJTD-2018-01），北京市自然科学基金委（Z180008），北京市科委（Z171100002017018，Z181100004218005，Z181100004218001）的资助。

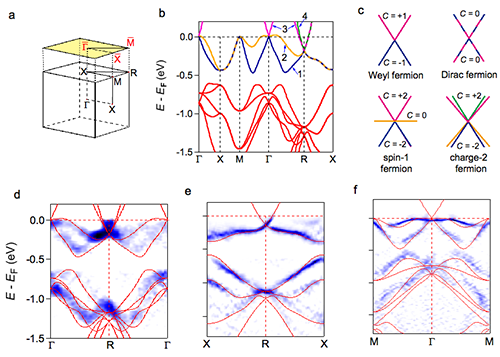图1. CoSi的体态电子结构。（a）体布里渊区和（001）表面布里渊区。（b）第一性原理计算的沿着高对称线的体态能带结构。（c）外尔费米子、狄拉克费米子、spin-1费米子、charge-2费米子的能带结构示意图。（d-f）沿Г-R、R-X、Г-M方向测量的体态能带色散，实验数据是在体态灵敏的软X射线下采集的，红色曲线是理论计算结果。

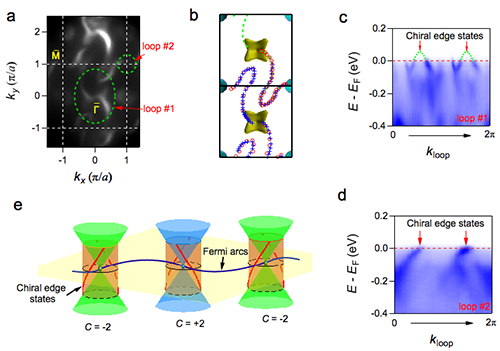图2. CoSi的（001）表面态。（a）在（001）表面上实验测量的表面态的费米面，实验数据是在表面态灵敏的极紫外光下采集的。（b）从费米面数据中提取出的表面态费米弧。（c,d）在围绕体态能带简并点的表面投影的闭合路径loop #1和loop #2上的能带色散。（e）陈数符号相反的体态能带简并点在表面上的投影被手性相反的表面态环绕，这样的表面态的等能面就是拓扑稳定的费米弧连接它们的投影。

s41586-019-1031-8.pdf