最近,中国科学院物理研究所/北京凝聚态物理国家研究中心理论室副研究员方辰和博士研究生宋志达、张田田的研究在很大程度上解决了这一难题。他们的研究指出:在自旋轨道耦合可忽略的非磁性系统中,一般位置上的拓扑能带交叉的存在性以及性质都可以由少数高对称点上的对称操作的本征值给出,例如能带交叉类型(点或者线)、拓扑荷、能带交叉数量、形状、位置。有了能带拓扑和能带表示之间的判据,物理学家只需要几个高对称点上的能带对称性数据就可以得到该材料的拓扑不变量以及能带交叉点的存在性以及性质。这一理论大大简化了识别拓扑材料的艰巨任务,为高通量搜索拓扑半金属铺平了道路。目前该工作已经发表在《Physical review X》上【Phys. Rev. X 8, 031069 (2018)】。
本工作基于最近提出的拓扑量子化学【1】、对称性指标【2】等理论。文献【1】系统地研究了原子绝缘体的能带连接关系,又称为“相容性关系”,并指出如果一组能带不能分解为原子绝缘体的对称性数据,那么这组能带必定是拓扑非平庸的。如果一组能带满足文献【1】中提出的相容性关系,那么这个系统要么是有能隙的绝缘体,要么是在非高对称点有能带交叉的半金属。文献【2】则指出任何在高对称线上有直接能隙的系统,其价带对称性数据都可以压缩为几个对称性指标,这些对称性指标的取值为一些有限的整数。文献【3】在文献【2】的基础上给出了有自旋轨道耦合的非磁性系统的对称性指标与拓扑不变量之间的具体关系,也称为“拓扑字典”。本文致力于完成在自旋轨道耦合可忽略的、满足兼容性关系的非磁性能带系统中,研究其对称性指标与拓扑不变量之间的映射关系。首先,作者推导出了所有有对称性指标的空间群的公式;其次,对于每一种对称性指标都列举出其对应的能带交叉点的类型、形状、数量、位置以及拓扑荷。这里以2号空间群的CaP3【4】为例来演示如何使用对称性判据:
第一步,计算CaP3高对称点上占据态能带的对称性数据,这一步可以由第一性计算软件完成;
第二步,把对称性数据代入附件公式(4)中计算对称性指标,得到(0101);
第三步,查找附件中表3,发现2号空间群(0101)对应的能带交叉是一个节点环的形状,围绕在高对称点Y且无拓扑荷。
【1】Bradlyn, B. et al. Topological quantum chemistry. Nature 547, 298–305 (2017).
【2】Po, H. C., Vishwanath, A. & Watanabe, H. Complete theory of symmetry-based indicators of band topology. Nature Communications 8, 50 (2017).
【3】Song, Z., Zhang, T., Fang, Z., & Fang, C. (2018). Quantitative mappings between symmetry and topology in solids. Nature communications, 9(1), 3530.
【4】Xu, Q., Yu, R., Fang, Z., Dai, X. & Weng, H. Topological Nodal Line Semimetals in CaP3 family of materials. Phys. Rev. B 95, 045136 (2017).
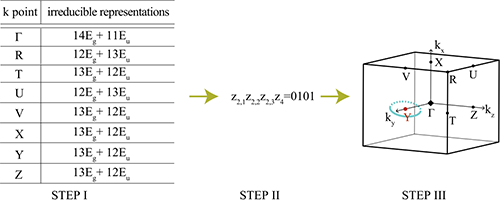 |
| 图1:对称性判据的使用方法,以2号空间群的CaP3为例。左侧表格是第一性原理计算得到的对称性数据,左列是高对称点的名称,右列是高对称点上导带的能带表示名称及其出现的次数。将此表格中的对称性数据代入附件中公式(4)即可得到对称性指标(0101)。查找附件中表3即可得到CaP3中的能带交叉点是一个围绕Y点的节点环,这与文献【4】中计算的结构相匹配。 |
PhysRevX.8.031069.pdf
