删除或更新信息，请邮件至freekaoyan#163.com(#换成@)

一维与二维爆轰传播的时空关联特性数值研究

本站小编 Free考研考试/2022-01-01


引 言


爆轰是一种在预混可燃气体中以超声速传播的极端燃烧现象, 具有自持、自组织和增压燃烧特征[1]. 在自然界中, 爆轰可能发生于煤矿爆炸和化工厂事故, 在Ia型超新星爆炸研究和航空航天新型动力的探索领域也得到越来越广泛的关注[2-4]. 19世纪末以来, 人们从各个角度探索了气体爆轰的起爆、传播规律和精细结构, 在理论和实验认知方面都取得了重大进展. 近年来, 姜宗林[5]在前人研究的基础上, 结合自己的研究成果, 提出气体爆轰物理的统一框架理论, 总体地概括了气相爆轰波起爆和传播的主要规律和关键物理参数的依存与竞争关系, 为进一步分析爆轰现象建立了一个具有启示性的理论基础.

斜爆轰的研究起步较晚, 由于应用需求推动其得到了越来越多的关注. 斜爆轰波是一种驻定爆轰波(standing detonation wave), 当高速可燃气体经过尖劈、钝体等结构时产生斜激波, 波后温度升高引发燃烧反应, 燃烧带与斜激波耦合构成斜爆轰波. Li等[6]的早期数值模拟研究揭示了斜爆轰波的基本起爆结构. Figueira da Silva和Deshaies[7]通过数值模拟发现了两种差异显著的起爆结构, 分别称为光滑型和突变型. Teng和Jiang[8]提出斜激波与斜爆轰波之间的角度差可以作为两种起爆结构的判据. Choi等[9]通过高分辨率的数值模拟发现斜爆轰波面也能够演化出类似正爆轰的胞格结构, Gui等[10]根据波面形状特征将斜爆轰波面结构分为3个区域. Teng等[11]的数值模拟结果表明高活化能、小楔角条件下更容易出现胞格结构. Fusina等[12]模拟了斜爆轰波面在非均匀来流条件下的响应, 说明斜爆轰波具有一定的抗干扰能力. Yang等[13]的研究表明斜爆轰波在非定常来流条件下也能保持一定的稳定性.

斜爆轰的形成和发展过程与正爆轰有一定的相似性, 但其起爆结构和胞格演化规律存在显著区别, 明确两者的关联和差异对深入理解和应用斜爆轰现象有重要意义. Ghorbanian和Sterling[14]发现双楔诱导斜爆轰的波系结构与变速活塞的t-y图有相似的特征, Daimon和Matsuo[15]数值模拟比较了半无限长楔诱导斜爆轰与活塞驱动正爆轰的起爆结构, 并通过活塞运动类比出多种楔面诱导的斜爆轰起爆结构. Higgins[16]指出, 利用斜爆轰与活塞驱动正爆轰的相似性, 可以直观地理解冲压加速器燃烧室内的波系结构. 上述这些研究结果表明, 斜爆轰是驻定的, 正爆轰是非定常的, 考虑正爆轰的时间维度, 两种爆轰的流场结构存在一定的时空关联关系, 即时空坐标下的非定常正爆轰与空间坐标下的定常斜爆轰有一定的相似性. 这种时空关联研究有助于理解斜爆轰与正爆轰在本质上的联系, 深化对爆轰现象的认识.

斜爆轰结构具有多尺度特征[17], 包含化学反应的控制方程求解存在刚性问题[18], 斜爆轰波的起爆、胞格等局部精细结构与流场中其他区域相比要求更高的时空分辨率, 高超声速边界处理也有很高的计算方法要求. 因此, 对斜爆轰的二维流场开展大尺度、高精度的数值模拟需要较大的计算量和较复杂的计算方法. 一维正爆轰的计算量小, 而且有经典理论和较丰富的实验验证. 如果能够借助正爆轰与斜爆轰的时空关联特性, 通过一维数值模拟获得二维斜爆轰流场的主要规律, 不仅具有工程应用价值, 也能加深对斜爆轰起爆机理等基础问题的理解.

然而, 过去的研究[14-16]侧重于利用斜爆轰与正爆轰的相似关系来理解斜爆轰现象, 采用了理想的半无限长楔构型和抽象的化学反应模型, 主要开展定性的讨论, 缺乏定量研究, 目前尚不清楚这种时空关联的精确度, 难以投入工程应用. 为了深入探索正爆轰与斜爆轰现象的时空关联特性, 从定量上获得两种爆轰现象的关联规律, 本文在文献[15]工作的基础上, 利用多组分Euler方程和基元反应模型模拟了有限长楔诱导定常斜爆轰波和相同过驱动度条件下的活塞驱动非定常正爆轰波, 通过两者流场特征的对比研究, 阐述两种爆轰相似性和差异, 并给出了时空关联关系.


1.
数值计算方法


一维爆轰理论是建立在定常流动的基础上的, 其预测结果和实验符合良好, 原因在于黏性对爆轰波流动结构的影响较小[19]. 本文的重点在于时空关联问题, 因此采用多组分Euler方程统一描述一维和二维爆轰波的起爆和传播过程. 该方程可表述如下







$$frac{{partial {boldsymbol{U}}}}{{partial t}} + frac{{partial {boldsymbol{F}}}}{{partial x}} + frac{{partial {boldsymbol{G}}}}{{partial y}} + {{boldsymbol{S}}_{
m{c}}} = {boldsymbol{0}}$$
(1)

式中






$$begin{array}{l} {boldsymbol{U}} = {[ {{
ho _1}},;{{
ho _2}},; cdots ;{{
ho _n}},;{
ho u},;{
ho v},;e ]^{
m T}} {boldsymbol{F}} = {[ {{
ho _1}u},;{{
ho _2}u},; cdots ;{{
ho _n}u},;{
ho {u^2} + p},;{
ho vu},;{left( {e + p}
ight)u} ]^{
m T}} {boldsymbol{G}} = {[ {{
ho _1}v},;{{
ho _2}v},; cdots ;{{
ho _n}v},;{
ho uv},;{
ho {v^2} + p},;{left( {e + p}
ight)v} ]^{
m T}} {{boldsymbol{S}}_{
m{c}}} = {[ {{{dot omega }_1}},;{{{dot omega }_2}},; cdots ;{{{dot omega }_n}},;0,;0,;0 ]^{
m T}} end{array} $$

对于一维爆轰的数值模拟






$$begin{array}{l} {boldsymbol{U}} = {[ {{
ho _1}},;{{
ho _2}},; cdots ;{{
ho _n}},;{
ho u},;e ]^{
m T}} {boldsymbol{F}} = {[ {{
ho _1}v},;{{
ho _2}v},; cdots ;{{
ho _n}v},;{
ho {v^2} + p},;{left( {e + p}
ight)v} ]^{
m T}} {{boldsymbol{S}}_{
m{c}}} = {[ {{{dot omega }_1}},;{{{dot omega }_2}},; cdots ;{{{dot omega }_n}},;0,;0 ]^{
m T}} end{array} $$

式中$;{
ho _i}left( {i = 1,2, cdots,n}
ight)$为第i个组分的密度, $n$为化学反应模型中包含的组分数. 混合气体的总密度为$
ho = displaystylesumlimits_{i = 1}^n {{
ho _i}} $, $u$和$v$分别为$x$方向和$y$方向的气体速度, $e$为气体单位体积的总能, 与气体的焓、压力和动能有关, 表达式为







$$e = sumlimits_{i = 1}^n {{
ho _i}{h_i} - p + frac{1}{2}}
ho left( {{u^2} + {v^2}}
ight)$$
(2)

式中${h_i}$为第i个组分单位质量的焓值, 本文将混合气体的每一个组分处理为热完全气体, 其定压比热${C_{pi}}$为温度的单值函数, 由多项式拟合得到







$$begin{split}& dfrac{{{C_{pi}}}}{{{R_i}}} = {a_{1i}}{T^{ - 2}} + {a_{2i}}{T^{ - 1}} + & qquad{a_{3i}} + {a_{4i}}T + {a_{5i}}{T^2} + {a_{6i}}{T^3} + {a_{7i}}{T^4} end{split} $$
(3)

进一步积分得到各组分的焓值







$$begin{split}& frac{{{h_i}}}{{{R_i}T}} = - {a_{1i}}{T^{ - 2}} + {a_{2i}}{T^{ - 1}}ln T + & qquad{a_{3i}} + frac{{{a_{4i}}}}{2}T + frac{{{a_{5i}}}}{3}{T^2} + frac{{{a_{6i}}}}{4}{T^3} + frac{{{a_{7i}}}}{5}{T^4} + {b_{1i}}{T^{ - 1}} end{split} $$
(4)

式中的拟合常数${a_{ji}}left( {j = 1,2, cdots,7}
ight)$和${b_{1i}}$参考文献[20]. 结合理想气体状态方程和道尔顿分压定律, 混合气体的压力$p$为







$$p = sumlimits_{i = 1}^n {{
ho _i}{R_i}T} $$
(4)

式中${R_i}$为第i个组元的气体常数, T为混合气体的温度. 式(1)中的化学反应源项${{boldsymbol{S}}_{
m{c}}}$包括$n$个组分单位体积的质量生成率${dot omega _i}$, 根据质量作用定律







$$begin{split}& {{dot omega }_i} = {M_i}sumlimits_{i = 1}^{{n_r}} {left( {{{nu ''_{ik}}} - {{nu '_{ik}}}}
ight)} left[ {sumlimits_{i = 1}^n {left( {{alpha _{ik}}{c_i}}
ight)} }
ight] cdot &qquad left[ {{k_{fk}}prodlimits_{i = 1}^n {{{left( {{c_i}}
ight)}^{{{nu '_{ik}}}}} - {k_{bk}}prodlimits_{i = 1}^n {{{left( {{c_i}}
ight)}^{{{nu ''_{ik}}}}}} } }
ight] end{split} $$
(5)

式中${M_i}$为第i个组分的物质的量, ${n_r}$为化学模型包含的反应数, ${nu ''_{ik}}$, ${nu '_{ik}}$, ${alpha _{ik}}$分别为第k个反应中第i个组分在生成物一侧的计量数、在反应物一侧的计量数和第三体增强系数, ${c_i}$为第i个组分的物质的量浓度, ${k_{fk}}$, ${k_{bk}}$分别为第k个反应的正、逆反应速率, 一般通过Arrhenius定律计算${k_{fk}}$







$${k_{fk}} = {A_k}{T^{{n_k}}}exp left( {frac{{{E_{ak}}}}{{{R_u}T}}}
ight)$$
(6)

式中${A_k}$, ${n_k}$, ${E_{ak}}$分别为第k个反应的频率因子、温度指数和活化能, ${R_u}$为普适气体常数. 进一步结合反应平衡常数可计算出${k_{bk}}$







$${k_{bk}} = frac{{{k_{fk}}}}{{{k_{ck}}}}$$
(7)

预混可燃气体为化学当量的氢气/空气混合气, 反应过程采用高压修正的Jachimowski机理[21], 包含H2, O2, H, O, OH, HO2, H2O2, H2O, N2共9种组分和19个化学反应. 二维数值模拟采用非结构四边形网格, 平均网格间距为50 μm, 通过有限体积法和二阶TVD格式离散求解, 界面通量通过HLLC(Harten-Lax-van Leer contact)近似黎曼求解器[22]计算. 一维数值模拟采用结构网格, 网格间距为10 μm, 采用频散控制耗散(dispersion controlled dissipation, DCD)格式[23]离散求解, 时间推进采用3阶Runge-Kutta法, 时间步长由CFL数控制, 计算中CFL数取0.1.


2.
计算模型的验证


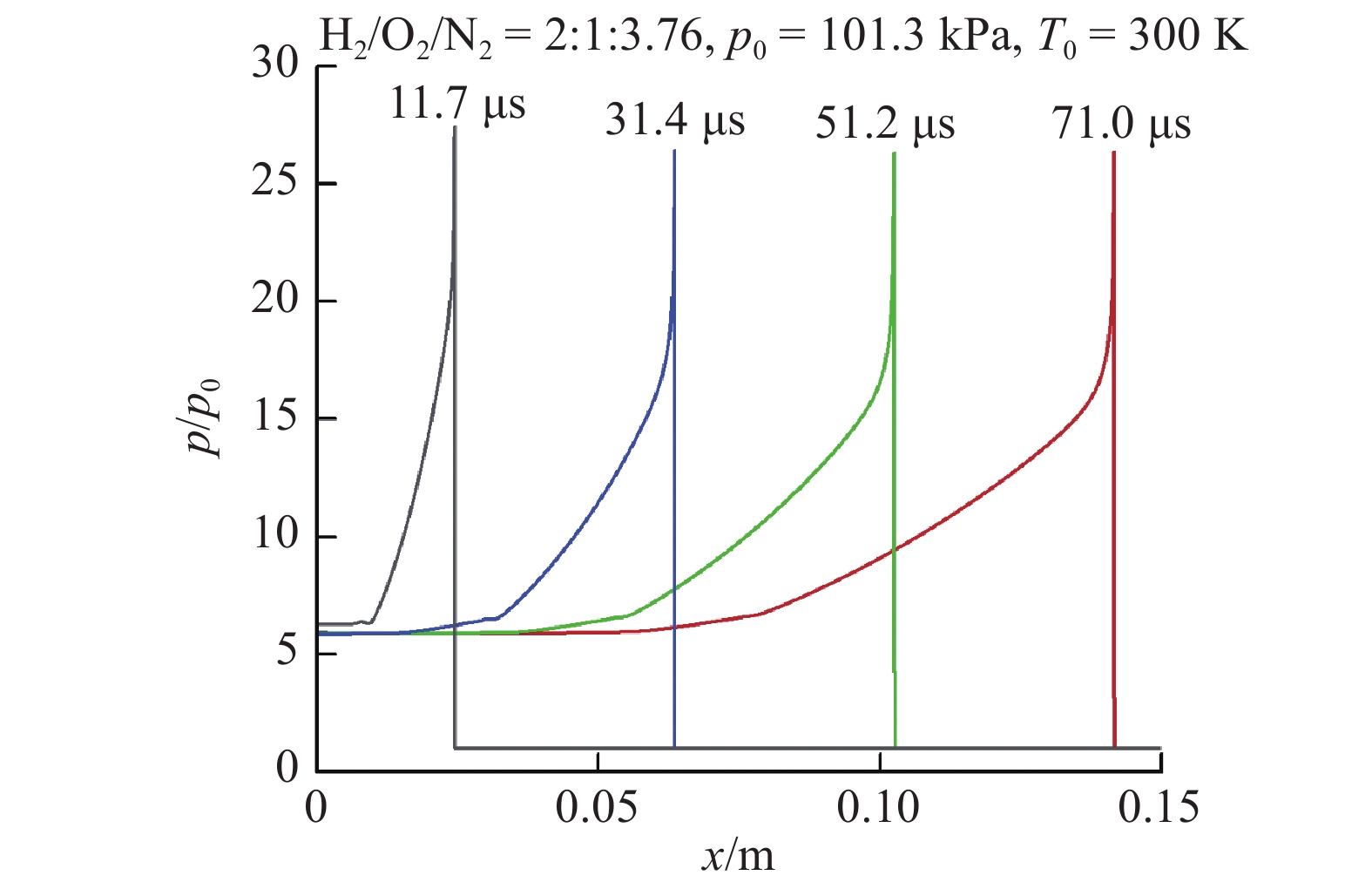
选取两个已知解析解的问题分别对一维和二维计算模型进行验证. 图1为一维爆轰波在光滑直管道中的传播问题, 计算得到不同时刻的压力分布. 31.4 μs后, 压力波形几乎不变, 通过捕捉激波位置变化得到爆轰波速为1970.71 m/s, GASEQ软件计算出的Chapman-Jouguet (CJ)爆速为1979.33 m/s, 两者的相对误差为?0.436%, 说明一维计算模型比较可靠.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/7//20-411-1.jpg'"
class="figure_img
figure_type1 bbb " id="Figure1" />



图
1
典型一维爆轰波的数值模拟结果



Figure
1.
Typical pressure profile of one-dimensional detonation in the numerical simulation



下载:
全尺寸图片
幻灯片


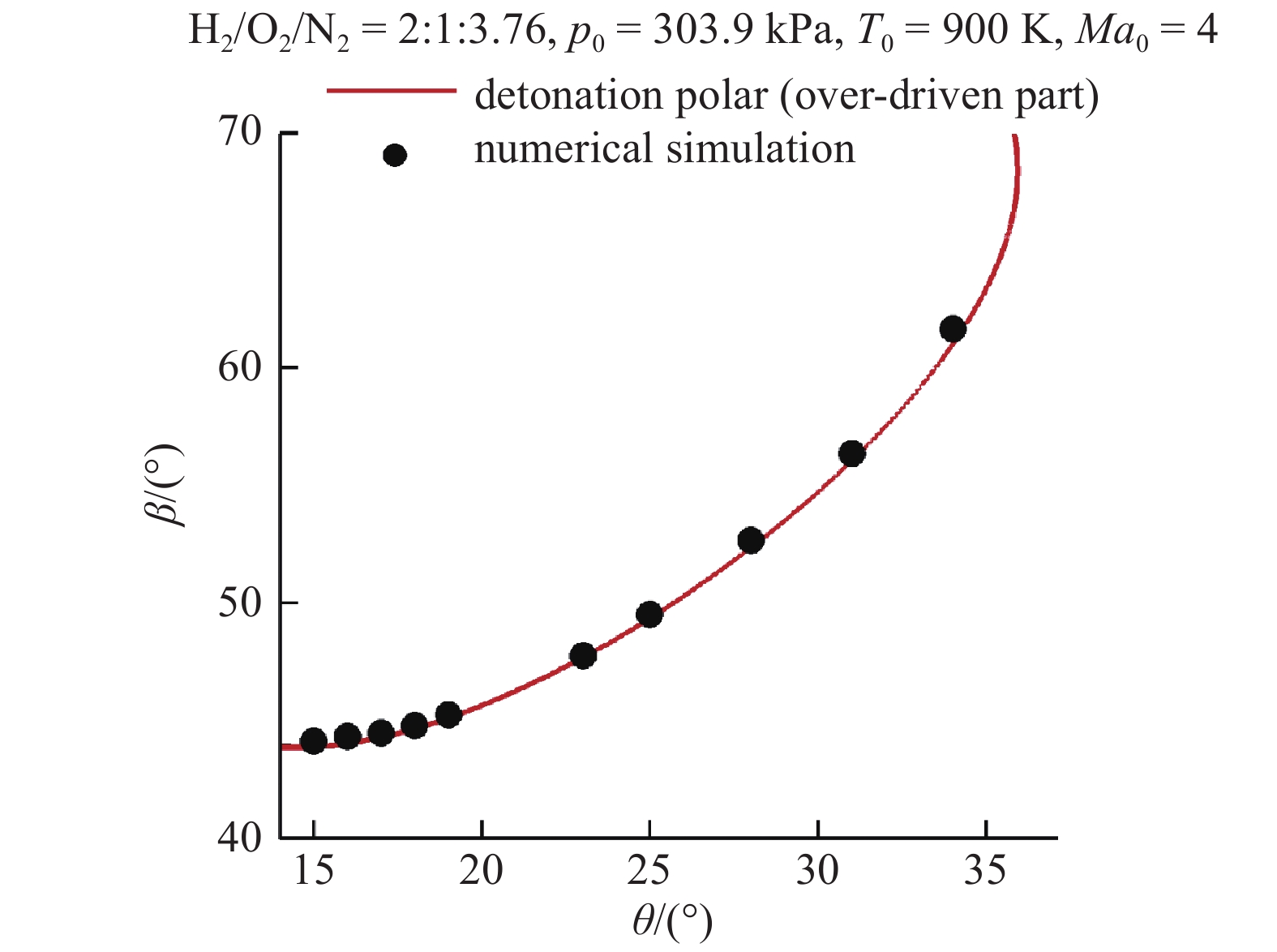
图2为半无限长楔诱导的斜爆轰问题, 当楔面足够长时, 可以忽略起爆结构的影响, 在下游测量爆轰角. 分别在10个角度下进行了数值模拟, 均在楔面上得到了驻定的斜爆轰波(见表1). 通过化学反应平衡的斜激波求解方法[24]得到理论解, 数值模拟和理论求解采用相同的化学反应模型, 表1中两者的相对误差几乎都在1%以下, 其中相对误差







$${E_{
m{r}}}{
m{ = }}frac{{{beta _{{
m{num}}}}{
m{ - }}{beta _{{
m{theory}}}}}}{{{beta _{{
m{theory}}}}}} times 100{text{%}} $$
(8)

从图2可以看出数值模拟得到的爆轰角βnum随着楔面折角θ的变化规律与理论解符合, 说明二维计算模型比较可靠.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/7//20-411-2.jpg'"
class="figure_img
figure_type1 bbb " id="Figure2" />



图
2
半无限长楔面数值模拟的爆轰角与爆轰极曲线对比



Figure
2.
Detonation angle of numerical simulation vs. detonation polar diagram



下载:
全尺寸图片
幻灯片





表
1
半无限长楔面数值模拟的爆轰角与爆轰极曲线对比



Table
1.
Detonation angle of numerical simulation vs. that of detonation polar diagram under various wedge angles



table_type1 ">
θ/(°)βtheory/(°)βnum/(°)Er/%
1543.8644.120.59
1644.0044.330.75
1744.2744.480.47
1844.6344.780.34
1945.0945.250.35
2347.6747.770.21
2549.3549.520.34
2852.3552.660.59
3156.0556.360.55
3461.0061.651.07





下载:
导出CSV
|显示表格



3.
计算结果分析


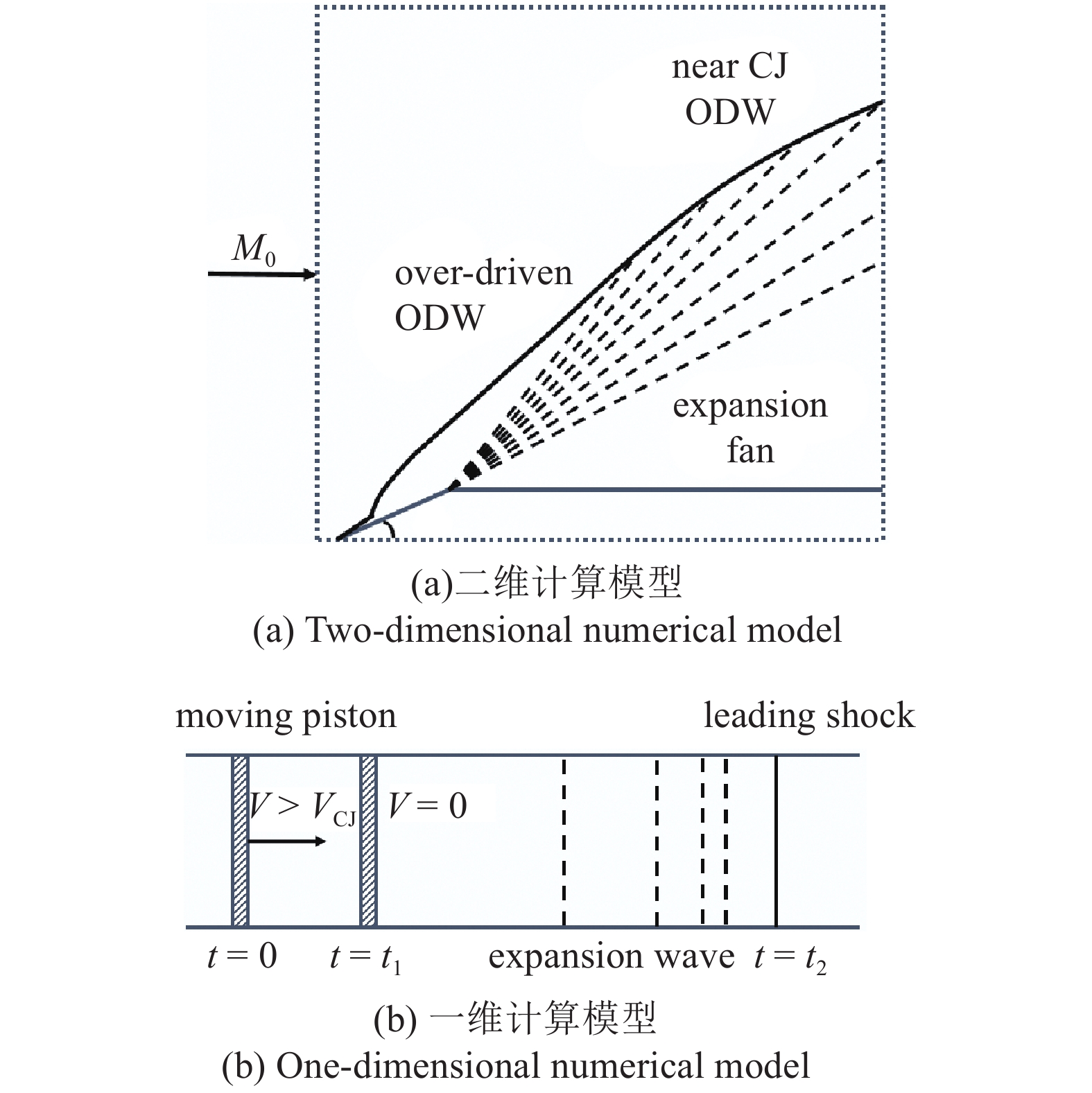
本文重点研究有限长楔诱导的定常斜爆轰波与非定常活塞驱动的正爆轰波的时空关联特性, 计算域及初始条件设置见图3. 二维数值模拟的计算域为12 cm × 12 cm的方形区域, 楔角θ为25°, 楔面长度2 cm, 楔面末端出现折角, 在折角下游, 壁面与来流方向平行.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/7//20-411-3.jpg'"
class="figure_img
figure_type1 bbb " id="Figure3" />



图
3
计算模型示意图



Figure
3.
Schematic diagram of numerical model



下载:
全尺寸图片
幻灯片


沿用Daimon和Matsuo[15]的近似方法, 建立壁面参考系, 时空变换关系表述为: 壁面法向流动对应一维流场, 壁面切向流动对应一维时间推进. 一维算例如图3(b)所示, 将活塞的非定常运动分为两个阶段. 第一阶段初始时刻, 活塞以1450.73 m/s匀速运动, 该速度高于CJ状态的气体速度1130.59 m/s, 诱导产生过驱动正爆轰波. 数值模拟中, 正爆轰波的过驱动度与25°楔面产生的过驱动斜爆轰波相同, 均为1.235, 过驱动度f定义为







$$f = {left( {frac{{{M_{
m{n}}}}}{{{M_{{
m{CJ}}}}}}}
ight)^2}$$
(9)

式中${M_{
m{n}}}$为来流在爆轰波面法向的速度对应的马赫数, ${M_{{
m{CJ}}}}$为相同来流条件下CJ状态的激波马赫数[25]. 来流为预混氢气/空气混合气, 来流压力${p_0} = $ 101.3 kPa, 来流温度${T_0} = 300;{
m{K}}$, 当量比为1, 对应的${M_{{
m{CJ}}}} = 4.843$. 当正爆轰波面与活塞的距离和斜爆轰波面与楔面的距离相同时, 第一阶段结束, 活塞停止. 第二阶段中, 活塞保持不动, 爆轰波继续向前传播. 根据时空变换关系, 上述活塞运动方式与二维有限长楔构型的壁面变化规律一致. 为阐述斜爆轰与正爆轰的时空关联特性将分别从波系结构、壁面参数、波形变化和时间尺度4个方面对二维和一维数值模拟结果进行对比.


3.1
波系结构


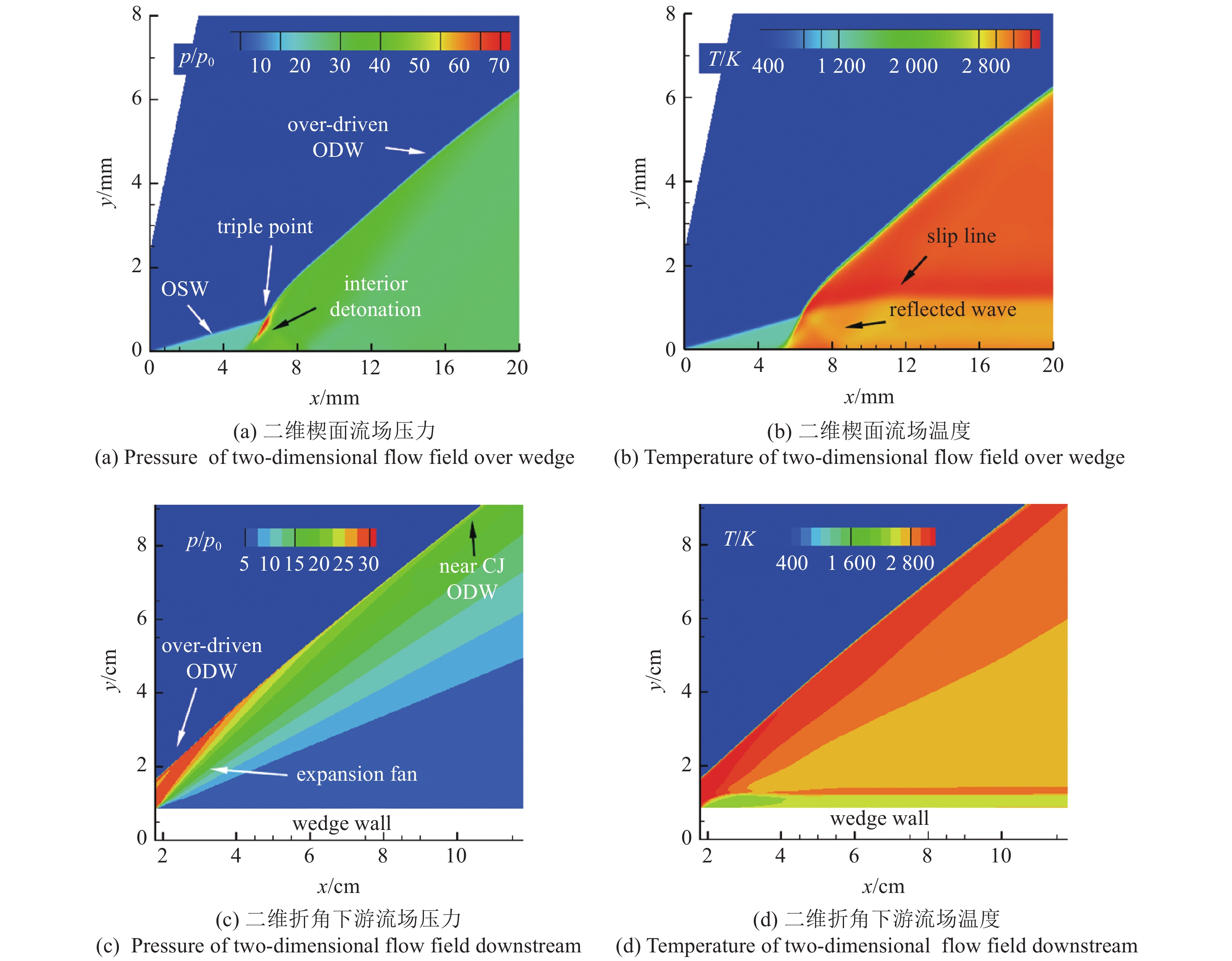
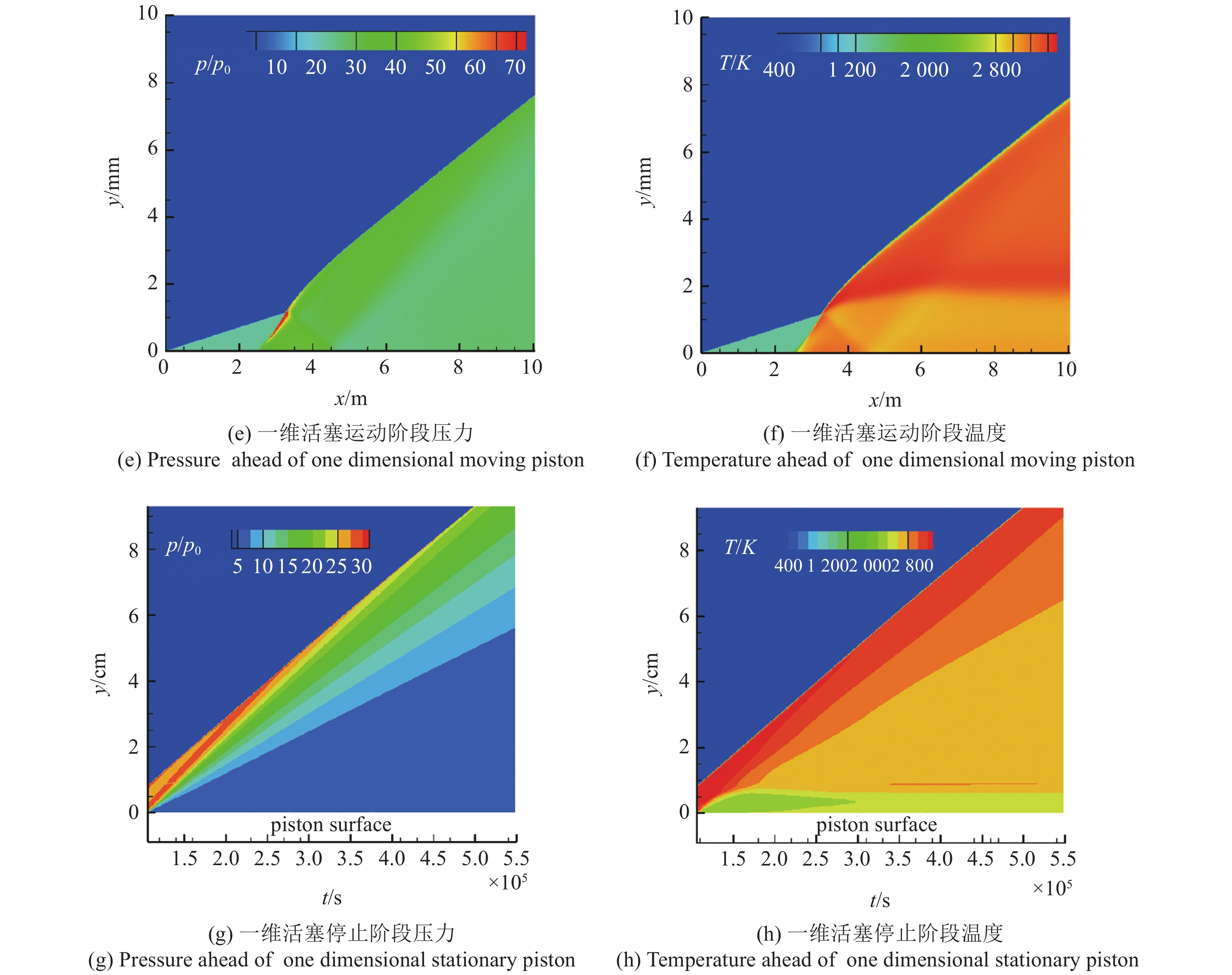
图4(a) ~ 图4(d)为二维有限长楔诱导的斜爆轰数值结果, 依次为楔面上的压力、温度流场和折角后的压力、温度流场, 图4中坐标原点在楔面起点处, x轴与来流方向平行, y轴与来流方向垂直. 在楔面上, 为了方便与一维计算结果比较, 对坐标轴进行了旋转, 旋转后x轴与楔面重合, y轴与楔面垂直. 图4(a)和图4(b)采用了旋转后的坐标系, 来流经过楔面被压缩, 壁面附近的压缩波汇聚[26]为斜激波(oblique shock wave, OSW), 波后温度约为1260 K, 诱发可燃气体自点火. 经过一定的起爆区距离, 可燃气体发生剧烈的放热反应, 燃烧反应带角度快速抬升并与斜激波相交, 燃烧和激波面强耦合诱导出过驱动的斜爆轰(oblique detonation wave, ODW). 同时三波点下游出现滑移线和反射波, 反射波在壁面上再次反射产生膨胀波, 膨胀波在滑移线上透射与过驱动斜爆轰波相交. 在本文的计算条件下, 斜爆轰波面较为稳定, 未发展出斜爆轰胞格结构[10]. 在图4(c)和图4(d)中, 折角处出现膨胀扇, 气流通过膨胀扇后与壁面平行. 一段距离后, 膨胀扇追上过驱动斜爆轰波使其激波角减小, 最终在计算域下游形成近CJ斜爆轰波, 其激波角为37.63°, 与CJ斜爆轰波的激波角37.03°接近. 气流通过近CJ斜爆轰波时熵增最小, 总压损失最小[27], 此时燃烧室出口总压恢复系数最高, 有利于产生更大的推力, 这是有限长楔构型在斜爆轰发动机中应用的一大优势.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/7//20-411-4-1.jpg'"
class="figure_img
figure_type2 ccc " id="Figure4-1" />



4
不同工况下压力及温度的数值模拟云图



4.
Numerical contours of pressure and temperature under different conditions



下载:
全尺寸图片
幻灯片




onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/7//20-411-4.jpg'"
class="figure_img
figure_type2 ccc " id="Figure4" />



图
4
不同工况下压力及温度的数值模拟云图(续)



Figure
4.
Numerical contours of pressure and temperature under different conditions (continue)



下载:
全尺寸图片
幻灯片


图4(e) ~ 图4(h)为一维数值模拟结果, 将时间作为一个维度与二维云图比较. 可以看出, 一维数值模拟在时空坐标下的温度、压力流场具有二维流场的全部特征, 包括激波、燃烧波、三波点、过驱动爆轰波、滑移线、反射波、膨胀扇等. 这初步验证了一维非定常活塞驱动正爆轰与二维有限长楔诱导定常斜爆轰的时空关联特性. 在一维流场中, 活塞压缩产生的高温高压区域从壁面向外扩张, 活塞表面附近的气体加热时间最长, 因此放热反应发源于壁面向前传播(interior detonation). 从时空关联的角度, 可以判断二维楔面上燃烧波从壁面引发的现象并不是边界层黏性效应的影响, 而是壁面压缩效应的结果.


3.2
壁面参数


进一步对二维和一维数值模拟结果的时空关联作定量研究, 沿用Daimon和Matsuo[15]的做法, 用楔面末端气流速度将楔面x坐标转化为时间t, 用靠近壁面的气流出口速度将壁面x坐标转化为时间t, 从而与一维壁面参数进行对比, 如图5所示. 需要指出, 本研究不考虑黏性, 壁面上采用滑移边界条件. 考虑黏性影响时, 楔面上发展出边界层, 边界层内的气流在黏性的阻滞下速度较低, 此时利用靠近壁面的气流出口速度进行时空关联并不合适. 研究表明, 黏性对斜爆轰流场的影响主要局限在边界层内部, 对斜爆轰波系结构和主流区的影响很小[28-29]. 因此, 开展黏性数值模拟时, 应选取边界层外的气流出口速度做时空转换, 此时本文研究的时空关联特性仍是成立的.

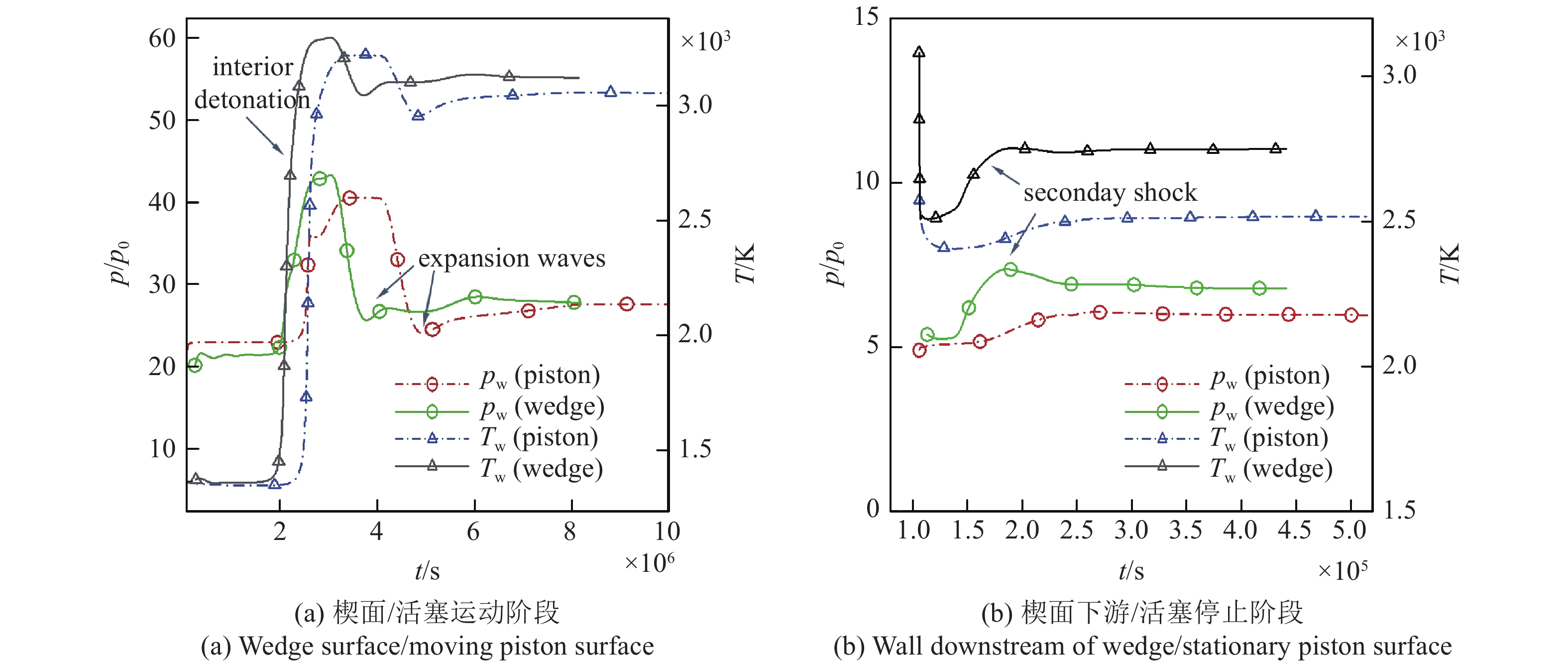
图5(a)为楔面压力、温度与活塞运动阶段表面的压力、温度对比. 可燃气体在激波后自点火产生的爆轰波造成温度、压力跃升, 产生局部高温高压. 气流通过壁面反射的膨胀波后, 温度、压力有所下降, 之后保持平稳. 图中两算例, 气体自点火的时间有一定差别, 压力、温度线型有0.4 μs左右的相位差, 其原因在3.4节中进行分析. 其他的壁面参数相差很小, 可以认为两者定量符合. 图5(b)为折角下游壁面压力、温度与活塞停止后表面压力、温度的对比. 在膨胀扇的作用下, 图5(b)的入口温度、压力低于图5(a)的出口温度、压力, 膨胀扇下游温度、压力保持平稳. 在二维数值模拟中, 折角处除膨胀扇外还产生一道二次激波, 在二次激波作用下, 壁面温度、压力有所上升, 而一维流场没有受到二次激波的影响.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/7//20-411-5.jpg'"
class="figure_img
figure_type2 ccc " id="Figure5" />



图
5
壁面压力、温度变化



Figure
5.
Wall pressure and temperature profiles



下载:
全尺寸图片
幻灯片



3.3
波形变化


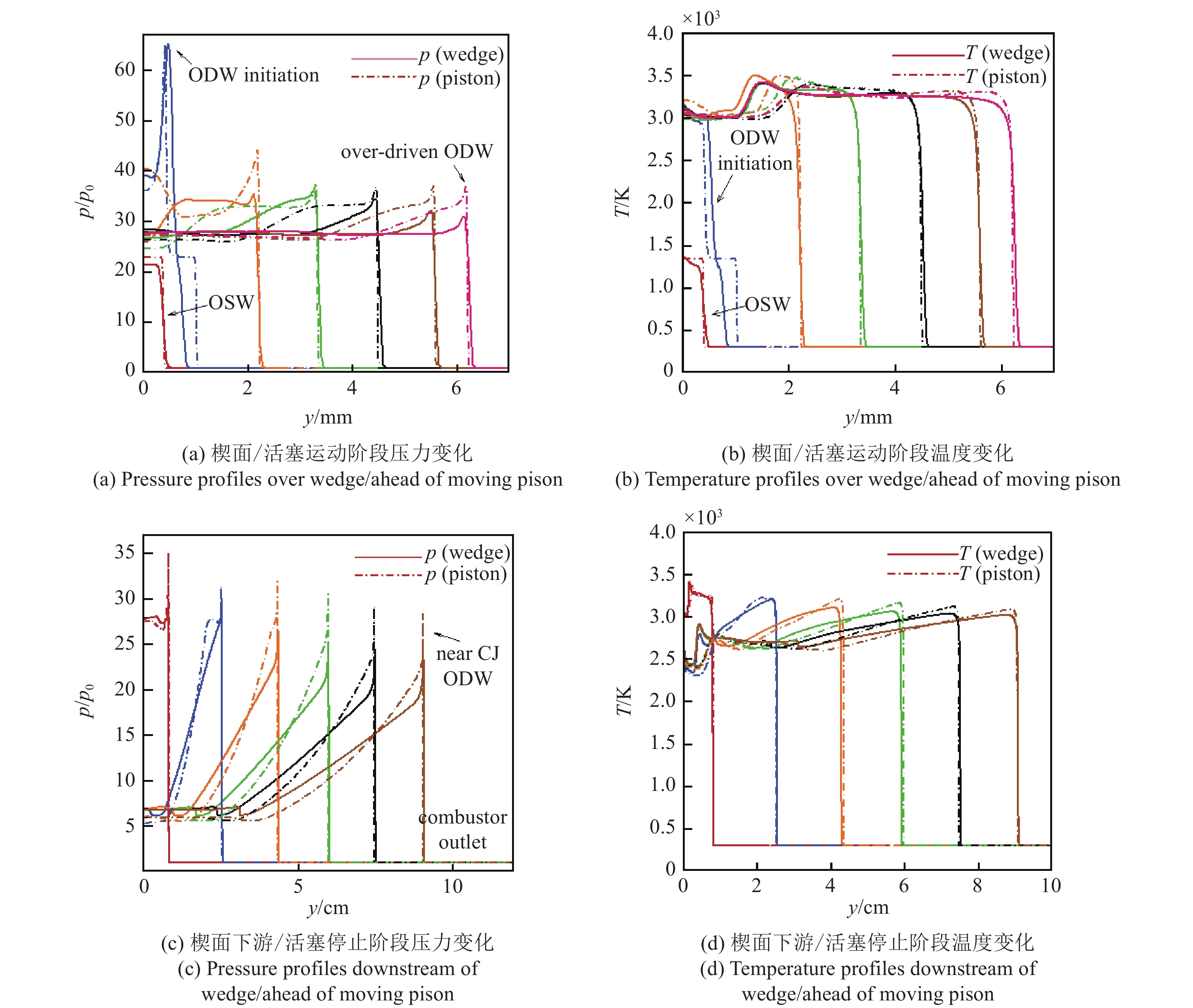
图6(a)和图6(c)显示了壁面与激波面距离相等的一系列位置处, 二维和一维压力波形的变化, 可分辨出图4(a)、图4(c)、图4(e)、图4(g)中的波系结构变化特征, 包括激波波形、起爆波形、过驱动爆轰波形和近CJ爆轰波形. 各位置处二维与一维波形定性相同, 呈现出相同的变化规律, 壁面附近压力平台的数值很接近, 但活塞驱动正爆轰的von Neumann压力峰值比斜爆轰高, 在近CJ状态下, 二维von Neumann压力峰值约为23, 而一维压力峰值约为28, 这可能是由于一维数值模拟空间分辨率更高, 得到的压力峰值更准确. 同时, 一维数值模拟结果中过驱动爆轰向CJ爆轰的演化比二维慢, 在$y = 0.06;{
m{m}}$后, 有限长楔上的压力波形基本保持不变, 而一维活塞流场在$y = 0.09;{
m{m}}$处的压力波形与$y = 0.075;{
m{m}}$处相比仍存在明显差别, 其原因在3.4节中进行分析.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/7//20-411-6.jpg'"
class="figure_img
figure_type2 ccc " id="Figure6" />



图
6
压力、温度波形变化



Figure
6.
Variation of pressure and temperature profile



下载:
全尺寸图片
幻灯片


图6(b)、图6(d)显示了与图6(a)、图6(c)对应的温度波形变化, 同样可以分辨出图4(b)、图4(d)、图4(f)、图4(h)中的结构变化特征, 包括激波波形、起爆波形、过驱动爆轰波形和近CJ爆轰波形. 由于二维和一维数值模拟的起爆距离有一定差别, 而起爆的时间尺度很短, 起爆阶段中相同位置处的波形有一定差异. 除此之外, 二维与一维的温度波形变化定量一致.


3.4
时间尺度


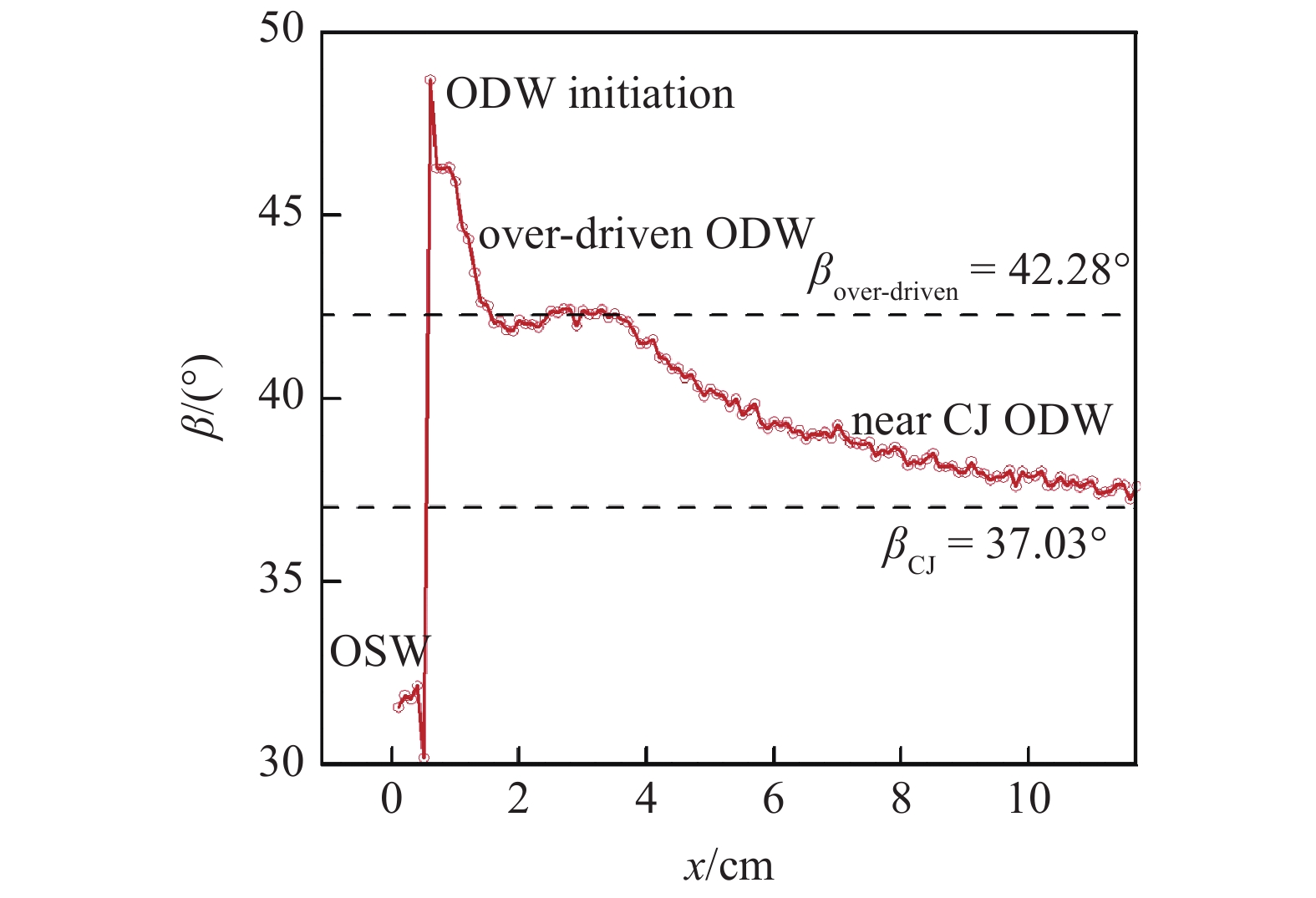
活塞运动中产生的激波、过驱动爆轰波和近CJ爆轰波处于定常状态, 而这些状态之间的转变是非定常过程, 经过时空变换后对应二维流场的结构特征. 图7显示了二维数值模拟结果中斜激波角β随坐标x的变化, 从图7中可以看出波系结构变化的各个阶段. 与斜爆轰波相比, 斜激波与来流方向的夹角较小, 约为32.20°, 与理论值32.73°接近. 斜激波与燃烧波相交形成三波点, 三波点下游波后温度迅速升高, 为了匹配波面前后的压力、温度, 斜激波变强, 激波角增大, 在三波点附近激波角达到最大值48.82°. 三波点处的反射波在壁面上再次反射, 产生膨胀波, 膨胀波透过滑移线作用在激波面上, 使激波角减小, 形成较稳定的过驱动斜爆轰波, 本文计算条件下过驱动爆轰波的激波角理论值为42.28°, 数值模拟结果与理论值符合. 楔面末端折角处的膨胀扇与过驱动斜爆轰波作用, 进一步使激波角降低, 计算条件下CJ状态的激波角为37.03°, 由图7可以看出在计算域下游激波角趋近于理论CJ激波角, 达到近CJ状态. 一维算例中激波马赫数随时间的变化也具有上述变化特征.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/7//20-411-7.jpg'"
class="figure_img
figure_type1 bbb " id="Figure7" />



图
7
有限长楔面上的斜激波角的变化



Figure
7.
Variation of oblique shock wave angle over finite wedge



下载:
全尺寸图片
幻灯片


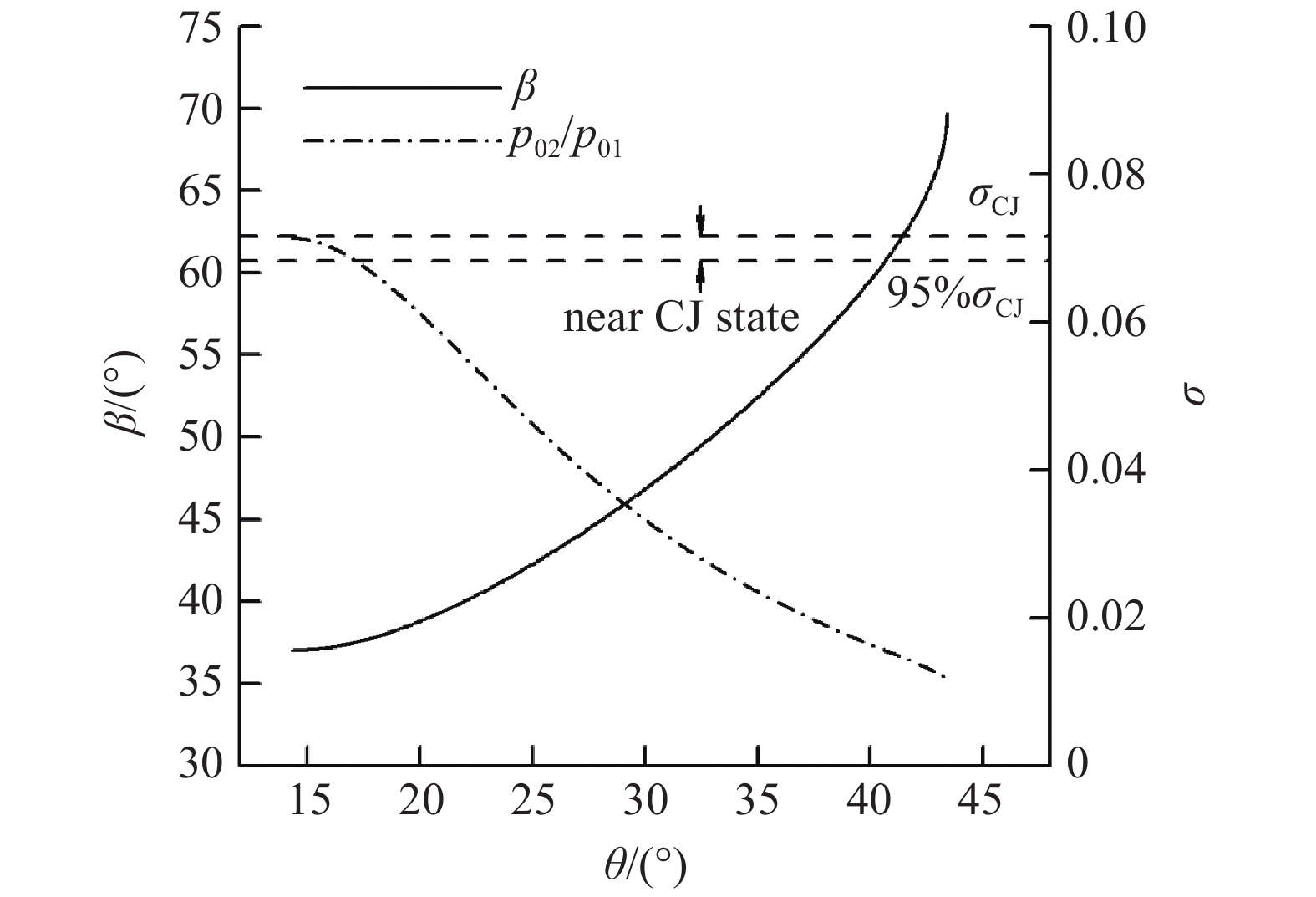
表2将一维数值模拟中非定常过程的弛豫时间与时空变换后的二维计算结果作了对比. 其中t1为激波转爆轰时间, 在计算条件下, 可燃混合气的点火延迟时间为2.59 μs, 楔面和活塞数值模拟中t1分别为2.87 μs和2.58 μs, 根据Teng等[30]的分类, 这种情况属于动力学控制(kinetics-controlled)起爆, 起爆的时间尺度与点火延迟时间相当. t2为起爆和产生稳定过驱动爆轰波之间的时间, 即壁面反射膨胀波的作用时间, 二维数值模拟得到的t2约为一维的2倍. 流动通过楔面折角或活塞停止时, 产生的膨胀扇以当地声速传播, 由于过驱动爆轰波波后是亚声速的, 膨胀扇经过t3后追上过驱动爆轰波使其弱化, 二维数值模拟得到的t3约为一维的1/2. t4为过驱动爆轰波与近CJ爆轰波之间的弛豫时间, 二维数值模拟得到的t4约为一维的1/3. 目前对近CJ状态还没有定量的界定, 本文中近CJ状态定义为气体流过波面时总压恢复σ达到CJ状态总压恢复σCJ的95%以上时的状态范围, 如图8所示.




表
2
爆轰波各发展阶段的时间尺度



Table
2.
Time duration of different stages in the development of detonation wave



table_type1 ">
Stagetwedge/μstpiston/μs
t12.872.58
t25.652.72
t35.8213.50
t425.3875.14





下载:
导出CSV
|显示表格




onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/7//20-411-8.jpg'"
class="figure_img
figure_type1 bbb " id="Figure8" />



图
8
近Chapman-Jouguet斜爆轰波的定量定义



Figure
8.
Quantitative definition of near Chapman-Jouguet oblique detonation wave



下载:
全尺寸图片
幻灯片


除起爆时间t1外, 二维与一维数值模拟结果在非定常尺度上存在显著差别. 根据理论分析, 只有波后气体在壁面切向的运动速度不变的情况下, 二维楔面诱导斜爆轰波后的气体运动方程才与一维活塞驱动正爆轰的波后气体运动方程一致. 然而在上述非定常过程中, 均存在波系相互作用, 气体速度在壁面法向的梯度较大, 选择一个特定的速度将二维空间坐标x转换为时间坐标t时存在较大误差. 因而通过活塞数值模拟无法准确预测楔面算例的非定常时间, 这种差异本质上是流动的二维效应造成的.


4.
结论


经过时空变换, 有限长楔诱导的定常斜爆轰与非定常活塞驱动的正爆轰具有相同的波系结构, 虽然两者的非定常时间尺度存在一定差异, 但爆轰参数、波形结构演化规律在定性和定量上均有较好的一致性, 体现出二维斜爆轰与一维非定常正爆轰现象存在着时空关联特性.

通过一维活塞驱动正爆轰计算, 经过时空变换方法, 能够获得相同过驱动度下的二维斜爆轰流场. 由于一维活塞驱动正爆轰理论完备, 计算结果精度高, 在斜爆轰发动机燃烧室设计等工程应用中能够有效节约计算时间、成本和复杂度. 另外, 两者的对比研究, 可以区分壁面效应、边界层效应和黏性效应的影响, 为进一步研究斜爆轰的波系结构和复杂流动提供了一种新方法.

相关话题/结构 计算 图片 运动 传播

Free考研考试FreeKaoYan.Com
欢迎来到Free考研考试，"为实现人生的Free而奋斗"

© 2020 FreeKaoYan! . All rights reserved.