 ,*,†,**,2), 包福兵*, 汪钰锟*, 杨森森*
,*,†,**,2), 包福兵*, 汪钰锟*, 杨森森*BUBBLE SLIPPING ON A SUPERHYDROPHOBIC PLANAR STRAIGHT TRAJECTORY UNDER DIFFERENT SURFACE ORIENTATIONS1)
Ye Yuhang*, Tu Chengxu ,*,†,**,2), Bao Fubing*, Wang Yukun*, Yang Sensen*
,*,†,**,2), Bao Fubing*, Wang Yukun*, Yang Sensen*通讯作者: 2)凃程旭,副教授,主要研究方向:多相流. E-mail:tuchengxu@cjlu.edu.cn
收稿日期:2020-12-1接受日期:2021-02-28网络出版日期:2021-04-08
| 基金资助: |
Received:2020-12-1Accepted:2021-02-28Online:2021-04-08
作者简介 About authors

摘要
利用特定几何分布的超疏水表面实现气泡定向输运在矿物浮选和生物孵化等领域具有广阔的应用前景, 对平面直线超疏水轨道而言, 其壁面取向是相关工程结构的关键参数, 但超疏水壁面取向对倾斜壁面气泡滑移的影响尚不明确. 本文采用高速阴影成像系统研究了不同壁面取向($-90^\circ\leqslant \beta \leqslant 90^\circ$)及轨道倾角($45^\circ\leqslant \alpha \leqslant 75^\circ$)下, 气泡($D_{eq}=2.4$ mm, $Re=500$ $\sim$ 700, $We=7$ $\sim$ 13)在轨道宽度为2 mm的超疏水直线轨道上的运动特性. 气泡在轨道上的滑移近似为匀速, 形状为具有多脊的半子弹型. 根据气液界面波动程度的不同, 滑移气泡可分为波动型和稳定型, 稳定型气泡只在较小倾角且较大方位角时出现($45^\circ\leqslant \alpha < 70^\circ$, $| \beta | \geqslant 45^\circ$). 根据倾角不同, 滑移速度关于$\beta $有2种变化规律: 当$\alpha \leqslant 65^\circ$, 气泡滑移速度近似为关于$\beta =0^\circ$ 的单峰分布($\beta =0^\circ$时, 气泡滑移速度最大); 当$\alpha \geqslant 70^\circ$, 气泡滑移速度在不同的方位角下基本保持稳定. 气泡的最大滑移速度可达0.66 m/s ($\beta =0^\circ$, $\alpha =70^\circ$), 远大于相同尺度的自由上升气泡($\approx0.25$ m/s), 这主要是壁面浸润性分布和惯性力的耦合效应所致. 轨道取向(方位角$\beta )$及轨道倾角($\alpha )$通过改变气泡沿轨道方向的驱动力和气泡迎风面积影响气泡的滑移速度和气液界面稳定性.
关键词:
Abstract
Bubble directional transportation using the superhydrophobic surfaces of different specific geometry in the water has broad application prospects in the fields of mineral flotation and biological incubation. The surface orientation of the planar straight superhydrophobic surfaces is a crucial parameter for the related engineering structures. However, it is still unclear that the effect of surface orientation on the bubble slipping along the inclined surface. The high-speed shadowgraphy is used to study the movement characteristics of the slipping bubble ($D_{eq}=2.4$ mm, $Re=500$ $\sim$ 700, $We=7$ $\sim$ 13) on the superhydrophobic linear trajectory with the width of 2 mm under different surface orientations ($-90^\circ\leqslant \beta \leqslant 90^\circ$) and inclination angles ($45^\circ\leqslant \alpha \leqslant 75^\circ$). The slipping velocity of the bubble ($u)$ on the trajectory is approximately stable, and the shape like semi-bullet with multi-ridges. The slipping bubble can be divided into two shape types: the stable and the unstable according to the fluctuation level of the gas-liquid interface. Stable bubble only appear when the inclination angle is small and the azimuth angle is large ($45^\circ\leqslant \alpha <70^\circ$, $| \beta | \geqslant 45^\circ$). As $\alpha $ changes, two kinds of $u$-$\beta $ relations can be found: When $\alpha \leqslant 65^\circ$, the slipping velocity is approximately a unimodal distribution about $\beta =0^\circ$ (the maximum sliding velocity at $\beta =0^\circ$); When $\alpha \geqslant 70^\circ$, the azimuth angle has no significant influence on $u$. The maximum sliding velocity can be upto 0.66 m/s ($\beta =0^\circ$, $\alpha =70^\circ$), which is much higher than that of the free-rising bubble of the similar size ($\sim$0.25 m/s), mainly as a combined effect of the wall-wettability and the inertial force. Surface orientation ($\beta$) and trajectory inclination angle ($\alpha$) affect the slipping velocity and the stability of the gas-liquid interface by changing the driving force, as a buoyance component, of the bubble along the trajectory direction and the bubble frontal area.
Keywords:
PDF (4828KB)元数据多维度评价相关文章导出EndNote|Ris|Bibtex收藏本文
本文引用格式
叶煜航, 凃程旭, 包福兵, 汪钰锟, 杨森森. 不同壁面取向下超疏水平面直轨道上的气泡滑移1). 力学学报[J], 2021, 53(4): 962-972 DOI:10.6052/0459-1879-20-405
Ye Yuhang, Tu Chengxu, Bao Fubing, Wang Yukun, Yang Sensen.
引言
气液两相系统在自然界和工业过程中广泛存在, 包括细胞孵化[1]、矿物浮选[2]、电解[3-6]等. 例如在电解过程中基底表面的气泡堆积会导致能耗提高[4-6], 因此需要降低气泡在壁面的停留时间. 相反, 矿物浮选过程中则希望气泡与矿物浆液充分接触使其表面附着更多的待选矿物[2]. 气泡运动速度的大小影响着化学反应器中的反应效率[7]. 因此, 气泡在壁面附近的运动模式及其操控对上述过程至关重要.近来, 具有特定浸润性几何分布的表面被用于气泡的定向输运, 其相关研究获得高度关注, 工程应用前景广阔. 截至目前, 在水环境中主要通过Laplace压差或者浮力两种方式实现气泡自发的定向输运[8]. 近年来的许多研究中, 科研人员通过具有壁面润湿性的几何梯度构建Laplace压差来实现气泡的输运, 具体壁面形式为超疏水铜锥[9-12]、梯形超疏水轨道[13-15]、楔形线性阵列超疏水轨道[16]、超疏水 非平行双轨道[8]. 除了超疏水双轨道外, 气泡总是从轨道窄的一端自发移动到宽的一端. 在一定几何梯度下的超疏水表面能够实现气泡的抗浮力输运[10,13,17]. 然而, 基于Laplace压差法定向输运气泡仅限于短距离($\sim$ O(10 mm))低速($\sim$ O(10 mm/s))的定向运输[9,14], 未能解决气泡长距离高速输运问题. 基于浮力法则可实现气泡的长距离定向连续输运, 超疏水轨道可以是直线[18-19]、S形[20]、螺旋形[21]. 当壁面的倾角较小时($\theta < 30^\circ$), 气泡的滑移速度较小. 随着壁面的倾斜度增大, 浮力的作用显著提升, 气泡在轨道上的滑移速度增大. 当壁面倾角较大($\theta > 30^\circ$)时, 尽管存在局部浮力效应[22], 但壁面的超疏水性仍促使气泡在水中滑动速度比气泡自由上升的速度快[18], 在不同疏水性的倾斜下表面, 毫米级气泡(直径1.79$\sim$3.06 mm)的最大滑移速度发生在$60^\circ\leqslant \theta \leqslant 70^\circ$[18]. 对于垂直疏水表面($120^\circ \leqslant CA \leqslant 125^\circ$), Jeong和Park[23]的研究发现, 在很小的初始距离下气泡可以在这些表面上滑动而不逃逸, 但气泡不能在渗透壁或弱亲水性表面黏附和滑动, 这与最近的数值结果[24]相矛盾.
上述气泡滑移现象的物理本质是气泡与周围流体的相互作用伴随三相接触线的钉扎和解钉[25-27]. 接触线在固体表面上的钉扎主要是由于受固体表面粗糙度或表面化学不均匀性的影响[25]. 对于自由上升气泡, 气泡的形状决定了气泡滑移的终了速度, 而气泡形状由浮力、形状阻力、表面张力等力的平衡所确定[24]. 相对于自由上升气泡, 贴壁气泡需额外考虑壁面剪切力、接触线钉扎等因素. 值得注意的是, 基于浮力的简单模型($F_{B}=\rho gV$)不适用于倾斜壁面的气泡动力学的精确分析[22]. 目前, 倾斜超疏水壁面的倾角对气泡滑移运动的相关研究较少[18], 超疏水壁面取向对气泡滑移的影响尚不清楚, 而壁面取向是诸多工程结构的重要参数, 如精馏塔翅片. 为此, 本文采用高速阴影成像系统对不同壁面取向及倾角下气泡在超疏水轨道上的运动特性进行了实验研究(雷诺数$Re=500\sim700$, 韦伯数$We=7\sim13$), 以期为该气泡操控技术在核反应堆、矿物浮选、池沸腾等领域的应用提供科学依据和创新思路.
1 实验方法
1.1 超疏水直线轨道(SHBT)的制作
在洁净的玻璃基底表面贴上预留有后续喷涂区域的掩膜, 将纳米SiO$_{2}$溶液(Glaco, Soft99 Co., Japan, SiO$_{2}$初始粒径为30 nm, 溶剂为异丙醇)喷涂在玻璃基底上, 多次喷涂烘干后在玻璃基底表面形成SiO$_{2}$纳米涂层, 由此得到超疏水轨道. 如图1(a)所示, 玻璃基底表面附着有一层致密的纳米二氧化硅涂层, 表面粗糙度约为100 nm[28]. SHBT表面存在大量的微孔结构, 夹带着气体形成气穴和薄气膜, 水滴沉积其上表现出超疏水性, 而在水环境中呈现出超亲气性, 因此超疏水表面在水环境中对气泡具有极强的附着力. 详细的超疏水轨道制作方法参见Tu等[29]最近的研究结果. 利用上述方法得到的超疏水轨道其表观接触角如图1(b), 约为162$^\circ$, 滚动角$<2^\circ$.图1
 新窗口打开|下载原图ZIP|生成PPT
新窗口打开|下载原图ZIP|生成PPT图1超疏水轨道实物图
Fig.1Physical picture of superhydrophobic trajectory
1.2 实验装置
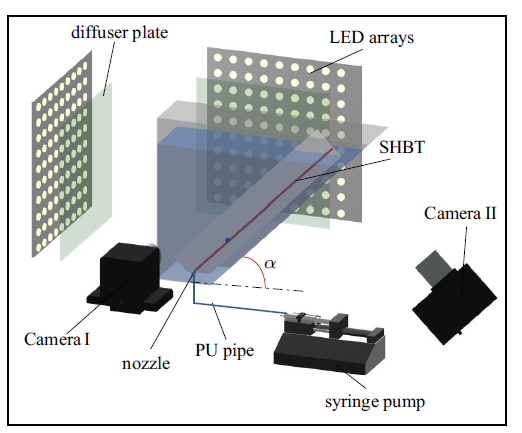
本研究采用的气泡生成装置和高速阴影成像系统如图2所示. 由注射泵(Harvard Pump 11 Elite, Hollision, MA)推动注射器往不锈钢喷嘴(喷嘴内径为0.26 mm)注气, 从而在水箱底部产生气泡. 注射器与喷嘴通过聚氨酯圆管(PU管)连接, 注射泵注射流量设定为0.1 mL/min. 实验采用纯净水, 水箱为亚克力透明水箱, 且其中一个侧面为倾斜面(倾角$\alpha $ (图2)).图2
 新窗口打开|下载原图ZIP|生成PPT
新窗口打开|下载原图ZIP|生成PPT图2实验装置图
Fig.2Experimental setup
气泡从喷嘴处自由脱离后具有高度轴对称性, 根据此刻的气泡投影轮廓计算得到气泡的等效直径($D_{eq})$是2.4 mm、体积($V)$为7.3 $\mu $L. 高速阴影成像系统由两台高速CCD相机(FASTCAM Mini UX, Photron)、微距镜头(AT-X Pro, Nikon)和LED阵列组成, 从两个正交视角同步记录气泡的上升, 高速相机帧率为2000, 相应分辨率为1280 $\times$ 1024像素. 一台相机视场平行于SHBT中心线且在竖直面内(相机I), 另一台相机视场与水箱倾斜面平行(相机II), 结合LED阵列和匀光板构成双视角的高速阴影成像系统, 捕捉气泡在超疏水轨道上的滑移.
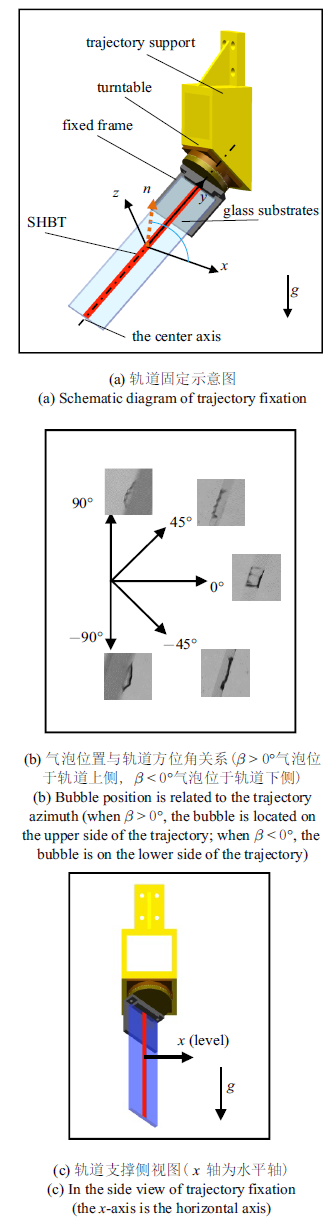
具有超疏水轨道的玻璃基底通过固定架与转台固定, $g$为重力加速度(图3), 图中$y$轴沿轨道中心轴线方向(斜向上为正), $x$轴在水平面内且垂直于$y$轴(当基底平面为竖直平面时, $x$轴恰好与基底的法线方向重合), $z$轴与$xy$平面垂直, $m$轴为$xz$平面与基底平面的交线, 玻璃基底平面法线$n$位于$xz$平面内, 与$x$轴的夹角为$\beta $, 通过转动转台使超疏水轨道绕其中心轴线转动, 改变轨道表面取向, 即改变$\beta $ (方位角, $-90^\circ\leqslant \beta \leqslant 90^\circ$), 间隔15$^\circ$ 取一个工况. $\beta > 0^\circ$ 气泡位于轨道上侧, $\beta < 0^\circ$ 气泡位于轨道下侧. 图4(a) $\sim\!$图4(c)为相机I在3个重要方位角($-90^\circ$, 0$^\circ$, 90$^\circ$)所拍摄的典型气泡图像. 图4(a) $\beta = -90^\circ$, 气泡位于轨道下方; 图4(b) $\beta =0^\circ$, 气泡位于竖直面内; 图4(c) $\beta =90^\circ$, 气泡位置位于轨道上方. 转台固定于轨道支撑, 使得图3中轨道与水平面夹角为$\alpha $角(轨道倾角, $\alpha =45^\circ$, 60$^\circ$, 65$^\circ$, 70$^\circ$, 75$^\circ$).
图3
 新窗口打开|下载原图ZIP|生成PPT
新窗口打开|下载原图ZIP|生成PPT图3倾斜超疏水轨道支撑装置示意图
Fig.3Schematic diagram of inclined superhydrophobic trajectory fixation
图4
 新窗口打开|下载原图ZIP|生成PPT
新窗口打开|下载原图ZIP|生成PPT图4$\alpha =70^\circ$ 时3个重要方位角的典型气泡图像(相机I测得)
Fig.4Typical bubble images captured using Camera I in three important azimuths at $\alpha =70^\circ$
超疏水轨道底端在竖直方向上距喷嘴顶端约为4 mm. 浮力作用下, 气泡从喷嘴口完全脱离后, 在壁面与气泡之间的流体开始以一定的速度流动, 此时周围流体产生的正压力驱动气泡向壁面迁移[23,30], 气泡与壁面之间的流体变薄并最终发生破裂, 气泡受到壁面的气膜黏性效应影响附着于轨道表面. 实验过程中每个工况重复5 $\sim$ 10次, 终了速度误差范围在10${\%}$以内.
2 实验方法
2.1 气泡稳定性
针对气泡在不同方位角的SHBT上滑移的稳定性, 本文从气泡形状和气泡上升速度两方面进行分析.超疏水轨道表面存在一层薄气膜, 长期置于水中会造成气膜不稳定导致轨道失效[18,31], 此外轨道放入水中的浸没速度对轨道表面气膜的形成至关重要[32], 而在本文的实验过程中, 连续有气泡在SHBT上滑移, 其稳定的终了速度表明气膜的厚度是较为稳定的. 由于轨道表面铠甲状气膜的存在[28]和三相接触线在轨道表面的钉扎, 使得气泡稳定附着于壁面. 当气泡所受浮力克服壁面对气泡的钉扎, 气泡将沿着壁面开始滑移[25]. SHBT特殊的表面微观结构(CAH($\Delta \theta < 2^\circ$))可以较好维持其水下壁面气膜的稳定, 极小的亲气角(等价较大的疏水角)表明其轨道的表面能极低, 使得气泡在浮力的作用下能够轻松克服表面缺陷能垒而滑移[33], 而滑移的过程实际是三相接触线的滑移-钉扎状态(stick-slip 状态).
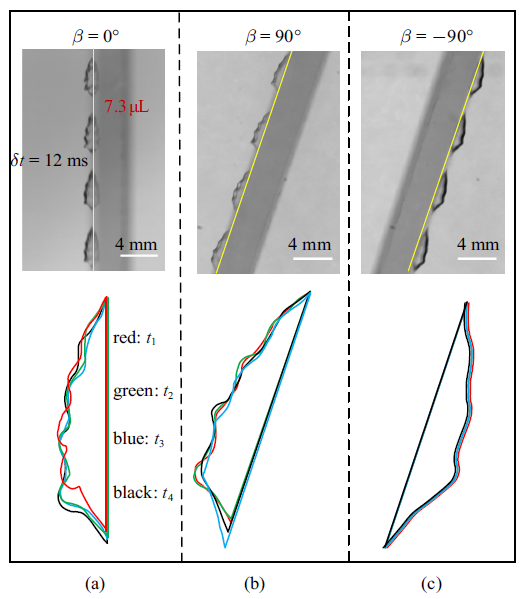
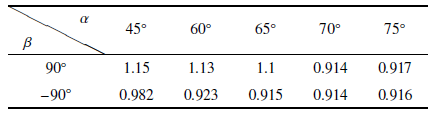
如图5, 当$V=7.3$ $\mu $L的气泡在$W=2.0$ mm的超疏水轨道上运动, 气泡整体呈现为具有多个峰脊的半子弹型, $Re=500$$ \sim$ 700. 图5为$\alpha =70^\circ$, $\beta =90^\circ$, 0$^\circ$, $-90^\circ$, 不同时刻下气泡的阴影成像轮廓(图下侧轮廓线分别为4个时刻($t_{1}=0$ ms, $t_{2}=12$ ms, $t_{3}=24$ ms, $t_{4}=36$ ms)气泡轮廓的叠加, 黄色线为壁面). 由于气泡表面毛细波的存在, 气泡在运动过程中呈现出多脊型[34], 根据气泡的气液界面是否存在显著波动可分为波动型和稳定型. 波动型如图5(a)和图5(b)所示, 气泡在运动过程中, 气液界面存在剧烈波动, 图中气泡轮廓线重合度较低, 而稳定型在气泡运动过程中, 形状基本保持稳定, 不同时刻下气泡轮廓线高度一致(图5(c)). 当轨道倾角较低时($\alpha \leqslant 65^\circ$), 随着$\beta $从$\pm90^\circ$ 逐渐接近0$^\circ$, 气液界面由稳定状态向非稳定状态转变, 失稳的临界点均在$\sim$ 30$^\circ\leqslant | \beta | \leqslant 45^\circ$. 随着$\alpha $的增大, 失稳临界点向$| \beta |\sim 90^\circ$ 逐渐靠近, 气泡在SHBT上方($\beta > 0^\circ$)较之气泡在SHBT下方($\beta < 0^\circ$)更易产生波动, 这可能与气液界面在$m$轴方向受到的静压大小有关. 当$\beta =\pm90^\circ$ 时, 气液界面所受的静压在$xz$平面上的分量方向与壁面法线方向重合, $m$轴方向受到的静压分量为0, 气液界面较为稳定. 随着$\beta $从$\pm90^\circ$ 逐渐接近0$^\circ$, $xz$平面上的静压分量的方向偏离壁面法线方向, $m$轴方向受到的静压分量增加, 气液界面受力对称性破坏, 导致气液界面逐渐失稳. 当气泡在轨道正上方滑移时($\beta =90^\circ$), 气泡在轨道法向上的高度(类似于粗糙元特征尺度)大于气泡在轨道正下方($\beta =-90^\circ$)滑移时的高度, 使得后者的气泡形状稳定性高于前者(表1).
图5
 新窗口打开|下载原图ZIP|生成PPT
新窗口打开|下载原图ZIP|生成PPT图5SHBT轨道上, 不同时刻气泡形状($\alpha =70^\circ$, $t_{1}=0$ ms, $t_{2}=12$ ms, $t_{3}=24$ ms, $t_{4}=36$ ms)
Fig.5Bubble shapes at different times in the SHBT trajectory ($\alpha =70^\circ$, $t_{1}=0$ ms, $t_{2}=12$ ms, $t_{3}=24$ ms, $t_{4}=36$ ms)
Table 1
表1
表1$\beta =\pm90^\circ$ 不同$\alpha $下的气泡高度 (mm)
Table 1
 |
新窗口打开|下载CSV
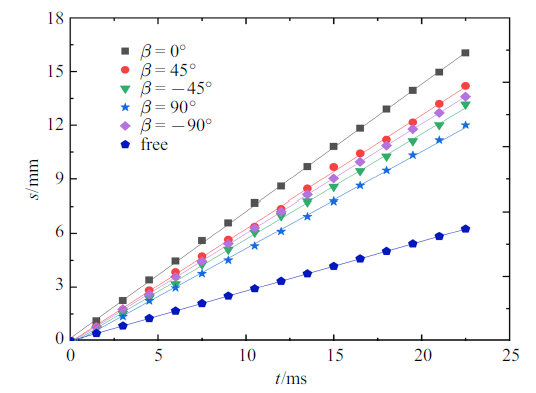
通过监测滑移过程中气泡质心的位置随时间的变化, 可以确定气泡在超疏水轨道上运动的稳定性. 如图6给出了$\alpha =60^\circ$, 不同$\beta$下气泡在超疏水轨道上滑移距离随时间的变化, 以气泡完整出现在相机视场中作为统计气泡位置的初始时刻. 图中纵坐标为气泡沿轨道方向上质心相对于初始时刻位置的位移, 横坐标为气泡在轨道上的运动时间. 无论是自由上升气泡还是在SHBT上滑移的气泡, 其位移与运动时间($s$-$t)$二者强线性相关(图6), 线性函数的斜率(即气泡的运动速度)随方位角的不同而不同, 但都大于自由上升气泡. $s$-$t$的高水平线性相关说明气泡沿轨道的终了速度波动很小, 气泡近似处于受力平衡状态. Jeong和Park[23]的研究成果也表明气泡在竖直均匀疏水壁面的滑移速度基本恒定.
图6
 新窗口打开|下载原图ZIP|生成PPT
新窗口打开|下载原图ZIP|生成PPT图6$\alpha =60^\circ$, 不同$\beta $下, 气泡沿轨道方向滑移距离$s$随时间$t$变化图
Fig.6$\alpha =60^\circ$, the sliding distance of bubble along the trajectory direction varies with time under the different $\beta $
2.2 受力分析
气泡在超疏水轨道上运动时受到浮力、形状阻力、轨道表面分裂力(源于接触线在SHBT表面上的钉扎)及附加质量力的影响.壁面的存在会导致气泡的局部浮力效应[22], 浮力的本质是静水压差, 可将静压对气泡的作用力分为竖直作用力$F_{V}$和水平作用力$F_{H}$. 竖直方向静压力$F_{V}$是在气液界面$A$上对静压二重积分, 可利用高斯公式, 将其转化为气泡的体积分, 并减去轨道$B$面所受竖直方向的静水压力, 所以竖直方向静压力$F_{V}$方程右边第一项表示等效直径气泡所受竖直方向上的静水压力, 第二项表示轨道气固界面(面$B$)所受竖直方向的静水压力. 式中, $\rho $为水的密度, $g$为重力加速度, 为9.81 m/s$^{2}$, $V$为气泡等效体积, $W$为轨道宽度, $\theta _{f}$为曲面微元d$S$法线方向与竖直方向(向上)的夹角, $L$为气泡与轨道单侧接触线长度.
静水压力对气液界面$A$在水平方向上的作用力为$F_{H}$
式中$\theta_1$为轨道壁面与水平面的夹角$(\alpha\leqslant\theta1\leqslant90^{\circ})$.
气泡运动过程中的驱动力$F_{driven}=F_{V}\sin{\alpha}+F_{H}\cos\theta_2$
式中
$\begin{eqnarray*} f(\alpha,\beta,\theta_1,\theta_2)=\sin^2\alpha\cos\alpha \vert \sin\beta \vert -\sin\alpha \cos \theta_2 \sin^2 \theta_1 \end{eqnarray*}$
式中$\theta_2$为水平静压力$F_{H}$与轨道中心线($y$轴正向)的夹角($\alpha \leqslant \theta_2\leqslant 90^{\circ}$), 不同$\alpha$, $\beta$对应的$\theta_1$, $\theta_2$的值参见附件表1.
气泡在水环境中受到的形状阻力$F_{D}$
$C_{D}$为阻力系数(包括形状阻力和黏滞阻力); $A_{f}$为迎风面积, 实验结果表明气泡滑移时的迎风面积与超疏水轨道的倾角及方位角高度相关.
因为超疏水表面的低表面能, 接触线钉扎解钉所需的轨道表面分裂力$\Delta F$可采用[25,35]
式中, $\kappa $为欧拉常数, $\lambda $为典型缺陷尺寸, $f_{c}$为逃脱能垒的临界力, $a/\lambda $为缺陷线密度, $k_{B}$为玻尔兹曼常数, $T$为弛豫率, $f_{T}$为热力, $K_{0}$为尝试频率, $E_{b}$为潜在的能量势垒, $k_{s}$为气液界面的弹性系数.
对于静止液体中加速的气泡, 附加质量力[23-24]如下
其中, $C_{m}$为附加质量系数, $\rho_{b}$为气体密度, 对于扁球形气泡, $C_{m}$取决于气泡的纵横比.
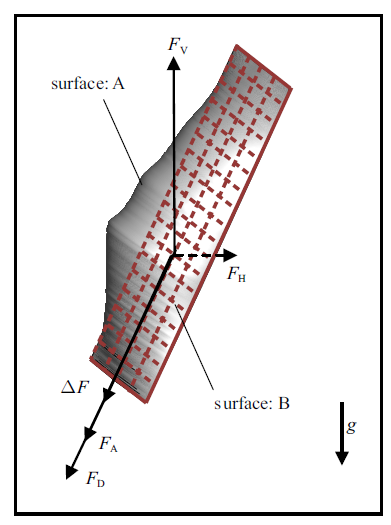
综上, SHBT上滑移气泡的受力模型如图7所示, 忽略气泡受到的重力, 气体与壁面间的黏性阻力(nN量级)远小于驱动力及形状阻力(约50 $\mu $N), 从而忽略不计.
图7
 新窗口打开|下载原图ZIP|生成PPT
新窗口打开|下载原图ZIP|生成PPT图7气泡运动受力模型
Fig.7Motion force model of bubble
故沿轨道方向气泡受力方程为
如前文所述, 气泡在轨道上可近似为匀速运动, 因此附加质量力可以忽略, 此外超疏水轨道滚动角较小, 接触角滞后力可忽略不计, 接触线耗散弱, 轨道表面分裂力量级较小(约0.1 $\mu$N)[36]. 因此式子(7)可简化为
故气泡运动主要受(气液界面静压产生的)驱动力及形状阻力影响. 联立方程式(3)、式(4)和式(8), 可得气泡滑移速度与迎风面积的关系
由实验结果反映的气泡迎风面积与倾角和方位角的相关性, 结合式(4)和式(9)可知, 倾角和方位角对气泡滑移速度的影响机制在于, 倾角和方位角的改变导致了气泡迎风面积和有效浮力的变化, 而后两者是气泡滑移速度的关键影响因素.
2.3 轨道倾角和方位角对气泡滑移速度影响
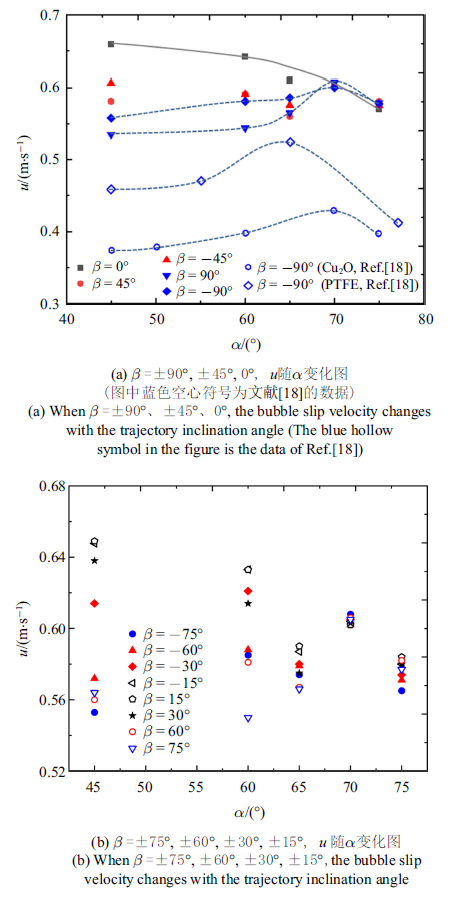
图8给出了不同方位角下, 气泡沿轨道方向的滑移速度随着$\alpha $增加的变化曲线. 对于$45^\circ\leqslant \alpha \leqslant 75^\circ$, 不同方位角下气泡的滑移速度相对于自由上升气泡(0.2 $\sim$ 0.3 m/s)始终维持在一个较高的水平(0.53 m/s $\leqslant u \leqslant 0.66$ m/s). 气泡等效直径$D_{eq}=2.4$ mm, 在轨道上的滑移速度最快可达0.66 m/s, 明显大于其他类型超疏水表面的结果[18]. Maleprade等[37]采用尼龙绳控制气泡倾斜运动, 速度也仅为0.1 m/s. Wu等[18]使用的Cu$_{2}$O超疏水轨道($\theta \approx 160^\circ$)和聚四氟乙烯超疏水轨道(PTFE, $\theta \approx 175^\circ$), 粉末粒径约为74 $\mu $m, 轨道表面粗糙度为微米级, 两种超疏水倾斜表面上的气泡最高速度分别约为0.42 m/s (Cu$_{2}$O超疏水轨道)和0.53 m/s (PTFE超疏水轨道). Glaco Soft 99溶液静置干燥形成的超疏水轨道, 表面粗糙度约100 nm[28], 本研究利用阴影成像测量经Glaco Soft 99喷涂干燥的轨道表面所附着的气膜厚度在微米级, 与Landau-Levich公式计算的理论值[32]很接近. 无论是静置还是喷涂得到的水平超疏水表面, 气泡在其上铺展时, 三相接触线的铺展演化过程都非常相似, 最高运动速度都可达1.0 m/s[28-29,38]. 对表面微观形貌而言, 由于Cu$_{2}$O轨道和纳米SiO$_{2}$轨道表面粗糙度差异较大, 使得Cu$_{2}$O轨道的钉扎作用强于纳米SiO$_{2}$轨道[25-26,34], 而且三相接触线在Cu$_{2}$O轨道移动时其在轨道法线方向上需克服的浸润距离(约 10$^{2}$ $\mu $m)[34]远大于纳米级的SiO$_{2}$轨道, 因此气泡在两种轨道上运动存在明显的速度差. 相同大小的气泡在超疏水轨道上呈多脊型, 气泡的迎风面积远小于单丝上滑移的类球形气泡[37].图8
 新窗口打开|下载原图ZIP|生成PPT
新窗口打开|下载原图ZIP|生成PPT图8不同$\beta $下, 气泡滑移速度$u$随$\alpha $变化图
Fig.8Bubble slip velocity changes with the trajectory inclination angle for different azimuth angles
此外, 气泡滑移速度随$\alpha $增大的变化规律根据$\beta$的不同可归纳为3种基本模态:
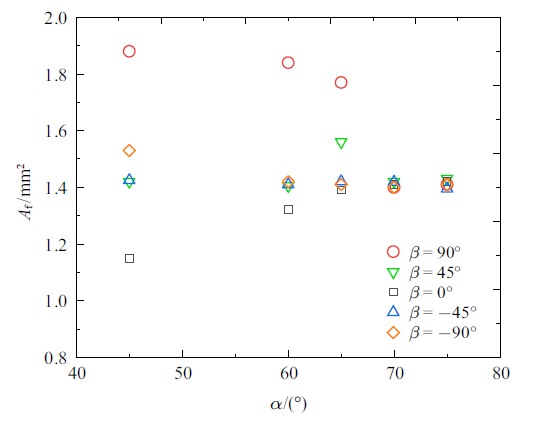
(1) 当$\beta =-90^\circ$, 随着$\alpha $的增大, 气泡受到的驱动力$F_{driven}$增强, 气泡沿轨道方向滑移速度增大, 在$\alpha =70^\circ$ 时, 滑移速度达到最大值$u=0.6$ m/s. 随着倾角继续增大, 滑移速度下降. 该特性与Wu等[18]实验结果一致. $\beta =90^\circ$, 气泡滑移速度随着$\alpha $的增大先增大后减小, 其规律与$\beta =-90^\circ$ 相似, 变化趋势更为剧烈. 特别当$\beta =\pm90^\circ$, 气泡滑移速度在$\alpha > 70^\circ$ 开始下降, 图9的气泡迎风面积数据表明这很可能是由于迎风面积的增大导致的. 其余角度下的气泡迎风面积难以提取, 仅能获取到$\beta =\pm90^\circ$, $\beta =\pm45^\circ$, $\beta =0^\circ$ 这5个典型的角度下的气泡迎风面积.
图9
 新窗口打开|下载原图ZIP|生成PPT
新窗口打开|下载原图ZIP|生成PPT图9不同$\beta $下气泡迎风面积与$\alpha $关系
Fig.9Relation between the frontal area of bubble and $\alpha $ under different $\beta $
(2) 当$\beta =0^\circ$, 气泡位于竖直面内, 滑移速度随着倾角的增大而减小. 显然也是受到气泡的迎风面积的影响(图9), 随着$\alpha $的增大气泡迎风面积明显增大, 形状阻力对气泡运动的影响占主导.
(3) 当$\beta =\pm45^\circ$时, $Re\sim$ O(10$^{2})$, 高$We\sim$ O(10)数的近壁气泡运动过程中, 惯性力起主导作用, 气泡开始出现形状不稳定[39], 且气泡界面压力在垂直于运动方向平面($xz$平面)内的分力偏离壁面法线方向, 破坏了气液界面对称性, 气液界面产生波动. 气泡的迎风面积$A_{f}$随着轨道倾角的变化存在一定的波动(图9), 与气泡的滑移速度呈负相关.
图8(b)表明$\pm$75$^\circ\leqslant \beta \leqslant \pm90^\circ$, 气泡滑移速度随$\alpha $的变化规律与模态I相似, $0^\circ\leqslant \beta \leqslant \pm15^\circ$, 滑移速度随着倾角的变化与模态II相似. $\pm30^\circ\leqslant \beta \leqslant \pm65^\circ$, 气泡滑移速度随着$\alpha $的变化与模态III相似.
有趣的是, 不同$\beta $气泡滑移速度的变化曲线, 都在$\alpha =70^\circ$ 处开始交汇. 通过对比$\beta =\pm90^\circ$, $\beta =\pm45^\circ$, $\beta =0^\circ$下, 气泡迎风面积随$\alpha $的变化规律(图9), 结果表明在$\alpha \leqslant 65^\circ$时, 不同方位角下气泡的迎风面积存在较大的差异; 当$\alpha \geqslant 70^\circ$ 时, 不同方位角下气泡迎风面积基本重合(图9; 不同方位角下气泡迎风面积的比值参见附表2). 因此, 在$\alpha \geqslant 70^\circ$ 时, $\beta $对气泡滑移速度影响较小, 此时不同$\beta$下的气泡滑移速度非常接近.
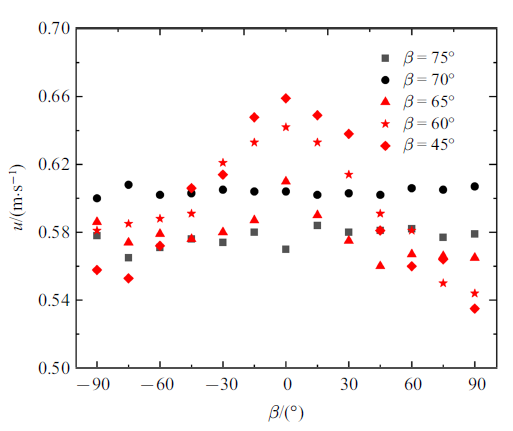
气泡沿着超疏水轨道的滑移速度随着轨道方位角的增加呈现出2种不同的变化趋势. 不同倾角下, 滑移速度随方位角的变化特性如图10所示.
图10
 新窗口打开|下载原图ZIP|生成PPT
新窗口打开|下载原图ZIP|生成PPT图10不同轨道倾角下, 气泡沿轨道滑移速度$u$随$\beta $变化图
Fig.10Sliding velocity of bubble along the trajectory varies with the azimuth angle for different trajectory inclination angles
第一种$u$-$\beta $分布: 当轨道倾角$45^\circ\leqslant \alpha \leqslant65^\circ$ 时, 气泡滑移速度随着$\beta $从$-90^\circ$ 逐渐增大至90$^\circ$, 其值先增大后减小, 近似为关于$\beta=0^\circ$ 的单峰分布. $\alpha =45^\circ$, $\beta =0^\circ$ 时, 气泡的滑移速度最大(约0.66 m/s). 较小倾角下($\alpha <70^\circ$), $\beta$直接决定了气泡滑移时的基本形态, 不同的方位角下气泡的形态不同(图11, 黄线为壁面, 正视图(相机I)). 气泡的迎风面积受$\beta $的影响(图9), 随着$\beta =\pm90^\circ$ 趋近于$\beta =0^\circ$, 气泡的迎风面积逐渐减小.
图11
 新窗口打开|下载原图ZIP|生成PPT
新窗口打开|下载原图ZIP|生成PPT图11$\alpha =45^\circ$, 不同方位角下气泡形态图
Fig.11When $\alpha =45^\circ$, the shape of bubble at different azimuths
第二种$u$-$\beta $分布: 当$\alpha \geqslant 70^\circ$ 时, 随着方位角变化, 气泡的滑移速度围绕某一定值小幅波动. 图12 (黄线为壁面, 正视图(相机I))中所示不同方位角下, 气泡运动形状基本一致, 迎风面积$A_{f}$的值较为相近 (图9), 对方位角的改变不敏感. 方位角的变化对大倾角($\alpha \geqslant 70^\circ$)下气泡滑移速度的影响较小, 且当$\alpha =70^\circ$ 时不同方位角下的气泡滑移速度最为相近.
图12
 新窗口打开|下载原图ZIP|生成PPT
新窗口打开|下载原图ZIP|生成PPT图12$\alpha =70^\circ$, 不同方位角下气泡形态图
Fig.12When $\alpha =70^\circ$, the shape of bubble at different azimuths
气泡沿轨道方向上的驱动力$F_{driven}$是气泡滑移的主要动力, 也是出现上述两种$u$-$\beta $分布的关键因素之一. 当$\alpha $恒定时, 式(3)中气泡驱动力$F_{driven}$中第一项$\rho gV\sin\alpha $为一定值, 第二项$\rho gWL^{2}f(\alpha $, $\beta $, $\theta_{1}$, $\theta_{2})$/2随着$\beta $的改变而改变, 即随着$\beta $从$-90^\circ$ 到90$^\circ$, 第二项的值先减小后增大(拐点为$\beta =0^\circ$). 因此, 驱动力先增大, 在$\beta =0^\circ$ 时达到最大值($\rho gV\sin\alpha)$, 然后减小. 当$\beta =\pm90^\circ$, 局部浮力效应[22]最明显, 气泡驱动力最小.
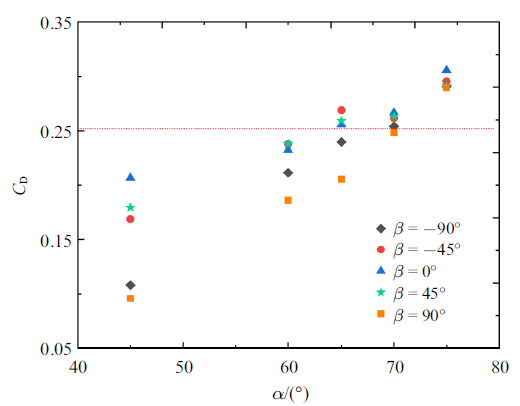
气泡在小倾角($45^\circ\leqslant \alpha \leqslant 65^\circ$)轨道上滑移, 由于$\alpha $较小, 第一项($\rho gV\sin \alpha )$占比较小, 所以驱动力中第二项的值对驱动力的大小影响较大, 故气泡的$u$-$\beta $分布在小倾角下表现为近似于驱动力关于$\beta =0^\circ$ 的($F_{driven}$ - $\beta )$单峰正弦分布. 对于大倾角($70^\circ \leqslant\alpha \leqslant 75^\circ$)轨道, 第二项随$\alpha $的增大单调递减($f(\alpha $, $\beta $, $\theta_{1}$, $\theta _{2})$的值变化见附件表3), 同时$\alpha $的增大使得第一项($\rho gV\sin \alpha )$的值增加, 因此第二项的占比进一步减小, 对驱动力大小的影响较小. 当$\alpha =90^\circ$ (壁面竖直), 驱动力的第二项为0, 即方位角的变化对气泡滑移时的驱动力没有影响. 另一方面, 当$\alpha \geqslant 70^\circ$, 不同$\beta $下气泡滑移时的迎风面积基本一致(见图9), 表明大倾角下$A_{f}$与$\beta $无关. 综述两方面, 大倾角下气泡在轨道上滑移的驱动力和迎风面积在不同的$\beta $下非常接近, 这很可能是大倾角下气泡滑移速度随$\beta $的增加基本保持不变的原因(第二种$u$-$\beta $分布). 气泡在超疏水轨道上的运动主要受浮力及形状阻力的影响, 而气泡的形状阻力可以通过阻力系数($C_{D})$进行量化. 对于自由上升的气泡($Re\sim$ O(10$^{2}))$, 其$C_{D}\approx 0.25$[40], 而本文中超疏水轨道上运动的多脊型气泡阻力系数$C_{D}\approx 0.1\sim0.3$, 变化范围较大, 且不同方位角下的阻力系数与倾角存在明显的正相关(图13, 红色虚线为自由上升气泡的$C_{D})$.
图13
 新窗口打开|下载原图ZIP|生成PPT
新窗口打开|下载原图ZIP|生成PPT图13不同$\beta $下, 多脊型气泡$C_{D}$随$\alpha $增大的变化
Fig.13Relation of bubble $C_{D}$ with $\alpha $ under the different $\beta $
3 结论
本文采用具有正交视场的高速阴影成像系统, 研究了毫米气泡($D_{eq}=2.4$ mm, $Re=500\sim700$, $We=7\sim13$)在不同轨道表面取向下(方位角$\beta )$, 倾斜超疏水轨道($W=2$ mm)上的滑移特性, 重点分析了方位角($-90^\circ\leqslant \beta \leqslant90^\circ$)和倾角($45^\circ\leqslant \alpha \leqslant 75^\circ$)对气泡形态和滑移速度的影响. 结果表明, 气泡黏附到超疏水轨道上后会经历短暂的加速, 而后迅速达到近似匀速的三相接触线钉扎-解钉运动状态. 由于表面毛细波的存在气泡滑移时形状为多脊型, 根据气液界面波动程度的不同滑移气泡可分为波动型和稳定型. 稳定型气泡只出现在较小倾角且较大方位角的超疏水轨道上($\alpha < 70^\circ, 45^\circ\leqslant\ | \beta | )$. 气液界面上的静压在$m$轴方向上的分量大小对气泡滑移过程中的形状稳定性有决定性的影响, 当该分量为零($\beta =\pm90^\circ$), 气泡形状最稳定. 当气泡在轨道正上方滑移时($\beta =90^\circ$), 气泡在轨道法向上的高度大于气泡在轨道正下方($\beta =-90^\circ$)滑移时的高度, 使得后者的气泡形状稳定性高于前者.方位角对气泡滑移速度的影响存在2种趋势:
(1) $45^\circ\leqslant \alpha \leqslant 65^\circ$, 气泡滑移速度近似为关于$\beta =0^\circ$ 的单峰分布($\beta =0^\circ$ 时, 气泡滑移速度最大), 此时沿轨道方向的驱动力起主导作用;
(2) $70^\circ\leqslant \alpha \leqslant 75^\circ$, 气泡滑移速度对方位角的改变不敏感, 此时气泡的迎风面积是影响滑移速度的主要因素.
综上, 壁面取向(方位角$\beta )$及轨道倾角($\alpha)$通过改变气泡沿轨道方向的驱动力和气泡滑移时的迎风面积影响气泡在超疏水表面上的滑移速度和气液界面稳定性. 这一新的认识有望为该气泡操控技术在核反应堆、矿物浮选、池沸腾等领域的应用提供科学依据和创新思路.
参考文献 原文顺序
文献年度倒序
文中引用次数倒序
被引期刊影响因子
DOIURLPMID [本文引用: 1]

Under laser illumination, a solid-state surface or nanostructure can turn into a micro/nano heating source with the so-called optothermal effect. This effect allows for non-invasive control of heat at the micro/nanoscale. In the presence of a liquid, a surface bubble can be generated on top of the solid surface or nanostructure at a temperature much higher than the boiling point of the liquid. The high temperature and the fluid flow associated with the optothermally generated surface bubble enable many intriguing applications, ranging from the micro/nano-manipulation of fluids, particles, cells, and light to the synthesis of micro/nano-structures under ambient conditions. In this review article, we present the fundamentals, recent developments, and future perspectives in this emerging field.
[本文引用: 2]
[本文引用: 1]
[本文引用: 1]
DOIURLPMID [本文引用: 2]

Efficient and low-cost electrocatalysts for the oxygen evolution reaction (OER) are essential components of renewable energy technologies, such as solar fuel synthesis and water splitting processes for powering fuel cells. Here, ultrathin NiCoFe layered double hydroxide (LDH) nanoplates, which directly grow on a cobalt-based nanowire array, forming a hierarchical nanoarray structure, are constructed as efficient oxygen evolution electrodes. In alkaline media, the ordered ultrathin hierarchical LDH nanoarray electrode shows dramatically increased catalytic activity compared to that of LDH nanoparticles and pure nanowire arrays due to the small size, large surface area, and high porosity of the NiCoFe LDH nanoarray. Only a small water oxidation overpotential (eta) of 257 mV is needed for a current density of 80 mA cm(-2) with a Tafel slope of 53 mV per decade. The hierarchical LDH nanoarray also shows excellent structural stability in alkaline media. After continuous testing under a high OER current density ( approximately 300 mA cm(-2)) for 10 h, the sample maintains the ordered hierarchical structure with no significant deactivation of the catalytic properties.
[本文引用: 1]
[本文引用: 2]
[本文引用: 2]
DOIURLPMID [本文引用: 1]

Microbubbles are tiny bubbles with diameters below 50 mum. Because of their minute buoyant force, the microbubbles stagnate in aqueous media for a long time, and they sometimes cause serious damage. Most traditional methods chosen for elimination of gas bubbles utilize buoyancy forces including chemical methods and physical methods, and they only have a minor effect on microbubbles. Several approaches have been developed to collect and transport microbubbles in aqueous media. However, the realization of innovative strategies to directly collect and transport microbubbles in aqueous media remains a big challenge. In nature, both spider silk and cactus spines take advantage of their conical-shaped surface to yield the gradient of Laplace pressure and surface free energy for collecting fog droplets from the environment. Inspired by this, we introduce here the gradient of Laplace pressure and surface free energy to the interface of superhydrophobic copper cones (SCCs), which can continuously collect and directionally transport CO2 microbubbles (from tip side to base side) in CO2-supersaturated solution. A gas layer was formed when the microbubbles encounter the SCCs. This offers a channel for microbubble directional transportation. The efficiency of microbubble transport is significantly affected by the apex angle of SCCs and the carbon dioxide concentration. The former provides different gradients of Laplace pressure as the driving force. The latter represents the capacity, which offers the quantity of CO2 microbubbles for collection and transportation. We believe that this approach provides a simple and valid way to remove microbubbles.
[本文引用: 1]
DOIURLPMID [本文引用: 2]

The maneuver of small bubbles in a programmed way will advance numerous processes, including gas evolution reaction and aeration. Unlike in-air droplets, rapidly rising bubbles in liquid medium can hardly be steered through interaction with solid substrates, causing difficulties in maneuvering bubbles. We pattern and lubricate nanoporous substrates with regions of contrasting wettability that is similar to the back of Namib desert beetles and subsequently immerse the lubricated surface underwater to spontaneously form spatially patterned Nepenthes-inspired slippery surfaces after the dewetting of lubricants. As a result, bubbles are confined on lubricant-infused surfaces, with their high mobility well preserved. The interfacial states of attached bubbles are analyzed, and their dynamic sliding velocities are quantified. Using the lubricated patterned surfaces, we further demonstrate the predefined motion of bubbles driven by buoyancy at a small tiling angle, as well as a self-propulsion of bubbles driven by surface tension force at a tilting angle of 0 degrees , respectively. The spatially lubricated surfaces simplify gas handling in liquid medium and have potential applications in fields where bubble handling is crucial.
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
DOIURLPMID [本文引用: 1]

A series of well-ordered, 3D gradient porous interconnected network surfaces composed of micro-nano hierarchical geometries is constructed on a copper wire. A continuous gas film can be trapped around its interface in an aqueous medium acting as an effective channel for gas transportation. Driving by the difference of the Laplace pressure, gas bubbles can be transported spontaneously and directionally.
DOIURLPMID [本文引用: 8]

Tiny bubbles readily stick onto substrates owing to contact angle hysteresis (CAH). Nevertheless, they can slide slowly on a tilted surface with ultralow CAH because capillarity is overcome by buoyancy. It is surprising to observe experimentally that bubbles of 3-15 muL (diameter 1.79-3.06 mm) slide beneath a tilted superhydrophobic surface at a vertical ascent rate faster than that of freely rising ones of high Reynold numbers approximately O(10(2)). As the tilting angle increases, the drag coefficient remains essentially the same as that of a freely rising bubble, but the frontal area of the flat bubble rises monotonically. Nonetheless, the frontal area of the sliding bubble always stays much smaller than that of a freely rising bubble. Consequently, the small drag force associated with the sliding bubbles is attributed to their substantially small frontal areas on superhydrophobic surfaces.
DOIURLPMID [本文引用: 1]

Superhydrophobic surfaces have long been considered as superaerophilic surfaces while being placed in the aqueous environment. However, versatile gas/solid interacting phenomena were reported by utilizing different superhydrophobic substrates, indicating that these two wetting states cannot be simply equated. Herein, we demonstrate how the hydrophilic defects on the superhydrophobic track manipulate the underwater gas delivery, without deteriorating the water repellency of the surface in air. The versatile gas-transporting processes can be achieved on the defected superhydrophobic surfaces; on the contrary, in air, a water droplet is able to roll on those surfaces indistinguishably. Results show that the different media pressures applied on the two wetting states determine the diversified fluid-delivering phenomena; that is, the pressure-induced hydrophilic defects act as a gas barrier to regulate the bubble motion behavior under water. Through the rational incorporation of hydrophilic defects, a series of gas-transporting behaviors are achieved purposively, for example, gas film delivery, bubble transporting, and anisotropic bubble gating, which proves the feasibility of this underwater air-controlling strategy.
URLPMID [本文引用: 1]
[本文引用: 1]
[本文引用: 4]
[本文引用: 4]
[本文引用: 3]
DOIURLPMID [本文引用: 5]

We report on direct atomic-force-microscope measurements of capillary force hysteresis (CFH) and relaxation of a circular moving contact line (CL) formed on a long micron-sized hydrophobic fiber intersecting a water-air interface. The measured CFH and CL relaxation show a strong asymmetric speed dependence in the advancing and receding directions. A unified model based on force-assisted barrier crossing is utilized to find the underlying energy barrier Eb and size lambda associated with the defects on the fiber surface. The experiment demonstrates that the pinning (relaxation) and depinning dynamics of the CL can be described by a common microscopic framework, and the advancing and receding CLs are influenced by two different sets of relatively wetting and nonwetting defects on the fiber surface.
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
DOIURLPMID [本文引用: 4]

While the dynamics of complete wetting has been widely studied for liquids, the way a gas spreads on a solid is by far less known. We report here the events following the rise of a millimeter-size air bubble towards a textured material immersed in water and covered by a thin plastron of air. Bubbles contact the material either directly at the end of the rise, or after a few rebounds, which affects the initial shape of the bubble and the resulting dynamics of contact. Then, air spreads on the material, owing to surface tension and later buoyance, which tends to flatten further the bubble. The corresponding dynamics are shown to result from the inertial resistance of water, which explains how spreading bubbles reach centimeter sizes in typically 10 ms.
[本文引用: 2]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 2]
DOIURLPMID [本文引用: 1]

We report a systematic study of contact angle hysteresis (CAH) with direct measurement of the capillary force acting on a contact line formed on the surface of a long glass fiber intersecting a liquid-air interface. The glass fiber of diameter 1-2mum and length 100-200mum is glued onto the front end of a rectangular cantilever beam, which is used for atomic force microscopy. From the measured hysteresis loop of the capillary force for 28 different liquids with varying surface tensions and contact angles, we find a universal behavior of the unbalanced capillary force in the advancing and receding directions and the spring constant of a stretched meniscus by the glass fiber. Measurements of the capillary force and its fluctuations suggest that CAH on an ambient solid surface is caused primarily by two types of coexisting and spatially intertwined defects with opposite natures. The contact line is primarily pinned by the relatively nonwetting (repulsive) defects in the advancing direction and by the relatively wetting (attractive) defects in the receding direction. Based on the experimental observations, we propose a
[本文引用: 3]
[本文引用: 3]
URLPMID [本文引用: 1]
DOIURLPMID [本文引用: 1]

We report a direct measurement of the friction coefficient of a fluctuating (and slipping) contact line using a thin vertical glass fiber of diameter d with one end glued onto a cantilever beam and the other end touching a liquid-air interface. By measuring the broadening of the resonant peak of the cantilever system with varying liquid viscosity eta, we find the friction coefficient of the contact line has a universal form, xi(c) approximately 0.8pideta, independent of the liquid-solid contact angle. The obtained scaling law is further supported by the numerical simulation based on the phase field model under the generalized Navier boundary conditions.
[本文引用: 2]
DOIURLPMID [本文引用: 1]

In this paper, a phenomenon of air bubbles quickly bursting within several milliseconds on a
[本文引用: 1]
[本文引用: 1]
