张洋^*,?,**, 陈科^,*,**,2), 尤云祥^*,**, 盛立^??* 上海交通大学海洋工程国家重点实验室, 上海 200240
? 普渡大学机械工程系, 美国西拉法叶 47907
** 高新船舶与深海开发装备协同创新中心, 上海 200240
?? 中国人民解放军92537部队, 北京 100161

BOUNCING BEHAVIORS OF A BUOYANCY-DRIVEN BUBBLE ON A HORIZONTAL SOLID WALL ¹⁾

Zhang Yang^*,?,**, Chen Ke^,*,**,2), You Yunxiang^*,**, Sheng Li^??* State Key Laboratory of Ocean Engineering$,$ Shanghai Jiao Tong University$,$ Shanghai 200240, China
? School of Mechanical Engineering$,$ Purdue University$,$ West Lafayette 47907$,$ United States
** Collaborative Innovation Center for Advanced Ship and Deep-Sea Exploration$,$ Shanghai 200240, China
?? No. 92537 Unit of PLA$,$ Beijing 100161, China

通讯作者: 2) 陈科, 博士后研究员, 主要研究方向：水动力学.E-mail:raulphan@sjtu.edu.cn

收稿日期:2019-03-26网络出版日期:2019-09-18

基金资助:

1) CSC项目.201806230204 航天先进制造联合基金项目资助..USCAST2016-2

Received:2019-03-26Online:2019-09-18
作者简介 About authors


摘要
黏性液体中的气泡浮升运动有趣而又复杂,而气泡与固壁边界的相互作用更是广泛存在于实际工程中.基于轴对称数值计算,模拟了浮力驱动下气泡在黏性液体中上升并与顶部水平固壁面碰撞、回弹的过程.采用考虑表面张力的不可压、变密度Navier-Stokes方程来描述气液两相流流动,并通过基于分级八叉树的有限体积法进行数值求解.为准确捕捉气泡在回弹过程中局部而迅速的拓扑变化,采用了动态自适应网格技术耦合流体体积法(volume of fluid,VOF)来重构气泡的形状. 从气泡对壁面的碰撞和回弹的基本现象入手,研究了伽利略数 Ga和接触速度$U_{a}$对气泡回弹动力学特性的影响, 分析了气泡碰撞过程中涡结构的变化.用回弹高度$H$、回弹周期$T$、长宽比{$A_{r}$}、浮升速度$U$、轴向位置$z$和回复系数$C_{r}$等参数来表征不同条件时气泡的运动和形状特性. 研究结果表明,气泡的回弹运动特性对 Ga十分敏感. Ga的增大可加剧气泡形变, 促进气泡的回弹运动, 增多回弹次数,增大回弹参数($T$和$H)$, 提升回复系数. 然而,接触速度并非决定气泡回弹动力学的控制参数, $U_{a}$的改变并不会改变回复系数.
关键词： 气泡回弹动力学;自适应VOF;伽利略数;接触速度

Abstract
It is not only interesting but also complex that buoyancy-driven bubbles rising in viscous liquids. In particular, the interactions between bubbles and boundaries (e.g., solid walls) is relevant in practical applications and these interactions may have a significant effect in the global behaviors of the multi-phase fluids. In this work, the rising, collision and bouncing to a horizontal solid wall for a single bubble are studied by axisymmetric computations. The incompressible, density-variable Navier-Stokes equations with surface tension are used to describe the gas-liquid flow and are solved by a tree-based finite volume method (FVM). The evolution of bubble shape is implemented by using a volume of fluid (VOF) approach that combines a balanced surface tension force calculation and a height-function curvature estimation. To finely resolve the local but fast topological evolutions of bubble, the technique of adaptive mesh refinement (AMR) is used. Starting with the basic phenomenon of bubble impacting and bouncing, we explore the effects of Galilei number Ga and approach velocity $U_{\rm a}$. To study the bubble behaviors under different conditions both qualitatively and quantitatively, the evolution of the velocity vector field and a lot of parameters such as bouncing height $H$, bouncing period $T,$rising velocity $U$, axial coordinate $z$and coefficient of restitution $C_{\rm r }$are analyzed. Based on the results, we find that the bubble bouncing behaviors are pretty sensitive to the Galilei number. The increase of Ga promotes the bouncing and signifies the deformation of bubbles, increasing the collisions of bubbles, bouncing parameters and the coefficient of restitution. However, the value of $C_{\rm r}$is nearly unaffected by the variation of the approach velocity, indicating that $U_{\rm a}$is not a governing parameter for the bubble bouncing motion.
Keywords：bubble bouncing dynamics;AMR-VOF;Galilei number;approach velocity


PDF (6112KB)元数据多维度评价相关文章导出EndNote|Ris|Bibtex收藏本文
本文引用格式
张洋, 陈科, 尤云祥, 盛立. 浮力气泡对水平壁面的回弹动力学特性 ¹⁾. 力学学报[J], 2019, 51(5): 1285-1295 DOI:10.6052/0459-1879-19-071
Zhang Yang, Chen Ke, You Yunxiang, Sheng Li. BOUNCING BEHAVIORS OF A BUOYANCY-DRIVEN BUBBLE ON A HORIZONTAL SOLID WALL ¹⁾. Chinese Journal of Theoretical and Applied Mechanics[J], 2019, 51(5): 1285-1295 DOI:10.6052/0459-1879-19-071

引言

气泡流不仅存在于日常生活中, 也拥有广泛的工业应用背景,例如二氧化碳的采集和储存、可燃冰的开采、石油的炼化以及核反应的堆冷却等.以上所有工业过程的准确实施,均以了解认识黏性液体中气泡的物理机制为前提,其中一个重要的问题即是气泡与外部边界的相互作用问题^[1-7].

过去数十年来,****对于气泡流动力学的研究主要集中在开放流场(即无界流域)中的单泡动力学问题,这是泡状流问题的一个最基础构型.对单泡问题的研究主要在形状、速度、路径和尾流结构等方面,前人已经开展了大量的实验^[8-11]或数值^[12-14]研究,代表性的综述可参见文献^[15,16]. 总的来说,气泡的动力学特性由表面张力、黏性、惯性、气泡表面杂质(如果存在)等因素共同决定.

根据$\pi $定理可知,开放流场中的单泡动力学问题可以用4个无量纲参数描述^[17-18], 分别是艾特华数(Eo= $\rho $$_{\rm l}$gd$^{2}$/$\sigma $)、伽利略数Ga= $\rho$$_{\rm l}g^{1 / 2}d^{3 / 2}$/$\mu $$_{l})$、密度比($\rho $$_{\rm r}$= $\rho $$_{l}$/ $\rho $$_{\rm g})$和黏度比( $\mu $$_{\rm r}$= $\mu $$_{l}$/ $\mu $$_{\rm g})$.艾特华数代表重力与表面张力的比值,而伽利略数表示重力与黏性力的比值. 从定义上, 可以看出, Eo和 Ga分别是韦伯数( We = $\rho $$_{l}U^2_{\rm t} d$/ $\sigma $)和雷诺数( Re = $\rho$$_{\rm l}gU_{\rm t}$/$\mu _{\rm l})$的变种. 不过,前面两者是以$\sqrt {gd} $为特征速度,而后面两者是以气泡终态速度$U_{\rm t}$为特征速度. 因此, 更严谨地讲, We和 Re是给定( Eo, Ga, $\rho $$_{r}$, $\mu $$_{\rm r})$条件下的后验参数或结果参数,而非先验参数或控制参数. 此外, 也可用莫顿数( Mo = Eo$^{3}$/ Ga$^{4})$来描述. 对于给定液体而言, Mo为常数.

近年来, 越来越多的****们开始关注气泡与表面的耦合作用. 此种情况下,气泡的动能会转移到表面能上, 当满足一定条件时,气泡会出现回弹(弹跳)运动.

Tsao等^[19]在实验中观测到气泡会在黏性耗散动能之前在水平壁面处完成数次回弹运动.Klaseboer等^[20]进行了液滴对水平壁面冲击的实验研究并提出了一个考虑了液膜排液效应的回弹轨迹模型.而后,Legemdre研究小组^[21-22]开展了一系列对气泡和液滴在固壁面附近回弹运动的实验研究,他们提出了回复系数($C_{\rm r}$, the coefficent ofrestitution)的概念,用来量化气泡碰撞前后的速度变化.Zawala的研究小组^[23-25]先后研究了气泡与气液交界面和固液交界面的碰撞回弹运动.他们发现, 在固液交界面的情况下,碰撞过程中的能量耗散总量远小于气液交界面的情况.这是因为气液表面可以产生形变.Fujasová-Zedníková等^[26]观测发现,对于固体边界的情况,气泡回弹运动特性与固壁面的材料特性无关,而表面活性剂(杂质)显著影响气泡回弹运动和变形.邱超等^[2]研究发现, 黏度相同时,气泡碰撞过程中的最大变形程度随雷诺数(Re)增大而增大.Pelletier等^[27]通过测量两种初始条件下自来水中气泡撞击水平壁面的过程发现,气泡长宽比是影响回弹过程的关键参数.

以上研究均是通过实验手段完成的. 然而, 由于条件的局限和限制,时至今日用实验手段探究气泡动力学问题仍极具挑战性.随着建模方法、数值算法以及计算能力的高速发展,数值模拟成为研究这一问题的一种极具前景的研究手段^[28-29]. 目前, 这方面的文献还相对较少.

Canot等^[30]在势流理论中加入润滑理论,模拟了二维气泡的回弹运动. 李帅等^[1]基于势流理论, 将Canot等^[30]的二维气泡模型推广到了轴对称的情况,研究了气泡与水平壁面碰撞的平衡构型,并指出韦伯数是影响气泡最终稳态构型的重要影响因素.Omori等^[31]采用界面追踪法(fronttracking)分析了气泡与壁面碰撞过程中的能量耗散过程. Qin等^[32]采用任意拉格朗日--欧拉方法, 研究了大莫顿数(0.1$\le$Mo $\le$16)条件下(即液体黏性很高时)气泡与水平固壁面相互作用的情况.根据气泡进入稳态后的形状的不同, 耦合类型被分成了三类.在他们的研究中, 流场是以有限元的模式计算的, 忽略了泡内的流体流动.气泡表面的捕捉依赖于动网格,液膜排液是通过自适应网格来确保壁面和气泡表面之间至少有3个单元.这样就不能模拟出液膜撕裂的过程,液膜厚度低于气泡半径的1/100时计算便无法继续.Zawala等^[33]成功应用流体体积法(volume of fluid,VOF)研究了顶部壁面做正弦振动时的气泡碰撞动力学问题,侧重分析了液膜的稳定性. 他们发现,液膜稳定性不仅依赖于壁面亲疏水特性,也与多相流系统中的能量传递有关.Albadawi等^[34]评估了VOF方法对气泡碰撞壁面问题的适用性.他们指出了精细地捕捉相间表面的液膜的重要性,特别是对于具有强疏水性能表面的材料而言. 然而,他们采用的是局部加密的静止网格,所以对大接触角时的三相接触线形成的问题对网格数量和计算量要求特别高.最近,Denner^[35]采用VOF法研究了蠕动流条件下的气泡与壁面的碰撞运动,揭示了壁面与气泡碰撞对于毛细管数 Ca的自相似特性.

时至今日, 人们对气泡在水平表面处的回弹动力学的认识还很初步. 例如,已有的实验一般是从有量纲参数出发, 研究水中气泡等少数的情况,而数值研究方兴未艾^[36-39]. 虽然,李帅等^[1]研究了浮力和表面张力对气泡回弹特性的影响,但目前为止, 尚未见到对气泡惯性影响的报道. 此外, 现实情况中,气泡在与顶部壁面碰撞或接触之前并不一定进入了终态,即壁面位置并非处于理想高度,所以研究气泡接触速度的影响也极具现实意义. 有鉴于此,本工作拟采用计算流体力学(computational fluid dynamis, CFD)方法,从无量纲的视角出发, 研究伽利略数 Ga和接触速度$U_{\rm a}$对气泡在壁面回弹的影响, 力求得到更具普遍性的结论.

1 数值方法

1.1 控制方程

针对气液两相流问题, 假设流动为不可压的层流流动, 流体等热且不相融.不考虑由于流体剪切而使黏性发生改变, 即关注的流体是牛顿的.为描述这样的两相流问题, 控制方程是密度可变的Navier-Stokes方程

(1)$$\delta\cdot {{ u}} = 0 $$

(2)$$\rho (\frac{\partial }{\partial t}{{ u}} + {{ u}} \cdot \nabla {{ u}})\mbox{ = } - \nabla p + \nabla (2\mu {D} ) + \rho {{ g}}\mbox{ + }\sigma \kappa \delta _s {{ n}} $$

其中, ${ u}$是速度矢量, $\rho $是密度, $t$是时间,$p$是压力, $\mu $是动力黏度, ${{ D}} = {\left( {\nabla {{ u}} + \nabla {{ u}}^{\rm T}} \right)} /2$是变形张量,${ g}$是重力加速度. 表面张力通过动量方程中右边最后一项加入. $\delta $$_{\rm s}$是狄拉克分布函数,表征表面张力集中在两相的表面上. $\sigma $, $\kappa $,${ n}$分别是相间表面张力系数、曲率以及表面法向单位向量.

气液两相流中的物性参数是根据体积加权平均获得的

(3)$$\rho = c\rho _{\rm l} + (1 - c)\rho _{\rm g} $$

(4)$$\mu =c\mu _{\rm l} + (1 - c)\mu _{\rm g} $$

其中, 下标l和g分别表征液体和气体.通过引入体积分数$c$和求解体积分数输运方程来记录气液表面

(5)$$\frac{\partial c}{\partial t} + \nabla \cdot (c{{ u}}) =0 $$

1.2 空间离散

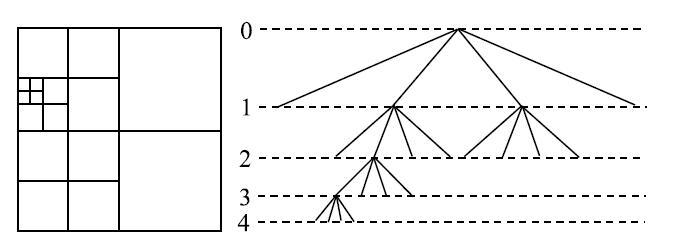
对于CFD而言, 由于气泡回弹过程涉及快速的局部拓扑变化,这对网格分辨率以及计算量要求很高,如使用均匀的静态网格无疑耗费巨大的计算量.本文采用动态自适应网格加密技术(adaptive mesh refiment, AMR).采用结构的笛卡尔网格, 空间域的离散采用分级的八叉树方法^[40].二维问题则采用四叉树方法. 如图1所示, 初始时,计算域都是由正方形构成. 每个原始正方形可以再被细分(加密)成4个子块.根据设定的加密标准, 每个原始正方形可以不断细分. 针对气泡流问题,考虑到体积分数和尾流对流场的决定性影响,同时设置了如下两种加密 标准

(6)$$\frac{\left| {\nabla \times {{ u}}} \right|\Delta }{\max(\left| {{ u}} \right|)} < \varepsilon $$

(7)$$\left| {\nabla c} \right|\Delta < \varepsilon\quad~ $$

图 1

新窗口打开|下载原图ZIP|生成PPT
图 1四叉树离散示意图

Fig. 1Example of quadtree discretisation and corresponding tree representation



其中, $\varepsilon $是标准阈值, 本文统一设定为0.01.以上两种标准的设定可以确保在气泡表面和大涡量处有很高的网格分辨率.自适应的网格加密方法为捕捉流场细节提供了更多的灵活性,平衡了计算量与精度的需求.

1.3 时间离散

时间域的离散上采用的是经典的时间分裂投影算法^[41],得到如下的离散方程组

(8)$$\rho _{n + 1 /2} (\frac{{{ u}}_\ast - {{ u}}_n }{\Delta t} + {{ u}}_{n + 1 /2} \cdot \nabla {{ u}}_{n + 1 /2} - {{ g}})\mbox{ = } \nabla [ {2\mu _{n + 1 /2} ({{ D}}_n + {{ D}}_\ast )} ]\mbox{ + }(\sigma \kappa \delta _s {{ n}})_{n + 1 /2} $$

(9)$$\frac{c_{n + 1 /2} - c_{n - 1 /2} }{\partial t} + \nabla \cdot (c_n {{ u}}_n ) = 0 $$

(10)$${{ u}}_{n{ + }1} = {{ u}}_{\ast } - \frac{\Delta t}{\rho _{n + 1 /2} }\nabla p_{n + 1 / 2}$$

(11)$$\nabla \cdot {{ u}}_{n + 1 /2} \mbox{ = }0 $$

要获得$n$+1时间步的校正后的速度场, 需要先求解泊松方程

(12)$$\nabla \cdot \left( {\frac{\Delta t}{\rho _{n + 1 /2} }\nabla p_{n + 1/2} } \right) = \nabla \cdot {{ u}}_{\ast } $$

然后, 动量方程(8)可写成如下的Helmholtz形式

(13)$$\frac{\rho _{n + 1 /2} {{ u}}_\ast }{\Delta t} - \nabla \cdot \left( {\mu _{n + 1 /2} {{ u}}_\ast } \right) = \nabla \cdot \left( {\mu _{n + 1 /2} {{ u}}_\ast } \right) + (\sigma \kappa \delta _s {{ n}})_{n + 1 /2} + \rho _{n + 1 /2} \left( {\frac{{{ u}}_n }{\Delta t} - {{ u}}_{n + 1 /2} \cdot \nabla {{ u}}_{n + 1 /2} + {{ g}}} \right) $$

上式中,黏性项的Crank-Nicholson离散是无条件稳定的并在时间域上具有标准的二阶精度.速度对流项的离散采用Bell-Colella-Glaz不分裂迎风格式^[42],当库朗数$f_{\rm c}<1$时满足稳定性要求.为精细捕捉气泡变形即气泡周围流场变化, 往往需要大量的时间步.本文取$f_{\rm c}$= 0.3, 时间步由下式控制

(14)$$f_{\rm c} =\frac{\Delta t}{\min \left(\dfrac{\varDelta }{\left| {{{ u}}_i} \right|},\dfrac{\rho \Delta ^2}{\mu },\sqrt {\dfrac{\rho \Delta^3}{\sigma }} \right)} $$

其中, $\varDelta $是局部网格尺寸, ${ u}_{i}$是单元中心或面心在$i$方向的速度.

1.4 VOF方法

体积分数输运方程的求解采用的是分段线性几何VOF方法,可分为以下两步：

(1) 相间表面重构;

(2) 几何通量计算和相间表面对流.

在步骤(1)中, 计算单元里的相间表面采用下式

(15)$${{ m}} \cdot {{ x}} = \alpha $$

其中, ${ m}$是相间表面法向量, ${ x}$是位置向量.给定$c$和${ m}$,通过确定计算单元里在平面之下流体体积就可以得到 $\alpha $的值.法向向量${ m}$可以通过近似相邻单元里的体积分数来获得.

完成相间表面重构后,笛卡尔网格上的方向分裂集合通量也可轻松得到^[43].而后得到的二阶精度的对流项可确保形成锋利的相间表面.

对于表面张力的计算是基于平衡力表面张力离散格式^[43],该格式纳入了高度函数(height-function)曲率计算. 经此处理,曲率半径与局部网格尺寸相当,可以得到具有二阶精度和数值平衡的相间表面构型. 这种表面张力的处理,可有效避免VOF模拟中常常遇到的寄生流(parasitic currents)问题.

本工作的建模和模拟都是在基于有限体积法的开源代码Gerris^[40,43]中实现的, 并在Dell Precision Tower 7910工作站上完成并行计算的.

1.5 问题描述

Sharaf等^{[9, 17]}和Cano-Lozana等^[44-45]两个 研究小组对单泡动力学的系统性研究表明, 对于Eo和 Ga的值均较小的气泡而言, 其形状是轴对称的,上升轨迹也是垂直向上的. 本工作将分析限制在轴对称条件下, 即讨论Eo和Ga的值均较小的孤立浮升气泡与顶部水平固壁面碰撞、回弹的动力学过程.

如图2所示, 本工作的计算在一个轴对称域中进行. 除轴边界外,其余边界均采用无滑移边界条件. 为避免侧边面的影响,计算域宽度即圆柱形容器半径取4^[3]. 为壁面底部边界的影响,至少在底部壁面以上2.5$d$位置静止释放, 气泡距离顶部壁面距离为$L$.为保证气泡在与顶部壁面碰撞之前可到达末态, 计算域高度设置为48$d$.初始时刻, 流场静止, 气泡以球形形状在轴线上静止释放.下文中的所有计算结果均以无量纲的形式呈现, 分别以$d$, $\sqrt {d /g} $, $\sqrt {gd} $为长度、时间和速度特征量.

图 2

新窗口打开|下载原图ZIP|生成PPT
图 2计算域示意图

Fig. 2Geometry of the computational domain.

2 自由气泡的浮升运动

本章将通过模拟自由上升的浮力气泡的浮升过程,来验证本文所采用数值方法的可靠性和准确性. 所谓自由气泡,即气泡不受边界影响或处于开放流域中的情况. 本章中,密度比和黏度比分别固定为1000和100.

2.1 收敛性分析

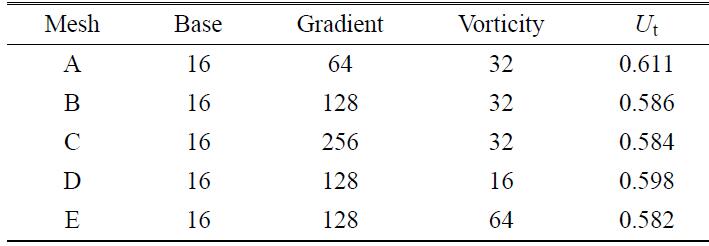
气液交界面和气泡尾流都是影响气泡动力学的关键因素, 均需精确捕捉.为此, 本节设计了一个网格收敛性测试,采用了5组不同的网格来进行收敛性分析. 条件参数 Eo = 116, Ga = 23.07. 根据表1的结果可知, 采用网格B时计算收敛. 也即是说,在气泡表面附近, 每单位长度(气泡直径$d)$有128个计算单元;而在大涡量处, 每单位长度有32个计算单元.而在远离气泡表面或者涡量很小的区域,网格密度为每单位长度16个计算单元.

Table 1
表1
表1网格对结果的影响
Table 1Effect of grid size on results

新窗口打开|下载CSV

2.2 与前人实验结果的对比

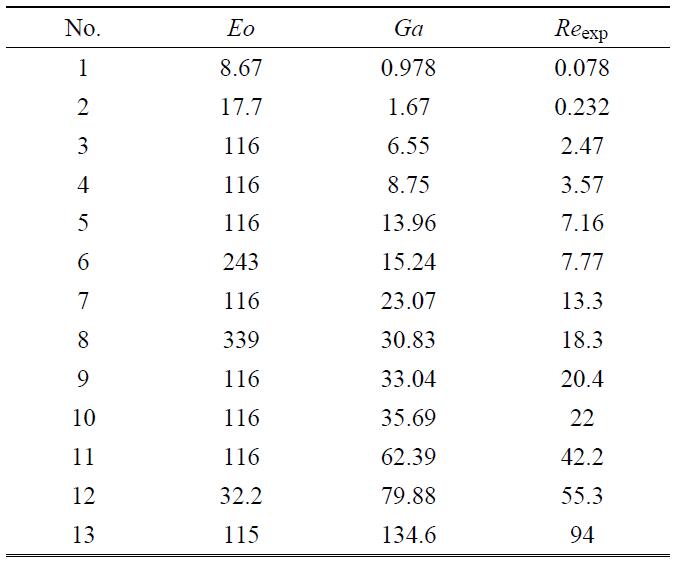
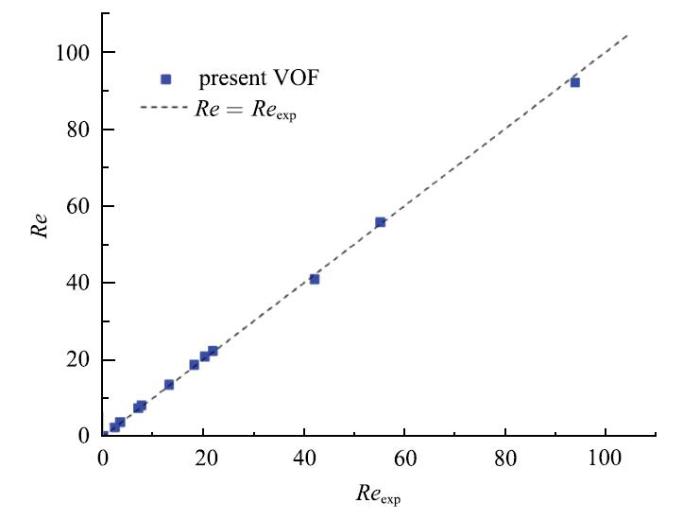
首先, 本文模拟了开放的静止流场中单气泡浮升运动的过程,并将得到的终态雷诺数和气泡构型与前人的实验结果相比较.

表2给出了选取了13组工况的条件参数, 全部来自Bhaga等^[8]的实验.图3比较了本文计算得到的雷诺数Re和前人实验测量的结果$Re_{\exp}$可以看到,虽然本文模拟了很多种工况, 覆盖了大范围的条件参数,但是每组模拟结果与实验结果均吻合良好, 相对误差在3%以内.

Table 2
表2
表2气泡参数表
Table 2Parameters of single bubble cases

新窗口打开|下载CSV

图 3

新窗口打开|下载原图ZIP|生成PPT
图 3气泡终态雷诺数对比

Fig. 3Comparison of terminal Reynolds numbers



图4比较了气泡进入终态后的稳定构型,其中实线曲线表示模拟得到的气泡轮廓. 可以看到,本文的模拟结果与实验观测的气泡形状吻合良好.

图 4

新窗口打开|下载原图ZIP|生成PPT
图 4气泡形状对比图

Fig. 4Comparison of terminal bubble shape

2.3 伽利略数的影响

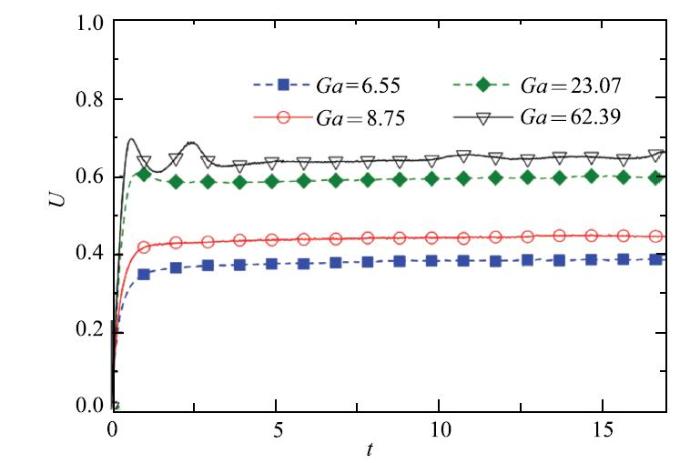
注意到, 表2中, 工况3$\sim $5, 7, 9$\sim $11其艾特华数 Eo相同, 而伽利略数 Ga不同. 本节将分析Ga的变化对自由气泡的浮升动力学动力学特性.

如图5所示, Ga改变, 最后得到的终态速度$U_{\rm t}$也不同.总的来说, Ga越大, $U_{\rm t}$也越大.这是由于黏性力的影响减弱, 而惯性力增大引起的. 与此同时,气泡在进入终态之前, 瞬时上升速度的波动在大 Ga时更加明显.当 Ga = 23.07时, 气泡从释放后逐渐加速到最大速度,再呈现微弱的减速到达其终态速度. 而当 Ga = 62.39时,气泡在大约$t$= 1.2时刻到达最大速度后, 会呈现剧烈的波动.气泡速度呈现下降、上升、下降趋势, 在$t$=4.8时刻左右再次得到极大值后, 气泡速度逐渐平稳下来. 相反, Ga$<$10时, 气泡速度变化过程平缓, 从初始释放后, 逐渐加速到终态速度.

图 5

新窗口打开|下载原图ZIP|生成PPT
图 5气泡速度时历曲线

Fig. 5Time histories of bubble rising velocity



对于不同的 Ga的气泡而言, 气泡浮力固定, 黏性阻力随Ga增大而减小, 所以气泡在释放后获得的加速度会随着Ga增大而增大, 这样 Ga更大时可以获得更大的终态速度.

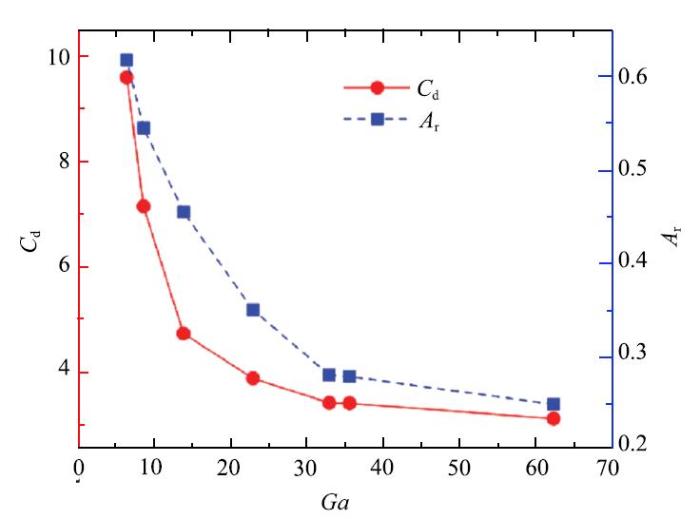
以上现象可以根据气泡的形状衍化过程解释. 从图3可知, Ga增大,气泡的形状变形更为明显. 为表征气泡的形状特性, 本文采用长宽比$A_{\rm r}$(气泡径向宽度$d_{\rm w}$与轴向高度$d_{h}$之比)来定量地分析气泡的形状.图6给出了气泡进入终态后的长宽比与伽利略数的关系. 可以看到,随着 Ga的增大, 气泡长宽比变小, 气泡扁平程度增大. 此外,根据前面的定义可知, $Re = {U_{\rm t} Ga} /{\sqrt {\mbox{g}d} }$,而从图5可知 Ga增大使得$U_{\rm t}$也增大, $\sqrt {\mbox{g}d}$为定值1, 这样可以解释 Ga增大使得 Re增大的原因.

图 6

新窗口打开|下载原图ZIP|生成PPT
图 6Eo = 116时不同 Ga的$A_{\rm r}$和$C_{\rm d}$

Fig. 6{$C_{\rm d}$} and $A_{\rm r}$for various Ga under Eo = 116



根据得到的气泡终态速度, 可通过下式$C_{\rm d} = {4\left( {\rho_{\rm l} - \rho _{\rm g} } \right)\left| g \right|d} /{\left({3\rho _{\rm l} U_{\rm t}^2 }\right)}$得到气泡进入终态后的阻力系数^[46]. 结果如图6所示,伽利略数越大, 气泡所受阻力系数更小.

3 气泡在顶部壁面处的回弹运动

前一章研究了开放流域中自由上升的气泡的动力学特性,本章将讨论顶部边界为固体壁面的情况.

3.1 与前人实验结果的对比

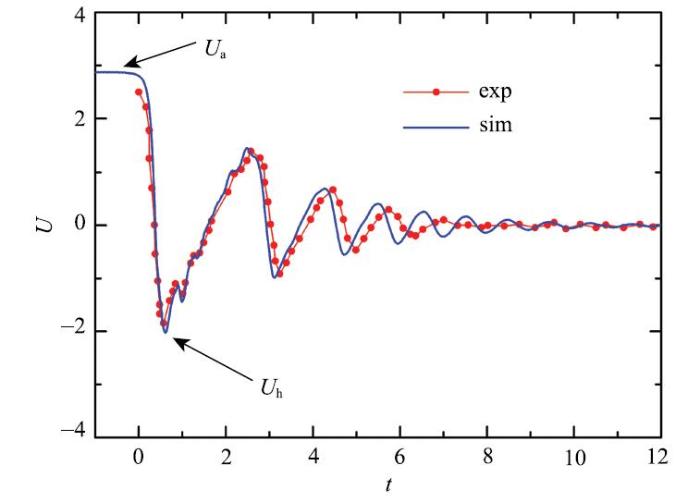
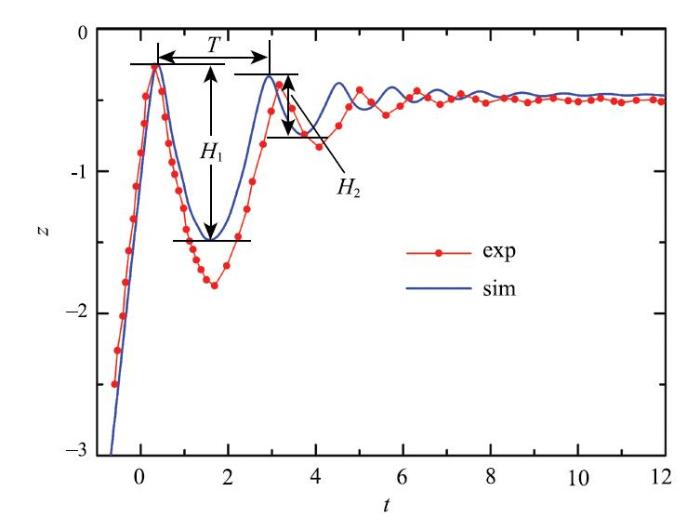
首先, 对比Kosior等^[23]的实验结果,进一步验证代码的准确性和适用性. 条件参数为： Ga = 178.33, Eo = 0.2984, $\rho $$_{\rm r}$= 769, $\mu$$_{\rm r}$= 42.74, 顶部壁面平衡接触角 $\theta $$_{\rm c}$= 0.

图7和图8分别给出了气泡瞬时速度和位置的时历曲线. 注意$t$=0时刻代表气泡开始受到壁面影响的时刻(根据速度判定). 可以看到,模拟结果尤其是速度与实验数据非常接近,而气泡质心位置的轨迹也与实验结果基本吻合.误差主要体现在气泡的回弹间隔上,即模拟中回弹比实验中发生地稍早一些. 换言之,模拟中墙壁对气泡的阻尼更大一些,所以气泡与壁面相撞后的回弹距离较实验值稍小一些,但该差异随着回弹次数的增加而逐渐减小.

Albadawi等^[34]的研究表明,气泡与固壁面之间处的网格分辨率对于准确模拟气泡与壁面的碰撞至关重要.因此,本文也对近壁面区域(距壁面的2$d$而距轴线也是2$d$的矩形区域)进行均匀的网格加密,以期缩小与实验数据的误差. 结果表明,即使近壁面区域加密到每单位长度256个计算单元时,与原有结果也无明显变化. 因此,作者认为本文模拟与实验数据之间的误差是由于数学模型、实验误差等不可避免的一些因素造成,是可接受的.

图 7

新窗口打开|下载原图ZIP|生成PPT
图 7气泡回弹过程中的速度时历曲线

Fig. 7Time history of bubble velocity during oscillations beneath solid wall

图 8

新窗口打开|下载原图ZIP|生成PPT
图 8回弹过程中的气泡质心轨迹

Fig. 8Trajectory of bubble centroid during oscillations beneath solid wall



图9给出了回弹过程中的长宽比 Ar的时历曲线. 同图7和图8一样,不论是数值上还是趋势上, 模拟结果与实验结果吻合度很高. 整体而言,依然可以清晰辨认出至少5次明显的回弹过程. 在气泡靠近壁面的过程中,气泡在轴向上被不断挤压(参见图10),泡内气体向径向扩散使得径向宽度增加而轴向高度减小,导致长宽比急剧增大. 在气泡逐渐脱离壁面的过程中,气泡形状呈相反的变化趋势, 致使$A_{\rm r}$迅速减小.

图 9

新窗口打开|下载原图ZIP|生成PPT
图 9回弹过程中的气泡长宽比时历曲线

Fig. 9Time history of bubble aspect ratio during oscillations beneath solid wall

图 10

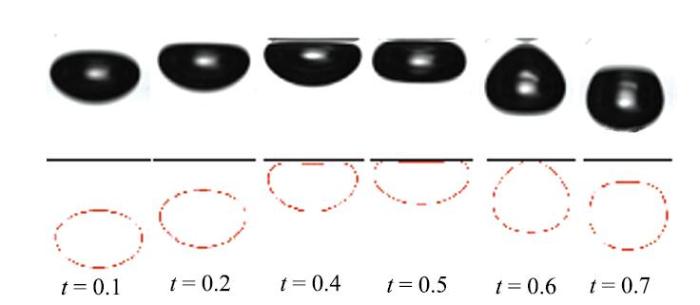
新窗口打开|下载原图ZIP|生成PPT
图 10首次碰撞至回弹过程中的形状衍化

Fig. 10Bubble shape evolution during the first collision-bouncing



在气泡向下回弹的末端, 气泡长宽比时历曲线会经历几次迅速的波动,这比图7中速度轨迹的波动更为剧烈. 这主要是因为, 在某些时刻,气泡内部轴向速度的方向并不完全一致造成的,而气泡速度$U$的是由气相的轴向速度的积分平均而定义的. 相似的是,不论是图7或是图9中, 这种波动随着回弹次数的增多而逐渐消失.

图10给出了气泡在第一次与墙壁碰撞并回弹的发展过程,其中粗直线表示顶部壁面. 从气泡的瞬时形状可见,数值模拟很好的重构了实验中气泡的变形过程.

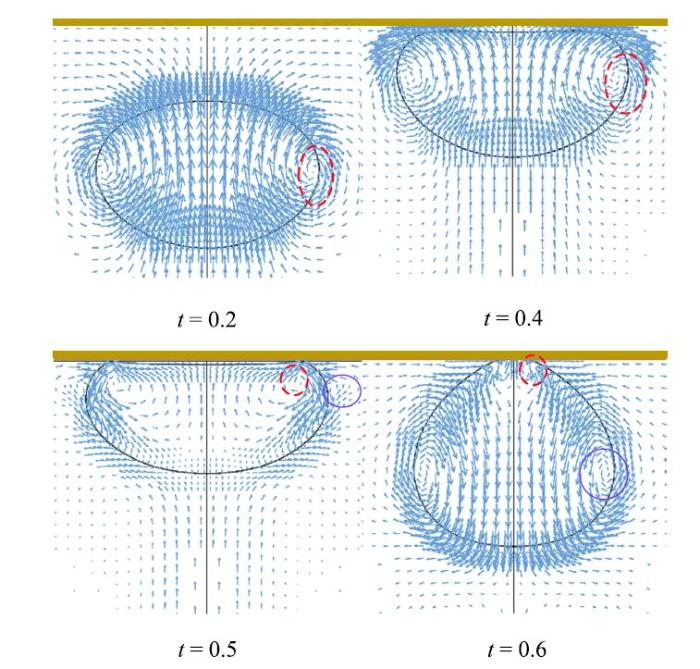
为分析气泡碰撞和回弹过程中的涡结构变化,图11就图10中4个代表时刻给出了气泡周围流场的速度矢量图,其中粗直线表示顶部固壁面. 从中可以看到,在气泡靠近并碰撞壁面的阶段(即从$t$= 0.1到$t$= 0.4),气泡径向边缘的涡环$V_{1}$逐渐由气泡的中部位置向顶部位置转移,同时$V_{1}$强度逐渐减弱、涡环半径逐渐增大,这使得诱导液体产生的向上的射流强度减弱, 气泡的尾流效应减弱,流场中的循环流动逐渐减弱, 气泡随之渐渐减速. 当$t$= 0.5时,受壁面挤压的作用, 气泡边缘处的$V_{1}$径向上向内侧偏移,即此时$V_{1}$完全处于气泡内. 这种气泡内旋涡裹挟着气体的现象,作者曾在之前对于裙带气泡在极度受到径向壁面约束的情况下观察到^[3].不过, 这里旋涡$V_{1}$的强度已经很弱. 当$t $= 0.6时,气泡顶部即将离开壁面, 呈桃形. 此时,$V_{1}$转移到这个``桃子''的顶端最终消失($t $= 0.7时已不能捕捉) .有趣的是, 与此同时, 在气泡的径向表面周围,一个新的旋涡$V_{2}$逐渐形成.它的产生是由于壁面附近液体径向上向轴线方向冲击气泡并与泡内旋涡相互作用形成的.需要注意的是, $V_{2}$的方向与$V_{1}$相反, 随着气泡远离壁面,$V_{2}$的强度增大, 诱导出向下的液体射流, 气泡开始做向下的加速运动.

图 11

新窗口打开|下载原图ZIP|生成PPT
图 11首次碰撞至回弹过程中的速度矢量图, 虚线圈表示旋涡$V_{1}$, 实线圈表示旋涡$V_{2}$

Fig. 11Velocity vectors during the first collision-bouncing,the dashed and the solid curves denote the vortex $V_{1}$and $V_{2}$, respectively



此外, 可以注意到, 图11中靠近壁面的旋涡的强度均较小,这即是之前对于壁面附近网格加密而结果并无改变的原因.

3.2 伽利略数的影响

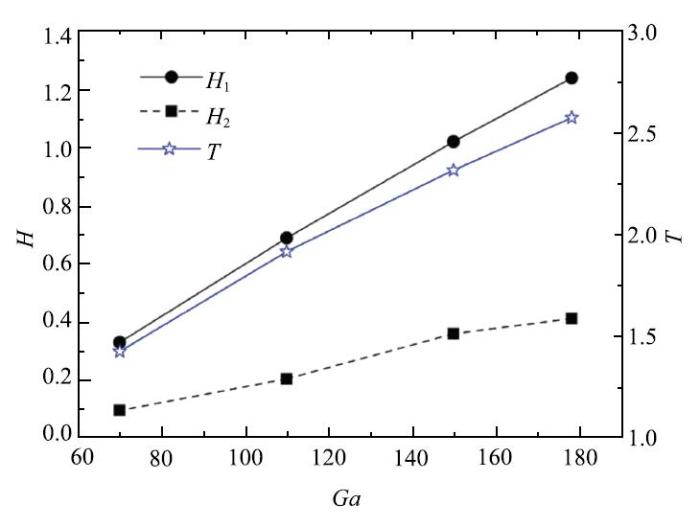
本节将研究不同 Ga时气泡在顶部壁面处的回弹动力学特性,分析气泡惯性在回弹动力学中的影响. Eo, $\rho $$_{\rm r}$, $\mu $$_{\rm r}$和 $\theta $$_{\rm c}$均与上节参考算例中的参数保持一致, Ga取70, 110,150和178.33(参考算例).

图12给出了不同伽利略数时的回弹高度$H$和回弹周期$T$的结果(参数定义示意图见图8).结果显示, Ga对这几个回弹参数的影响是单调递增的,即$H$和$T$均随着 Ga的增大而增大, 增长规律是近似线性的.

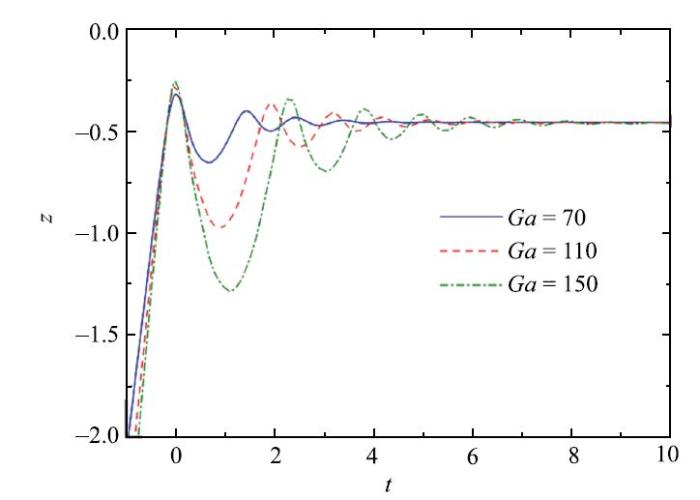
可以从气泡能量转换的角度解释$H$随 Ga增大的原因.以第一次碰撞为例, Ga增大,气泡碰撞后变形程度更大(从图13可知), 附加质量更大. 而由图14可知, Ga更大时, 气泡的质心位置极大值更大,即碰撞时重力势能更小(以底部边界为参考线). 需要强调的是,虽然变形更大使得气泡在碰撞时能量的黏性耗散增大,但这里可以不用考虑能量黏性耗散的影响. 这是因为,Zawala等^[24]对能量的定量分析表明,气泡能量的黏性耗散几乎在碰壁时存在且量级远低于重力势能和动能.再考虑到, Ga更大时, 气泡获得的接触速度本就更大,动能也就更大. 自然地,当气泡向下运动到动能为0(将动能转化为势能)所需的距离必然更长.

图 12

新窗口打开|下载原图ZIP|生成PPT
图 12Ga对回弹高度及周期的影响

Fig. 12Effect of Ga on bouncing parameters

图 13

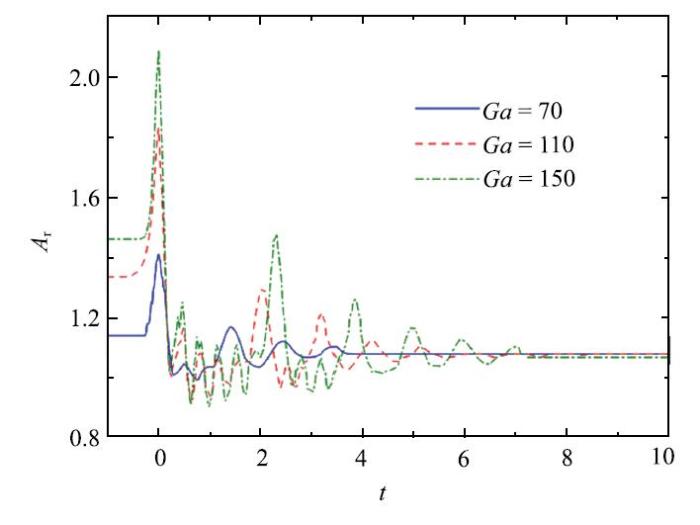
新窗口打开|下载原图ZIP|生成PPT
图 13不同 Ga时的$A_{\rm r}$时历曲线

Fig. 13Time histories of $A_{\rm r}$under different Ga

图 14

新窗口打开|下载原图ZIP|生成PPT
图 14不同 Ga时的气泡质心时历曲线

Fig. 14Time histories of bubble centroid under different Ga



Ga增大时, 液体黏性减弱, 气泡运动所受到的黏性阻力降低.这样气泡碰撞后的加速度数值上会更小, 先加速再减速的过程会更慢.因此, 气泡回弹周期$T$也更大.

图13对比了不同 Ga时的气泡长宽比时历曲线. 根据定义可知,液体黏性和 Ga成反比. 因此, 在液体黏性强(小 Ga)时,气泡变化所受阻力大, 气泡在与壁面碰撞后形变程度也随之较小,经历小幅度的回弹后气泡即可稳定地贴附于壁面. 这即是 Ga = 70时,只观察到3次明显的回弹且大致在$t$= 4时刻后{$A_{\rm r}$}值就趋于稳定. 相反地, Ga更大时,气泡由于获得更大惯性在碰撞之前获得了更多的动能,受阻尼消耗所需的时间也就更长.

引言中提到, 回复系数($C_{\rm r}$= $U_{\rm b}$/$U_{\rm a})$是描述气泡对壁面回弹运动特性的一个重要的概括性参数. 这里,$U_{\rm a}$是气泡接触壁面前的速度, $U_{\rm b}$是气泡离开壁面后的速度(示意图可见图7). 从图15可知, Ga对回复系数$C_{\rm r}$的影响是正相关的.

图 15

新窗口打开|下载原图ZIP|生成PPT
图 15Ga对回复系数的影响

Fig. 15Effect of Ga on the coefficient of restitution

3.3 接触速度的影响

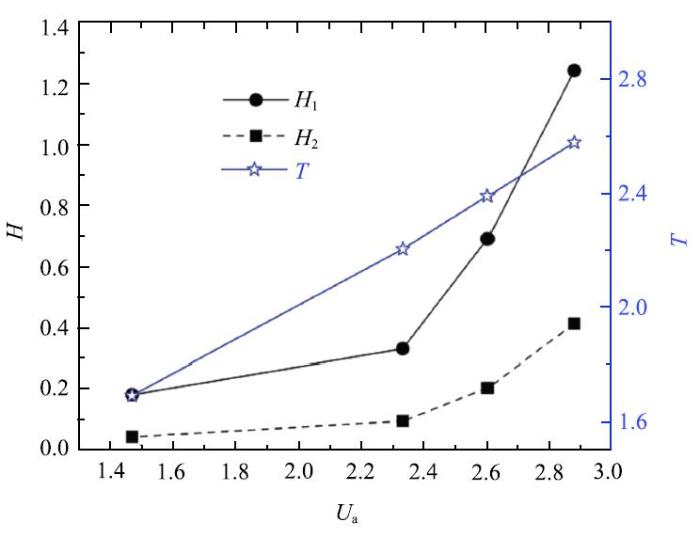
现实情况中, 气泡在与顶部壁面碰撞或接触之前并不一定进入了终态.例如, 气泡所在流域的高度可能是受限的,这样气泡与壁面碰撞前并未获得终态上升速度$U_{\rm t}$.本节通过改变初始时刻气泡的释放位置(气泡与壁面的初始间距$L)$,获得不同接触速度$U_{\rm a}$, 以分析对结果的影响.

图16展示了接触速度的变化对回弹高度和周期的影响. 接触速度更大时,即气泡距离顶部水平壁面的初始距离$L$更大,气泡从释放之后的加速过程更长更充分,在接触碰撞壁面之前获得的动能也就更大. 因此, 可以看到,图16中回弹高度和周期均随$U_{\rm a}$增大而增大. 需要注意,与图14中的变化趋势不同的是, 回弹高度随$U_{\rm a}$变化的规律并非线性的. 当$U_{\rm a}$超过2.34之后,两次回弹高度$H_{1}$和$H_{2}$均开始大幅度增大.

图 16

新窗口打开|下载原图ZIP|生成PPT
图 16$U_{\rm a}$对回弹高度及周期的影响

Fig. 16Effect of $U_{\rm a}$on bouncing parameters



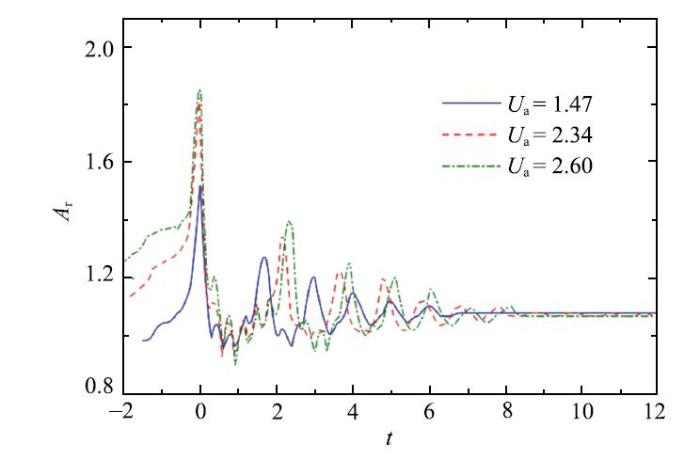
图17用长宽比表征了气泡在整个碰撞{--}回弹过程中的形状变化.虽然{$U_{\rm a}$}增大后气泡的变形程度显著增大, 然而,但长宽比时历曲线变化趋势大致相同, 即使{$U_{\rm a}$}从2.6降低到1.47, 仍可观测到4$\sim $5次明显的回弹过程.对比3.2节的情况可知, 相比于伽利略数的影响,气泡的回弹运动特性受接触速度的影响相对较小. 需要注意的是,当气泡稳定附在壁面上(长宽比保持定值)时, 图14和图16均未有明显变化,这是因为气泡接触壁面后的稳定构型主要是由于接触角决定的.

图 17

新窗口打开|下载原图ZIP|生成PPT
图 17不同$U_{\rm a}$时的$A_{\rm r}$时历曲线

Fig. 17Time histories of $A_{\rm r}$under different $U_{\rm a}$



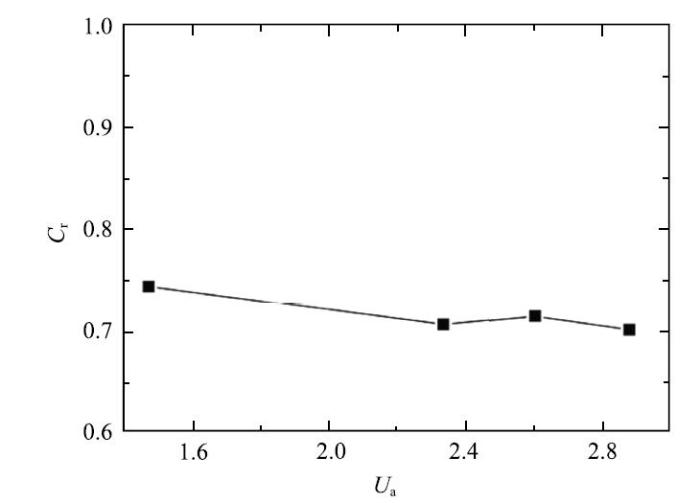
从图18可见, 接触速度的改变并未对回复系数造成太多改变, 这说明$C_{\rm r}$并不依赖于$U_{\rm a}$,这与Zenit等^[22]的实验观测结果一致. 进一步地讲, 这表明,$U_{\rm a}$并不是决定气泡回弹动力学特性的控制参数.

图 18

新窗口打开|下载原图ZIP|生成PPT
图 18$U_{\rm a}$对回复系数的影响

Fig. 18Effect of $U_{\rm a}$on the coefficient of restitution

4 结 论

本文基于动态自适应网格技术结合VOF方法, 模拟了直线上升轨迹(the rectilinear regime^[45]的浮力气泡撞击顶部壁面而回弹的运动过程,研究了气泡对壁面的回弹动力学特性.

研究表明, 伽利略数 Ga对浮力气泡与壁面的碰撞过程具有重要影响. Ga的增大, 气泡受到的黏性阻力减小, 惯性增大,可获得更大的接触速度(以及动能).回弹参数(回弹高度和回弹周期)、回复系数均与 Ga正相关, 所以Ga增大可支持气泡与壁面碰撞后发生更持久的回弹,气泡形变程度更为剧烈.

接触速度$U_{\rm a}$的改变在一定程度上可产生与$Ga$类似的影响,即增大$U_{\rm a}$可促进气泡碰撞产生更为剧烈的形变、更大的回弹高度及周期. 然而,回复系数并不受$U_{\rm a}$的影响.

下一步工作中, 将采用完全三维数值模拟,即研究具有气泡不稳定性的情况,以求进一步认识气泡对于顶部壁面的回弹动力学特性.

参考文献 View Option 原文顺序
文献年度倒序
文中引用次数倒序
被引期刊影响因子

[1] 李帅, 张阿漫 . 上浮气泡在壁面处的弹跳特性研究
物理学报, 2014,63(5):054705
[本文引用: 3]

( Li Shuai, Zhang Aman . Study on a rising bubble bouncing near a rigid boundary
Acta Physica Sinica, 2014,63(5):054705 (in Chinese))
[本文引用: 3]

[2] 邱超, 张会臣 . 单个上升空泡撞击顶部壁面的变形和回弹特性研究
机械工程学报, 2014,50(14):191-196
[本文引用: 1]

( Qiu Chao, Zhang Huichen . Deformation and rebound characteristics of single rising bubble impacting against top wall. Chin
[J] Mech Eng-EN, 2014,50(14):191-196 (in Chinese))
[本文引用: 1]

[3] 张洋, 陈科, 尤云祥 等. 壁面约束对裙带气泡动力学的影响
力学学报, 2017,49(5):1050-1058
[本文引用: 2]

( Zhang Yang, Chen Ke, You Yun-xiang , et al. Confinement effect on the rising dynamics of a skirted bubble
Chin J Theor Appl Mech, 2017,49:1050-1058(in Chinese))
[本文引用: 2]

[4] Liu LT, Yao XL, Zhang AM , et al. Numerical analysis of the jet stage of bubble near a solid wall using a front tracking method
Phys Fluids, 2017,29(1):012105


[5] 张阿漫, 姚熊亮 . 近壁面气泡的运动规律研究
物理学报, 2008,57(3):1662-1671


( Zhang Aman, Yao Xiongliang . The law of the bubble motion near the wall
Acta Physica Sinica, 2008,57(3):1662-1671 (in Chinese))


[6] 刘海龙, 沈学峰, 王睿 等. 纳米流体液滴撞击壁面铺展动力学特性研究
力学学报, 2018,50(5):1024-1231


( Liu Hailong, Shen Xuefeng, Wang Rui , et al. Study on spreading characteristics of nanofluid droplet impacting on solid surface
Chinese Journal of Theoretical and Applied Mechanics, 2018,50(5):1024-1231 (in Chinese))


[7] 周剑宏, 童宝宏, 王伟 , 等. 含气泡油滴撞击油膜壁面时气泡的变形与破裂
力学学报, 2018,50(2):427-37
[本文引用: 1]

( Zhou Jianhong, Tong Baohong, Wang Wei , et al. Deformation and rupture of bubble when the hollow droplet impacts on the film
Chinese Journal of Theoretical and Applied Mechanics, 2018,50(2):427-437 (in Chinese))
[本文引用: 1]

[8] Bhaga D, Weber ME . Bubbles in viscous liquids: Shapes, wakes and velocities
J Fluid Mech, 1981,105(-1):61-85
[本文引用: 2]

[9] Sharaf DM, Premlata AR, Tripathi MK , et al. Shapes and paths of an air bubble rising in quiescent liquids
Phys Fluids, 2017,29(12):122104
[本文引用: 1]

[10] Clift R, Grace JR, Weber ME. Bubbles , Drops, Particles. New York: Academic Press, 2005


[11] 闫红杰, 赵国建, 刘柳 等. 静止水中单气泡形状及上升规律的实验研究
中南大学学报(自然科学版), 2016,47(7):2513-2520
[本文引用: 1]

( Yan Hongjie, Zhao Guojian, Liu Lin , et al. Experimental study on shape and rising behavior of single bubble in stagnant water
J Cent South Univ, 2016,47(7):2513-2520 (in Chinese))
[本文引用: 1]

[12] 李帅, 孙龙泉, 张阿漫 . 水中上浮气泡动态特性研究
物理学报, 2014,63(18):287-299
[本文引用: 1]

( Li Shuai, Sun Longquan, Zhang Aman . Dynamic behavior of rising bubble
Acta Physica Sinica, 2014,63(18):287-299 (in Chinese))
[本文引用: 1]

[13] 孙鹏楠, 李云波, 明付仁 . 自由上浮气泡运动特性的光滑粒子流体动力学模拟
物理学报, 2015,64(17):174701


( Sun Pengnan, Li Yunbo, Ming Furen . Numerical simulation on the motion characteristics of freely rising bubbles using smoothed particle hydrodynamics method
Acta Physica Sinica, 2015,64(17):174701 (in Chinese))


[14] Zhang J, Ni M . What happens to the vortex structures when the rising bubble transits from zigzag to spiral?
J Fluid Mech, 2017,828:353-373
[本文引用: 1]

[15] Joshi JB, Nandakumar K, Evans GM , et al. Bubble generated turbulence and direct numerical simulations
Chem Eng Sci, 2017,157:26-75
[本文引用: 1]

[16] Magnaudet J, Eames I . The motion of high-Reynolds-number bubbles in inhomogeneous flows
Annu Rev Fluid Mech, 2000,32(1):659-708
[本文引用: 1]

[17] Tripathi MK, Sahu KC, Govindarajan R . Dynamics of an initially spherical bubble rising in quiescent liquid
Nat Commun, 2015,6:6268
[本文引用: 2]

[18] Zhang Y, Chen K, You Y , et al. Coalescence of two initially spherical bubbles: Dual effect of liquid viscosity
Int J Heat Fluid Fl, 2018,72:61-72
[本文引用: 1]

[19] Tsao HK, Koch DL . Observations of high Reynolds number bubbles interacting with a rigid wall
Phys Fluids, 1997,9(9):44-56
[本文引用: 1]

[20] Klasevoer E, Chevaillier J-P, Maté A , et al. Model and experiments of a drop impinging on an immersed wall
Phys Fluids, 2001,13(1):45-57
[本文引用: 1]

[21] Legendre D, Daniel C, Guiraud P . Experimental study of a drop bouncing on a wall in a liquid
Phys Fluids, 2005,17(9):097105
[本文引用: 1]

[22] Zenit R, Legendre D . The coefficient of restitution for air bubbles colliding against solid walls in viscous liquids
Phys Fluids, 2009,21(8):083306
[本文引用: 2]

[23] Kosior D, Zawala J, Malysa K . Influence of n-octanol on the bubble impact velocity, bouncing and the three phase contact formation at hydrophobic solid surfaces
Colloid Surface A, 2014,441:88-95
[本文引用: 2]

[24] Zawala J, Dabros T . Analysis of energy balance during collision of an air bubble with a solid wall
Phys Fluids, 2013,25(12):123101
[本文引用: 1]

[25] Zawala J, Krasowska M, Dabros T , et al. Influence of bubble kinetic energy on its bouncing during collisions with various interfaces
Can J Chem Eng, 2007,85(5):669-78
[本文引用: 1]

[26] Fujasová-Zedníková M, Vobecká L, Vejrazka J . Effect of solid material and surfactant presence on interactions of bubbles with horizontal solid surface
Can J Chem Eng, 2010,88(4):473-81
[本文引用: 1]

[27] Pelletier E, Béguin C, étienne S . Experiments of air bubbles impacting a rigid wall in tap water
Phys Fluids, 2015,27(12):123302
[本文引用: 1]

[28] Zhang A, Sun P, Ming F . An SPH modeling of bubble rising and coalescing in three dimensions
Comput Method Appl M, 2015,294:189-209
[本文引用: 1]

[29] Wu W, Liu Y, Zhang A . Numerical investigation of 3D bubble growth and detachment
Ocean Eng, 2017,138:86-104
[本文引用: 1]

[30] Canot é, Davoust L, Hammoumi ME , et al. Numerical simulation of the buoyancy-driven bouncing of a 2-D bubble at a horizontal wall
Theor Comp Fluid Dyn, 2003,17(1):51-72
[本文引用: 2]

[31] Omori T, Kayama H, Tukovic Z , et al. Interface resolving simulation of bubble-wall collision dynamics//Proceedings of the International Conference on Multiphase Flow,
F, 2010
[本文引用: 1]

[32] Qin T, Ragab S, Yue P . Axisymmetric simulation of the interaction of a rising bubble with a rigid surface in viscous flow
Int J Multiphas Flow, 2013,52:60-70
[本文引用: 1]

[33] Zawala J . ``Immortal'' liquid film formed by colliding bubble at oscillating solid substrates
Phys Fluids, 2016,28(5):057103
[本文引用: 1]

[34] Albadawi A, Donoghue DB, Robinson AJ , et al. On the assessment of a VOF based compressive interface capturing scheme for the analysis of bubble impact on and bounce from a flat horizontal surface
Int J Multiphas Flow, 2014,65:82-97
[本文引用: 2]

[35] Denner F . Wall collision of deformable bubbles in the creeping flow regime. Eur J Mech B-fluid, 2018,70:36-45
[本文引用: 1]

[36] Zhang A, Li S, Cui J . Study on splitting of a toroidal bubble near a rigid boundary
Phys Fluids, 2015,27(6):062102
[本文引用: 1]

[37] Zawala J, Kosior D, Dabros T , et al. Influence of bubble surface fluidity on collision kinetics and attachment to hydrophobic solids
Colloid Surface A, 2016,505:47-55


[38] 史冬岩, 王志凯, 张阿漫 . 相同尺度下气泡与复杂壁面的耦合特性研究
物理学报, 2014,63(17):533-538


( Shi D, Wang Z, Zhang A . Study on coupling characteristics between bubble and complex walls at the same scale
Acta Physica Sinica, 2014,63(17):533-538 (in Chinese))


[39] Ye X, Yao X, Han R . Dynamics of cavitation bubbles in acoustic field near the rigid wall
Ocean Eng, 2015,109:507-516
[本文引用: 1]

[40] Popinet S . Gerris: a tree-based adaptive solver for the incompressible Euler equations in complex geometries
J Comput Phys, 2003,190(2):572-600
[本文引用: 2]

[41] Chorin AJ . On the convergence of discrete approximations to the Navier-Stokes equations
Math Comput, 1989,23(106):35-47
[本文引用: 1]

[42] Bell JB, Colella P, Glaz HM . A second-order projection method for the incompressible Navier-Stokes equations
J Comput Phys, 1989,85(2):257-283
[本文引用: 1]

[43] Popinet S . An accurate adaptive solver for surface-tension-driven interfacial flows
J Comput Phys, 2009,228(16):5838-5866
[本文引用: 3]

[44] Cano-Lozano JC, Bohorquez P, Martínez-Bazán C . Wake instability of a fixed axisymmetric bubble of realistic shape
Int J Multiphas Flow, 2013,51:11-21
[本文引用: 1]

[45] Cano-Lozano JC, Martínez-Bazán C, Magnaudet J , et al. Paths and wakes of deformable nearly spheroidal rising bubbles close to the transition to path instability
Phys Rev Fluids, 2016,1(5):053604
[本文引用: 2]

[46] Gumulya M, Joshi JB, Utikar RP , et al. Bubbles in viscous liquids: Time dependent behaviour and wake characteristics
Chem Eng Sci, 2016,144:298-309
[本文引用: 1]