Muhammad Nadeem ^1,
, Md. Shakilur Rahman ^2,
, Muhammad Shahid ^1,
, Guinyun Kim ^1,,
, Haladhara Naik ^3,
, Nguyen Thi Hien ^1,
,

Corresponding author: Guinyun Kim, gnkim@knu.ac.kr

1.Department of Physics, Kyungpook National University, Daegu 41566, Korea
2.Institute of Nuclear Science and Technology, Bangladesh Atomic Energy Commission, Savar, Dhaka, Bangladesh
3.Radiochemistry Division, Bhabha Atomic Research Centre, Mumbai 400085, India
Received Date:2021-07-07
Available Online:2021-12-15
Abstract:The flux-weighted average cross sections of ^natCd(γ, xn)^{115g,m,111m,109,107,105,104}Cd and ^natCd(γ, x)^{113g,112,111g,110m}Ag reactions were measured at the bremsstrahlung end-point energies of 50 and 60 MeV. The activation and off-line γ-ray spectrometric technique was carried out using the 100 MeV electron linear accelerator at the Pohang Accelerator Laboratory, Korea. The ^natCd(γ, xn) reaction cross sections as a function of photon energy were theoretically calculated using the TALYS-1.95 and the EMPIRE-3.2 Malta codes. Then, the flux-weighted average cross sections were obtained from the theoretical values of mono-energetic photons. These values were compared with the flux-weighted values from the present study and were found to be in general agreement. The measured experimental reaction cross-sections and integral yields were described for cadmium and silver isotopes in the ^natCd(γ, xn)^{115g,m,111m,109,107,105,104}Cd and ^natCd(γ, x)^{113g,112,111g,110m}Ag reactions. The isomeric yield ratio (IR) of ^115g,mCd in the ^natCd(γ, xn) reaction was determined for the two bremsstrahlung end-point energies. The measured isomeric yield ratios of ^115g,mCd in the ^natCd(γ, xn) reaction were also compared with the theoretical values of the nuclear model codes and previously published literature data of the ¹¹⁶Cd(γ, n) and ¹¹⁶Cd(n, 2n) reactions. It was found that the IR value increases with increasing projectile energy, which demonstrates the characteristic of excitation energy. However, the higher IR value of ^115g,mCd in the ¹¹⁶Cd(n, 2n) reaction compared to that in the ¹¹⁶Cd(γ, n) reaction indicates the role of compound nuclear spin alongside excitation energy.

HTML

--> --> -->

Measurements of photon induced reaction cross-sections of natural cadmium are connected with different fields of science, such as the production of medically useful radioisotopes and yield measurements of long-lived radioactive products for radioactive waste handling and dose estimations. Cadmium isotopes are also used in nuclear technology as an important material to make bearings and alloys as well as for electroplating. Therefore, its activation can be used to estimate the radiation dose deposited inside materials for industrial or even medical purposes. In ^natCd, there are eight different isotopes [1]: ¹¹⁶Cd (7.49%), ¹¹⁴Cd (28.73%), ¹¹³Cd (12.22%), ¹¹²Cd (24.13%), ¹¹¹Cd (12.8%), ¹¹⁰Cd (12.49%), ¹⁰⁸Cd (0.89%), and ¹⁰⁶Cd (1.25%). The proton induced reactions of ^natCd are good sources for the production of medically important indium radioisotopes [2]. The radioisotopes ^111mCd and ¹¹¹In play a crucial role in time dependent perturbed angular correlation (TDPAC) studies for the investigation of material properties [3]. The radioisotope ¹⁰⁹Cd is frequently used for detector calibration due to its long half-life and high γ-ray abundance [4]. Cadmium isotopes are also used to enhance the coherence length and output power of HeCd metallic lasers [5]. Important radioactive isotopes of Cd can be produced from the photon-induced reactions of ^natCd. Similarly, the photon-induced reactions of ^natCd produce different radioisotopes of Ag. Among them, ^110mAg is frequently used as a γ-ray reference source. The radioisotopes ^111gAg and ^110mAg are also medically important radioisotopes for radiotherapy and imaging purposes [2, 6].
To maintain an optimal radioisotope production database, the addition of new, reliable experimental data is always important [7]. Previous studies were conducted in the giant dipole resonance (GDR) energy region for the production of ^115mCd [8] and ^111mCd [8, 9] using a γ-ray spectrometry technique; however, the [8, 9] results were higher than the estimated values. No further literature data have been found for any of the nuclides of interest, even in the GDR region. In a nuclear reaction, daughter products may have ground and meta-stable states with different nuclear spins. The ratio between the reaction cross sections of isomers with high spin $ {(\sigma }_{\rm H} $) and low spin $ \left({\sigma }_{\rm L}\right) $ is known as the isomeric yield ratio $ \left({{\sigma }_{\rm H}}/{{\sigma }_{\rm L}}\right) $ [10]. There are few earlier experimental studies on the IR of ^115m,gCd produced from the ¹¹⁶Cd(γ, n)^115m,gCd reaction in the giant dipole resonance region [11-14], based on mono-energetic photon beams. However, the measured IR of ^g,m115Cd in the ¹¹⁶Cd(γ, n) reaction using bremsstrahlung endpoint energies of 50, 60, and 70 MeV is available in literature [15], and the IR at high neutron energies for the ¹¹⁶Cd(n, 2n)^115m,gCd reactions [16] is also cited.
Based on these data, in this study, well-established radiation activation and off-line γ-ray spectrometrywere employed to determine the nuclear reaction cross-sections and integral yields of the ^{115g,m,111m,109,107,105,104}Cd and ^{113g,112,111g,110m}Ag radionuclides produced from ^natCd with the bremsstrahlung end-point energies of 50 and 60 MeV. The IR of ^115m,gCd produced in the ^natCd(γ, n) reactions was also measured using the activation technique with these bremsstrahlung end-point energies. For comparison, the ^natCd(γ, xn)^{115g,m,111m,109,107,105,104}Cd and ^natCd(γ, pxn)^{113g,112,111g,110m}Ag reaction cross sections were also theoretically calculated by employing the computer codes TALYS-1.95 [17] and EMPIRE-3.2 Malta [18]. The IR values from the present study with the bremsstrahlung end-point energies of 50 and 60 MeV are compared with the calculated values [17, 18] as well as with the available literature data [11-15].

Pulsed electron beams from the 100 MeV electron LINAC installed at the Pohang Accelerator Laboratory (PAL), Korea, were utilized for bremsstrahlung production. The 50 and 60 MeV electron beams were individually bombarded, one energy beam at a time, onto a tungsten converter foil with a thickness of 0.1 mm and a size of 10 cm × 10 cm, which was placed at a distance of 18 cm from its exit window. Details regarding the bremsstrahlung production using the linear accelerator are described elsewhere [19, 20]. The high-purity (99.99%) natural cadmium and ¹⁹⁷Au metal foils were irradiated by bremsstrahlung radiation with end-point energies of 50 and 60 MeV. Two sets of 0.1 mm thick ^natCd foils with weights of 0.1782 and 0.1231 g and two sets of 0.1 mm thick ¹⁹⁷Au foils with weights of 0.2478 and 0.2668 g were placed in air at a distance of 12 cm from the W-target in a perpendicular direction to the electron beam. These targets were irradiated for 236 and 125 min with the bremsstrahlung radiation with end-point energies of 50 and 60 MeV, respectively. The average beam current during irradiation was 20-36 mA with a repetition rate of 15 Hz and a pulse width of 2 μs.
The samples irradiated by the bremsstrahlung radiation with end-point energies of 50 and 60 MeV were taken out after sufficient cooling time. The off-line γ-ray counting was performed using a pre-calibrated HPGe detector coupled with a PC-based 4K channel analyzer. The HPGe detector used for γ-ray counting is an Ortec detector from Canberra. The dead time of the detector during the γ-ray counting was kept below 2% by changing the distance between the detector and irradiated samples; this prevented pile up and coincidence-summing effects. The resolution of the HPGe detector was 1.8 keV at full-width at half width (FWHM) at the photopeak of 1332.5 keV γ-ray of ⁶⁰Co. The total detector efficiency was 20% at the 1332.5 keV γ-ray peak relative to a 7.62 cm × 7.62 cm NaI(Tl) detector. Typical γ-ray spectra of the reaction products produced from the ^natCd and ¹⁹⁷Au monitor samples irradiated with bremsstrahlung radiation with an end-point energy of 60 MeV are shown in Fig. 1(a-c). The produced radionuclides were identified based on the respective γ-ray energies and half-lives of the radioactive isotopes [21, 22], as presented in Table 1.
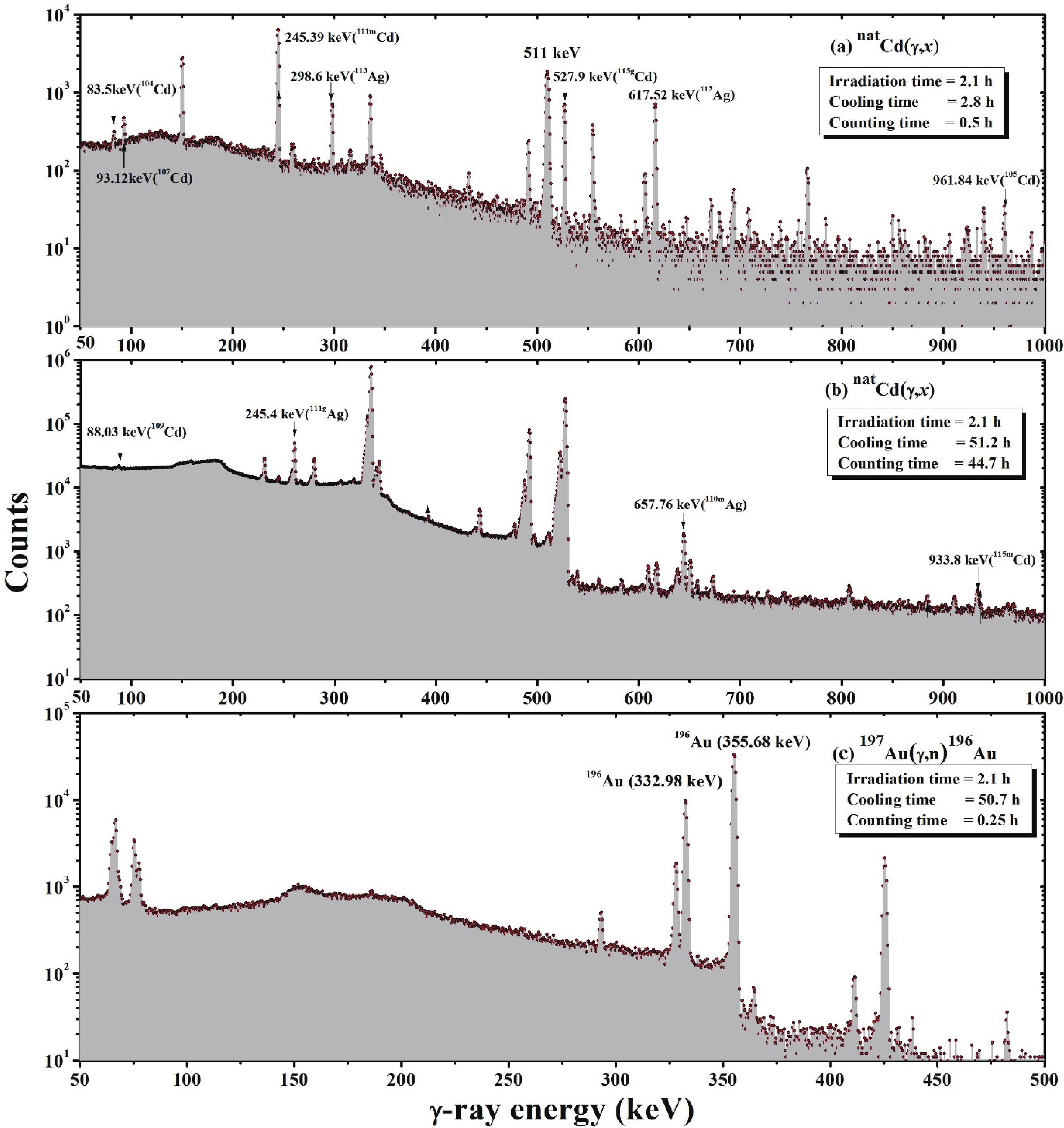Figure1. (color online) Typical γ-ray spectra of the products of the ^natCd(γ, x) reactions with cooling times of (a) 2.8 h and (b) 51.2 h, and (c) those of the ¹⁹⁷Au(g, n) reaction with a cooling time of 50.7 h. The bremsstrahlung end-point energy used for the irradiation was 60 MeV.

Nuclides (spin & parity)	Half-life	Decay mode (%)	g-ray energy /keV	γ-ray abundance (%)	Reactions	Q-value /MeV	Threshold /MeV
115gCd (1/2)+	53.46 h	β- : 100.00	336.24	45.9	116Cd(γ, n)	?8.699	8.700
					Decay of 115mAg (T1/2 = 18 s) by β-(79%)
			527.90	27.45	Decay of 115gAg (T1/2 = 20 m) by β-(100%)
115mCd (11/2)-	44.56 d	β-: 100.00	158.03	0.02	116Cd(γ, n)	?8.699	8.700
			484.47	0.29	Decay of 115Ag (T1/2 = 20 m) by β-(100%)
			933.80	2
111mCd (11/2)-	48.5 m	IT : 100	150.82	29.1	111Cd(γ, g’)	0.0	0.0
					112Cd(γ, n)	?9.394	9.394
					113Cd(γ, 2n)	?15.934	15.935
			245.39	94	114Cd(γ, 3n)	?24.977	24.980
					116Cd(γ, 5n)	?39.817	39.824
109Cd (5/2)+	461.9 d	EC: 100	88.03	3.64	110Cd(γ, n)	?9.915	9.915
					111Cd(γ, 2n)	?16.891	16.892
					112Cd(γ, 3n)	?26.285	26.288
					113Cd(γ, 4n)	?32.824	32.829
					114Cd(γ, 5n)	?41.867	41.875
					116Cd(γ,7n)	?56.707	56.722
107Cd (5/2)+	6.5 h	EC :100	93.12	4.7	108Cd(γ, n)	?10.334	10.334
					110Cd(γ, 3n)	?27.572	27.575
					111Cd(γ, 4n)	?34.547	34.553
					112Cd(γ, 5n)	?43.941	43.950
			828.93	0.163	113Cd(γ, 6n)	?50.481	50.493
					114Cd(γ, 7n)	?59.524	59.541
					116Cd(γ, 9n)	?74.364	74.390
105Cd (5/2)+	55.5 m	EC :100	346.87	4.2	106Cd(γ, n)	?10.870	10.870
					108Cd(γ, 3n)	?29.133	29.137
			433.24	2.81	110Cd(γ, 5n)	?46.371	46.381
					111Cd(γ, 6n)	?53.346	53.360
			961.84	4.7	112Cd(γ, 7n)	?62.740	62.759
					113Cd(γ, 8n)	?69.280	69.303
104Cd (0)+	57.7 m	EC :100			106Cd(γ, 2n)	?19.306	19.308
			66.6	2.4	108Cd(γ, 4n)	?37.569	37.576
			83.5	47	110Cd(γ, 6n)	?54.808	54.822
			709.3	19.5	111Cd(γ, 7n)	?61.783	61.802
					112Cd(γ, 8n)	?71.177	71.201
113gAg (1/2)-	5.37 h	β- : 100.00	258.72	1.64	114Cd(γ, p)	?10.277	10.278
					116Cd(γ, p2n)	?25.117	25.120
			298.6	10	Decay of 113mAg
					(T1/2 = 62 s, spin=7/2+) by IT(64%)
Continued on next page

Table1.Nuclear spectroscopic data of the products of the ^natCd(γ, xn), ^natCd(γ, pxn), and ¹⁹⁷Au(γ, n) reactions. The photo-peak activities of γ-ray energies marked with bold letters were used for calculations.

2

-->

A.Determination of photon flux

The photon fluxes (${{\rm{\phi}} _{{E_{\rm e}}}}\left( {{E_\gamma }} \right)$) as a function of photon energy (E_γ) for the bremsstrahlung spectra with electron beam energies (E_e) of 50 and 60 MeV were simulated using the GEANT4 code [23] and are shown in Fig. 2. The integrated photon flux $\Phi \left( {{E_{\rm e}}} \right)\left( { = \int_{{E_{\rm th}}}^{{E_{\rm e}}} {{{\rm{\phi}} _{{E_{\rm e}}}}\left( {{E_\gamma }} \right){\rm d}{E_\gamma }} } \right)$ from the threshold to the electron beam energy was measured using the photo-peak activity of a 355.68 keV (Iγ =87%) γ-line of ^196gAu produced from the ¹⁹⁷Au(γ, n)^196gAu monitor reaction. The observed number of counts ($N_{\rm obs}^{{E_{\rm e}}}$) for the 355.68 keV γ-line of ^196gAu was calculated by summing the counts under the full energy peak and subtracting the linear Compton back-ground, which is related to the integrated photon flux $\Phi \left( {{E_{\rm e}}} \right)$ as follows [24]:
Figure2. (color online) Typical bremsstrahlung spectra for the end-point energies of 50 and 60 MeV simulated using the GEANT4 code.

$\Phi \left( {{E_{\rm e}}} \right) = \frac{{N_{\rm obs}^{{E_{\rm e}}}\left( {CL/LT} \right)\lambda }}{{n\left\langle {{{\rm{\sigma}} _R}\left( {{E_{\rm e}}} \right)} \right\rangle {I_\gamma }{{\rm{\varepsilon}} _\gamma }\left( {1 - {{\rm e}^{ - \lambda {T_{\rm irr}}}}} \right){{\rm e}^{ - \lambda {T_{\rm C}}}}\left( {1 - {{\rm e}^{ - \lambda CL}}} \right)}},$

(1)

where n and λ are the number of atoms in the flux monitor (Au) sample and the decay constant for ^196gAu, respectively. I_γ and ε_γ are the branching intensity and detection efficiency of the selected γ-line, respectively. T_irr and T_C, are the irradiation and the cooling times, respectively. CL and LT are the clock and live counting times, respectively. The detection efficiencies were measured using the standard calibration sources of ¹⁵²Eu and ¹³³Ba. $\left\langle {{{\rm{\sigma}} _R}\left( {{E_{\rm e}}} \right)} \right\rangle $ is the known average cross section of the ¹⁹⁷Au(γ,n)^196gAu monitor reaction taken from Ref. [24], which is 103.3±12.1 mb and 102.4±9.5 mb for the bremsstrahlung end-point energies of 50 and 60 MeV, respectively. Nuclear data, such as the half-lives, γ-ray abundances, reaction Q-values, and threshold energies of the products, are given in Table 1 [21, 22].

Table 1-continued from previous
Nuclides (spin & parity)	Half-life	Decay mode (%)	g-ray energy /keV	γ-ray abundance (%)	Reactions	Q-value /MeV	Threshold /MeV
112Ag (2)-	3.13 h	β- : 100.00	606.82	3.1	113Cd(γ, p)	?9.749	9.749
			617.52	43	114Cd(γ, pn)	?18.792	18.793
			694.87	2.9	116Cd(γ, p3n)	?33.632	33.637
111gAg (1/2)-	7.45 d	β- : 100.00	245.40	1.24	112Cd(γ, p)	?9.648	9.649
					113Cd(γ, pn)	?16.188	16.189
					114Cd(γ, p2n)	?25.231	25.234
			342.13	7	116Cd(γ, p4n)	?40.071	40.079
					Decay of 111mAg (T1/2 = 1.08 m, spin=7/2+) by IT (99.3%)
110mAg (6)+	249.83 d	IT : 1.33	657.76	95.61	111Cd(γ, p)	?9.084	9.084
					112Cd(γ, pn)	?18.478	18.479
					113Cd(γ, p2n)	?25.018	25.021
		β- : 98.67	884.67	75	114Cd(γ, p3n)	?34.061	34.066
					116Cd(γ, p5n)	?48.901	48.912
196gAu (2)-	6.18 d	EC : 92.8 β- : 7.2	355.68	87.0	197Au(γ, n)	?8.072	8.073

2 -->

B.Calculation of normalized yield and correction factor

Natural cadmium has eight stable isotopes with different isotopic abundances. The yield of the produced radionuclides is the sum of the isotope contributions based on their production threshold energies, as shown in Table 1. The eleven radio nuclides in Table 1 can be produced from ^natCd(γ, x)j reactions with different threshold values. The normalized yield contribution (${Y_{i,j}}\left( {{E_{\rm e}}} \right)$) for each reaction of ⁱCd(γ, x)j was obtained as follows [25]:

${Y_{i,j}}\left( {{E_{\rm e}}} \right) = \frac{{\displaystyle\int_{{E_{\rm th}}}^{{E_{\rm e}}} {{A_i}\;{{\rm{\sigma}} _{i,j}}\left( {{E_\gamma }} \right){\rm{\phi}} \left( {{E_\gamma }} \right){\rm d}{E_\gamma }} }}{{\displaystyle\sum\limits_{k = 1}^8 {\int_{{E_{\rm th}}}^{{E_{\rm e}}} {{A_k}\;{{\rm{\sigma}} _{k,j}}\left( {{E_\gamma }} \right){\rm{\phi}} \left( {{E_\gamma }} \right){\rm d}{E_\gamma }} } }},$

(2)

where i and k are eight stable isotopes (i, k = 106, 108, 110, 111, 112, 113, 114, 116) in ^natCd, and j is eleven produced isotopes (^{115g,m,111m,109,107,105,104}Cd and ^{113g,112,111g,110m}Ag). ${\rm{\phi}} \left( {{E_\gamma }} \right)$ is the photon flux calculated using the GEANT4 code [23], A_i(k) is the isotopic abundance, and ${{\rm{\sigma}} _{i,j}}\left( {{E_\gamma }} \right)$ is the cross section for the ⁱCd(γ, x)j reactions at the photon energy E_γ, which was calculated using the TALYS 1.95 code [17]. The normalized yield contributions for eleven radio isotopes j produced from various ⁱCd(γ, x)j reactions are given in Table 2.

Produced Nuclei	Reaction	Eth/MeV	E e =50 MeV			Ee =60 MeV
			${Y_{i,j}}\left( {{E_{\rm e}}} \right)$	${F_{i,j}}\left( {{E_{\rm e}}} \right)$		${Y_{i,j}}\left( {{E_{\rm e}}} \right)$	${F_{i,j}}\left( {{E_{\rm e}}} \right)$
115gCd	116Cd(γ, n)	8.70	Y116,115= 100	F116,115= 0.934		Y116,115 = 100	F116,115= 0.940
115mCd	116Cd(γ, n)	8.70	Y116,115= 100	F116,115= 0.934		Y116,115 = 100	F116,115= 0.940
111mCd	111Cd(γ, g’)	0.0	Y111,111= 1.70	F111,111= 2.910		Y111,111 =1.40	F111,111= 2.710
	112Cd(γ, n)	9.39	Y112,111= 64.9	F112,111= 0.890		Y112,111=62.6	F112,111= 0.901
	113Cd(γ, 2n)	15.94	Y113,111= 18.5	F113,111= 0.554		Y113,111= 19.0	F113,111= 0.592
	114Cd(γ, 3n)	24.96	Y114,111= 14.5	F114,111= 0.306		Y114,111= 16.0	F114,111= 0.359
	116Cd(γ, 5n)	39.82	Y116,111= 0.40	F116,111= 0.080		Y116,111= 1.00	F116,111= 0.148
109Cd	110Cd(γ, n)	9.92	Y110,109= 75.7	F110,109= 0.848		Y110,109= 74.1	F110,109= 0.863
	111Cd(γ, 2n)	16.89	Y111,109= 18.7	F111,109= 0.518		Y111,109= 18.7	F111,109= 0.560
	112Cd(γ, 3n)	26.29	Y112,109= 4.60	F112,109= 0.278		Y112,109= 5.00	F112,109= 0.333
	113Cd(γ, 4n)	32.83	Y113,109= 0.80	F113,109= 0.168		Y113,109= 1.10	F113,109= 0.231
	114Cd(γ, 5n)	41.86	Y114,109= 0.20	F114,109= 0.059		Y114,109= 1.10	F114,109= 0.127
107Cd	108Cd(γ, n)	10.33	Y108,107= 67.5	F108,107= 0.823		Y108,107= 59.2	F108,107= 0.840
	110Cd(γ, 3n)	27.58	Y110,107= 24.7	F110,107= 0.255		Y110,107= 24.5	F110,107= 0.316
	111Cd(γ, 4n)	34.55	Y111,107= 7.30	F111,107= 0.145		Y111,107= 10.1	F111,107= 0.210
	112Cd(γ, 5n)	43.95	Y112,107= 0.50	F112,107= 0.039		Y112,107= 5.80	F112,107= 0.108
	113Cd(γ, 6n)	50.49	Y113,107= 0.00	F113,107= 0.00		Y113,107= 0.40	F113,107= 0.052
105Cd	106Cd(γ, n)	10.87	Y106,105= 98.6	F106,105= 0.786		Y106,105= 96.4	F106,105= 0.806
	108Cd(γ, 3n)	29.14	Y108,105= 1.40	F108,105= 0.227		Y108,105= 1.60	F108,105= 0.286
	110Cd(γ, 5n)	46.38	Y110,105= 0.00	F110,105= 0.020		Y110,105= 1.90	F110,105= 0.086
	111Cd(γ, 6n)	53.36	Y111,105= 0.00	F111,105= 0.000		Y110,105= 0.10	F111,105= 0.033
104Cd	106Cd(γ, 2n)	19.31	Y106,104= 98.2	F106,104= 0.443		Y106,104= 96.2	F106,104= 0.488
	108Cd(γ, 4n)	37.58	Y108,104= 1.80	F108,104= 0.107		Y108,104= 3.60	F108,104= 0.174
	110Cd(γ, 6n)	54.82	Y110,104= 0.00	F110,104= 0.000		Y110,104= 0.20	F110,104= 0.016
113Ag	114Cd(γ, p)	10.28	Y114,113= 88.1	F114,113= 0.823		Y114,113= 92.9	F114,113= 0.840
	116Cd(γ, p2n)	25.12	Y116,113= 11.9	F116,113= 0.302		Y116,113= 7.10	F116,113= 0.356
112Ag	113Cd(γ, p)	9.75	Y113,112= 27.0	F113,112= 0.862		Y113,112= 21.9	F113,112= 0.875
	114Cd(γ, pn)	18.79	Y114,112= 71.8	F114,112= 0.460		Y114,112= 74.3	F114,112= 0.505
	116Cd(γ, p3n)	33.64	Y116,112= 1.20	F116,112= 0.156		Y116,112= 3.80	F116,112= 0.234
111Ag	112Cd(γ, p)	9.65	Y112,111= 56.9	F112,111= 0.862		Y112,111= 49.9	F112,111= 0.875
	113Cd(γ, pn)	16.19	Y113,111= 23.1	F113,111= 0.546		Y113,111= 23.0	F113,111= 0.585
	114Cd(γ, p2n)	25.23	Y114,111= 19.9	F114,111= 0.297		Y114,111= 26.5	F114,111= 0.352
	116Cd(γ, p4n)	40.08	Y116,111= 0.10	F116,111= 0.078		Y116,111= 0.60	F116,111= 0.146
110mAg	111Cd(γ, p)	9.08	Y111,110= 17.5	F111,110= 0.905		Y111,110= 10.7	F111,110= 0.914
	112Cd(γ, pn)	18.48	Y112,110= 58.7	F112,110= 0.466		Y112,110= 49.2	F112,110= 0.511
	113Cd(γ, p2n)	25.02	Y113,110= 16.4	F113,110= 0.301		Y113,110= 18.3	F113,110= 0.356
	114Cd(γ, p3n)	34.06	Y114,110= 7.40	F114,110= 0.151		Y114,110= 21.6	F114,110= 0.215
	116Cd(γ, p5n)	48.91	Y116,110= 0.00	F116,110= 0.004		Y116,110= 0.20	F116,110= 0.065

Table2.Normalized yield (%) and photon flux correction factor (${F_{i,j}}\left( {{E_{\rm e}}} \right)$) for the ⁱCd(γ, xn)j reactions.

The threshold value (E_th) of the monitor reaction ¹⁹⁷Au(γ, n)¹⁹⁶Au is 8.07 MeV, as seen in Table 1. However, the production thresholds for the elevenradionuclides (j =^{115g,m;111m;109m,107m;105m;104m}Cd and ^{113g;112;111g;110m}Ag) are different from the monitor reaction as listed in Table 1. Therefore, a flux correction factor is required to correct the measured photon flux from the ⁱCd(γ, x)j reactions to that from the monitor reaction. The photon flux correction factors ${F_{i,j}}\left( {{E_{\rm e}}} \right)$ for ⁱCd(γ, x)j were calculated as follows [25]:

${F_{i,j}}\left( {{E_{\rm e}}} \right) = {{\int\limits_{E_{\rm th}^{i,j}}^{{E_{\rm e}}} {{\rm{\phi}} \left( {{E_\gamma }} \right){\rm d}{E_\gamma }} } \Big/ {\int\limits_{E_{\rm th}^{\rm Au}}^{{E_{\rm e}}} {{\rm{\phi}} \left( {{E_\gamma }} \right){\rm d}{E_\gamma }} }},$

(3)

where i and j have the same definitions as in Eq. (2). $E_{\rm th}^{i,j}$ and $E_{\rm th}^{\rm Au}$ are the threshold energies for the ⁱCd(γ, x)j and ¹⁹⁷Au(γ,n)^196gAu reactions, respectively. ${\rm{\phi}} \left( {{E_\gamma }} \right)$ is the photon flux as a function of photon energy E_γ, taken from Fig. 2, which was simulated using the GEANT4 code [23]. The obtained correction factors to correct the different reactions to the monitor reaction are given in Table 2.
The yield-weighted flux correction factors $C_j^T\left( {{E_{\rm e}}} \right)$ for the ^jCd(γ, x)j reactions were calculated using Eqs. (2) and (3) as follows:

$C_j^T\left( {{E_{\rm e}}} \right) = {{\sum\limits_i {\left( {{Y_{i,j}}\left( {{E_{\rm e}}} \right) \times {F_{i,j}}\left( {{E_{\rm e}}} \right)} \right)} } \Big/ {\sum\limits_i {{Y_{i,j}}\left( {{E_{\rm e}}} \right)} }}.$

(4)

The obtained yield-weighted flux correction factors $C_j^T\left( {{E_{\rm e}}} \right)$ for the eleven produced isotopes (j) are listed in Table 3. The yield-weighted photon flux $\Phi _j^C\left( {{E_{\rm e}}} \right)$ with the yield-weighted flux correction factors for the ^natCd(γ, x)j reactions were obtained as follows:

Nuclear reactions	Total correction factors ($C_j^T\left( { {E_{\rm e}} } \right)$)
	Bremsstrahlung end-point energy, Ee/MeV
	50	60
natCd(γ, n)115gCd	0.934	0.941
natCd(γ, n)115mCd	0.934	0.941
natCd(γ, xn)111mCd	0.774	0.774
natCd(γ, xn)109Cd	0.753	0.765
natCd(γ, xn)107Cd	0.629	0.602
natCd(γ, xn)105Cd	0.778	0.783
natCd(γ, xn)104Cd	0.437	0.476
natCd(γ, pxn)113gAg	0.761	0.806
natCd(γ, pxn)112Ag	0.565	0.576
natCd(γ, pxn)111gAg	0.676	0.665
natCd(γ, pxn)110mAg	0.492	0.416

Table3.Yield-weighted flux correction factor for the ^natCd(γ, x)j reactions.

$\Phi _j^C\left( {{E_{\rm e}}} \right) = C_j^T\left( {{E_{\rm e}}} \right) \times \Phi \left( {{E_{\rm e}}} \right).$

(5)

2 -->

C.Measurement of flux-weighted average cross sections

We determined the flux-weighted average cross sections using the yield-weighted photon flux $\Phi _j^C\left( {{E_{\rm e}}} \right)$ for the ^natCd(γ, x)j reactions (the produced nuclei j is given as ^{115gm,111m,109,107,105,104}Cd and ^{113g,112,111g,110m}Ag). The nuclear spectroscopic data for the reaction products were taken from Refs. [21, 22] and given in Table 1. Once the observed number counts under the photo-peak ($N_{\rm obs}^{{E_\gamma }}$) was acquired for the characteristic γ-ray energy of the produced radionuclide j, the flux-weighted average cross sections of the ^natCd(γ, x)j reactions were obtained as follows [25]:

$\left\langle {{\rm{\sigma}} _j^{\rm nat}\left( {{E_{\rm e}}} \right)} \right\rangle = \frac{{N_{\rm obs}^{{E_{\rm e}}}\left( {CL/LT} \right)\lambda }}{{n\Phi _j^C\left( {{E_{\rm e}}} \right){I_\gamma }{{\rm{\varepsilon}} _\gamma }\left( {1 - {{\rm e}^{ - \lambda {T_{\rm irr}}}}} \right){{\rm e}^{ - \lambda {T_C}}}\left( {1 - {{\rm e}^{ - \lambda CL}}} \right)}},$

(6)

where all terms have the same meaning as in Eq. (1) and $\Phi _j^C\left( {{E_{\rm e}}} \right)$ is the yield-weighted photon flux as given in Eq. (5).
2 -->

D.Theoretical calculations of flux-weighted average cross sections

The flux-weighted average cross sections were also theoretically calculated for all the residual nuclides of interest based on the TALYS 1.95 [17] and EMPIRE-3.2 Malta [18] nuclear codes and compared with the experimental data, which are presented in Table 4. The calculations based on TALYS 1.95 [17] and EMPIRE-3.2 Malta [18] were performed with their default parameters. The photon-induced reaction cross sections (${\rm{\sigma}} _R^x\left( {{E_i}} \right)$) for the ^natCd(γ, x) reactions were calculated based on mono-energetic photons using the TALYS 1.95 [17] and EMPIRE-3.2 Malta [18] codes. In the calculations, all possible exit channels of the nuclear reactions of the given projectile energy were considered. The flux-weighted average cross sections $\left( {\left\langle {{{\rm{\sigma}} _x}\left( E \right)} \right\rangle } \right)$ for the ^natCd(γ, x) reactions were calculated as follows:

Reaction	Bremsstrahlung end-point energy/MeV	Flux-weighted average cross-section $\left\langle {{\sigma _i}} \right\rangle $/mb
		Present work	Theoretical calculations
			TALYS 1.95 [17]	Empire 3.2 Malta [18]
natCd(γ, xn)115gCd	50	2.432 ± 0.345	2.521	3.631
	60	2.123 ± 0.261	2.330	3.544
natCd(γ, xn)115mCd	50	0.5 ± 0.071	0.534	0.778
	60	0.446 ± 0.059	0.493	0.760
natCd(γ, xn)111mCd	50	1.461 ± 0.219	0.458	0.811
	60	1.413 ± 0.212	0.449	0.785
natCd(γ, xn)109Cd	50	12.346 ± 1.786	9.082	8.381
	60	10.210 ± 1.501	8.466	7.724
natCd(γ, xn)107Cd	50	0.733 ± 0.101	0.788	0.656
	60	0.681 ± 0.094	0.834	0.711
natCd(γ, xn)105Cd	50	0.43 ± 0.065	0.669	0.702
	60	0.385 ± 0.059	0.632	0.651
natCd(γ, xn)104Cd	50	0.105 ± 0.015	0.121	0.112
	60	0.087 ± 0.011	0.112	0.086
natCd(γ, xn)113g+mAg	50	0.534 ± 0.075	0.057	0.108
	60	0.501 ± 0.061	0.057	0.110
natCd(γ, xn)112Ag	50	0.318 ± 0.043	0.068	0.159
	60	0.367 ± 0.046	0.081	0.172
natCd(γ, xn)111g+mAg	50	0.126 ± 0.019	0.0425	0.121
	60	0.123 ± 0.018	0.045	0.119
natCd(γ, xn)110mAg	50	0.026 ± 0.005	0.017	0.032
	60	0.027 ± 0.004	0.026	0.035

Table4.Flux-weighted average cross sections for the ^natCd(γ, xn) and ^natCd(γ, pxn) reactions.

$\left\langle {{\sigma _x}\left( E \right)} \right\rangle = {{\int\limits_{{E_{\rm th}}}^{{E_{\gamma \max }}} {\sigma _R^x({E_i})\;\varphi ({E_i}){\rm d}E} }\Bigg/ {\int\limits_{{E_{\rm th}}}^{{E_{\gamma \max }}} {\varphi ({E_i}){\rm d}E} }},$

(7)

where $ \left({E}_{i}\right) $ is the bremsstrahlung photon flux as a function of energy (E) simulated by the GEANT 4 code [23], as shown in Fig. 2.

The measured flux-weighted average cross sections are presented in different figures along with theoretical calculations and previously published data. The numerical values of all the cross sections and the uncertainties are given in Table 4. As previously stated, natural cadmium has eight stable isotopes (^{116,114,113,112,111,110,108,106}Cd). Thus, during irradiation, the production of a specific radionuclide is prone to contribution from many reaction channels based on the projectile energy.
The overall uncertainties in the results were calculated by taking the square root of the quadratic sum of all independent statistical and systematic uncertainties [19]. The resulting statistical uncertainties were mainly contributed by the counting statistics from the observed number of counts under the photo-peak of each γ-line (1.5%~10.5%). This was estimated by accumulating the data for an optimum time that depends on the half-life of the produced nuclides. In contrast, the systematic uncertainties were calculated from the uncertainties of the flux estimation (~11.5%), the detector efficiency (~3%), the half-life of the reaction products (~2%), the distance between the sample and detector (~2%), the γ-ray abundance (~2%), the irradiation and cooling time (~2%), the current and electron beam energy (~1%), and the number of cadmium target nuclei (~0.3%). The total systematic uncertainty is approximately 12.58%. The overall uncertainty is found to be between ~12.67% and ~16.07%.
2

-->

A.Measured photo-nuclear reaction cross sections of cadmium isotopes

When natural cadmium is irradiated with bremsstrahlung radiation with end-point energies of 50 and 60 MeV, six cadmium isotopes are directly produced through ^natCd(γ, xn) reactions, except the ^115g,mCd nuclides, which can be indirectly produced from the β^- decay of ^115g,mAg, as given in Table 1.
In this study, the flux-weighted average cross sections of the ^natCd(γ, xn)^{115g,m,111m,109,107,105,104}Cd reactions at the bremsstrahlung end-point energies of 50 MeV and 60 MeV are determined for the first time and presented in Table 4. All measurements of the produced cross sections of the cadmium isotopes are exclusive, that is, there is no contribution from any other short-lived radionuclides in the measurements. Even the ^{109,107,105,104}Cd radionuclides have no isomers; hence, their reaction cross sections are also independent. For comparison, the cross sections for the reactions as a function of the mono-energetic photons were calculated using the TALYS-1.95 and Empire 3.2 codes with default parameters; the flux-weighted average cross sections were then calculated using Eq. (7).
3 -->

1.^natCd(γ, n)^{115g, 115m}Cd reaction

The radioisotope ¹¹⁵Cd is produced directly through the ¹¹⁶Cd(γ, n) reaction and indirectly through the β^- decay of ¹¹⁵Ag. It has a short-lived ground state ^115gCd (T_1/2=53.46 h) and a long-lived meta-stable state ^115mCd (T_1/2=44.56 d). The simplified energy level and the decay scheme of ^115m,gCd is shown in Fig. 3. The meta-stable state ^115mCd with a half-life of 44.6 d decays directly to the ground state of ¹¹⁵In by the β^- process with a branching ratio of 97%. Meanwhile, approximately 1.7% of the meta-stable state decays to the ground state of ¹¹⁵In (j^π=9/2⁺) through the excited state of ¹¹⁵In (j^π=7/2⁺) by emitting a 933.8 keV γ-ray. The unstable ground state ^115gCd (j^π=1/2⁺) decays to the 336.24 keV state of ¹¹⁵In (J^π = 1/2^-) by a β^- process with a branching ratio of 62.6%, which decays to the ground state of ¹¹⁵In (J^π = 9/2⁺) via M4 transition by emitting a characteristic γ-ray of 336.2 keV. On the other hand, the unstable ground state ^115gCd decays to the 864.1 keV state of ¹¹⁵In (J ^π = 1/2⁺) by a β^- process with a branching ratio of 33.1%, which then decays to the 336.2 keV state of ¹¹⁵In (J ^π = 1/2^-) by emitting a 527.9-keV γ-ray. In order to identify the ^115m,gCd isomeric pairs, we used the 933.8 keV and 527.9 keV photo-peaks for the ^115mCd and ^115gCd nuclides, respectively. It is observed that both the metastable and ground states seem to be individual.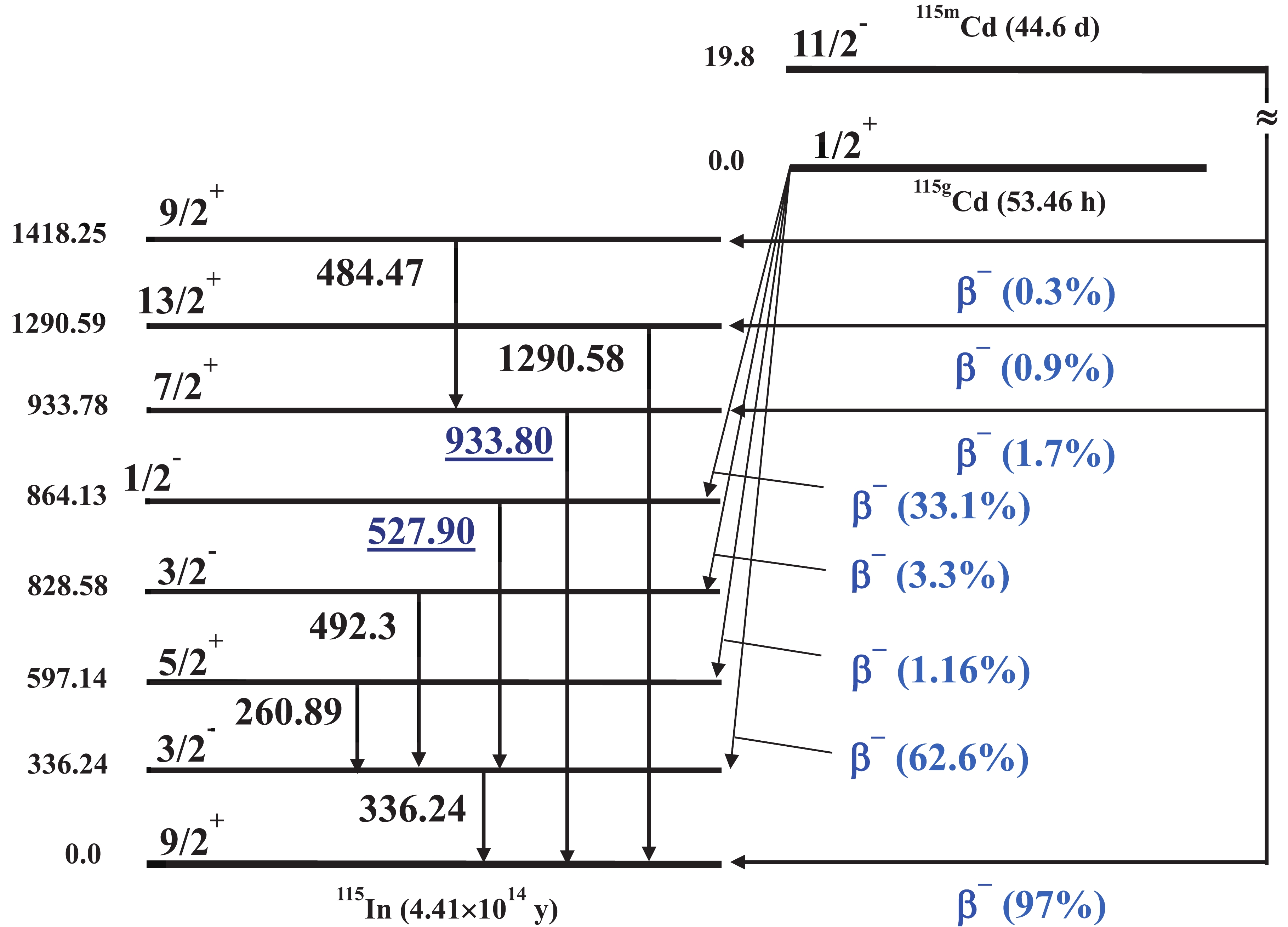
Figure3. (color online) Simplified decay scheme of the ^115g,,mCd isomers.

The measured results for the ^natCd(γ, xn)^115g;115mCd reactions are compared with the theoretical values obtained with the TALYS-1.95 and Empire 3.2 codes, as shown in Fig. 4. There is no literature data for the ^natCd(γ, xn)^115gCd reaction. It is clear that the theoretical values from both the TALYS-1.95 and Empire 3.2 codes are in agreement with the data from this study, as shown in Fig. 4. However, there is only one set of literature data regarding the low energy side of the GDR region for the ^natCd(γ, xn)^115mCd reaction [8], which was obtained with mono-energetic photons. To compare those results with the results of this study, we calculated the flux-weighted average cross section for the literature value using Eq. (7), as shown in Fig. 4. The flux-weighted average cross sections for literature data in the low energy region were higher than the theoretical results. However, the present results are lower than the values obtained with the TALYS-1.95 and Empire 3.2 codes, as shown in Fig. 4.
Figure4. (color online) The experimental flux-weighted average cross sections of ^natCd(γ, xn)^115gCd and ^natCd(γ, xn)^115mCd reactions as a function of bremsstrahlung end-point energy along with the theoretical calculations using the TALYS-1.95 and EMPIRE-3.2 codes.

Based on the measured experimental cross sections of the metastable and ground states from Table 4, we obtained the isomeric yield ratio (IR=σ_h/σ_l) of ^115gCd (nuclear spin=1/2⁺) and ^115mCd (nuclear spin=11/2^-) in the ^natCd(γ, xn) reactions, which are given in Table 5 for various bremsstrahlung end-point energies. The photon-induced IR values from this study, the literature data in the GDR region [11-14], and our previous results [15] are listed in Table 5 and shown in Fig. 5. The IR values for neutron-induced ¹¹⁶Cd(n, 2n)^115g,mCd reactions taken from previous data [16] and those theoretically calculated using TALYS-1.95, EMPIRE-3.2 Malta, and TENDL-2019 [26] are also presented in Table 5 and Fig. 5.

Reaction	Projectile energy/MeV	Excitation energy/MeV	Isomeric ratio (${IR} = { { {\sigma _{\rm HighSpin} } }/{\sigma _{\rm LowSpin} } }$)
			Experimental work [Ref.]	Theoretical calculations
				TALYS 1.95 [17]	Empire 3.2 Malta [18]
natCd(γ, xn)115g,mCd	50	13.922	0.206 ± 0.041 [A]	0.212	0.214
	60	13.928	0.210 ± 0.038 [A]	0.212	0.214
116Cd(γ, n)115gmCd	9.43	9.072	0.180 ± 0.019 [12]	0.015	0.004
116Cd(γ, n)115g,mCd	20	13.803	0.117 ± 0.012 [14]	0.205	0.213
116Cd(γ, n)115g,mCd	20	13.803	0.148 ± 0.020 [11]	0.205	0.214
116Cd(γ, n)115g,mCd	22	13.841	0.120 ± 0.020 [13]	0.209	0.214
116Cd(γ, n)115g,mCd	23.5	13.857	0.158 ± 0.016 [14]	0.209	0.214
116Cd(γ, n)115g,mCd	50	13.922	0.186 ± 0.020 [15]	0.212	0.214
116Cd(γ, n)115g,mCd	60	13.928	0.202 ± 0.020 [15]	0.212	0.214
116Cd(γ, n)115g,mCd	70	13.933	0.209 ± 0.019 [15]	0.212	0.214
116Cd(n, 2n)115g,mCd	13.4	19.04	0.95 ± 0.13 [16]	1.321	1.189
116Cd(n, 2n)115g,mCd	14	19.64	0.98 ± 0.14 [16]	1.360	1.246
116Cd(n, 2n)115g,mCd	14.68	20.32	1.0 ± 0.14 [16]	1.398	1.295
116Cd(n, 2n)115g,mCd	14.81	20.45	1.05 ± 0.15 [16]	1.410	1.295
116Cd(n, 2n)115g,mCd	16.5	22.14	1.25 ± 0.18 [16]	1.510	1.364
116Cd(n, 2n)115g,mCd	17.95	23.59	1.36 ± 0.19 [16]	2.810	2.690
116Cd(n, 2n)115g,mCd	19.76	25.40	1.59 ± 0.22 [16]	3.461	3.101
[A] Present work.

Table5.Isomeric yield ratio of ^115m,gCd from the ¹¹⁶Cd(γ, n) and ¹¹⁶Cd(n, 2n) reactions.

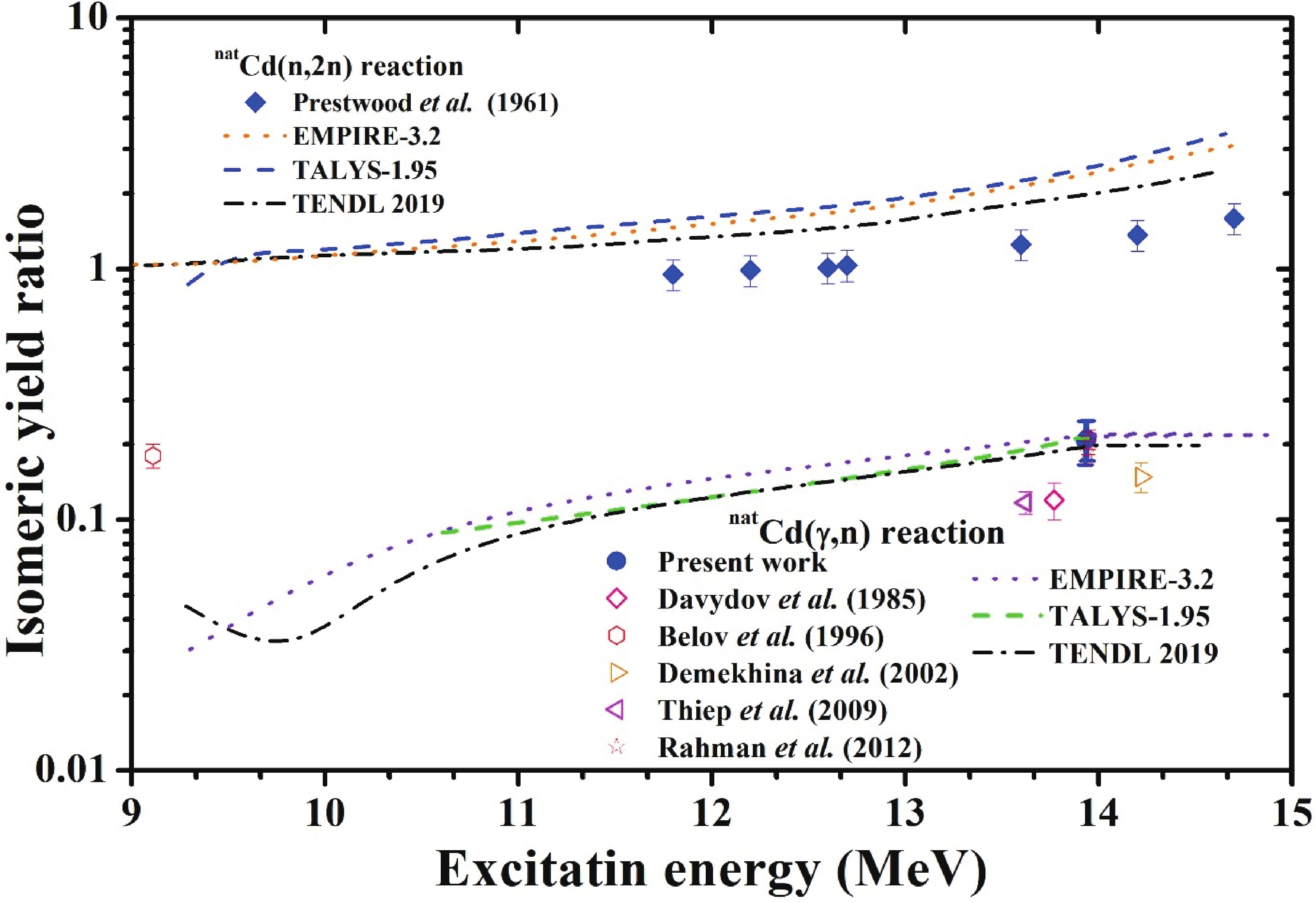Figure5. (color online) Isomeric cross section ratio (IR=σ_h/σ_l) of ^115g,mCd in the (γ, n) and (n, 2n) reactions as a function of excitation energy of the compound nucleus.

In order to understand the effects of spin and input angular momentum, outgoing particles, and excitation energy, the IR values from the different reaction channels were compared. The average excitation energy $ \left( {\left\langle {{E^*}\left( E \right)} \right\rangle } \right) $ of the compound nucleus from the threshold energy (E_th) to the bremsstrahlung end-point energy (E_e) was determined using the following expression [27, 28]:

$\left\langle {{E^*}\left( {{E_{\rm e}}} \right)} \right\rangle = \frac{{\int_{{E_{\rm th}}}^{{E_{\rm e}}} {{\rm{\phi}} \left( E \right){{\rm{\sigma}} _R}\left( E \right)E{\rm d}E} }}{{\int_{{E_{\rm th}}}^{{E_{\rm e}}} {{\rm{\phi}} \left( E \right)} {{\rm{\sigma}} _R}\left( E \right){\rm d}E}},$

(8)

where ${\rm{\phi}} \left( E \right)$ represents the photon flux as a function of photon energy (E) for the bremsstrahlung spectra, which was calculated using the Geant4 code, as shown in the Fig. 2. The reaction cross section (${{\rm{\sigma}} _R}\left( E \right)$) was calculated using the default option in the TALYS-1.95 code. The calculated average excitation energies for the ¹¹⁶Cd(γ,n) reaction corresponding to different bremsstrahlung end-point energies are given in Table 5.
The excitation energy (E^*) of the compound nucleus in the neutron and charged particle induced reactions was calculated as follows:

${E^*} = {E_{\rm p}} + \left( {{\Delta _{\rm T}}\, + \,{\Delta _{\rm p}}} \right)\, - \,{\Delta _{\rm CN}},$

(9)

where E_p is the projectile energy, and ${\Delta _{\rm CN}}$, ${\Delta _{\rm T}}$, and ${\Delta _{\rm p}}$ are the mass excess values of the compound nucleus, target, and projectile, respectively. The mass excess values are taken from the Nuclear Wallet Cards [29].
As seen in Fig. 5, the experimental IR values in the ¹¹⁶Cd(γ, n) reaction are in agreement with the theoretical values. However, in the ¹¹⁶Cd(n, 2n) reaction, the theoretical values from TALYS-1.95, EMPIRE-3.2, and TENDL-2019 are higher than the experimental values. Additionally, in the ¹¹⁶Cd(n, 2n) reaction, the theoretical values from TALYS-1.95 and EMPIRE-3.2 are slightly different. TENDL-2019 data are lower than the TALYS-1.95 data but are close to the experimental data. These differences are due to the use of default parameters in the current calculations with TALYS-1.95. Furthermore, the figure shows that the IR values of ^115m,gCd increase with increasing excitation energy. However, at the same excitation energy, the IR values of ^115m,gCd in the ¹¹⁶Cd(n, 2n) reaction are significantly higher than those in the ¹¹⁶Cd(γ, n) reaction. In the ¹¹⁶Cd(γ, n) reaction, the compound nucleus is ¹¹⁶Cd^*, which has a 0⁺ spin. On the other hand, in the ¹¹⁶Cd(n, 2n) reaction, the compound nucleus is ¹¹⁷Cd^*, which has a 11/2^- spin in the excited state and ?⁺ spin in the ground state. At a high excitation energy, the compound nucleus of ¹¹⁷Cd^* with a high spin value of 11/2^- will be favorable in the ¹¹⁶Cd(n, 2n) reaction. Thus, the high spin isomeric product ^115mCd with a spin state of 11/2^- will preferably be populated in the ¹¹⁶Cd(n, 2n) reaction, which results in a high IR value. This observation indicates the role of the spin of a compound nucleus alongside excitation energy. A similar observation can be made from our previous studies on the isomer ratio of ^106m,gAg and ^104m,gAg from the ^natAg (γ, xn) [30] and ^natAg(n, xn) [28] reactions, which support our present observations.
3 -->

2.^natCd(γ, xn)^111mCd reaction

The isomeric state ^111mCd (48.5 min, 11/2⁺) was identified by the pure and independent 245.39 keV γ-line. For the production of ^111mCd from the ¹¹²Cd target, only two previous experimental data sets in the GDR energy region based on mono-energetic photons were available [8, 9]; these were found to be higher than the theoretical values obtained using the TALYS-1.95 and EMPIRE-3.2 Malta codes as shown in Fig. 6 and provided in Table 4. The figure and table also show that the current results follow the graphical shape but are higher than the theoretical values; they are the closest to the values calculated using the Empire-3.2 code.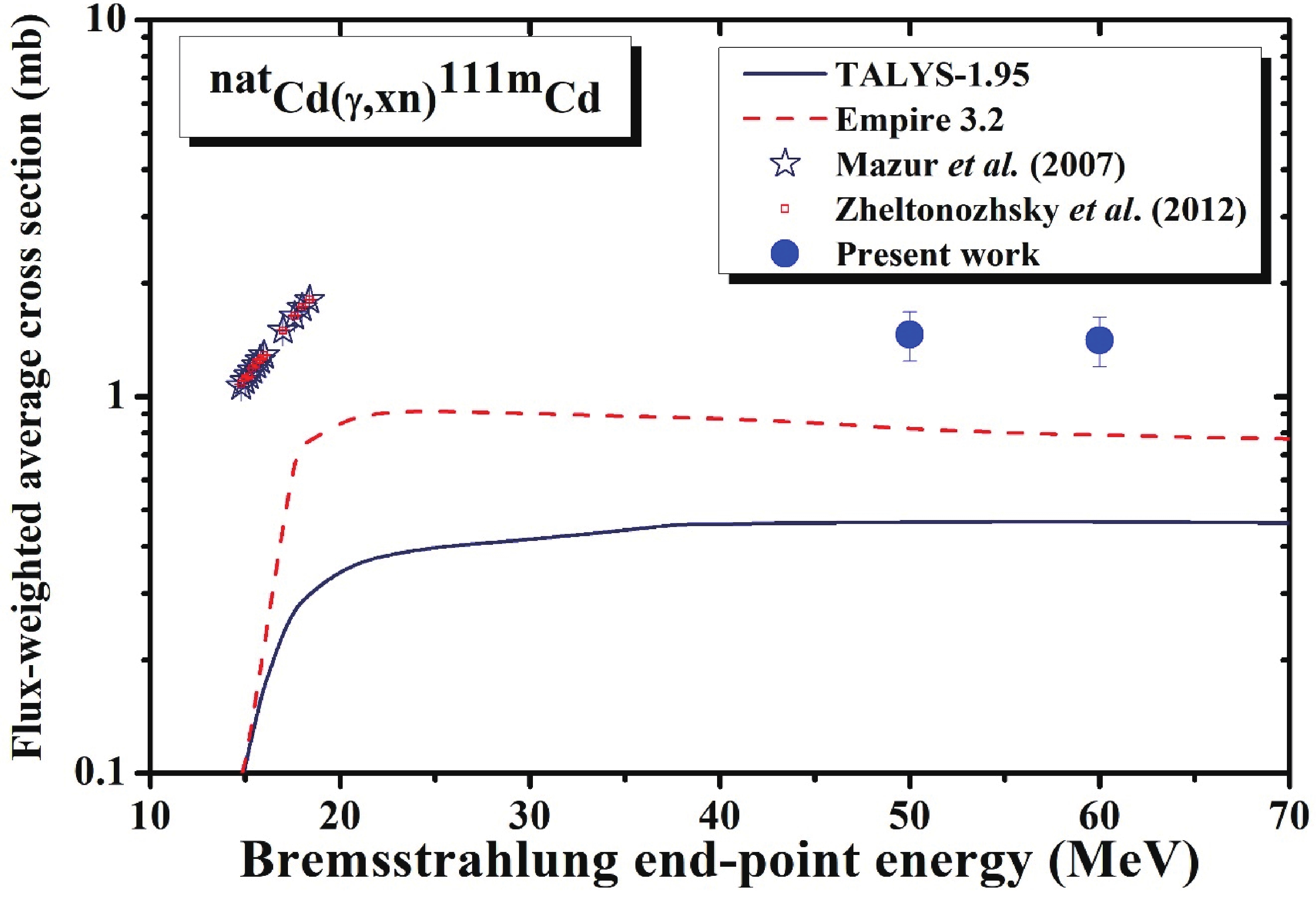
Figure6. (color online) Experimental flux-weighted average cross sections of the ^natCd(γ, xn)^111mCd reaction as a function of bremsstrahlung end-point energy along with the theoretical calculations using the TALYS-1.95 and EMPIRE-3.2 codes.

3 -->

3.^natCd(γ, xn)¹⁰⁹Cd reaction

The radionuclide ¹⁰⁹Cd (461.9 d, 5/2⁺) was identified by the pure and independent 88.03 keV γ-line. The measured ^natCd(γ, xn)¹⁰⁹Cd reaction cross-sections could onlybe compared with the theoretical calculations because no previous data has been found, as shown in Fig. 7 and tabulated in Table 4. In the figure, it is clear that the currently measured and theoretical values are in good agreement, in terms of not only shape but also magnitude.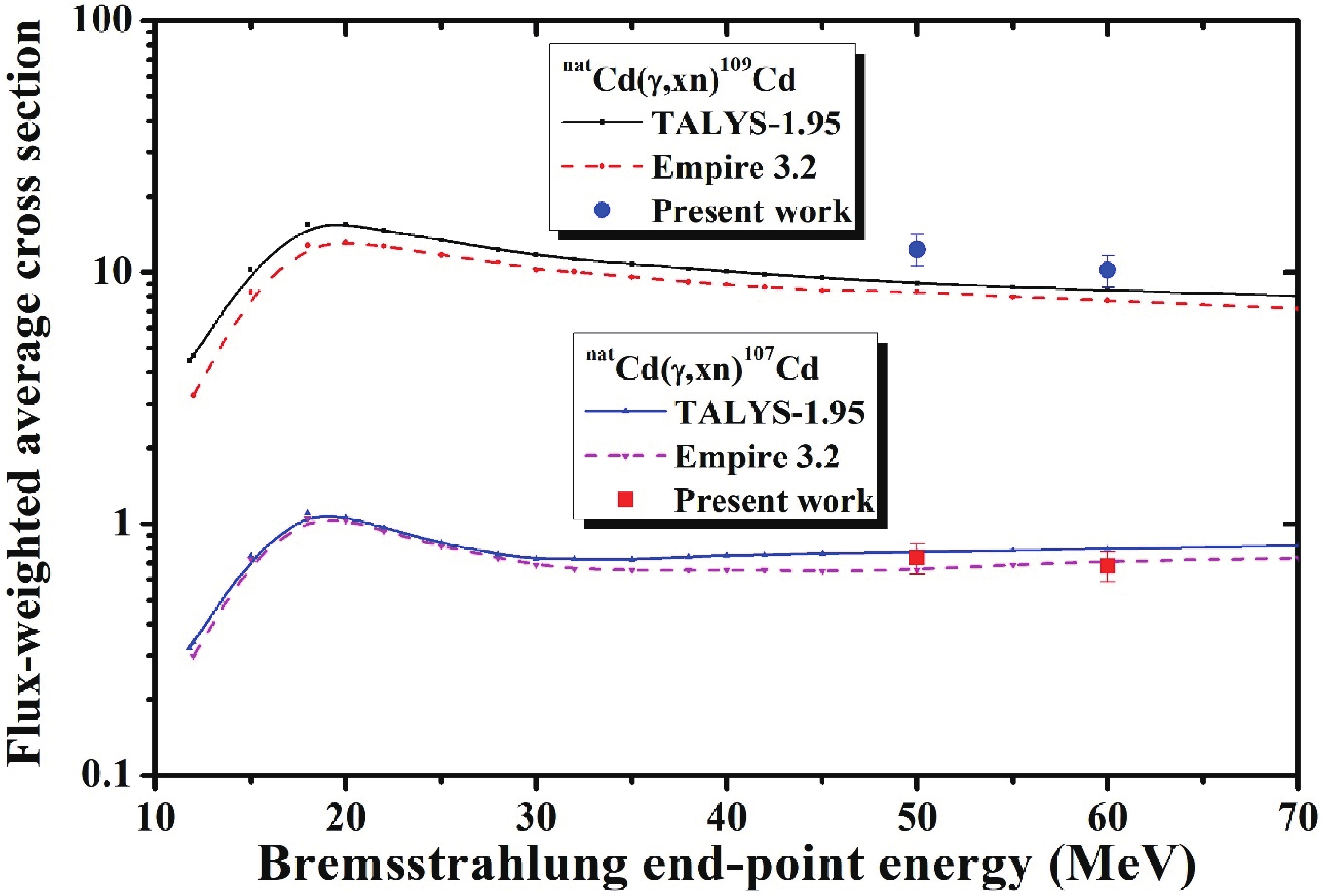
Figure7. (color online) Experimental flux-weighted average cross sections of the ^natCd(γ, xn)¹⁰⁹Cd and ^natCd(γ, xn)¹⁰⁷Cd reactions as a function of bremsstrahlung end-point energy along with the theoretical calculations using the TALYS-1.95 and EMPIRE-3.2 codes.

3 -->

4.^natCd(γ, xn)¹⁰⁷Cd reactions

The flux-weighted average formation cross sections of ¹⁰⁷Cd (6.5 h, 5/2⁺) were measured based on the 93.12 keV γ line. The measurements for the ^natCd(γ, xn)¹⁰⁷Cd reaction were performed for the first time and thus could only be compared with the theoretical values. Fig. 7 shows that the measurements are in good agreement with both of the calculations, but they are closer to the EMPIRE-3.2 Malta calculations.
3 -->

5.^natCd(γ, xn)¹⁰⁵Cd reactions

The flux-weighted average formation cross sections for ¹⁰⁵Cd (55.5 min, 5/2⁺) were measured based on the independent 961.84 keV γ-line. The radioisotope (¹⁰⁵Cd) is without an isomer. For this reaction, no literature data were available; hence, its measurements were also only compared with the theoretical calculations. In Fig. 8 and Table 4, it is clear that the flux-weighted average reaction cross sections calculated by the EMPIRE-3.2 Malta and TALYS-1.95 codes are almost the same, but they are higher than the currently presented results for the ^natCd(γ, xn)¹⁰⁵Cd reaction.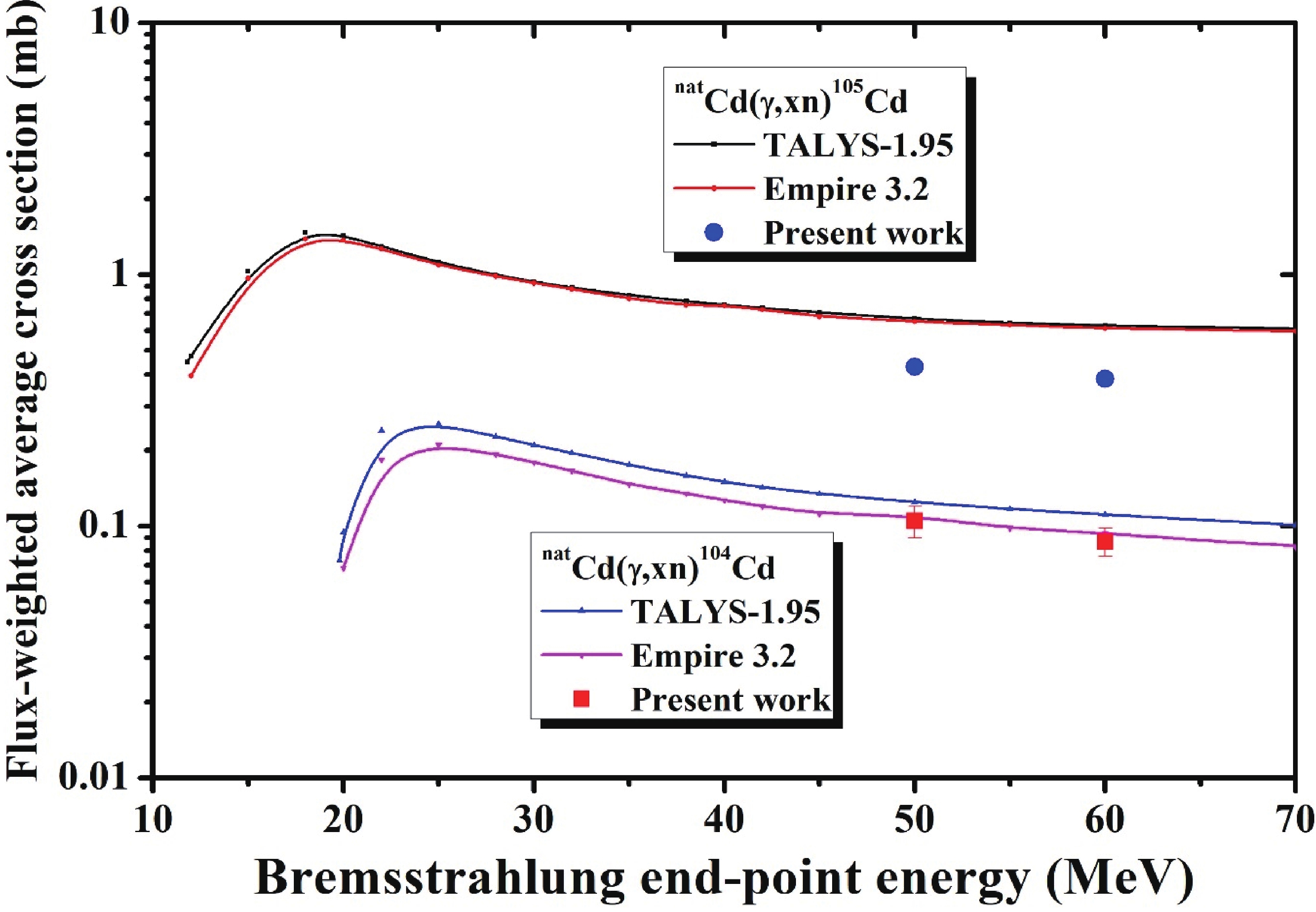
Figure8. (color online) Experimental flux-weighted average cross sections of the ^natCd(γ, xn)¹⁰⁵Cd and ^natCd(γ, xn)¹⁰⁴Cd reactions as a function of bremsstrahlung end-point energy along with the theoretical calculations using the TALYS-1.95 and EMPIRE-3.2 codes.

3 -->

6.^natCd(γ, xn)¹⁰⁴Cd reaction

The flux-weighted average formation cross section measurements of ¹⁰⁴Cd (57.7 min, 0⁺) were also performed based onthe independent 83.5 keV γ-line. This reaction was studied for the first time and thus could only be compared with the theoretical values. In Table 4 and Fig. 8, the measured cross sections for the ^natCd(γ, xn)¹⁰⁴Cd reaction are shown to be in good agreement with both calculations in terms of shape and magnitude, but they are more precisely matched with the EMPIRE-3.2 Malta calculations.
2 -->

B.Measured reaction cross-sections of silver radionuclides

Radioisotopes of silver (^{113g,112,111g,110m}Ag) were formed directly through (γ, pxn) reactions. During theirdirect production, ^113gAg and ^111gAg were populated by their short-lived metastable states by isomeric transition (IT). Therefore, their reaction cross sections were considered as cumulative values. ¹¹²Ag has no isomer, while ^110mAg has no contribution from any other radioisotope for its production; hence, their formation cross sections are exclusive and independent. Further details on silver residual nuclides are given below.
3 -->

1.Cumulative ^natCd(γ, pxn)^113gAg reaction

The deduced cumulative formation cross sections of ^113gAg (5.37 h, 1/2^-) include the direct production and the production through decay of the short-lived isomeric state ^113mAg (62 s, 7/2⁺), as presented in Fig. 9 and listed in Table 4. Measurements of the ^natCd(γ, pxn)^113gAg reaction cross sections were performed using the 298.6 keV γ-line. Moreover, it is important to note that the production probability of the meta-stable state is low due to its high spin state (7/2⁺); therefore, we may conclude that ^113mAg has a low contribution to the cumulative formation cross section of ^113gAg. The measurements from the reaction were only compared with the theoretical values due to unavailability of published data. In Fig. 9(a), it is shown that the measured values for the reaction are higher than the calculated values; however, they exhibit the same tendency as the incident photon energy increases.
Figure9. (color online) Experimental flux-weighted average cross sections of the (a) ^natCd(γ, x)^113gAg and (b) ^natCd(γ, xn)¹¹²Ag reactions as a function of bremsstrahlung end-point energy along with the theoretical calculations using the TALYS-1.95 and EMPIRE-3.2 codes.

3 -->

2.^natCd(γ, pxn)¹¹²Ag reaction

The ^natCd(γ, pxn)¹¹²Ag reaction cross-sections were measured based on the 617.52 keV γ-line of ¹¹²Ag (3.13 h, 2^-). This γ-line is also contributed to by ¹⁰⁵Cd and ^106mAg. However, after separating the contributions, it was found that their combined contribution to the 617.52 keV γ-line was only ~2%-3%, and thus, they were added to the photo peak area uncertainty. These measurements were only compared with the theoretical values due to unavailability of published data. In Fig. 9(b) and Table 4, the measured values are revealed to be higher than the calculated values; however, both follow a similar trend when the incident photon energy is increased. Moreover, the magnitude of the current measurements are shown to be closer to the EMPIRE-3.2 calculation than the TALYS calculation.
3 -->

3.Cumulative ^natCd(γ, pxn)^111gAg reaction

For measurements of the flux-weighted average production cross section of ^111gAg (7.45 d, 1/2^-), the situation is the same as in the previous case with (^113gAg). It is formed directly via the (γ, pxn) reaction and through the IT (99.3%) decay of the simultaneously produced short-lived ^111mAg (1.08 min, 7/2⁺). In this case,the nuclear spin of the metastable state is higher; hence, its production probability is lower than that of the ground state. Based on this, we may once again conclude that the cumulative cross section measurements of ^111gAg have a low ^111mAg decay contribution. A comparison of the present results with theoretical values is shown in Fig. 10(a) and Table 4.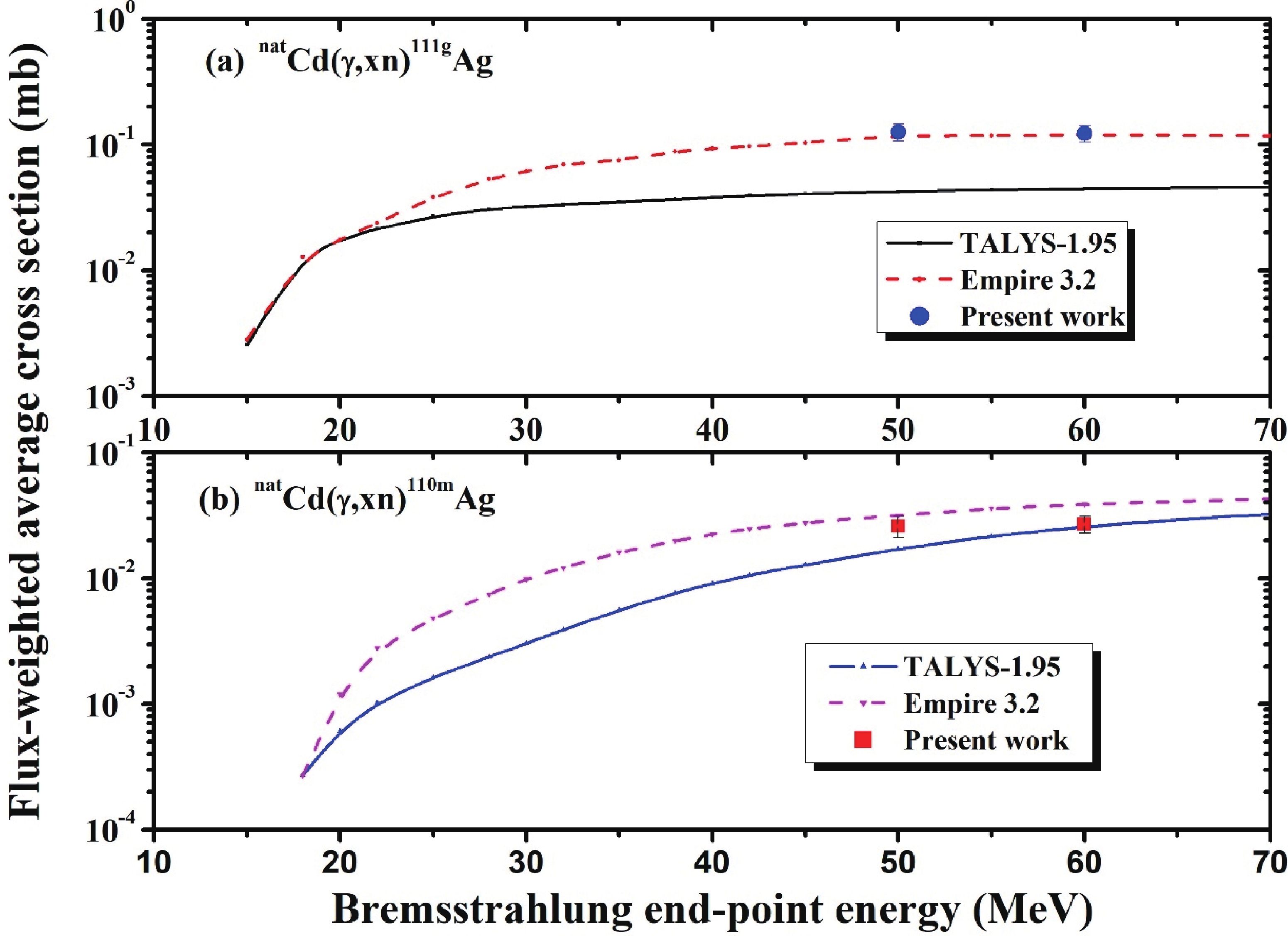
Figure10. (color online) Experimental flux-weighted average cross sections of the (a) ^natCd(γ, xn)^111gAg and (b) ^natCd(γ, xn)^110mAg reactions as a function of bremsstrahlung end-point energy along with the theoretical calculations using the TALYS-1.95 and EMPIRE-3.2 codes.

3 -->

4.^natCd(γ, pxn)^110mAg reaction

Flux-weighted average production cross sections of ^110mAg (249.83 d, 6⁺) were measured based on the 657.76 keV γ-line. The gamma-ray spectrum was taken after sufficient time had passed to ensure other short-lived nuclides such as ¹⁰⁵Cd, which contaminate the 657.76 keV γ-line, had sufficiently decayed. The measured results, along with the calculated values, are shown in Fig. 10(b) and listed in Table 4. Both of the results are consistent and higher than the theoretical values but closer to the values calculated using the EMPIRE-3.2 code.
2 -->

C.Integrated yield (Bq/g.μAh)

The production of cadmium and silver isotopes are important for medical and industrial applications and for a better understanding of their production in photon induced nuclear reactions. Therefore, the integrated yields (Bq/g.μAh) of cadmium and silver isotope productions from ^natCd(γ, x) reactions were measured in a procedure similar to that used for the integral yields of rhodium isotopes from the ¹⁰³Rh(γ, x) reaction [19, 31]. The integral yields of cadmium and silver isotope productions from ^natCd(γ, x) reactions are given in Table 6.

Reaction	Isotope	Yields/(Bq/g·A·h)
		Bremsstrahlung end-point energy/MeV
		50	60
natCd(γ, xn)115gCd	115gCd	(8.83±0.57)×106	(8.52±0.60)×107
natCd(γ, xn)115mCd	115mCd	(1.86±0.12)×106	(1.80±0.19)×107
natCd(γ, xn)111mCd	111mCd	(4.48± 0.28)×106	(8.99±0.61)×107
natCd(γ, xn)109Cd	109Cd	(3.62±0.26)×107	(2.49±0.21)×108
natCd(γ, xn)107Cd	107Cd	(1.71±0.12)×106	(1.73± 0.12)×107
natCd(γ, xn)105Cd	105Cd	(1.44±0.13)×106	(1.17±0.14)×107
natCd(γ, xn)104Cd	104Cd	(1.8±0.12)×105	(1.73±0.15)×106
natCd(γ, pxn)113g+mAg	113m+gAg	(1.58±0.11)×106	(1.67±0.11)×107
natCd(γ, pxn)112Ag	112Ag	(7.0±0.41)×105	(8.74±0.53)×106
natCd(γ, pxn)111g+mAg	111gAg	(3.3±0.24)×105	(3.55±0.32)×106
natCd(γ, pxn)110mAg	110mAg	(6.0±0.65)×104	(5.6±0.40)×105

Table6.Integral isotopic yield of different products from the ^natCd(γ, xn) and ^natCd(γ, pxn) reactions.

The flux-weighted average photon induced nuclear reaction cross-sections for the ^natCd(γ, xn; x=1-6)^{115g,m,111m,109,107,105,104}Cd and ^natCd(γ, xnyp; y=1 x=1-5)^{113g,112,111g,110m}Ag reactions as well as the isomeric yield ratios of ^115g,mCd in the ¹¹⁶Cd(γ, n) reaction were measured with the bremsstrahlung end-point energies of 50- and 60- MeV. Integral yield was also measured to assess the activities produced in the nuclear reactions. The photon induced formation reaction cross sections of ^natCd and the IR value of ¹¹⁵Cd were calculated using the TALYS-1.95 and EMPIRE-3.2 codes and the evaluated data taken from the TENDL-2019 library. In most of the cases, calculated values from the TALYS and EMPIRE codes matched each other and the experimental value. It was also found that the flux-weighted average cross sections increased sharply in the GDR region due to photo absorption and then decreased slightly in QDR region due to the opening of particle emission reaction channels. The isomeric yield ratio of ^115g,mCd in the ¹¹⁶Cd(γ, n) reaction from this study and previously published data was compared with literature data for the ¹¹⁶Cd(n, 2n) reaction. It was found that the experimental IR values of ^115g,mCd in the ^natCd(γ, xn) reaction agree with the calculations but were well below the IR values due to the ¹¹⁶Cd(n, 2n) reaction. The isomeric yield ratio previously measured in the ¹¹⁶Cd(n, 2n) reaction was lower than the calculated values for the same reaction; this is most likely due to the use of default parameters in the theoretical calculations. It was also observed that the theoretical and experimental values increased with excitation energy. However, at the same excitation energy, the IR values in the ¹¹⁶Cd(n, 2n) reaction were significantly higher than those in the ¹¹⁶Cd(γ, n) reaction due to the higher spin of the compound nucleus in the former. This indicates the role of compound nucleus spin alongside the effect of excitation energy.

The authors express their sincere thanks to the staff of the Pohang Accelerator Laboratory (PAL), Pohang, Korea, for the excellent operation and their support during the experiment.