Yi-Long Yang
, Ya-Kun Wang ^,
,

Corresponding author: Ya-Kun Wang, wangyk15@pku.edu.cn

State Key Laboratory of Nuclear Physics and Technology, School of Physics, Peking University, Beijing 100871, China
Received Date:2019-10-28
Available Online:2020-03-01
Abstract:Nuclear masses of even-even nuclei with the proton number $8\leqslant Z\leqslant 50$ (O to Sn isotopes) from the proton drip line to neutron drip line are investigated using the triaxial relativistic Hartree-Bogoliubov theory with the relativistic density functional PC-PK1. Further, the dynamical correlation energies (DCEs) associated with the rotational motion and quadrupole-shaped vibrational motion are taken into account by the five-dimensional collective Hamiltonian (5DCH) method. The root-mean-square deviation with respect to the experimental masses reduces from 2.50 to 1.59 MeV after the consideration of DCEs. The inclusion of DCEs has little influence on the position of drip lines, and the predicted numbers of bound even-even nuclei between proton and neutron drip lines from O to Sn isotopes are 569 and 564 with and without DCEs, respectively.

HTML

--> --> -->

Nuclear mass is one of the most fundamental properties of nuclei. It is of great importance in nuclear physics and also astrophysics [1, 2]. For example, the masses of nuclei widely ranging from the valley of stability to the vicinity of neutron drip line are involved in simulating the rapid neutron capture (r-process) of stellar nucleosynthesis [3]. Although considerable achievements have been made in mass measurement [4], a large amount of nuclei on the neutron-rich side away from the valley of stability still cannot be observed experimentally in the foreseeable future. Therefore, reliable nuclear models for high-precision description of nuclear masses are urgently required.
During the past decades, various global nuclear models have been proposed to describe the nuclear mass, including the finite-range droplet model (FRDM) [5, 6], semi-empirical Weizs?cker-Skyrme (WS) model [7, 8], non-relativistic [9-12] and relativistic [13-17] density functional theories (DFTs). Nuclear DFTs start from the universal density functionals with a few parameters determined by fitting the properties of finite nuclei or nuclear matter. They can describe the nuclear masses and ground and excited state properties in a unified manner [18-20]. In particular, because of the consideration of the Lorentz symmetry, the relativistic or covariant density functional theory (CDFT) naturally includes the nucleonic spin degree of freedom and time-odd mean fields, which play an essential role in describing the moments of inertia for nuclear rotations [21-24]. Thus far, the CDFT has received considerable attention because of its successful description of many nuclear phenomena [18, 20, 25-29].
In the framework of CDFT, masses for over 7000 nuclei with $ 8\leqslant Z\leqslant100 $ up to proton and neutron drip lines have been investigated based on the axial relativistic mean field (RMF) theory [13]. Then, to explore the location of the proton and neutron drip lines, a systematic investigation has been performed for even-even nuclei within the axial relativistic Hartree-Bogoliubov (RHB) theory [14, 15, 30]. Recently, the ground-state properties of nuclei with $ 8\leqslant Z\leqslant 120 $ from the proton drip line to the neutron drip line have been calculated using the spherical relativistic continuum Hartree-Bogoliubov (RCHB) theory, in which the couplings between the bound states and the continuum can be considered properly [31]. The root-mean-square (rms) deviation with respect to the experimental nuclear masses in these pure CDFT calculation is typically around several MeV. To achieve higher precision, one needs to go beyond the mean-field approximation and consider the beyond-mean-field dynamical correlation energies (DCEs).
In Ref. [32], low-lying states of 1712 even-even nuclei from $ Z = 10 $ to $ Z = 110 $ were studied using the five-dimensional collective Hamiltonian (5DCH) method with the collective parameters determined by the Gogny-Hartree-Fock-Bogoliubov calculations. It was found that the DCEs given by 5DCH significantly improve the accuracy of the two-particle separation energies. In Ref. [16], Zhang et al. carried out a global calculation of the binding energies for 575 even-even nuclei ranging from $ Z = 8 $ to $ Z = 108 $ based on the axial RMF, and the Bardeen-Cooper-Schrieffer (BCS) approximation was adopted to consider the pairing correlations. In this axial RMF+BCS calculation, the DCEs, namely the rotational and vibrational correlation energies were obtained by the cranking approximation. After including the DCEs, the rms deviation for binding energies of the 575 even-even nulcei reduced from 2.58 to 1.24 MeV. Later, the DCEs of these nuclei were revisited in Ref. [17] using the 5DCH method with the collective parameters determined by the CDFT calculations [33, 34]. The 5DCH method takes into account the DCEs in a more proper way, and the resulting rms deviation reduces from 2.52 to 1.14 MeV. Note that in Ref. [16], the adopted experimental mass data are taken from Ref. [35], while in Ref. [17], the experimental mass data are from Ref. [36]. Moreover, compared to the theoretical results shown in Ref. [16], the energies associated with triaxial deformation are further included in Ref. [17].
The studies shown in Refs. [16, 17] demonstrate that the inclusion of DCEs can significantly improve the description of nuclear masses. Thus far, the inclusion of DCEs in the CDFT is still confined to nuclei with known mass, and the DCEs of most neutron-rich nuclei crucial in simulating the r-process are uninvestigated. Therefore, it is necessary to extend the investigation from nuclei with known mass to the boundary of nuclear landscape. Meanwhile, the pairing correlations were treated by the BCS approximation in Refs. [16, 17]. For the description of nuclei around the neutron drip line, this approximation is questionable because the continuum effect cannot be taken into account properly [37]. Nevertheless, the methods with the Bogoliubov transformation can provide a better description for the pairing correlations in weakly bound nuclei. Therefore, in the present study, the nuclear masses of even-even nuclei from O to Sn isotopes ranging from the proton drip line to the neutron drip line are performed within the triaxial RHB theory [38], and the beyond mean-field quadrupole DCEs are considered by the 5DCH method.

The detailed theoretical formulae of CDFT and 5DCH have been presented in Refs. [33, 34, 39, 40]. Here, the framework of 5DCH and CDFT will be present briefly for completeness. The 5DCH is expressed by the two intrinsic deformation parameters $ \beta $ and $ \gamma $, as well as three Euler angles $ (\phi,\theta,\psi)\equiv\Omega $ defining the orientation of three intrinsic principal axes with respect to the laboratory frame. The collective Hamiltonian of 5DCH can be written as [33, 34],

$ \hat{H}_{\rm{coll}}(\beta,\gamma) = \hat{T}_{\rm{vib}}(\beta,\gamma) + \hat{T}_{\rm{rot}}(\beta,\gamma,\Omega) + V_{\rm{coll}}(\beta,\gamma), $

(1)

which includes a vibrational kinetic energy term,

$ \begin{split}{{\hat T}_{{\rm{vib}}}}(\beta ,\gamma ) \!=\!& -\! \frac{{{\hbar ^2}}}{{2\sqrt {\omega r} }}\!\!\left\{ \frac{1}{{{\beta ^4}}}\!\!\left[\frac{\partial }{{\partial \beta }}\!\!\sqrt {\frac{r}{\omega }} {\beta ^4}{B_{\gamma \gamma }}\frac{\partial }{{\partial \beta }}\! -\! \frac{\partial }{{\partial \beta }}\!\!\sqrt {\frac{r}{\omega }} {\beta ^3}{B_{\beta \gamma }}\frac{\partial }{{\partial \gamma }}\right]\right.\\& + \frac{1}{{\beta \sin 3\gamma }}\left[ - \frac{\partial }{{\partial \gamma }}\sqrt {\frac{r}{\omega }} \sin 3\gamma {B_{\beta \gamma }}\frac{\partial }{{\partial \beta }}\right. \\&\left.\left.+ \frac{1}{\beta }\frac{\partial }{{\partial \gamma }}\sqrt {\frac{r}{\omega }} \sin 3\gamma {B_{\beta \beta }}\frac{\partial }{{\partial \gamma }}\right]\right\} ,\end{split}$

(2)

a rotational kinetic energy term,

$ \hat{T}_{\rm{rot}} = \frac{1}{2}\sum_{k = 1}^3\frac{\hat{J}^2_k}{{\cal I}_k}, $

(3)

and a collective potential $ V_{\rm{coll}}(\beta,\gamma) $. The operator $ \hat{J}_k $ represents the total angular momentum components in the body-fixed frame. The moment of inertia $ {\cal I}_k $ and mass parameters $ B_{\beta\beta}, B_{\beta\gamma}, B_{\gamma\gamma} $ depend on the quadrupole deformation parameters $ \beta $ and $ \gamma $. Two additional quantities r and $ \omega $ in $ \hat{T}_{\rm{vib}}(\beta,\gamma) $ are used to determine the volume element in the collective space and their explicit expressions are provided in Refs. [33, 34]. The Hamiltonian in Eq. (1) can be diagonalized by the complete set of basis in Ref. [33]; thus, the eigenvalues and corresponding eigenfunctions can be obtained.
In the framework of the CDFT-based 5DCH approach, all the collective parameters including the collective potential $ V_{\rm{coll}} $, the moments of inertia $ {\cal I}_k $, and mass parameters $ B_{\beta\beta}, B_{\beta\gamma}, B_{\gamma\gamma} $ are determined by the microscopic CDFT calculations.
Within the point-coupling CDFT, the unified and self-consistent treatment of mean fields and pairing correlations can be realized by solving the following RHB equation [39],

$ \left( {\begin{array}{*{20}{c}}{{{\hat h}_{\rm D}} - \lambda }&{\hat \Delta }\\{ - {{\hat \Delta }^ * }}&{ - {{\hat h}^ * } + \lambda }\end{array}} \right)\left( {\begin{array}{*{20}{c}}{{U_k}}\\{{V_k}}\end{array}} \right) = {E_k}\left( {\begin{array}{*{20}{c}}{{U_k}}\\{{V_k}}\end{array}} \right),$

(4)

where

$ \hat{h}_{\rm D} = -{\rm i}\mathit{{\alpha}}\cdotp\mathit{{\nabla}} + \beta(m+S) + V $

(5)

is the single-nucleon Dirac Hamiltonian. $ U_k $ and $ V_k $ are the quasiparticle wavefunctions, and $ E_k $ is the corresponding quasiparticle energies. The scalar and vector mean fields in Eq. (5) are given by

$ \begin{split}S =& {\alpha _S}{\rho _S} + {\beta _S}\rho _S^2 + {\gamma _S}\rho _S^3 + {\delta _S}\Delta {\rho _S},\\V =& {\alpha _V}{\rho _V} \!+\! {\gamma _V}{({\rho _V})^3} \!+\! {\delta _V}\Delta {\rho _V} \!+\! {\tau _3}{\alpha _{TV}}{\rho _{TV}} \!+\! {\tau _3}{\delta _{TV}}\Delta {\rho _{TV}} \!+\! e{A^0},\end{split}$

(6)

where $ eA^0 $ is the electromagnetic field and the densities $ \rho_S, \rho_V $, and $ \rho_{TV} $ can be expressed in terms of quasiparticle wavefunctions $ V_k $ as

$ \begin{split}{\rho _S} = \sum\limits_{k > 0} {V_k^\dagger } {\gamma ^0}{V_k},\quad{\rho _V} = \sum\limits_{k > 0} {V_k^\dagger } {V_k},\quad{\rho _{TV}} = \sum\limits_{k > 0} {V_k^\dagger } \vec \tau {V_k},\end{split}$

(7)

where the sum over $ k>0 $ corresponds to the “no-sea approximation” [39]. The matrix element of pairing field $ \hat{\Delta} $ can be written in the form,

$ \Delta_{ab} = \frac{1}{2}\sum_{cd}\langle ab|V^{pp}|cd\rangle_a\kappa_{cd}. $

(8)

Here, $ \kappa = V^\ast U^T $ is the pairing tensor, and $ V^{pp} $ is the pairing force for which a finite range separable pairing force [41] is adopted in the present work.
By solving Eq. (4) iteratively, the total energy in the laboratory can be obtained,

$ \begin{split} E_{\rm{tot}} =& \int {\rm d}^3r\sum_{k>0}V^\dagger_k[\mathit{{\alpha}}\cdotp\mathit{{p}}+\beta m]V_k\\ &+ \int {\rm d}^3r\biggl\{\frac{1}{2}\alpha_S\rho_S^2+ \frac{1}{3}\beta_S\rho_S^3+\frac{1}{4}\gamma_S\rho^4_S+\frac{1}{2}\delta_S\rho_S\Delta\rho_S\\ &+\frac{1}{2}\alpha_V\rho_V^2+\frac{1}{2}\alpha_{TV}\rho_{TV}^2+\frac{1}{4}\gamma_V\rho_V^4+\frac{1}{2}\delta_V\rho_V\Delta\rho_V \\& +\frac{1}{2}\delta_{TV}\rho_{TV}\Delta\rho_{TV}\}.\end{split} $

(9)

The map of the potential energy surface as functions of quadrupole deformation parameters $ \beta $ and $ \gamma $ can be obtained by constraining the axial and triaxial mass quadrupole moments. As shown in Refs. [33, 34], the quadratic constraint method uses an unrestricted variation of the function

$ \langle H\rangle + \sum_{\mu = 0}^2C_{2\mu}(\langle\hat{Q}_{2\mu}\rangle-q_{2\mu})^2, $

(10)

where $ \langle H\rangle $ is the total energy and $ \langle\hat{Q}_{2\mu}\rangle $ the expectation value of the following mass quadrupole operator,

$ \hat{Q}_{20} = 2z^2-x^2-y^2,\quad \hat{Q}_{22} = x^2-y^2. $

(11)

Here, $ q_{2\mu} $ represents the desired values of the quadrupole moments, and $ C_{2\mu} $ is the corresponding stiffness constant [42].

In this section, adiabatic deformation constrained RHB calculations are performed to obtain the mean-field states in the full $ (\beta,\gamma) $ energy surface. The relativistic density functional PC-PK1 [40] is used in the particle-hole channel. This density functional particularly improves the description for the isospin dependence of binding energies, and it has been successfully used for describing the Coulomb displacement energies among mirror nuclei [43], nuclear masses [17, 44], quadrupole moments [45-47], superheavy nuclei [48-51], nuclear shape phase transitions [52, 53], magnetic and antimagnetic rotations [27, 54-56], chiral rotations [57], etc. For the particle-particle channel, we adopted the finite range separable pairing force with pairing strength $ G = -728 $ MeV as proposed in Ref. [41]. The triaxial RHB equation was solved by expanding the quasiparticle wavefunctions in terms of three-dimensional harmonic oscillator bases, which are the eigenfunctions of a three-dimensional harmonic oscillator potential in the Cartesian coordinates [39]. The oscillator frequencies in the $ x, \;y,\; z $ directions are $ \hbar\omega_x = \hbar\omega_y = \hbar\omega_z = \hbar\omega_0 = 41 A^{-1/3} $ MeV, and the corresponding oscillator lengths are $ b_x = b_y = b_z = \sqrt{\hbar/m\omega_0} $. The spatial part of these bases are labeled by the quantum numbers $ n_x,\; n_y $, and $ n_z $, and the spin part is chosen as the eigenfunctions of the x-simplex operator ${{\dot S} } = \hat{P}{\rm e}^{-{\rm i}\pi {\hat{J}}_x} $, in which $ \hat{P} $ is the parity operator. The detailed formulas of three-dimensional harmonic oscillator basis can be found in Refs. [39, 58]. In the present calculations, we used 12 major shells for nuclei with proton number $ Z<20 $ and 14 major shells for nuclei with proton number $ 20\leq Z\leq50 $, which was confirmed by checking the convergence of the obtained binding energies and charge radii. The obtained quasiparticle energies and wavefunctions are used to calculate the mass parameters, moments of inertia, and collective potentials of in 5DCH; all of these quantities are associated with the quadrupole deformation parameters $ \beta $ and $ \gamma $. The dynamical correlation energy $ E_{\rm{corr}} $ is given by the energy difference between the lowest mean-field states and the $ 0_1^+ $ states from the 5DCH calculations.

The bound nuclear regions from O to Sn isotopes predicted by the triaxial RHB approach with and without DCEs are shown in Fig. 1. The discrepancies of the calculated binding energies with respect to the data are scaled by colors. The binding energies calculated by the triaxial RHB approach shown in panel (a) are given by the binding energies of the lowest mean-field states, while in panel (b), the DCEs are taken into account.
Figure1. (color online) Even-even nuclei from O to Sn isotopes predicted by the triaxial RHB approach with (panel (b)) and without (panel (a)) dynamical correlation energies. Discrepancies of the calculated binding energies with the data [4] are denoted by colors. The proton and neutron drip lines predicted by spherical RCHB (PC-PK1) [31], axial RHB (DD-PC1) [15], and axial RMF+BCS (TMA) [13] are also plotted for comparison.

In the triaxial RHB calculations without DCEs, it was found that the binding energies are systematically underestimated. Most deviations are in the range of $ 0.5\;\sim\;4.5 $ MeV, resulting in the rms deviation of 2.50 MeV. We compared our results with the those of Ref. [15], where the ground state observables of even-even nuclei were investigated based on CDFT with the DD-PC1 density functional in particle-hole channel and the separable pairing force in the particle-particle channel. The rms deviation in Ref. [15] for the even-even nuclei from O to Sn is 2.29 MeV, which is consistent with our results. Moreover, we also compared our results with those in Ref. [17]. For the pure mean-field calculations in Ref. [17], same density functional, namely PC-PK1, was used in the particle-hole channel, while a density dependent delta force was adopted in the particle-particle channel. Because the calculations in Ref. [17] were performed for the nuclei with known mass, the location of these nuclei are still far from the neutron drip line. For most nuclei with known mass, the energy difference between the RHB and the RMF+BCS calculations is less than 0.2 MeV, and the final rms deviation is only 0.09 MeV. However, evident energy differences occur in Cd and Sn isotopes with neutron number $ N = 56 \sim 66 $. It is found that for these specific nuclei, the pairing energies obtained from th RMF+BCS are stronger than those from RHB, which is not the same as the usual case. This might be because two different pairing forces are adopted in the RMF+BCS and RHB calculations. As mentioned before, for the lowest mean field calculations, a density dependent $ \delta $ pairing force was used in Ref. [17], while a separable pairing force was used in the present calculations. The stronger pairing correlations given by yhr RMF+BCS make these nuclei more binding, thus increasing the discrepancy between the two calculations.
By including the DCEs, the underestimation of the binding energies is improved significantly, and the rms deviation is reduced from 2.50 MeV to 1.59 MeV. However, in the region $ (N,Z)\sim(24,12) $, large deviations exist even though the DCEs are considered. This might be associated with the complex shell evolution around this region. To obtain a better description of the binding energies in this region, the tensor interaction [59] may need to be included in the adopted density functional, which is beyond the scope of the present investigation.
To estimate the number of bound nuclei from O to Sn isotopes, two-proton and two-neutron drip lines predicted by the present triaxial RHB approach with and without DCEs are also plotted in Fig. 1. The predicted number of bound even-even nuclei between the proton and neutron drip lines from O to Sn isotopes without DCEs is 569. The inclusion of DCEs has little influence on the proton and neutron drip lines, and the corresponding number of bound nuclei is 564. For comparison, the drip lines predicted by the spherical RCHB (PC-PK1) [31], axial RHB(DD-PC1) [15], and axial RMF+BCS(TMA) [13] are also shown. It is found that theoretical differences for the proton drip lines are rather small. However, the neutron drip lines predicted by different approaches differ considerably, and the differences increase with the mass number. The neutron drip line predicted by the triaxial RHB approach is located between those predicted by the axial RHB and spherical RCHB approaches.
Besides the binding energies, the charge radii calculated by the triaxial RHB were been compared with available data [60] in Fig. 2. The experimental charge radii are well reproduced, and most deviations between the calculated results and the data are in the range of $ -0.03\sim 0.03 $ fm.
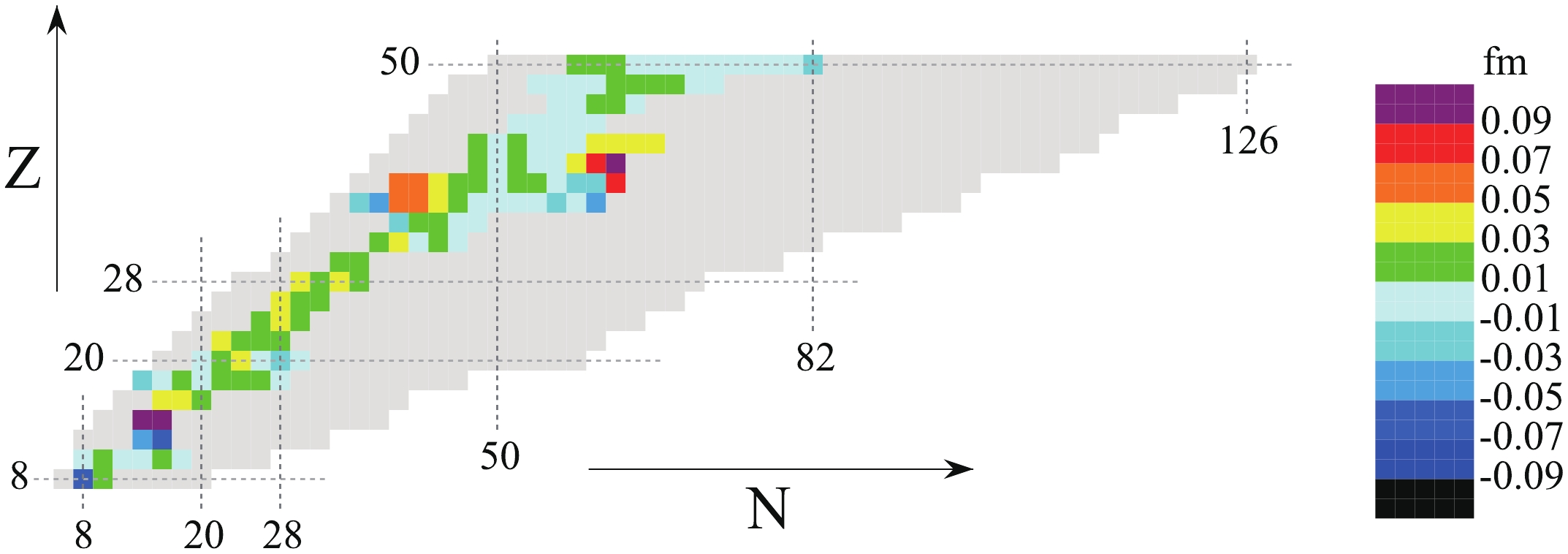Figure2. (color online) Charge radii of nuclei from O to Sn and their comparison with available data [60]. Discrepancies of the calculated charge radii with data are denoted by different colors.

Figure 3 shows the contour map of the dynamical correlation energies $ E_{\rm{corr}} $ calculated by the 5DCH model based on the triaxial RHB calculations. The calculated $ E_{\rm{corr}} $ ranges from 0 to 5 MeV and varies mainly in the region of $ 2.0-4.0 $ MeV. Owing to shape fluctuations, the dynamical correlation energies are pronounced for the nuclei around $ Z \sim 32, \;40 $ and $ N \sim 34, \;60 $. Similar to the results of Ref. [17], the dynamical correlation energies for the semi-magic nuclei with $ Z = 28,\; 50 $ and $ N = 28, \;82 $ are nonzero or larger. This is because the potential energy surfaces for these nuclei are either soft or with shape coexisting phenomena.
Figure3. (color online) Contour map of the dynamical correlation energies E_corr calculated by the 5DCH model based on triaxial RHB calculations as functions of neutron and proton numbers.

In Ref. [17], the binding energies of 575 even-even nuclei in the region of $ 8\leqslant Z\leqslant 108 $ were calculated using the 5DCH method in the framework of the triaxial RMF+BCS. For the 228 nuclei with $ 8\leqslant Z\leqslant50 $ in Ref. [17], the rms deviation with respect to data was 1.23 MeV, whereas the rms deviation in the present calculations for these nuclei is 1.47 MeV. The lowest mean-field binding energies given by these two calculations have little difference; therefore, the differences mainly arise because of $ E_{\rm{corr}} $.
The dynamical correlation energies $ E_{\rm{corr}} $ calculated by 5DCH based on the triaxial RHB and triaxial RMF+BCS are plotted in Fig. 4 as functions of the neutron number N. Although the systematics of $ E_{\rm{corr}} $ are similar for both calculations, the triaxial RHB-based $ E_{\rm{corr}} $ are systematically larger than those based on the triaxial RMF+BCS. The rms deviation between these two results is 0.53 MeV, and this leads to an overall difference in the binding energies. The systematic difference of $ E_{\rm{corr}} $ might be caused by the different treatments of pairing correlations. The pairing correlations in the present calculations are considered by the Bogoliubov transformation, while in Ref. [17], they are considered by the BCS approximation. To understand the origin of the discrepancy of the dynamical correlation energies between the RHB and RMF+BCS calculations, the pairing energies $ E_{\rm{pair}} $, moments of inertia $ {\cal I}_x $, collective masses $ B_{\beta\beta} $ and $ B_{\gamma\gamma} $ for nucleus ⁷⁶Ge calculated by RHB and RMF+BCS were compared in detail. It is found that pairing correlations calculated from the RHB are stronger than those from the RMF+BCS, which leads to smaller collective parameters $ {\cal I}_x $, $ B_{\beta\beta} $, and $ B_{\gamma\gamma} $ and thus, larger dynamical correlation energies $ E_{\rm{corr}} $. Similar conclusions were made in Ref. [61]. Moreover, compared with the DCEs obtained from the 5DCH method based on Gogny-Hartree-Fock-Bogoliubov theory [32], the triaxial RHB-based DCEs are systematically smaller, and the rms deviation between two calculations is 1.59 MeV. As demonstrated in Ref. [17], this discrepancy might be due to the collective parameters, which are sensitive to the effective interactions, in particular the pairing properties.
Figure4. (color online) Dynamic correlation energies calculated by 5DCH based on triaxial RHB (circles) compared with those based on triaxial RMF+BCS [17] (triangles).

The contour map of the triaxial RHB calculated quadrupole deformation $ \beta $ are presented in Fig. 5. The quadrupole deformation corresponds to the energy minima on the whole $ (\beta,\gamma) $ plane. Here, $ \beta $ is defined as positive for $ 0^\circ\leqslant \gamma<30^\circ $ and negative for $ 30^\circ<\gamma\leqslant 60^\circ $. In general, the nuclei near magic numbers possess small or vanishing deformation. However, it is found that single magic numbers do not enforce sphericity, especially for neutron-rich nuclei. For example, neutron-rich isotones with $ N = 28, \;Z<20 $ and $ N = 50,\; Z<28 $ show remarkable deformation. In addition, the deformation develops when moving away from the magic numbers, either isotopically or isotonically. There are four large deformed regions located at $ (N, Z)\sim (24,14), \;(34,32), \;(60,40) $ and $ (94,46) $. These regions with large deformation correspond to the regions with large DCEs as shown in Fig. 3.
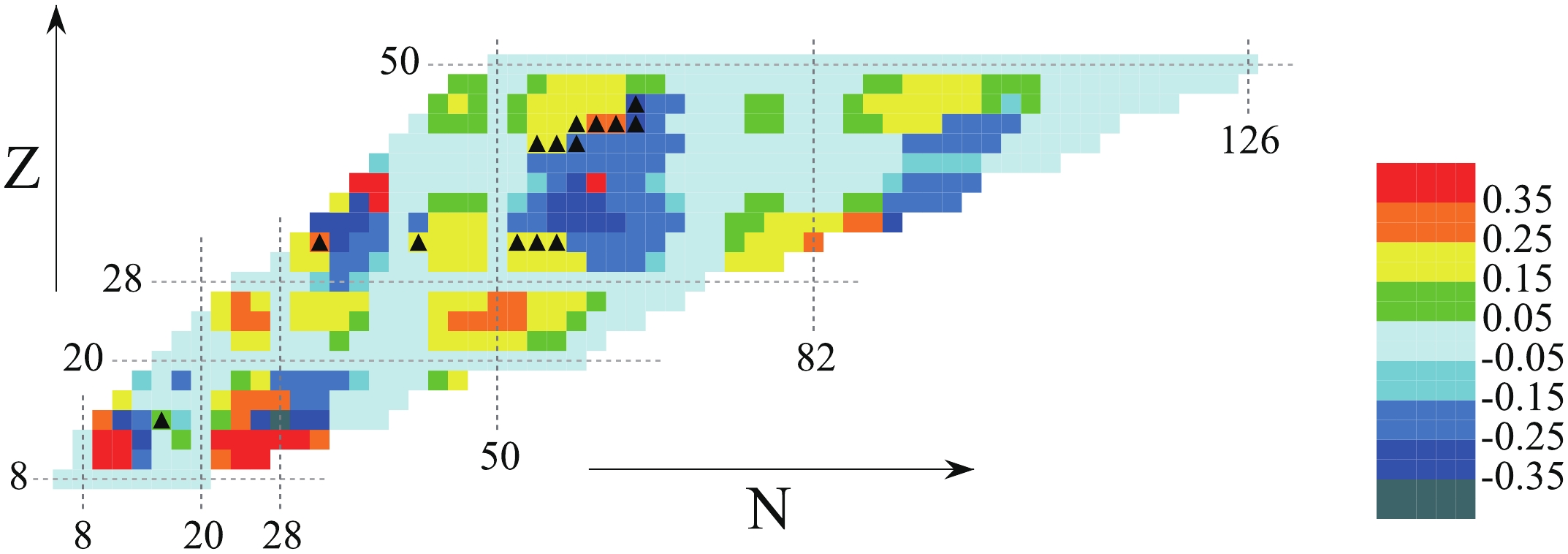Figure5. (color online) Contour map of quadrupole deformation β calculated by the triaxial RHB approach as functions of the neutron and proton numbers. Nuclei with triaxial deformation are denoted by black triangles.

The nuclei with triaxial deformation i.e. $ \gamma\neq 0^\circ,\; 60^\circ $, are also shown in Fig. 5. It is found that the static triaxial nuclei occur mainly in the region with $ (N, Z)\sim(56, 46) $, which is consistent with the results given by finite-range liquid-drop model [62]. There are 14 nuclei with triaxial deformation, and most of them belong to the Ge, Mo, and Ru isotopes. The inclusion of static triaxial deformation makes these nuclei more binding at a value of $ \sim0.3 $ MeV. For our present beyond mean-field calculations, the triaxial deformation was not only static but also dynamic. The effects of triaxial deformation play a role in the description of binding energy especially for a nucleus with a $ \gamma $ soft potential energy surface. The final aim of this project is to build a whole nuclear mass table including both triaxial degrees of freedom and dynamical correlation energies. Similar works on this topic are in progress.

In summary, the nuclear masses of even-even nuclei with $ 8\leqslant Z\leqslant 50 $ ranging from the proton drip line to the neutron drip line are systematically investigated using the triaxial RHB theory with the relativistic density functional PC-PK1, and the quadrupole dynamical correlation energies are taken into account by solving the 5DCH. By including the dynamic correlation energies, the prediction of triaxial RHB theory for 252 nuclei masses was improved significantly, with the rms deviation reducing from 2.50 to 1.59 MeV. The dynamic correlation energies have little influence on the positions of proton and neutron drip lines, and the predicted numbers of bound even-even nuclei between proton and neutron drip lines with and without dynamical correlation energies are 569 and 564, respectively. In the present calculations, the obtained dynamical correlation energies ranged from 0 to 5 MeV, which are slightly larger than the results of a previous work [17]. The discrepancies might be caused by the different treatments of the pairing correlations, which would lead to different zero point energies, and thus different dynamical correlation energies. The contour map of quadrupole deformation $ \beta $ and $ \gamma $ associated with the dynamic correlation energies is also discussed in detail. Fourteen nuclei are predicted to have triaxial deformation, which are good candidates for the experimental study of the possibility of triaxial deformations. The final aim of this project is to build a whole nuclear mass table including both triaxial degrees of freedom and dynamical correlation energies. Similar works on this topic are still in progress.
The authors are grateful to Prof. ZhiPan Li and Prof. PengWei Zhao for providing the numerical computation codes and the fruitful discussions, as well as for the critical readings of our manuscript.