Jing-Jing Liu ^,
, Dong-Mei Liu ^,
, Liang-Huan Hao
,

Corresponding author: Jing-Jing Liu, syjjliu68@qzu.edu.cn

Corresponding author: Dong-Mei Liu, liudongmei72@126.com

College of Science, Hainan tropical ocean University, Sanya 572022, China
Received Date:2018-12-03
Accepted Date:2019-03-26
Available Online:2019-06-01
Abstract:In this study, we investigate the ion-ball screening model (model (I)), focused on the screening electrostatic potential per electron under the Wigner-Seitz approximation and the Q-value correction. By considering the changes of the Coulomb free energy and the effects of strong electron screening (SES) on the Q-value and the Coulomb chemical potential, we discuss the linear-response screening model (model (II)). We also analyze the influence of the SES on the $ \beta^- $ decay antineutrino energy loss rate by considering the corrections of the Q-value, the electron chemical potential, and electron energy, as well as the shell and pair effects. The antineutrino energy loss rate is found to increase by two orders of magnitude (e.g., the SES enhancement factor reaches 651.9 for model (II)) due to the SES effect.

HTML

--> --> -->

The beta decay antineutrino energy loss rates (AELR) of ⁵⁶V, ⁵⁶Cr, ⁵⁶Mn, ⁵⁶Fe, ⁵⁶Co, and ⁵⁶Ni are key parameters in numerical simulation of supernova. The neutrinos and antineutrinos are transparent to the stellar matter and cause stellar core cooling. The neutrino energy loss rates caused by the beta decay and electron capture (EC) in presupernova have been investigated in previous studies (e.g., Fuller et al. [1, 2] (FFN) ; Aufderheide et al. [3, 4] (AUFD); Langanke et al. [5, 6]). In our previous studies [7–9], we have discussed the electron capture and beta decay reactions along with the related issues. The AELR by EC has likewise posed an interesting problem in the investigation of cooling of a neutron star [10–13], because the EC rates could be affected by many factors, such as density of the matter, electron fractions [14–16], temperature, and magnetic field strength, which may in turn influence the equation of state and spin evolution of the star [17-20]. However, all of the studies mentioned above neglected the effect of strong electron screening (SES) on the neutrino energy loss rates.
Some astrophysicists (e.g., studies depicted Refs. [20–26]) discussed the SES problem in detail. Many works (e.g., Refs. [27–30]) also addressed the the effects of ion and electron screening on thermonuclear reaction rates. However, these studies did not consider the influence of SES on the chemical potential, Q-value, shell and pair effects. The SES strongly influences the beta decay threshold energy and the chemical potential. Thus, it is very important to accurately investigate the beta decay neutrino energy loss in the SES.
Our previous studies [31, 32] demonstrated that the SES affects the beta decay rates and neutrino cooling to a great degree. However, these studies neglected the SES effect on the chemical potential in the beta decay. Toki et al. [33] have calculated $ \beta $-transition rates for the URCA process using the $ s-d $ shell model. They considered many $ \beta- $transitions, including excited states necessary for the electron capture and $ \beta- $decay at high density and high temperature. Recently, Suzuki et al. [34] also evaluated the electron capture and $ \beta $-decay rates based on the $ s-d $ shell model for electron-degenerate $ \rm{O-Ne-Mg} $ cores with initial masses of 8–10 $ M_{\bigodot} $($ M_{\bigodot} $ denotes the solar mass).
Our studies differ from these works [33, 34] in discussing the SES effects on the beta decay and neutrino cooling. First, these works discussed the weak interaction rates for some $ \rm{O-Ne-Mg} $ nuclei based on the $ s-d $ model theory, whereas in the present paper, we focus on the some iron group nuclei and discuss the beta decay reaction based on the $ p-f $ shell model. Second, there are two Coulomb effects due to SES: one is the screening effect of the electrons, and the other is the change of threshold energy due to the change of chemical potential of the ions. Nuclear reaction rates in dense plasmas depend in a number of crucial ways on their thermodynamic functions. Enhancement due to internuclear multiparticle processes is described in terms of increments in the excess of chemical potentials before and after nuclear reactions. Screening distances of internuclear potentials are likewise described by the compressibility of the electron gas. These studies discussed the effect caused by the correction of the chemical potential of the nucleus due to the interactions between nucleus and electron background based on the Ichimaru model [35]. We discussed the SES problem based on the Potekhin model [36, 37]. The polarizable electron background is calculated for ion charges $ Z = 26 $ and a wide domain of plasma parameters ranging from the Debye limit to the crystallization point. Our calculations are based on the linear-response theory for the electron-ion interaction, including the local-field corrections in the electronic dielectric function. Finally, their studies only discussed the effect of SES on the weak interaction reaction and the neutrino cooling by considering the corrections of the Q-value, electron chemical potential, and the electron energy. Following the study from Ref. [38], we calculate the half-lives of some iron group nuclei of $ \beta^- $-decay, taking into account shell and pair effects. Based on the ion ball screening model (IBSM) (i.e., SES model(I)) [10], and the linear-response theory model (LRTM)(i.e., SES model(II)) [36, 37, 39], we calculate the screening corrections to AELR by $ \beta^- $ decay for ⁵⁶V, ⁵⁶Cr, ⁵⁶Mn, ⁵⁶Fe, ⁵⁶Co, and ⁵⁶Ni. We also discuss and compare the results of model (I) with those of the SES model (II).
The SES model (I) is mainly focused on the screening electrostatic potential per electron under the Wigner-Seitz approximation and Q-value correction based on the IBSM from Ref. [20]. The SES model (II) is mainly focused on the linear response theory by considering the effect of the SES on the Q-value and Coulomb chemical potential due to the change of Coulomb free energy (see Refs. [36, 37, 39] for a detailed discussion)
We organize this paper as follows. In Section 2, we study the beta decay AELR and the half-lives in the absence of SES. In Section 3, we discuss the screening potential, and the screening corrections to the Q-value and the AELR for the model (I). In Section 4, we discuss the AELR and the screening corrections of the Q-value, the electron chemical potential for the model (II). We analyze the influence of SES on the AELR. Our results and discussions are provided in Section 5. In Section 6, we present our conclusions.

In the absence of SES, the AELR by $ \beta^- $ decay at temperature $ T $ is given by (e.g., Refs. [1-4])

$ \lambda_{\rm{AELR}}^0 = \ln2 \sum\frac{(2J_i+1){\rm e}^{\frac{-E_i}{k_{B}T}}}{G(Z, A, T)} \sum\limits_{f} \frac{\xi(\rho, T, Y_e, Q_{ij})}{ft_{ij}}, $

(1)

where $ G(Z, A, T) $ is the nuclear partition function; $ Z, A, T $ are the electric charge on nucleus, mass number, and the temperature, respectively; $ ft_{ij} $ is the comparative half-life connecting states of $ i $ and $ j $; $ k_{B} $ is the Boltzmann constant, and $ J_i $ is the spin. $ Q_{ij} $ is the nuclear energy difference between the states of $ i $ and $ j $, respectively. $ Q_{00} = M_{p}c^2-M_{d}c^2 $, $ M_p $ and $ M_d $ are the masses of the parent nucleus and the daughter nucleus, respectively, $ E_i $ and $ E_j $, are the excitation energies of the $ i $ th and $ j $ th nuclear state. The $ \xi(\rho, T, Y_e, Q_{ij}) $ in Eq.(1) for the AELR by $ \beta^- $ decay is

$ \begin{split} \xi(\rho, T, Y_e, Q_{ij}) =& \frac{c^3}{(m_ec^2)^5}\int_1^{Q_{ij}}{\rm d}\varepsilon_e \varepsilon_e(\varepsilon_e^2-1)^{1/2} \\& \times (Q_{ij}-\varepsilon_e)^3\frac{F(Z+1, \varepsilon_e)}{1+\exp[(U_F-\varepsilon_e)/k_{B}T]}, \end{split} $

(2)

where $ F(Z+1, \varepsilon_e) $ is the Coulomb wave correction. $ \varepsilon_e $ is the electron energy, and $ U_F, m_e, p $ are the electron's chemical potential, mass, and momentum, respectively.
In the pre-collapse phase, the electron chemical potential is given by [30]

$ U_F = 1.11(\rho_7Y_e)^{1/3}\left[1+\left(\frac{\pi}{1.11}\right)\frac{(k_BT)^2}{(\rho_7Y_e)^{2/3}}\right]^{-1/3}\; \; \rm{MeV} . $

(3)

Ref. [38] discussed the beta-decay half-lives of the r-process nuclei with a consideration of the shell and pair effects, as well as the decay energy $ Q $. Then, the comparative half-life $ ft_{ij} $ is written as

$ \begin{split} \ln(ft_{ij}) =& a_1+\left(\alpha^2Z^2-5+a_2\frac{N-Z}{A}\right)\ln(Q_{if}-a_3\delta) \\& +(a_4\alpha^2Z^2)+\frac{1}{3}\alpha^2Z^2\ln(A)-\alpha Z\pi+S(N, Z), \end{split} $

(4)

where the fine structure constant $ \alpha = 1/137 $, and $ \delta = (-1)^N+(-1)^Z $. Taking into account the pairing effects on Q-values, and the shell effects, the correction factor $ S(N, Z) $ is written as [28]

$ \begin{split} S(N, Z) =& a_5\exp(-((N-28)^2+(N-20)^2)/12)\\& +a_6\exp(-((N-50)^2+(N-38)^2)/43)\\ &+a_7\exp(-((N-82)^2+(N-50)^2)/13)\\& +a_8\exp(-((N-82)^2+(N-58)^2)/24)\\& +a_9\exp(-((N-110)^2+(N-70)^2)/244), \end{split} $

(5)

where $ {a_i(i = 1, 2, 3, ...9)} $ are 11.09, 1.07, ?0.935, ?5.398, 3.016, 3.879, 1.322, 6.030, 1.669, respectively, in Eqs.(4–5).

The free electron gas is relativistic and completely degenerated in a supernova. The incoming (outgoing) electrons in the EC (beta decay) process mainly originate from near the Fermi surface. Their Fermi energy is $ E_F>1 $ MeV when the density is $ \rho>10^7\rm{g/cm^3} $. The screening electrostatic potential in the pre-supernova core is much stronger than the one in the main sequence stars. Based on the ion ball screening model (IBSM), the screening electrostatic potential per electron under the Wigner-Seitz approximation is determined by [20]

$ D_1 = 1.784\times10^{-5}\left(\frac{Z^{5/3}}{AY_e^{2/3}}\right)\rho^{1/3}\; \; \; \rm{MeV}. $

(6)

Due to the SES effect, the beta decay Q-value will change by a factor of (e.g., Refs. [1, 2])

$ \Delta Q\approx 2.940\times10^{-5}Z^{2/3}(\rho Y_e)^{1/3}\; \; \; \rm{MeV}. $

(7)

Therefore, the Q-value of beta decay changes from $ Q_{if} $ to $ Q_{if}^s({\rm I}) = Q_{if}-\Delta Q $.
We can not neglect the SES influence at high density, as the screening energy is high. The electron energy will change from $ \varepsilon_e $ to $ \varepsilon^{s}_e({\rm I}) = \varepsilon_e+D_1 $ in the beta decay. Due to SES, the threshold energy for the beta decay decreases from $ Q_{if} $ to $ Q_{if}^s({\rm I}) = Q_{if}-\Delta Q $. The $ \xi(\rho, T, Y_e, Q_{ij}) $ in Eq. (2) is also replaced by $ \xi^s(\rho, T, Y_e, Q^s_{ij}(\rm{I})) $, given by

$ \begin{split} \xi^s(\rho, T, Y_e, Q_{ij}^s)(\rm{I}) =& \frac{c^3}{(m_ec^2)^5}\int_{1+D_1}^{Q_{ij}^s(\rm{II})+D_1}{\rm d}\varepsilon_e^s \varepsilon_e^s\\ &\times((\varepsilon^s_e)^2-1)^{1/2}(Q^s_{ij}-\varepsilon_e^s)^3\\ &\times \frac{F(Z+1, \varepsilon_e^s)}{1+\exp[(U_F-\varepsilon_e^s)/k_{B}T]}. \end{split} $

(8)

Therefore, according to Eq. (1), the AELR by beta decay in the SES is given by

$ \lambda_{\rm AELR}^s({\rm I}) = \ln2 \sum\frac{(2J_i+1){\rm e}^{\frac{-E_i}{k_{B}T}}}{G(Z, A, T)} \sum\limits_{{f}} \frac{\xi^s(\rho, T, Y_e, Q^s_{ij})}{ft^s_{ij}}, $

(9)

where $ ft^s_{ij} $ is the half-life in the SES

$ \begin{split} \ln(ft^s_{ij})(\rm{I}) =& a_1+\left(\alpha^2Z^2-5+a_2\frac{N-Z}{A}\right)\ln(Q^s_{if}-a_3\delta)\\& +(a_4\alpha^2Z^2)+\frac{1}{3}\alpha^2Z^2\ln(A)-\alpha Z\pi+S(N, Z). \end{split} $

(10)

Itoh et al. [40] investigated the influence of the screening potential on EC by the linear-response theory model (LRTM). The condition is

$ T\ll T_F = 5.930\times10^9\left\{\left[1+1.018\left(\frac{Z}{A}\right)^{2/3}(10\rho_7)^{2/3}\right]^{1/2}-1\right\}, $

(11)

where $ T_{\rm{F}} $ is the electron Fermi temperature, and $ \rho_7 $ is the mass density in units of $ 10^7\rm{g/cm^3} $.
The static longitudinal dielectric function has been discussed by Jancovici et al. [41] for relativistic degenerate of electron fluid. Because of the SES effect, the electron potential energy is given by

$ V(r) = -\frac{Ze^2(2k_{\rm F})}{2k_{\rm F}r}\frac{2}{\pi}\int_0^\infty \frac{\sin[(2k_{\rm F}r)]q}{q\epsilon(q, 0)}{\rm d}q, $

(12)

where $ k_{\rm{F}} $ is the electron Fermi wave-number, and $ \epsilon(q, 0) $ is Jancovici's static longitudinal dielectric function.
According to the linear response theory, the screening potential is determined by

$ D_2 = 7.525\times10^{-3}Z\left(\frac{10Z\rho_7}{A}\right)^{\frac{1}{3}}J(r_s, R) ~(\rm{MeV}), $

(13)

where the parameters $ J(r_s, R) $, $ r_s $, and $ R $ are given in Ref. [40]. Eq. (13) and $ 10^{-5}\leqslant r_s \leqslant 10^{-1}, 0\leqslant R\leqslant 50 $ are fulfilled in the pre-supernova environment.
It is well known that the SES also plays a key role in determining the thermodynamical properties at high density plasma surrounding [42]. When one includes the contribution of the SES, the chemical potential for nuclei is given by

$ U_F^s = U_F^0+U_{iC}, $

(14)

where $ U_F^0 $ is the chemical potential in the absence of Coulomb effects, and $ \Delta U_F $ is the contribution to the chemical potential due to the interaction of the nuclei $ i $ with the electron background.
Because the stellar core can comprise multi-component plasma, all the thermodynamic quantities are computed as the sum of the individual quantities for each species. If one further assumes that the electron distribution is not affected by the presence of the nuclear charges (uniform background approximation), the correction from Coulomb chemical potential of the nuclei $ i $ is given by [32]

$ U_{iC} = kTf_C(\Gamma_i), $

(15)

where $ k $ is Boltzmanns constant, $ f_C $, and $ \Gamma_i = Z_i^{5/3}\Gamma_e $ are the Coulomb free energy per ion in units of $ kT $, and the ion-coupling parameter, respectively. $ \Gamma_e = e^2/a_ekT $, and $ a_e = (3/(4\pi n_e))^{1/3} $ is the electron sphere radius, while $ n_e $ depicts the electron number density.
According to the discussions for the Coulomb free energy, we will use the expression of (e.g., [36, 37])

$ f_C(\Gamma) = -\Gamma_e\frac{c_{\rm{DH}}\sqrt{\Gamma_e}+ac_{\rm{TF}}\Gamma_e^\nu g_1(r_s)h_1(x)}{1+[b\sqrt{\Gamma_e}+ag_2(r_s)\Gamma_e/r_s]h_2(x)}, $

(16)

where the parameter

$ c_{\rm{DH}} = \frac{Z}{\sqrt{3}}[(1+Z)^{3/2}-Z^{3/2}-1], $

(17)

and the parameter $ c_{\rm{TF}} $ determines the screening in the limit of large $ \Gamma_e $ and small $ r_s $, given by

$ c_{\rm{TF}} = c_{\infty}Z^{7/3}[1-Z^{-1/3}+0.2Z^{-1/2}], $

(18)

where $ c_{\infty} = 0.253 $ is consistent with the Thomas-Fermi approximation [20], and the parameters $ a = 1.11Z^{0.475} $, $ b = 0.2+0.078(\ln Z)^2 $, and $ \nu = 1.16+0.08\ln(Z) $. The functions $ g_1(r_s) $ and $ g_2(r_s) $ are written as

$ g_1(r_s) = 1+\frac{0.78}{21+\Gamma_e(Z/r_s)^3}\left(\frac{\Gamma_e}{Z}\right)^{1/2}, $

(19)

and

$ g_2(r_s) = 1+\frac{Z-1}{9}\left(1+\frac{1}{0.001Z^2+2\Gamma_e}\right)\frac{r_s^3}{1+6r_s^2}, $

(20)

respectively. In Eq. (16), the factor $ h_1(x) = $ $ [1+(V_F/c)^6Z^{-1/3}]^{-1} $, where $ x = P_F/(m_ec) $, and $ P_F, m_e, c $ are the zero-temperature Fermi momentum of electrons, electron mass, and the speed of light, respectively. Here $ V_F = cx/\sqrt{1+x^2} $ is the electron Fermi velocity, and $ h_2(x) = (1+x^2)^{-1/2} $ is the relativistic correction that may be omitted when $ x\ll 1 $.
The Coulomb corrections contribute to changing the threshold energy in beta decay by

$ \Delta Q^s_{if}({\rm II}) = U_{C}(Z+1)-U_C(Z). $

(21)

Thus, the beta-decay threshold energy becomes

$ Q^s_{if}({\rm II}) = Q^{ss}_{if} = Q_{if}+\Delta Q^s_{if}(\rm{II}). $

(22)

Due to the SES, the electron energy increases from $ \varepsilon_e $ to $ \varepsilon^{s}_e({\rm II}) = \varepsilon^{ss}_e = \varepsilon_e+D $ in beta decay, and the threshold energy decreases from $ Q_{if} $ to $ Q^{ss}_{if} $. The chemical potential also changes from $ U_F $ to $ U^s_F $, and $ \xi(\rho, T, Y_e, Q_{ij}) $ is replaced by $ \xi^{ss}(\rho, T, Y_e, Q^{ss}_{ij})(\rm{II}) $ in Eq. (2). Thus, we have

$ \begin{split} \xi^{ss}(\rho, T, Y_e, Q_{ij}^{ss})(\rm{II}) =& \frac{c^3}{(m_ec^2)^5}\int_{1+D_2}^{Q_{ij}^{ss}+D_2}{\rm d}\varepsilon_e^{ss} \varepsilon_e^{ss} \\ &\times((\varepsilon^{ss}_e)^2-1)^{1/2}(Q^{ss}_{ij}-\varepsilon_e^{ss})^3\\& \times\frac{F(Z+1, \varepsilon_e^{ss})}{1+\exp[(U^s_F-\varepsilon_e^{ss})/k_{B}T]}.\end{split} $

(23)

According to Eq. (1), the AELR by beta decay in the SES is given by

$ \lambda_{\rm{AELR}}^s({\rm II}) = \ln2 \sum\frac{(2J_i+1){\rm e}^{\frac{-E_i}{k_{B}T}}}{G(Z, A, T)} \sum\limits_{f} \frac{\xi^{ss}(\rho, T, Y_e, Q^{ss}_{ij})}{ft^{ss}_{ij}(\rm{II})}, $

(24)

where the half-life $ ft^{ss}_{ij} $ in the SES for the model (II) is

$ \begin{split} \ln(ft^{ss}_{ij}(\rm{II})) =& a_1+\left(\alpha^2Z^2-5+a_2\frac{N-Z}{A}\right)\ln(Q^{ss}_{if}-a_3\delta)\\ &+(a_4\alpha^2Z^2)+\frac{1}{3}\alpha^2Z^2\ln(A)-\alpha Z\pi+S(N, Z). \end{split} $

(25)

For the purpose of numerical simulation, we define a SES enhancement factor $ C $, which is expressed as

$ C(i) = \frac{\lambda_{\rm{AELR}}^s(i)}{\lambda_{\rm{AELR}}^0}\; \; (i = 1, 2), $

(26)

where $ i = 1, 2 $ correspond to model (I) and model (II), respectively.

Figures 1and 2 show the ratios of $ \bigtriangleup Q/U_F $ and ($ D/U_F $) as a function of electron density $ \rho_7 $ for the model (I). We find that $ \bigtriangleup Q/U_F $, and ($ D/U_F $) decrease significantly as the density increases. However, there is a small effect on $ \bigtriangleup Q/U_F $ when $ \rho_7>10 $ from Fig. 1(a). Therefore, the beta decay with a low threshold energy is easier to change than that at higher density environment. Figure 1(b) also shows that $ D/U_F $ decreases with the density, and that it is hardly related with the matter density when $ \rho_7>10^2 $. For example, $ D/U_F $ for ⁵⁶Fe is 0.03281, 0.02243, 0.01847, 0.01735 at $ \rho_7 = 10, 10^2, 10^3, 10^4 $, respectively, as shown in Fig. 1. Therefore, the AELR at higher density may be less dependent on the matter density in the SES.
Figure1. (color online) $ \bigtriangleup Q/U_F $ ratio for Q-value correction, and electron Fermi energy as a function of electron density $ \rho_7 $ at several typical temperature points for the model (I).

Figure2. (color online) $ D/U_F $ ratio for screening potential, and electron Fermi energy correction as a function of electron density $ \rho_7 $ at several typical temperature points for model (I).

Figures 3 and 4 show the ratios $ \bigtriangleup Q/U_F^s $, and ($ D/U_F^s $) as a function of the electron density $ \rho_7 $ for the model (II). $ \bigtriangleup Q/U_F^s $, and ($ D/U_F^s $) likewise decrease significantly as the density increases. However, there is little effect on $ \bigtriangleup D/U_F^s $ when $ \rho_7>10 $ at a relatively higher temperature (e.g., $ T_9\geqslant 5.33 $), as shown in Fig. 4. Higher temperatures lead to larger electron energy. The higher the density, the lager the electron chemical potential becomes. According to Eqs. (8, 13–19), the screening effect on $ D/U_F^s $ may not strongly depend on the mass density when $ \rho_7>10 $. However, the screening affects $ \bigtriangleup Q/U_F^s $ significantly, as shown in Fig. 3.
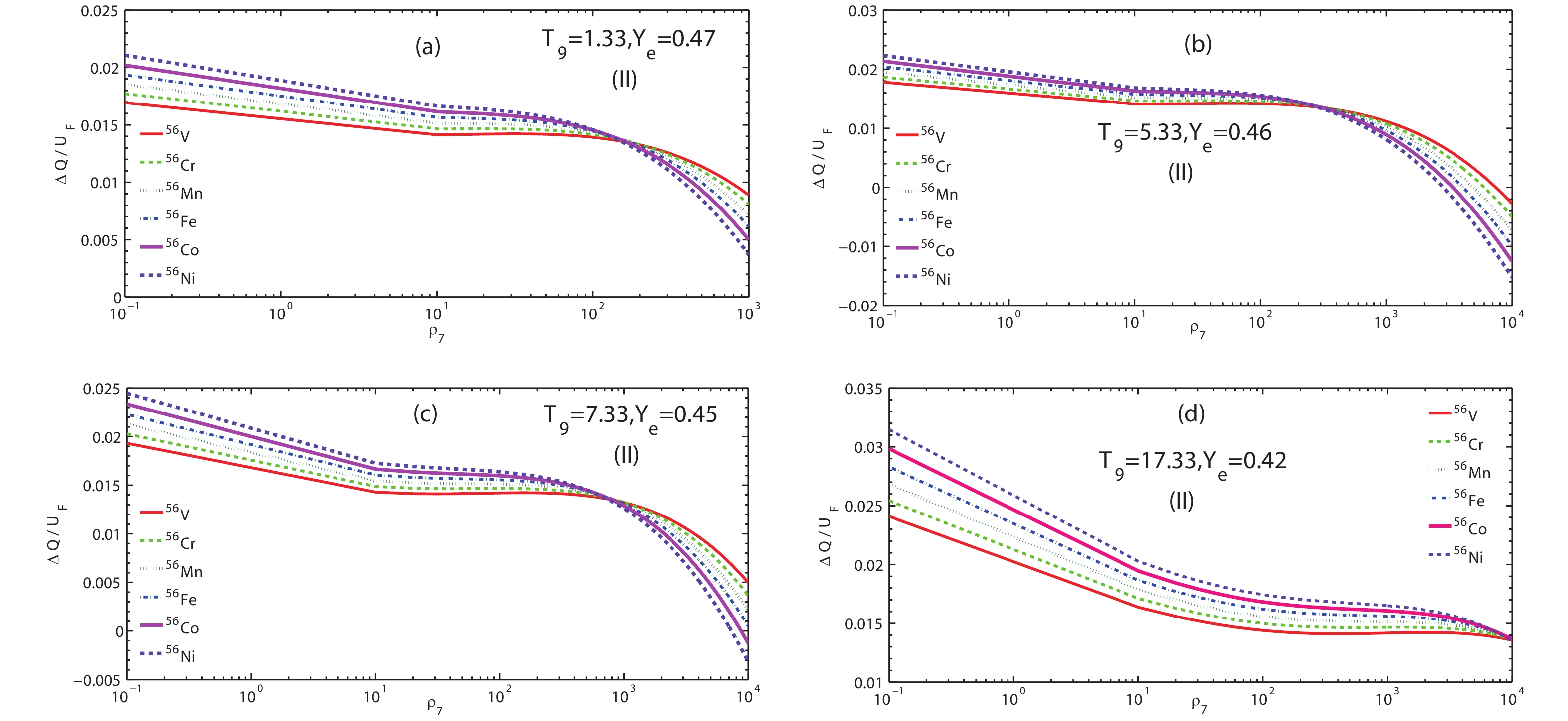Figure3. (color online) $ \bigtriangleup Q/U_F $ ratio for the corrections of Q-value, and electron Fermi energy as a function of electron density $ \rho_7 $ at several typical temperature points for model (II).

Figure4. (color online) $ D/U_F $ ratio for the correction of screening potential, and electron Fermi energy as a function of electron density $ \rho_7 $ at several typical temperature points for model (II).

The screening factors $ C $ as a function of $ \rho_7 $ for the models (I) and (II) are shown in Figs. 5–8 at different densities and temperatures. The effect of the SES on $ C $ decreases as the temperature increases for a given density. For example, at $ \rho_7 = 10^3 $ for model (I), the maximum $ C $ for ⁵⁶Ni decreases from 7.272 to 1.014, as shown in Fig. 5, and from 33.14 to 4.319 as shown in Fig. 8 for model (II).
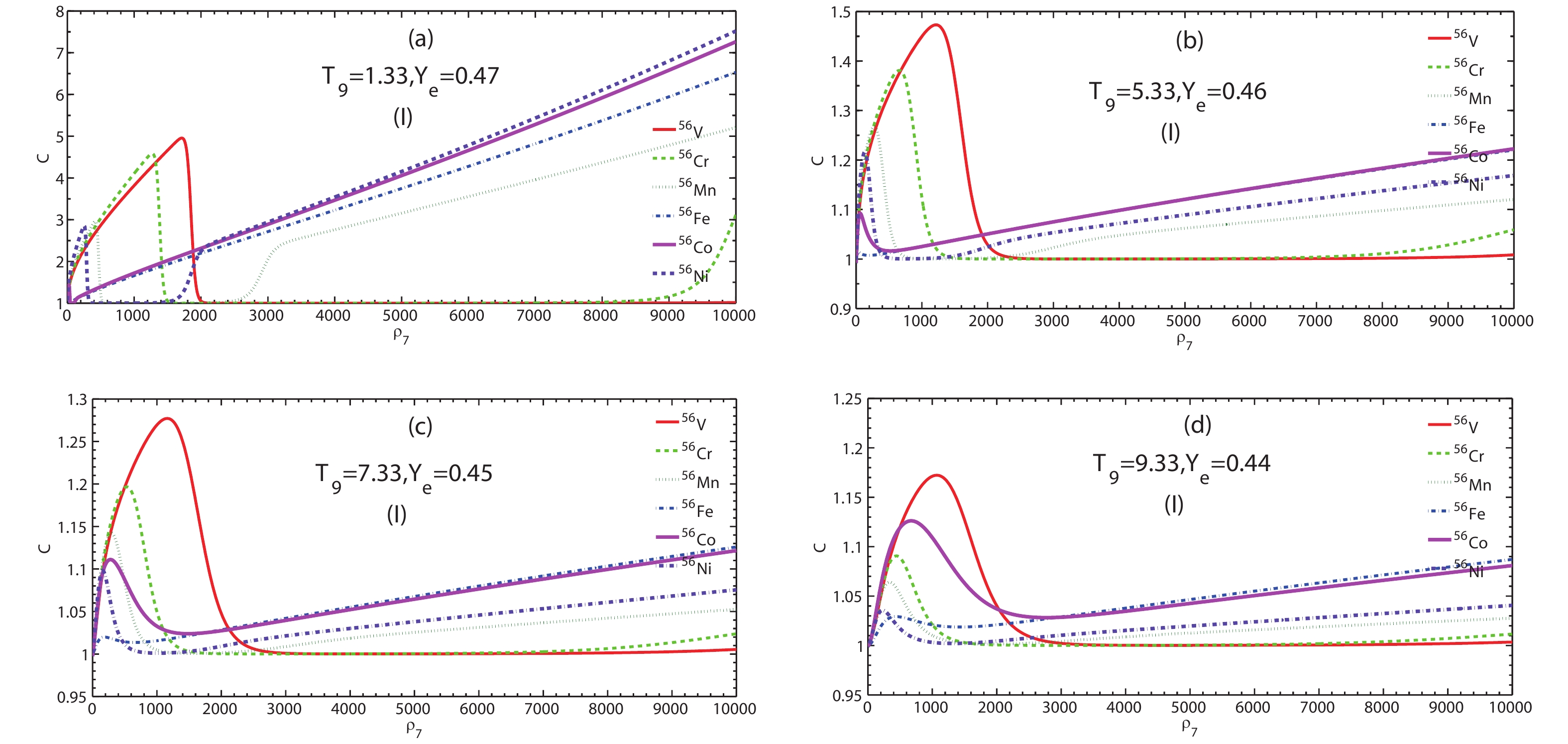Figure5. (color online) Screening enhancement factor C by beta decay of ⁵⁶V, ⁵⁶Cr, ⁵⁶Mn, ⁵⁶Fe, ⁵⁶Co, and ⁵⁶Ni as a function of electron density $ \rho_7 $ at relatively lower ($ T_9 = 1.33, 5.33 $) and medium temperatures ($ T_9 = 7.33, 9.33 $) for model (I).

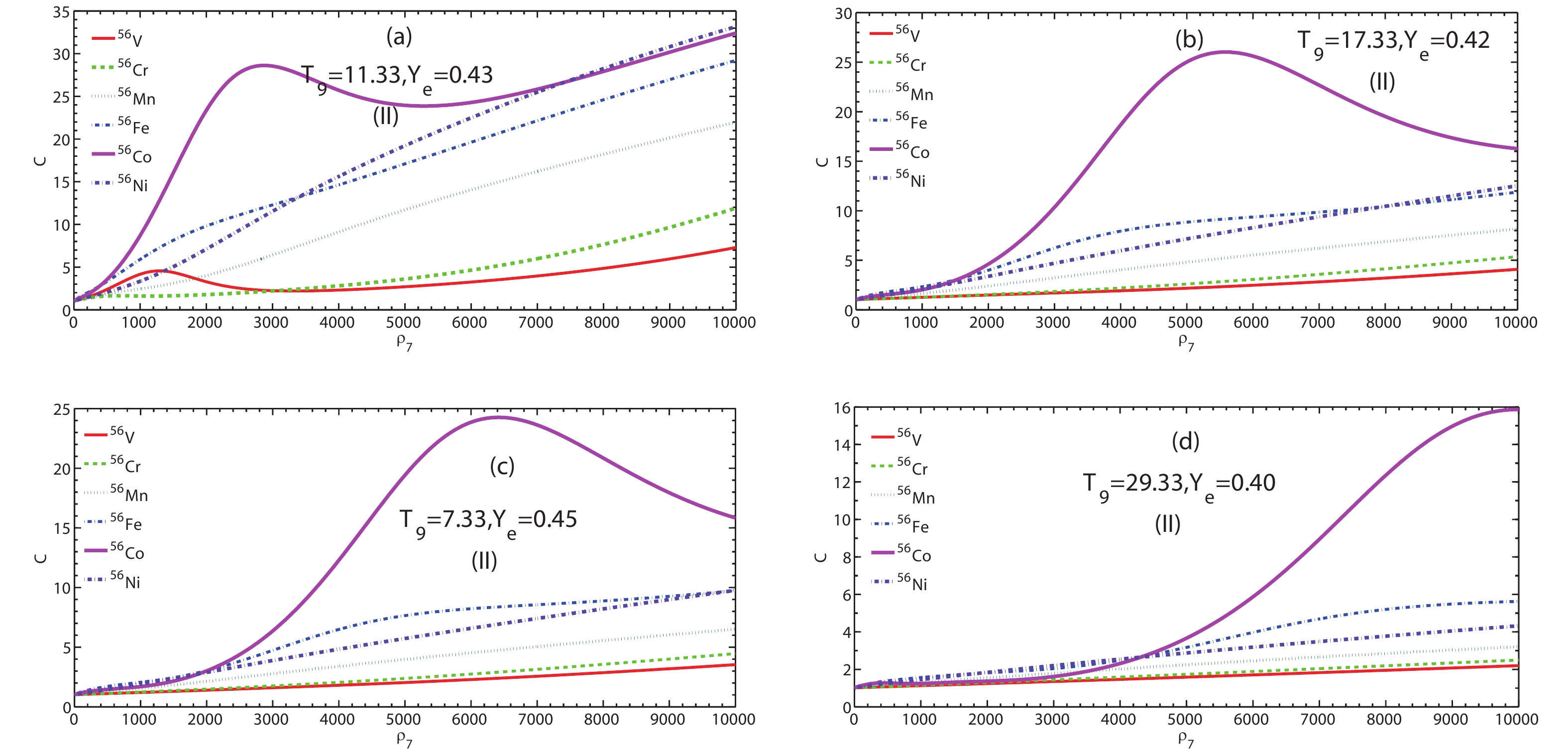Figure8. (color online) Screening enhancement factor C by beta decay of ⁵⁶V, ⁵⁶Cr, ⁵⁶Mn, ⁵⁶Fe, ⁵⁶Co, and ⁵⁶Ni as a function of electron density $ \rho_7 $ at relatively high temperature range ($ T_9>11 $) for model (II).

At relatively low ($ T_9 = 1.33, 5.33 $) and moderate temperatures ($ T_9 = 7.33, 9.33 $), we compare the results of Figs. 5 and 6. Herein, the factor $ C $ in model (II) is significantly larger than that of model (I). For example, $ C $ for ⁵⁶V has a value of 4.955 in model (I), whereas it has a value of 651.9 in model (II) at $ T_9 = 1.33 $. The same conclusions can be derived from Figs. 7 and 8 for higher temperatures. We compare the calculations for Figs. 5 and 6 with those of Figs. 7 and 8 for model (I) and (II). Finally we conclude that the lower the temperature, the smaller the electron kinetic energy becomes. Hence, the SES effect on $ C $ and AELR is large.
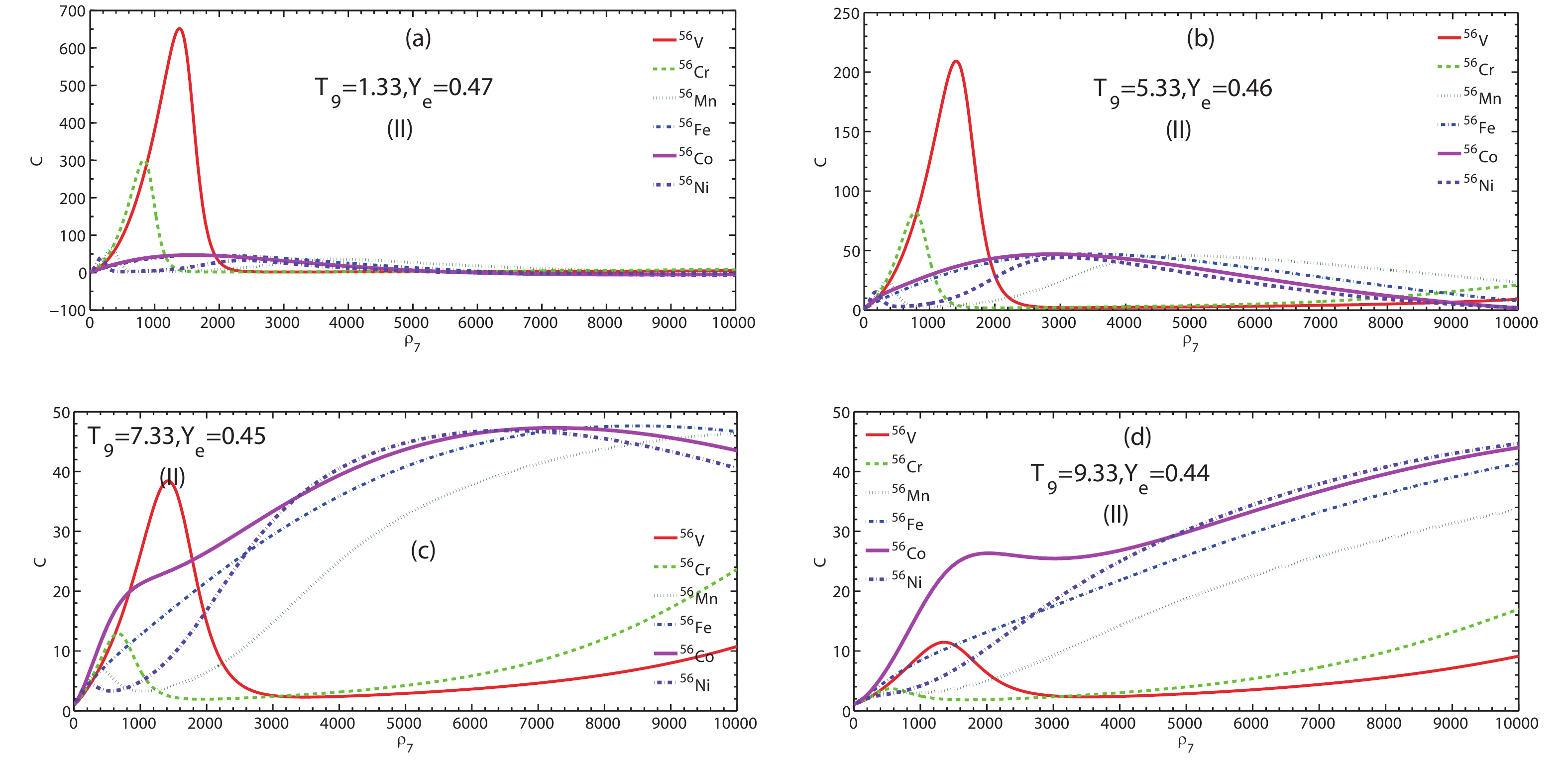Figure6. (color online) Screening enhancement factor C by beta decay of ⁵⁶V, ⁵⁶Cr, ⁵⁶Mn, ⁵⁶Fe, ⁵⁶Co, and ⁵⁶Ni as a function of electron density $ \rho_7 $ at relatively lower ($ T_9 = 1.33, 5.33 $) and medium temperatures ($ T_9 = 7.33, 9.33 $) for model (II).

Figure7. (color online) Screening enhancement factor C by beta decay of ⁵⁶V, ⁵⁶Cr, ⁵⁶Mn, ⁵⁶Fe, ⁵⁶Co, and ⁵⁶Ni as a function of electron density $ \rho_7 $ at relatively high temperature range ($ T_9>11 $) for model (I).

Judging from the influence of SES on nuclear physics and nuclear structure, the electron screening potential can significantly increase the energy of outgoing electrons during the beta decay process. In addition, the SES can also increase the energy of individual particles, whereas it relatively decreases the threshold needed for beta decay reactions because of the increase in the number of high-energy electrons. Indeed, the SES greatly accelerates the progress of beta decay.
Tables 1–4 show our results in terms of the screening enhancement factor $ C $. The AELR increases greatly due to SES from the information provided by $ C $, especially for model (II). Tables 1 and 2 show the maximum value of the screening factor for ⁵⁶V, ⁵⁶Cr, ⁵⁶Mn, ⁵⁶Fe, ⁵⁶Co, and ⁵⁶Ni at several medium temperatures for model I and II. For example, at $ T_9 = 5.33, Y_e = 0.46 $ the maximum value of enhancement factor $ C $ for ⁵⁶V, ⁵⁶Cr, ⁵⁶Mn, ⁵⁶Fe, ⁵⁶Co, and ⁵⁶Ni are 1.473, 1.381, 1.266, 1.222, 1.223, 1.213 for model (I), whereas they are 209.3, 81.98, 44.58, 43.12, 47.02, 44.26 for model (II), respectively.

nuclei	T9 = 1.33, Ye = 0.47			T9 = 5.33, Ye = 0.46			T9 = 7.33, Ye = 0.45			T9 = 9.33, Ye = 0.44
	ρ7	C(max)		ρ7	C(max)		ρ7	C(max)		ρ7	C(max)
56V	1712	4.955		1221	1.473		1161	1.277		1071	1.172
56Cr	1271	4.584		650.7	1.381		520.6	1.197		440.5	1.091
56Mn	10000	5.208		260.4	1.266		270.4	1.141		340.4	1.064
56Fe	10000	6.532		10000	1.222		10000	1.126		10000	1.087
56Co	10000	7.257		10000	1.223		10000	1.122		670.8	1.126
56Ni	10000	7.272		150.2	1.213		150.2	1.098		10000	1.041

Table1.Maxima of strong screening enhancement factor C at several typical temperatures within the medium temperature range for model (I).

nuclei	T9 = 1.33, Ye = 0.47			T9 = 5.33, Ye = 0.46			T9 = 7.33, Ye = 0.45			T9 = 9.33, Ye = 0.44
	ρ7	C(max)		ρ7	C(max)		ρ7	C(max)		ρ7	C(max)
56V	1391	651.9		1411	209.3		1422	38.45		1331	11.45
56Cr	810.9	298.2		780.9	81.98		10000	23.66		10000	17.00
56Mn	330.4	64.80		4455	44.58		10000	46.70		10000	33.67
56Fe	1772	46.38		3564	47.12		8509	47.63		10000	41.34
56Co	1452	46.74		2883	47.02		7277	47.31		10000	44.65
56Ni	1703	40.90		3093	44.26		6527	46.85		10000	44.66

Table2.Maxima of strong screening enhancement factor C at several typical temperatures within the medium temperature range for model (II).

nuclei	T9 = 11.33, Ye = 0.43			T9 = 17.33, Ye = 0.42			T9 = 19.33, Ye = 0.41			T9 = 29.33, Ye = 0.40
	ρ7	C(max)		ρ7	C(max)		ρ7	C(max)		ρ7	C(max)
56V	10000	7.286		10000	4.087		10000	3.523		10000	2.196
56Cr	10000	11.86		10000	5.343		10000	4.447		10000	2.492
56Mn	10000	21.91		10000	8.139		10000	6.501		10000	3.205
56Fe	10000	29.16		10000	11.86		10000	9.745		10000	5.622
56Co	2382	32.37		5526	26.01		6326	24.24		10000	15.86
56Ni	10000	33.14		10000	12.49		10000	9.746		10000	4.319

Table4.Maxima of strong screening enhancement factor C at several typical temperatures in the relatively high temperature range for model (II).

The results of $ C $ at relatively higher temperatures are presented in Tables 3 and 4. We find that there is small enhancement in $ C $ at the higher temperature. For example, the maximum value of the enhancement factor $ C $ is 1.099 (e.g., for ⁵⁶V) in Table 3, whereas is 33.14 (e.g., for ⁵⁶Ni) in Table 4. This is because the higher the temperature leads to a larger electron energy at a given density. The effect of the SES on beta decay may be weakened due to higher electron energy.

nuclei	T9 = 11.33, Ye = 0.43			T9 = 17.33, Ye = 0.42			T9 = 19.33, Ye = 0.41			T9 = 29.33, Ye = 0.40
	ρ7	C(max)		ρ7	C(max)		ρ7	C(max)		ρ7	C(max)
56V	991.1	1.099		1542	1.004		10000	1.001		10000	1.001
56Cr	410.5	1.024		10000	1.002		10000	1.002		10000	1.002
56Mn	460.6	1.021		10000	1.005		10000	1.004		10000	1.003
56Fe	10000	1.067		10000	1.040		10000	1.036		10000	1.023
56Co	1171	1.126		2833	1.099		3413	1.089		6486	1.047
56Ni	10000	1.025		10000	1.009		10000	1.007		10000	1.003

Table3.Maxima of strong screening enhancement factor C at several typical temperatures in the relatively high temperature range for model (I).

To summarize the above analysis, the $ C $ and AELR are both influenced greatly by the SES as the density increases, as seen in Figs. 5-8. This is because the SES has a strong influence on the Q-value of the beta decay. As the density increases, $ D/U_F $ and $ \bigtriangleup Q/U_F $ decrease. However, they have little relation with mass density when $ \rho_7>10^2 $, as shown in Figs. 1–4. The AERL is also strongly dependent on the beta decay Q-value. The higher the energy of the outgoing electron, the larger the AERL becomes, in the case where the electron energy is higher than the threshold energy.
For model (I), the SES significantly alters the Q-value, the electron energy, and the half-life for the beta decay. According to Eqs. (7) and (10), due to the Q-value correction, the comparative half-life increases with the increase the Q-value. Because of the interactions among the electrons in plasma, the nuclear binding energy decreases. The effective nuclear Q-value ($ Q_{\rm{if}} $) varies at high density because of the effect of the charge dependence on the binding energy. Based on Eqs. (8) and (9), the beta decay increases due to the SES.
For model (II), we discuss the influence of the SES on the enhancement factor and AERL by beta decay, by considering the corrections of the Q-value, electron energy, and the half-life, as well as the electron chemical potential. According to Eqs. (13–22, 25), the half-life and electron chemical potential increase due to the the Q-value correction in the SES. The nuclear binding energy also decreases due to interactions with the dense electron gas in the SES. Based on Eqs. (13–24), the beta decay increases greatly due to the SES. Comparison of the results of model (I) with those of model (II), as shown in Figs. 5-8, shows that an improved estimation of the SES for AERL is given in the model (II).
In contrast, the pairing effect and Q-values with the neutron number of the parent nuclei play key roles in the $ \beta^- $ decay reaction. For instance, the half-lives with Q-values are strongly influenced by them. As shown in Fig. 2 of Ref. [36], when the number of neutrons increases, the comparative half-live decreases, whereas the Q-value increases.
The shell and pairing effects are very important in the nuclear structure. Some information on the pairing effects on $ \beta^- $ decay half-lives and Q-values is described by the parameter $ \delta $. When the number of nuclear neutrons increases, the beta decay reaction can be more active because of the pairing effect. Thus, the AERL increases.
Because of the quantum effect, the shell effect strongly changes the nuclear structure and influences the $ \beta^- $ decay comparative half-lives. A complete correction of shell effects should include all major shell, as well as sub-shell closures. A reasonable approximation is given by Eq. (4), when we consider the shell effects and pairing effects.
Based on Eqs. (7) and (10) for the model (I) (Eqs. (15–22) and Eq. (25) for the model (II)), the SES influences the Q-value and decay half-lives. From Figs. 1–4, we find that the enhancement factor $ C $ rises and falls because of to the shell effects and the pairing effect in the SES, as well as the corrections of the Q-value.

We investigate the influence of SES on the AELR by beta decay for several iron group nuclei, based on two different SES models. We calculate the screening potential based on IBSM and LRTM. We compare the effect of the SES from two screening models on AELR by considering the corrections of the Q-value, electron chemical potential, and the shell and pair effects. We find that the AELR by beta decay increases by two orders of magnitude, and the enhancement factor can reach 651.9 compared to the case without SES as the density increases in model (II). Meanwhile, this value is 7.272 in model (I) for a given temperature. As the temperature increases, the influence of SES on AELR is weakened. Comparing the results of model (I) with those of model (II), we find that the study of AERL in model (II) may represent an improved estimation.
The AELR by beta decay plays a key role in stellar cooling evolution. Our results may have important consequences for astrophysical applications, and in particular, for the burst mechanism of supernovae explosion and cooling numerical simulations.