基于Meta-Gaussian模型的中国农业干旱预测研究

删除或更新信息，请邮件至freekaoyan#163.com(#换成@)

本站小编 Free考研考试/2021-12-29

吴海江^,¹^,², 粟晓玲^,¹^,², 张更喜¹

1.西北农林科技大学水利与建筑工程学院,杨凌 712100

2.西北农林科技大学旱区农业水土工程教育部重点实验室,杨凌 712100

Prediction of agricultural drought in China based on Meta-Gaussian model

WU Haijiang^,¹^,², SU Xiaoling^,¹^,², ZHANG Gengxi¹

1. College of Water Resources and Architectural Engineering, Northwest A&F University, Yangling 712100, Shaanxi, China

2. Key Laboratory for Agricultural Soil and Water Engineering in Arid Area of Ministry of Education, Northwest A&F University, Yangling 712100, Shaanxi, China

通讯作者: 粟晓玲(1968-), 女, 四川开江人, 教授, 博导, 主要从事水文模拟研究。E-mail: xiaolingsu@nwafu.edu.cn

收稿日期:2020-02-17修回日期:2020-10-28网络出版日期:2021-03-25

基金资助:

国家自然科学基金项目.51879222

Received:2020-02-17Revised:2020-10-28Online:2021-03-25

Fund supported:

National Natural Science Foundation of China.51879222

作者简介 About authors
吴海江(1994-), 男, 山西大同人, 硕士生, 研究方向为干旱预测。E-mail: haijiangwu@nwafu.edu.cn

摘要
在全球气候变化背景下,干旱愈加频发,有效且可靠的农业干旱预测对于保障粮食安全和水资源安全具有重要意义。以标准化降水指数（SPI）和联合标准化土壤湿度指数（JSSI）分别表征气象干旱和农业干旱,以前期的气象干旱和农业干旱指数作为预测因子,在1~3个月预见期下基于Meta-Gaussian（MG）模型对中国1961—2015年6—8月的农业干旱进行预测,并采用Brier Skill Score（BSS）和纳什效率系数（NSE）评价MG模型的预测性能。结果表明：① 将1个月、3个月、6个月、9个月和12个月时间尺度的标准化土壤湿度指数（SSI）结合起来得到的JSSI能够对中国农业干旱的综合状况进行客观评价。② 以中国2010年和2014年遭受严重的干旱事件为例,预见期为1~3个月时,除新疆南部、青海西部以及内蒙古西部等沙漠地区外,MG模型对6—8月农业干旱预测结果的分布范围与实际干旱的分布区域较吻合,预见期越短,吻合越好。③ 预见期为1个月时,6—8月BSS ≥ 0.5的面积比例分别为0.714、0.642和0.640,NSE ≥ 0.5的面积比例分别为0.903、0.829和0.837,表明MG模型能够对中国大部分区域的农业干旱作出可靠的预测。本文结果可为中国农业干旱的监测、预警及干旱决策提供科学指导。
关键词： 农业干旱;干旱预测;预测概率;Meta-Gaussian模型

Abstract

It is predicted that many regions will witness higher frequencies of drought events under global climate change, which could pose a threat to crop yield and water security. Therefore, the development of efficient and reliable methods for agricultural drought prediction is crucial. This study used the Standardized Precipitation Index (SPI) based on monthly precipitation at a 6-month time scale as an indicator of meteorological drought. The Joint Standardized Soil Moisture Index (JSSI) was used to assess the comprehensive situation of agricultural drought and was derived by combining the Standardized Soil Moisture Index (SSI) over 1-, 3-, 6-, 9-, and 12-month time scales based on monthly root zone soil moisture. Using the antecedent SPI and the persistent JSSI as predictors, the Meta-Gaussian (MG) model was applied to predict agricultural drought in China from June to August in 1961-2015. The Brier Skill Score (BSS) and Nash-Sutcliffe Efficiency Coefficient (NSE) were adopted for the evaluation of the prediction performance of the MG model. The results showed that the JSSI was capable of capturing both emerging and prolonged agricultural droughts in a timely manner, which is significant for agricultural drought monitoring. The spatial distribution of predictions of severe agricultural droughts with the 1- to 3-month lead by the JSSI for June to August in 2010 and 2014 resembled the corresponding observations for most parts of China. Moreover, the areas with a predicted higher probability of JSSI falling below -0.5 corresponded well with areas that experienced agricultural drought according to observed data (JSSI ＜ -0.5). The BSS and NSE results confirmed that the MG model was able to provide reliable predictions of agricultural drought for June to August in most parts of China. The prediction of JSSI from June to August by the MG model with the 1-month lead showed that the proportions of the total area with BSS ≥ 0.5 were 0.714, 0.642, and 0.640, respectively, whereas the proportions of the total area with NSE ≥ 0.5 were 0.903, 0.829, and 0.837, respectively. However, the MG model performed poorly in desert areas, including southern Xinjiang, western Qinghai and western Inner Mongolia, which may have been due to the extremely arid conditions of these regions with soil water mostly related to condensation water rather than rainfall. The results of this study can provide scientific basis for agricultural drought monitoring, early warning, and decision-making in China.

Keywords：agricultural drought;drought prediction;prediction probability;Meta-Gaussian model

PDF (11145KB)元数据多维度评价相关文章导出EndNote|Ris|Bibtex 收藏本文
本文引用格式
吴海江, 粟晓玲, 张更喜. 基于Meta-Gaussian模型的中国农业干旱预测研究. 地理学报[J], 2021, 76(3): 525-538 doi:10.11821/dlxb202103003
WU Haijiang, SU Xiaoling, ZHANG Gengxi. Prediction of agricultural drought in China based on Meta-Gaussian model. Acta Geographica Sinice[J], 2021, 76(3): 525-538 doi:10.11821/dlxb202103003

1 引言

干旱是对粮食生产、水资源管理和生态系统等造成恶劣影响和巨大经济损失的极端事件之一^[1,2,3,4]。气候的剧烈变化和人类对自然的过度干预,使得中国局域极端事件频发,如2009—2010年中国西南地区百年一遇的干旱事件^[5,6,7]、2014年中国26个省（自治区、直辖市）发生的旱灾^[8,9]等,这些严重的干旱事件对农业经济造成了灾难性的影响。因此,亟需一种有效的干旱预测方法来减轻干旱对农业生产的潜在影响。

干旱可以分为气象干旱、农业干旱、水文干旱和社会经济干旱。近半个世纪以来,用于表征干旱类型的干旱指数众多,其中被广泛使用的气象干旱指数有：标准化降水指数（Standardized Precipitation Index, SPI）^[10]和标准化降水蒸散指数（Standardized Precipitation Evapotranspiration Index, SPEI）^[11]等;广泛使用的农业干旱指数有：帕尔默干旱指数（Palmer Drought Severity Index, PDSI）^[12]和标准化土壤湿度指数（Standardized Soil Moisture Index, SSI）^[13]等。干旱一般起源于气象干旱（降水减少或蒸发量增大）,进而向农业干旱（土壤水含量减少）^[14,15]发展。为捕捉和刻画更为复杂的干旱事件^[16,17],众多****将气象干旱和水文干旱^{[1, 14, 18-19]}、气象干旱和农业干旱^{[17, 20]}两两联合起来,但大多基于单一的时间尺度进行研究。由于单一时间尺度的干旱指数只能表征某一特定类型的干旱特性,往往与实际情况有较大偏差。针对这个问题,Kao等^[21]通过结合不同时间尺度的SPI并提出了联合亏缺指数（Joint Deficit Index, JDI）来综合反映不同时间尺度下的干旱状况。因此,根据JDI的计算方法,考虑将不同时间尺度的SSI结合起来并用于农业干旱预测有望提高模型的预测精度。

Meta-Gaussian（简称MG）是Elliptical Copula函数族中最常用的模型之一,它能够建立多种与边缘分布无关的相依结构且其条件分布函数有解析形式^[1]。MG模型作为一种有效联合多维变量的工具,在进行干旱预测时被广泛使用并取得了良好的效果。如Hao等^[1]以水文干旱的持续性（SRI）和前期的气象干旱（SPI）作为预测因子,基于MG模型对美国德克萨斯州的水文干旱进行了概率预测,并与集合预报模型（Ensemble Streamflow Prediction, ESP）进行比较,结果表明,当预见期为1~2个月时,MG模型的预测性能优于ESP;Hao等^[16]基于MG模型对南非夏季的复合干热事件进行预测研究,并与随机预测以及确定性预测进行比较,结果表明,当预见期为3个月时,MG模型的预测性能仍优于随机预测和确定性预测。一般在夏季（6—8月）干旱事件频发^{[7, 22]},对粮食生产、水资源安全和生态等产生了严重的影响。选用6个月时间尺度的SPI来表征气象干旱是由于其可以很好的反映中国的气象干旱状况^[23]。根区土壤湿度是作物和植被生长的主要控制因子,且基于根区土壤湿度得到的SSI可以用来监测和评估农业干旱^[24]。但由于农业干旱的动态复杂性,单一时间尺度的SSI往往不能够全面反映农业干旱的综合状况,因此,拟将1个月、3个月、6个月、9个月和12个月时间尺度的SSI结合起来得到联合标准化土壤湿度指数（Joint Standardized Soil Moisture Index, JSSI）以表征农业干旱的综合状况。本文主要研究内容包括：JSSI和不同时间尺度SSI的计算与比较;滞时为1~3个月时,对6—8月JSSI的自相关、JSSI与SPI之间的互相关进行Pearson相关分析;预见期为1~3个月时,以JSSI的持续性和前期的SPI作为两个预测因子,利用MG模型对6—8月的农业干旱进行预测,并采用Brier Skill Score（BSS）和纳什效率系数（Nash-Sutcliffe Efficiency Coefficient, NSE）对MG模型的预测性能进行评价。研究结果可为中国农业干旱的监测、预警以及抗旱减灾等提供科学指导。

2 数据资料

本文使用的月根区土壤湿度数据来自全球陆地数据同化系统（Global Land Data Assimilation System, GLDAS）数据集（https://ldas.gsfc.nasa.gov/gldas/）,空间分辨率为0.25°×0.25°,采用的时间范围是1961年1月—2015年12月,该数据集利用地面观测数据和卫星遥感数据并结合陆面过程模型如VIC、NOAH等模拟生成全球地表水文变量和通量数据^[9],已被广泛应用于水资源调查、天气预报、水循环以及干旱的监测和预警^[20]等方面。月降水数据来自东英格利亚大学气候研究中心（Climatic Research Unit, CRU）（http://www.cru.uea.ac.uk/data）,空间分辨率为0.5°×0.5°,时间范围是1901年1月—2018年12月。为与GLDAS数据集中的月根区土壤湿度数据的空间分辨率和时间序列长度一致,取CRU中1961—2015年的月降水数据并重采样为0.25°×0.25°空间分辨率。

3 研究方法

3.1 干旱指数

为避免对分布函数的假设和减少拟合分布参数的计算^[9],本文使用非参数化的Gringorten位置划分公式^[25]来计算月根区土壤湿度和月降水量的经验累积概率（P'）：

(1)

P^{'} = \frac{# (x x_{i}) - 0.44}{n + 0.12}

式中：n表示数据系列长度;x为根区土壤湿度或降水的月值数据在不同时间尺度下的累积量（如1个月、3个月或6个月等）;#(x x_i)表示x的序统计量。

对P'进行正态分位数转换（Normal Quantile Transformation, NQT）^[26]得到标准化干旱指数（Standardized Drought Index, SDI）：

（2）

SDI = Φ^{- 1} (P^{'})

式中：

Φ^{- 1}

表示高斯逆变换;SDI可以为不同时间尺度的SSI或SPI。

由于干旱的动态复杂性,不同时间尺度的同一个干旱指数在监测和表征干旱时可能会出现不一致的情况,如短时间尺度的干旱指数可以表征新发展的干旱事件^[27]（即短时间尺度的干旱指数值表现为较严重的干旱而长时间尺度的干旱指数值则表现为无旱）,而长时间尺度的干旱指数则能够更好地反映持续性或长期干旱^{[21, 27]}。因此,本文将1个月、3个月、6个月、9个月和12个月尺度的SSI结合起来以综合反映土壤水分的盈亏状况,具体计算方法如下。

K_C（Kendall Copula）分布函数被广泛用于构造联合分布,对于5维K_C累积联合概率K_C(s)^{[21, 27]}的表达式为：

（3）

\begin{array}{l} K_{C} (s) = P [C_{U_{1}, U_{3}, U_{6}, U_{9}, U_{12}} (u_{1}, u_{3}, u_{6}, u_{9}, u_{12}) \leq s] \\ s = P [U_{1} \leq u_{1}, U_{3} \leq u_{3}, U_{6} \leq u_{6}, U_{9} \leq u_{9}, U_{12} \leq u_{12}] \end{array}

式中：u_i为i个月时间尺度下的SSI对应的累积概率;

U_{i}

为对应于u_i的随机变量。

由于K_C的解析表达式对于非Archimedean Copula函数族可能不存在^[2],根据Kao等^[21]的研究结果,可以用经验分布函数K_Cn来替代K_C^[28],即：

（4）

\begin{array}{l} K_{Cn} (s) = \frac{1}{n} \overset{n}{\sum_{i = 1}} I (α_{i} \leq s) \\ α_{i} = \frac{1}{n} \overset{n}{\sum_{j = 1}} I (u_{1 j} u_{1 i}, u_{3 j} u_{3 i}, u_{6 j} u_{6 i}, u_{9 j} u_{9 i}, u_{12 j} u_{12 i}) \end{array}

式中：I(x)为逻辑表达式,当x中的条件满足时,I取1,否则取0。

对K_Cn(s)进行NQT转换得到联合标准化土壤湿度指数（JSSI）,其表达式为：

（5）

JSSI = Φ^{- 1} (K_{Cn} (s))

3.2 Meta-Gaussian模型

设两个连续随机变量分别为X₁、X₂,对其进行NQT转换分别得到标准化正态随机变量Z₁和Z₂,则基于MG模型的表达式为^{[1, 29]}：

（6）

P (X_{1} \leq x_{1}, X_{2} \leq x_{2}) = Φ_{2} (Z_{1}, Z_{2} | μ, \sum)

式中：

Φ_{2}

为均值为

μ

、协方差为

\sum

的二元正态分布。

基于多元正态分布函数的性质,其条件分布函数也服从正态分布^{[1, 24]}。在给定X的条件下,Y发生的概率记为P(Y|X),那么条件均值

μ_{Y | X}

和方差

σ_{Y | X}^{2}

表达式分别为^[29]：

（7）

μ_{Y | X} = μ_{Y} + ρ \frac{σ_{Y}}{σ_{X}} (X - μ_{X})

（8）

σ_{Y | X}^{2} = σ_{Y}^{2} (1 - ρ^{2})

式中：

μ_{X}

、

μ_{Y}

、

σ_{X}

、

σ_{Y}

分别为X、Y的均值和均方差;

ρ

为Pearson相关系数。

受全球以及区域水文循环的影响,各气象水文变量之间存在着密切的联系。一段时期内,降水的持续亏缺可能导致气象干旱,降水不足使得土壤水分的补给来源减少,进而诱发农业干旱,即气象干旱先于农业干旱发生并向农业干旱传递。此外,干旱的发展过程一般比较缓慢,一场干旱事件可能持续数月甚至数年^[1]。因此,考虑将前期的气象干旱和农业干旱的持续性（或记忆性）分别作为农业干旱的驱动因素和初始条件,即在MG模型中将前期的气象干旱和农业干旱的持续性作为预见期农业干旱的两个预测因子来对预见期的农业干旱进行预测。设前期的气象干旱、前期的农业干旱和预见期的农业干旱分别为X₁、X₂、Y,将公式（6）~（8）推广到3个变量情形下,特别地,当向量X=[X₁, X₂],则基于MG模型可以推导出在给定X₁和X₂的条件下Y的条件分布为^[1]：

（9） $Y|\left(X_{1}, X_{2}\right) \sim \Phi\left(\mu_{Y|\left(X_{1}, X_{2}\right)}, \sum_{Y|\left(X_{1}, X_{2}\right)}\right)$

其中条件均值 $\mu_{Y|\left(X_{1}, X_{2}\right)}$和协方差 $\sum_{Y|\left(X_{1}, X_{2}\right)}$的表达式为：

（10）

μ_{Y | (X_{1}, X_{2})} = μ_{y} + \sum_{yx} \sum_{xx}^{- 1} (x - μ_{x})

（11）

\sum_{Y | (X_{1}, X_{2})} = \sum_{yy} - \sum_{yx} \sum_{xx}^{- 1} \sum_{xy}

式中：

μ_{x}

、

μ_{y}

分别表示向量X、变量Y的均值;

\sum_{xx} 、 \sum_{xy} 、 \sum_{yx} 、 \sum_{yy}

表示X和Y的协方差矩阵。

MG模型还可以用来进行概率预测^{[1, 16]},即在给定X₁和X₂的条件下,由公式（9）~（11）预测发生农业干旱概率P的表达式为：

（12）

P (s_{0}; μ_{Y | (X_{1}, X_{2})}, \sum_{Y | (X_{1}, X_{2})} = \int_{-^{\infty}}^{s_{0}} \frac{1}{\sqrt[]{2 π \sum_{Y | (X_{1}, X_{2})}}} \exp [- \frac{(t - μ_{Y | (X_{1}, X_{2})})^{2}}{2 \sum_{Y | (X_{1}, X_{2})}}] dt

式中：s₀为发生农业干旱的阈值（取-0.5）。

条件均值

μ_{Y | (X_{1}, X_{2})}

可以作为预见期农业干旱的预测值^{[1, 16]}。条件均值

μ_{Y | (X_{1}, X_{2})}

和预测概率P可为管理者提供有用的决策信息,从而有助于开展旱情管理工作^[1]。

3.3 预测性能评价

Brier Score（BS）是概率预测中最常用的精度评价指标之一,实质上是预测概率和观测概率的均方误差^[30],其表达式为：

（13）

BS = \frac{1}{n} \overset{n}{\sum_{i = 1}} (P P_{i} - O P_{i})^{2}

式中：n为预测值的个数;取发生农业干旱的阈值为-0.5;PP_i为第i个JSSI的预测值小于-0.5发生的概率（公式（12））;OP_i为第i个JSSI的观测值小于-0.5时对应的观测概率,如果JSSI的观测值小于-0.5,OP_i = 1,否则OP_i = 0。

以随机预测模型作为参考,采用BSS对MG模型的预测性能进行评价时,表达式为^[30]：

（14）

BSS = 1 - BS / [\bar{x} (1 - \bar{x})] BSS \in (- \infty, 1]

式中：

\bar{x}

表示JSSI的阈值取-0.5时对应的累积概率为0.3^{[16, 24]};BSS越接近于1,表明MG模型的预测性能越好,BSS ≤ 0,表明MG模型的预测性能较差^{[16, 30]}。

NSE也可以用来检验MG模型的预测性能,其表达式为：

（15）

NSE = 1 - \frac{\overset{n}{\sum_{i = 1}} (P_{i} - O_{i})^{2}}{\overset{n}{\sum_{i = 1}} (O_{i} {- \bar{O})}^{2}} NSE \in (- \infty, 1]

式中：P_i为MG模型的预测值;O_i为对应的观测值;

\bar{O}

为观测样本O的均值。

4 结果分析

4.1 JSSI与不同时间尺度SSI的比较

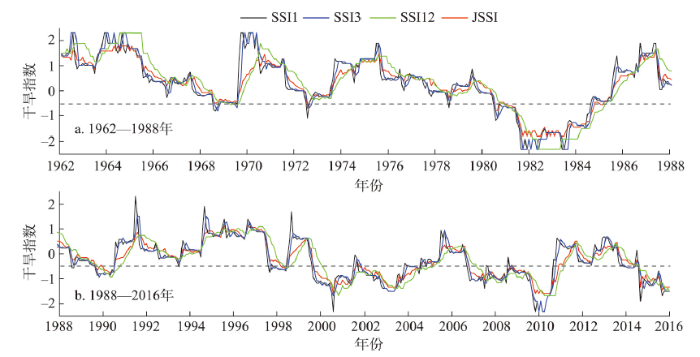
为更好的展示JSSI和不同时间尺度下SSI对农业干旱的表征能力,以栅格（120°E, 42°N）为例,将1962—2015年的JSSI序列与SSI1（表示1个月尺度）、SSI3和SSI12序列进行比较（图1）。

图1

新窗口打开|下载原图ZIP|生成PPT
图11962—2015年栅格(120°E, 42°N)中JSSI与SSI1、SSI3和SSI12的比较

Fig. 1Comparison of the JSSI with the SSI1, SSI3, and SSI12 in the grid (120°E, 42°N) in 1962-2015

如图1所示,SSI1和SSI3的变化幅度比较剧烈,而SSI12和JSSI的变化幅度较平缓,且JSSI不仅能够反映出由SSI12描述的持续性干旱（如2000—2004年、2007—2010年等）,也能够捕捉到像SSI1表征的新发展干旱（如1972年7月、1999年8月等）。因此,以JSSI作为农业干旱的监测指标能够客观地评价农业干旱的综合状况且比单时间尺度的SSI在表征农业干旱上更有说服力。

4.2 相关性分析

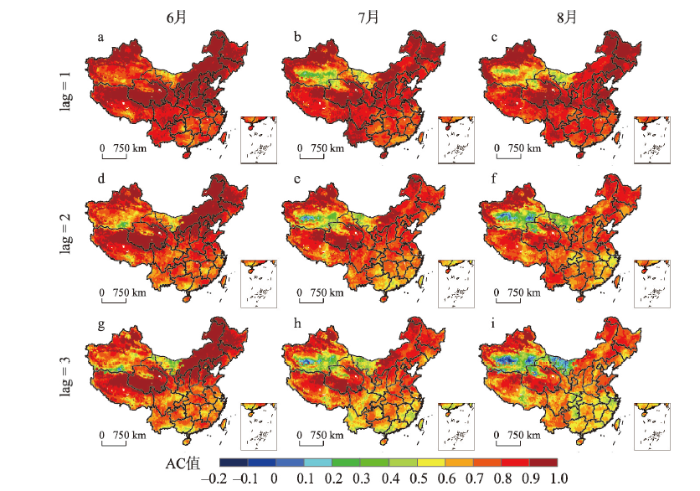
在进行农业干旱预测前,必须考虑不同变量之间的相关性^{[24, 31]}。因此,需在不同的滞时下对JSSI的自相关（Autocorrelation, AC）以及JSSI与SPI的互相关（Cross-correlation, CC）进行分析。AC值越高,表明JSSI对干旱的记忆性越好,而CC值越高,表明前期的气象干旱可以为后期的农业干旱提供有效的预测信息。首先,滞时（Lag）为1~3个月时,对6—8月JSSI的AC进行Pearson相关分析（图2）。由于计算时段长度为55年,所以5%的显著性水平对应的Pearson相关系数值为0.26。如图2所示,滞时为1~3个月时,6—8月的AC值在中国的大部分区域均在0.5以上,表明JSSI对农业干旱的记忆性较好。在滞时为2~3个月时,在部分沙漠地区如新疆南部、青海西部以及内蒙古西部等的AC值多在0.5以下,但大多仍呈显著正相关。因此,AC分析表明JSSI的持续性可以为农业干旱预测提供有效的信息。

图2

新窗口打开|下载原图ZIP|生成PPT
图21961—2015年6—8月滞时1~3个月时JSSI自相关系数AC的空间分布

注：基于自然资源部标准地图服务网站审图号GS(2020)4630号标准地图制作,底图无修改。
Fig. 2Autocorrelation (AC) of the JSSI for the 1- to 3-month time lags from June to August in 1961-2015

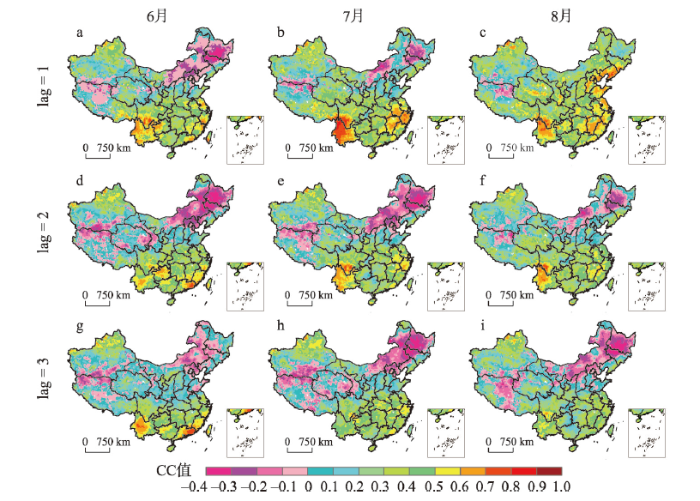
当滞时为1~3个月时,进一步对6—8月JSSI和SPI之间的CC进行Pearson相关分析。如图3所示,在大部分区域,JSSI和SPI呈显著正相关,表明前期的气象干旱对后期的农业干旱有较大影响。除图3c外,如在东北地区以及内蒙古的大部分区域,CC值小于0且呈显著负相关,可能是由于降水不足（气象干旱）往往伴随着温度升高,这有助于冰雪融化或季节性冻土解冻等,使其土壤水分得到补充。

图3

新窗口打开|下载原图ZIP|生成PPT
图31961—2015年6—8月滞时1~3个月时SPI与JSSI互相关系数CC的空间分布

注：基于自然资源部标准地图服务网站审图号GS(2020)4630号标准地图制作,底图无修改。
Fig. 3Cross-correlation between the SPI and JSSI for the 1- to 3-month time lags from June to August in 1961-2015

4.3 农业干旱条件预测

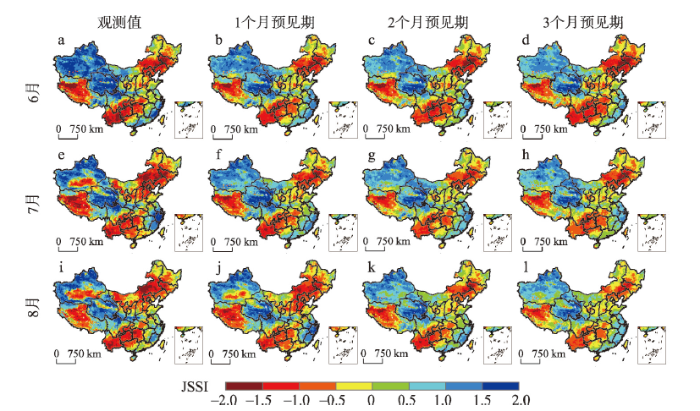
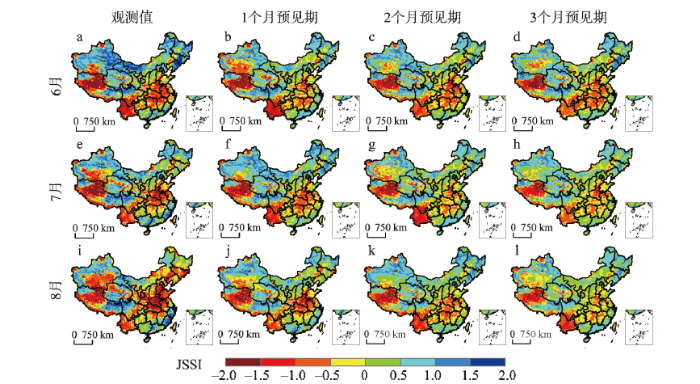
图2和图3的分析结果表明,前期的气象干旱和农业干旱的持续性可以为预见期的农业干旱提供有效的预测信息。因此,考虑预见期为1~3个月,利用MG模型并采用留一交叉验证法^{[16, 32]},对1961—2015年中国6—8月的JSSI进行预测,取-0.5作为发生农业干旱的阈值。以2010年夏季在中国西南地区和东北地区等发生的严重干旱事件^[5,6,7]以及2014年中国共有26个省（自治区、直辖市）遭受旱灾^[8,9]为例进行分析。

如图4所示,不同预见期下6—8月JSSI的预测值和其对应的观测值都很好的反映了西南、东北、华北以及西藏等大部分区域严重的干旱事件,且其在空间分布上基本相似。以6月为例（图4a~4d）,预见期为1~2个月时,JSSI预测值的分布区域与观测值的展布范围基本一致,即使在预见期为3个月时,预测发生农业干旱事件的分布区域与观测到的干旱事件的范围仍吻合较好。但对于部分沙漠地区如新疆南部、内蒙古西部等（图4e~4l）,JSSI的预测值与其对应的观测值相差较大,这可能是由于这些区域的土壤水更多的依赖于大气凝结水,其对干旱的记忆性相对较差（图2）,也可能是由于CRU数据集中降水的模拟或GLDAS数据集中根区土壤水的模拟在这些区域存在较大偏差引起的。如图5所示,JSSI的观测值和预测值均很好的反映了2014年中国大范围内发生的干旱事件。仍以6月为例（图5a~5d）,预见期为1~2个月时,JSSI预测值的分布区域与观测值的展布范围基本一致。预见期为1个月时（图5b、5f、5j）,6—8月预测发生农业干旱事件的分布区域与观测到的发生农业干旱事件的范围基本吻合（图5a、5e、5i）。当预见期为3个月时,7—8月MG模型的预测性能有所降低（图5h、5l）。同样地,对于部分沙漠地区,MG模型对农业干旱的预测效果较差。

图4

新窗口打开|下载原图ZIP|生成PPT
图42010年6—8月预见期1~3个月下JSSI的观测值与MG模型预测值的空间分布

注：基于自然资源部标准地图服务网站审图号GS(2020)4630号标准地图制作,底图无修改。
Fig. 4The JSSI observation values vs. 1- to 3-month lead prediction values from June to August in 2010

图5

新窗口打开|下载原图ZIP|生成PPT
图52014年6—8月预见期1~3个月下JSSI的观测值与MG模型预测值的空间分布

注：基于自然资源部标准地图服务网站审图号GS(2020)4630号标准地图制作,底图无修改。
Fig. 5The JSSI observation values vs. 1- to 3-month lead prediction values from une to August in 2014

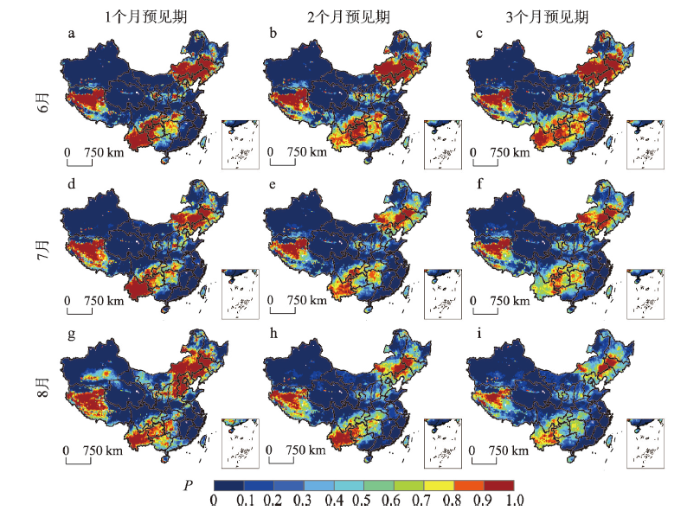
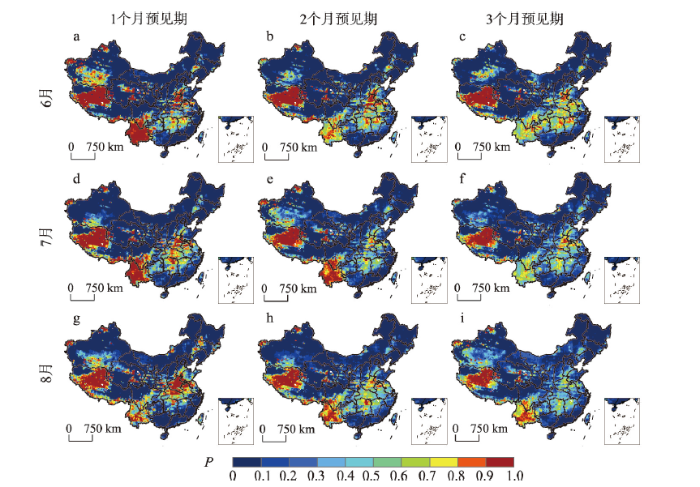
MG模型可以用来预测发生农业干旱事件（JSSI ＜ -0.5）的概率。以2010年和2014年为例,基于MG模型由公式（12）预测6—8月发生JSSI ＜ -0.5的概率（图6、图7）。在不同的预见期下,2010年6—8月预测JSSI ＜ -0.5发生概率较高的区域与图4a、4e、4i中干旱事件的分布区域吻合较好,如东北地区、西南地区、西藏以及内蒙古东部等。预测JSSI ＜-0.5发生概率接近于0的区域,可以反映该区域为无旱或湿润状态。同样地,在沙漠地区的预测结果较差。如图7所示,2014年6—8月预测JSSI ＜ -0.5发生概率较高的区域与图5a、5e、5i中干旱事件的分布范围基本一致,主要集中在华北、西南以及西藏等大部分区域。在华北地区预见期为3个月时,MG模型预测其发生农业干旱的概率减小（图7c、7f、7i）,表明在该区域MG模型的预测性能有所下降,但MG模型预测其发生农业干旱的概率仍大于0.4。

图6

新窗口打开|下载原图ZIP|生成PPT
图62010年6—8月预见期1~3个月下JSSI < -0.5的预测概率空间分布

注：基于自然资源部标准地图服务网站审图号GS(2020)4630号标准地图制作,底图无修改。
Fig. 6Prediction probability (JSSI < -0.5) of the 1- to 3-month lead predictions from June to August in 2010

图7

新窗口打开|下载原图ZIP|生成PPT
图72014年预见期1~3个月下6—8月JSSI < -0.5的预测概率空间分布

注：基于自然资源部标准地图服务网站审图号GS(2020)4630号标准地图制作,底图无修改。
Fig. 7Prediction probability (JSSI < -0.5) of the 1- to 3-month lead predictions from June to August of 2014 in China

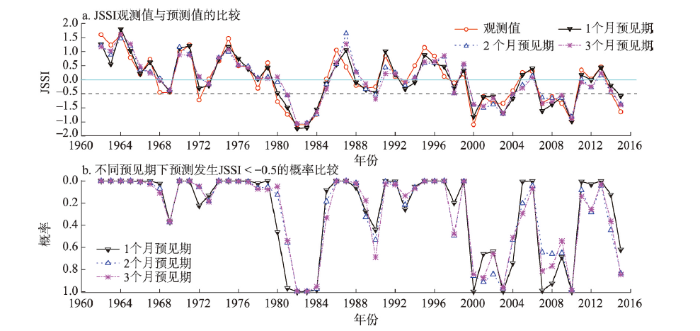
预见期为1~3个月时,以栅格（120°E, 42°N）7月的农业干旱预测为例,将MG模型得到的1962—2015年JSSI的预测值与其对应的观测值进行比较（图8a）以及得到相应的预测JSSI ＜ -0.5发生的概率（图8b）。如图8a所示,预见期为1个月时,7月JSSI的预测值与观测值对应最好,随着预见期的延长,吻合程度有所降低,但仍能捕捉到主要的干旱事件,如1982—1984年7月、2000年7月和2010年7月等。同时在不同的预见期下,当JSSI的观测值小于-0.5时（图8a）,预测其发生农业干旱（JSSI ＜ -0.5）的概率明显增大（图8b）,且对严重的干旱事件（图8a中的异常低值点）,预测其发生JSSI ＜ -0.5的概率在不同的预见期下都接近于1（图8b）,表明MG模型在长预见期下仍能很好的预测到严重的干旱事件。当JSSI的观测值大于0时,在不同的预见期下,预测其发生农业干旱的概率接近于0,表明其发生农业干旱的可能性非常小,这与实际情况基本相符。

图8

新窗口打开|下载原图ZIP|生成PPT
图81962—2015年7月在栅格(120°E, 42°N)上预见期1~3个月下MG模型JSSI的预测值

Fig. 8The predictions of the JSSI with the 1- to 3-month lead for July in 1962-2015 in the grid (120°E, 42°N)

4.4 MG模型预测性能评价

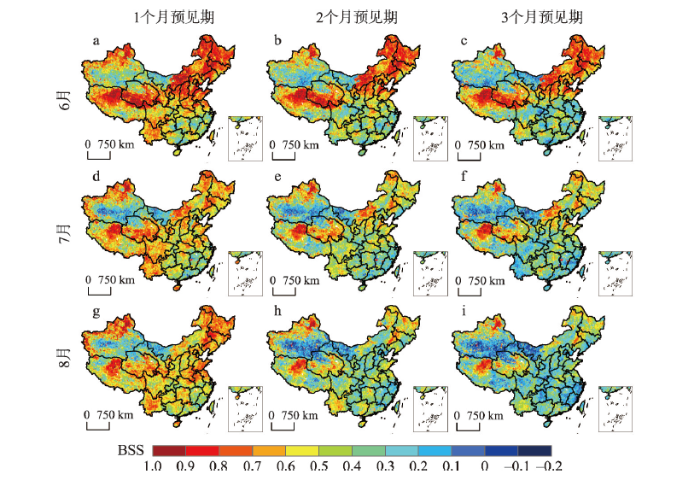
以随机预测作为参考,当预见期为1~3个月时,6—8月BSS的空间分布如图9所示,在大部分区域BSS > 0,表明MG模型的预测性能较好。预见期为1个月时,在大部分区域BSS > 0.5,MG模型的预测性能明显优于随机预测（图9a、9d、9g）。随着预见期的延长,BSS > 0.5的区域有所减少,如预见期为3个月时,在大部分区域BSS > 0.2（图9c、9f、9i）,表明MG模型的预测性能有所降低。此外,预见期为1~3个月时,6月MG模型的预测性能总体上优于7—8月（图9a~9c）,特别是在东北、华北地区和青藏高原等大部分区域。不同预见期下,在新疆南部、青海西部以及内蒙古西部等部分沙漠地区BSS ＜ 0,表明MG模型在这些区域的预测性能较差。

图9

新窗口打开|下载原图ZIP|生成PPT
图91961—2015年6—8月1~3个月预见期下BSS的空间分布

注：基于自然资源部标准地图服务网站审图号GS(2020)4630号标准地图制作,底图无修改。
Fig. 9BSS of the JSSI predictions with the 1- to 3-month lead from June to August in 1961-2015

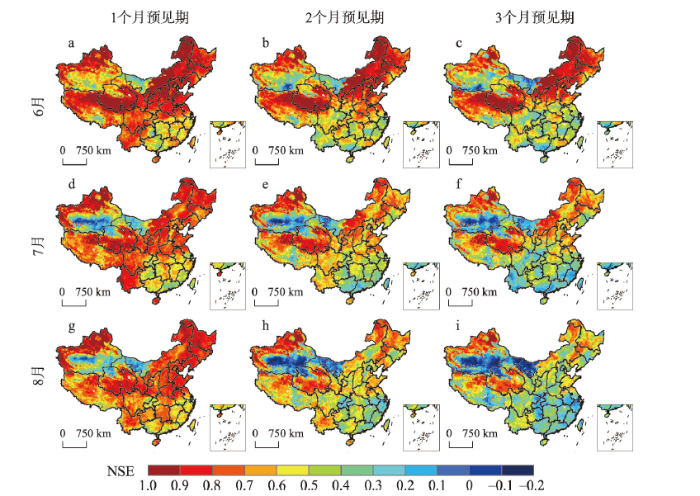
不同预见期下6—8月NSE的空间分布如图10所示,大部分区域NSE > 0.3,特别是在东北、华北地区和青藏高原的大部分区域,NSE达到0.5以上（图10a~10h）。而在新疆南部、青海西部以及内蒙古西部等部分沙漠地区NSE ＜ 0,表明MG模型在这些区域的预测性能较差,这与图9的分析结果基本一致。预见期为2~3个月时,在部分南方湿润区,NSE大都介于0.3~0.5,表明在这些区域农业干旱对气象干旱的响应以短滞时为主。总之,由BSS和NSE的预测性能评价结果来看（图9、图10）,预见期为1~3个月时,MG模型能够对中国大部分区域6—8月的农业干旱作出可靠的预测。

图10

新窗口打开|下载原图ZIP|生成PPT
图101961—2015年6—8月1~3个月预见期下NSE的空间分布

注：基于自然资源部标准地图服务网站审图号GS(2020)4630号标准地图制作,底图无修改。
Fig. 10NSE of the JSSI predictions with the 1- to 3-month lead from June to August in 1961-2015

为了进一步对MG模型的预测性能进行评价,分别计算图9、图10中BSS ≥ 0.5和NSE ≥ 0.5的面积比例。如表1所示,预见期为1个月时,6—8月BSS ≥ 0.5和NSE ≥ 0.5的面积比例最大,预测性能最好,其中6—8月BSS ≥ 0.5、NSE ≥ 0.5的面积占比分别为0.714和0.903、0.642和0.829、0.640和0.837。随着预见期的延长,BSS ≥ 0.5和NSE ≥ 0.5面积比例逐渐减小,表明预测性能有所降低。当预见期相同时,6—8月BSS ≥ 0.5和NSE ≥ 0.5的面积比例总体上呈逐渐减小的变化趋势。

Tab. 1
表1
表11961—2015年1~3个月预见期下6—8月BSS ≥ 0.5和NSE ≥ 0.5的面积占比
Tab. 1The proportions of the total area for the 1- to 3-month lead JSSI predictions with obtained BSS ≥ 0.5 and NSE ≥ 0.5 for June to August in 1961-2015

BSS ≥ 0.5	预见期			NSE ≥ 0.5	预见期
BSS ≥ 0.5	1个月	2个月	3个月	NSE ≥ 0.5	1个月	2个月	3个月
6月	0.714	0.556	0.489	6月	0.903	0.763	0.672
7月	0.642	0.386	0.309	7月	0.829	0.662	0.530
8月	0.640	0.309	0.190	8月	0.837	0.592	0.406

新窗口打开|下载CSV

5 结论与讨论

利用GLDAS数据集中的月根区土壤湿度数据和CRU数据集中的月降水数据,计算得到了JSSI和6个月尺度的SPI,并分别用来表征农业干旱和气象干旱。本文以前期的SPI和JSSI的持续性作为预测因子,基于MG模型对6—8月的农业干旱进行预测并采用BSS和NSE对其预测性能进行评价。主要得到以下结论：

（1）利用经验Kendall Copula分布函数将1个月、3个月、6个月、9个月和12个月时间尺度的SSI结合起来得到JSSI并用来表征农业干旱,能够及时地捕捉到短时间尺度下的新发展干旱和长时间尺度下的持续性干旱,可以客观地对农业干旱的综合状况作出评价。

（2）预见期为1~3个月时,6—8月JSSI的预测值和其对应的观测值在空间分布上基本相似,且预测发生农业干旱（JSSI ＜ -0.5）概率较高的区域与观测到的实际发生农业干旱的区域在空间分布上基本吻合。其中,预见期为1~2个月时,农业干旱的预测值及其预测概率与观测值在空间分布上吻合较好。但对部分沙漠地区如新疆南部、青海西部以及内蒙古西部等,MG模型的预测结果较差,可能是由于这些区域的土壤水更多的依赖于大气凝结水引起的。

（3）BSS和NSE的预测性能评价结果表明,除新疆南部、青海西部以及内蒙古西部等沙漠地区外,MG模型能够对中国大部分区域6—8月的农业干旱作出可靠的预测。

降水不足和高温是土壤水分散失（农业干旱）的2个重要的驱动因素,且作物和植被的生长在很大程度上取决于水热条件。在进行农业干旱预测时考虑温度的影响有望提高模型的预测精度,但如何在高维情形下（≥ 4维）有效地构建预测模型仍存在不少的挑战。中国幅员辽阔、气候类型变化多样,各气候区之间气候环境差异较大,在不同的气候区采用同一时间尺度的SPI在表征气象干旱时可能存在差异。因此,在不同的气候区关于SPI时间尺度的选取问题还有待进一步研究。

参考文献原文顺序
文献年度倒序
文中引用次数倒序
被引期刊影响因子

[1]

Hao Z

, Hao F

, Singh V

, et al. Probabilistic prediction of hydrologic drought using a conditional probability approach based on the meta-Gaussian model
Journal of Hydrology, 2016,542:772-780.

[本文引用: 11]

[2]

Hao Z

, Hao F

, Singh V

, et al. An integrated package for drought monitoring, prediction and analysis to aid drought modeling and assessment
Environmental Modelling & Software, 2017,91:199-209.

[本文引用: 2]

[3]

Hao Z

, Hong

, Xia Y

, et al. Probabilistic drought characterization in the categorical form using ordinal regression
Journal of Hydrology, 2016,535:331-339.

[本文引用: 1]

[4]

Hao Z

, Singh V

, Xia Y

. Seasonal drought prediction: Advances, challenges, and future prospects
Reviews of Geophysics, 2018,56(1):108-141.

[本文引用: 1]

[5]

Li X

, Li

, Chen A

, et al. The impact of the 2009/2010 drought on vegetation growth and terrestrial carbon balance in Southwest China
Agricultural and Forest Meteorology, 2019,269/270:239-248.

[本文引用: 2]

[6]

Zeng Z

, Wu W

, Li Z

, et al. Agricultural drought risk assessment in Southwest China
Water, 2019,11(5):1064. DOI: 10.3390/w11051064.

[本文引用: 2]

[7]

Wang

, Yu

, Yang M

, et al. A drought index: The standardized precipitation evapotranspiration runoff index
Journal of Hydrology, 2019,571:651-668.

[本文引用: 3]

[8]

Zhang

Gengxi

, Su

Xiaoling

, Hao

Lina

, et al. Response of vegetation to drought based on NDVI and scPDSI data sets from 1982 to 2015 across China
Transactions of the Chinese Society of Agricultural Engineering, 2019,35(20):145-151.

[本文引用: 2]

[ 张更喜, 粟晓玲, 郝丽娜, 等. 基于NDVI和scPDSI研究1982—2015年中国植被对干旱的响应
农业工程学报, 2019,35(20):145-151.]

[本文引用: 2]

[9]

Qin

, Zhang

Qiang

, Huang

Qingzhong

, et al. Nonparametric integrated agro-meteorological drought monitoring in China: New monitoring technique and applicability
Acta Geographica Sinica, 2018,73(1):67-80.

[本文引用: 4]

[ 李勤, 张强, 黄庆忠, 等. 中国气象农业非参数化综合干旱监测及其适用性
地理学报, 2018,73(1):67-80.]

[本文引用: 4]

[10]

Amrit

, Mishra S

, Pandey R

, et al. Standardized precipitation index-based approach to predict environmental flow condition
Ecohydrology, 2019,12(7):e2127. DOI: 10.1002/eco.2127.

[本文引用: 1]

[11]

Vicente-Serrano S

, Beguería

, López-Moreno J

. A multiscalar drought index sensitive to global warming: The standardized precipitation evapotranspiration index
Journal of Climate, 2010,23(7):1696-1718.

[本文引用: 1]

[12]

Yu H

, Zhang

, Xu C

, et al. Modified palmer drought severity index: Model improvement and application
Environment International, 2019,130:104951. DOI: 10.1016/j.envint.2019.104951.

URLPMID:31272019 [本文引用: 1]

[13]

Xu Y

, Wang

, Ross K

, et al. Standardized soil moisture index for drought monitoring based on soil moisture active passive observations and 36 years of north american land data assimilation system data: A case study in the Southeast United States
Remote Sensing, 2018,10(3):301. DOI: 10.3390/rs10020301.

[本文引用: 1]

[14]

Sattar M

, Lee J

, Shin J

, et al. Probabilistic characteristics of drought propagation from meteorological to hydrological drought in south Korea
Water Resources Management, 2019,33(7):2439-2452.

[本文引用: 2]

[15]

Gevaert A

, Veldkamp T

I E

, Ward P

. The effect of climate type on timescales of drought propagation in an ensemble of global hydrological models
Hydrology and Earth System Sciences, 2018,22(9):4649-4665.

[本文引用: 1]

[16]

Hao Z

, Hao F

, Singh V

, et al. Statistical prediction of the severity of compound dry-hot events based on El Ni?o-Southern Oscillation
Journal of Hydrology, 2019,572:243-250.

[本文引用: 7]

[17]

Hao Z

, Hao F

, Singh V

, et al. Quantifying the relationship between compound dry and hot events and El Ni?o-southern Oscillation (ENSO) at the global scale
Journal of Hydrology, 2018,567:332-338.

[本文引用: 2]

[18]

Byakatonda

, Parida B

, Kenabatho P

. Relating the dynamics of climatological and hydrological droughts in semiarid Botswana
Physics and Chemistry of the Earth, 2018,105:12-24.

[本文引用: 1]

[19]

Sattar M

, Kim

T-W

. Probabilistic characteristics of lag time between meteorological and hydrological droughts using a Bayesian model. Terrestrial,
Atmospheric and Oceanic Sciences, 2018,29(6):709-720.

[本文引用: 1]

[20]

Hao Z

, Aghakouchak

, Nakhjiri

, et al. Global integrated drought monitoring and prediction system
Scientific Data, 2014,1:140001. DOI: 10.1038/sdata.2014.1.

[本文引用: 2]

[21]

Kao S

, Govindaraju R

. A copula-based joint deficit index for droughts
Journal of Hydrology, 2010,380(1/2):121-134.

[本文引用: 4]

[22]

Gao C

, Chen H

, Sun S

, et al. A potential predictor of multi-season droughts in southwest China: Soil moisture and its memory
Natural Hazards, 2018,91(2):553-566.

[本文引用: 1]

[23]

Hao Z

, Hao F

, Singh V

, et al. Quantitative risk assessment of the effects of drought on extreme temperature in eastern China
Journal of Geophysical Research: Atmospheres, 2017,122(17):9050-9059.

[本文引用: 1]

[24]

Hao Z

, Hao F

, Singh V

, et al. A multivariate approach for statistical assessments of compound extremes
Journal of Hydrology, 2018,565:87-94.

[本文引用: 4]

[25]

Gringorten I

. A plotting rule for extreme probability paper
Journal of Geophysical Research, 1963,68(3):813-814.

[本文引用: 1]

[26]

Bogner

, Pappenberger

, Cloke H

. Technical note: The normal quantile transformation and its application in a flood forecasting system
Hydrology and Earth System Sciences, 2012,16(4):1085-1094.

[本文引用: 1]

[27]

Mirabbasi

, Anagnostou E

, Fakheri-Fard

, et al. Analysis of meteorological drought in northwest Iran using the Joint Deficit Index
Journal of Hydrology, 2013,492:35-48.

[本文引用: 3]

[28]

Genest

, Rémillard

, Beaudoin

. Goodness-of-fit tests for copulas: A review and a power study
Insurance: Mathematics and Economics, 2009,44(2):199-213.

[本文引用: 1]

[29]

Kelly K

, Krzysztofowicz

. A bivariate meta-Gaussian density for use in hydrology
Stochastic Hydrology and Hydraulics, 1997,11(1):17-31.

[本文引用: 2]

[30]

Wilks D

. Sampling distributions of the Brier score and Brier skill score under serial dependence
Quarterly Journal of the Royal Meteorological Society, 2010,136(653):2109-2118.

[本文引用: 3]

[31]

Hao Z

, Singh V

. Review of dependence modeling in hydrology and water resources
Progress in Physical Geography: Earth and Environment, 2016,40(4):549-578.

[本文引用: 1]

[32]

Bayat

, Nasseri

, Zahraie

. Identification of long-term annual pattern of meteorological drought based on spatiotemporal methods: Evaluation of different geostatistical approaches
Natural Hazards, 2015,76(1):515-541.

[本文引用: 1]