基于多源遥感影像的洞庭湖地形提取方法

删除或更新信息，请邮件至freekaoyan#163.com(#换成@)

本站小编 Free考研考试/2021-12-29

隆院男¹^,², 闫世雄¹, 蒋昌波^,¹^,², 吴长山²^,³, 李志威¹^,², 唐蓉¹

1.长沙理工大学水利工程学院,长沙 410114

2.洞庭湖水环境治理与生态修复湖南省重点实验室,长沙 410114

3.美国威斯康星大学密尔沃基分校地理系,美国密尔沃基 WI53211

A new method for extracting lake bathymetry using multi-temporal and multi-source remote sensing imagery: A case study of Dongting Lake

LONG Yuannan¹^,², YAN Shixiong¹, JIANG Changbo^,¹^,², WU Changshan²^,³, LI Zhiwei¹^,², TANG Rong¹

1.School of Hydraulic Engineering, Changsha University of Science & Technology, Changsha 410114, China

2.Key Laboratory of Dongting Lake Aquatic Eco-Environmental Control and Restoration of Hunan Province, Changsha 410114, China

3.Department of Geography, University of Wisconsin-Milwaukee, Milwaukee, WI 53211, USA

通讯作者: 蒋昌波(1970-), 男, 陕西石泉人, 博士, 教授, 研究方向为河流动力过程及其模拟技术。E-mail: jiangchb@csust.edu.cn

收稿日期:2018-04-3修回日期:2019-03-11网络出版日期:2019-07-25

基金资助:

国家自然科学基金项目.91647118
国家自然科学基金项目.51809020
湖南省自然科学基金项目.2016JJ3011
湖南省自然科学基金项目.2018JJ3535

Received:2018-04-3Revised:2019-03-11Online:2019-07-25

Fund supported:

Natural Science Foundation of China.91647118
Natural Science Foundation of China.51809020
Natural Science Foundation of Hunan Province.2016JJ3011
Natural Science Foundation of Hunan Province.2018JJ3535

作者简介 About authors
隆院男(1985-),男,湖南宁乡人,博士,讲师,研究方向为水文遥感和流域水文模型E-mail:lynzhb@csust.edu.cn。

摘要
湖底地形数据是湖泊流域规划与治理、湖区冲淤变化研究、水资源利用和生态环境保护的重要基础。但传统的大型湖泊湖底地形数据获取手段耗时长、投入大,因此,有必要研究一种基于遥感影像快速获取湖底地形数据的方法。本文以洞庭湖为研究对象,采用Landsat和MODIS系列遥感影像提取湖区边界,基于趋势面分析法和克里金插值法,反演湖区边界各点对应的水位,将带有水位信息的边界点作为高程点实现湖底地形反演,进一步用实测湖底地形验证反演方法的可靠性。研究结果表明,克里金插值法水位反演效果较好,交叉验证的误差标准平均值在0.2 m以内,水位样本点分布较多处,基于克里金法的地形反演绝对误差在1 m以内。本文利用湖泊淹没区域变化的特点快速获取湖底地形,对湖区演变分析、综合治理与保护等具有重要意义。
关键词： 湖底地形;水位;遥感影像;湖泊边界;水位反演;洞庭湖

Abstract

Lake bathymetry can provide abundant information for basin planning and governance, watershed erosion and siltation management, water resource utilization, as well as environmental protection. In particular, lake bathymetry is essential for lake development and conservation, and is also closely related to sediment deposition and removal. A number of sounding techniques, such as single-beam sonar sounding, multi-beam sonar sounding, and unmanned ship sounding, have been applied to extract underwater topography of lakes. These techniques, albeit with high measurement accuracy, are time-consuming and costly. Therefore, it is of great need to develop a simple and cost-effective method. To reach this goal, recent advances of remote sensing technologies provide an alternative means of accurately measuring lake bathymetry information. Taking Dongting Lake as the study area, this paper estimated the lake bathymetry through extracting the boundaries of lake areas using multi-temporal Landsat and MODIS image series. In particular, the water level corresponding to each reference point of the lake boundary is retrieved based on trend surface analysis and kriging interpolation technology. Then the water levels of these points are regarded as the elevation points to retrieve the landform of the lakebed of the Dongting Lake. The reliability and accuracy of the developed methods were assessed through the comparsion with the actual measurements. Results indicate that the kriging interpolation technology performs well, with the average of cross-validated error target less than 0.2 meter, and the retrieval error of lake boundary with more reference points less than 1 meter. This paper suggests that an improved method for accurately and rapidly extracting lake bathymetry information can be achieved through examining the changes of water levels. This method might be of great significance for further study on lake evolution, lake development planning, and water ecological protection.

Keywords：lake bathymetry;water level;remote sensing imagery;lake boundary;water retrieval;Dongting Lake

PDF (0KB)元数据多维度评价相关文章导出EndNote|Ris|Bibtex 收藏本文
本文引用格式
隆院男, 闫世雄, 蒋昌波, 吴长山, 李志威, 唐蓉. 基于多源遥感影像的洞庭湖地形提取方法. 地理学报[J], 2019, 74(7): 1467-1481 doi:10.11821/dlxb201907015
LONG Yuannan. A new method for extracting lake bathymetry using multi-temporal and multi-source remote sensing imagery: A case study of Dongting Lake. Acta Geographica Sinice[J], 2019, 74(7): 1467-1481 doi:10.11821/dlxb201907015

随着河长制、湖长制的深入实施和河湖综合治理的推进,各类水域的规划建设不断增加,对待开发水域水下地形的勘测是一项重要工作^[1,2]。对内陆湖泊而言,一方面,基于实测地形数据,开展湖泊演变过程和冲淤变化研究,探求湖泊调蓄能力和江湖连通性的变化规律^[3,4,5,6];另一方面,为开展水动力计算和水质建模等研究提供基础资料^[7],指导湖区规划和生态环境保护^[8]。可见,水下地形数据既是规划设计必不可少的基础数据,也是研究湖泊诸多问题的基础。

针对水下地形勘测,基于专业设备的测深技术,如人工水深测量技术、单波束声呐测深技术以及多波束声呐测深技术等,对水下地形进行细致勘测,此类方法测量精度高,但处理周期长、操作难度大^[9,10,11]。基于光学遥感影像,利用不同深度水体遥感图像的色度不同这一特点,进行水下地形反演,此方法操作简单且处理周期较短,但在浑浊水体应用的效果不佳^[12]。部分****通过遥感影像及测高卫星,提取不同水位时的水域边界,以提取的水域边界作为相应水位高度的等高线,生成数字高程模型^{[13,14,15,16]},目前,大多应用Landsat系列或MODIS系列遥感影像进行水域边界提取,以局部水位代表整个水域水位来标定水域边界高程。然而,采用局部水位直接标定时,对于大跨度湖泊湖底地形反演可能产生较大误差,Feng等^[1]用此原理反演鄱阳湖湖底地形时,认为湖区内纬度跨度较大的两点,存在水位梯度,单一水位站的水位数据无法代表整个湖区水位,因此,Feng等建立了水位与纬度相关关系,并将所得关系应用于整个湖区,确定水域边界的水位,最终得到了鄱阳湖湖底地形。

前人研究为湖区边界提取及水位反演提供了思路,而这些研究多选取某一水文站水位为代表水位,边界提取大多仅应用Landsat系列或MODIS系列影像,缺乏足够代表性。洞庭湖覆盖范围广,采用单一水文站的水位不能较好的反演湖区边界水位,同时,其水位与经度和纬度均存在一定的相关关系。因此,本文在Feng等^[1]提出方法的基础上,通过收集洞庭湖10个水文站点水位资料,基于Landsat和MODIS系列遥感影像多源数据,提取洞庭湖边界,综合考虑水位与经度和纬度的相关关系,应用趋势面分析法及克里金插值法,反演水域边界各点水位,开展洞庭湖湖底地形的提取和验证研究。

1 研究区概况

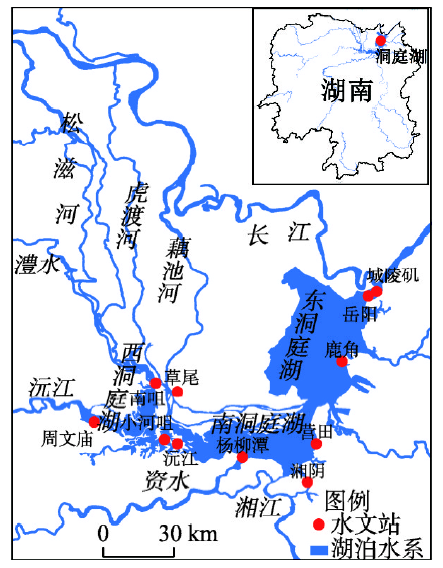
洞庭湖位于长江中游南岸,跨湘、鄂两省,位于27°39'N~30°25'N、111°19'E~113°34'E之间,为中国第二大淡水湖。其由东、南、西3个湖泊组成,北面的松滋河、虎渡河、藕池河分别从松滋、太平、藕池三口分泄长江中游水沙入湖,即三口水系。南、西两面有湘江、资水、沅江、澧水四水入湖,四水水系入湖后,经湖泊调蓄,自湖口城陵矶（七里山）泄入长江,是典型的吞吐型湖泊（图1）。

图1

新窗口打开|下载原图ZIP|生成PPT
图1研究区域及湖区主要控制站分布

Fig. 1Study area and hydrological station distribution

近几十年来,受四水以及长江三口分支入湖洪水和泥沙的影响,洞庭湖地形变化从未停止,加之人类活动如梯级水库、采砂和围垦,使洞庭湖区内湖底地形变化剧烈,洞庭湖面积和容积也随之改变,导致洞庭湖调节径流和调蓄洪水的能力减弱^[17,18]。洞庭湖区由于泥沙淤积加之人为影响,地形情况复杂,对湖底地形的勘测尤为困难,地形数据相对较少,因而通过遥感方法对洞庭湖的地形进行估算十分必要。

2 数据来源与处理

本文采用的数据包括多源遥感影像、实测水位以及实测湖底地形。多源遥感影像数据包括2003年Landsat 5、Landsat 7、MODIS 09GA以及MODIS 09GQ遥感影像。洞庭湖区横跨两幅 Landsat系列影像,编号分别为123/40、124/40,所需MODIS系列影像编号为h27v06（表1）;实测水位数据包括洞庭湖周边水文站、水位站2003年实测水位（日期与遥感影像获取时间一致,表1）,站点包括城陵矶、岳阳、鹿角、营田、湘阴、草尾、杨柳潭、沅水、南咀、小河咀10个站点,根据“洞庭湖区水文（位）站高程换算值表”将各个水文站冻结基面高程统一转换为黄海高程;实测湖底地形数据为洞庭湖湖区2003年实测1∶10000地形资料,通过ArcGIS 10.3软件Projections and Transformations工具将高程点坐标系统转换为WGS 84坐标系。

Tab. 1
表1
表1遥感影像数据获取日期及传感器
Tab. 1Date of the remote sensing image and the sensor

影像获取时间	卫星/传感器名称	影像获取时间	卫星/传感器名称
2003-01-17	Landsat 5/TM	2003-08-25	MODIS 09
2003-04-15	Landsat 5/TM	2003-09-06	Landsat 5/TM
2003-05-01	Landsat 5/TM	2003-09-12	MODIS 09
2003-07-04	Landsat 5/TM	2003-09-22	Landsat 5/TM
2003-07-14	MODIS 09	2003-09-30	Landsat 7/ETM+
2003-07-20	Landsat5/TM	2003-10-07	Landsat 7/ETM+
2003-07-23	MODIS 09	2003-10-16	Landsat 7/ETM+
2003-07-27	MODIS 09	2003-10-18	MODIS 09
2003-07-28	Landsat 7/ETM+	2003-10-24	Landsat 5/TM
2003-08-01	MODIS 09	2003-11-01	Landsat 7/ETM+
2003-08-06	MODIS 09	2003-12-27	Landsat 5/TM

新窗口打开|下载CSV

Landsat系列影像数据分辨率为30 m,利用ENVI 5.3.1图像处理软件进行处理,首先进行辐射定标和大气校正,再对图像进行裁剪和重采样。MODIS 09数据为地面Ⅱ级数据,一般可不做辐射定标和大气校正,但需进行坐标重投影,采用MRT工具或ENVI中MODIS-Conversion-Toolkit工具实现,重投影完成后,进一步将影像数据进行裁剪和重采样,完成对原始遥感影像数据的前期处理,方便后期的水体提取。

3 原理与方法

3.1 湖泊地形估算的原理

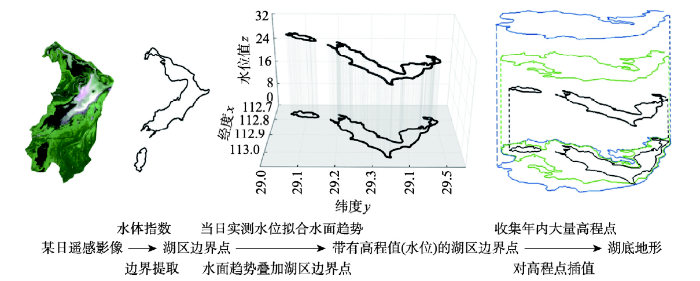
利用湖泊淹没区域快速变化的特点获取湖底地形。首先利用水体指数将水体凸现出来,提取当日湖区边界并转化为边界点;然后进行边界水位矫正反演,基于控制水文站点分布情况及当日水位数据,利用趋势面分析法及克里金插值法对当日湖区水面趋势进行模拟,将拟合的水面趋势与当日湖区边界点叠加,计算湖区边界点水位值,得到当日带有高程值（水位）的边界点,利用年内多日遥感影像可获取大量高程点,经过插值可得湖底地形（图2）。在湖底地形生成过程中,湖区边界提取和边界水位矫正反演的精度,直接影响最终地形的估算精度。

图2

新窗口打开|下载原图ZIP|生成PPT
图2地形反演原理示意图

Fig. 2Diagram of terrain computational principle

3.2 地形估算方法

由上述提取原理可知,湖底地形的估算精度取决于湖区边界提取精度与边界水位反演的精度,提高湖区边界提取精度主要从两个方面考虑：① 采用高分辨率的遥感影像数据,提高对细节地形的识别;② 寻找适合高分辨率影像的水体提取方法进行湖区边界的提取。针对水位反演结果的不确定性,本文采用趋势面分析法和克里金插值法反演水位,提高边界水位反演精度。

3.2.1 湖区边界提取本文采用水体指数法提取湖区边界,该方法操作简单且在实际应用中取得较好的效果。本文选取常用的3种水体指数（AWEI^[19]、NDWI^[20]、MNDWI^[21]）提取洞庭湖水域边界并分析3种水体指数在洞庭湖区的提取效果。

改进的水体指数AWEI：

（1）

AWE I_{ns h} = 4 \times (band 2 - band 5) - (0.25 \times band 4 + 2.75 \times band 7)

（2）

AWE I_{s h} = band 1 + 2.5 \times band 2 - 1.5 \times (band 4 + band 5) - 0.25 \times band 7

式中：AWEI_nsh表示剔除非水体像元,如建筑用地等的水体指数;AWEI_sh表示进一步剔除AWEI_nsh结果中与水体信息发生混淆的地物后的水体指数,如阴影等;band 1、band 2、band 4、band 5和band 7分别指Landsat影像的蓝光、绿光、近红外、短波红外1及短波红外2波段的反射率,对应于Landsat数据的1、2、4、5和7波段,对应于MOD09数据的3、4、2、6和7波段。

归一化差分植被指数NDWI：

（3）

NDWI = \frac{(Green - NIR)}{(Green + NIR)}

式中：Green、NIR分别指绿光波段、近红外波段的反射率,对应于Landsat数据的2波段、4波段;MOD09数据的4波段、2波段。

改进的归一化差分水体指数MNDWI：

（4）

MNDWI = \frac{(Green - MIR)}{(Green + MIR)}

式中：Green、MIR分别指绿光波段、短波红外波段的反射率,对应于Landsat数据的2波段、5波段;MOD09数据的4波段、6波段。

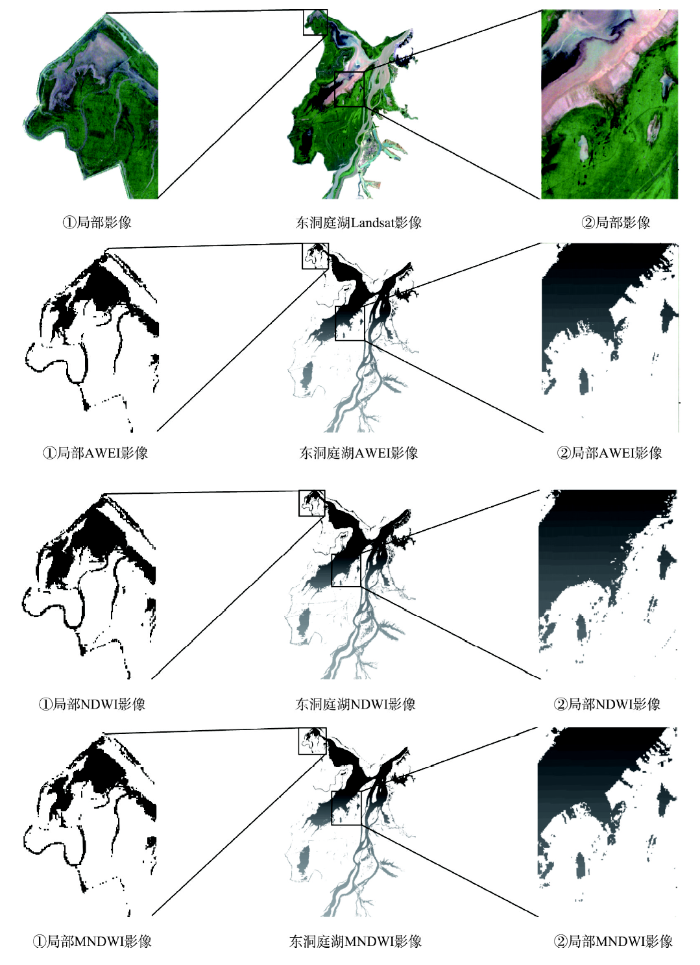
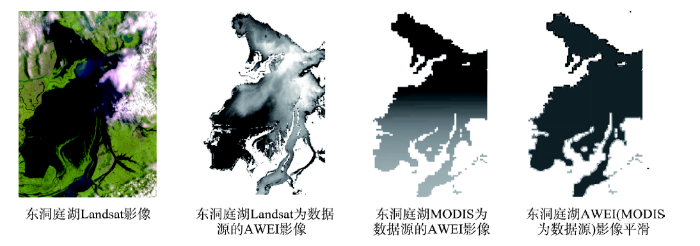
基于Landsat数据,采用3种水体指数提取东洞庭湖水体边界（图3）,通过观察总体、细节对比效果以及阈值选取的准确性,AWEI水体指数对洞庭湖区边界的提取效果较好。考虑到Landsat时间分辨率较低,尤其是洞庭湖区6-8月阴雨天较多,Landsat的低时间分辨率导致在此期间可用图像较少,部分图像因云量过多无法使用。采用6-8月多阴雨期的MODIS图像进行平滑处理,来补充同期缺失的Landsat影像。分析结果表明,由于洞庭湖6-8月水位较高,大部分湖底地形已被淹没,需要反映的边界细节特征减少,提高了MODIS数据的可用性,高水位时MODIS数据能够满足生成地形的精度要求（图4）。

图3

新窗口打开|下载原图ZIP|生成PPT
图3东洞庭湖3种水体指数提取效果对比图

Fig. 3Comparison of the extraction results about three kinds of water index in East Dongting Lake

图4

新窗口打开|下载原图ZIP|生成PPT
图4东洞庭湖遥感影像处理对比图

Fig. 4The comparison of the processing results in East Dongting Lake

3.2.2 边界水位矫正反演本文分别采用趋势面分析法和克里金插值法进行洞庭湖边界水位反演,并探讨两种方法在湖底地形反演时的精度。

（1）趋势面分析法。

趋势面分析法是一种整体内插算法,利用插值函数在区域内进行特征拟合,插值算法包括多项式趋势面拟合、傅里叶分析及小波变换等^[22],其中较为常用是多项式趋势面拟合,即用多项式对目标的空间分布进行分析,用多项式代表的曲面对变量真实分布情况进行拟合,趋势面模型的多项式形式根据阶次不同分为一次多项式模型、二次多项式模型等^[23]。本文采用该方法模拟不同湖区水位在经纬度影响下的空间分布及变化趋势。Feng等^[1]在反演鄱阳湖湖底地形时,基于控制水文站水位及站点纬度,建立水位与纬度的函数相关关系进行边界水位反演,最终得到了鄱阳湖湖底地形。

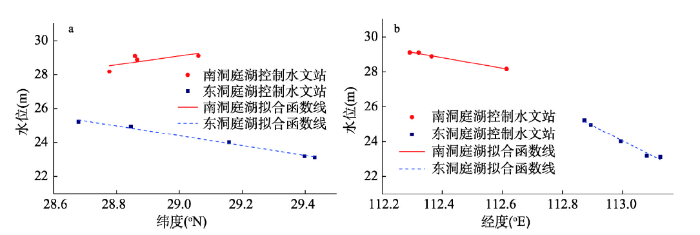
基于Feng等^[1]方法,对水位与经度、纬度的相关性进行分析（图5）。由图5可知,由于洞庭湖形态特点与鄱阳湖不同,湖泊西南部为上游,东北部为下游,上下游之间水位比降显著^[24],洞庭湖水位与经、纬度都存在一定相关关系;同时,由于洞庭湖东、南湖区水力条件不同^[25],在不同湖区,水位与经纬度之间的相关关系也不同。

图5

新窗口打开|下载原图ZIP|生成PPT
图5水位与经纬度相关关系图

Fig. 5The relationship between the water level and the geographical factor

考虑到洞庭湖水面趋势变化较为缓和,本文趋势面模型采用一次多项式模型进行水位反演,模型为：

（5）

z_{1} = A_{1} x_{1} + B_{1} y_{1} + C_{1}

（6）

z_{2} = A_{2} x_{2} + B_{2} y_{2} + C_{2}

式中：x₁表示东洞庭湖水位点经度;y₁表示东洞庭湖水位点纬度;z₁表示东洞庭湖水位点水位值;x₂表示南洞庭湖水位点经度;y₂表示南洞庭湖水位点纬度;z₂表示南洞庭湖水位点水位值;A₁、B₁、C₁表示东洞庭趋势面分析参数;A₂、B₂、C₂表示南洞庭趋势面分析参数。

为检验趋势面模型的拟合程度,本文应用拟合度系数R²测定回归模型拟合情况^[22]：

（7）

R^{2} = \frac{S S_{R}}{S S_{T}} = \frac{\overset{n}{\sum_{i = 1}} {({\overset{?}{z}}_{i} - \overset{?}{z})}^{2}}{\overset{n}{\sum_{i = 1}} {(z_{i} - {\overset{?}{z}}_{i})}^{2} + \overset{n}{\sum_{i = 1}} {({\overset{?}{z}}_{i} - \overset{?}{z})}^{2}} = 1 - \frac{S S_{D}}{S S_{T}}

式中：SS_D为剩余平方和,表示随机因素对因变量z的离差的影响;SS_R为回归平方和,表示自变量对因变量z的离差的总影响;R²的数值越大,表明趋势面拟合效果越好。

由表2可知,趋势面分析法在不同湖区都有较好的水位拟合效果,拟合度系数多在0.9以上。相比于Feng等^[1]的水位反演方法,趋势面分析法同时考虑经、纬度对水位反演的影响,以当日实测水位数据为基础,可以更好地描述湖区水位的空间分布及变化趋势;通过拟合度分析,最终拟合度系数也普遍高于Feng等^[1]在鄱阳湖水位反演中的线性回归拟合系数,证明趋势面分析法在反演真实水位变化上有较好效果。

Tab. 2
表2
表2趋势面分析参数表
Tab. 2Parameters of trend surface analysis

日期	A₁	B₁	C₁	R²	日期	A₂	B₂	C₂	R²
2003-01-17	-0.865	-4.520	11.635	0.995	2003-01-17	-8.248	-4.798	40.726	0.909
2003-04.15	-1.045	-5.069	12.043	0.996	2003-04-15	-5.135	-3.015	25.268	0.981
2003-05-01	-3.031	-1.900	17.566	0.996	2003-05-01	-7.684	-2.517	34.238	0.951
2003-07-04	-0.692	-0.372	4.078	0.974	2003-07-04	-1.334	1.855	4.299	0.934
2003-07-14	-1.294	-0.393	5.957	0.965	2003-07-14	-1.118	2.205	2.950	0.868
2003-07-23	-0.732	-0.177	3.878	0.984	2003-07-23	-0.713	2.440	1.337	0.846
2003-07-27	-1.452	-0.199	6.726	0.986	2003-07-27	-0.940	1.739	2.875	0.866
2003-07-28	-1.582	-0.162	7.252	0.965	2003-07-28	-0.928	1.648	2.935	0.896
2003-08-06	-0.802	-0.176	4.521	0.988	2003-08-06	-1.941	1.916	6.932	0.953
2003-08-25	-0.010	-0.316	1.397	0.974	2003-08-25	-2.900	2.259	10.853	0.970
2003-09-22	-0.941	0.014	133.436	0.984	2003-09-22	-1.220	3.262	71.385	0.901
2003-10-16	-0.460	-0.183	82.091	0.973	2003-10-16	-6.933	2.301	741.180	0.971
2003-10-18	-0.130	-0.307	48.045	0.974	2003-10-18	-7.369	2.187	793.331	0.983
2003-11-01	0.170	-0.897	27.823	0.994	2003-11-01	-9.443	-0.762	1109.852	0.904
2003-12-27	7.030	-4.881	-633.028	0.999	2003-12-27	-12.739	-5.299	1610.931	0.953

新窗口打开|下载CSV

（2）克里金插值法。

克里金插值法又称空间可局部插值法,是以变异函数理论和结构分析为基础,在有限区域内对区域化变量进行无偏最优估计的一种方法^[25]。趋势面法构建的趋势面受阶次的限制,低阶次用于拟合变化缓和的趋势,高阶次用于拟合变化剧烈的趋势,对于复杂变化趋势,趋势面法的逼近效果有限^[26]。相比趋势面分析法,克里金插值法通过变异函数自身的函数结构及其各项参数,从不同角度反映变量的空间变异性,能更好地描述变量在空间中如何随位置变化而变化。而变异函数通过设定变程、基台、块金常数等,对复杂趋势的逼近效果较好。克里金插值法除用于地理统计外,各个领域都已广泛应用^[27],如研究区域降雨量时,根据雨量站实测点雨量,结合克里金插值法可近似推求研究区域面雨量,并得到了较好的应用效果^[28,29]。

克里金插值法有多种类型,各有其适用的条件,主要有以下几类：区域化变量满足二阶平稳性假定的普通克里金法和简单克里金法,区域化变量存在漂移现象的泛克里金法,多个协同变量参与插值的协同克里金法,变量服从对数正态分布的对数克里金法以及适用于非连续性取值的指示克里金、析取克里金和概率克里金法等,考虑到本文接下来要进行的连续性湖区边界水位反演,以及水位变量所服从的分布,选取普通克里金法和泛克里金法进行研究。

克里金插值法的简单表达如下：

（8）

Z (s) = μ (s) + ε (s)

式中：Z(s)为s位置处的变量值;μ(s)为s位置处的趋势值;ε(s)为s位置处的自相关随机误差。式（8）表明,区域内各位置的变量值在空间上大体服从某一趋势,每个位置都有一个对应的趋势值,各点变量值围绕对应位置趋势值上下波动,波动值即为自相关随机误差。普通克里金法与泛克里金法的区别在于对空间变量趋势的描述：普通克里金法假定趋势值μ(s)为某一恒定未知常数,空间内各位置的变量值围绕该常数值上下波动,即区域化变量满足二阶平稳性假定;泛克里金法假定趋势值μ(s)不为常数且服从趋势方程,方程自变量为空间坐标,即趋势值随空间位置改变而改变,存在漂移现象^[30]。由于已知水位点较少,无法准确判定水位变量是否满足二阶平稳性假定以及是否存在明显漂移现象,本文选取普通克里金法、泛克里金法同时进行水位反演,并对反演效果进行评价,根据评价结果选取合适的插值方法。

本文利用ArcGIS 10.3中分析扩展模块（Geostatistical Analyst）的趋势分析工具（Trend Analysis）对数据进行分析,包括QQPlot图、直方图、Voronoi图以及全局趋势分析,发现水位数据在南北和东西方向具有“U”型曲线趋势;利用地统计分析向导（Geostatistical Wizard）进行克里金插值,在克里金类型（Kriging type）一栏选取相应克里金方法,“Transformation”里选择Log变换,“Order of trend removal”里选择“second”用以拟合水位数据在南北和东西方向呈现出的“U”型曲线趋势;然后选取一种变异函数,种类包括Spherical、Exponential等,选定各向异性,插值中采用四分的椭圆形邻域进行搜索,每个邻域搜索点数最大设置为5个,最少为2个;最终可得到克里金插值出的水面趋势^[31]。

考虑到进行克里金插值时,10个样本点相对较少,本文采用交叉验证法对水位反演的精度进行评价,对于反演精度较低的情况,通过不断调整变异函数等设置以提高精度,弃用误差始终较大的趋势面,尽可能降低由样本点较少引起的误差随机性较大的问题。交叉验证法具体步骤如下^[30]：① 根据采样数据的空间结构特征等选择变异函数模型及相关参数;② 将第一个测量值Z₁暂时从水位数据系列中除去;③ 选用已设定好的变异函数对其余测量值进行克里金插值,估算测量值Z₁位置处的值Z₁^*;④ 将第一个测量值Z₁放回数据系列,依次对剩余测量值重复②③步骤,估算所有测量值相应位置处的值Z_i^*（i = 1, 2, 3…, n）;⑤ 将实测水位值及相同位置反演水位值进行对比统计,判断水位反演的精度。

交叉验证法得到相应统计指标,符合以下标准则被认为是拟合效果较好;标准平均值（mean standardized）最接近于0,均方根预测误差（root mean square）最小,平均标准误差（average standard error）最接近于均方根预测误差,标准均方根预测误差（root mean square standardized）最接近1^[31]。

表3为交叉验证的统计结果,采用同样变异函数的情况下,相比于普通克里金法,泛克里金法的标准平均值更接近于0,标准均方根预测误差接近于1,平均标准误差更接近均方根预测误差,说明在水位样本点较少的情况下,水位变量无法很好地满足二阶平稳性假定,存在一定的漂移现象,泛克里金法更适合于进行该情况下的水位反演;同时,在多次插值后发现,应用Spherical变异函数可以在大部分情况下获得较高的反演精度。综上所述,在水位样本点较少的情况下,泛克里金法拟合效果优于普通克里金法,本文最终选用泛克里金法反演水位。

Tab. 3
表3
表3克里金法对比表
Tab. 3Kriging interpolation with different variogram models

插值法	变异函数	均方根预测误差	标准平均值	标准均方根预测误差	平均标准误差
普通克里金	Spherical	1.589	0.566	2.166	0.596
	Exponential	1.592	0.524	2.102	0.594
	K-Bessel	1.591	0.486	2.056	0.583
泛克里金	Spherical	1.636	0.166	1.330	0.916
	Exponential	1.624	0.160	1.359	0.882
	K-Bessel	1.614	0.149	1.380	0.851

新窗口打开|下载CSV

4 结果与分析

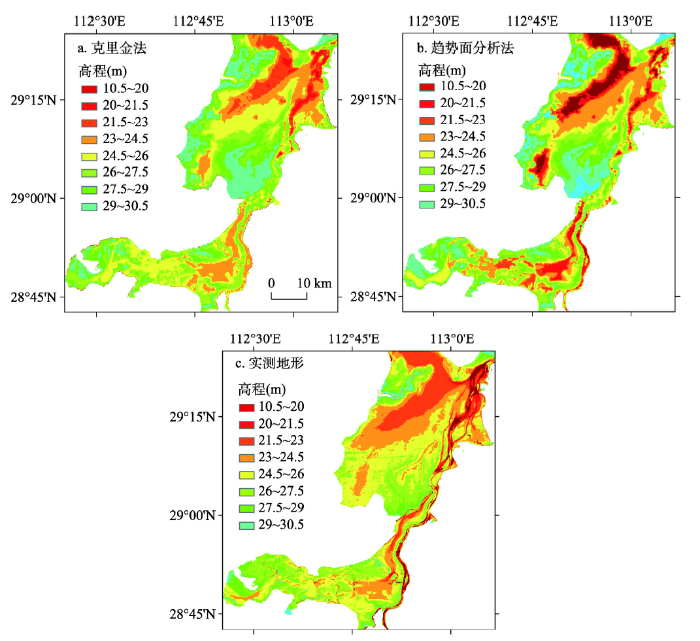
利用Landsat、MODIS系列遥感影像数据,通过ENVI、ArcMap提取湖区边界并转化为离散点的形式,采用趋势面分析法、克里金插值法,由各控制站点水位值及边界经纬度计算出当日湖区边界逐点水位,进而得到具有经纬度、水位值的离散高程点,将离散点栅格化生成地形高程（图6a、6b）。同时,将实测地形高程点栅格化生成实测地形高程（图6c）,对比可知,两种方法反演的地形起伏的轮廓与实测地形轮廓基本一致,且基于克里金法反演得到的地形与实测地形更一致,精度更高。

图6

新窗口打开|下载原图ZIP|生成PPT
图6洞庭湖湖底地形

Fig.6Lake bathymetry model in the Dongting Lake area

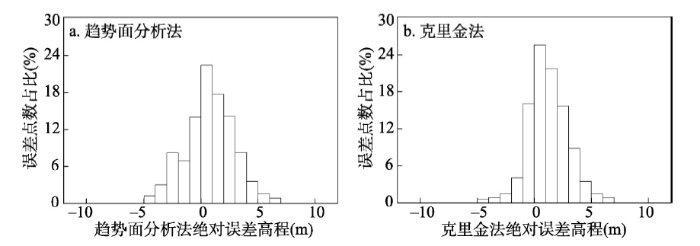
为了进一步比较两种方法精度,利用实测高程检核点进行精度评价,将克里金法和趋势面分析法分别内插得到检核点处高程,由于湖底地形复杂多变,因而将两种方法反演结果与实测地形高程之差定义为绝对误差高程,以此作为评价指标。图7及表4表明,克里金法绝对误差值分布范围较为集中,主要分布在-1~3 m间,共213378个点,约占总数的79%,趋势面分析法绝对误差在 -1~3 m区间内的离散点,约占总数的67%,表明克里金法在湖底地形反演方面具有更高的精度。

图7

新窗口打开|下载原图ZIP|生成PPT
图7绝对误差柱状图

Fig. 7Histogram of absolute error

Tab. 4
表4
表4克里金法、趋势面分析法误差统计信息(m)
Tab. 4Comparisons between the Kriging model, trend surface analysis model and shipborne points (m)

	平均绝对误差	标准偏差	均方根误差
趋势面分析法	1.76	2.08	2.21
克里金法	1.60	1.69	2.06

新窗口打开|下载CSV

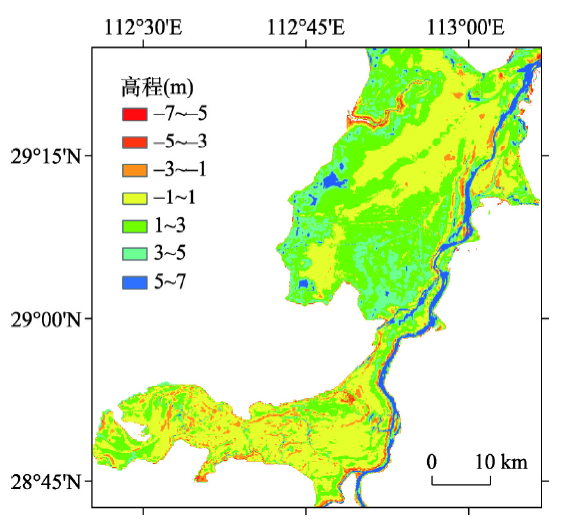
由图8可知,东洞庭湖误差大于南洞庭湖。在东洞庭湖112°45'E~113°0'E部分区域绝对误差在2 m以上,南洞庭湖误差大多在±1 m之间。造成误差的原因主要有：① 水位控制站点有限,无法有效覆盖到整个湖区,在东洞庭湖112°45'E~113°0'E区域无水位控制站点,致使该区水位反演产生较大误差;② 湖区边界的提取精度不高,导致坡度较陡的地形处出现不同水位下边界重合甚至高水位边界与低水位边界交叉的现象,产生较大的误差。

图8

新窗口打开|下载原图ZIP|生成PPT
图8克里金法与实测地形差值图

Fig. 8Comparison of the results of Kriging model withmeasured data grided model (m)

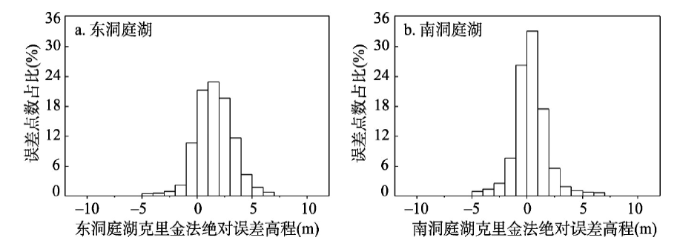
为了更好的确定克里金法误差产生的原因,分别对东、南洞庭湖的地形反演精度进行比较。由表5及图9可知,南洞庭湖绝对误差分布较集中,主要分布在-1~1 m,东洞庭湖绝对误差主要分布在-1~4 m,克里金法在南洞庭湖能够获得较高的精度,这与水文站点分布有关,表明地形反演效果依赖于水位样本点的分布情况,站点分布越均匀,反演地形效果越好。

Tab. 5
表5
表5两湖区克里金法误差统计信息(m)
Tab. 5Comparisons of absolute error in two lakeareas about Kriging model (m)

	平均绝对误差	标准偏差	均方根误差
东洞庭湖	1.84	1.64	2.27
南洞庭湖	1.08	1.43	1.47

新窗口打开|下载CSV

图9

新窗口打开|下载原图ZIP|生成PPT
图9不同分区绝对误差柱状图

Fig. 9Histogram of absolute error of differences in two lake areas

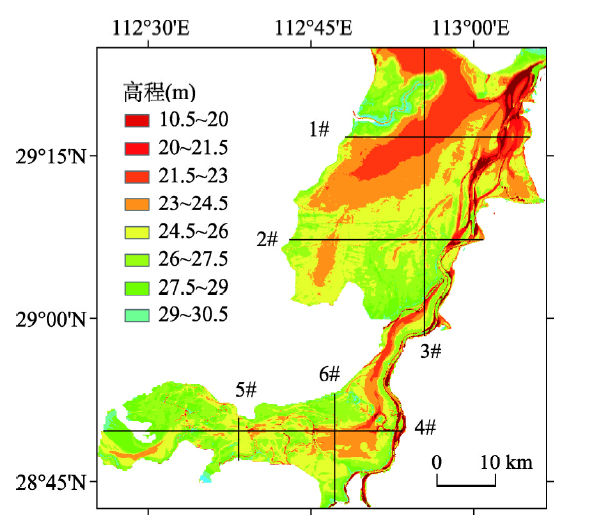
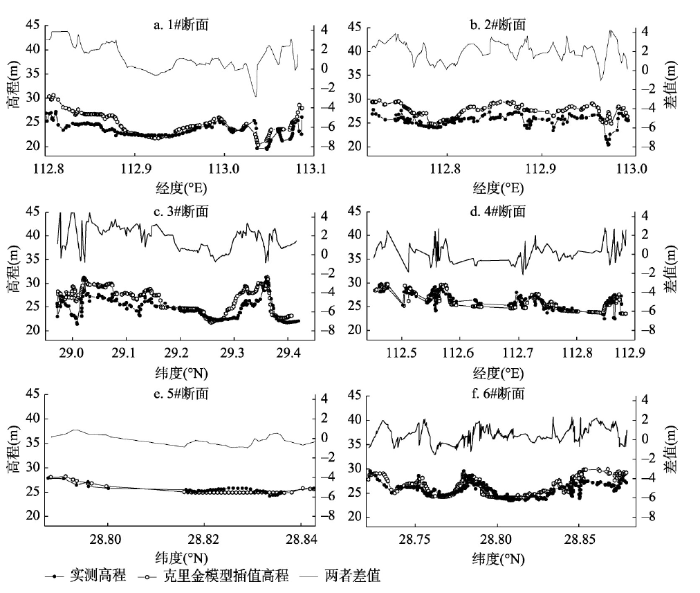
克里金法的反演精度不仅与水位样本点分布有关,还与湖区边界提取的精度有关。选取湖区6个断面,对比分析反演地形和实测地形。图10为6个断面所在位置,对比验证结果如图11所示。南洞庭湖地形反演精度较高;同时,在地形平缓处,地形反演的精度较高;在地形变化复杂区域,如河道,地形反演的精度较低,表明遥感影像提取的精度在大部分平缓区域精度较高,但在河道等地形复杂区域仍需提高精度。

图10

新窗口打开|下载原图ZIP|生成PPT
图10研究水域及验证横断面位置

Fig. 10Tested areas and checked cross-section

图11

新窗口打开|下载原图ZIP|生成PPT
图11地形精度验证的横断面对比

Fig. 11Comparison of measured and extracted cross-sections

误差产生主要有两类,第一类误差存在于湖底地形变化较大的区域,如上述河道或高程起伏较大处,无法准确反映河道和湖底起伏情况,导致该处误差较大,此类误差源于遥感影像提取;第二类误差主要分布在东洞庭湖水位样本点较少的区域,其误差主要来源于水位反演;在样本点分布均匀,水位反演精度较高的南洞庭湖,此类误差较小。

上述分析解释了误差产生的原因,表明在无样本点的情况下,水位反演存在困难。同时由图11可知,地形反演中大于1 m的误差绝大部分属于上述的第二类误差,即由水位反演产生的误差,说明在洞庭湖湖底地形反演中,水位反演精度对地形反演的最终效果影响较大。

5 结论

本文以洞庭湖为例,根据湖泊水域年内多变可间接反映湖底地形的原理,用遥感影像结合城陵矶等10个水文站点水位数据,反演得到了洞庭湖湖底地形,并以实测湖底地形对其精度进行评价,得到以下主要结论：

（1）采用遥感影像和水位数据,结合边界提取和水位反演方法可以有效获取洞庭湖湖底地形,结果较可靠且操作周期短。

（2）通过比较2种水位反演方法,克里金法的反演精度优于趋势面分析法;同时,在水位样本点覆盖全面的水域,水位反演精度较高,地形反演误差可缩小到±1 m。

（3）克里金法精度不仅与水位样本点分布情况有关,还与遥感影像提取湖区边界的精度有关,在地形复杂多变且湖底坡度较陡的水域,其边界提取精度有限,会产生较大误差。地形坡度变化平缓水域的预测精度明显高于复杂地形水域。

（4）本方法重点在于湖区边界的提取精度和水位反演精度,运用多源遥感影像可提高湖区边界的时空分辨率,但上述边界提取及水位反演方法仍有改进空间。边界提取方面,首先,30 m分辨率的Landsat系列遥感影像无法反映小于30 m的细节地貌特征,对于陡峭地形处水位起伏造成的湖区边界变化,会因小于30 m无法被有效区分。其次,年内较少的影像获取数量也有可能忽略掉某些湖底特征地貌,Landsat影像分辨率及较长重访周期增加了湖区边界提取的不确定性;无地形资料湖区的水位反演方面,首先,可以通过其他监测方式在已建站点实测水位数据的基础上,增加水位样本点数量。其次,考虑从地统计学等角度优化水位反演模型及精度验证方法,尽可能降低水位反演中因水位样本点数量较少产生的不确定性,更好的拟合水位在湖区内的变化趋势。通过提高边界提取及水位反演精度可进一步减少地形反演误差,相关问题有待深入研究。

参考文献原文顺序
文献年度倒序
文中引用次数倒序
被引期刊影响因子

[1]

Feng

, Hu C

, Chen X

, et al. MODIS observations of the bottom topography and its inter-annual variability of Poyang Lake
Remote Sensing of Environment, 2011,115(10):2729-2741.

DOI:10.1016/j.rse.2011.06.013 URL [本文引用: 7]

[2]

Wang C

, Philpot W

. Using airborne bathymetric LIDAR to detect bottom type variation in shallow waters
Remote Sensing of Environment, 2007,106(1):123-135.

DOI:10.1016/j.rse.2006.08.003 URL [本文引用: 1]

[3]

Tao

, Xiong

Lihua

, Yi

Fanghui

, et al. Relation of the water area of Dongting Lake to the water levels of hydrological stations based on MODIS images
Resources and Environment in the Yangtze Basin, 2012,21(6):756-765.

Magsci [本文引用: 1]

针对洞庭湖区，以30 m分辨率的环境减灾卫星CCD影像为参考，对比分析了归一化差异植被指数（NDVI）和比值植被指数（RVI）应用于MODIS遥感影像水体面积提取的优缺点。研究发现，选取NDVI并且赋予各月份各自适应的阈值进行水体面积提取，有效避免了采取单一阈值造成的枯水期水体误提以及丰水期水体漏提问题。将提取湖区面积与相应日期水位数据组成水位面积组，建立湖区面积水位相关关系。考虑到建立湖区面积与单一水文站点水位间相关关系存在一定空间不合理性，选取逐步多元回归法建立2003~2006年湖区面积与多站点水位间相关关系。结果表明：在高水位和低水位处，洞庭湖面积水位关系年际间变化不太明显，但在中等水位处（如24~29 m），湖区面积水位关系有比较明显的变化，同一水位处湖区面积有逐年减小的趋势。

[ 杜涛, 熊立华, 易放辉 , 等. 基于MODIS数据的洞庭湖水体面积与多站点水位相关关系研究
长江流域资源与环境, 2012,21(6):756-765.]

Magsci [本文引用: 1]

Zhu

Lingling

, Chen

Jianchi

, Yuan

Jing

, et al. Sediment erosion and deposition in two lakes connected with the middle Yangtze River and the impact of Three Gorges Reservoir
Advances in Water Science, 2014,25(3):348-357.

Magsci [本文引用: 1]

长江中游江湖关系复杂，分布有中国第一、二大淡水湖泊，江湖关系演变对防洪、生态等影响重大。通过分析反应长江中游洞庭湖和鄱阳湖泥沙冲淤的实测水沙和地形资料，初步掌握了湖区泥沙冲淤特征及主要影响因素，并着重探讨了三峡水库蓄水对两湖泥沙冲淤的影响。结果表明，近10年洞庭湖和鄱阳湖湖区泥沙淤积速度明显减缓，部分年份出现冲刷，其中洞庭湖湖区泥沙沉积率下降主要由来沙减少引起，三峡水库拦沙作用的影响明显；鄱阳湖区冲刷主要集中在入江水道，采砂活动影响显著，三峡水库蓄水影响尚不明显。

[ 朱玲玲, 陈剑池, 袁晶 , 等. 洞庭湖和鄱阳湖泥沙冲淤特征及三峡水库对其影响
水科学进展, 2014,25(3):348-357.]

Magsci [本文引用: 1]

Jingbao

, Wang

Kelin

, Qin

Jianxin

, et al. The evolution of annual runoff and sediment in the Dongting Lake and their driving forces
Acta Geographica Sinica, 2005,60(3):503-510.

[本文引用: 1]

[ 李景保, 王克林, 秦建新 , 等. 洞庭湖年径流泥沙的演变特征及其动因
地理学报, 2005,60(3):503-510.]

[本文引用: 1]

[6]

Jingbao

, Yin

Hui

, Lu

Chengzhi

, et al. Impact of sedimentation on Doingting Lake
Acta Geographica Sinica, 2008,63(5):514-523.

[本文引用: 1]

[ 李景保, 尹辉, 卢承志 , 等. 洞庭湖区的泥沙淤积效应
地理学报, 2008,63(5):514-523.]

[本文引用: 1]

[7]

Tang

Guoan

. Progress of DEM and digital terrain analysis in China
Acta Geographica Sinica, 2014,69(9):1305-1325.

[本文引用: 1]

[ 汤国安 . 我国数字高程模型与数字地形分析研究进展
地理学报, 2014,69(9):1305-1325.]

[本文引用: 1]

[8]

Jiang

Feng

, Qi

Shuhua

, Liao

Fuqiang

, et al. Hydrological and sediment effects from sand mining in Poyang Lake during 2001-2010
Acta Geographica Sinica, 2015,70(5):837-845.

[本文引用: 1]

[ 江丰, 齐述华, 廖富强 , 等. 2001-2010年鄱阳湖采砂规模及其水文泥沙效应
地理学报, 2015,70(5):837-845.]

[本文引用: 1]

[9]

Carbonneau P

, Lane S

, Bergeron

. Feature based image processing methods applied to bathymetric measurements from airborne remote sensing in fluvial environments
Earth Surface Processes & Landforms, 2006,31(11):1413-1423.

[本文引用: 1]

[10]

Gao

. Bathymetric mapping by means of remote sensing: methods, accuracy and limitations
Progress in Physical Geography, 2009,33(1):103-116.

DOI:10.1177/0309133309105657 URL [本文引用: 1]

[11]

Liu

Shudong

, Tian

Junfeng

. Development of bathyorographic survey technique
Port & Waterway Engineering, 2008(1):11-15.

[本文引用: 1]

[ 刘树东, 田俊峰 . 水下地形测量技术发展述评
水运工程, 2008(1):11-15.]

[本文引用: 1]

[12]

Changyou

, Sun

Biao

, Gao

Zhanyi

, et al. Retrieval model of water depth in Hulun Lake using multi-spectral remote sensing
Journal of Hydraulic Engineering, 2011,42(12):1423-1431.

[本文引用: 1]

[ 李畅游, 孙标, 高占义 , 等. 呼伦湖多波段遥感水深反演模型研究
水利学报, 2011,42(12):1423-1431.]

[本文引用: 1]

[13]

Shen

Xin

, Ouyang

Zhiyun

, Leeuw

. Constructing a DEM of Baiyang Lake Area from a series of Landsat images
Geography and Geo-Information Science, 2005,21(2):16-19.

[本文引用: 1]

[ 沈欣, 欧阳志云 Jande

LEEUW

, . 利用多时相Landsat影像生成白洋淀湖底DEM的研究
地理与地理信息科学, 2005,21(2):16-19.]

[本文引用: 1]

[14]

Liu

Dong

, Li

Yan

. The calculation of area and storage of Poyang Lake based on remote sensing technology
Remote Sensing Information, 2012(2):57-61.

[本文引用: 1]

[ 刘东, 李艳 . 基于遥感技术的鄱阳湖面积库容估算
遥感信息, 2012(2):57-61.]

[本文引用: 1]

[15]

Duan

, Bastiaanssen

W G M

. Estimating water volume variations in lakes and reservoirs from four operational satellite altimetry databases and satellite imagery data
Remote Sensing of Environment, 2013,134(5):403-416.

DOI:10.1016/j.rse.2013.03.010 URL [本文引用: 1]

[16]

Zhu

Changming

, Zhang

Xin

, Lu

Ming

, et al. Lake storage change automatic detection by multi-source remote sensing without underwater terrain data
Acta Geodaetica et Cartographica Sinica, 2015,44(3):309-315.

DOI:10.11947/j.AGCS.2015.20130438 Magsci [本文引用: 1]

针对现有库容遥感监测方法对无湖盆数据区域的湖泊动态库容难以直接测算问题,提出了未知湖泊水下地形数据的遥感湖泊动态库容监测方法.该方法通过多源遥感数据,匹配相对时相的湖泊面积和水位信息,构建并模拟湖盆DEM数据,据此来估算湖泊的动态库容.在算法实现上,首先采用分布迭代水体提取从遥感影像提取湖泊的多期动态边界;其次,从ICEsat GLAS激光测高数据中反演出湖泊的动态水位高程;第三,依据时间水位信息,通过邻近时相匹配,将水位高程赋给湖泊边界线,生成湖泊等水位线;第四,通过等水位线构建TIN(triangulated irregular network)和Kriging 插值,得到模拟湖盆数字高程模型;最后,依据模拟湖盆DEM和水体面积分布、水位信息,计算湖泊动态库容.试验通过对博斯腾湖的多年动态库容监测与真实性检验,结果显示:最大误差为2.21×108 m3,最小误差为0.000 02×108 m3,平均误差为0.044×108 m3,均方根为0.59,相关系数达到0.99.

[ 朱长明, 张新, 路明 , 等. 湖盆数据未知的湖泊动态库容遥感监测方法
测绘学报, 2015,44(3):309-315.]

DOI:10.11947/j.AGCS.2015.20130438 Magsci [本文引用: 1]

Yin

Hui

, Yang

, Jiang

Zhongcheng

, et al. Mutual effects between morphological characteristics and variations of flow-sediment process of Dongting Lake during 1951-2009
Geographical Research, 2012,31(3):471-483.

[本文引用: 1]

[ 尹辉, 杨波, 蒋忠诚 , 等. 近60年洞庭湖泊形态与水沙过程的互动响应
地理研究, 2012,31(3):471-483.]

[本文引用: 1]

[18]

Jiang

Jiahu

, Huang

Qun

. Analysis of the lake basin change and the rushing-silting features in the past decades of Doingting Lake
Journal of Lake Sciences, 2004,16(3):209-214.

Magsci [本文引用: 1]

洞庭湖是我国著名的五大淡水湖泊之一,位于长江中游荆江段南岸,湖南省境内.历史时期,曾经是我国第一大淡水湖,直至新中国成立初期,湖泊面积仍然有4350km2,居我国淡水湖泊之首位.但由于洞庭湖承纳"四水",吞吐长江,长江大量水沙涌入洞庭湖,造成了湖盆迅速淤高,加之由此诱发的人类大规模地湖泊垦殖活动,湖泊急剧萎缩.目前,洞庭湖已退居鄱阳湖之后,为我国第二大淡水湖泊.湖泊的严重泥沙淤积,已经造成了湖泊调蓄长江中游洪水功能的严重衰退,不但危及湖南省的防洪的安全,而且危及长江中下游地区的防洪安全,研究洞庭湖的湖盆冲淤演变具有重要意义.本文根据1974、1988和1998年洞庭湖1:25000水下地形资料,并针对洞庭湖具有显著上下游水位落差的实际,分不同高程和不同水位情况下,分析洞庭湖湖泊面积和容积演变特征,探讨洞庭湖近几十年来的湖盆变化及冲淤规律,试图揭示洞庭湖湖泊调蓄能力的变化过程.

[ 姜加虎, 黄群 . 洞庭湖近几十年来湖盆变化及冲淤特征
湖泊科学, 2004,16(3):209-214.]

Magsci [本文引用: 1]

Jiang

, Feng

, Zhu Y

, et al. An automated method for extracting rivers and lakes from landsat imagery
Remote Sensing, 2014,6(6):5067-5089.

DOI:10.3390/rs6065067 URL [本文引用: 1]

[20]

Gao B

. NDWI: A normalized difference water index for remote sensing of vegetation liquid water from space
Remote Sensing of Environment, 1996,58(3):257-266.

DOI:10.1016/S0034-4257(96)00067-3 URL [本文引用: 1]

[21]

Hanqiu

. A study on information extraction of water body with the modified normalized difference water Index (MNDWI)
Journal of Remote Sensing, 2005,9(5):589-595.

DOI:10.3321/j.issn:1007-4619.2005.05.012 URL Magsci [本文引用: 1]

在对M cfeeters提出的归一化差异水体指数(NDWI)分析的基础上,对构成该指数的波长组合进行了修改,提出了改进的归一化差异水体指数MNDWI(M odified NDWI),并分别将该指数在含不同水体类型的遥感影像进行了实验,大部分获得了比NDWI好的效果,特别是提取城镇范围内的水体。NDWI指数影像因往往混有城镇建筑用地信息而使得提取的水体范围和面积有所扩大。实验还发现MNDWI比NDWI更能够揭示水体微细特征,如悬浮沉积物的分布、水质的变化。另外,MNDWI可以很容易地区分阴影和水体,解决了水体提取中难于消除阴影的难题。

[ 徐涵秋 . 利用改进的归一化差异水体指数(MNDWI)提取水体信息的研究
遥感学报, 2005,9(5):589-595.]

DOI:10.3321/j.issn:1007-4619.2005.05.012 URL Magsci [本文引用: 1]

Wang

Dandan

. Spatial statistic analysis and its application in agricultural land classification
[D]. Xi'an: Chang'an University, 2008.

[本文引用: 2]

[ 王丹丹 . 空间统计分析及其在农用地分等中的应用
[D]. 西安: 长安大学, 2008.]

[本文引用: 2]

[23]

Chen

, Li

Zhengpin

, Yang

Linbo

, et al. Underwater trend surface analysis based on geostatistics and kriging methodology
Geomatics & Spatial Information Technology, 2016(7):82-84.

[本文引用: 1]

[ 陈科, 李正品, 杨林波 , 等. 基于地统计学和克里金法的水下趋势面分析
测绘与空间地理信息, 2016(7):82-84]

[本文引用: 1]

[24]

Tan

Xiaoming

. Study on characteristics of water level variation in Dongting Lake
Hunan Hydro & Power, 2002(2):25-26.

[本文引用: 1]

[ 谭晓明 . 洞庭湖水位变化特性
湖南水利水电, 2002(2):25-26.]

[本文引用: 1]

[25]

Sun

Zhaohua

, Li

, Yan

Xin

, et al. Analysis of the critical relationship between the water levels of Dongting Lake and Chenglingji station
Advances in Water Science, 2017,28(4):496-506.

[本文引用: 2]

[ 孙昭华, 李奇, 严鑫 , 等. 洞庭湖区与城陵矶水位关联性的临界特征分析
水科学进展, 2017,28(4):496-506.]

[本文引用: 2]

[26]

Liu

Zhilong

, Yu

Mukui

, Ma

Yue

, et al. A trend surface analysis of geographic variation in the traits of seeds and seedlings from different Quercus acutissima provenances
Acta Ecologica Sinica, 2011,31(22):6796-6804.

Magsci [本文引用: 1]

麻栎(Quercus acutissima Carr.)是优良的能源和用材树种,在我国分布广泛并已有悠久栽培利用的历史,研究其种子和苗木性状地理变异规律对选择优良种源和适生区十分必要。研究收集了13个省(区)36个种源的麻栎种子,在测定麻栎种子性状的基础上,在安徽省滁州市红琊山林场进行了苗期试验和苗木性状测定,并采用趋势面分析方法对这些性状在经纬2维方向的地理变异模式进行了剖析。结果表明:1)麻栎种源间种子长度、宽度、百粒重和营养内含物存在极显著差异。种子百粒重、长度和宽度总体表现双向渐变趋势,随经度增高而增大,随纬度增高而减小,主要受到经度的控制;以西南到东北为中间地带,可溶性糖含量向东南表现先下降后上升的趋势,向西北则相反;淀粉含量从西北到东南呈逐渐减小的趋势。2)麻栎种源苗高、地径、生物量、热值和木材化学组分存在极显著差异。苗高、地径和生物量均呈双向渐变,经正向变异且变化幅度较大,纬负向变异且变化幅度较小,经度影响大于纬度;热值拟合回归方程不显著,方程无意义。木质素含量北部大于南部,但北部以西北部最高,南部以东南部最高。3)研究显示,麻栎种子和苗木性状多数存在显著的地理变异模式,这也是麻栎在长期进化过程中为适应复杂多变的环境而产生与之相适应的遗传变异结果。

[ 刘志龙, 虞木奎, 马跃 , 等. 不同种源麻栎种子和苗木性状地理变异趋势面分析
生态学报, 2011,31(22):6796-6804.]

Magsci [本文引用: 1]

Tingting

, Lin

Min

. Models comparison for water interpolation based on kriging method
Science Technology and Engineering, 2015,15(4):135-139.

[本文引用: 1]

[ 陆婷婷, 林敏 . 基于克里金的水深插值模型比较
科学技术与工程, 2015,15(4):135-139.]

[本文引用: 1]

[28]

Tianxian

, Wang

Yukuan

, Fu

Bin

. Interpolation analysis of precipitation spatial distribution in Sichuan Province
Yangtze River, 2010,41(10):9-12.

[本文引用: 1]

[ 徐天献, 王玉宽, 傅斌 . 四川省降水空间分布的插值分析
人民长江, 2010,41(10):9-12.]

[本文引用: 1]

[29]

Wang

Yinghua

, Zhang

Xin

. Analysis of spatial and temporal distribution of precipitation in Xining City
Yellow River, 2012,34(10):80-82.

[本文引用: 1]

[ 王颖华, 张鑫 . 西宁市降水量时空分布规律分析
人民黄河, 2012,34(10):80-82.]

[本文引用: 1]

[30]

Yang

Gongliu

, Zhang

Guimin

, Li

Shixin

. Application of universal Kriging interpolation in geomagnetic map
Journal of Chinese Inertial Technology, 2008,16(2):162-166.

[本文引用: 2]

[ 杨功流, 张桂敏, 李士心 . 泛克里金插值法在地磁图中的应用
中国惯性技术学报, 2008,16(2):162-166.]

[本文引用: 2]

[31]

Junxiao

, Li

Chaokui

, Yin

Zhihui

. ArcGIS based kriging interpolation method and its application
Bulletin of Surveying and Mapping, 2013(9):87-90.

[本文引用: 2]

[ 李俊晓, 李朝奎, 殷智慧 . 基于ArcGIS的克里金插值方法及其应用
测绘通报, 2013(9):87-90.]

[本文引用: 2]