删除或更新信息，请邮件至freekaoyan#163.com(#换成@)

基于析因数值实验方法的蒸发皿蒸发归因研究

本站小编 Free考研考试/2021-12-29

王婷婷¹^,²^,, 孙福宝¹^,²^,³^,⁴^,, 章杰¹, 刘文彬¹, 王红¹

1. 中国科学院地理科学与资源研究所陆地水循环及地表过程重点实验室,北京 100101

2. 中国科学院大学,北京 100049

3. 河西学院祁连山生态研究院,张掖 734000

4. 中国科学院水资源中心,北京 100101

A new method to attribute changes of pan evaporation: The experimental detrending approach

WANGTingting¹^,²^,, SUNFubao¹^,²^,³^,⁴^,, ZHANGJie¹, LIUWenbin¹, WANGHong¹

1. Key Laboratory of Water Cycle and Related Land Surface Processes, Institute of Geographic Sciences and Natural Resources Research, CAS, Beijing 100101, China

2. College of Resources and Environment, University of Chinese Academy of Sciences, Beijing 100049, China

3. Ecology Institute of Qilian Mountain, Hexi University, Zhangye 734000, Gansu, China

4. Center for Water Resources Research, CAS, Beijing 100101, China

通讯作者:通讯作者：孙福宝(1979-), 男, 河北唐山人, 研究员, 主要从事水文水资源方面的研究。E-mail: sunfb@igsnrr.ac.cn
收稿日期:2017-09-27
修回日期:2018-07-21
网络出版日期:2018-11-25
版权声明:2018《地理学报》编辑部本文是开放获取期刊文献，在以下情况下可以自由使用：学术研究、学术交流、科研教学等，但不允许用于商业目的.
基金资助:

中国国家重点研究发展计划(2016YFA0602402, 2016YFC0401401); 中国科学院重点部署项目课题(ZDRW-ZS-2017-3-1), 中国科学院****(孙福宝)

作者简介:
-->作者简介：王婷婷(1989-), 女, 安徽安庆人, 博士生, 主要从事水文水资源方面的研究。E-mail: wangtt778@163.com

展开

摘要
蒸发皿蒸发是唯一可长时间大范围观测的潜在蒸发,其准确估算和长时间序列趋势变化归因分析,对变化环境下干旱研究、水文过程理解分析与预估具有重要意义。本文筛选出416个具有连续观测的气象台站资料,率定了PenPan模型中适合模拟中国20 cm口径（D20）蒸发皿蒸发的风速函数,发展了基于去趋势法的析因数值实验归因法,对比了此方法与常用的偏导归因法在1960-2014年、1960-1993年（“蒸发悖论”时段）及1993-2014年（“蒸发悖论”消失）蒸发皿蒸发趋势变化的归因结果。结果表明,使用新率定的风速函数f_q(u₂)=3.977×10^-8(1+0.505u₂)能更准确模拟中国D20蒸发皿蒸发;相较于偏导归因法结果,析因数值实验法也能对蒸发皿蒸发趋势变化进行定量归因分析,且归因结果略优于偏导归因法结果;此外,可利用析因数值实验法的基准态信息来对偏导归因法结果进行校正,从而更准确地对蒸发皿蒸发趋势变化进行归因分析,加深对蒸发皿蒸发趋势变化的理解,为水文水循环研究准确分析提供保障。

关键词：析因数值实验法;蒸发皿蒸发;归因分析;偏导归因法
Abstract
Pan evaporation is the only long-term observation of potential evaporation around the world. In analyzing and predicting how droughts and hydrological cycles might change in a warming climate, change of pan evaporation is one crucial element to be understood. In this paper, we chose 416 sites with continuous monthly observations over 1960-2014 in China. We calibrated the wind function in the PenPan model to improve the estimation of pan evaporation. We developed a new approach, i.e., the experimental detrending (ED) approach, and made comparison with the traditional partial differential (PD) method in attributing changes of pan evaporation for the periods of 1960-2014, 1960-1993 (evaporation paradox) and 1993-2014 (evaporation paradox disappeared). The results first showed that improvement in estimating pan evaporation can be made when using the new calibrated wind function: f_q(u₂)=3.977×10^-8(1+0.505u₂). The comparison then showed that both methods can well attribute changes of pan evaporation, and the ED approach performs slightly better than the traditional PD method. In addition, the ED approach can help make effective adjustment for the PD method in attribution analysis so as to better understand the change of pan evaporation. Hence, the ED approach is recommended to assist a better understanding and prediction of water-energy cycles in a changing climate.

Keywords：experimental detrending approach;pan evaporation;attribution analysis;partial differential method

-->0
PDF (4660KB)元数据多维度评价相关文章收藏文章
本文引用格式导出EndNote Ris Bibtex 收藏本文-->
王婷婷, 孙福宝, 章杰, 刘文彬, 王红. 基于析因数值实验方法的蒸发皿蒸发归因研究[J]. 地理学报, 2018, 73(11): 2064-2074 https://doi.org/10.11821/dlxb201811002
WANG Tingting, SUN Fubao, ZHANG Jie, LIU Wenbin, WANG Hong. A new method to attribute changes of pan evaporation: The experimental detrending approach[J]. Acta Geographica Sinica, 2018, 73(11): 2064-2074 https://doi.org/10.11821/dlxb201811002

1 引言

蒸散发是地表水热平衡的重要参量,是联系水循环和能量循环的纽带。蒸发皿蒸发作为唯一可长时间大范围观测的潜在蒸发,其准确估算及长时间序列变化分析对理解变化环境下干旱成因机制、水热循环变化具有重要意义^[1,2]。而全球范围内蒸发皿观测数据显示,从20世纪50年代开始到90年代初,潜在蒸发呈下降趋势,这与全球变暖则蒸发皿蒸发增加的预期相悖,又称“蒸发悖论”^{[1, 3-4]}。国内外****纷纷对“蒸发悖论”现象展开研究并对其成因进行分析^{[4,5,6,7,8,9,10,11]}并综述报道^{[12,13,14,15]}。
蒸发皿蒸发的长时间序列趋势变化及归因分析,对于准确理解陆—气蒸发需求变化、分析潜在蒸发对气象要素的敏感性及定量研究气候变化对流域水循环的影响具有重要意义^{[4, 16]}。相关/回归分析方法,如多元线性回归法,常用于分析各气象要素对蒸发皿蒸发变化的敏感性^{[4, 10, 16]};但它要求各输入变量相互独立,而各气象要素间存在很强的共线性问题^[17],因此,基于相关/回归分析法的归因结果存在一定偏差。Roderick等^[2]发展了一种利用偏导方程对蒸发皿蒸发趋势变化进行归因的方法（简称：偏导归因法）,能很好的对影响蒸发皿蒸发趋势变化的气象要素（辐射、风速、气温和相对湿度）进行定量归因分析。这种方法具有一定的数理机理,且被广泛用于定量评估潜在蒸发敏感性分析研究中^{[11, 18-23]}。然而,在复杂方程或水文模型的归因分析研究中,因无法直接获取其偏导解析式,偏导归因法应用受限。针对此不足,Zhang等^[24]在去趋势法的基础上发展了析因数值实验法,首次定量评估影响帕尔默干旱指数（PDSI）的各气象要素的贡献,这是偏导归因法难以实现的。
目前为止,对于析因数值实验法的相关研究仍存在大量空白,相比较于常用的偏导归因法,析因数值实验法的归因分析能力如何仍未可知。为此,本文以中国20 cm口径（D20）蒸发皿蒸发趋势变化归因分析为例,来详细介绍这两种方法,并对比分析其归因结果。本文旨在主要对比和推广析因数值实验归因法,以期更准确解释“蒸发悖论”现象产生机制,同时利用析因数值实验法来改进偏导归因法结果,从而加深对蒸发皿蒸发趋势变化的理解,从而更好理解和预测变化环境下蒸散发规律。

2 数据与方法

2.1 数据与质量控制

本研究选取PenPan模型来模拟蒸发皿蒸发,选取中国气象数据共享网（http://data.cma.cn/）提供的1960-2014年月平均气象数据、辐射数据来模拟中国D20蒸发皿蒸发,进而对其趋势变化进行归因分析。所需数据包括：756个气象站的平均气温（T_a）、风速（u₂）、日照时数（Sd）、相对湿度（Rh）和D20蒸发量（1960-2001年资料完整,2002-2014年部分台站缺测）及130个台站太阳辐射资料。为了提高统计结果的可靠性和准确性,去除因数据不连续导致的偏差,首先对所需气象要素数据和站点选取进行质量控制：剔除存在长时间缺测的站点,最终选取416个具有连续月平均观测数据的气象站（图1）。此外,选取对应的蒸发皿蒸发数据和入射太阳辐射观测资料来对PenPan模型模拟的蒸发皿蒸发进行率定和验证。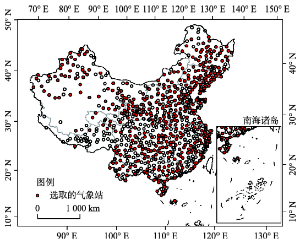

显示原图|下载原图ZIP|生成PPT
图1研究区站点分布
-->Fig. 1Spatial distribution of the meteorological stations in China
-->

2.2 PenPan模型

Rotstayn等^[25]通过耦合蒸发的动力作用^[26]和辐射作用^[27],提出了基于物质平衡和能量平衡的PenPan模型（方程（1））来模拟蒸发皿蒸发。此模型在全球各区域蒸发皿蒸发模拟研究中取得较好结果^{[2, 11, 18, 22]}。

E_{pan} = E_{p, R} + E_{p, A} = (\frac{Δ}{Δ + aγ} \frac{R_{n}}{λ}) + (\frac{aγ}{Δ + aγ} f_{q} (u_{2}) \times e_{s} (1 - Rh))

（1）
式中：E_pan、E_p,R和E_p,A分别为蒸发皿蒸发速率、辐射作用的蒸发速率和动力作用蒸发速率（单位：kg/（m²·s）,即mm/s）;e_s为饱和水汽压（单位：Pa）,Rh为相对湿度;

Δ

为2 m处饱和水汽压—温度曲线斜率（单位：Pa/K）,

γ

为湿度计常数（单位：Pa/K）;

λ

是汽化热（单位：J/kg）;a为常数,表征蒸发皿水—热转化有效面积比例,在本研究中,D20蒸发皿的a取4.2。

f_{q} (u_{2})

（单位：kg/（m²·s·Pa））多采用Thom等^[26]基于经验拟合的风速函数：

f_{q} (u_{2}) = 1.39 \times 10^{- 8} (1 + 1.35 u_{2})

;R_n（单位：W/m²）为净辐射,由净短波辐射和净长波辐射组成,具体计算方法：

R_{n} = (1 - A_{p}) R_{sp} + R_{l, in} - R_{l, out}

（2）
式中：R_sp为蒸发皿中水体吸收的太阳辐射,且由于蒸发皿四周壁也参与吸收太阳辐射的缘故,其数值应大于太阳辐照度;A_p（约0.14）为蒸发皿反射率;

(1 - A_{p}) R_{sp}

表示蒸发皿吸收的净短波辐射;R_l,in、R_l,out分别为入射和出射长波辐射。假设D20蒸发皿为黑体,则有：

R_{l, in} = σ {T_{a}}^{4} (1 - (0.34 - 0.14 \sqrt[]{\frac{e_{a}}{1000}}) (1.35 R_{s} / (R_{0} (0.75 + 2 \times 10^{- 5} z)) - 0.35))

（3）
式中：

σ

为Stefan-Boltzmann常数;e_a为实际水汽压（单位：Pa）;z为台站高程（m）;R_o详见FAO-Penman潜在蒸散发^[28]计算。R_s为入射太阳辐射：

R_{s} = (a_{s} + b_{s} \frac{n}{N}) R_{a}

（4）
式中：n为月日照时数;N为月最大可照时数;R_a为大气层外太阳辐射;a_s和b_s为经验拟合的参数,常取0.25和0.5。由于中国地域广阔,且跨越不同的气候带,因此全国用同一组定值会造成较大误差^[4]。因此,本文利用辐射站观测的太阳辐射数据,对参数a_s和b_s进行优化,以期能更准确估算太阳辐射。

2.3 偏导法

自2007年Roderick等^[2]利用偏导解析式（Partial Differential, PD）对基于PenPan模型模拟的蒸发皿蒸发趋势变化进行归因分析后,此方法被广泛用于潜在蒸散发趋势变化归因分析,以解析“蒸发悖论”现象成因机制,并定量分析各气象要素（辐射、风速、气温和相对湿度）对蒸发皿蒸发趋势变化的贡献^{[11, 18, 20, 22, 29]}。蒸发皿蒸发（E_pan）趋势变化可被视为辐射项（E_p,R）和动力项（E_p,A）趋势变化之和,即：

\frac{d E_{pan_PD}}{dt} = \frac{d E_{p, R}}{dt} + \frac{d E_{p, A}}{dt}

（5）
为进一步分析各输入气象要素对E_pan趋势变化的贡献率,辐射项和动力项趋势变化可被进一步归因为：

\frac{d E_{p, R}}{dt} = \frac{? E_{p, R}}{? R_{n}} \times \frac{d R_{n}}{dt} + \frac{? E_{p, R}}{? Δ} \times \frac{dΔ}{d T_{a}} \times \frac{d T_{a}}{dt}

（6）

\frac{d E_{p, A}}{dt} = \frac{? E_{p, A}}{? u_{2}} \times \frac{d u_{2}}{dt} + \frac{? E_{p, A}}{? Rh} \times \frac{d Rh}{dt} + \frac{? E_{pan}}{? T_{a}} \times \frac{d T_{a}}{dt}

（7）
由于Δ和e_s是由温度计算得到,因此,在蒸发皿趋势变化中,气温的贡献可分别由辐射项和动力项中Δ和e_s的气温贡献作用共同组成。即：

\frac{? E_{pan_PD}}{? T_{a}} \times \frac{d T_{a}}{dt} = \frac{? E_{p, R}}{? Δ} \times \frac{dΔ}{d T_{a}} \times \frac{d T_{a}}{dt} + \frac{? E_{p, A}}{? Δ} \times \frac{dΔ}{d T_{a}} \times \frac{d T_{a}}{dt} + \frac{? E_{p, A}}{? e_{s}} \times \frac{d e_{s}}{d T_{a}} \times \frac{d T_{a}}{dt}

（8）
因此,E_pan趋势变化可近似看成由R_n、Rh、u₂和T_a的贡献量共同组成,即：

\frac{d E_{pan_PD}}{dt} = \frac{d E_{p, R}}{? R_{n}} \times \frac{d R_{n}}{dt} + \frac{d E_{pan}}{? T_{a}} \times \frac{d T_{a}}{dt} + \frac{d E_{p, A}}{? u_{2}} \times \frac{d u_{2}}{dt} + \frac{? E_{p, A}}{? Rh} \times \frac{d Rh}{dt}

（9）
基于偏导法归因结果（

d E_{pan_PD} / dt

）将与模拟的蒸发皿蒸发趋势变化（

d E_{pan} / dt

）比较,以评价基于此方法归因结果的准确性。

2.4 析因数值实验法

目前,对气候变化相关研究主要集中于其趋势分析,尤其是线性趋势变化方面研究。去趋势法可有效去除要素的趋势,从而有效分离趋势项和波动项,在气候变化、干旱研究中应用广泛^[30,31]。Zhang等^[24]在去趋势法基础上,发展了一种析因数值实验方法,即设计一系列的单一气候变化情景（去除其他要素自变量趋势,仅保留单一自变量趋势）实验,将PDSI趋势变化定量归因到各输入气象要素中。现将此方法命名为“析因数值实验方法”（Experimental Detrending, ED）,利用此方法对蒸发皿蒸发趋势变化归因过程为：
（1）去趋势数据集的构建
对于去趋势气温数据集,即直接减去其趋势项：

{T_{a}}_{_detrend, i, j} = {T_{a_}}_{observed, i, j} - k (i - i_{pivot})

（10）
式中：T_{a_detrend,i,j}为去趋势后的月气温;T_{a_observed,i,j}为原始观测的月气温;k为每个站点的年际变化趋势;i为年,如1960, 1961, …, 2014;j为月（1, 2, …, 12）;i_pivot为选取的研究时间段起始年份,在本研究中,分别为1960（1960-2014年和1960-1993年时段）和1993（1993-2014年时段）。
风速、辐射和相对湿度数据在去趋势后数值应大于0,且相对湿度还需小于等于1,所以这3种气象要素的去趋势数据集构建可采用公式（11）和（12）：

F_{detrend, i, j} = F_{observed, i, j} - k (i - i_{pivot})

（11）

F_{detrend, i, j} = F_{observed, i, j} (\frac{F_{detrend, i}}{F_{observed, i}})

（12）
式中：F_detrend,i分别表示去趋势后的风速、辐射和相对湿度;F_observed,i为对应的历史观测数据集。
当每个站点的去趋势数据集构建完成后,新数据的各气象要素虽年际趋势被去除,但年际—年内波动得到有效保留。
（2）析因数值实验法归因
当各气象要素的年际趋势从原始观测数据中去除后,基于此数据集（即用T_{a_detrend,i,j}代替原始月平均气温,F_detrend,i,j代替观测的风速、辐射和相对湿度）计算的E_pan可看作为无气候变化（无气温、风速、辐射和相对湿度变化）影响情景下的蒸发皿蒸发,可被视为基准情景（“BaseCase”）下E_pan,记为E_BaseCase。
逐一释放单一气象要素趋势,并分别计算该情景下的E_pan。如,在释放气温趋势情景下,使用原始观测平均气温数据（T_{a_observed,i,j}）和去趋势后风速、辐射和相对湿度数据（F_detrend,i,j）来计算E_pan,此E_pan即为只有气温变化影响下的蒸发皿蒸发。同理,逐一释放风速、辐射和相对湿度的趋势,分别计算的E_pan即为只有该气象要素变化影响情景下的蒸发皿蒸发,记为：E_detrend,f（下标f分别表征气温、风速、辐射和相对湿度）。
E_detrend,f和E_BaseCase间趋势差异即为每个站的该气象要素在E_pan趋势变化的贡献（C_f）。即：

C_{f} = d E_{detrend, f} / d t - d E_{BaseCase} / d t

（13）
（3）归因结果验证
以上计算的4种气象要素贡献之和,即可视为基于析因数值实验法归因的E_pan趋势变化（

d E_{pan_ED} / dt

）,即：

\frac{d E_{pan_ED}}{dt} = C_{T_{a}} + C_{u_{2}} + C_{Sd} + C_{Rh}

（14）
此结果（

d E_{pan_ED} / dt

）将会与原始蒸发皿蒸发趋势（

d E_{pan} / dt

）进行比较,用以评估析因数值实验方法归因结果的优劣。

2.5 偏导归因法校正

在析因数值实验法中,基准态情景下模拟的蒸发皿蒸发（E_BaseCase）可看作无气候变化影响情景下的蒸发皿蒸发,则E_BaseCase的趋势（dE_BaseCase/dt）变化即可看作除4个主要气象要素影响外,受其他可能要素对蒸发皿蒸发趋势变化的影响。因此,利用析因数值实验法中的基准态信息,可对偏导法归因结果进行校正,校正公式如方程（15）：

d {E_{pan}}_{_P D_{Adj}} / dt = d {E_{pan}}_{_PD} / dt + d E_{BaseCase} / dt

（15）
式中：

d {E_{pan}}_{_P D_{Adj}} / dt

即为偏导法归因校正后结果。
同理,校正后的归因结果（

d {E_{pan}}_{_P D_{Adj}} / dt

）将与

d E_{pan} / dt

进行比较,用以评估校正后的偏导归因法优劣。

3 结果与讨论

3.1 PenPan模型校正

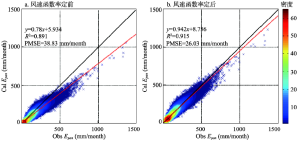
基于率定后的太阳辐射数据计算的E_pan,与观测的蒸发皿蒸发相比,偏差较大,RMSE达38.83 mm/month（图2a）。由于在PanPan模型中,除风速函数外,各参量均具有一定物理机理^[25],因此,本文利用中国观测D20蒸发皿蒸发数据,对原适合于美国Class A型蒸发皿蒸发的风速函数^[26]进行率定,得到新函数：

f_{q} (u_{2}) = 3.977 \times 10^{- 8} (1 + 0.505 u_{2})

（16）
利用此风速函数最终计算的E_pan,对比观测的蒸发皿蒸发,结果有了明显改进,RMSE降至26.03 mm/month（图2b）。因此,此率定后的E_pan能更准确模拟中国D20蒸发皿蒸发,为接下来的归因研究奠定基础。

显示原图|下载原图ZIP|生成PPT
图2风速函数率定前(a)、后(b)模拟和观测的月蒸发皿蒸发比较
-->Fig. 2Comparison between observed and calculated E_pan before (a) and after (b) using the calibrated wind function at monthly timescale
-->

3.2 蒸发皿蒸发变化归因结果比较和分析

研究表明偏导归因法能有效定量评估各气象要素对蒸发皿蒸发趋势变化的贡献^{[2, 11, 18, 22]},并对“蒸发悖论”现象给出较为合理解释与分析。为评估析因数值实验法对E_pan趋势变化归因分析的能力,本研究利用选取的416个站点,分别比较1960-2014年、1960-1993年（中国“蒸发悖论”存在^{[4, 11]}）和1993-2014年（“蒸发悖论”消失）这3个时段,两种方法的归因结果（图3,表1）。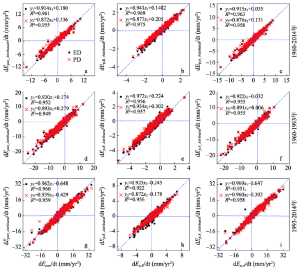

显示原图|下载原图ZIP|生成PPT
图3基于析因数值实验法(ED)和偏导法(PD)的归因结果比较
-->Fig. 3Comparison of attributing results based on the experimental detrending (ED) approach and partial differential (PD) method
-->

Tab. 1
表1
表1两种方法归因结果统计
Tab. 1Statistical information of attributing results based on two methods

		均值(mm/yr²)				RMSE(mm/yr²)
		dE/dt	ED	PD		ED	PD
1960-2014年	E_pan	-0.016	0.166	0.322		0.727	0.864
	E_p,R	-0.116	0.039	0.103		0.234	0.285
	E_p,A	0.101	0.127	0.219		0.664	0.749
1960-1993年	E_pan	-3.110	-2.720	-2.500		1.228	1.373
	E_p,R	-0.858	-0.610	-0.500		0.382		0.458
	E_p,A	-2.252	-2.110	-2.000	1.044		1.100
1993-2014年	E_pan	4.162	3.356	3.477	2.011	2.089
	E_p,R	0.316	0.098	0.029	0.499		0.621
	E_p,A	3.846	3.379	3.326	1.806		1.748

新窗口打开
对比3个时段直接计算的蒸发皿蒸发、其辐射项和动力项的趋势（即dE_pan/dt,dE_p,R/dt和dE_p,A/dt）,两种方法归因结果均分布在1∶1线附近,拟合的R²高于0.90,大部分情况下超过0.95（图3）。表明析因数值实验法和偏导法一样,也能合理且较为准确的定量分析E_pan趋势变化。结合416个台站归因结果的简单统计（表1）显示,基于析因数值实验方法的结果,其均值更接近直接计算的趋势,且除1993-2014年时段的动力项外,析因数值实验方法归因结果的RMSE均小于偏导归因法结果。具体说来,E_p,R归因结果（图3b、3e、3h和表1）显示,偏导法归因结果的误差略大于析因数值实验方法结果,尤其在1960-2014年时段的E_p,R最大负趋势区域,偏导法归因结果存在较为明显的低估现象;在E_p,A的归因分析中,析因数值实验方法也体现出微弱的优势;析因数值实验方法在E_p,R和E_p,A的优势综合到E_pan归因结果上,表现出与偏导结果相当甚至更优点效果。这充分说明,析因数值实验法归因结果略优于偏导法结果。
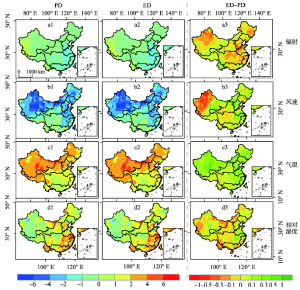
为比较基于上述两种归因方法归因到各输入变量间的差异,本文选取“蒸发悖论”时段（1960-1993年）数据的归因分析结果,来展示各气象要素对蒸发皿蒸发趋势变化敏感性的空间分布（图4）。结果显示,两种方法的归因结果空间分布基本相似,但存在微小差异。其中气温和相对湿度的归因结果差异主要集中在-0.5 mm/yr²~+0.5 mm/yr²（图4c3、4d3）;相对而言,偏导法和析因数值实验方法在辐射和风速的归因结果则差异较大,差异主要集中在-1 mm/yr²~0.1 mm/yr²范围（图4a3、4b3）,尤其在西北地区,两种方法对辐射和风速的归因结果差异达-1 mm/yr²以上。

显示原图|下载原图ZIP|生成PPT
图41960-1993年时段各气象要素对Epan趋势变化敏感性的空间分布
-->Fig. 4Spatial distribution of the sensitivity of each meteorological variable to the change of E_pan during the period of 1960-1993
-->

从全国范围来看,风速下降时造成“蒸发悖论”的主要原因,直接导致蒸发皿蒸发趋势变化达-2.56 mm/yr²,占蒸发皿蒸发趋势总变化的60%左右。不同地区,风速贡献存在空间差异较大,尤其在北方和西北地区,对蒸发皿趋势变化影响贡献均在-4 mm/yr²以上,部分地区超过-6 mm/yr²,远大于辐射、气温和相对湿度的敏感性。此外,相对湿度和辐射的下降也对蒸发皿蒸发趋势下降有一定作用,如辐射下降的影响导致E_pan趋势下降达-0.95 mm/yr²,近乎抵消了由于气温增加导致的E_pan趋势增加部分（0.92 mm/yr²）。4种气象要素综合作用,致使蒸发皿蒸发整体呈现负增长的趋势,从而导致“蒸发悖论”现象出现。

3.3 基于校正后的偏导法归因结果

综上所述,基于偏导法的4种气象要素的总贡献,能解释约90%的蒸发皿蒸发趋势变化,但相对于观测的蒸发皿趋势变化仍存在较小偏差。为此,本文利用析因数值实验法中基准态信息来对偏导法归因结果进行校正（公式（15））,对比校正前后归因结果,来验证校正后偏导归因法的优劣。针对选取的416个站点归因结果比较显示（图5）,校正后的偏导归因结果能更好的对蒸发皿蒸发趋势进行归因。对比计算的蒸发皿蒸发趋势,校正后的归因结果更贴近1∶1线,R²达0.99,且RMSE降至0.50 mm/yr²,相对于校正前结果,有了非常明显的改进。即除4种气象要素外,其他可能要素也会对蒸发皿蒸发趋势变化产生影响,而析因数值实验法的基准态信息能有效识别部分贡献率。这说明,析因数值实验法能有效弥补偏导法在归因分析的不足,这对于更准确估算蒸发皿蒸发趋势变化、分析水文气象过程敏感性,并对其他基于偏导法的应用和分析提供更可靠的保障。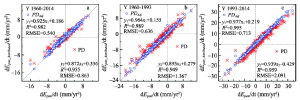

显示原图|下载原图ZIP|生成PPT
图5校正前后偏导法归因结果比较
-->Fig. 5Comparison of the attributing results based on partial differential methods before and after adjustment
-->

3.4 析因数值实验法优势

对比常用的偏导法在归因分析研究中,析因数值实验法具有以下几个优点：
（1）在对可获取偏导形式解析式的方程进行定量归因分析中,析因数值实验法具有与偏导法相匹配甚至更优的归因分析能力。如本研究对基于PenPan模型模拟的蒸发皿蒸发趋势变化归因分析中,偏导法和析因数值实验法均能准确的对其定量归因,二者归因结果很相近,且析因数值实验法归因结果略微优于偏导法分析结果。
（2）在对无法应用偏导法进行归因分析情况下,如无法获取偏导形式解析式的方程或更为复杂的模型中,偏导法难以用于趋势变化归因分析研究,而析因数值实验法不受此限制,且能发挥有效作用。如Zhang等^[24]利用此方法有效对干旱指数PDSI趋势变化进行定量归因分析,这是偏导法难以实现的。因此,相比较偏导法,析因数值实验法在趋势变化归因分析中具有更广阔的应用前景。
（3）析因数值实验法中的基准态信息,能在一定程度上表征除4种主要气象要素外其他要素对蒸发皿蒸发趋势变化影响的贡献,在析因数值实验法归因分析中承担“校零”的作用。此外,此基准态信息能对偏导法归因结果进行校正,从而有效弥补其不足,为基于偏导法归因分析的应用和理解提供更可靠的保障。
（4）利用析因数值实验法构建去趋势数据集过程中,每种情景仅保留单一或选定气候要素的趋势,而不受到其他气象要素趋势的影响,各模拟情景能最大程度地保留各气候要素间“响应—反馈”的水循环过程的内在属性。

4 结论

本文详细介绍了偏导法和析因数值实验法这两种归因方法,选取中国416个具有连续观测（1960-2014年）气象资料的台站数据,基于PenPan模型模拟了中国D20蒸发皿蒸发,比较了两种方法的归因结果,得到以下结论：
（1）重新率定了PenPan模型中的风速函数：

f_{q} (u_{2}) = 3.977 \times 10^{- 8} (1 + 0.505 u_{2})

,相比较于常用的Thom等的风速函数,使用新风速函数的PenPan模拟结果有了较大改进,RMSE从原始的38.83 mm/month降至26.03 mm/month,为更准确的模拟及分析中国D20蒸发皿蒸发提供基础。
（2）析因数值实验法能合理有效的对蒸发皿蒸发趋势变化进行定量归因分析,其归因效果略微优于偏导法的归因结果,尤其是对辐射项归因,析因数值实验法表现出一定优势。这说明,在能利用偏导法进行归因分析的情况下,析因数值实验法亦能表现出与之相当的归因分析能力。
（3）在偏导法无法直接获取复杂方程及模型的偏导解析式,从而进行归因分析的情况下,此析因数值实验法亦能对其进行归因分析,如Zhang等^[24]的研究。这意味着析因数值实验法在趋势变化归因研究中具有更广阔的应用前景,能为复杂水文气象过程敏感性分析提供基础,为定量分析气候变化研究及其致因提供可能。
（4）利用析因数值实验法的基准态信息来对偏导法归因结果进行校正,能有效改进偏导归因结果,进而对蒸发皿蒸发趋势变化进行更准确的归因分析,同时为其他基于偏导法的应用和分析提供更可靠的保障。
The authors have declared that no competing interests exist.

基于析因数值实验方法的蒸发皿蒸发归因研究

本站小编 Free考研考试/2021-12-29

A new method to attribute changes of pan evaporation: The experimental detrending approach

1 引言