删除或更新信息，请邮件至freekaoyan#163.com(#换成@)

滑动平均差检测法的提出及验证

本站小编 Free考研考试/2021-12-29

包为民, 沈丹丹, 倪鹏, 周俊伟, 孙逸群
河海大学水文水资源学院,南京 210098

Proposition and certification of moving mean difference method for detecting abrupt change points

BAOWeimin, SHENDandan, NIPeng, ZHOUJunwei, SUNYiqun
College of Hydrology and Water Resources, Hohai University, Nanjing 210098, China
收稿日期:2017-12-25
修回日期:2018-06-25
网络出版日期:2018-11-25
版权声明:2018《地理学报》编辑部本文是开放获取期刊文献，在以下情况下可以自由使用：学术研究、学术交流、科研教学等，但不允许用于商业目的.
基金资助:

国家重点研发计划专项(2016YFC0402703);中央级公益性科研院所基本科研业务专项(HKY-JBYW-2017-12);江苏省研究生科研与实践创新计划项目(KYCX17_0423);中央高校基本科研业务费专项资金(2017B 684X14)

作者简介:
-->作者简介：包为民(1956-), 男, 浙江省金华人, 教授, 博士生导师, 主要从事水文物理规律模拟方面研究。E-mail: wmbao163@163.com

展开

摘要
时间序列突变点的检测研究是当前气候变化问题的关键环节,其方法和成果也较多,传统的检测方法因统计量结构不合理、假设条件不符合实际以及受主观因素影响等,结果常常缺乏可信度。本文提出一种新的时间序列突变点的检测方法——滑动平均差检测法,将该方法分别用理想时间序列和实际观测序列进行应用检验,并与现有常用的4种突变检验方法比较,发现滑动平均差法具有：① 结构简单、物理意义明确;② 检测突变点更精确;③ 能同时检测出所有突变点的突变位置和其突变强度3个明显的优势。综合利用滑动平均差检测法和传统的4种方法,对黄河流域几个重点水文控制站实测输沙量资料进行突变分析,结果表明：黄河上游输沙量在1986年发生突变,黄河中游输沙量在1979年和1996年发生突变,华县站和潼关站输沙量在1979年、1996年和2003年发生突变,造成输沙量突变的主要因素为水利工程建设和大规模水土保持措施等人类活动。

关键词：滑动平均差检测法;时间序列;突变检验;黄河流域;输沙量
Abstract
The abrupt change point detection is an important content in the research of current climate change problem. And many methods and achievements have already been proposed. The results of traditional methods are often considered to be unpersuasive due to the irrational structure of statistics, ideal assumptions and subjectivity. In this paper, a new method called moving mean difference method for abrupt change points detection is proposed. It is compared with four widely used methods via both hypothetic series and observed data. The results show that the moving mean difference method has three advantages: (1) The method has a simple structure and definite physical meaning; (2) It is more accurate to detect the mutation point; (3) It can simultaneously detect all the mutation points and calculate the corresponding intensity of the mutations. The sediment discharge abrupt changes in different reaches of the Yellow River are analyzed through the five methods, based on the annual data obtained from the main hydrological stations in the Yellow River Basin. The results indicate that the sediment discharge in the upper reaches the river mutated in 1986, while that in the middle reaches changed suddenly in 1979 and 1996. The mutations of sediment discharge at Huaxian and Tongguan stations occurred in 1979, 1996 and 2003. The main factors for the mutation are human activities, including hydraulic engineering construction and large-scale water and soil conservation measures.

Keywords：moving mean difference method;time series;abrupt change point detection;Yellow River;sediment discharge

-->0
PDF (2014KB)元数据多维度评价相关文章收藏文章
本文引用格式导出EndNote Ris Bibtex 收藏本文-->
包为民, 沈丹丹, 倪鹏, 周俊伟, 孙逸群. 滑动平均差检测法的提出及验证[J]. 地理学报, 2018, 73(11): 2075-2085 https://doi.org/10.11821/dlxb201811003
BAO Weimin, SHEN Dandan, NI Peng, ZHOU Junwei, SUN Yiqun. Proposition and certification of moving mean difference method for detecting abrupt change points[J]. Acta Geographica Sinica, 2018, 73(11): 2075-2085 https://doi.org/10.11821/dlxb201811003

1 引言

突变理论最早可追溯至20世纪60年代末期,法国数学家R.Thom创立了以常微分方程为数学基础的突变理论^[1],其要点在于考察某种系统或过程从一种稳定状态到另一种稳定状态的飞跃^[2]。随后,突变理论在数学、生物、天文、气象、社会科学等领域得到了广泛的应用^[3,4,5,6,7]。从统计学的角度,可以把突变现象定义为从一个统计特性到另一个统计特性的急剧变化,如考察均值、方差等特征量的急剧变化^[8]。目前,常见的气候突变是指气候从一个平均值到另一个平均值的急剧变化,称为均值突变^[9]。迄今为止,针对均值突变的情形,已经发展出很多突变检测的方法,包括较为传统的低通滤波法、滑动t检验法、Cramer法、Yamamot法,以及后来被提出并广泛使用的Mann-Kendall突变检验法^{[10,11,12,13,14]}、Pettitt法、有序聚类分析（OC）法^[15]和BG（Bernaola-Galvan）分割法等^[16,17]。传统的4种方法都因检测结果带有主观性,所以缺乏可信度。而后4种方法虽解决了传统检测方法突变点漂移和受主观因素影响的缺点^[3],但统计量结构的合理性有待讨论,另外,这些方法都是基于序列只有一个突变点的假设条件,但是气候序列是多尺度的,大小涨落（距平）都有,且具有周期性变化的特点,因此,这些方法很难找出不同尺度和层次上的所有突变点,进而影响对突变成因的分析。因此,本文提出一种新的时间序列突变点的检测方法,并与现有常用的Mann-Kendall突变检验法、Pettitt法、OC法和BG分割法4种方法相比较,证明了该方法有诸多优点且行之有效。利用这种方法分析黄河中上游输沙量序列资料,探讨黄河泥沙的突变时间及可能的影响因素,为黄河水沙治理提供支撑。

2 滑动平均差检测法

时间序列突变点的检测,均以样本观测序列为基础,根据某种统计假设,计算其检测统计量,进而确定其突变点。这过程都会受到3个关键环节因素的影响：① 样本观测序列获得过程产生的误差,这包括基本资料观测误差、样本选择误差等。这类误差随机过程一般都具有零均值和常方差的平稳过程特征。② 时间序列本身所具有的周期性变化。这变化受时间变量本身的常规物理属性驱使,在一定的周期内有确定性变化规律,而周期与周期之间的均值接近常数。当时间变量的某个物理属性驱动因子出现异常,导致这周期均值出现显著改变时,就是时间序列要检测的突变点。③ 当检测时间序列具有反复变化（正向和反向交替出现或连续多个突变）的多个突变点时,如何能有效地检测出这些突变点,是突变检测方法的难点所在。
为解决第一个因素的影响,样本序列误差消除的有效方法是期望均值计算,而解决第二和第三个环节问题的有效手段是把周期均值作为考察变量,三个环节因素综合兼顾考虑,选择以时间变量常规物理周期为滑动期的滑动平均变量作为突变点的新考察序列是较为理想的。如时间序列X_i（i=1, 2, …, n）变量的常规物理周期为p,则可以构建正向滑动平均序列：

M U_{i} = \frac{1}{k} \overset{k}{\sum_{j = 1}} X_{i - j} i = 2,3, ?, n; k = \min (p, i - 1)

（1）
类似地可以构建逆向滑动平均序列：

M D_{i} = \frac{1}{k} \overset{k}{\sum_{j = 1}} X_{i + j - 1} i = 2,3, ?, n; k = \min (p, n - i + 1)

（2）
由式（1）和式（2）可知,MU_i和MD_i即第i个样本点前后两个子序列的均值。考察一个突变点的最简单理想时间序列（没有观测误差、突变点前后都为常数）,如：

X_{i} = \{\begin{matrix} 10,1 \leq i \leq 25 \\ 0,26 \leq i \leq 50 \end{matrix}

（3）
计算其正逆向滑动平均序列得：

M U_{i} = \{\begin{matrix} 10,2 \leq i \leq 26 \\ 36 - i, 27 \leq i \leq 36 \\ 0,37 \leq i \leq 50 \end{matrix} M D_{i} = \{\begin{matrix} 10,2 \leq i \leq 16 \\ 26 - i, 17 \leq i \leq 26 \\ 0,27 \leq i \leq 50 \end{matrix}

（4）
其正逆向滑动平均序列差为：

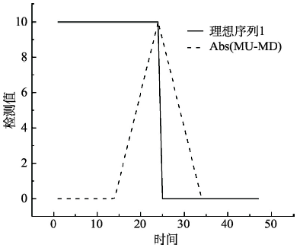
Δ M_{i} = |M U_{i} - M D_{i}| = \{\begin{matrix} \begin{matrix} 0,2 \leq i \leq 26 \\ i - 16,17 \leq i \leq 26 \end{matrix} \\ \begin{matrix} 36 - i, 27 \leq i \leq 36 \\ 0,37 \leq i \leq 50 \end{matrix} \end{matrix}

（5）
把序列（3）和（5）作图,如图1所示。发现正逆向滑动平均序列的最大差值正对应的点就是突变点I_cr,其含义为该点前后均值差值达到最大,而且其突变强度为其最大差值。因此,统计量ΔM_i的极大值点表示该样本点前后子序列均值发生了急剧变化,即极大值点有可能是突变点,由此提出时间序列突变点的滑动平均差位置检测指标为：

I_{cr} = \max_{i} \{Δ M_{i}\}

（6）

显示原图|下载原图ZIP|生成PPT
图1无误差单突变点真值序列和滑动平均差序列
-->Fig.1Single mutation point series without errors and moving mean difference series
-->

和强度检测指标M_cr：

M_{cr} = \frac{\max_{Δ M} \{Δ M_{i}\}}{M U_{Icr}}

（7）

3 不同检测方法理想时间序列突变点检验比较

由上节介绍可知,滑动平均差检测方法的结构很简单,其几何解释也非常直观易理解,但方法的合理性和准确性还有待检验。为此,这里把滑动平均差检测方法与目前较为常用的BG分割法、Mann-Kendall突变检验法、Pettitt法和OC法4种方法应用于理想序列进行突变点检测比较,分别从无误差单突变点、无误差多突变点和有误差多突变点3种情况进行检验分析。在理想序列的检验中,考虑到所构造的理想序列的特点,滑动平均法的滑动周期取p = 10。

3.1 无误差单突变序列检验

无误差单突变序列如式（3）所列样本,分别用5种检测方法进行检验,结果如表1、图2和图3所示。为了把不同检测指标序列显示在同一张图中,图中的样本序列和前4种方法的检测指标都进行了标准化转换。即：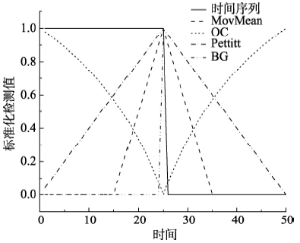

x_{i}^{'} = \frac{x_{i} - \min \{x_{i}\}}{\max \{x_{i}\} - \min \{x_{i}\}}

（8）

显示原图|下载原图ZIP|生成PPT
图2无误差单突变点时间序列各方法检测结果
-->Fig. 2Detection results of different methods on single mutation point series without errors
-->

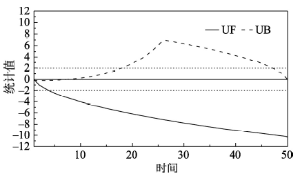显示原图|下载原图ZIP|生成PPT
图3无误差单突变点序列Mann-Kendall突变检验法检测结果
-->Fig. 3Detection result of Mann-Kendall method on single mutation point series without errors
-->

Tab. 1
表1
表1无误差单突变序列突变点检测结果
Tab. 1Detection results of single mutation point series without errors

检测内容	实际序列	MovMean	BG	OC	Pettitt	MannKendall
突变位置	25~26	25~26	25~26	25~26	25~26	No
检测值	10	10	1.64×10⁹	5.55×10^(-13)	625

新窗口打开
从表1和图2、图3结果可知,5种方法除Mann-Kendall突变检验法外,都准确地找出了突变点发生的位置,滑动平均差方法还准确地算出了突变强度。而Mann-Kendall突变检验法的两个序列根本就没有交点,所以没有探测出序列的突变点。

3.2 无误差多突变序列检验

无误差多突变点的序列,设计有5个突变点,其突变点发生的位置和各点的突变强度如表2所示,5种方法检测结果如表2和图4所示。
Tab. 2
表2
表2无误差多突变点序列检测结果
Tab. 2Detection results of multi-mutation points series without errors

检测内容	实际序列	MovMean	BG	OC	Pettitt	Mann-Kendall
突变位置1	15~16	15~16	15~16	15~16	15~16	No
检测值1	5	5	54.6	503.2	915	-
突变位置2	28~29	28~29	No	No	No	No
检测值2	2	2	-	-	-	-
突变位置3	43~44	43~44	43~44	43~44	43~44	No
检测值3	4	4	11.3	693.9	463	-
突变位置4	59~60	59~60	No	No	No	No
检测值4	3	3	-	-	-	-
突变位置5	76~77	76~77	76~77	76~77	76~77	No
检测值5	6	6	60.3	468.6	1037	-

新窗口打开

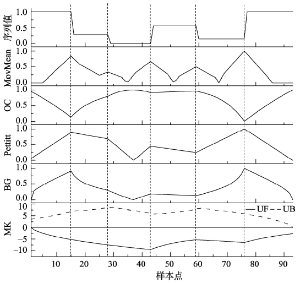显示原图|下载原图ZIP|生成PPT
图4无误差多突变点序列各方法检测结果
-->Fig. 4Detection results of different methods on multi-mutation points series without errors
-->

图4中的样本序列和前4种方法的检测指标都进行了标准化转换。由表2和图4结果可知,滑动平均差方法都一次检测出了所有突变点和其突变强度,而且位置和强度都没有误差。BG法和OC法检测出1和5两个突变点位置,Pettitt方法从统计量曲线上看有1、3和5三个局部极值点,但3突变点的信号较弱,没有通过其显著性水平检验,而对于2与4两个突变点BG法、OC法和Pettitt方法均没有检测出。按照这些方法设计,依次去除已检测出突变点的序列,再重复检测剩余序列,能检测出剩余的突变点。具体结果类似于3.1节的单突变点检测结果。同样的也只有Mann-Kendall突变检验法,对所有5个突变点都没有能检测出。
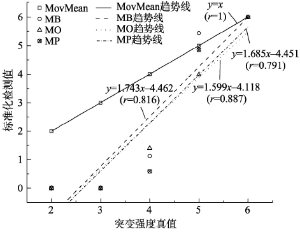
把表2各突变点突变强度与各方法突变点检测值进行比较,发现各方法突变点检测值都与其突变强度真值成正比关系（图5）。为把不同方法的检测值在同一图中方便表达,图5中进行了检测值数值转换,其转换公式为：

MB = 6 \times BG / 60.3

（9）

MO = 6 \times 68.6 / (OC - 400)

（10）

MP = 6 \times (Pettitt - 400) / 637

（11）

显示原图|下载原图ZIP|生成PPT
图5各突变方法检测值与突变强度真值关系图
-->Fig. 5The relationship between the detection value of each method and the true value of the mutation intensity
-->

各方法的检测值与实际突变强度比较,发现滑动平均差法的检测值等于其实际突变强度,方法构造信号检测值过程中没有损失其有效信息,所以所有突变点都准确无误的检测到了。而其他3种方法,构造信号检测值过程中都损失了有效信息,而且突变强度越低相对损失越大,所以对2和4两个突变点的突变强度低些,其有效信息就被全部损失而无法检测到了。这是这3种方法存在的共同缺点。
分析BG法、OC法和Pettitt法3种方法有效信息损失的原因,笔者认为主要是方法本身检测指标结构的不合理引起的。3种方法都有一个暗指的假设,即只有一个突变点,且突变点前和后为两个均值不同的平稳序列,所以当有多突变点时,突变强度低的点其信息被强度高的点所“掩盖”而不起作用。特别如BG分割法,检测指标式为

MO = |\frac{μ_{left} - μ_{right}}{s_{d}}|

（12）

s_{d} = {(\frac{s_{left}^{2} + s_{right}^{2}}{n_{left} + n_{right} - 2})}^{\frac{1}{2}} \times {(\frac{1}{n_{left}} + \frac{1}{n_{right}})}^{\frac{1}{2}}

（13）
式中：μ_left和μ_right分别为每个点左边子序列的平均值和右边子序列的平均值^{[3, 16]}。
其中,结构

{(\frac{1}{n_{left}} + \frac{1}{n_{right}})}^{\frac{1}{2}}

的最大值发生在两端（n_left×n_right为最小值时）、最小值发生在中间（n_left×n_right为最大值时）,与突变点毫无关系,所以不仅不能挖掘突变点的有效信息,而且还会提供与突变点无关的有害信息。

3.3 有误差多突变序列检验

有误差多突变序列,其真值序列和突变点同上,加入随机误差序列后,其突变点位置与突变强度如表3所示。
Tab. 3
表3
表3有误差多突变点序列检测结果
Tab. 3Detection results of multi-mutation points series with errors

检测内容	实际序列	MovMean	BG	OC	Pettitt	Mann-Kendall
位置1	15~16	15~16	15~16	15~16	17~18	No
检测值1	5	4.97	45.0	663	938	-
位置2	28~29	28~29	No	No	No	No
检测值2	2	1.83	-	-	-	-
位置3	43~44	45~46	No	No	No	No
检测值3	4	3.2	-	-	-	-
位置4	59~60	59~60	No	No	No	No
检测值4	3	2.9	-	-	-	-
位置5	76~77	76~77	76~77	76~77	76~77	85~86
检测值5	6	6.3	49.2	600	1006	-

新窗口打开
滑动平均差检测法、BG分割法、OC法、和Pettitt法4种方法检测结果与无误差多突变序列相差无几,依旧只有滑动平均差检测出了所有突变点且同时准确计算出了突变强度,而其他3种方法没有检测出突变强度较弱的3个突变点。Mann-Kendall突变检验法检测结果差别较大,该方法检测出序列的突变点在85~86位置,但这个突变点显然不是检测序列实际的突变点。

4 不同检测方法的实际时间序列检验结果分析

4.1 研究区及资料概况

20世纪70年代以来,由于气候变化和人类活动的双重影响,黄河水沙条件发生了巨大变化,黄河水沙特别是泥沙量发生趋势性锐减。潼关站平均输沙量从天然情况的16亿t减至不足1亿t^{[18,19,20,21,22,23]}。依地理位置和河流特征,黄河可分为上、中、下游三段,其中由内蒙古托克托县的河口镇至龙门为中游段,流经黄土高原和丘陵区,水土流失尤为严重,是黄河泥沙的主要来源区,因此,本文选取黄河中游干流控制站头道拐、龙门和潼关,窟野河控制站温家川、汾河控制站河津以及渭河控制站华县6个水文站点的年输沙量序列,检验不同方法在实际序列中的检测效果。站点基本情况介绍如表4所示,研究区和站点位置如图6所示。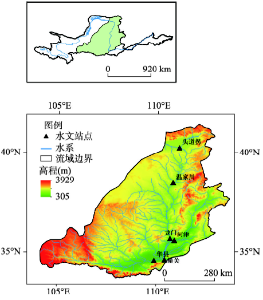

显示原图|下载原图ZIP|生成PPT
图6研究区和站点位置图
-->Fig. 6Study region and location of the hydrological stations
-->

Tab. 4
表4
表4水文站点基本信息
Tab. 4Information of the hydrological stations

站名	水系	经度(E)	纬度(N)	控制面积(km²)	资料系列
头道拐	黄河干流	111°04′	40°15′	367898	1964-2015
温家川	窟野河	110°45′	38°29′	8515	1960-2015
龙门	黄河干流	110°35′	35°40′	497552	1964-2015
河津	汾河	110°48′	35°34′	39728	1964-2015
华县	渭河	109°46′	34°35′	106498	1962-2015
潼关	黄河干流	110°18′	34°37′	682166	1950-2015

新窗口打开

4.2 潼关断面年输沙量突变点检测

年输沙量时间序列通常都包含年输沙量观测过程产生的误差和样本序列的年际周期变化。降雨等气候因子、植被变化和人类活动等是引起水文序列变化的主要因素,为了研究人类活动和植被变化对水文序列的影响,准确检测出水文序列的突变点,应尽可能减小或抵消降雨等气候因子的周期震荡对水文序列突变点检测的影响。因此,滑动平均差检测法的滑动周期应取气候周期,以消除气候震荡带来的误差。滑动周期太短抵消不了样本序列的观测误差和年际波动,容易造成突变点的漂移,而滑动周期过长,会导致序列过渡平滑,淹没突变点。结合黄土高原地区地形及气候变化周期特点,本研究中滑动平均差检测法的滑动周期取p = 16 a,潼关断面1950-2015年输沙量序列和不同方法的计算结果如图7所示。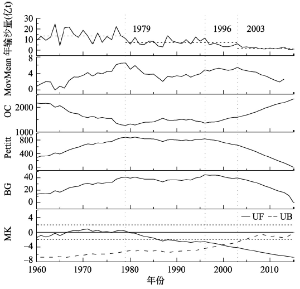

显示原图|下载原图ZIP|生成PPT
图7潼关输沙量检测结果
-->Fig. 7Detection results of sediment discharge at Tongguan Station
-->

从图7结果看,滑动平均差法检测出两个显著的突变点,分别在1979年和2003年,对应的突变强度分别为6.528和5.467。OC法和Pettitt法检测出突变点在1979年,BG法方法检测出的突变点在1996年,Mann-Kendall法UF和UB曲线在2000年有一个交点,但该交点不在0.1置信区间内,因此该交点不能算显著突变点。但从BG法、OC法和Pettitt法4种方法统计量曲线来看,曲线都有两个明显的极值点,第一个极值点在1979年,据年输沙量序列和滑动平均差检测结果可知,1979年前后的突变强度最大,所以该突变点的检测结果较为一致和可信;第二个极值点在1996年,从滑动平均差法曲线可以看出1996年也是一个局部极值点,突变强度为4.868,相较于1979年和2003年,该点的突变强度较弱。BG法检测出的最大突变点不是发生在均值变化最大的1979年,而是发生在突变强度很弱的1996年,且2003年应该是突变强度仅次于1979年的突变点,但BG法、OC法和Pettitt法均没有检测出。这均是由“序列只有一个突变点”的暗指假设与实际不符所导致的。综上,潼关站输沙量序列有两个显著突变点,分别发生在1979年和2003年。

4.3 其他序列突变点检测检验

头道拐、龙门、温家川、河津和华县五个断面年输沙量序列各方法的检测结果如表5所示。分析表5可得,① 当时间序列有且仅有一个突变点,且为显著突变（如头道拐年输沙量序列）时,5种方法均可检测出该突变点,且结果基本一致;② 当突变点为两个或两个以上时,只有滑动平均差检测法能同时一次性准确检测出所有突变点及相应的突变强度,BG法、OC法和Pettitt法检测出的突变点也都是滑动平均差法检测出的突变点之一,但不一定是最大突变强度的突变点,甚至出现检测出的突变点是几个突变点中突变强度最弱的情况,即3种方法都存在着突变点漂移的问题;③ Mann-Kendall方法在序列存在多个突变点的时候,统计曲线在其置信区间内无交点,找不到突变点,方法几乎崩溃。
Tab. 5
表5
表5本研究其他5个水文站点年输沙量序列检测结果
Tab. 5Detection results of sediment discharge at the other five selected stations

站名	检测内容	MovMean	OC	Pettitt	BG	Mann-Kendall
头道拐	位置1	1986	1985	1986	1985	1985
头道拐	突变强度	0.76	13.77	561	29.44	-
龙门	位置1	1979	1979	1979	1979	No
	突变强度	5.76	711.68	468	27.44	-
	位置2	1996	1996	1996	1996	No
	突变强度	4.31	840.43	591	29.05	-
温家川	位置1	1979	1979	1979	1979	No
	突变强度	0.66	27.86	460	21.94	-
	位置2	1996	1996	1996	1996	No
	突变强度	0.69	26.76	663	29.83	-
河津	位置1	1979	1979	No	1979	No
	突变强度	0.24	0.77	-	26.08	-
	位置2	1996	No	1996	No	No
	突变强度	0.044	-	585	-	-
华县	位置1	1979	1979	No	-	No
	突变强度	1.75	204.85	-	-	-
	位置2	1996	1996	1996	1996	No
	突变强度	1.48	204.34	503	23.96	-
	位置3	2003	No	No	2003	No
	突变强度	1.87	-	-	24.14	-

新窗口打开
黄河流域上游输沙量在1986年发生显著突变,20世纪80年代,黄河上游生产生活用水大大增加,比50年代增长约52%^[24],且20世纪60年代后,黄河上游干流水利工程的修建极大地改变了上游水沙的年际和年内分配,如1986年龙羊峡水库建成后,与刘家峡水库联合调度,拦蓄了大量的径流和泥沙^[25],使上游输沙量大大降低;黄河中游段输沙量主要有两个突变点,分别在1979年和1996年,黄河中游段流经黄土高原,20世纪70年代后黄土高原大规模的水土保持措施对水沙的减少有很大的促进作用^[26],90年代初期,黄土高原地区进一步展开水土保持二期治理工程（包括退耕还林、封山禁牧和大量的植树造林）,使得植被覆盖度进一步增加,水沙进一步锐减^[27]。渭河流域在1979年、1996年和2003年发生突变,且2003年和1979年为主要突变点,这一结果与潼关站检验结果相一致。潼关站在黄河流域干流的下游,来水来沙由龙门、汾河、北洛河和渭河共同组成,各种人类活动的综合作用是黄河流域输沙量减少的主要原因^[28]。

5 结论

（1）本文提出了一种新的突变点检测方法——滑动平均差检测方法,该方法能同时检测出时间序列的多个突变点及相应的突变强度。将该方法运用到理想时间序列和实际观测时间序列中进行检验,并与现有常用的4种突变检验方法的检测结果作比较,发现传统4种方法存在如下不足：① 4种方法都有“序列只有一个突变点”的默认假设,当实际情况与假设条件不符时,则统计量计算会损失有效信息而使突变强度较低的突变点无法检测出;② BG法的指标结构不太合理。而滑动平均差检测方法比较这4种检测方法具有3个明显的优势：一是结构简单、直观易理解;二是检测突变点更精确;三是能同时检测出所有突变点的突变位置和突变强度,这为流域水沙突变点检测提供了较为科学、准确的方法,值得推广使用。
（2）对黄河流域几大重点水文控制站输沙量资料进行突变分析,结果显示：黄河流域上游输沙量在1986年发生显著突变;中游段输沙量在1979年和1996年发生突变,其中1979年为主要突变点;渭河流域和潼关站输沙量有两个主要突变点,分别在1979年和2003年,大型水利工程建设和大规模水土保持措施的实施等人类活动是导致黄河流域泥沙突变的主要因素。
The authors have declared that no competing interests exist.

滑动平均差检测法的提出及验证

本站小编 Free考研考试/2021-12-29

Proposition and certification of moving mean difference method for detecting abrupt change points

1 引言

2 滑动平均差检测法