删除或更新信息，请邮件至freekaoyan#163.com(#换成@)

中国城市能源消费碳排放的区域差异、空间溢出效应及影响因素

本站小编 Free考研考试/2021-12-29

王少剑¹^,, 苏泳娴²^,³, 赵亚博⁴

1. 中山大学地理科学与规划学院广东省城市化与地理环境空间模拟重点实验室,广州 510275

2. 广州地理研究所,广州 510070

3. 广东省地理空间信息技术与应用公共实验室,广州 510070

4. 广州大学地理科学学院,广州 510006

Regional inequality, spatial spillover effects and influencing factors of China's city-level energy-related carbon emissions

WANGShaojian¹^,, SUYongxian²^,³, ZHAOYabo⁴

1. Guangdong Provincial Key Laboratory of Urbanization and Geo-simulation, School of Geography and Planning, SunYat-sen University, Guangzhou 510275, China

2. Guangzhou Institute of Geography, Guangzhou 510070, China

3. Guangdong Open Laboratory of Geospatial Information Technology and Application, Guangzhou 510070, China

4. School of Geographical Sciences, Guangzhou University, Guangzhou 510006, China

收稿日期:2017-04-21
修回日期:2017-11-18
网络出版日期:2018-03-21
版权声明:2018《地理学报》编辑部本文是开放获取期刊文献，在以下情况下可以自由使用：学术研究、学术交流、科研教学等，但不允许用于商业目的.
基金资助:

国家自然科学基金项目(41601151)

广东省自然科学基金项目(2016A030310149)

广州市珠江科技新星

作者简介:
-->作者简介：王少剑(1986-), 男, 河南驻马店人, 博士, 副教授, 中国地理学会会员(S110011019M), 主要研究方向为城市地理、城市与区域规划。E-mail: 1987wangshaojian@163.com

展开

摘要
基于1992-2013年中国城市遥感模拟反演碳排放数据,采用空间自相关、空间马尔科夫矩阵和动态空间面板数据模型,在同时考虑碳排放的时空滞后效应和不同地理经济空间权重矩阵的条件下,对城市碳排放的演化路径和关键影响因素进行了定量识别和减排政策探讨。研究表明,中国城市能源消费碳排放的区域差异正逐步缩小,空间上呈现出明显的高排放俱乐部集聚特征,同时碳排放类型演化具有明显的路径依赖特征;面板数据模型估计结果表明经济增长与人均碳排放呈现显著的倒“U”型曲线关系,而绝大多数城市的人均碳排放处于随经济发展而增加的阶段,二产偏重的经济结构和投资的粗放增长共同正向作用于城市碳排放,而人口的集聚效应、技术水平的提升、对外开放度和公路运输强度的增加则共同抑制城市碳排放水平的提高。因此未来要抑制促增因素和发挥促降因素的作用才能有效降低城市碳排放;优化产业结构、精简粗放投资、增加研发强度以及提升公路通达性是未来实现中国城市节能减排的有效途径。

关键词：城市碳排放;空间溢出效应;动态空间面板模型;减排政策;EKC曲线;中国
Abstract
Carbon emissions are increasing due to human activities related with the energy consumptions for economic development. Thus, attention has been paid to the reduction of the growth of carbon emissions and formulation of policies for addressing climate change. Although most studies have explored the driving forces behind carbon emissions in China, literature lacks studies at the city-level due to a limited availability of statistics on energy consumptions. In this study, based on China's city-level remote sensing carbon emissions from 1992 to 2013, we applied the spatial autocorrelation, spatial Markov-chain transitional matrices, dynamic spatial panel model and Sys-GMM to empirically estimate the key determinants of carbon emissions at the city-level and discuss its spatial spillover effects in consideration of spatiotemporal lag effects and different geographical and economic weighting matrices. Results indicated that the regional inequalities of city-level carbon emissions decreased over time and presented an obvious spatial spillover effect and high-emission "club" agglomeration. In addition, the evolution of the emission pattern has the characteristic of obvious path dependence. Panel data analysis results indicated that there was a significant U-shaped curve that can reflect the relationship between carbon emissions and GDP per capita. In addition, carbon emissions per capita are increasing with economic growth for most cities. High-proportion of secondary industry and extensive growth of investment exerted significantly positive effects on China's city-level carbon emissions. Conversely, rapid population agglomeration, the improvement of technology level, the increase of trade openness and road density play an inhibiting role in carbon emissions. Therefore, in order to reduce carbon emissions, the Chinese government should inhibit the effects of promotion factors and enhance the effects of mitigation factors. Combining with the analysis of results, we argued that optimizing the industrial structure, streamlining the extensive investment, increasing the level of technology and improving the road accessibility are the effective ways to increase energy savings and reduce carbon emissions in China.

Keywords：carbon emissions;spatial spillover effect;dynamic spatial panel data model;emission policies;EKC curve;China

-->0
PDF (3312KB)元数据多维度评价相关文章收藏文章
本文引用格式导出EndNote Ris Bibtex 收藏本文-->
王少剑, 苏泳娴, 赵亚博. 中国城市能源消费碳排放的区域差异、空间溢出效应及影响因素[J]. 地理学报, 2018, 73(3): 414-428 https://doi.org/10.11821/dlxb201803003
WANG Shaojian, SU Yongxian, ZHAO Yabo. Regional inequality, spatial spillover effects and influencing factors of China's city-level energy-related carbon emissions[J]. Acta Geographica Sinica, 2018, 73(3): 414-428 https://doi.org/10.11821/dlxb201803003

1 引言

化石能源的大量消耗,使得以气候变暖为主要特征的全球气候变化成为最受关注的国际环境问题,减少温室气体排放,推行低碳发展已刻不容缓^[1]。自《京都协议书》生效以来,各国对低碳经济发展模式开始逐步重视。在2009年的哥本哈根世界气候大会上,与会各国达成了减排的基本共识。中国是第一个提出节能减排目标的发展中国家,中国政府承诺,2020年碳排放强度将会降至2005年55%~60%^[2]。2014年11月中国政府在“中美气候变化联合声明”提出2030年左右碳排放将达到峰值且争取尽快实现^[3,4]。随后很多地方政府也陆续颁布了各自的低碳行动计划,彰显了“低碳”发展的决心。
中国已成为碳排放大国,尽管存在能源资源消耗量过大等问题,但同时也是发展方式粗放、产业结构偏重、排放绩效偏低和环境治理低效等一系列问题综合影响的结果^[5]。节能减排是减缓全球变暖的关键措施,同时也是倒逼经济发展方式转变和产业结构转型升级的重要途径。然而引致碳排放的社会经济因素众多^[6],在碳减排的背景下,定量识别影响碳排放的因素、量化关键因子的作用机理,将有助于制定切实可行的减排措施^[7]。由于中国实行自上而下的能源统计系统,统计部门仅公开了省域和少数发达城市的能源消费平衡表,受此限制,学界目前主要从国家和区域层面对碳排放进行研究,而对全国城市尺度碳排放的影响机制与减排策略所开展的系统研究却较为匮乏^[8]。已有研究表明,城市地区消耗了全球60%~80%以上的能源,排放了全球70%以上的温室气体;显然,城市地区已成为节能减排的重要区域^[9,10]。因此,以城市为基本分析尺度,开展关于全国碳排放影响机制和减排策略的研究,对指导低碳经济发展将具有重要的理论与现实意义。
近年来,国内外****对不同尺度的碳排放及其成因做了大量分析研究,这些研究从研究方法上来看主要可以分为以下四类。① 在投入产出分析框架下,结合投入产出表和投入产出模型,通过结构分解技术（SDA）对碳排放的影响因素进行识别^[11,12,13]。例如,王长建等利用改进的IO-SDA技术,分析了新疆的碳排放影响因素,发现经济规模和人口规模是引起碳排放变化的重要指标^[14]。Feng等发现1997-2007年美国经济增长是促进碳排放增加的第一驱动要素,而2007-2013年能源结构的变化则是抑制其碳排放增长的重要因素^[15]。然而这类研究往往依赖投入产出表进行非连续性的跨期分析,而且分析的影响因素种类也十分有限,不能较为全面的考察多类社会经济指标的影响。② 基于扩展和改进的Kaya恒等式,通过指数分解技术（IDA）对能源消费碳排放的要素进行分析^[16,17]。例如,王长建等采用LMDI法发现人口规模效应与经济产出效益促使新疆能源消费碳排放增加,而能源替代与能源结构效应则使其减少^[18]。Yao等通过IDA发现经济与人口的增长是驱动G20国家碳排放增长的第一要素,而能源效率的提高和碳排放强度的降低是抑制碳排放增长的关键因素^[19]。虽然IDA可以通过恒等变换对碳排放进行完全无剩余分解,但其考虑的社会经济因素却有限,较少涉及交通、贸易等因素对碳排放的影响^[20]。③ 基于可计算一般均衡模型（CGE）对经济产业结构优化、科技水平、清洁能源替代率与不同减排政策组合进行情景分析。尽管CGE模型可以在一般均衡条件下模拟各社会经济因素与碳排放之间的关系,但其模拟分析主要依托投入产出表进行,所以对碳排放的研究也很难进行时间上的连续研究^[21,22]。④ 依靠计量经济模型来研究影响碳排放的因素^[23,24]。计量分析方法可以对多项社会经济因素进行时间序列的分析,从而可以考察时间上连续的多种指标对碳排放的动态影响。然而,上述四类方法大都将碳排放单元看作是均质个体且相互独立,却忽略了各单元之间的空间联系和相关性,即使有少数研究关注了这一问题^{[5, 25]},但其研究方法采用的是不考虑碳排放变化“路径依赖”特征和解释变量“内生性”问题的空间计量方法,所构造的空间权重矩阵也是最为简单的邻接矩阵,没有考虑不同权重矩阵对研究结果的影响^[26]。
基于以上分析,本文以中国城市单元的碳排放为研究对象,采用动态空间面板数据模型,对中国城市碳排放的区域差异、空间溢出效应和驱动机制进行了较为全面的考察。首先利用基尼系数和泰尔指数^[27,28]分析了城市碳排放的区域差异,创建地理、经济和地理经济等3种距离空间权重矩阵,利用空间自相关和空间马尔科夫链方法对中国城市碳排放的空间溢出效应进行了实证分析;并采用系统广义距估计方法,在同时考虑城市碳排放的时间滞后、空间滞后和时空滞后效应下,对城市碳排放影响因素进行了较为全面的分析。本文旨在通过以上一系列探索性研究工作,分析中国城市碳排放的区域差异及空间溢出效应,识别影响碳排放的关键因素,从而为科学制定中国城市的节能减排政策提供依据。

2 研究方法与数据来源

2.1 基于全域和局域空间自相关分析碳排放的空间集聚特征

文章采用ESDA中的空间自相关分析法对城市碳排放的空间溢出效应进行检验。全域空间自相关一般采用Moran's I系数进行考察,其具体的模型表达为^[5]：

\begin{matrix} I = \frac{[m \overset{m}{\sum_{i = 1}} \overset{m}{\sum_{j = 1}} ω_{ij} (x_{i} - \overset{?}{x}) (x_{j} - \overset{?}{x})]}{[\overset{m}{\sum_{i = 1}} \overset{m}{\sum_{j = 1}} ω_{ij} \overset{m}{\sum_{i = 1}} (x_{i} {- \overset{?}{x})}^{2}]} \end{matrix}

（4）
式中：m为全国城市的数量;w_ij表示空间权重;x_i、x_j分别为i城市和j城市的人均碳排放;

\begin{matrix} \overset{?}{x} \end{matrix}

为全国城市人均碳排放均值。为了对城市碳排放的空间关联特征进行较为全面的检测,本文根据已有文献建立了两种空间权重矩阵。一种是地理空间权重矩阵（W₁）,其权重w_ij用各城市之间距离的倒数来表示。考虑到城市经济体之间一般会存在空间关联的情况,为增强结果的可对比性,本文采用了经济发展背景下的经济距离权重矩阵（W₂）,其权重w_ij表示i城市人均收入均值与j城市人均收入均值绝对值差的倒数。如果单纯的以地理或经济权重来考虑空间关联性可能会存在偏差,本文还考虑了地理权重与经济权重嵌套的矩阵（W₃）,W₃= （1-α）W₁+αW₂,α的取值范围在0~1之间,α表示以经济构建的权重所占的比例,在本文中α取值为0.5,即地理空间权重等于经济权重。W₃同时考虑了地理空间权重的影响,同时也反映了经济水平存在空间溢出效应的事实,所以可以更加全面客观的反映城市碳排放的空间关联模式。
全域空间自相关忽略了局部地区空间的非典型特征,而局域空间自相关检验则有助于弥补这一不足。局域Moran's I指数是普遍使用的局域空间指标,其可表示为^[26]：

\begin{matrix} I_{i} = [(x_{i} - \overset{?}{x}) / S^{2}] \times \sum ω_{ij} (x_{j} - \overset{?}{x}); ? ? S^{2} = \frac{[\sum (x_{i} {- \overset{?}{x})}^{2}]}{m} \end{matrix}

（5）
式中：I_i>0,表示高碳排放城市与低碳排放城市在空间上分别集聚,分别形成高—高型和低—低型的空间格局;I_i<0,则表示高碳排放城市与低碳排放城市错位集聚,分别形成高—低型和低—高型格局。

2.2 基于空间马尔科夫链分析碳排放的空间溢出效应

通过马尔科夫链和空间马尔科夫链方法可以较好地分析城市碳排放过程中的空间相互作用关系（空间溢出效应）。马尔科夫链是一种离散的马尔可夫过程^[29]。首先将城市人均碳排放分为K种类型,再分别计算各个类型所占城市总数的概率以及其转移概率的未来变化^[30]。元素m_ijt表示t年到t+1年某城市人均碳排放所属类型由i转变为j的概率。相邻两年的概率矩阵关系可以表示为：

\begin{matrix} R_{t + 1} = M \times R_{t} \end{matrix}

（6）
式中：M为K×K的转移矩阵;R_t为t年份K种类型的概率矩阵^[30]。
空间马尔科夫法由马尔科夫法与空间滞后相结合而形成^[30],它将传统转移矩阵分解为条件转移矩阵。元素m_ijt(k)表示以城市人均碳排放类型在t年份属于i为空间滞后条件,从而计算在t+1年份碳排放类型由i转为j的转移概率。通过对比空间与非空间矩阵中相对应的元素,能得出城市碳排放类型转移的概率与周围相邻城市间的关系,可以揭示以不同类型城市为邻居下的城市碳排放类型转移的空间溢出效应。如果相邻城市碳排放类型对特定城市碳排放类型转移没影响,则有两矩阵中对应的所有元素都相同^[30]。参考已有研究成果,空间溢出效应的分析主要是基于人均指标来实现的^[29,30]。

2.3 城市碳排放影响因素的计量模型设定

为了更好地揭示城市碳排放空间溢出效应的影响因素,本文改进了两种动态空间面板数据模型来分别探测城市碳排放的空间依赖特征和空间误差特征。城市碳排放可表示为^[26]：

\begin{matrix} C E_{it} = α_{1} X_{it} + ρ \sum ω_{ij} C E_{jt} + γ \sum ω_{ij} C E_{jt - 1} + μ_{it} \end{matrix}

（7）

\begin{matrix} C E_{it} = β_{1} X_{it} + ξ μ_{t - 1} + λ \sum ω_{ij} μ_{it} + φ_{it} \end{matrix}

（8）
式中：CE为城市的人均碳排放量;i代表截面城市;t代表年份;X为自变量组成的特征向量;α₁和β₁为系数自变量向量;

\begin{matrix} φ_{it} = ε_{it} + μ_{it} \end{matrix}

,ε_it和μ_it是服从正态分布的扰动项;ρ是当期空间滞后系数;γ是滞后一期空间滞后效应系数,λ为空间误差系数。
公式（7）和（8）设立的条件是,城市碳排放量会随本城市相应影响因素的变化而立马做出相应变化,也即是说自变量和因变量之间不存在调整性的时间滞后效应。但事实上包括碳排放在内的社会经济变量演化趋势通常都呈现出一定的路径依赖特征,即当期的变化势必会受到前期或者上一期的本底水平的影响。一些影响城市碳排放的关键因素,如人口密度、产业结构、外商直接投资等因素的自身变化就具有明显的滞后性和依赖特征,从而可能相应的使得城市碳排放的预期变化也随之滞后。所以,对城市碳排放量变化的时间滞后效应进行检测具有十分重要的现实意义。基于此,本文将式（7）和式（8）进行局部调整,从而得到动态空间面板数据模型的空间滞后效应和空间误差效应的计算公式：

\begin{matrix} C E_{it} = θC {E_{it}}_{- 1} + α_{1} X_{it} + ρ \sum ω_{ij} C E_{jt} + γ \sum ω_{ij} C E_{jt - 1} + μ_{it} \end{matrix}

（9）

\begin{matrix} C E_{it} = θ^{'} C E_{it - 1} + β_{1} X_{it} + ξ μ_{t - 1} + λ \sum ω_{ij} μ_{it} + φ_{it} \end{matrix}

（10）
式中：θ和θ'分别为时间滞后系数,用来衡量时间滞后效应的强度,表示上一年碳排放对当期碳排放的影响。值得提出的是动态空间面板数据模型能够更加全面地对城市碳排放的滞后效应进行考察,检测的滞后效应包括时间滞后、空间滞后和时空滞后效应。

2.4 变量选取

环境库兹涅茨曲线（EKC）理论和IPAT模型是研究环境压力影响因素的常用理论,本文将依据二者共同来研究城市碳排放的影响因素。IPAT模型的扩展形式STIRPAT模型的面板形式为：

\begin{matrix} I_{it} = a P_{it}^{b} A_{it}^{c} T_{it}^{d} e \end{matrix}

（11）
式中：I、P、A和T分别表示环境压力、人口数据、人均收入和科技水平;e为误差项。对等式两边同时取对数后模型可表示为^[4]：

\begin{matrix} \ln I_{it} = a + bln P_{it} + cln A_{it} + dln T_{it} + e_{it} \end{matrix}

（12）
STIRPAT模型的优点是可以对各系数a、b、c和d作为参数进行估计,同时又允许对模型中的变量进行分解^[4]。具体而言,在本文中表示城市人均碳排放量CE,对于等式右边的影响因素及其指标的选择说明如下：① 人口密度（POPD）。人口密度用来代替式中的城市人口规模,用来探讨人口集聚对于碳排放的影响。通常人口集聚通常可以通过规模效应和集聚效应对碳排放造成影响,一是人口规模的增加势必会造成直接和间接能源消耗的增加,进而提高排放量;一是由于人口集聚产生的集聚效应,会在一定程度上的改善科技水平,从而降低排放量。② 经济增长（GDPPC）。经济增长通常用人均GDP表示,用来考察传统的EKC假设,检测城市人均碳排放和经济增长之间是否会出现倒U型曲线,本文用人均GDP的一次项和二次项来探究碳排放与经济增长之间的关系。③ 技术水平（TC）。考虑到城市尺度相关数据的匮乏性,本文采用科学事业费用支出来表征技术水平,通常其值越大反映各城市的研发投入强度越大。④ 产业结构（SIND）。来自第二产业（特别是重工业）的化石能源的燃烧是人为碳排放的重要组成部分。本文选用第二产业增加值占GDP的比重来反映产业结构对城市碳排放的影响。⑤ 路网密度（ROAD）。在考虑同样交通运输量的情况下,路网密度越大,交通拥堵越轻,从而机动车尾气排放的效率就会越高。本文用单位面积公路里程数来探究交通因素对城市碳排放的影响。⑥ 固定资产投资（FAI）。中国大部分城市的经济增长是投资拉动型,而粗放型的投资对产业结构调整和科技水平提高都有显著影响。文章用城市固定资产投资来分析投资水平对碳排放的影响。⑦ 对外开放（TO）。由城市实际利用外资额占GDP比重来反映对外开放程度对城市碳排放的影响。使用外资对碳排放具有双重影响,一方面,有****认为通过利用外资可以更多引进环境友好型技术来提高能源利用效率,进而降低能源利用碳排放;另一方面,有****认为外资的引入会通过高能耗和高排放产业向东道国转移碳排放进而提高了能源利用碳排放量。

2.5 数据来源

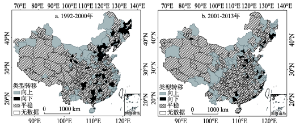
由于中国实行的是自上而下的能源统计制度,目前只有区域尺度具有能源消费平衡表,在城市尺度能源消费数据十分匮乏,只有少数发达地区的城市除外,为解决城市碳排放历史数据缺失的问题,本文采用已有能源统计资料和夜间灯光数据的模拟反演来核算城市尺度碳排放,具体方法可参看Su等^[31]、Zhu等^[32]和Wang等^[33]的研究。首先根据IPCC温室气体排放清单核算具有城市能源消费数据的能源消费碳排放,其次根据DMSP/OLS夜间灯光影像,获取城市范围内的夜间灯光数据,并统计夜间灯光总值,然后与相应的碳排放量统计值进行拟合分析,为确保碳排放量模拟值的可靠性,将其与基于统计数据计算的地级市碳排放量进行比照,结果发现,模拟的碳排放量与统计数据计算值的相对误差为7.65%。可见,基于夜间灯光数据模拟所得碳排放量的精度良好,可用来开展全国碳排放量的区域差异及影响机制研究,考虑到篇幅的限制,部分年份模拟反演的城市人均碳排放数据如图1所示。除城市碳排放外,其他相关数据均来源于《中国城市统计年鉴》、《中国区域经济统计年鉴》及各相关省市的年鉴。在进行模型回归时剔除了社会经济指标统计不全的城市。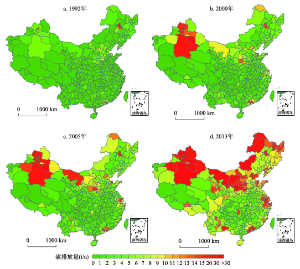

显示原图|下载原图ZIP|生成PPT
图11992-2013年中国城市碳排放的时空格局变化
-->Fig. 1Spatiotemporal pattern of per capita carbon emissions at city level in China, 1992-2013
-->

3 研究结果与分析

3.1 城市碳排放的区域差异及空间溢出效应检验

在探讨城市碳排放的空间溢出效应之前,本文首先关注的是城市碳排放的变化趋势和区域差异。图2表明中国城市人均碳排放呈逐年上升的趋势。1992-2013年,中国城市人均碳排放量从1.72 t增至10.37 t,年均增长8.93%。同时借助于基尼系数发现,在1992-2013年期间,城市碳排放的区域差异正在逐步缩小,基尼系数从1992年的0.72逐步下降到2013年的0.32。由此,虽然全国城市人均碳排放呈上升趋势,而城市间的差异正逐步降低。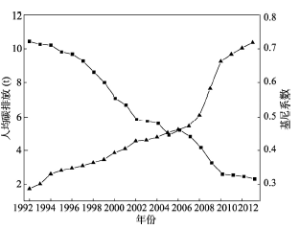

显示原图|下载原图ZIP|生成PPT
图21992-2013年中国城市人均碳排放及其基尼系数
-->Fig. 2Average per capita carbon emissions at city level and its Gini index in China, 1992-2013
-->

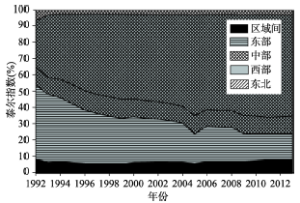
泰尔指数作为测度区域差异众多方法中的一种,相比于基尼系数,在识别区域组间和组内差异上具有较大的优势,因此常被用来分析区域组间和组内差异对整体区域差异的贡献性。对中国东部、中部、西部和东北地区城市人均碳排放组内差异及其组间差异进行分析,结果表明（图3）,1992-1995年期间,东部城市间的人均碳排放差异对城市人均碳排放总体差异的贡献最大,其次是西部、中部、区域间和东北。1995-2013年期间,西部城市间的人均碳排放差异贡献率最大,并呈逐步升高趋势;东部城市间的人均碳排放差异贡献额逐步缩小,而中部、东部和区域间的贡献性呈微弱的波动性变化。要探讨其形成原因,首先是东部城市人均碳排放虽然呈逐步升高趋势,但其城市间的碳排放差异正逐步缩小,这说明东部城市间的能源消耗和产业结构有趋同趋势,逐步向可再生能源为主的能源消费结构和服务业为主的产业结构演化;其次是西部城市人均碳排放在呈上升趋势的同时,城市间的碳排放差异也在逐步增加,这说明在经济增长的过程中,西部城市对化石能源依赖的程度呈现出显著的差异。

显示原图|下载原图ZIP|生成PPT
图31992-2013年中国四大区域内部及区域间人均碳排放差异对碳排放总体差异的贡献率
-->Fig. 3The contributions of reginal inequalities between groups and within groups to overall inequality of per capita carbon emissions at city level in China, 1992-2013
-->

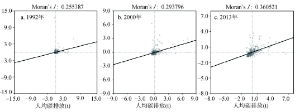
无论是基尼系数或是泰尔指数及其分解都没有考虑数据的空间相关性,地理学第一定律揭示任何空间事物及其属性都相关,且相关性与空间距离呈反比。在分析区域事物发展演化的过程中,如果忽略了事物的空间自相关性,势必会对结果造成影响或偏差。基于此,本文计算了不同权重（W₁、W₂、和W₃）的全域空间自相关,结果显示在W₁和W₃权重矩阵下,全域Moran's I值均大于0且均具有不小于1%的显著性,表明城市人均碳排放呈现出了高值集聚区和低值集聚区的空间正相关特征。但在经济权重（W₂）下全域Moran's I均不具有显著性,说明城市人均碳排放并不具有单纯的经济发展差异的空间关联特征,而是在地理、地理和经济的综合空间上呈现出空间自相关性。全域空间自相关反映了空间数据的整体空间关联特征,但往往也会忽略局部地区的空间的非典型性特征。因此,文章通过局部空间自相关监测来探究局部城市人均碳排放的区域空间集聚特征。图4给出了地理空间权重矩阵下3个代表年份全国城市人均碳排放分布的散点图,其纵轴为城市人均碳排放的空间滞后值,横轴为标准化的城市人均碳排放量。从图4可知,大部分城市位于第一象限和第三象限,从而更进一步的说明城市人均碳排放存在显著的高排放和低排放俱乐部集聚特征。

显示原图|下载原图ZIP|生成PPT
图4部分年份地理空间权重矩阵下中国城市人均碳排放的局域关联性的散点图
-->Fig. 4Moran scatterplot of per capita carbon emissions at city level using geospatial weight matrix for selected years
-->

虽然空间自相关分析揭示了城市人均碳排放的全域或局域空间关联集聚特征,但并没有考虑空间溢出效应的动态性。而比较马尔科夫转移矩阵和空间马尔科夫转移矩阵的结果,将有助于更好揭示城市人均碳排放的动态空间溢出效应。文章首先将城市人均碳排放分为4种类型：低水平（人均碳排放位于全国均值的50%及以下）;中低水平（人均碳排放位于全国均值的51%~100%）;中高水平（人均碳排放位于全国均值的101%~150%）;高水平（人均碳排放高于全国均值的150%）。
为便于对比分析,本文将整个研究过程划分为两个时间段：1992-2000年和2001-2013年（表1,图5）。表1对角线上的元素表示城市碳排放类型发生未发生转变的概率,非对角线上的元素则表示城市碳排放类型发生转变的概率。由表1可知,所有对角线的元素要高于非对角线的,说明城市碳排放类型更倾向于保持不变。对角线上的值介于0.848~0.970之间,表明城市碳排放类型不发生转变的最小概率为84.8%;而非对角线上的最大值为0.071,说明城市碳排放类型发生转变的最大概率仅为7.1%;此外,城市碳排放类型即使发生转变也是发生在相邻两类型之间,城市碳排放类型转变的跳跃式发展是几乎不存在的（跨越转变的概率几乎为0）。初始类型为高水平碳排放的城市,在接下来的年份中城市类型保持高水平的概率至少为92.8%,类型向下转移的概率仅为7.2%;而初始类型为低水平的城市,在未来年份仍然保持低水平类型的概率最小为94.9%,类型向上转移的概率最大仅为5.1%。上述发现说明城市碳排放类型在演化过程中存在趋同趋势的空间溢出效应。总的来看,1992-2000年城市碳排放类型转移上升的概率为17.9%,但下降的概率为19%;2001-2013年转移上升的概率为13.5%,下降的概率为9.3%。两个阶段转移结果表明,第一阶段城市碳排放类型转移的负向溢出效应是明显高于第二阶段。
Tab. 1
表1
表11992-2013年中国城市人均碳排放类型的马尔科夫转移矩阵
Tab. 1Markov-chain transitional matrices for per capita carbon emission at city level in China, 1992-2013

	n	P (≤ 50%)	L (51%~100%)	D (101%~150%)	R (≥ 150%)
1992-2013年
P	3098	0.957	0.043	0.000	0.000
L	2002	0.024	0.936	0.040	0.000
D	872	0.005	0.054	0.873	0.068
R	1252	0.005	0.006	0.034	0.955
1992-2000年
P	1342	0.949	0.049	0.001	0.001
L	657	0.037	0.906	0.055	0.002
D	323	0.016	0.065	0.848	0.071
R	430	0.014	0.014	0.044	0.928
2001-2013年
P	1756	0.964	0.036	0.000	0.000
L	1345	0.016	0.951	0.033	0.000
D	549	0.000	0.047	0.887	0.066
R	822	0.000	0.001	0.029	0.970

注：P：低水平城市;L：中低水平城市;D：中高水平城市;R：高水平城市。

新窗口打开

显示原图|下载原图ZIP|生成PPT
图51992-2013年中国城市人均碳排放类型转移的空间分布格局
-->Fig. 5Spatial patterns of per capita carbon emissions class transitions at city level in China, 1992-2013
-->

中国城市人均碳排放类型的空间马尔科夫转移矩阵如表2所示。对比表1、表2发现,与高水平类型相邻的城市,其人均碳排放类型向上转移的概率较大,而向下转移的概率较低;反之亦然。例如,1992-2000年,低水平城市碳排放类型向上转移的概率平均为0.051,而与中低水平、中高水平城市为邻时,其转移概率分别增加到0.087和0.098,而当与低水平类型为邻时,其向上转移的概率降至0.038;2001-2013年,高水平城市类型向下转移的概率为0.030,而当与高水平城市类型为邻时,其向下转移的概率降到0.007。综上,城市邻居溢出效应的方向对城市本身发展具有显著的影响,从而导致了城市类型发展的路径依赖。总体来说,马尔科夫链和空间马尔科夫链为城市类型发展具有的路径依赖特征提供了理论和现实依据。
Tab. 2
表2
表21992-2013年中国城市人均碳排放类型的空间马尔科夫转移矩阵
Tab. 2Spatial Markov-chain transitional matrices for per capita carbon emissions at city level in China, 1992-2013

		1992-2000年				2001-2013年
		P	L	D	R	P	L	D	R
P	P	0.962	0.038	0.000	0.000	0.972	0.028	0.000	0.000
	L	0.043	0.904	0.053	0.000	0.091	0.902	0.025	0.000
	D	0.057	0.096	0.836	0.011	0.000	0.112	0.864	0.024
	R	0.000	0.000	0.000	1.000	0.000	0.000	0.000	1.000
L	P	0.913	0.087	0.000	0.000	0.946	0.054	0.000	0.000
	L	0.027	0.926	0.047	0.000	0.042	0.942	0.016	0.000
	D	0.017	0.154	0.818	0.011	0.000	0.063	0.916	0.021
	R	0.000	0.000	0.066	0.934	0.000	0.000	0.064	0.936
D	P	0.902	0.098	0.000	0.000	0.868	0.132	0.000	0.000
	L	0.015	0.931	0.054	0.000	0.061	0.928	0.011	0.000
	D	0.000	0.139	0.814	0.038	0.000	0.088	0.884	0.018
	R	0.000	0.000	0.072	0.928	0.000	0.000	0.036	0.964
R	P	1.000	0.000	0.000	0.000	0.784	0.216	0.000	0.000
	L	0.015	0.931	0.054	0.000	0.075	0.914	0.011	0.000
	D	0.000	0.108	0.863	0.029	0.000	0.000	0.908	0.092
	R	0.000	0.000	0.013	0.987	0.000	0.000	0.007	0.993

注：P：低水平城市;L：中低水平城市;D：中高水平城市;R：高水平城市。

新窗口打开

3.2 城市碳排放的关键影响因素识别和减排政策分析

本文选用robust LM检验来比较空间滞后模型和空间误差模型,探究哪一个更适合城市碳排放的关键因素识别。通常根据LM统计量和robust LM统计量的显著性进行比选^[34]。由表3可知,在地理空间权重矩阵（W₁）及地理权重与经济权重嵌套矩阵（W₃）下,空间滞后模型的robust LM的检验效果都明显高于空间误差模型,这表明前者较后者适合模型参数估计。因此,本文采用空间滞后模型的结果进行分析。由于变量内生性问题,运用系统广义距估计（Sys-GMM）来进行动态空间面板模型的估计会比一般估计方法更具有效性。另外,在没有指定工具变量的情况下,系统广义距估计（Sys-GMM）可以依靠变量的时间变化趋势来自动识别合理的工具变量。所以本文选用Sys-GMM方法对模型进行参数估计。
Tab. 3
表3
表3空间面板模型的LM检验
Tab. 3The LM tests of spatial panel models

LM检验	权重矩阵：W₁			权重矩阵：W₃
LM检验	χ²		p值	χ²	p值
no lag	1675.474	0.000		1684.328	0.000
no lag (robust)	25.856	0.000		26.732	0.002
no error	1671.253	0.000		1669.529	0.000
no error (robust)	18.712	0.248		14.967	0.169

新窗口打开
表4是两种空间权重矩阵（W₁和W₃）设定下的估计结果。Sargan和Arellano-Bond的检验结果均符合Sys-GMM的要求,这表明模型所选用工具变量的合理有效性。另外需要指出的是,当样本工具变量较弱时,工具变量的选用可能会对Sys-GMM的结果造成影响或偏差。文章对面板混合最小二乘法（PLOS）和面板固定效应模型（FE）的估计结果进行比较分析,以进一步检验Sys-GMM的结果。有关研究表明,PLOS方法的估计系数是向上偏移的,而FE方法估计的结果是向下偏移的,因此如果Sys-GMM的估计系数介于二者之间,则进一步说明了Sys-GMM估计结果的有效性。从表4可以发现,Sys-GMM的城市碳排放时间滞后项系数均大于PLOS估计系数而都小于FE估计系数,表明Sys-GMM估计并未因工具变量的选择产生偏差而具有较高的有效性。另外,Sys-GMM估计系数的显著性明显高于其他两种方法的估计结果,说明变量内生性问题会对模型估计结果产生重要影响,所以本文选择动态空间面板数据模型对城市碳排放的时间和空间滞后效应同时予以反映,同时还利用Sys-GMM模型处理了变量内生性问题。基于以上分析,本文将重点讨论Sys-GMM模型的估计结果。
Tab. 4
表4
表4动态空间面板模型估计结果
Tab. 4Estimation results of dynamic spatial panel data models

变量	权重矩阵：W₁			权重矩阵：W₃
变量	PLOS	FE	Sys-GMM	PLOS	FE	Sys-GMM
ln(CE_t-1(θ))	0.864^***	0.266^***	0.703^***	0.864^***	0.268^***	0.702^***
ωln(CE(ρ))	1.455^***	1.622^***	1.082^***	1.396^***	1.624^***	0.179^***
ωln(CE_t-1(γ))	0.688^***	0.247^***	0.726^***	0.687^***	0.249^***	0.724^***
ln(GDPPC)	0.578^*	0.642^***	0.594^***	0.580	0.638^***	0.596^***
ln(GDPPC)²	-0.017^*	0.034^**	0.026^***	0.019	0.035^**	0.025^***
ln(POPD)	0.142	-0.247^**	-0.386^***	0.104	-0.246^**	-0.388^***
ln(TC)	-0.053^***	-0.049^***	-0.064^***	-0.054^***	-0.048^***	-0.064^***
ln(SIND)	0.099^***	0.163^***	0.254^***	0.104^***	0.164^***	0.255^***
ln(ROAD)	-0.067^*	-0.123^***	-0.154^***	-0.066^**	-0.123^**	-0.155^***
ln(FAI)	0.057^***	0.086^***	0.066^***	0.057^***	0.085^***	0.067^***
ln(TO)	-0.023^*	-0.018^***	-0.027^***	0.023^*	-0.019^***	-0.028^***
Sargan P			0.675			0.663
AR(2) P			0.816			0.892

注：^*：表示示在10%的水平上显著;^**：表示在5%的水平上显著;^***：表示在1%的水平上显著。

新窗口打开
首先关注时间效应,城市人均碳排放的时间滞后系数θ在地理权重和地理经济权重下均呈现较高的显著性且系数为正,表明城市人均碳排放变化存在着路径依赖,也即当前碳排放水平对未来水平会产生一定影响,具体表现为当期碳排放水平每提高1%会造成下期碳排放水平提高约0.7%。其次从空间效应来看,空间滞后系数ρ同样在地理权重和地理经济矩阵设定下均呈现较高显著性且系数为正,这也再次表明城市人均碳排放存在明显的空间集聚特征。在W₁和W₃权重矩阵设定下,邻近地区城市人均碳排放水平每提高1%,本地区城市的人均碳排放水平会提高约1.08%。从时空效应来看,城市人均碳排放的时空滞后系数γ在地理权重和地理经济权重矩阵设定下均在1%的水平上显著为正,表明上一期地理或地理经济临近地区较高的城市碳排放水平同样会促使本地区当期城市排放水平的降低。
本文首先考察了经济增长与人均碳排放之间的EKC曲线关系。由表4可知,经济增长的一次项系数显著为正,而二次项系数显著为负,说明城市人均碳排放与城市经济增长之间存在倒“U”型曲线关系。从本文计算的各城市碳排放量来看,大部分城市人均碳排放都还处于增长阶段,说明各城市人均GDP均位于倒“U”型曲线拐点的左侧,也即是说未来一段时间内各城市的碳排放水平与经济增长之间将继续处于正相关阶段,传统的EKC假说所表示的排放与增长之间的“脱钩”阶段还没有到来,从而再次说明城市节能减排任务的紧迫性和重要性。由于经济发展阶段所限,城市经济增长是绝大多数地方政府的首要任务,快速的经济增长势必导致城市碳排放的快速增加,即使是在国际和国内减排压力背景下,城市也不可能完全靠以牺牲经济增长来降低碳排放水平,所以,城市未来更应该强调绿色可持续发展,进一步引导城市居民的低碳出行和绿色消费,才能实现经济稳定增长和碳排放持续下降的双赢局面。
人口密度对城市碳排放水平的负向作用明显。一般来讲,人口密度的增加可以通过两个方面来影响碳排放,一个是集聚效应,另一个是规模效应。人口密度的增加往往会产生集聚效应,进而会提高技术水平、公共交通分担率和能源利用效率以及共享减排设施等手段来降低碳排放。另一方面,人口密度的提升会直接或间接导致能源消费的增加,从而形成碳排放增加的首要因素;此外,人口密度的增加也会增加交通拥堵,从而导致机动车燃料燃烧不充分而增加碳排放。估计结果表明,人口密度的集聚效应明显高于规模效应,也即是说明人口集聚带来的能源利用效率提升明显高于人口规模扩大带来的碳排放量增加。所以,未来更应该关注人口集聚在资源利用效率提升的作用进而有效缓解人口规模效应对碳排放的影响。
技术进步对城市碳排放水平的负向作用显著。技术进步往往可以通过生产技术和减排技术两个方面来作用于碳排放,生产技术主要通过影响要素的生产率,而减排技术主要关注排放强度。也即是说技术进步可以促进能源强度降低,减少碳排放,同时也会推动经济增长增加碳排放。本文的结果表明中国的科学事业费用支出在提高节能技术方面发挥了有效作用,从而引致能源使用效率的提高而对城市碳排放表现出了一定的抑制作用。同时这也提醒我们要继续加大技术创新的投入、提高研发强度,更好地发挥科技水平在节能减排方面的有效作用。
第二产业比重的提升对城市碳排放水平的正向作用显著。伴随着工业化进程的快速推进,第二产业特别是重工业如能源密集型和高碳密集型产业发展迅速,成为经济发展的主要动力,然而以第二产业为主的产业结构加上当前的粗放的工业化模式则构成了城市碳排放的主要驱动因素。产业结构升级是指在技术进步的影响下,产业不断淘汰落后产能、改造传统技术,并发展、转变为技术含量高、附加值高等技术密集型产业的过程,因此,促进产业结构的优化与转型升级、加大对绿色产业扶持等将是降低碳排放的有效举措。
路网密度增加在1%的水平上对碳排放的抑制作用显著。在考虑同样交通运输量的情况下,路网密度越大,交通拥堵越轻,从而有利于机动车燃料的充分燃烧。未来应积极建设便捷高效的公共交通网络,提高公共交通的运输能力,大力宣传和提高城市居民的低碳出行意识,这些举措应该成为降低碳排放的重要措施。
固定资产投资估计系数在1%的水平显著为正,说明固定资产投资的增加提升了碳排放水平。中国城市经济的快速增长是投资拉动型的,而经济增长对化石能源依赖的程度也日益增大。中国固定资产投资主要集中于第二产业,而第二产业的发展对能源的依赖程度最高,其碳排放相比于一、三产业也最大。同时,对第二产业的粗放投资不利于产业结构调整,而粗放投资则更多地被用于促进生产技术进步而非绿色技术进步,引致生产规模扩大而对城市碳排放具有正向促进作用。综上,中国城市政府在进行固定资产投资时需对其进行低碳甄别,提高投资的环境准入门槛,使投资更多地用于促进绿色技术进步,进而引致由于技术进步效应提升的作用以有效缓解规模效应对碳排放的影响。
对外开放度的提高对城市碳排放表现出了明显的促降作用。事实上,实际利用外资可以通过收入效应和技术外溢效应等方式来提高环境质量。实际利用外资额的增加有利于生产规模的扩大进而提高居民的收入水平,从而可以为节能减排提供资金保障,并且随着收入水平的增加,居民的生态环保意识也会相应提高,对生态环境质量的要求也会提高,进而可以通过这种非正式环境规制倒逼环境质量的改善,降低城市碳排放水平。另外,外商直接投资会带来国外环境友好的技术与产品,这会产生清洁技术溢出效应,进而提高中国的绿色技术水平,并达到降低中国的碳排放水平的效果。因此,中国城市政府在引入外商投资时需对其进行低碳甄别,提高外资的环境准入门槛,充分发挥外资在改善环境质量方面的技术优势和外溢效应,积极发挥外资在降低碳排放上的作用。

4 结论

基于1992-2013年中国城市遥感模拟反演碳排放数据,本文首先采用基尼系数分析了中国城市碳排放的区域差异,发现虽然人均碳排放水平不断提升,但城市间的差异正逐步缩小;泰尔指数分解模型的结果显示,西部城市间的差异对碳排放总体差异的贡献份额最大,东部和中部地区次之,而地区间和东北地区的贡献份额较小。在3种不同空间权重矩阵下,城市碳排放的空间相关性并不具有单纯的经济发展差异的空间关联特征,而是在地理空间及地理经济综合空间上呈现出了明显的高排放俱乐部集聚特征。马尔科夫矩阵和空间马尔科夫矩阵的动态分析结果表明中国城市碳排放类型演化具有明显的空间溢出效应和路径依赖特征,类型转移方面受相邻城市的影响显著,当与较高排放水平城市为邻时,其向上转移的概率会增加,而向下转移会减少;反之亦然。
基于动态空间面板数据模型,在同时考虑碳排放的时间滞后、空间滞后和时空滞后效应的条件下,对城市碳排放的关键影响因素进行了定量识别和减排政策探讨。结果表明,人均碳排放与人均GDP之间存在显著的倒“U”型关系,并且大部分城市的人均碳排放处于随经济增长而增加的阶段,二产偏重的产业结构和投资的粗放增长共同引致于城市人均碳排放水平的提升。虽然人口的集聚效应高于规模效应对城市碳排放表现出了显著的抑制作用,但其影响程度较小。科技水平的提升、对外开放度和公路运输强度的增加则共同促使城市碳排放水平的降低,因此未来要抑制促增因素和发挥促降因素的作用才能有效降低城市碳排放水平。上述研究结论对如何通过社会经济手段实现中国城市的低碳发展具有重要的政策意义,未来中国应继续优化产业结构、精简粗放投资、增加研发强度以及提升道路通达性进而实现中国城市节能减排的目标^{[35,36,37,38]}。
The authors have declared that no competing interests exist.

中国城市能源消费碳排放的区域差异、空间溢出效应及影响因素

本站小编 Free考研考试/2021-12-29

Regional inequality, spatial spillover effects and influencing factors of China's city-level energy-related carbon emissions

1 引言