Florent BRIENT^,

Corresponding author: Florent BRIENT,florent.brient@gmail.com

CNRM, Université de Toulouse, Météo-France, CNRS, Toulouse, 31057, France
Manuscript received: 2019-06-24
Manuscript revised: 2019-09-10
Manuscript accepted: 2019-09-19
Abstract:Models disagree on a significant number of responses to climate change, such as climate feedback, regional changes, or the strength of equilibrium climate sensitivity. Emergent constraints aim to reduce these uncertainties by finding links between the inter-model spread in an observable predictor and climate projections. In this paper, the concepts underlying this framework are recalled with an emphasis on the statistical inference used for narrowing uncertainties, and a review of emergent constraints found in the last two decades. Potential links between highlighted predictors are explored, especially those targeting uncertainty reductions in climate sensitivity, cloud feedback, and changes of the hydrological cycle. Yet the disagreement across emergent constraints suggests that the spread in climate sensitivity can not be significantly narrowed. This calls for weighting the realism of emergent constraints by quantifying the level of physical understanding explaining the relationship. This would also permit more efficient model evaluation and better targeted model development. In the context of the upcoming CMIP6 model intercomparison a growing number of new predictors and uncertainty reductions is expected, which call for robust statistical inferences that allow cross-validation of more likely estimates.
Keywords: climate modeling,
emergent constraint,
climate change,
climate sensitivity
摘要:很多模式在对气候变化的很多响应上存在分歧，如气候反馈、区域变化、气候平衡态敏感性的强度等。观测涌现约束方法(以下称为“涌现约束”)是找到关于预报因子的多模式间预报离散性和气候预测的关系，来减少模式间预报的不确定性。本文回顾了在涌现约束这个框架下的一些基本概念，强调了用于缩小不确定性的统计推断，此外文章还对过去二十年间关于涌现约束的研究做了回顾。本文探索了重要因子之间的潜在联系，尤其是尝试缩小气候敏感度、云反馈和水循环的变化的不确定性。但涌现约束结果的不统一表明目前的方法还不能显著地缩小气候敏感度的不确定性范围。这要求通过对这个关系的物理理解的水平进行量化来加强涌现约束真实性。这可能也需要更有效率的模式评估和更有针对性地发展模式。在即将到来的CMIP6模式间比较中，我们希望看到更多的预报因子并且希望预报不确定性能缩小，这需要可靠的统计推断，以便对更有可能的估计进行交叉验证。
关键词:气候模式,
观测涌现约束,
气候变化,
气候敏感性

HTML

--> --> -->

For more than two centuries, steadily increasing carbon dioxide (CO₂) concentrations in the atmosphere have been warming the Earth. Today it is 0.8°C warmer than in the preindustrial period in the middle of the 19th century (Morice et al., 2012). Global climate models project how this global warming will continue given the expected continuous increase in human-made CO₂ emissions. While models agree on the sign of a number of climate change signals, they often disagree on their amplitude (Flato et al., 2013). A well-known example is the equilibrium climate sensitivity (ECS), i.e., the equilibrium global-mean surface temperature increase resulting from a sustained doubling of CO₂ concentrations (Gregory et al., 2004). For decades, models have exhibited widely differing climate sensitivities, yet with a range remaining roughly between 2°C and 5°C (Charney et al., 1979; Bony et al., 2013). To correctly predict how much the Earth will warm, one must know at least (1) how CO₂ concentrations will evolve (Stocker et al., 2013), and (2) the correct value of climate sensitivity.
A doubling of the CO₂ concentration would warm the Earth by 1.2°C $ \pm $ 0.1°C (Dufresne and Bony, 2008). However, this warming induces changes that can amplify or dampen the initial temperature response through feedback processes (Bony et al., 2006). For example, the CO₂-induced global warming allows the atmosphere to hold more water vapor. This acts as a positive feedback on the surface warming, because water vapor itself is a powerful greenhouse gas that, like CO₂, absorbs and re-emits longwave radiation back to the surface. This is somewhat compensated by the negative temperature lapse rate feedback that allows more outgoing longwave emission to be emitted out of the atmosphere. The initial warming also reduces the surface albedo by melting snow and sea ice, which also constitutes a positive feedback because snow and ice are effective reflectors of sunlight. Models agree on the sign and approximately the amplitude of these two feedback processes (Ceppi et al., 2017). The water vapor, lapse rate, and ice-albedo feedbacks in isolation enhance the global warming due to increasing CO₂ concentrations to around +2.2°C (Dufresne and Bony, 2008). Models disagree on the cloud response to surface warming, which is primarily why they produce a wide range of ECS values, e.g., between 2.1°C and 4.7°C for climate models participating in phase 5 of the Coupled Model Intercomparison Project (CMIP5) (Flato et al., 2013). Since clouds have dynamical scales in the order of tens to hundreds of meters, climate models with grid boxes of hundred of kilometers cannot explicitly resolve cloud processes. Empirically based assumptions are thus used to relate unresolvable small-scale dynamics to properties (temperature, humidity etc.) on the models' grid scale. Those parameterizations are the heart of biases in reproducing the present-day climate and of uncertainties in climate change projections (e.g., Qu et al., 2014; Webb et al., 2015; Brient et al., 2016; Geoffroy et al., 2017). This calls for new and efficient process-oriented methods for understanding the leading causes behind these uncertainties and for establishing better model evaluation and development.

2

-->

2.1. Definition

Recently, a methodology called "emergent constraint" has been developed for reducing uncertainties in climate change projections. This framework is based on:
(1) Identifying responses to climate change perturbations in which models disagree (e.g., cloud feedback).
(2) Relating the intermodel spread in the climate change responses to present-day biases or short-term variations that can be observed.
This could be achieved by identifying an empirical relationship between the intermodel spread of an observable variable (hereafter named A) and spread of a response to a given perturbation (B). The variable A is called the predictor and the variable B the predictand. Because observed measurements of the predictor A can then be used to constrain the models' responses, B, the relationship between A and B is called an emergent constraint (Klein and Hall, 2015). The variable A may represent a metric that characterizes the climate system (e.g., humidity, winds) or some natural variability (e.g., in the seasonal cycle, or from year to year). The response B can be the global-mean response of the climate system (e.g., ECS) or a local response to perturbations (e.g., a regional climate feedback). Therefore, the goal is to find a predictor that, given its relation to a climate response, emerges as a constraint on future projections.
Once variable A is estimated observationally, the emergent constraint can be used to assess the realism of models and to eventually narrow the spread of climate change projections. As an idealized example, Fig. 1 shows a randomly generated relationship between a predictor A simulated by 29 climate models and a projection of future climate changes (in principle, any climate change response may be considered). The green distribution represents an observational measurement and its uncertainties. We see that differences in A are significantly associated with differences in B, here with a correlation coefficient of r = 0.83. By constraining A through potential observations (green distribution), this example suggests that some models are more realistic and, by inference, are associated with a more realistic predictand. The degree to which the models' A deviates from the observed A can be used to derive weights for the models to compute a weighted average of the models' response, B (see section 2.2.3).
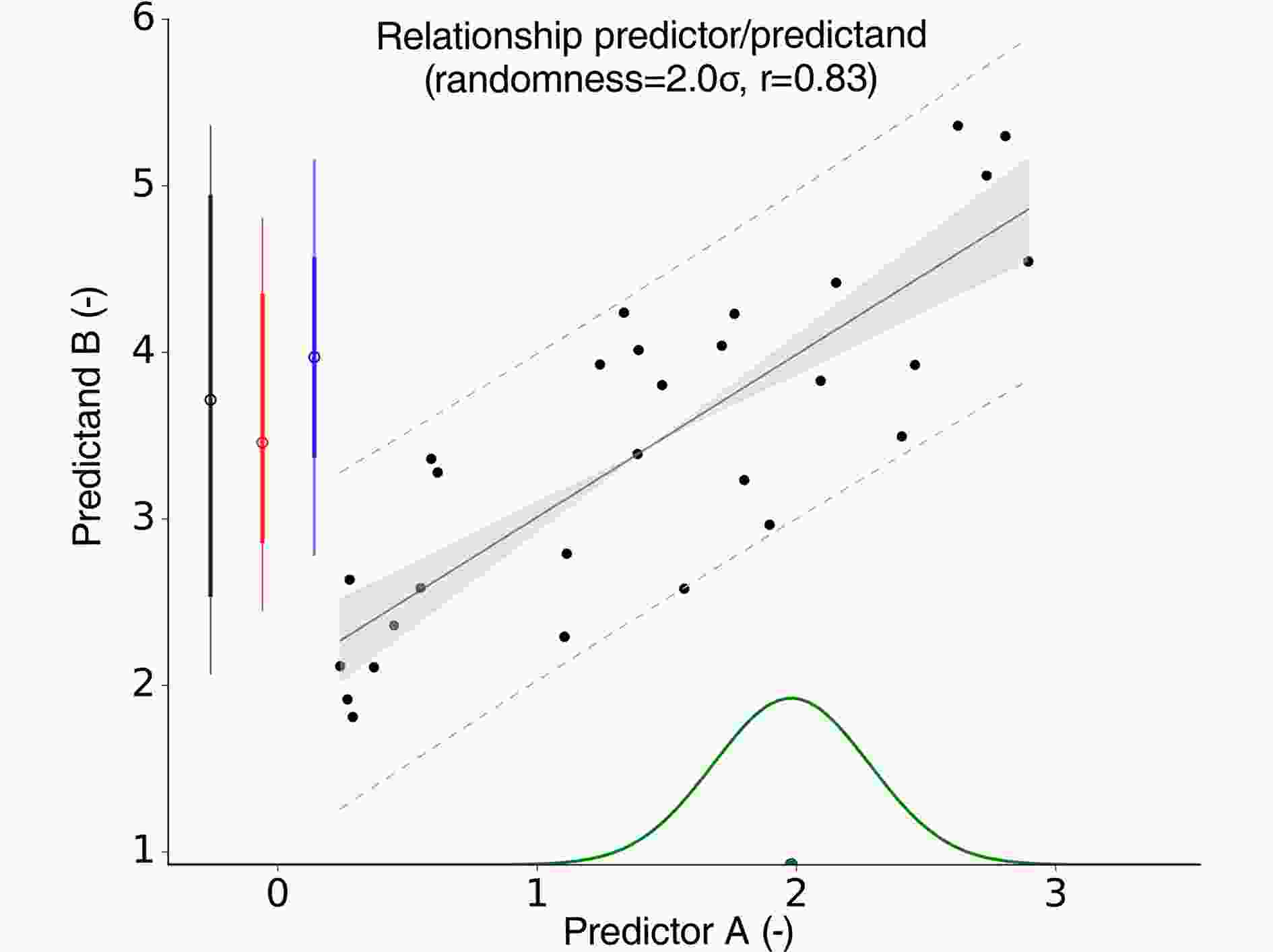Figure1. Idealized relationship between a predictor and a predictand. The 29 models (dots) are associated with randomly generated values of the predictor A ( x-axis, between 0 and 3). The predictand B, on they-axis follows the idealized relationship $ y' = ax+b $, with a = 1 and b = 2, plus a random deviation $ \Delta $ following a normal distribution with $ \sigma $ = 2 [such as $ y = y'+\Delta(y') $]. The dashed lines and blue shades represent the 90% prediction limits and the 90% confidence limits of the slope, respectively. The green distribution on the x-axis represents an idealized observed distribution of the predictor, assuming a normal distribution (here with $ \mu $ = 1.98 and $ \sigma $ = 0.3). Prior and posterior distributions of the predictand are represented as vertical lines in the left part, with the mode (circle), 66% (thick) and 90% (thin) confidence intervals. Black lines represent the prior distribution, red lines represent the posterior distribution obtained by a weighted average of the climate models through a Kullback–Leibler divergence, and blue lines are the distribution inferred using the slope and its uncertainties. In this randomly generated example, posterior estimates are sensitive to the way inference is computed.



2 -->

2.2. Criterion and uncertainties

3 -->

2.2.1. Physical understanding

An emergent constraint can be trusted if it meets certain criteria. The most important one is an understanding of physical mechanisms underlying the empirical relationship, which is the key to increasing the plausibility of a proposed emergent constraint. Several methods have recently been suggested to verify the level of confidence in emergent constraints (Caldwell et al., 2018; Hall et al., 2019). One of these methods consists of checking the reliability of an emergent constraint by developing sensitivity tests that would modify A for some models (if there is a straightforward way of manipulating A). For accurate model comparison, this would require coupled model simulations with global-mean radiative balance as performed in CMIP. If the models' behavior after the modification deviates from that expected from the emergent constraint, the relationship may have been found by chance. A study showed that this risk is not negligible (Caldwell et al., 2014), primarily because climate models are not independent, often being derived from each other (Masson and Knutti, 2011; Knutti et al., 2013). Keeping only models with enough structural differences often reduces the reliability of identified emergent constraints. The search for correlations with no obvious physical understanding could lead to such spurious results. Conversely, if those sensitivity tests confirm the intermodel relationship, the credibility of assumed physical mechanisms and observational constraints on climate change projections increases. Those tests could be performed through an ensemble of simulations over which either parameterizations or uncertain parameters are modified. This would help (1) disentangle structural and parametric influence on the multimodel spread in predictor A and (2) highlight underlying processes explaining the empirical relationship (Kamae et al., 2016).

3 -->

2.2.2. Observation uncertainties

The second criterion is related to the correct use of observations. Uncertainties tied to the observation of the predictor must be small enough so that not all models remain consistent with the data. This criterion may not be satisfied if observations are available only over a short time period [as is the case for the vertical structure of clouds, (e.g.,Winker et al., 2010)], or if the predictor is defined through low-frequency variability (trends, decadal variability), or if there is a lack of consistency among available datasets [as in the case for global-mean precipitation and surface fluxes, (e.g.,G?inu??-Bogdan et al., 2015)]. Finally, some observational constraints rely on parameterizations used in climate models, e.g., reanalysis data that use sub-grid assumptions for representing clouds (e.g.,Dee et al., 2011) or data products for clouds that use sub-grid assumptions for radiative transfer calculations (Rossow and Schiffer, 1999).

3 -->

2.2.3. Statistical inference

Emergent constraints can allow us to narrow uncertainties and quantify more likely estimates of climate projections, i.e., a constrained posterior range of a prior distribution. However, not all emergent constraints should be given the same trust. Hall et al. (2019) suggested to relate this trust to the level of physical understanding associated with the emergent relationship. This means making predictions only for confirmed emergent constraints.
Posterior estimates are influenced by the way the statistical inference has been performed. However, no consensus has yet emerged for this inference. A first method for quantifying this constraint is to directly use uncertainties underlying the observational predictor and project it onto the vertical axis using the emergent constraint relationship. This method takes into account uncertainties in both observations and the estimated regression model, through bootstrapping samples for instance (Huber et al., 2011). Most studies use this straightforward framework. In our idealized example, this would give a posterior estimate that is slightly larger and narrower than the prior estimate (Fig. 1). However, several problems with this kind of inference might be highlighted, as suggested by Schneider (2018):
● Most fundamentally, the inference generally revolves around assuming that there exists a linear relationship, and estimating parameters in the linear relationship from climate models. However, it is not clear that such a linear relationship does in fact exist, and estimating parameters in it is strongly influenced by models that are inconsistent with the observations (extreme values). In other words, the analysis neglects structural uncertainty about the adequacy of the assumed linear model, and the parameter uncertainty the analysis does take into account is strongly reduced by models that are "bad" according to this model–data mismatch metric. Thus, outliers strongly influence the result. However, the influence of models consistent with the data but off the regression line is diminished. Given that there is no strong a priori knowledge about any linear relationship (this is why it is an "emergent" constraint), it seems inadvisable to make one's statistical inference strongly dependent on models that are not consistent with the data at hand.
● Often, analysis parameters are chosen so as to give strong correlations between the response of models to perturbations and the predictor. This introduces selection bias in the estimation of the regression lines. This leads to underestimation of uncertainties in parameters, such as the slope of the regression line, which propagates into underestimated uncertainties in the inferred estimate.
● When regression parameters are estimated by least squares, the observable on the horizontal axis is treated as being a known predictor, rather than as being affected by error (e.g., from sampling variability). This likewise leads to underestimation of uncertainties in regression parameters. This problem can be mitigated by using errors-in-variables methods.
A second method consists of estimating a posterior distribution by weighting each model's response by the likelihood of the model given the observations of the predictor. This can be accomplished by a Bayesian weighting method (e.g.,Hargreaves et al., 2012) or through information theory (e.g.,Brient and Schneider, 2016), such as the Kullback–Leibler divergence or relative entropy (Burnham and Anderson, 2003). This method does not use linear regression for estimating the posterior distribution and therefore favors realistic models and de-emphasizes outliers inconsistent with observations. For instance, the Kullback–Leibler divergence applied to our idealized example (assuming an identical standard deviation between observation and each model) suggests a posterior estimate lower and narrower than the prior estimate (Fig. 1).
This more justifiable inference still suffers from several shortcomings (Schneider, 2018). For example, it suffers from selection bias, and it treats the model ensemble as a random sample (which it is not). It also only weights models, suggesting that climate projections far outside the range of what current models produce will always come out as being very unlikely. Given uncertainties underlying each method, posterior estimates should thus be quantified using different methods [as previously done in Hargreaves et al. (2012), for instance], which must be explicitly described.
Figure 2 provides a tangible example for explaining the importance of statistical inference. It shows the relation in 29 current climate models between ECS and the strength with which the reflection of sunlight in tropical low-cloud regions covaries with surface temperature (Brient and Schneider, 2016). That is, the horizontal axis shows the percentage change in the reflection of sunlight per degree of surface warming, for deseasonalized natural variations. It is clear that there is a strong correlation (correlation coefficient of about ?0.7) between ECS on the vertical axis and the natural fluctuations on the horizontal axis. The green line on the horizontal axis indicates the probability density function (PDF) of the observed natural fluctuations. What many previous emergent-constraint studies have done is to take such a band of observations and project it onto the vertical ECS axis using the estimated regression line between ECS and the natural fluctuations, taking into account uncertainties in the estimated regression model. If we do this with the data here, we obtain an ECS that likely lies within the blue band: between 3.1 and 4.2 K, with a most likely value of 3.6 K. Simply looking at the scatter of the 29 models in this plot indicates that this uncertainty band is too narrow. For example, model 7 is consistent with the observations, but has a much lower ECS of 2.6 K. The regression analysis would imply that the probability of an ECS this low or lower is less than 4%. Yet, this is one of 29 models, and one of relatively few (around 9) that are likely consistent with the data. Obviously, the probability of an ECS this low is much larger than what the regression analysis implies. As explained before, these flaws could be reduced by weighting ECS by the likelihood of the model given the observations. Models such as numbers 2 and 3, which are inconsistent with observations, would receive essentially zero weight (unlike in the regression-based analysis, they do not influence the final result). No linear relationship is assumed or implied, so models such as 7 receive a large weight because they are consistent with the data, although they lie far from any regression line. The resulting posterior PDF for ECS is shown by the orange line in Fig. 1b. The most likely ECS value according to this analysis is 4.0 K. It is shifted upward relative to the regression estimate, toward the values in the cluster of models (around numbers 25 and 26) with relatively high ECS that are consistent with the observations. The likely ECS range stretches from 2.9 to 4.5 K. This is perhaps a disappointingly wide range. It is 50% wider than what the analysis based on linear regressions suggests, and it is not much narrower than what simple-minded equal weighting of raw climate models gives (gray line in Fig. 1b). It is, however, a much more statistically defensible range.
Figure2. (a) Scatterplot of ECS versus deseasonalized covariance of marine tropical low-cloud reflectance $ \alpha_c $ with surface temperature T in CMIP5 models (numbered in order of increasing ECS). Gray lines represent a robust regression line (solid), with the 90% confidence interval of the fitted values (dashed) estimated by a bootstrap procedure. The green line at the lower axis indicates the PDF of the α_c variation with T inferred from observations. The vertical green band indicates the 66% band of the observations. The blue circle and horizontal band show the mode and the likely (66%) ECS range inferred from a linear regression procedure, respectively, taking into account uncertainties estimated by bootstrapping predictions with estimating regression models. (b) Posterior PDF of ECS (orange) obtained by a weighted average of the climate models, given the observations. The bars with circles represent the mode and confidence intervals (66% and 90%) implied by the posterior (orange) PDF and the prior (gray) PDF. Adapted from Brient and Schneider (2016)


In order to generalize the sensitivity of inferred estimates to the statistical methodology, 10⁴ random emergent relationships are generated. Figure 3 shows the statistics of inferences (mode, confidence intervals) as a function of correlation coefficients. Averaged modes and confidence intervals obtained from the two inference methods are consistent with each other. However, the variance of inferred best estimates (modes) using the weighting method is larger than the one using the inference method. This is in agreement with results obtained from the tangible example from Brient and Schneider (2016), which show different most-likely values (Fig. 2). Therefore, this suggests the best estimate is significantly influenced by the way statistical inference is performed.
Figure3. Relationship between modes and correlation coefficient (r) of 10⁴ randomly generated emergent constraints, as per the example shown in Fig. 1. Thick lines, dashed lines and shades represent the average mode, the average 66% confidence interval and the standard deviation of the mode across the set of emergent relationships. Characteristics of the prior distributions are represented in black color. Posterior estimates using the slope inference or the weighting averaging are represented in blue and red, respectively, using an idealized observed distribution of the predictor as defined in Fig. 1. The PDF of correlation coefficients is shown as a thin black line on the x-axis. This figure shows that average modes and confidence intervals remain independent of the inference method, but the uncertainty of the mode value is larger for the weighting method.


Finally, uncertainties underlying these estimates may be influenced by the level of structural similarity between climate models. Indeed, adding models with only weak structural differences (e.g., model versions with different resolution, interactive chemistry) can artificially strengthen the correlation coefficient of the empirical relationship and the inferred best estimate (Sanderson et al., 2015). This coefficient is usually the first criterion that quantifies the statistical credibility of an emergent constraint, i.e., the larger the correlation coefficient, the more trustworthy the regression-based inference will be. However, it remains unknown what level of statistical significance justifies an emergent constraint and whether these correlations best characterize their credibility.

In the following sections, emergent constraints that have been highlighted within the last two decades are listed and described. Table 1 summarize them, along with prior and posterior estimates of the models' predictands. The mean and uncertainties (one standard deviation) are based on the inference provided in the reference if available, or roughly derived through their empirical relationship and observational uncertainties (for qualitative assessment).

Reference		Predictand	Original	Constrained
A	Covey et al. (2000)	ECS (K)	3.4±0.8	–
A	Volodin (2008) (RH)	ECS (K)	3.3±0.6	3.4±0.3
A	Volodin (2008) (cloud)	ECS (K)	3.3±0.6	3.6±0.3
A	Trenberth and Fasullo (2010)	ECS (K)	3.3±0.6	> 4.0
A	Huber et al. (2011)	ECS (K)	3.3±0.6	3.4±0.6
A	Fasullo and Trenberth (2012)	ECS (K)	3.3±0.6	4.1±0.4*
A	Sherwood et al. (2014)	ECS (K)	3.4±0.8	4.5±1.5*
A	Su et al. (2014)	ECS (K)	3.4±0.8	>3.4
A	Zhai et al. (2015)	ECS (K)	3.4±0.8	3.9±0.5
A	Tian (2015)	ECS (K)	3.4±0.8	4.1±1.0*
A	Brient and Schneider (2016)	ECS (K)	3.4±0.8	4.0±1.0*
A	Lipat et al. (2017)	ECS (K)	3.4±0.8	2.5±0.5*
A	Siler et al. (2018)	ECS (K)	3.4±0.8	3.7±1.3
A	Cox et al. (2018)	ECS (K)	3.4±0.8	2.8±0.6
B	Qu et al. (2014)	Low-cloud amount feedback (% K?1)	?1.0±1.5	?
B	Gordon and Klein (2014)	Low-cloud optical depth feedback (K?1)	0.04±0.03	?
B	Brient and Schneider (2016)	Low-cloud albedo change (% K?1)	?0.12±0.28	?0.4±0.4*
B	Siler et al. (2018)	Global cloud feedback (% K?1)	0.43±0.30	0.58±0.31
C	Allen and Ingram (2002)	Global-mean precipitation	?	?
C	O’Gorman (2012)	Tropical precipitation extremes (% K?1)	2?23	6?14
C	DeAngelis et al. (2015)	Clear-sky shortwave absorption (W m2 K?1)	0.8±0.3	1.0±0.1
C	Li et al. (2017)	Indian monsoon rainfall changes (% K?1)	6.5±5.0	3.5±4.0
C	Watanabe et al. (2018)	Hydrological sensitivity (% K?1)	2.6±0.3	1.8±0.4
D	Cox et al. (2013)	Tropical land carbon release (GtC K?1)	69±39	53±17
D	Wang et al. (2014)	Tropical land carbon release (GtC K?1)	79±43	70±45*
D	Wenzel et al. (2014)	Tropical land carbon release (GtC K?1)	49±40	44±14
D	Hoffman et al. (2014)	CO2 concentration in 2100 (ppm)	980±161	947±35
D	Wenzel et al. (2016)	Gross primary productivity (%)	34±15	37±9
D	Kwiatkowski et al. (2017)	Tropical ocean primary production (% K?1)	?4.0±2.2	?3.0±1.0
D	Winkler et al. (2019)	Gross primary production (PgC yr?1)	2.1±1.9	3.4±0.2
E	Plazzotta et al. (2018)	Global-mean cooling by sulfate [K (W m?2)?1]	0.54±0.33	0.44±0.24
F	Hall and Qu (2006)	Snow-albedo feedback (% K?1)	?0.8±0.3	?1.0±0.1*
F	Qu and Hall (2014)	Snow-albedo feedback (% K?1)	?0.9±0.3	?1.0±0.2*
F	Boé et al. (2009)	Remaining Arctic sea-ice cover in 2040 (%)	67±20*	37±10*
F	Massonnet et al. (2012)	Years of summer Arctic ice-free	(2029–2100)	(2041–2060)
F	Bracegirdle and Stephenson (2013)	Arctic warming (°C)	~2.78	<2.78
G	Kidston and Gerber (2010)	Shift of the Southern Hemispheric jet (°)	?1.8±0.7	?0.9±0.6
G	Simpson and Polvani (2016)	Shift of the Southern Hemispheric jet (°)	~?3	~?0.5* (winter)
G	Gao et al. (2016)	Shift of the Northern Hemispheric jet (°)	~0	~?2 (winter)
G	Gao et al. (2016)	Shift of the Northern Hemispheric jet (°)	~+1.5	~?1 (spring)
G	Douville and Plazzotta (2017)	Summer midlatitude soil moisture	?	?
G	Lin et al. (2017)	Summer US temperature changes (°C)	6.0±0.8	5.2±1.0*
G	Donat et al. (2018)	Frequency of heat extremes (?)	?	?
H	Hargreaves et al. (2012)	ECS (K)	3.1±0.9	2.3±0.9
H	Schmidt et al. (2013)	ECS (K)	3.3±0.8	3.1±0.7

Table1. List of 45 published emergent constraints, the predictand they constrain, and the original and constrained ranges. The mean and standard deviations of prior and posterior estimates are listed where available. An asterisk signifies that the moments of the distribution are not directly quantified in the reference paper but derived from their emergent relationship and the observational constraint, and thus should be understood only as a qualitative assessment. Letters correspond to groups of emergent constraints with related predictands


In the late 1990s, signs of climate feedback started to be constrained from climate models and observations (e.g., Hall and Manabe, 1999). Usually analyzing one unique model, these studies improved our understanding of physical mechanisms driving climate feedback. However, the lack of intermodel comparisons in these studies did not allow quantifying the relative importance of feedbacks in driving uncertainties in climate change projections. Model intercomparisons during this period identified the cloud response to global warming as being the key contributor of intermodel spread in climate projections (Cess et al., 1990, 1996). Both types of studies pave the way toward process-oriented analysis for understanding intermodel differences in climate projections.
To the best of my knowledge, the first attempt at introducing the concept of emergent constraints was made by Allen and Ingram (2002). The authors tried to constrain the spread in global-mean future precipitation change simulated by the set of climate models participating in CMIP2 (Meehl et al., 2000) through observable temperature variability and a simple energetic framework. Despite the inability to robustly narrow future precipitation changes, they introduced the concepts that establish emergent constraints: the need for physical understanding and the ability of observations to constrain the model predictor.
An early application of emergent constraints concerns the snow-albedo feedback. Hall and Qu (2006) showed that differences among models in seasonal Northern Hemisphere surface albedo changes are well correlated with global-warming albedo changes in CMIP3 models. The three main criteria for a robust emergent constraint are satisfied: the physical mechanisms are well understood, the statistical relationship between the quantities of interest is strong, and uncertainties in the observed variations are weak, allowing the authors to constrain the Northern Hemisphere snow-albedo feedback under global warming. Despite this successful application, the generation of models that followed (CMIP5) continued to exhibit a large spread in seasonal variability of snow-albedo changes (Qu and Hall, 2014). This could be narrowed through targeted process-oriented model development based on the evaluation of snow and vegetation parameterizations (Thackeray et al., 2018). Yet, this study can be seen as the first confirmed emergent constraint (Klein and Hall, 2015; Hall et al., 2019).
The success of the Hall and Qu (2006) study led a number of studies to seek emergent constraints able to narrow climate change responses. In the following sections, these studies aimed at constraining ECS, cloud feedback, or various changes in Earth system components, such as the hydrological cycle or the carbon cycle, are described.

Uncertainties in ECS usually scale with uncertainties in regional climate changes (Seneviratne et al., 2016). Therefore, constraining ECS would help in better estimating regional responses to climate change, which matter the most for impact studies and risk assessment. Therefore, most emergent constraints prioritize providing a better range for ECS, as shown in Table 1.
The main predictors used to constrain the spread in ECS consist of observable climatological characteristics of the current climate. The first study using this approach was Volodin (2008), which found that CMIP3 models with large ECS are more likely to exhibit (1) large differences in cloud cover between the tropics and the extratropics and (2) low tropical relative humidity.
Using a cloud climatology from geostationnary satellites, Volodin (2008) provides a first more likely ECS range of 3.6±0.3 K. This range is slightly higher than the multimodel average, with a reduced variance (Table 1). However this study does not address the physical understanding of links between clouds, moisture, and climate feedbacks, which reduce the credibility of this estimate. A more recent study, Siler et al. (2018), provides a physical interpretation underlying this cloud constraint. They hypothesize that the need for a global-mean radiative balance (through model tuning) forces a link between warm and cold regions, i.e., models having fewer clouds in the tropical area will very likely simulate more extratropical clouds in the current climate. Given that global warming will expand tropical warm regions at the expense of extratropical cold regions, these models will increase the spatial coverage of areas with weak cloudiness relative to the multimodel mean, leading to more positive low-cloud feedback and high climate sensitivity. Using observations for characterizing the spatial coverage of cloud albedo, Siler et al. (2018) found a best ECS estimate of 3.7±1.3 K, in agreement with Volodin (2008). However, the credibility of this estimate is questionable, because physical mechanisms explaining the emergent relationships are not testable (Caldwell et al., 2018).
The second estimate suggested by Volodin (2008) is related to relative humidity and uses reanalysis outputs to provide a more likely ECS range of 3.4±0.3 K. In CMIP3, models with the largest zonal-mean relative humidity over the subtropical free troposphere are those with the lowest climate sensitivity. Given that models generally overestimate this predictor, this suggests the highest ECS values are more realistic. This is in agreement with Fasullo and Trenberth (2012), who found the same relationship and a best ECS estimate of around 4 K (Table 1). This emergent relationship is explained to a certain extent by the broadening of the tropical dry zones with global warming, which implies a drying of the subsiding branches. Thus, the drier the free troposphere in the current climate, the stronger the boundary-layer drying and cloud feedback with global warming. This mechanism may also explain the positive low-cloud feedback in climate models, e.g., the IPSL-CM5A (Brient and Bony, 2013). Conversely, Volodin (2008) hypothesized that the relationship is related to the role of relative humidity in convective parameterization. These different physical interpretations suggest that emergent constraints arise from intermodel differences in structural (local) uncertainties, (remote) biases in large-scale dynamics, and the interactions between them.
This dichotomy is addressed by Sherwood et al. (2014). They quantified the low-tropospheric convective mixing through the sum of two metrics : an index related to small-scale mixing and an index linked to large-scale mixing. The former aims to represent errors in parameterized processes such as shallow convection, turbulence, or precipitation. The latter quantifies model errors in reproducing the tropical dynamical circulation, which can also be affected by parameterizations of deeper convection remotely affecting low clouds. The CMIP3 and CMIP5 intermodel spread of this predictor is well correlated to uncertainties in ECS. Observations (here, reanalysis) suggest that most models underestimate this large-scale mixing, indicating a most likely ECS value larger than 3 K (Table 1). The level of confidence in this estimate is related to the trust one gives to the link between the low-tropospheric characteristics these indices aim to quantify and the low-cloud feedback, which primarily controls the intermodel spread in ECS. In that regard, Caldwell et al. (2018) suggest that constraints suggested by Sherwood et al. (2014) are only partly credible and metrics need to be studied separately. The observational constraint should also be viewed with caution since it is based on reanalysis data and hence is influenced by parameterizations.
The mixing indexes suggested by Sherwood et al. (2014) highlight that errors in representing the coupling between low clouds and tropical dynamics explain a significant part of the spread in ECS, in agreement with Volodin (2008) and Fasullo and Trenberth (2012). This was confirmed by follow-up studies that suggested significant correlations between ECS and indexes of the tropical dynamics, such as the strength of the double-ITCZ bias (Tian, 2015) or the strength of the Hadley circulation (Su et al., 2014). Both show that models better representing the tropical large-scale dynamics are those with the highest climate sensitivities (≈4 K). However, the lack of robust physical mechanisms explaining these emergent constraints reduces the trustworthiness of these inferences, but it also prompts for better theoretical understanding of links between cloud and circulation. This question can be investigated by analyzing the driving influence of clouds on the energetic balance of the atmosphere for explaining large-scale dynamical biases, whether clouds are located in the Southern Hemisphere (Hwang and Frierson, 2013) or in the tropical subsiding regions (Adam et al., 2016, 2017). Together, these studies suggest hidden relationships between low clouds, circulation, and climate sensitivity, which remain to be clarified.
The spread in ECS can also be constrained through the past variability in global-mean temperature, as suggested by Cox et al. (2018). Observations suggest that most models overestimate temperature variations and year-to-year autocorrelation, providing a most likely posterior ECS estimate of 2.8±0.6 K (Table 1). Contrary to most emergent constraints, this study thus suggests a relative low best estimate for climate sensitivity. The absence of links between the mathematical framework used to build the predictor and clouds might reduce the confidence in this estimate, despite the fact that Cox et al. (2018) constraint seems strongly dominated by the spread in shortwave cloud feedback (Caldwell et al., 2018). Given that the low-frequency natural variability of tropical temperature is partly related to cloud variability (e.g., Zhou et al., 2016), it cannot be excluded that all these emergent constraints are related to each other through cloud processes. Process-oriented cross-metric analysis would be necessary to support this hypothesis (e.g., Wagman and Jackson, 2018).

The spread of climate sensitivity is significantly related to the spread in cloud feedback, and mostly to uncertainties in low-cloud responses. It therefore appears obvious that constraining how low clouds respond to global warming would very likely reduce the spread of climate sensitivity among models, and that many emergent constraints on ECS can be understood as encoding properties of shortwave low-cloud feedbacks (Qu et al., 2018). Conversely, emergent constraints that are only indirectly related to clouds should be viewed with caution.
A number of studies have highlighted relationships between low-cloud amount changes under global warming and modeled variations of low clouds with changes in specific meteorological conditions, such as surface temperature, inversion strength, or subsidence (Myers and Norris, 2013, 2015; Qu et al., 2014, 2015; Brient and Schneider, 2016). These studies suggest two robust low-cloud feedbacks: a decrease in low-cloud amount with surface warming (related to increasing boundary-layer ventilation) and an increase in low-cloud amount with inversion strengthening (related to a reduced cloud-top entrainment of dry air). Models show that the former feedback mostly dominates the latter under global warming, and that the more realistic models exhibit larger low-cloud feedback (Qu et al., 2014, 2015; Brient and Schneider, 2016). The convergence of studies using different methodologies and different observations increases our confidence that low-cloud amount feedback more likely lies in the upper range of simulated estimates. Given the credibility of physical mechanisms explaining cloud feedback emergent relationships, reproducibility with the CMIP6 models is expected but yet to be confirmed.
Given that the strength of low-cloud amount feedback strongly correlates with ECS, temporal variations in low-cloud albedo appears to be one of the most credible metrics for constraining ECS (Caldwell et al., 2018). Observations suggest most likely ECS estimates of around 4 K, roughly identical for different temporal frequencies of cloud variations (Zhai et al., 2015; Brient and Schneider, 2016). Despite this robustness, these conclusions are sensitive to the short time period (around a decade) over which observations provide accurate enough characteristics of low clouds. Low-cloud short-term variations might only partly reflect long-term feedback (Zhou et al., 2015), likely because of slow-evolving spatial patterns of surface temperature that delay inversion changes and cloud feedback in subsiding regions (Ceppi and Gregory, 2017; Andrews et al., 2018).
Although low-cloud amount feedback is the main driver of uncertainties in climate sensitivity, other cloud responses contribute to the spread as well. One of them is the low-cloud optical feedback, which is defined by the radiative influence of changes in optical properties given unchanged cloud amount and altitude. Gordon and Klein (2014) show that the natural variability of midlatitude cloud optical depth with temperature is well correlated with its changes with global warming. This relationship stems from fundamental thermodynamics, i.e., the increase in water content with warming (Betts and Harshvardhan, 1987), and microphysical changes, i.e., the relative increase in liquid content relative to ice within clouds (Mitchell et al., 1989). This supports a robust negative cloud optical feedback with warming. Observations suggest that models are usually biased high, thus overestimating the negative midlatitude low-cloud optical feedback. A misrepresentation of mixed-phase processes within these extratropical clouds may explain this bias (McCoy et al., 2015), which has been pinpointed as being a key driver of differences in cloud feedback and climate sensitivity estimates (Tan et al., 2016).
The cloud altitude response to global warming may also amplify the original warming, and models continue to disagree on the strength of this feedback (Zelinka et al., 2013). Physical mechanisms of high cloud elevation with warming are well understood (Hartmann and Larson, 2002), making high-cloud altitude feedback very likely positive. Yet, it remains unknown to what extent the high-cloud amount and the high-cloud optical depth change with warming. These changes are related to upper-tropospheric divergence and microphysics, which need to be constrained individually. Some studies suggest a decreasing high-cloud amount due to more efficient large-scale organization with warming (e.g. Bony et al., 2016), which points the way towards mechanistic emergent constraints on high-cloud feedback.
Better constraining cloud feedback will therefore very likely lead to better constraints on the ECS. This target should be addressed through process-based understanding of individual cloud changes, such as how the relative coverage of tropical low clouds evolves, how high-cloud fractions change as they move upward, or to what extent small-scale microphysical changes perturb the climate system. Merging realistic estimates of these feedbacks would provide a step forward for accurately constraining the ECS.

In the last decade, the concept of emergent constraints has begun to be widely applied in different branches of climate science that allow constraining uncertain responses of the Earth system, such as the hydrological cycle, the carbon cycle, or various regional changes.

2

-->

6.1. The hydrological cycle

Uncertainties in the response of precipitation to global warming are important and remain to be narrowed. Increasing the confidence in precipitation changes would provide important benefits for regional climate projections and risk assessment (Christensen et al., 2013). Links between natural variability of extreme precipitation and temperature offer possible observational constraints for changes in climate extremes, especially because the underlying physical mechanisms are relatively well understood (O’Gorman and Schneider, 2008). These constraints usually suggest a strong intensification of heavy rainfall with warming (O’Gorman, 2012; Borodina et al., 2017). Changes in the hydrological cycle can partly be attributed to changes in the clear-sky shortwave absorption, which is related to models' radiative transfer parameterizations (DeAngelis et al., 2015). Watanabe et al. (2018) followed this path by providing a best estimate for both hydrological sensitivity and shortwave cloud feedback, through the surface longwave cloud radiative effect climatology. This study then connected the intermodel spread of changes in the water cycle and ECS. Process-oriented analysis of specific emergent constraints might thus lead to targeted model development for narrowing the spread in climate projections.

2 -->

6.2. The carbon cycle

A second topic that has also received considerable attention is the sensitivity of the carbon cycle to climate change. Cox et al. (2013) found a robust relationship that links interannual covariations between tropical temperature and carbon release into the atmosphere (the predictor) and the weakening in carbon storage under global warming. Observations highlight that most climate models overestimate the present-day sensitivity of land CO₂ changes, suggesting an overly strong weakening of the CO₂ tropical land storage with climate change (Table 1). This constraint has been confirmed in subsequent analysis (Wang et al., 2014; Wenzel et al., 2014). Additional studies have aimed to constrain other aspects of the climate–carbon cycle feedback, such as terrestrial photosynthesis (Wenzel et al., 2016), sinks and sources of CO₂ (Hoffman et al., 2014; Winkler et al., 2019), and tropical ocean primary production (Kwiatkowski et al., 2017).

2 -->

6.3. Geoengineering

Constraining uncertainties in geoengineering simulations has also been addressed. Intermodel differences in the climate response to an artificial increase in sulfate concentrations are correlated to intermodel differences in the simulated cooling by past volcanic eruptions (Plazzotta et al., 2018). Physical assumptions underlying this relationship consist of assuming that volcanic eruptions can be understood as an analogue of solar radiation management (Trenberth and Dai, 2007). Observations from satellites suggest that models overestimate the cooling by volcanic eruptions, thus overestimating the potential cooling effect by an addition of aerosols in the stratosphere.

2 -->

6.4. Regional climate changes

While most emergent constraints focus on global scales, several aim to better understand and constrain regional climate changes. So far, these studies mostly focus on extratropical climate responses, as was the case for the pioneering work of Hall and Qu (2006). Attempts in constraining changes of extreme temperature have recently showed that models slightly overestimate the increasing frequency of heat extremes with global warming in Europe and North America (Donat et al., 2018), in relation to overly strong soil drying (Douville and Plazzotta, 2017). Changes in the extratropical circulation have also been studied. Models show a robust poleward shift of the Southern Hemisphere jet with global warming, and are uncertain about the sign of the shift in the Northern Hemisphere jet. Emergent constraints suggest that models overestimate the Southern Hemispheric poleward shift (Kidston and Gerber, 2010; Simpson and Polvani, 2016) and predict that the Northern Hemisphere jet will likely move poleward (Gao et al., 2016). Finally, a number of studies have sought to constrain changes over the Arctic region. Their results show that most models delay the year when summertime sea-ice cover is likely to disappear (Boé et al., 2009; Massonnet et al., 2012) and slightly overestimate the strength of the polar amplification (Bracegirdle and Stephenson, 2013).
Regional emergent constraints remain rare, which reduces the ability to compare metrics and observations to one another. Results are thus not yet robust, and should be viewed with caution. However, knowing the large uncertainties underlying regional climate projections and the advantages local populations will get from better model projections (Christensen et al., 2013), I expect in the near future to see numerous new emergent constraints aimed at narrowing uncertainties in regional climate changes. Nevertheless, this should be addressed through rigorous physical understanding given the numerous multi-scale interactions and adjustments that induce regional differences.

2 -->

6.5. Paleoclimate

The sensitivity of global-mean temperature to Earth's orbital variations and/or CO₂ natural changes might be considered an analogue of the warming induced by the artificial CO₂ increase, i.e., the climate sensitivity to past climate change as an analogue to the ECS [as defined by Gregory et al. (2004)]. When imposing such past variations, climate models suggest different responses in the strength of global-mean cooling that may be related to the spread in ECS. For instance, Hargreaves et al. (2012) showed that the simulated global-mean cooling during the Last Glacial Maximum (LGM, 19–23 ka before present) is inversely correlated with ECS in CMIP3 models. Constraining the LGM cooling from proxy data yields a most likely climate sensitivity of around 2.3 K, which is lower than inferred estimates based on the mean state or variability (Table 1). A number of criticisms may arise from this inference, such as the realism of the LGM CMIP simulations, uncertainties underlying proxies used for observational reference, and the use of paleoclimates as a surrogate for global warming (differences in temperature patterns, albedo feedback etc.). These uncertainties may partly explain the frequent weak correlations found between paleoclimate indices and climate projections, and the difficulty in narrowing the spread in models' climate sensitivity estimates from paleoclimate-based emergent constraints (Schmidt et al., 2013; Harrison et al., 2015).

Table 1 lists 14 emergent constraints that provide best estimates for climate sensitivity using various predictors (without paleoclimate indexes). Here, I consider whether, taken together, they reduce the raw model uncertainty (e.g., 3.4$ \pm $0.8 K for CMIP5 models). For that purpose, a density estimate is generated based on 11 ECS emergent constraints that provide the mean and standard deviation of more likely ranges (Table 1). These values correspond to moments provided by the authors if available, or estimated from the emergent relationship (and thus correspond to a raw estimate of the real posterior estimate). Due to the small sample, I use a kernel bandwidth of 1.0°C. This provides a density distribution with a 5%–95% range of 2.2°C–4.9°C and a median of 3.8°C. Figure 4 shows that this unweighted distribution is close to the prior distributions, yet slightly skewed towards high ECS values (explained by most emergent constraints with higher-than-average ECS values).
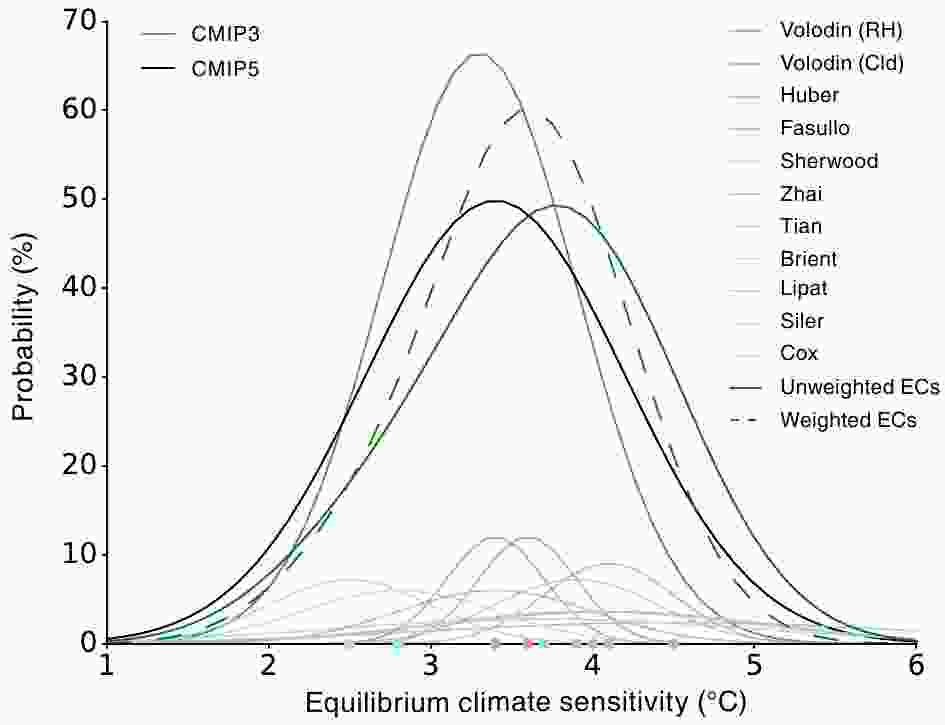Figure4. Probability density distributions of ECS. The black and gray density distributions show the original CMIP3 and CMIP5 model distributions. The 11 emergent constraints of ECS are shown as a normal distributions, with the mean (color dots) and standard deviation listed in Table 1. Unweighted and weighted density distributions aggregated over the 11 emergent constraints are shown as green full and dashed lines respectively. A kernel bandwidth of 1.0°C is used and weights are computed as the reciprocal of the variance.


Here, an equal weight is attributed to each distribution, which assumes that emergent constraints are equally valuable. Knowing the various levels of credibility emergent constraints could receive (Caldwell et al., 2018), this assumption remains a crude approximation. Conversely, quantifying this credibility would permit weighting each emergent constraint and providing more reliable posterior distributions. However, various ways of combining and weighting the constraints exist. Standard deviation $ \sigma $ associated with each constraint is somehow related to this level of confidence, given its link with the model ensemble (section 2.2.3) and observation uncertainties (section 2.2.2). Thus, I attribute a relative weight of $ \dfrac{1}{\sigma^2} $ to each emergent constraint, which corresponds to an optimal weighting method under the assumption that distributions are independent and normally distributed. Figure 4 shows that the weighted density distribution is closer to the raw CMIP distributions and narrower that the unweighted distribution (a 5%–95% range of 2.3°C–4.6°C and a median of 3.7°C). Differences between unweighted and weighted distributions are partly related to the strong relative weight given to some emergent constraints (e.g., Volodin, 2008). The weighting framework suffers from several biases, such as the lack of statistical consistency across various constraints, the overconfidence of observational estimates, or the different set of models used for computing emergent constraints.
The disagreement between emergent constraints and their large uncertainties therefore does not significantly narrow the original spread in ECS. This suggests that emergent constraints need to be better assessed through a verification of physical mechanisms explaining the relationship (Caldwell et al., 2018; Hall et al., 2019). This would help in providing better weights quantifying the credibility of emergent constraints and thus provide more reliable averaged ranges for narrowing the spread in climate change projections. Finally, statistical inference and observational uncertainties must be better informed for cross-validation of posterior estimates.

This paper presents the concept of emergent constraints, a methodology that aims to narrow uncertainties in climate change projections by identifying a link between them and the intermodel spread in an observable predictor. In the last decade, the number of studies using this framework has grown significantly and provided constraints on various climate projections (an exhaustive list of published emergent constraints is presented in Table 1). The majority focused on narrowing uncertainties in ECS, cloud feedback, and carbon cycle feedbacks. Others focused on components of the climate system in relation to changes in the hydrological cycle, the cryosphere, or the dynamical shift of the midlatitude jet, among others. Predictors can be grouped in two main categories: natural variations of the variable of interest with temperature variability, or a mean feature of the climate system. This sometimes leads to metrics not directly related to the considered predictand. Physical explanations for emergent constraints are diverse and thus most of them remain to be confirmed. Weighting the credibility of emergent constraints would very likely increase the confidence in posterior estimates aimed at narrowing the spread in climate projections.
The diversity of emergent constraints highlights the commitment of the climate community to narrowing uncertainties in climate projections. This interest will likely continue to grow since a large number of changes in climate phenomena simulated by models remain uncertain, even when fundamental mechanisms are relatively well understood (e.g., changes in monsoons, heat waves, cyclones). The emergent constraint framework can thus be seen as a new and promising way to evaluate climate models (Eyring et al., 2019; Hall et al., 2019), especially with the upcoming CMIP6, which will very likely boost this enthusiasm. However, this calls for robust statistical inference for providing credible uncertainty reductions. In that respect, the code used for quantifying inference and uncertainties in Fig. 4 with two different methods is shared^①. Quantifying posterior estimates with different frameworks (either from inference or model weighting) allows testing the confidence in predictions. Further work would consist of continuing to test different statistical inference procedures and build multi-predictor weighting methods to benefit from the number of proposed emergent constraints.
Beyond the post-facto model evaluation, it will ultimately be interesting to see whether new climate models take advantage of emergent constraints to improve their simulation of present-day climate and to reduce uncertainties in future projections.
Acknowledgements. This work received funding from the Agence Nationale de la Recherche (ANR) [grant HIGH-TUNE ANR-16-CE01-0010]. I thank Tapio SCHNEIDER for the numerous discussions we had on this topic, and for sharing his thoughts on statistical inference. I also thank Ross DIXON for interesting discussions and for proofreading the manuscript. Finally, I thank the two anonymous reviewers for their insightful comments on the manuscript. Routines for the randomly generated relationship and the statistical inferences are available on the Github website (https://github.com/florentbrient/emergent_constraint/).