JIAO Xiaoxiang, XIN Jialin
School of Mathematical Sciences, University of Chinese Academy of Sciences, Beijing 100049, China

Received 20 November 2019; Revised 4 February 2020
Foundation items: Supported by the National Natural Science Foundation of China (11871450)
Corresponding author: XIN Jialin, E-mail: xinjialin17@mails.ucas.ac.cn

Abstract: We present a construction of the complex Grassmannian G(2, n+2) as a quotient of some minimal submanifold Qⁿ⁺¹ of $\mathbb{H}$Pⁿ⁺¹, then show that a surface in G(2, n+2) can be horizontally lifted to Qⁿ⁺¹ if and only if it is totally real.
Keywords: Grassmanniantotally real surfacehorizontal lift
复Grassmann流形中全实曲面的构造
焦晓祥, 辛嘉麟
中国科学院大学数学科学学院, 北京 100049
摘要: 给出复Grassmann流形G（2，n+2）的全实曲面的一种构造方法，也就是把G（2，n+2）看作$\mathbb{H}$Pⁿ⁺¹中极小子流形Qⁿ⁺¹的商，并证明G（2，n+2）中的曲面可以水平提升到Qⁿ⁺¹中当且仅当它是全实的。
关键词: Grassmann流形全实曲面水平提升
The theory of minimal surfaces is an important part of modern differential geometry. The theory is particularly fruitful when the ambient space is a symmetric space. Calabi^[1] proved a rigidity theorem for minimal two-spheres of constant curvature in Sⁿ. Bolton et al.^[2] constructed all the minimal two-spheres of constant curvature in $\mathbb{C}$Pⁿ, and showed that a totally real minimal two-sphere in $\mathbb{C}$Pⁿ can be mapped, by a holomorphic isometry of $\mathbb{C}$Pⁿ, into $\mathbb{R}$Pⁿ?$\mathbb{C}$Pⁿ. Then He and Wang^[3] proved a similar rigidity result for totally real minimal two-spheres in $\mathbb{H}$Pⁿ.
In this paper, we present a construction of the complex Grassmannian G(2, n+2) due to Berndt^[4], which considers G(2, n+2) as a quotient of some minimal submanifold Qⁿ⁺¹ of $\mathbb{H}$Pⁿ⁺¹. A Riemannian metric can be given on G(2, n+2) so that the projection π: Qⁿ⁺¹→G(2, n+2) is a Riemannian submersion. Then we show that a surface in G(2, n+2) can be horizontally lifted to Qⁿ⁺¹ if and only if it is totally real.
Our result is a special case of Ref.[5], where the author considered a general Riemannian submersion N→B, and characterized the existence of horizontal lifts of a submanifold of B using a family J of (1, 1)-tensors on B. In our paper, we make use of the fact that the projection Qⁿ⁺¹→G(2, n+2) is a principal bundle, thus obtain a characterization by a first order PDE. Our method is largely inspired by Ref.[3], where the authors considered the Riemannian submersion S⁴ⁿ⁺³→$\mathbb{H}$Pⁿ.
1 PreliminariesWe denote by $\mathbb{H}$ the algebra of quaternions. This is a 4-dimensional vector space over $\mathbb{R}$ with basis {1, i, j, k}, and the multiplication is defined by

$\mathrm{i}^{2}=\mathrm{j}^{2}=\mathrm{k}^{2}=-1,$

$\mathrm{ij}=\mathrm{k}=-\mathrm{ji}, \mathrm{jk}=\mathrm{i}=-\mathrm{kj}, \mathrm{ki}=\mathrm{j}=-\mathrm{ik} .$

Thus $\mathbb{H}$ is associative but not commutative. $\mathbb{R}$ and $\mathbb{C}$ are naturally embedded into $\mathbb{H}$ as follows:

$\mathbb{R}=\mathbb{R} \cdot 1 \subset \mathbb{H}, \quad \mathbb{C}=\mathbb{R} \cdot 1 \oplus \mathbb{R} \cdot \mathrm{i} \subset \mathbb{H},$

and we sometimes express an element of $\mathbb{H}$ as q=z+wj, where z, w∈$\mathbb{C}$.
Conjugation is defined for quaternions:

$\overline{a+b \mathrm{i}+c \mathrm{j}+d \mathrm{k}}=a-b \mathrm{i}-c \mathrm{j}-d \mathrm{k}(a, b, c, d \in \mathbb{R}).$

Or equivalently,

$\overline{z+w \mathrm{j}}=\bar{z}-w \mathrm{j}(z, w \in \mathbb{C}).$

Then we have pq=qp, for any p, q∈$\mathbb{H}$.
Let $\mathbb{H}$ⁿ be the space of n-dimensional quaternion column vectors. We consider it as a right $\mathbb{H}$-module. If p=(p₁, …, p_n)^T, q=(q₁, …, q_n)^T∈$\mathbb{H}$ⁿ, two inner products of p, q are defined:

$\langle\boldsymbol{p}, \boldsymbol{q}\rangle_{\mathbb{H}}=\sum\limits_{l} \bar{p}_{l} q_{l},\langle\boldsymbol{p}, \boldsymbol{q}\rangle_{\mathbb{R}}=\operatorname{Re}\langle\boldsymbol{p}, \boldsymbol{q}\rangle_{\mathbb{H}}.$

It is easily verified that 〈, 〉_$\mathbb{R}$ is just the usual Euclidean inner product if $\mathbb{H}$ⁿ is identified as $\mathbb{R}$⁴ⁿ, and that the following properties hold:

$\langle\boldsymbol{p} x, \boldsymbol{q} y\rangle_{\mathbb{H}} =\bar{x}\langle\boldsymbol{p}, \boldsymbol{q}\rangle_{\mathbb{H}} y, $

$\langle\boldsymbol{p}, \boldsymbol{q}\rangle_{\mathbb{H}} =\overline{\langle\boldsymbol{q}, \boldsymbol{p}\rangle}_{\mathbb{H}},$

where p, q∈$\mathbb{H}$ⁿ, x, y∈$\mathbb{H}$.
Similarly, for z=(z₁, …, z_n)^t, w=(w₁, …, w_n)^t∈$\mathbb{C}$ⁿ, we define their inner products:

$\langle \boldsymbol{z}, \boldsymbol{w}\rangle_{\mathbb{C}}=\sum\limits_{1} \overline{\mathrm{z}}_{1} \mathrm{w}_{1},\langle \boldsymbol{z}, \boldsymbol{w}\rangle_{\mathbb{R}}=\operatorname{Re}\langle \boldsymbol{z}, \boldsymbol{w}\rangle_{\mathbb{C}}.$

We will often omit the subscripts $\mathbb{C}$and $\mathbb{H}$ for simplicity.
Next we consider the quaternion projective space $\mathbb{H}$Pⁿ, the set of quaternionic lines in $\mathbb{H}$ⁿ⁺¹. Equivalently, $\mathbb{H}$Pⁿ=S⁴ⁿ⁺³/Sp(1), where S⁴ⁿ⁺³ is the unit sphere in $\mathbb{H}$ⁿ⁺¹$\cong \mathbb{R}$⁴ⁿ⁺⁴, and Sp(1), the multiplicative group of unit quaternions, acts on S⁴ⁿ⁺³ by right multiplication. Since this is an isometric action, there is a unique Riemannian metric on $\mathbb{H}$Pⁿ, called the Fubini-Study metric, such that the quotient map τ: S⁴ⁿ⁺³→$\mathbb{H}$Pⁿ is a Riemannian submersion. For any q∈S⁴ⁿ⁺³, let H_q be the horizontal space of τ at q, i.e. the normal space to the fibre τ^-1(τ(q)). Then H_q={q′∈$\mathbb{H}$ⁿ⁺¹|〈q, q′〉_$\mathbb{H}$=0}. Let τ_q=dτ_q|_Hq. By assumption, τ_q: H_q→T_τ(q)$\mathbb{H}$Pⁿ is a linear isometry.
2 The submanifold Qⁿ⁺¹?$\mathbb{H}$Pⁿ⁺¹; the complex Grassmannian G(2, n+2)We quote some results from Ref.[4].
SU(n+2) acts on S⁴ⁿ⁺⁷?$\mathbb{H}$ⁿ⁺² isometrically via

$S U(n+2) \times S^{4 n+7} \rightarrow S^{4 n+7}, $

$(\boldsymbol{A}, \boldsymbol{z}+\boldsymbol{v} \mathrm{j}) \mapsto \boldsymbol{A} \boldsymbol{z}+(\boldsymbol{A} \boldsymbol{v}) \mathrm{j},$

where z, v∈$\mathbb{C}$ⁿ⁺², with |z|²+|v|²=1. This action commutes with the Sp(1)-action on S⁴ⁿ⁺⁷ defined in the last section, hence descends to an isometric action on $\mathbb{H}$Pⁿ⁺¹.
By some straightforward calculations, we find that this SU(n+2)-action on $\mathbb{H}$Pⁿ⁺¹ has only two singular orbits, namely,

$\mathbb{C} P^{n+1}=\left\{\boldsymbol{\tau}(\boldsymbol{z}+0 \cdot \mathrm{j}) \mid \boldsymbol{z} \in S^{2 n+3}\right\},$

(1)

and

$\begin{aligned}Q^{n+1} &=\{\boldsymbol{\tau}((1 / \sqrt{2})(\boldsymbol{z}+\boldsymbol{v} \mathrm{j})) \mid \boldsymbol{z},\\\boldsymbol{v} &\left.\in S^{2 n+3},\langle \boldsymbol{z}, \boldsymbol{v}\rangle=0\right\},\end{aligned}$

(2)

where S²ⁿ⁺³ is the unit sphere of $\mathbb{C}$ⁿ⁺².
We have the following proposition from Ref.[4]:
Proposition 2.1??The singular orbits of the SU(n+2)-action on $\mathbb{H}$Pⁿ⁺¹ are $\mathbb{C}$Pⁿ⁺¹ and Qⁿ⁺¹.Qⁿ⁺¹ has codimension 3 in $\mathbb{H}$Pⁿ⁺¹, and is isometric to the homogeneous space SU(n+2)/SU(2)×SU(n) equipped with a suitable invariant metric. Furthermore, Qⁿ⁺¹ is a minimal submanifold of $\mathbb{H}$Pⁿ⁺¹.
Now consider an action of U(1) on Qⁿ⁺¹:

$U(1) \times Q^{n+1} \rightarrow Q^{n+1},\left(\mathrm{e}^{\mathrm{i} t}, \boldsymbol{\tau}(\boldsymbol{q})\right) \mapsto \boldsymbol{\tau}\left(\mathrm{e}^{\mathrm{i} t} \boldsymbol{q}\right),$

where t∈$\mathbb{R}$. Again this is an isometric action. A vector field ξ on Qⁿ⁺¹ is defined:

$\begin{aligned}\boldsymbol{\xi}_{\boldsymbol{\tau}(\boldsymbol{q})} &=\left.\frac{\mathrm{d}}{\mathrm{d} t}\right|_{t=0} \mathrm{e}^{\mathrm{i} t} \cdot \boldsymbol{\tau}(\boldsymbol{q})=\left.\frac{\mathrm{d}}{\mathrm{d} t}\right|_{t=0} \boldsymbol{\tau}\left(\mathrm{e}^{\mathrm{i} t} \boldsymbol{q}\right) \\&=\mathrm{d} \boldsymbol{\tau}_{\boldsymbol{q}}(\mathrm{i} \boldsymbol{q})=\boldsymbol{\tau}_{\boldsymbol{q}}(\mathrm{i} \boldsymbol{q}).\end{aligned}$

(3)

Here $\boldsymbol{q}=\frac{1}{\sqrt{2}}(\boldsymbol{z}+\boldsymbol{v} \mathrm{j}) \in \boldsymbol{\tau}^{-1}\left(Q^{n+1}\right), \boldsymbol{z}, \boldsymbol{v} \in S^{2 n+3}$, 〈z, v〉=0. For the last equality, we note that 〈q, iq〉_$\mathbb{H}$=0 for q∈τ^-1(Qⁿ⁺¹), i.e., iq∈H_q. Thus ξ is the field of tangent vectors to the orbits of the U(1)-action.
Let Bⁿ⁺¹=Qⁿ⁺¹/U(1). Since U(1) acts on Qⁿ⁺¹ isometrically, there is a unique Riemannian metric on Bⁿ⁺¹ such that the natural projection π: Qⁿ⁺¹→Bⁿ⁺¹ is a Riemannian submersion.
For τ(q)∈Qⁿ⁺¹, let $\mathcal{H}$_τ(q) be the orthogonal complement of ξ_τ(q) in T_τ(q)Qⁿ⁺¹, i.e. the horizontal space of the Riemannian submersion π: Qⁿ⁺¹→Bⁿ⁺¹. Then the map $\pi_{\tau(\boldsymbol{q})}=\mathrm{d} \pi_{\tau(\boldsymbol{q})} \mid _{\mathcal{H}_{\tau(\boldsymbol{q})}}\;: \mathcal{H}_{\tau(\boldsymbol{q})}$→T_π(τ(q))Bⁿ⁺¹ is a linear isometry. By Ref.[4], the horizontal lift of $\mathcal{H}_{\tau(\boldsymbol{q})}$ through τ: S⁴ⁿ⁺⁷→$\mathbb{H}$Pⁿ⁺¹ is

$\boldsymbol{\tau}_{\boldsymbol{q}}^{-1} \mathcal{H}_{\boldsymbol{\tau}(\boldsymbol{q})}=\left\{\boldsymbol{X} \in \mathbb{H}^{n+2} \mid\langle\boldsymbol{X}, \boldsymbol{q}\rangle=\langle\boldsymbol{X}, \mathrm{i} \boldsymbol{q}\rangle=0\right\}.$

(4)

We define a (1, 1)-tensor φ on Qⁿ⁺¹ as φX=$-\nabla_{\boldsymbol{X}}^{Q^{n+1}} \boldsymbol{\xi}, \boldsymbol{X} \in T Q^{n+1}$, where $\nabla^{Q^{n+1}}$ is the Riemannian connection on Qⁿ⁺¹. Using the O'Neil formula for Riemannian submersions (see, for example, Proposition 4.5.1 of Ref.[6]), it can be shown that

$\varphi X= \begin{cases}0, & \boldsymbol{X}=\boldsymbol{\xi}, \\ \boldsymbol{\tau}_{\boldsymbol{q}}\left(-\mathrm{i} \cdot \boldsymbol{\tau}_{\boldsymbol{q}}^{-1}(\boldsymbol{X})\right), & \boldsymbol{X} \in \mathcal{H}_{\boldsymbol{\tau}(\boldsymbol{q})} .\end{cases}$

(5)

Since by definition T_τ(q)Qⁿ⁺¹=$\mathbb{R}$·$\boldsymbol{\xi}_{\tau(\boldsymbol{q})} \oplus \mathcal{H}_{\tau(\boldsymbol{q})}$, this completely determines φ. In particular, $\varphi(\mathcal{H})\subset \mathcal{H}$.
Finally, notice that φ commutes with the U(1)-action on Qⁿ⁺¹. In other words, if L_t denotes the map Qⁿ⁺¹→Qⁿ⁺¹, $\tau(\boldsymbol{q}) \mapsto \tau\left(\mathrm{e}^{\mathrm{i} t} \boldsymbol{q}\right)$, then $\mathrm{d} L_{t} \circ \varphi=\varphi \circ \mathrm{d} L_{t}$ for all t∈$\mathbb{R}$. Therefore, there exists a (1, 1)-tensor J on Bⁿ⁺¹ satisfying Jπ_*=π_*φ. As φ²X=-X for all $\boldsymbol{X} \in \mathcal{H}$, it follows that J is an almost Hermitian structure on Bⁿ⁺¹. Actually, as is proved in Ref.[4], J turns out to be K?hler, and Bⁿ⁺¹ is holomorphically isometric to the complex Grass-mannian

$G(2, n+2)=U(n+2) / U(2) \times U(n),$

where the metric on G(2, n+2) is induced by the following bi-invariant metric on U(n+2):

$\langle\boldsymbol{X}, \boldsymbol{Y}\rangle=-\frac{1}{4} \operatorname{tr}(\boldsymbol{X} \boldsymbol{Y}),(\boldsymbol{X}, \boldsymbol{Y} \in \mathfrak{U}(n+2)).$

Thus, for example, B² is isometric to G(2, 3)=$\mathbb{C}$P², with the Fubini-Study metric of constant holomorphic sectional curvature 8.
Remark??The isometry between G(2, n+2) and Bⁿ⁺¹ can be explicitly given as

$G(2, n+2) \rightarrow B^{n+1},$

$\mathbb{C} \boldsymbol{z} \oplus \mathbb{C} \boldsymbol{v} \mapsto \boldsymbol{\pi}\left(\boldsymbol{\tau}\left(\frac{1}{\sqrt{2}}(\boldsymbol{z}+\boldsymbol{v} \mathrm{j})\right)\right),$

where z, v∈$\mathbb{C}$ⁿ⁺², |z|=|v|=1, 〈z, v〉_$\mathbb{C}$=0.
3 The main theoremDefinition 3.1??Suppose N is a Hermitian manifold, J is its complex structure, f: M→N is an immersion from a surface M to N. Then f is called totally real if J Im f_*p⊥Imf_*p for all p∈M.
If we choose a local frame X, Y for M, then fis totally real if and only if Jf_*X⊥f_*Y everywhere. This follows easily from the Hermitian condition 〈Ju, Jv〉=〈u, v〉, J²=-1, where 〈, 〉 is the Riemannian metric on N.
Now we can state our main result.
Theorem 3.1??Suppose M is a surface, ψ: M→Bⁿ⁺¹ an immersion, then the following are equivalent:
1) ψ is totally real;
2) ψ has local horizontal lifts to Qⁿ⁺¹, that is, for any p∈M, there is a neighborhood U of p, and an immersion η: U→Qⁿ⁺¹, such that $\pi \circ \eta=\psi$, and Im $\eta_{*} \subset \mathcal{H}$.
Furthermore, η is minimal in Qⁿ⁺¹ if and only if ψ is minimal in Bⁿ⁺¹.
We prove the theorem step by step.
Step 1??Let U be an open subset of M, η: U→Qⁿ⁺¹ an immersion, we shall find a sufficient and necessary condition for η to be horizontal.
First, since τ: S⁴ⁿ⁺⁷→$\mathbb{H}$Pⁿ⁺¹ is a submersion, η can be lifted to S⁴ⁿ⁺⁷, that is, there is an immersion $\boldsymbol{q}=\frac{1}{\sqrt{2}}(\boldsymbol{Z}+\boldsymbol{V} \mathrm{j}): U \rightarrow \tau^{-1}\left(Q^{n+1}\right) \subset S^{4 n+7}$ such that $\eta=\tau \circ q$, where Z, V: U→$\mathbb{C}$ⁿ⁺², |Z|=|V|=1, 〈Z, V〉=0. Now

$\begin{aligned}\mathrm{d} \eta &=\mathrm{d} \boldsymbol{\tau} \mathrm{d} \boldsymbol{q} \\&=\mathrm{d} \boldsymbol{\tau}(\mathrm{d} \boldsymbol{q}-\boldsymbol{q}\langle\boldsymbol{q}, \mathrm{d} \boldsymbol{q}\rangle),\end{aligned}$

(6)

so the horizontal lift of dη to S⁴ⁿ⁺⁷ is τ_q^-1dη=dq-q〈q, dq〉, namely the orthogonal projection of dq onto H_q, the horizontal space of τ at q.
Recall from the last section that
η is horizontal with respect to π
$\Leftrightarrow \operatorname{Im}(\mathrm{d} \eta) \subset \mathcal{H}$
$\Leftrightarrow$〈τ_q^-1dη, q〉=〈τ_q^-1dη, iq〉=0
$\Leftrightarrow$〈dq-q〈q, dq〉, iq〉=0
$\Leftrightarrow$〈dq, iq〉=0.
For the last equivalence note that q∈τ^-1(Qⁿ⁺¹) implies 〈q, iq〉=0.
Write $\boldsymbol{q}=\frac{1}{\sqrt{2}}(\boldsymbol{Z}+\boldsymbol{V} \mathrm{j}), \mathrm{d} \boldsymbol{q}=\frac{1}{\sqrt{2}}(\mathrm{~d} \boldsymbol{Z}+\mathrm{d} \boldsymbol{V} \cdot \mathrm{j})$. Differentiating 〈V, V〉=1, 〈Z, V〉=0 gives

$\left\{\begin{array}{l}\langle\mathrm{d} \boldsymbol{V}, \boldsymbol{V}\rangle+\langle\boldsymbol{V}, \mathrm{d} \boldsymbol{V}\rangle=0, \\\langle\mathrm{d} \boldsymbol{Z}, \boldsymbol{V}\rangle+\langle\boldsymbol{Z}, \mathrm{d} \boldsymbol{V}\rangle=0.\end{array}\right.$

Then

$\begin{aligned}\langle&\mathrm{d} \boldsymbol{q}, \mathrm{i} \boldsymbol{q}\rangle=0 \\\Leftrightarrow 0=&\langle\mathrm{d} \boldsymbol{Z}+\mathrm{d} \boldsymbol{V} \cdot \mathrm{j}, \boldsymbol{Z} \mathrm{i}+\boldsymbol{V} \boldsymbol{\mathrm { k }}\rangle \\=&(\langle\mathrm{d} \boldsymbol{Z}, \boldsymbol{Z}\rangle-\langle\boldsymbol{V}, \mathrm{d} \boldsymbol{V}\rangle) \mathrm{i}+\\&(\langle\boldsymbol{Z}, \mathrm{d} \boldsymbol{V}\rangle+\langle\mathrm{d} \boldsymbol{Z}, \boldsymbol{V}\rangle) \mathrm{k} \\=&(\langle\mathrm{d} \boldsymbol{Z}, \boldsymbol{Z}\rangle+\langle\mathrm{d} \boldsymbol{V}, \boldsymbol{V}\rangle) \mathrm{i} .\end{aligned}$

In summary, we have proved
Lemma 3.1??Suppose $\eta=\tau\left(\frac{1}{\sqrt{2}}(\boldsymbol{Z}+\boldsymbol{V} \mathrm{j})\right)$: U→Qⁿ⁺¹ is an immersion. Then η is horizontal with respect to π: Qⁿ⁺¹→Bⁿ⁺¹ if and only if

$\langle\mathrm{d} \boldsymbol{Z}, \boldsymbol{Z}\rangle+\langle\mathrm{d} \boldsymbol{V}, \boldsymbol{V}\rangle=0.$

(7)

Step 2??Let ψ: M→Bⁿ⁺¹ be an immersion of a surface M into Bⁿ⁺¹. We look for the condition under which ψ has a local horizontal lift to Qⁿ⁺¹.
Let $\eta=\tau \circ \boldsymbol{q}=\tau\left(\frac{1}{\sqrt{2}}(\boldsymbol{Z}+\boldsymbol{V} \mathrm{j})\right): U \rightarrow Q^{n+1}$ be any local lift of ψ, and η₀ a horizontal lift of ψ. Recall that Bⁿ⁺¹ is defined as the quotient of Qⁿ⁺¹ under the U(1)-action e^it·τ(q)=τ(e^itq), then for any p∈U, η(p) and η₀(p) lie in the same orbit. It follows that there is a map λ: U→U(1) such that η₀(p)=λ(p)·η(p) for all p∈U. In short,

$\eta_{0}=\lambda \cdot \eta=\boldsymbol{\tau}\left(\frac{1}{\sqrt{2}}(\lambda \boldsymbol{Z}+\lambda \boldsymbol{V} \mathrm{j})\right).$

(8)

Since η₀ is horizontal, we apply Lemma 1 to obtain

$\begin{aligned}0 &=\langle\mathrm{d}(\lambda \boldsymbol{Z}), \lambda \boldsymbol{Z}\rangle+\langle\mathrm{d}(\lambda \boldsymbol{V}), \lambda \boldsymbol{V}\rangle \\&=\langle\mathrm{d} \lambda \cdot \boldsymbol{Z}+\lambda \mathrm{d} \boldsymbol{Z}, \lambda \boldsymbol{Z}\rangle+\langle\mathrm{d} \lambda \cdot \boldsymbol{V}+\lambda \mathrm{d} \boldsymbol{V}, \lambda \boldsymbol{V}\rangle \\&=\lambda \mathrm{d} \bar{\lambda}(\langle\boldsymbol{Z}, \boldsymbol{Z}\rangle+\langle\boldsymbol{V}, \boldsymbol{V}\rangle)+\lambda \bar{\lambda}(\langle\mathrm{d} \boldsymbol{Z}, \boldsymbol{Z}\rangle+\langle\mathrm{d} \boldsymbol{V}, \boldsymbol{V}\rangle) \\&=-2 \bar{\lambda} \mathrm{d} \lambda+\langle\mathrm{d} \boldsymbol{Z}, \boldsymbol{Z}\rangle+\langle\mathrm{d} \boldsymbol{V}, \boldsymbol{V}\rangle.\end{aligned}$

Here we have used λλ=1 and λdλ+λdλ=0. Since λdλ=λ^-1dλ=d(logλ) we get

$2 \mathrm{~d}(\log \lambda)=\langle\mathrm{d} \boldsymbol{Z}, \boldsymbol{Z}\rangle+\langle\mathrm{d} \boldsymbol{V}, \boldsymbol{V}\rangle.$

(9)

If we take a local coordinate (x, y) on M, this amounts to

$\left\{\begin{array}{l}2 \frac{\partial \log {\lambda}}{\partial x}=\left\langle\boldsymbol{Z}_{x}, \boldsymbol{Z}\right\rangle+\left\langle\boldsymbol{V}_{x}, \boldsymbol{V}\right\rangle, \\2 \frac{\partial \log \lambda}{\partial y}=\left\langle\boldsymbol{Z}_{y}, \boldsymbol{Z}\right\rangle+\left\langle\boldsymbol{V}_{y}, \boldsymbol{V}\right\rangle,\end{array}\right.$

(10)

where $\boldsymbol{Z}_{x}=\frac{\partial \boldsymbol{Z}}{\partial x}, \boldsymbol{Z}_{y}=\frac{\partial \boldsymbol{Z}}{\partial y}$, etc. This is a system of first-order PDEs inλ. By the Frobenius theorem for PDEs, an initial value problem of such a system is solvable if and only if the integrability condition

$\frac{\partial}{\partial y}\left(\frac{\partial \log \lambda}{\partial x}\right)=\frac{\partial}{\partial x}\left(\frac{\partial \log \lambda}{\partial y}\right),$

that is,

$\frac{\partial}{\partial y}\left(\left\langle\boldsymbol{Z}_{x}, \boldsymbol{Z}\right\rangle+\left\langle\boldsymbol{V}_{x}, \boldsymbol{V}\right\rangle\right)=\frac{\partial}{\partial x}\left(\left\langle\boldsymbol{Z}_{y}, \boldsymbol{Z}\right\rangle+\left\langle\boldsymbol{V}_{y}, \boldsymbol{V}\right\rangle\right)$

holds. This equation simplifies to

$\left\langle\boldsymbol{Z}_{x}, \boldsymbol{Z}_{y}\right\rangle+\left\langle\boldsymbol{V}_{x}, \boldsymbol{V}_{y}\right\rangle=\left\langle\boldsymbol{Z}_{y}, \boldsymbol{Z}_{x}\right\rangle+\left\langle\boldsymbol{V}_{y}, \boldsymbol{V}_{x}\right\rangle .$

(11)

Thus we obtain
Lemma 3.2??Suppose $ \psi=\pi \circ \tau\left(\frac{1}{\sqrt{2}}(\boldsymbol{Z}+\right.\boldsymbol{V}\text{ j) ) }$: M→Bⁿ⁺¹ is an immersion. Then ψ has local horizontal lifts to Qⁿ⁺¹ if and only if (11) holds.
Step 3??Let $\psi=\pi \circ \tau \circ q: M \rightarrow B^{n+1}$, where q=$\frac{1}{\sqrt{2}}(\boldsymbol{Z}+\boldsymbol{V} \mathrm{j}): M \rightarrow \tau^{-1}\left(Q^{n+1}\right) \subset S^{4 n+7}$. We shall find out the equation for ψ to be totally real.
We have

$\begin{aligned}\mathrm{d} \psi &=\mathrm{d} \pi \mathrm{d} \boldsymbol{\tau} \mathrm{d} \boldsymbol{q} \\&=\mathrm{d} \pi \mathrm{d} \boldsymbol{\tau}(\mathrm{d} \boldsymbol{q}-\boldsymbol{q}\langle\boldsymbol{q}, \mathrm{d} \boldsymbol{q}\rangle-\mathrm{i} \boldsymbol{q}\langle\mathrm{i} \boldsymbol{q}, \mathrm{d} \boldsymbol{q}\rangle) \\&=\mathrm{d} \pi \mathrm{d} \boldsymbol{\tau}\left(\mathrm{d} \boldsymbol{q}^{\mathcal{H}}\right),\end{aligned}$

(12)

where $\mathrm{d} \boldsymbol{q}^{\mathcal{H}}=\mathrm{d} \boldsymbol{q}-\boldsymbol{q}\langle\boldsymbol{q}, \mathrm{d} \boldsymbol{q}\rangle-\mathrm{i} \boldsymbol{q}\langle\mathrm{i} \boldsymbol{q}, \mathrm{d} \boldsymbol{q}\rangle$ is the orthogonal projection of dq onto $\tau_{\boldsymbol{q}}^{-1} \mathcal{H}_{\tau(\boldsymbol{q})}$. In other words, $\mathrm{d} \boldsymbol{q}^{\mathcal{H}}=\tau_{\boldsymbol{q}}^{-1} {\pi}_{\tau(\boldsymbol{q})}^{-1}(\mathrm{~d} \psi)$.
Choose a local coordinate (x, y) on M. Then, using the definitions of the tensors φ, J (see (5)), and the fact that τ, π are Riemannian submersions, we obtain
ψ is totally real

$\begin{aligned}\Leftrightarrow 0 &=\left\langle\psi_{x}, J \psi_{y}\right\rangle_{B^{n+1}} \\&=\left\langle\pi_{\boldsymbol{\tau}(\boldsymbol{q})}^{-1} \psi_{x}, \pi_{\boldsymbol{\tau}(\boldsymbol{q})}^{-1} J \psi_{y}\right\rangle_{Q^{n+1}} \\&=\left\langle{\pi}_{\boldsymbol{\tau}(\boldsymbol{q})}^{-1} \psi_{x}, {\varphi} \pi_{\boldsymbol{\tau}(\boldsymbol{q})}^{-1} \psi_{y}\right\rangle_{Q^{n+1}} \\&=\left\langle\boldsymbol{\tau}_{\boldsymbol{q}}^{-1} \pi_{\boldsymbol{\tau}(\boldsymbol{q})}^{-1} \psi_{x}, \boldsymbol{\tau}_{\boldsymbol{q}}^{-1} \varphi \pi_{\boldsymbol{\tau}(\boldsymbol{q})}^{-1} \psi_{y}\right\rangle_{\mathbb{R}} \\&=\left\langle\boldsymbol{\tau}_{\boldsymbol{q}}^{-1} \pi_{\boldsymbol{\tau}(\boldsymbol{q})}^{-1} \psi_{x},-\mathrm{i} \cdot \boldsymbol{\tau}_{\boldsymbol{q}}^{-1} \pi_{\boldsymbol{\tau}(\boldsymbol{q})}^{-1} \psi_{y}\right\rangle_{\mathbb{R}} \\&=\left\langle\boldsymbol{q}_{x}^{\mathcal{H}},-\mathrm{i} \boldsymbol{q}_{y}^{\mathcal{H}}\right\rangle_{\mathbb{R}} .\end{aligned}$

(13)

Since $\left\langle\boldsymbol{q}_{x}^{\mathcal{H}}, \mathrm{i} \boldsymbol{q}_{y}^{\mathcal{H}}\right\rangle_{\mathbb{R}}=\operatorname{Re}\left\langle\boldsymbol{q}_{x}^{\mathcal{H}}, \mathrm{i} \boldsymbol{q}_{y}^{\mathcal{H}}\right\rangle$, let us calculate $\left\langle\boldsymbol{q}_{x}^{\mathcal{H}}, \mathrm{i} \boldsymbol{q}_{y}^{\mathcal{H}}\right\rangle$ first. Now
For the second step note that q∈τ^-1(Qⁿ⁺¹) implies 〈q, iq〉=0. Differentiating〈q, q〉=1 yields

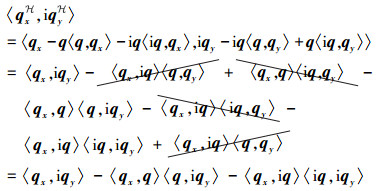$\begin{aligned}0 &=\left\langle\boldsymbol{q}_{x}, \boldsymbol{q}\right\rangle+\left\langle\boldsymbol{q}, \boldsymbol{q}_{x}\right\rangle \\&=\left\langle\boldsymbol{q}_{x}, \boldsymbol{q}\right\rangle+\overline{\left\langle\boldsymbol{q}_{x}, \boldsymbol{q}\right\rangle},\end{aligned}$

i.e., 〈q_x, q〉∈Im$\mathbb{H}$. Similarly, differentiating 〈q, iq〉=0 yields

$\begin{aligned}0 &=\left\langle\boldsymbol{q}_{y}, \mathrm{i} \boldsymbol{q}\right\rangle+\left\langle\boldsymbol{q}, \mathrm{i} \boldsymbol{q}_{y}\right\rangle \\&=-\left\langle\mathrm{i} \boldsymbol{q}_{y}, \boldsymbol{q}\right\rangle+\left\langle\boldsymbol{q}, \mathrm{i} \boldsymbol{q}_{y}\right\rangle \\&=-\overline{\left\langle\boldsymbol{q}, \mathrm{i} \boldsymbol{q}_{y}\right\rangle}+\left\langle\boldsymbol{q}, \mathrm{i} \boldsymbol{q}_{y}\right\rangle,\end{aligned}$

i.e., 〈q, iq_y〉∈$\mathbb{R}$. Therefore〈q_x, q〉〈q, iq_y〉∈Im$\mathbb{H}$. Similarly 〈q_x, iq〉〈iq, iq_y〉∈Im$\mathbb{H}$. Thus we get

$\begin{aligned}& 2\left\langle\boldsymbol{q}_{x}^{\mathcal{H}}, \mathrm{i} \boldsymbol{q}_{y}^{\mathcal{H}}\right\rangle_{\mathbb{R}} \\=& 2 \operatorname{Re}\left\langle\boldsymbol{q}_{x}^{\mathcal{H}}, \mathrm{i} \boldsymbol{q}_{y}^{\mathcal{H}}\right\rangle \\=& 2 \operatorname{Re}\left\langle\boldsymbol{q}_{x}, \mathrm{i} \boldsymbol{q}_{y}\right\rangle \\=& \operatorname{Re}\left\langle\boldsymbol{Z}_{x}+\boldsymbol{V}_{x} \mathrm{j}, \boldsymbol{Z}_{y} \mathrm{i}+\boldsymbol{V}_{y} \mathrm{k}\right\rangle \\=& \operatorname{Re}\left(\left\langle\boldsymbol{Z}_{x}, \boldsymbol{Z}_{y}\right\rangle \mathrm{i}-\left\langle\boldsymbol{V}_{y}, \boldsymbol{V}_{x}\right\rangle \mathrm{i}\right) \\=& \operatorname{Im}\left(\left\langle\boldsymbol{V}_{y}, \boldsymbol{V}_{x}\right\rangle-\left\langle\boldsymbol{Z}_{x}, \boldsymbol{Z}_{y}\right\rangle\right) .\end{aligned}$

(14)

Finally, from (13) and (14) we obtain
Lemma 3.3??$\psi=\pi \circ \tau\left(\frac{1}{\sqrt{2}}(\boldsymbol{Z}+\boldsymbol{V} \mathrm{j})\right): \boldsymbol{M}$→Bⁿ⁺¹ is totally real if and only if

$\operatorname{Im}\left(\left\langle\boldsymbol{V}_{y}, \boldsymbol{V}_{x}\right\rangle-\left\langle\boldsymbol{Z}_{x}, \boldsymbol{Z}_{y}\right\rangle\right)=0,$

or equivalently,

$\left\langle\boldsymbol{V}_{y}, \boldsymbol{V}_{x}\right\rangle-\left\langle\boldsymbol{Z}_{x}, \boldsymbol{Z}_{y}\right\rangle=\left\langle\boldsymbol{V}_{x}, \boldsymbol{V}_{y}\right\rangle-\left\langle\boldsymbol{Z}_{y}, \boldsymbol{Z}_{x}\right\rangle$

(15)

Comparing with Lemma 3.2, we find that ψ have a local horizontal lift to Qⁿ⁺¹ if and only if it is totally real.
Step 4??We need a simple lemma.
Lemma 3.4??Suppose $\pi: \bar{N} \rightarrow N$ is a Riemannian submersion, $\bar{M} \subset \bar{N}$ is a horizontal submanifold, and $M=\pi(\bar{M}) \subset N$. Then

$\boldsymbol{H}_{M}(\pi(p))=\pi_{*}\left(\boldsymbol{H}_{\bar{M}}(p)\right)$

for any p∈M. Furthermore, H_M is horizontal. Here H_M, H_M are the mean curvature vectors of M, M, respectively.
Proof??Let e₁, …, e_m be an orthonormal frame on M, then, since $\left.\pi\right|_{\bar{M}}: \bar{M} \rightarrow M$ is an isometry, e₁=π_*(e₁), _…, e_m=π_*(e_m) is an orthonormal frame on M. By O'Neil's formula, $\nabla_{\bar{\boldsymbol{e}}_{i}}^{\bar{N}} \bar{\boldsymbol{e}}_{i}$ is the horizontal lift of $\nabla_{\boldsymbol{e}_{i}}^{N} \boldsymbol{e}_{i}$, hence horizontal, and $\boldsymbol{B}_{\bar{M}}\left(\overline{\boldsymbol{e}}_{i}, \overline{\boldsymbol{e}}_{i}\right)$=$\nabla_{\overline{\boldsymbol{e}}_{i}}^{\bar{N}} \overline{\boldsymbol{e}}_{i}-\nabla_{\overline{\boldsymbol{e}}_{i}}^{\bar{M}} \overline{\boldsymbol{e}}_{i}$ is also horizontal. Thus H_M=$\sum\limits_{i} \boldsymbol{B}_{\bar{M}}\left(\overline{\boldsymbol{e}}_{i}, \overline{\boldsymbol{e}}_{i}\right)$ is horizontal. On the other hand,

$\begin{aligned}\nabla_{\boldsymbol{e}_{i}}^{N} \boldsymbol{e}_{i} &=\pi_{*}\left(\nabla_{\bar{\boldsymbol{e}}_{i}}^{\bar{N}} \overline{\boldsymbol{e}}_{i}\right) \\&=\pi_{*}\left(\nabla_{\bar{\boldsymbol{e}}}^{\bar{M}} \overline{\boldsymbol{e}}_{i}+\boldsymbol{B}_{\bar{M}}\left(\overline{\boldsymbol{e}}_{i}, \overline{\boldsymbol{e}}_{i}\right)\right) \\&=\nabla_{\boldsymbol{e}_{i}}^{M} \boldsymbol{e}_{i}+\pi_{*}\left(\boldsymbol{B}_{\bar{M}}\left(\overline{\boldsymbol{e}}_{i}, \overline{\boldsymbol{e}}_{i}\right)\right).\end{aligned}$

(16)

Comparing with the Gauss equation in N, we find that

$\boldsymbol{B}_{M}\left(\boldsymbol{e}_{i}, \boldsymbol{e}_{i}\right)=\pi_{*}\left(\boldsymbol{B}_{\bar{M}}\left(\overline{\boldsymbol{e}}_{i}, \overline{\boldsymbol{e}}_{i}\right)\right).$

(17)

The conclusion follows immediately.
From the above lemma, we see that H_M=$0 \Leftrightarrow \boldsymbol{H}_{\bar{M}}=0$. That is, $M {\rm { minimal }} \Leftrightarrow \bar{M} \rm { minimal }$. This applies to our situation and the main theorem is fully proved.

References

[1]	Calabi E. Minimal immersions of surfaces in Euclidean spheres[J]. Journal of Differential Geometry, 1967, 1(1): 111-125.
[2]	Bolton J, Jensen G R, Rigoli M, et al. On conformal minimal immersions of S2 into $\mathbb{C}$Pn[J]. Mathematische Annalen, 1988, 279(4): 599-620. DOI:10.1007/BF01458531
[3]	He Y, Wang C. Totally real minimal 2-spheres in quaternionic projective space[J]. Science in China. Series A. Mathematics, 2005, 48(3): 341-349. DOI:10.1360/03ys0295
[4]	Berndt J. Riemannian geometry of complex two-plane Grassmannians[J]. Rendiconti del Seminario Matematico. Università e Politecnico Torino, 1997, 55(1): 19-83.
[5]	Reckziegel H. Horizontal lifts of isometric immersions into the bundle space of a pseudo-Riemannian submersion[C]//Ferus D, Gardner R B, Helgason S, et al. Global differential geometry and global analysis 1984. Berlin: Springer, 1985: 264-279.
[6]	Petersen P. Riemannian geometry[M]. 3rd ed. Berlin: Springer, 2016.