

中国科学技术大学中国科学院无线光电通信重点实验室, 合肥 230027
2015年09月08日 收稿; 2015年12月28日 收修改稿
基金项目: 863计划项目(2014AA01A707)资助
通信作者: 邱玲,E-mail:lqiu@ustc.edu.cn
摘要: 考虑到MTCD数量巨大的特性,针对OFDMA蜂窝网络中H2H与M2M共存场景系统过载的情况,提出一种准入控制及资源分配联合优化算法.针对共存场景系统过载的情况,考虑控制信道的影响,本文形成了最大化准入MTCD数目的MINLP问题.由于难以求得其最优解,通过凸松弛将其转化为标准的凸问题,由此得到原问题解的上界,并进一步提出一种低复杂度的求解算法.仿真结果表明所提算法与上界相比性能损失小,且明显优于两种对比算法.
关键词: 机器通信准入控制资源分配控制信道
Admission control and resource allocation of H2H & M2M co-existence scenario
WANG Xin, QIU Ling


Key Laboratory of Wireless-Optical Communications of Chinese Academy of Sciences, University of Science and Technology of China, Hefei 230027, China
Abstract: This study focuses on the massive device characteristic of M2M communication. Considering the overload situation in H2H & M2M co-existence scenario of OFDMA cellular networks, we propose an admission control and resource allocation joint optimization algorithm. Considering the effect of control channel, we formulate a MINLP problem of maximizing the number of MTCDs admitted. Because of the complexity of MINLP problems, relaxed constraints are used to transform the MINLP problem into a convex problem, which is the upper-bound of the original problem. Furthermore, a low-complicity algorithm is proposed. Simulation results show that the algorithm has minor degradation compared with the upper-bound and is better than two other algorithms.
Key words: M2Madmission controlresource allocationcontrol channel
机器与机器(machine to machine,M2M)通信利用自动控制及网络通信等技术,在没有人为干预的情况下实现机器间自主数据通信及信息交互[1].3GPP预测未来有万亿级别的机器通信终端(machine type communication device,MTCD)接入无线通信网络中,比人与人(human to human,H2H)通信终端(user equipment,UE)要多出至少2个数量级[2].大规模M2M通信的实际部署依赖于网络的广泛覆盖及低复杂的连接,蜂窝网络成为最直接及最现实的解决方案[3].蜂窝网络主要为相对少量的UE而设计,但与H2H通信相比,M2M通信具有终端数量巨大,业务类型多,上行业务为主等显著特性,给蜂窝网络无线资源管理带来严峻挑战[4].
资源分配作为蜂窝网络无线资源管理的重要组成部分,可以有效挖掘系统的复用增益,得到了广泛而深入的研究.文献[5]研究上行OFDMA系统最大化H2H加权和速率问题,但没有考虑不同优先级混合业务的资源分配;针对H2H与M2M共存的场景,文献[4]提出一种基于网络效用最大化的资源分配算法,但其效用仅是UE和MTCD数据速率的函数,且没有考虑服务质量(quality of service,QoS)的约束;文献[6-7]分别研究共存场景最小化系统上行总发射功率及最大化系统上行能量效率的问题,且考虑了UE 和MTCD的QoS约束,但文献[6-7]仅研究了系统不过载情况,即系统资源能同时满足所有用户需求.对于存在大量MTCD的共存场景,需考虑系统过载的情况,此时,系统进行准入控制[8](admission control,AC),文献[9]对次用户进行准入控制,最大化系统所准入的次用户数目,同时保证主用户以及准入次用户的QoS需求,但仅考虑了单信道的情况,即仅分配上行发射功率.当考虑在蜂窝网络中部署M2M通信时,充分利用M2M通信的特性,研究多信道系统共存场景下系统过载情况的混合资源分配问题具有重要的理论意义及应用价值.此外,文献[10]指出对于存在大量MTCD的场景,控制信道也是制约系统性能的因素,文献[11]仿真分析控制信道对M2M通信随机接入过程的影响,因此,研究蜂窝网络中M2M通信的资源分配问题也需要考虑控制信道的影响.
针对研究现状,本文利用M2M通信的特性,研究上行OFDMA系统H2H与M2M共存场景下系统过载情况的混合资源分配问题,并同时考虑了控制信道对资源分配的影响,主要贡献总结如下:
关注MTCD数量巨大的特性,考虑共存场景系统过载的情况,将优化目标设为最大化系统准入的MTCD数目,区别于传统的最小化发射功率、最大化能量效率等目标;对于形成的准入控制及资源分配联合优化混合整形非线性规划(mixed-integer nonlinear programming,MINLP)问题,由于难以求得其最优解,本文通过凸松弛将其转化为标准凸问题,由求解凸问题得到原问题解的上界,并进一步提出一种低复杂度的求解算法,仿真结果表明所提算法与上界相比性能损失小,且明显优于2种对比算法.
1 系统模型考虑OFDMA蜂窝系统单小区上行链路.小区内设备集合为$k\triangleq ${1,…,K1,…,K},分为2个子集,UE集合${{k}_{\text{h}}}\triangleq ${1,…,K1},MTCD集合${{k}_{\text{m}}}\triangleq ${K1+1,…,K}.系统带宽为B,均匀划分成子载波集合$N\triangleq ${1,…,N}.设备最大上行发射功率为Pk,最小速率要求为RkT,ρk,n为子载波分配变量(值为1代表子载波n分配给设备k),pk,n代表设备k在子载波n上的发射功率,αk,n=|hk,n|2N/N0B代表设备k在子载波n上的信道SNR,其中k=1,2,…,K,n=1,2,…,N.
本文利用信令数据比(ratio of signaling to data,RSD)建模控制信道与数据信道间的数量关系[12],RSD值反映不同类型的业务对控制信道需求的大小:
| $RSD:f\text{=}\frac{控制信道子载波数}{数据信道子载波数}.$ |
2 M2M准入控制及资源分配2.1 问题形成针对MTCD数量巨大的特性,并考虑实际系统中控制信道的约束,H2H与M2M共存场景下系统过载情况的准入控制及资源分配问题形成如下:
| $\begin{align} & (\text{P}1)\underset{\{{{\rho }_{k,n}},{{p}_{k,n}}\}}{\mathop{\max }}\,\Sigma _{k={{K}_{1}}+1}^{K}{{X}_{k}} \\ & \text{s}.\text{t}.C1:\Sigma _{n=1}^{N}{{p}_{k,n}}\le {{P}_{k}},\forall k \\ & C2:\Sigma _{k=1}^{K}{{p}_{k,n}}\le 1,\forall n \\ & C3:\Sigma _{k=1}^{K}\Sigma _{n=1}^{N}{{f}_{k}}{{p}_{k,n}}\le C \\ & C4:{{p}_{k,n}}\ge 0,\forall k,n \\ & C5:{{p}_{k,n}}=\left\{ 0,1 \right\},\forall k,n \\ & C6:{{X}_{k}}=\left\{ 0,1 \right\},{{K}_{1}}+1\le k\le K \\ & C7:\Sigma _{n=1}^{N}{{p}_{k,n}}{{\log }_{2}}(1+{{p}_{k,n}}{{\alpha }_{k,n}})\ge R_{k}^{\text{T}},1\le k\le {{K}_{1}}. \\ & \\ \end{align}$ |
2.2 问题求解由于(P1)不易求解,因此分别对Xk和ρk,n进行凸松弛[8](Xk∈[0,1]表示系统准入所有速率大于0的用户;ρk,n∈[0,1]表示不同的用户可以共享同一个子载波,例如时域共享),将(P1)转化为(P2).
在(P2)中,sk,n=ρk,npk,n表示设备k在子载波n上实际的能量. 对于非线性约束7和8,令$g(\{{{\rho }_{k,n}}\},\{{{s}_{k,n}}\},{{X}_{k}})=\sum\limits_{n=1}^{N}{{{\rho }_{k,n}}}{{\log }_{2}}\left( 1+\frac{{{s}_{k,n}}{{\alpha }_{k,n}}}{{{\rho }_{k,n}}} \right)XR_{k}^{\text{T}}$,其中,$X=\left\{ \begin{array}{*{35}{l}} 1 & 1\le k\le {{K}_{1}} \\ {{X}_{k}} & {{K}_{1}}+1\le k\le K\prime \\\end{array} \right.$,由于其海森矩阵半负定,因此g({ρk,n},{sk,n},Xk)为凹函数.
| $\begin{align} & (\text{P2})\underset{\{{{\rho }_{k,n}},{{p}_{k,n}}\}}{\mathop{\max }}\,\Sigma _{k={{K}_{1}}+1}^{K}{{X}_{k}} \\ & \text{s}.\text{t}.C1:\Sigma _{n=1}^{N}{{S}_{k,n}}\le {{P}_{k}},\forall k \\ & C2:\Sigma _{k=1}^{K}{{p}_{k,n}}\le 1,\forall n \\ & C3:\Sigma _{k=1}^{K}\Sigma _{n=1}^{N}{{f}_{k}}{{p}_{k,n}}\le C \\ & C4:{{S}_{k,n}}\ge 0,\forall k,n \\ & C5:{{p}_{k,n}}=\left\{ 0,1 \right\},\forall k,n \\ & C6:{{X}_{k}}=\left\{ 0,1 \right\},{{K}_{1}}+1\le k\le K \\ & C7:\Sigma _{n=1}^{N}{{p}_{k,n}}{{\log }_{2}}(1+\frac{{{s}_{k,n}}{{\alpha }_{k,n}}}{{{\rho }_{k,n}}})\ge R_{k}^{\text{T}},1\le k\le {{K}_{1}} \\ & C8:\Sigma _{n=1}^{N}{{p}_{k,n}}{{\log }_{2}}(1+\frac{{{s}_{k,n}}{{\alpha }_{k,n}}}{{{\rho }_{k,n}}})\ge {{X}_{k}}R_{k}^{\text{T}},{{K}_{1}}+1\le k\le {{K}_{1}}. \\ \end{align}$ |
定义(P2)的拉格朗日函数如下:(其中拉格朗日乘子λ,β,μ,ν≥0)
| $\begin{align} & L(\{{{\rho }_{k,n}}\},\{{{s}_{k,n}}\},\{{{X}_{k}}\},\lambda ,\beta ,\mu ,\upsilon ) \\ & =\sum\limits_{k={{K}_{1}}+1}^{K}{{{X}_{k}}}\sum\limits_{k=1}^{{{K}_{1}}}{{{\lambda }_{k}}}\left( \sum\limits_{n=1}^{N}{{{p}_{k,n}}{{\log }_{2}}(1+\frac{{{s}_{k,n}}{{\alpha }_{k,n}}}{{{\rho }_{k,n}}})-R_{k}^{\text{T}}} \right)+ \\ & \sum\limits_{k={{K}_{1}}+1}^{K}{{{\lambda }_{k}}\left( \sum\limits_{n=1}^{N}{{{p}_{k,n}}{{\log }_{2}}(1+\frac{{{s}_{k,n}}{{\alpha }_{k,n}}}{{{\rho }_{k,n}}})-{{X}_{k}}R_{k}^{\text{T}}} \right)}+ \\ & \sum\limits_{k=1}^{K}{{{\beta }_{k}}\left( {{P}_{k}}-\sum\limits_{n=1}^{N}{{{S}_{k,n}}} \right)}+\sum\limits_{n=1}^{N}{{{\mu }_{n}}\left( 1-\sum\limits_{n=1}^{N}{{{p}_{k,n}}} \right)}+ \\ & v\left( C-\sum\limits_{k=1}^{K}{\sum\limits_{n=1}^{N}{{{f}_{k}}{{p}_{k,n}}}} \right) \\ \end{align}$ |
| $\beta _{k}^{*}\left( {{P}_{k}}-\sum\limits_{n=1}^{N}{S_{k,n}^{*}} \right)=0,$ | (1) |
| $\begin{align} & \frac{\partial L}{\partial S_{k,n}^{*}}=\lambda _{k}^{*}\rho _{k,n}^{*}\frac{{{\alpha }_{k,n}}}{\left( \rho _{k,n}^{*}+S_{k,n}^{*}{{\alpha }_{k,n}} \right)\ln 2}- \\ & \beta _{k}^{*}\left\{ \begin{array}{*{35}{l}} \text{=}0 & S_{k,n}^{*}>0 \\ <0 & S_{k,n}^{*}\text{=}0 \\\end{array}, \right. \\ \end{align}$ | (2) |
| $\begin{align} & \frac{\partial L}{\partial \rho _{k,n}^{*}}=\lambda _{k}^{*}\left[ {{\log }_{2}}\left( 1+\frac{S_{k,n}^{*}{{\alpha }_{k,n}}}{\rho _{k,n}^{*}} \right)-\frac{{{\alpha }_{k,n}}}{\left( \rho _{k,n}^{*}+S_{k,n}^{*}{{\alpha }_{k,n}} \right)\ln 2} \right]-\mu _{k}^{*}-{{v}^{*}}{{f}_{k}} \\ & \left\{ \begin{array}{*{35}{l}} <0 & \rho _{k,n}^{*}\text{=}0 \\ =0 & 0<\rho _{k,n}^{*}<1 \\ >0 & \rho _{k,n}^{*}=1 \\\end{array} \right.. \\ \end{align}$ | (3) |
证明 将拉格朗日函数对sk,n求偏导,可以得到(2)式,因此相应的功率分配方案为
| $\rho _{k,n}^{*}=\frac{S_{k,n}^{*}}{\rho _{k,n}^{*}}={{\left( \frac{\lambda _{k}^{*}}{\beta _{k}^{*}\ln 2}-\frac{1}{{{\alpha }_{k,n}}} \right)}^{+}},$ | (4) |
推论2.2 子载波倾向于分配给信道条件好,RSD值小的设备.
证明 将拉格朗日函数对ρk,n求偏导,可以得到(3)式,将(4)式代入(3)式中,可以得到:
| $\rho _{k,n}^{*}=\left\{ \begin{array}{*{35}{l}} 0, & {{H}_{k,n}}<\mu _{n}^{*} \\ \left( 0,1 \right), & {{H}_{k,n}}=\mu _{n}^{*} \\ 1, & {{H}_{k,n}}>\mu _{n}^{*} \\\end{array} \right.,$ | (5) |
上述在功率和子载波分配中基于KKT条件的推论,对于算法的设计具有重要的启示意义,本文后续所提算法将主要基于这些推论.
2.3 算法步骤算法以最大化准入的MTCD数目为目标,并将MTCD所占用的控制信道容量$$作为其是否准入的衡量标准,算法的主要步骤如下:
步骤1(初始化及UE的资源分配):
准入MTCD集合${{H}_{\text{a}}}\text{=}\varnothing $,未准入MTCD集合${{H}_{\text{u}}}\text{=}{{H}_{\text{m}}}$,可用子载波集合${{N}_{\text{a}}}\text{=}N$,分配给设备k的子载波集合${{\varphi }_{k}}=\varnothing ,1\le k\le H$;依次对${{H}_{\text{h}}}$中的UE按照信道条件分配子载波并满功率注水,直至满足速率约束,并将相应子载波从${{N}_{\text{a}}}$中去除;
步骤2(MTCD的资源分配):
依次将Na中的子载波添加到Ku中αk,n最大的MTCD的Sk中,计算分配当前子载波时该MTCD在Sk上满功率注水的可达速率Rm,若Rm≥RmT,则将该MTCD添加到Ka以及从Ku中去除,直至${{N}_{\text{a}}}\text{=}\varnothing $;
步骤3(控制信道约束):
1) 对Ka中的MTCD、Kh中的UE以及相应的Sk,计算所占用总的控制信道子载波数,若占满执行2),否则执行3);
2) 从Ka中删除$$最大的MTCD,将相应的Sm添加到Na,执行步骤2;
3)对Ku中的MTCD,按照fm(RmT-Rm)从小到大依次分配资源准入,直至控制信道或数据信道资源不能满足,算法结束.
该算法的复杂度近似为O(KuKN),其中Ku为系统未准入的MTCD数目.对于存在大量MTCD和子载波的系统,该算法复杂度远低于求解优化问题(P1)性能上界的内点法.
3 仿真结果与分析仿真场景为OFDMA系统上行单小区系统过载情况,MTCD和UE均匀分布在距离基站100m到500m的环形范围内,路径损耗为PL(dB)=128.1+37.6lgR(km),基站与设备间的信道服从独立同分布瑞利衰落,UE和MTCD的最大发射功率分别为20dBm和10dBm,系统共有50个子载波,每个子载波带宽为15kHz,噪声功率N0为-174dBm/Hz.
仿真将检验本文所提算法(proposed)与问题(P2)的最优解,即原问题(P1)的性能上界(upper bound)之间的差距,在此基础上,为了更好说明本文所提算法的性能,将与CNA[5]及Random Selecting算法进行对比.基于CNA的准入控制算法主要思想是:按照MTCD的平均信道条件与目标速率计算所需的子载波数目,并由此计算所需控制信道容量,按照其值从小到大的顺序依次准入;Random Selecting算法的主要思想是:随机选取MTCD准入.
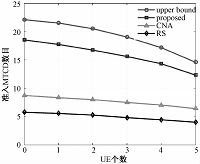
图 1表示RkT=450kbits/s,fk=0.5?k,C=20时,100个MTCD中准入的数目与UE数目之间的关系.随着UE数目的增加,UE占用的资源增多,准入的MTCD数目减少.
Fig. 1
 | Download: JPG larger image |
| 图 1 准入MTCD数目与UE数目关系Fig. 1 Number of MTCDs admitted versus UE number | |
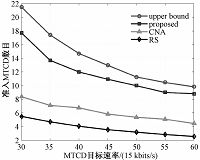
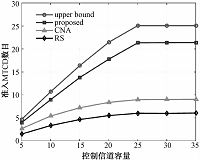
当系统中仅存在1个UE时,图 2与图 3分别表示系统准入的MTCD数目与目标速率及控制信道子载波数目之间的关系.随着目标速率的增加,每个MTCD占用的系统资源增多,准入数目减少;随着控制信道子载波数目的增加,MTCD可以使用的子载波数目增加,系统准入的MTCD数目增加.由于数据传输子载波总数为50,因此,当控制信道子载波数目大于25时,所有用于数据传输的子载波都被分配,因此,系统准入的MTCD数目不再增加.
Fig. 2
 | Download: JPG larger image |
| 图 2 准入MTCD数目与MTCD目标速率关系Fig. 2 Number of MTCDs admitted versus data rate | |
Fig. 3
 | Download: JPG larger image |
| 图 3 准入MTCD数目与控制信道容量关系Fig. 3 Number of MTCDs admitted versus control channel | |
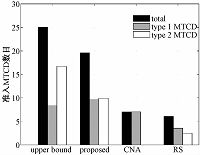
当系统中存在相同数目的2类MTCD,f1=0.25,f2=0.5,相应的目标速率分别为R1T=600 kbits/s,R2T=300 kbits/s时,图 4对比4种算法对不同类型MTCD的准入个数,所提算法更均衡地准入2种类型的MTCD.CNA算法由于按照MTCD占用控制信道的大小依次准入,因此,准入的MTCD都为第1种类型.
Fig. 4
 | Download: JPG larger image |
| 图 4 不同类型MTCD的准入数目比较Fig. 4 Numbers of MTCDs admitted of different types | |
4 结束语本文主要针对MTCD数量巨大的特性,研究OFDMA蜂窝网络中H2H与M2M共存场景下系统过载情况的准入控制以及资源分配问题.针对共存场景系统过载的情况,并且考虑控制信道的影响,形成了最大化准入MTCD数目的MINLP问题.由于MINLP问题难以求得最优解,本文通过凸松弛将其转化为标准凸问题,由求解凸问题得到原问题解的上界,并依据KKT条件的相关推论进一步提出一种低复杂度的求解算法,仿真结果表明所提算法与上界相比性能损失小,且明显优于2种对比算法.
参考文献
| [1] | 3GPP. Study on facilitating machine to machine communication in 3GPP systems (release 8) . Technical Report 22.868 V8.0.0, 2007,3. |
| [2] | 3GPP. Service requirements for machine-type communications (release 11) .Technical Specification,22.368 V11.5.0,2012,6. |
| [3] | Zanella A, Zorzi M, dos Santos A F, et al. M2M massive wireless access: challenges, research issues, and ways forward //Globecom Workshops (GC Wkshps), IEEE, 2013: 151-156. |
| [4] | Zheng K, Hu F, Wang W, et al. Radio resource allocation in LTE-advanced cellular networks with M2M communications[J].Communications Magazine, IEEE, 2012, 50(7):184–192.DOI:10.1109/MCOM.2012.6231296 |
| [5] | Huang J, Subramanian V G, Agrawal R, et al. Joint scheduling and resource allocation in uplink OFDM systems for broadband wireless access networks[J].Journal on Selected Areas in Communications, IEEE, 2009, 27(2):226–234.DOI:10.1109/JSAC.2009.090213 |
| [6] | Aijaz A, Aghvami H. On radio resource allocation in lte networks with machine-to-machine communications //Vehicular Technology Conference (VTC Spring), IEEE, 2013: 1-5. |
| [7] | Aijaz A, Tshangini M, Nakhai M R, et al. Energy-efficient uplink resource allocation in LTE networks with M2M/H2H co-existence under statistical QoS guarantees[J].Transactions on Communications, IEEE, 2014, 62(7):2352–2365. |
| [8] | Abdelnasser A, Hossain E, Kim D I. Tier-Aware resource allocation in OFDMA macrocell-small cell networks[J].Transactions on Communications, IEEE, 2015, 63(3):695–710.DOI:10.1109/TCOMM.2015.2397888 |
| [9] | Monemi M, Rasti M, Hossain E. On joint power and admission control in underlay cellular cognitive radio networks[J].Transactions on Wireless Communications, IEEE, 2015, 14(1):265–278.DOI:10.1109/TWC.2014.2340866 |
| [10] | Lien S Y, Chen K C, Lin Y. Toward ubiquitous massive accesses in 3GPP machine-to-machine communications[J].Communications Magazine, IEEE, 2011, 49(4):66–74.DOI:10.1109/MCOM.2011.5741148 |
| [11] | Osti P, Lassila P, Aalto S, et al. Analysis of PDCCH performance for M2M traffic in LTE[J].Transactions on Vehicular Technology, IEEE, 2014, 63(9):4357–4371.DOI:10.1109/TVT.2014.2314532 |
| [12] | Wu J, Zhou S, Niu Z, et al. Traffic-aware data and signaling resource management for green cellular networks // International Conference on Communications (ICC), IEEE, 2014: 3 499-3 504. |
