阮家麟, 王丽瑾
中国科学院大学数学科学学院, 北京 100049
摘要: 为一类高振荡随机哈密顿系统提出一种李代数数值方法。对一个具体的高振荡随机哈密顿系统，给出两个基于李代数方法的数值格式，并证明它们近似保辛结构。通过数值实验展示这两种格式的根均方收敛阶，以及它们在数值求解该高振荡随机哈密顿系统中的有效性和优越性。
关键词: 随机微分方程数值解随机哈密顿系统高振荡随机微分方程算子分裂方法李代数方法
Stochastic differential equations (SDEs) play an important role in the description of phenomena in many subjects^[1—2], such as biology, mechanics, chemistry, and microelectronics. The Hamiltonian system is one of the most important dynamical systems. All the real physical processes where the dissipation can be neglected can be formulated as Hamiltonian systems^[3]. Stochastic Hamiltonian systems (SHSs) are the Hamiltonian systems with stochastic disturbances.
A 2n-dimensional SHS can be written as the SDE of Stratonovich sense^[4-5] with initial values P(0)=p, Q(0)=q,

$\begin{array}{*{20}{c}}{{\rm{d}}P = \mathit{\boldsymbol{f}}\left( {t,P,Q} \right){\rm{d}}t + \sum\limits_{r = 1}^m {{\mathit{\boldsymbol{\sigma }}_r}\left( {t,P,Q} \right)} \circ {\rm{d}}{W_r}\left( t \right),}\\{{\rm{d}}Q = \mathit{\boldsymbol{g}}\left( {t,P,Q} \right){\rm{d}}t + \sum\limits_{r = 1}^m {{\mathit{\boldsymbol{\gamma }}_r}\left( {t,P,Q} \right)} \circ {\rm{d}}{W_r}\left( t \right),}\end{array}$

(1)

where f, g, σ_r, and γ_r, r=1, …, m, are n-dimensional column vectors, and W_r(t), r=1, …, m, are independent standard Wiener processes. There are functions H(t, P, Q), H_r(t, P, Q), r=1, …, m, such that

$\begin{array}{*{20}{c}}{{f^i} = - \partial H/\partial {q^i},{g^i} = \partial H/\partial {p^i},}\\{\sigma _r^i = - \partial {H_r}/\partial {q^i},\gamma _r^i = \partial {H_r}/\partial {p^i}\left( {i = 1, \cdots ,n} \right).}\end{array}$

(2)

Similar to deterministic Hamiltonian systems, the phase flow of SHS (1) preserves the symplectic structure characterized by

${\left( {\frac{{\partial Y\left( t \right)}}{{\partial {y_0}}}} \right)^{\rm{T}}}J\left( {\frac{{\partial Y\left( t \right)}}{{\partial {y_0}}}} \right) = J,\forall t \ge 0,{\rm{a}}.{\rm{s}}.,$

where Y(t)=(P(t)^T(Q(t)^T, y₀=(p^Tq^T)^T, J= $\left( {\begin{array}{*{20}{l}} 0&{{I_n}} \\ { - {I_n}}&0 \end{array}} \right)$.
The exact solutions to SDEs are in general very difficult to obtain. Therefore numerical methods become important tools for simulating solutions to SDEs. In recent decades, there arose many studies regarding different aspects of numerical methods of SDEs^[6—8]. The study of numerical solutions for highly oscillatory problems is an important branch, to which many works were devoted, such as Refs.[9-12]. Standard numerical methods are usually not suitable for treating such problems tecause they require very small time step sizes and thus make the computations prohibitively expensive.
In this work we focus on the stochastic highly oscillatory problem with initial values P(0)=p, Q(0)=q,

$\begin{matrix} \text{d}\mathit{\boldsymbol{P}}=\left( {{\epsilon }^{-1}}-f\left( \mathit{\boldsymbol{P}},\mathit{\boldsymbol{Q}} \right) \right)\mathit{\boldsymbol{Q}}\text{d}t-\sigma \mathit{\boldsymbol{Q}}\circ \text{d}W\left( t \right), \\ \text{d}\mathit{\boldsymbol{Q}}=\left( -{{\epsilon }^{-1}}+f\left( \mathit{\boldsymbol{P}},\mathit{\boldsymbol{Q}} \right) \right)\mathit{\boldsymbol{P}}\text{d}t+\sigma \mathit{\boldsymbol{P}}\circ \text{d}W\left( t \right), \\\end{matrix}$

(3)

where $ \epsilon $>0 is a small number, and f is a scalar function. It is called the highly oscillatory nonlinear Kubo oscillator with multiplicative noise^[10]. According to the integrability lemma^[13], it is not difficult to obtain that the oscillator (3) is a stochastic Hamiltonian system under the conditions

$\mathit{\boldsymbol{Pf}}_p^{\rm{T}} = {\mathit{\boldsymbol{f}}_p}{\mathit{\boldsymbol{P}}^{\rm{T}}},\mathit{\boldsymbol{Qf}}_p^{\rm{T}} = {\mathit{\boldsymbol{f}}_p}{\mathit{\boldsymbol{Q}}^{\rm{T}}},\mathit{\boldsymbol{Qf}}_p^{\rm{T}} = \mathit{\boldsymbol{Pf}}_p^{\rm{T}}.$

(4)

Our motivation is to employ the Lie algebraic approach to solve this class of highly oscillatory SHSs (3) with conditions (4), and we establish two numerical schemes for a concrete highly oscillatory SHS based on the Lie algebraic approach. Further, we analyze the symplecticity of the two schemes and prove that they nearly preserve the symplectic structure. Next we investigate their root mean-square convergence orders, efficiency, and superiority via numerical experiments.
1 The Lie algebraic approachLet (Ω, $ \mathscr{F} $, { $ \mathscr{F}$_t}_t≥0, P) be a complete probability space with filtration { $\mathscr{F}$_t}_t≥0. Consider the SDE of Stratonovich sense under the probability space Ω, $\mathscr{F} $, { $\mathscr{F} $_t}_t≥0, P), with initial value S(0)=s₀,

${\rm{d}}S\left( t \right) = b\left( {S\left( t \right)} \right){\rm{d}}t + \sum\limits_{j = 1}^r {{g_j}\left( {S\left( t \right)} \right)} \circ {\rm{d}}{W^j}\left( t \right),$

(5)

where b, g_j, j=1, …, r, are d-dimensional ${\mathbb{C}}$^∞ functions and W(t)=(W¹(t), …, W^r(t)) is a m-dimensional standard Wiener process. Define the $ {\mathbb{C}}$^∞ vector fields

${X_0} = \sum\limits_{i = 1}^d {{b^i}{\partial _i}} ,{X_j} = \sum\limits_{i = 1}^d {g_j^i{\partial _i}\left( {j = 1, \cdots ,r} \right)} ,$

(6)

where ?_i=?/?Sⁱ. There is a representation theorem in Ref.[14] for the solution of SDE (5), which is the base of the Lie algebraic approach. To state the theorem, we first introduce some notations.
Given a multi-index J=(j₁, …, j_m) and [X, Y]=XY-YX, X^J is defined as

${X^J} = \left[ {\left[ { \cdots \left[ {{X_{{j_1}}},{X_{{j_2}}}} \right], \cdots } \right],{X_{{j_m}}}} \right].$

The divided index ${\hat J}$ is a division of the multi-index J in the form

$\hat J = \left( {{J_1}, \cdots {J_{{k_1}}}} \right)\left( {{J_{{k_1} + 1}}, \cdots {J_{{k_2}}}} \right) \cdots \left( {{J_{{k_{l - 1}} + 1}}, \cdots {J_{{k_l}}}} \right).$

(7)

${\hat J}$ is called a single divided index when each J_k(k=1, …, k_l) contains a single element, and ${\hat J}$ is a double divided index if each J_k(k=1, …, k_l) has either one element or two duplicated elements.
For a single divided index ${\hat J}$, the multiple Stratonovich integral ${W^{\hat J}}(t)$ is defined as

${W^{\hat J}}\left( t \right): = \int { \cdots \int { \circ {\rm{d}}{W^{{j_1}}}\left( {{t_1}} \right) \cdots \circ {\rm{d}}{W^{{j_m}}}\left( {{t_m}} \right)} } ,$

(8)

where W⁰(t)=t. For a double divided index ${\hat J}$,

${W^{\hat J}}\left( t \right): = \int { \cdots \int { \circ {\rm{d}}{W^{{J_1}}}\left( {{t_1}} \right) \cdots \circ {\rm{d}}{W^{{J_{{k_l}}}}}\left( {{t_{{k_l}}}} \right)} } ,$

(9)

where

${W^{{J_k}}}\left( t \right) = \left\{ {\begin{array}{*{20}{c}}\begin{array}{l}{W^{{i_k}}}\left( t \right),\\t,\\0,\end{array}&\begin{array}{l}{\rm{if}}\;{J_k} = \left\{ {{i_k}} \right\},\\{\rm{if}}\;{J_k} = \left\{ {{i_k},{i_k}} \right\}\;{\rm{and}}\;{i_k} \ne 0,\\{\rm{if}}\;{J_k} = \left\{ {0,0} \right\}.\end{array}\end{array}} \right.$

Lemma 1.1 Suppose that the Lie algebra L=L(X₀, X₁, …, X_r) generated by X₀, X₁, …, X_r is nilpotent of step p. Then the solution S(t) of (5) with S(0)=s is represented as S(t)=exp(Y_t)(s), where Y_t(ω) is the vector field given by

${Y_t} = \sum\limits_{i = 0}^r {{W^i}\left( t \right){X_i}} + \sum\limits_{2 \le \left| J \right| \le p} {\left\{ {\sum\limits_J^ * {{c_{\hat J}}{W^{\hat J}}\left( t \right)} } \right\}{X^J}} $

(10)

almost surely for each t.
In (10), |J| denotes the length of the multi-index J, and $\sum\limits_{\hat J}^* {} $ is the sum taken over all single and double divided indices ${\hat J}$ of J. Besides, the coefficients ${c_{\hat J}}$ are given by

$\begin{array}{*{20}{c}}{{c_{\hat J}} = \frac{1}{m}\sum\limits_{s = 0}^{l - 1} {\sum\limits_ * {\left( {\begin{array}{*{20}{c}}{l - 1}\\s\end{array}} \right){{\left( { - 1} \right)}^{{u_1} + \cdots + {u_{{k_l}}} - s - 1}}} } \times }\\{\frac{{{{\left( {{u_1} + \cdots + {u_{{k_l}}} - s} \right)}^{ - 1}}}}{{n_1^{\left( 1 \right)}! \cdots n_1^{\left( {{u_1}} \right)}! \cdots n_{{k_l}}^{\left( 1 \right)}! \cdots n_{{k_l}}^{\left( {{u_{{k_l}}}} \right)}!}},}\end{array}$

(11)

where n_k^(v) (k=1, …, k_l, v=1, …, u_k) denotes the v-th element of J_k, and u_k is the number of elements of J_k.
Given a time discretization {t_n} of the interval [0, T] with an equidistant step size h, i.e., t_n=nh, n=0, 1, …, N. The Lie algebraic approach to construction of numerical methods follows the procedure^[2] as follows.
?Based on the representation of the solution of the SDE (5), write the time discretization scheme S_n+1=exp(Y_{n, h})(S_n);
?After obtaining a truncated vector field ${{\hat Y}_{n, h}}$ by discarding the higher order terms, construct the truncated scheme ${{\hat S}_{n + 1}} = \exp ({{\hat Y}_{n, h}})({{\hat S}_n})$
?Split ${{\hat Y}_{n, h}}$ into ${{\hat Y}_{n, h}}$=A_{n, h}+B_{n, h} where exp(A_{n, h}) and exp(B_{n, h}) can both be explicitly calculated. Then, use exp(A_{n, h}) exp(B_{n, h}) to approximate exp ${{\hat Y}_{n, h}}$ to get the numerical approximation ${{\tilde S}_{n + 1}} = \exp ({A_{n, h}})\exp({B_{n, h}})({{\tilde S}_n})$, with ${{\tilde S}_0} = {s_0}$.
2 The Lie algebraic methods for highly oscillatory SHSsAccording to Refs.[2, 14], we write the coefficients ${c_{\hat J}}$ in (11) for |J|=2, 3 explicitly. Furthermore, for convenience of calculations, we replace the multiple Stratonovich integrals in Y_t in (10) by their equivalent multiple ${\text{It}}\hat o$ integrals. For SDE (5) with one single noise, we have

$\begin{array}{l}{Y_t} = {I_{\left( 0 \right)}}\left( t \right){X_0} + {I_{\left( 1 \right)}}\left( t \right){X_1} + \\\;\;\;\;\;\;\frac{1}{2}\left( {{I_{\left( {0,1} \right)}}\left( t \right) - {I_{\left( {1,0} \right)}}\left( t \right)} \right)\left[ {{X_0},{X_1}} \right] + \\\;\;\;\;\;\;\frac{{{C_1}}}{{18}}\left[ {\left[ {{X_0},{X_1}} \right],{X_0}} \right] + \frac{{{C_2}}}{{18}}\left[ {\left[ {{X_0},{X_1}} \right],{X_1}} \right] + \\\;\;\;\;\;\;\frac{1}{{36}}\left\{ {{I_{\left( {0,0} \right)}} + {{\left\{ {{I_{\left( 0 \right)}}\left( t \right)} \right\}}^2}} \right\}\left[ {\left[ {{X_0},{X_1}} \right],{X_1}} \right] + \\\;\;\;\;\;\;\sum\limits_{4 \le \left| I \right|} {{H^J}\left( t \right){X^J}} ,\end{array}$

(12)

where H^J(t) is a version of $\sum\limits_{\hat J}^* {{c_{\hat J}}{W^{\hat J}}(t)} $, C₁=2I_{(0, 1, 0)}-2I_{(1, 0, 0)}+I₍₀₎I_{(1, 0)}-I₍₀₎I_{(0, 1)} and C₂=2I_{(0, 1, 1)}-2I_{(1, 0, 1)}+I₍₁₎I_{(1, 0)}-I₍₁₎I_{(0, 1)}.
Now let us consider the highly oscillatory SDE (3). Let f(P, Q)=P²+Q² and the dimension of the system d=2, i.e.,

$\begin{matrix} \text{d}\mathit{\boldsymbol{P}}=\left( {{\epsilon }^{-1}}-\left( {{\mathit{\boldsymbol{P}}}^{2}}+{{\mathit{\boldsymbol{Q}}}^{2}} \right) \right)\mathit{\boldsymbol{Q}}\text{d}t-\sigma \mathit{\boldsymbol{Q}}\circ \text{d}W\left( t \right), \\ \text{d}\mathit{\boldsymbol{Q}}=\left( -{{\epsilon }^{-1}}+\left( {{\mathit{\boldsymbol{P}}}^{2}}+{{\mathit{\boldsymbol{Q}}}^{2}} \right) \right)\mathit{\boldsymbol{P}}\text{d}t+\sigma \mathit{\boldsymbol{P}}\circ \text{d}W\left( t \right). \\\end{matrix}$

(13)

According to the conditions (4), it is clear that (13) is an SHS, with Hamiltonian functions

$H\left( \mathit{\boldsymbol{P}},\mathit{\boldsymbol{Q}} \right)=\frac{-{{\epsilon }^{-1}}}{2}\left( {{\mathit{\boldsymbol{P}}}^{2}}+{{\mathit{\boldsymbol{Q}}}^{2}} \right)+\frac{1}{4}{{\left( {{\mathit{\boldsymbol{P}}}^{2}}+{{\mathit{\boldsymbol{Q}}}^{2}} \right)}^{2}},$

${H_1}\left( {\mathit{\boldsymbol{P}},\mathit{\boldsymbol{Q}}} \right) = \frac{\sigma }{2}\left( {{\mathit{\boldsymbol{P}}^2} + {\mathit{\boldsymbol{Q}}^2}} \right).$

Therefore, (13) is a highly oscillatory SHS.
Performing the change of variable s=t/ $\epsilon$ in (13), we get the equivalent system of (13)

$\begin{matrix} \text{d}\mathit{\boldsymbol{P}}=\left( 1-\epsilon \left( {{\mathit{\boldsymbol{P}}}^{2}}+{{\mathit{\boldsymbol{Q}}}^{2}} \right) \right)\mathit{\boldsymbol{Q}}\text{d}s-\sqrt{\epsilon }\sigma \mathit{\boldsymbol{Q}}\circ \text{d}W\left( s \right), \\ \text{d}\mathit{\boldsymbol{Q}}=\left( -1+\epsilon \left( {{\mathit{\boldsymbol{P}}}^{2}}+{{\mathit{\boldsymbol{Q}}}^{2}} \right) \right)\mathit{\boldsymbol{P}}\text{d}s+\sqrt{\epsilon }\sigma \mathit{\boldsymbol{P}}\circ \text{d}W\left( s \right). \\\end{matrix}$

(14)

It is not difficult to see that (14) is also an SHS. Now we apply the Lie algebraic approach to system (14), for which

$\begin{align} &{{X}_{0}}=\left( 1-\epsilon \left( {{\mathit{\boldsymbol{P}}}^{2}}+{{\mathit{\boldsymbol{Q}}}^{2}} \right) \right)\mathit{\boldsymbol{Q}}\partial \mathit{\boldsymbol{P}}+ \\ &\ \ \ \ \ \ \ \ \left( -1+\epsilon \left( {{\mathit{\boldsymbol{P}}}^{2}}+{{\mathit{\boldsymbol{Q}}}^{2}} \right) \right)\mathit{\boldsymbol{P}}\partial \mathit{\boldsymbol{Q}}, \\ \end{align}$

${{X}_{1}}=-\sqrt{\epsilon }\sigma \mathit{\boldsymbol{Q}}\partial \mathit{\boldsymbol{P}}+\sqrt{\epsilon }\sigma \mathit{\boldsymbol{P}}\partial \mathit{\boldsymbol{Q}}.$

We take the truncation ${{\hat Y}_{n, h}}$=hX₀+ΔW_nX₁, and let

${{A}_{n,h}}=\left( \left( 1-\epsilon \left( {{\mathit{\boldsymbol{P}}}^{2}}+{{\mathit{\boldsymbol{Q}}}^{2}} \right) \right)Qh-\sqrt{\epsilon }\sigma \mathit{\boldsymbol{Q}}\Delta {{W}_{n}} \right)\partial \mathit{\boldsymbol{P}},$

$\begin{matrix} {{B}_{n,h}}=\left( \left( -1+\epsilon \left( {{\mathit{\boldsymbol{P}}}^{2}}+{{\mathit{\boldsymbol{Q}}}^{2}} \right) \right)Ph+ \right. \\ \left. \sqrt{\epsilon }\sigma \mathit{\boldsymbol{P}}\Delta {{W}_{n}} \right)\partial \mathit{\boldsymbol{Q}}. \\\end{matrix}$

For simplicity, we denote F(p, q)=(1- $\epsilon$(p²+q²))h- $\sqrt\epsilon$σΔW_n. If we choose the operator splitting ${{\hat Y}_{n, h}} = {A_{n, h}} + {B_{n, h}}$, we get the scheme

$\begin{align} &{{P}_{n+1}}={{P}_{n}}+F\left( {{P}_{n}},{{Q}_{n+1}} \right)\frac{\exp \left( -2\epsilon {{P}_{n}}{{Q}_{n+1}}h \right)-1}{-2\epsilon {{P}_{n}}h}, \\ &{{Q}_{n+1}}={{Q}_{n}}-F\left( {{P}_{n}},{{Q}_{n}} \right)\frac{\exp \left( 2\epsilon {{P}_{n}}{{Q}_{n}}h \right)-1}{2\epsilon {{Q}_{n}}h}. \\ \end{align}$

(15)

If we choose the operator splitting ${{\hat Y}_{n, h}} = \frac{{{B_{n, h}}}}{2} + {A_{n, h}} + \frac{{{B_{n, h}}}}{2}$, we obtain the scheme

$\begin{matrix} {{P}_{n+1}}={{P}_{n}}+F\left( {{P}_{n}},{{{\tilde{Q}}}_{n}} \right)\frac{\exp \left( -2\epsilon {{P}_{n}}{{{\tilde{Q}}}_{n}}h \right)-1}{-2\epsilon {{P}_{n}}h}, \\ {{Q}_{n+1}}={{{\tilde{Q}}}_{n}}-\frac{1}{2}F\left( {{P}_{n+1}},{{{\tilde{Q}}}_{n}} \right)\frac{\exp \left( 2\epsilon {{P}_{n+1}}{{{\tilde{Q}}}_{n}}h \right)-1}{2\epsilon {{{\tilde{Q}}}_{n}}h}, \\\end{matrix}$

(16)

where ${{\tilde Q}_n} = {Q_n} - \frac{1}{2}F({{P}_n}, {{Q}_n})\frac{{\exp (2{{P}_n}{{Q}_n}{h}) - 1}}{{2{{\tilde Q}_n}h}}$.
Theorem 2.1 The Lie algebraic schemes (15) and (16) for the highly oscillatory SHS (14) nearly preserve the symplectic structure with error of root mean-square order 3/2, i.e.,

${\left( {\frac{{\partial \left( {{P_{n + 1}},{Q_{n + 1}}} \right)}}{{\partial \left( {{P_n},{Q_n}} \right)}}} \right)^{\rm{T}}}\mathit{\boldsymbol{J}}\left( {\frac{{\partial \left( {{P_{n + 1}},{Q_{n + 1}}} \right)}}{{\partial \left( {{P_n},{Q_n}} \right)}}} \right) = \left( {1 + {R_s}} \right)\mathit{\boldsymbol{J}}$

(17)

with ${(E({R_s}))^2}{)^{\frac{1}{2}}} = O({h^{\frac{3}{2}}})$.
Proof (17) holds if and only if

$\frac{{\partial {P_{n + 1}}}}{{\partial {P_n}}}\frac{{\partial {Q_{n + 1}}}}{{\partial {Q_n}}} - \frac{{\partial {Q_{n + 1}}}}{{\partial {P_n}}}\frac{{\partial {P_{n + 1}}}}{{\partial {Q_n}}} = 1 + {R_s}$

(18)

with ${(E({R_s})^2}{)^{\frac{1}{2}}} = O({h^{\frac{3}{2}}})$.
For convenience, the left parts of (18) for the Lie algebraic schemes (15) and (16) are denoted by I₁ and I₂, respectively. Then, according to (15) and (16), we have

$\begin{align} &{{{\bar{I}}}_{1}}=1+{{\epsilon }^{\frac{3}{2}}}\sigma \left( 3q_{n}^{2}+p_{n}^{2} \right)h\Delta {{W}_{n}}+O\left( {{h}^{2}} \right), \\ &{{{\bar{I}}}_{2}}=1+{{\epsilon }^{\frac{3}{2}}}\sigma \left( 2q_{n}^{2}+\frac{5}{2}p_{n}^{2} \right)h\Delta {{W}_{n}}+O\left( {{h}^{2}} \right). \\ \end{align}$

Due to ${(E{(\Delta W)^2})^{\frac{1}{2}}} = {h^{\frac{1}{2}}}$, it is not difficult to get the conclusion.
3 Numerical experimentsIn this section, we illustrate the performance of the Lie algebraic schemes via numerical tests. Throughout the section, the reference solution is computed by high-order schemes with a sufficiently small step size.
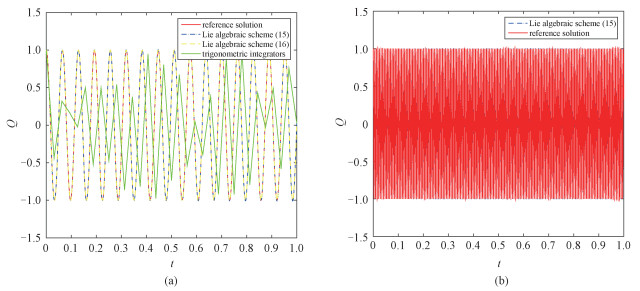
In Fig. 1(a) we show the sample trajectories of the numerical solutions (15) (blue), (16) (yellow), and a trigonometric integrator in Ref.[11] (green) for the highly oscillatory SHS (13), with the initial values p=0, q=1 and the parameters $\epsilon$=0.01, σ=0.3, on t∈[0, 1]. The step size is h=2^-5. The blue and yellow lines coincide visually with the red line which is the sample trajectory of the reference solution. Hereby we construct the two schemes (15) and (16) by involving the time-rescaling change of variable in our Lie algebraic methods, on the equivalent but time-rescaled system (14) of (13), and we apply the trigonometric method directly to (13) to draw the green line, with the same time step size h=2^-5.
Fig. 1

	Download: JPG larger image
Fig. 1 The sample trajectories

In Fig. 1(b) is the sample trajectory of the Lie algebraic scheme (15) under a higher frequency parameter $\epsilon$=0.001, which is also visually in goodcoincidence with the reference solution. The initial values are p=0, q=1. We take σ=0.3 and the step size h=2^-5.
In Fig. 2(a) and Fig. 2(b) we show the preservation of the invariant quantity P(t)²+Q(t)²=p²+q² of system (13)^[10] by the two Lie algebraic schemes.
Fig. 2

	Download: JPG larger image
Fig. 2 The phase trajectories

In Fig. 2, the initial values p=0, q=1 and the parameters $\epsilon$=0.01, σ=0.3. The step size is h=2^-5.
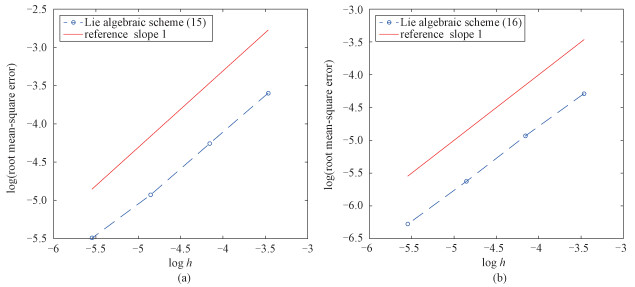
As shown in Fig. 3(a) and Fig. 3(b), the root mean-square convergence orders of the Lie algebraic schemes (15) and (16) are both 1. Here we compute the error at T=1 and take p=0, q=1, $\epsilon$=0.01, σ=0.3. Five hundred trajectories are sampled for approximating the expectation.
Fig. 3

	Download: JPG larger image
Fig. 3 The convergence orders

References

[1]	Higham D J. An algorithmic introduction to numerical simulation of stochastic differential equations[J]. SIAM review, 2001, 43(3): 525-546. DOI:10.1137/S0036144500378302
[2]	Misawa T. A Lie algebraic approach to numerical integration of stochastic differential equations[J]. SIAM Journal on Scientific Computing, 2001, 23(3): 866-890. DOI:10.1137/S106482750037024X
[3]	Feng K, Qin M. Symplectic geometric algorithms for hamiltonian systems[M]. Berlin: Springer, 2010.
[4]	Milstein G N, Repin Y M, Tretyakov M V. Symplectic integration of Hamiltonian systems with additive noise[J]. SIAM Journal on Numerical Analysis, 2002, 39(6): 2066-2088. DOI:10.1137/S0036142901387440
[5]	Milstein G N, Repin Y M, Tretyakov M V. Numerical methods for stochastic systems preserving symplectic structure[J]. SIAM Journal on Numerical Analysis, 2002, 40(4): 1583-1604. DOI:10.1137/S0036142901395588
[6]	Kloeden P E, Platen E. Numerical solution of stochastic differential equations[M]. Springer-Verlag, 1992.
[7]	Milstein G N. Numerical integration of stochastic differential equations[M]. Springer Science & Business Media, 1994.
[8]	Milstein G N, Tretyakov M V. Stochastic numerics for mathematical physics[M]. Springer Science & Business Media, 2013.
[9]	Chartier P, Makazaga J, Murua A, et al. Multi-revolution composition methods for highly oscillatory differential equations[J]. Numerische Mathematik, 2014, 128(1): 167-192. DOI:10.1007/s00211-013-0602-0
[10]	Vilmart G. Weak second order multirevolution composition methods for highly oscillatory stochastic differential equations with additive or multiplicative noise[J]. Siam Journal on Scientific Computing, 2015, 36(4): A1770-A1796.
[11]	Cohen D. On the numerical discretisation of stochastic oscillators[J]. Mathematics & Computers in Simulation, 2012, 82(8): 1478-1495.
[12]	Cohen D. Convergence analysis of trigonometric methods for stiff second-order stochastic differential equations[J]. Numerische Mathematik, 2012, 121(1): 1-29.
[13]	Hairer E, Lubich C, Wanner G. Geometric numerical integration:structure-preserving algorithms for ordinary differential equations[J]. Series in Computational Mathematics, 2006, 25(1): 805-882.
[14]	Kunita H. On the representation of solutions of stochastic differential equations[M]. Séminaire de Probabilités XIV 1978/79. Springer Berlin Heidelberg, 1980: 282-304.