舒持恺¹, 候星甫², 王建金¹, 杨侃¹
1. 河海大学 水文水资源学院, 南京 210098;
2. 河海大学 理学院, 南京 210098
2017年5月10日 收稿; 2017年9月26日 收修改稿
基金项目: 国家重点基础研究发展（973）计划（2012CB417006）、“十一五”国家科技支撑计划（2009BAC56B03）资助
通信作者: 杨侃, E-mail:kyang@hhu.edu.cn

摘要: 为更好地处理水质评价过程中的不确定信息，引入集对分析理论。针对水质分类级别细化问题，对集对分析理论中同、异、反联系度概念进行原创性扩展，将差异度细分为优异与劣异，对立度细分为优反与劣反。采用组合赋权进行指标权重计算，并考虑随机观测误差的影响对权重加以修正，同时利用差异系数与相关性优化指标体系。将模型应用于宜兴市地表水功能区水质评价，并将结果与人工神经网络、灰色理论法和投影寻踪法3种不确定性方法进行比较。在部分断面评价结果存在分歧时，本模型的水质分类结果与水质监测数据符合得最好，表明模型的评价结果更符合实际情况。
关键词: 水质评价集对分析理论组合赋权随机观测误差差异系数
Application of improved set pair analysis model for considering the influence of stochastic observation error in water quality fuzzy evaluation
SHU Chikai¹, HOU Xingfu², WANG Jianjin¹, YANG Kan¹
1. College of Hydrology and Water Resources, Hohai University, Nanjing 210098, China;
2. College of Science, Hohai University, Nanjing 210098, China


Abstract: In order to better deal with the uncertain information in the process of water quality evaluation, the theory of set pair analysis is used. Considering the water quality classification level refinement, we divide the diversity factor in set pair analysis theory into good-difference and bad-difference and divide the reverse factor into good-reverse and bad-reverse. The weight of the index is calculated by the combining weighting method and corrected by considering the influence of stochastic observation error. The difference coefficient and correlation are used to optimize the index system. This model is applied in the evaluation of ground water functional zone in Yixing. The results are compared with those obtained using the artificial neural network, gray theory, and projection pursuit methods. When the evaluation results of the four methods are different in some sections, we find that the results using this model are in the best agreement with the water quality monitoring data.
Keywords: evaluation of water qualityset pair analysis theorycombining weightingstochastic observation errordifference coefficient
一直以来，水环境问题是全球的研究热点，水质评价是水环境评价的重要内容。当前水质评价方法众多，一般可分为确定性与不确定性两类^[1]。其中确定性方法以综合指数法为主，虽然存在许多不足，但由于其计算简便、易于操作，仍然得到广泛应用。近年来，随着人们对模糊评价的深入研究，水质评价的不确定方法逐渐兴起，如人工神经网络^[2]、灰色理论法^[3]、投影寻踪法^[4]等。这些方法使得对水质评价中存在的不确定信息处理更加全面合理，相比确定性方法，是很大的进步。但不确定性方法也有各自的不足之处，如人工神经网络法中存在参数率定较难、收敛速度慢、易陷入局部极小等缺点^[1]；灰色理论法存在评价值趋于均化，分辨率不高等缺点^[5]；投影寻踪法存在优化投影方向问题，实现全局最优困难。相应理论还在摸索研究中^[1]。
水环境系统是一个不断演化、相互作用的大系统，有其复杂性与不确定性，在水质评价工作中应给予重视。水质评价过程就是将确定性的评价标准与不确定性的监测样本相结合进行比较分析的过程^[6]，如果仅依赖评价标准，而忽略其不确定性，得到结果不一定合理。如对于指标总氮，Ⅰ级标准为0.2mg/L，若实测值为0.19mg/L，则评价等级应为Ⅰ，若实测值为0.21mg/L，则评价等级应为Ⅱ，这显然是不合理的，忽略了观测过程中存在的随机误差^[7]，以及各个评价等级之间相互联系的事实。因此，在水质评价过程中需要考虑到随机观测误差的影响，同时针对各个评价等级之间相互联系的事实，引入集对分析理论。
集对分析理论是中国****赵克勤于1989年首次提出^[8]，该理论认为事物之间存在同、异、反三种联系，将事物之间进行巧妙的辩证统一分析，其包含随机、模糊、灰色等不确定性理论思想，对于水质评价过程中的不确定信息是一种很好的处理方法。但水质分类比较细化，评价等级可分为“Ⅰ、Ⅱ、Ⅲ、Ⅳ、Ⅴ、劣Ⅴ”，即存在着“好、稍好、一般、较差、差、很差”的概念区别，而集对分析中的同、异、反联系概念则比较泛化，对于水质评价结果区分不够理想。因此有必要对其进行细致刻画，构建改进集对分析模型，使其能够更好地适应水质评价问题中的复杂性与不确定性^{[1, 9]}。
1 改进集对分析模型1.1 集对分析基本理论集对分析理论^[8]认为两个事物存在同、异、反三种联系，可以很好地描述和处理事物之间存在的不确定信息。集对分析在对问题研究过程中先构建一个集对S=(E，F)，对集对S的特性进行展开分析，共得到M个特性，其中A个特性为集合E与集合F共同具有的，C个特性为集合E与集合F相互对立的，剩下的B=M-A-C个特性为集合E与集合F既不共同具有也不相互对立，则有

$\begin{array}{l}\mu = \frac{A}{M} + \frac{B}{M}i + \frac{C}{M}j = a + bi + cj,\\a + b + c = 1.\end{array}$

(1)

式中：μ为综合联系度；a、b、c为联系度分量，分别为同一度、差异度和对立度，并且满足归一化条件；i为差异度的系数，规定取值在[-1, 1]；j为对立度的系数，规定值为-1，需要说明的是同一度系数为1。
1.2 改进集对分析理论针对同异反联系度细致刻画问题，主要就是对差异度与对立度进行精确划分，使之能够适应水质分类要求^{[1, 9]}。在水质评价问题背景下，对于m个水质样本、n个指标，每个指标分为p个等级，

$集合\;{X_{ij}} = \left[ {\begin{array}{*{20}{c}}{{X_{11}}}&{{X_{12}}}& \cdots &{{X_{1n}}}\\{{X_{21}}}&{{X_{22}}}& \cdots &{{X_{2n}}}\\ \vdots&\vdots &{}& \vdots \\{{X_{m1}}}&{{X_{m2}}}& \cdots &{{X_{mn}}}\end{array}} \right],$

(2)

$其评价标准为\;{S_{kj}} = \left[ {\begin{array}{*{20}{c}}{{S_{11}}}&{{S_{12}}}& \cdots &{{S_{1n}}}\\{{S_{21}}}&{{S_{22}}}& \cdots &{{S_{2n}}}\\ \vdots&\vdots &{}& \vdots \\{{S_{p1}}}&{{S_{p2}}}& \cdots &{{S_{pj}}}\end{array}} \right],$

(3)

式中：X_ij表示第i个水质监测样本的第j个评价指标实测值；S_kj为第j个评价指标第k等级的标准值，1≤k≤p。传统集对分析中若X_ij处于评价标准S_kj中，则认为是同一；若X_ij处于评价标准S_kj相邻级别中，则认为是差异；若X_ij处于评价标准S_kj相隔级别中，则认为是对立。这样对于水质多级别判断会产生障碍，如当指标实测值处于标准Ⅲ，对于标准Ⅱ与Ⅳ都被认为是差异，对于标准Ⅰ和Ⅴ都被认为是对立，而无法区分优劣。针对于此，对集对分析中差异度与对立度作出改进。当X_ij处于评价标准S_kj相邻级别中，进一步考虑X_ij是在其优越级别中还是劣差级别中：若在其优越一边，则将这种差异认为是优异，记为b₁，若在其劣差一边，则将这种差异认为是劣异，记为b₂。同样，当X_ij处于评价标准S_kj相隔级别中：若是优越的一边，则认为这种对立是优反，记为c₁；若是劣差的一边，则认为这种对立是劣反，记为c₂。则式(1)可写为

$\begin{array}{l}\mu = a + bi + cj = a + \left( {{b_1} + {b_2}} \right)i + \left( {{c_1} + {c_2}} \right)j\\\;\;\; = a + {b_1}{i^ + } + {b_2}{i^ - } + {c_1}{j^ + } + {c_2}{j^ - },\end{array}$

(4)

式中：$a + {b_1} + {b_2} + {c_1} + {c_2} = 1, - 1 \le {i^ - } \le 0, 0 \le {i^ + } \le 1, {j^ + } = \left\{ {0, 1} \right\}, {j^ - } = - 1 $。
采用距离贴近度计算联系度分量a、b₁、b₂、c₁、c₂。若指标实测值处于评价级别标准中，则a=1，b₁、b₂、c₁、c₂=0。若指标实测值处于评价级别标准之外，则a < 1，并且越远离该等级标准，a越小，若是处于相邻等级且往等级优越一边远离，则b₁越大，b₂、c₁、c₂=0，若是处于相邻等级且往等级劣差一边远离，则b₂越大，b₁、c₁、c₂=0；若是处于相隔等级且往等级优越一边远离，则b₁越小、c₁越大，b₂、c₂=0，若是处于相隔等级且往等级劣差一边远离，则b₂越小、c₂越大，b₁、c₁=0。则改进的集对分析模型各等级联系度按下式计算：

${\mu _1} = \left\{ \begin{array}{l}1,{X_{ij}} \in \left[ {0,{S_{1j}}} \right]\\\frac{S}{X} + \frac{{X - S}}{X}{i^ - },{X_{ij}} \in \left[ {{S_{1j}},{S_{2j}}} \right]\\\frac{X}{S} + \frac{{S - S}}{X}{i^ - } + \frac{{X - S}}{X}{j^ - },{X_{ij}} \in \left[ {{S_{2j}}, + \infty } \right]\end{array} \right.,$

(5)

${\mu _2} = \left\{ \begin{array}{l}\frac{{{S_{2j}} - {S_{1j}}}}{{{S_{2j}} - {X_{ij}}}} + \frac{{{S_{1j}} - {X_{ij}}}}{{{S_{2j}} - {X_{ij}}}}{i^ + },{X_{ij}} \in \left[ {0,{S_{1j}}} \right]\\1,{X_{ij}} \in \left[ {{S_{1j}},{S_{2j}}} \right]\\\frac{{{S_{2j}} - {S_{1j}}}}{{{X_{ij}} - {S_{1j}}}} + \frac{{{X_{ij}} - {S_{2j}}}}{{{X_{ij}} - {S_{1j}}}},{X_{ij}} \in \left[ {{S_{2j}},{S_{3j}}} \right]\\\frac{{{S_{2j}} - {S_{1j}}}}{{{X_{ij}} - {S_{1j}}}} + \frac{{{S_{3j}} - {S_{2j}}}}{{{X_{ij}} - {S_{1j}}}} + \frac{{{X_{ij}} - {S_{3j}}}}{{{X_{ij}} - {S_{1j}}}},\\{X_{ij}} \in \left[ {{S_{3j}}, + \infty } \right]\end{array} \right.,$

(6)

${\mu _3} = \left\{ \begin{array}{l}\frac{{{S_{3j}} - {S_{2j}}}}{{{S_{3j}} - {X_{ij}}}} + \frac{{{S_{2j}} - {S_{1j}}}}{{{S_{3j}} - {X_{ij}}}} + \frac{{{S_{1j}} - {X_{ij}}}}{{{S_{3j}} - {X_{ij}}}},\\{X_{ij}} \in \left[ {0,{S_{1j}}} \right]\\\frac{{{S_{3j}} - {S_{2j}}}}{{{S_{3j}} - {X_{ij}}}} + \frac{{{S_{2j}} - {X_{ij}}}}{{{S_{3j}} - {X_{ij}}}},{X_{ij}} \in \left[ {{S_{1j}},{S_{2j}}} \right]\\1,{X_{ij}} \in \left[ {{S_{2j}},{S_{3j}}} \right]\\\frac{{{S_{3j}} - {S_{2j}}}}{{{X_{ij}} - {S_{2j}}}} + \frac{{{X_{ij}} - {S_{3j}}}}{{{X_{ij}} - {S_{2j}}}},{X_{ij}} \in \left[ {{S_{3j}},{S_{4j}}} \right]\\\frac{{{S_{3j}} - {S_{2j}}}}{{{X_{ij}} - {S_{2j}}}} + \frac{{{S_{4j}} - {S_{3j}}}}{{{X_{ij}} - {S_{2j}}}} + \frac{{{X_{ij}} - {S_{4j}}}}{{{X_{ij}} - {S_{2j}}}},\\{X_{ij}} \in \left[ {{S_{4j}}, + \infty } \right]\end{array} \right.,$

(7)

${\mu _4} = \left\{ \begin{array}{l}\frac{{{S_{4j}} - {S_{3j}}}}{{{S_{4j}} - {X_{ij}}}} + \frac{{{S_{3j}} - {S_{2j}}}}{{{S_{4j}} - {X_{ij}}}} + \frac{{{S_{2j}} - {X_{ij}}}}{{{S_{4j}} - {X_{ij}}}},\\{X_{ij}} \in \left[ {0,{S_{2j}}} \right]\\\frac{{{S_{4j}} - {S_{3j}}}}{{{S_{4j}} - {X_{ij}}}} + \frac{{{S_{3j}} - {X_{ij}}}}{{{S_{4j}} - {X_{ij}}}},{X_{ij}} \in \left[ {{S_{2j}},{S_{3j}}} \right]\\1,{X_{ij}} \in \left[ {{S_{3j}},{S_{4j}}} \right]\\\frac{{{S_{4j}} - {S_{3j}}}}{{{X_{ij}} - {S_{3j}}}} + \frac{{{X_{ij}} - {S_{4j}}}}{{{X_{ij}} - {S_{3j}}}},{X_{ij}} \in \left[ {{S_{4j}},{S_{5j}}} \right]\\\frac{{{S_{4j}} - {S_{3j}}}}{{{X_{ij}} - {S_{3j}}}} + \frac{{{S_{5j}} - {S_{4j}}}}{{{X_{ij}} - {S_{3j}}}} + \frac{{{X_{ij}} - {S_{5j}}}}{{{X_{ij}} - {S_{3j}}}},\\{X_{ij}} \in \left[ {{S_{5j}}, + \infty } \right]\end{array} \right.,$

(8)

${\mu _5} = \left\{ \begin{array}{l}\frac{{{S_{5j}} - {S_{4j}}}}{{{S_{5j}} - {X_{ij}}}} + \frac{{{S_{4j}} - {S_{3j}}}}{{{S_{5j}} - {X_{ij}}}} + \frac{{{S_{3j}} - {X_{ij}}}}{{{S_{5j}} - {X_{ij}}}},\\{X_{ij}} \in \left[ {0,{S_{3j}}} \right]\\\frac{{{S_{5j}} - {S_{4j}}}}{{{S_{5j}} - {X_{ij}}}} + \frac{{{S_{4j}} - {X_{ij}}}}{{{S_{5j}} - {X_{ij}}}},\\{X_{ij}} \in \left[ {{S_{3j}},{S_{4j}}} \right]\\1,{X_{ij}} \in \left[ {{S_{4j}},{S_{5j}}} \right]\\\frac{{{S_{5j}} - {S_{4j}}}}{{{X_{ij}} - {S_{4j}}}} + \frac{{{X_{ij}} - {S_{5j}}}}{{{X_{ij}} - {S_{4j}}}},\\{X_{ij}} \in \left[ {{S_{5j}},{S_{6j}}} \right]\\\frac{{{S_{5j}} - {S_{4j}}}}{{{X_{ij}} - {S_{4j}}}} + \frac{{{S_{6j}} - {S_{5j}}}}{{{X_{ij}} - {S_{4j}}}} + \frac{{{X_{ij}} - {S_{6j}}}}{{{X_{ij}} - {S_{4j}}}},\\{X_{ij}} \in \left[ {{S_{6j}}, + \infty } \right]\end{array} \right.,$

(9)

${\mu _6} = \left\{ \begin{array}{l}\frac{{{S_{6j}} - {S_{5j}}}}{{{S_{6j}} - {X_{ij}}}} + \frac{{{S_{5j}} - {S_{4j}}}}{{{S_{6j}} - {X_{ij}}}} + \frac{{{S_{4j}} - {X_{ij}}}}{{{S_{6j}} - {X_{ij}}}},\\{X_{ij}} \in \left[ {0,{S_{4j}}} \right]\\\frac{{{S_{6j}} - {S_{5j}}}}{{{S_{6j}} - {X_{ij}}}} + \frac{{{S_{5j}} - {X_{ij}}}}{{{S_{6j}} - {X_{ij}}}},{X_{ij}} \in \left[ {{S_{4j}},{S_{5j}}} \right]\\1,{X_{ij}} \in \left[ {{S_{5j}},{S_{6j}}} \right]\\\frac{{{S_{6j}} - {S_{5j}}}}{{{X_{ij}} - {S_{5j}}}} + \frac{{{X_{ij}} - {S_{6j}}}}{{{X_{ij}} - {S_{5j}}}},{X_{ij}} \in \left[ {{S_{6j}}, + \infty } \right]\end{array} \right.$

(10)

其中联系度μ₁、μ₂、μ₃、μ₄、μ₅、μ₆分别对应于水质等级Ⅰ类、Ⅱ类、Ⅲ类、Ⅳ类、Ⅴ类、劣Ⅴ类。
1.3 指标权重计算水环境质量往往受到多个因子的共同影响，在水质评价过程中每个指标因子都或多或少影响着评价结果，因此要慎重考虑各因子对评级结果的贡献^[10]。为客观评价水质状况，先采用熵值法计算客观权重，反映数据本身效用值，同时还要考虑超标因子对水质状况的影响，用超标倍数法反映超标因子的作用。在构建组合赋权，将两种权重方法结合，这样既能兼顾监测数据本身的效用值，又能突出超标因素的影响。此外，水质监测是一个随机观测过程，文献[7]运用最大熵原理与蒙特卡罗法证明水环境评价过程中随机观测误差影响的重要性。因此有必要考虑随机观测误差影响，对组合权重结果加以修正。
1.3.1 熵值法1) 将水质监测数据x_ij标准化，
2) 计算第j项指标下，第i个样本数据的比重y_ij，
3) 计算第j项指标的权重

${\omega _j} = \frac{{1 - {e_j}}}{{\sum\limits_{i = 1}^m {\left( {1 - {e_j}} \right)} }},$

(11)

其中$ {e_j} = - \frac{1}{{Inm}}\sum\limits_{i = 1}^m {{y_{ij}}In{y_{ij}}} $。
1.3.2 超标倍数法计算第j项指标权重

${\omega _j} = \frac{{{x_{ij}}/{{\bar z}_j}}}{{\sum\limits_{j = 1}^m {\left( {{x_{ij}}/{{\bar z}_j}} \right)} }},$

(12)

其中$ {{\bar z}_j}$是第j项指标各评价等级标准的均值。
1.3.3 组合赋权法由熵值法计算得到权重向量为ω₁，超标倍数法计算得到权重向量为ω₂，构建组合赋权ω：

$\mathit{\boldsymbol{\omega }} = \eta {\mathit{\boldsymbol{\omega }}_1} + \lambda {\mathit{\boldsymbol{\omega }}_2},$

(13)

$\eta + \lambda = 1.$

(14)

式中η、λ为两种权重方法的分配系数。
考虑两种权重方法计算的权重差异，按下式计算距离函数d(ω₁, ω₂)：

$d\left( {{\mathit{\boldsymbol{\omega }}_1},{\mathit{\boldsymbol{\omega }}_2}} \right) = {\left[ {\frac{1}{2}\sum\limits_{k = 1}^n {{{\left( {{\omega _{1k}} - {\omega _{2k}}} \right)}^2}} } \right]^{\frac{1}{2}}},$

(15)

其中ω_1k、ω_2k分别为权重向量ω₁、ω₂中第k个指标的权重值。
为平衡两种权重方法的差异，设定组合权重分配系数差异与两种权重方法计算差异保持一致^[11]，可使

${\left( {\eta - \lambda } \right)^2} = {d^2}\left( {{\mathit{\boldsymbol{\omega }}_1},{\mathit{\boldsymbol{\omega }}_2}} \right),$

(16)

结合式(14)，可以解得η、λ，代入式(13)即得组合权重向量ω。
1.3.4 随机观测误差权重的影响随机观测误差影响在评价过程中不容忽视，有时甚至可能改变评价结果。考虑随机观测误差影响的权重计算按下述步骤进行^[7]：
1) 计算各指标数据的均值与方差；
2) 将各指标均值与方差相除，然后与组合权重对应相乘，再进行归一化处理，即得考虑了随机观测误差影响的权重结果。
1.4 水质监测数据的优化水质监测的原始数据复杂而冗余，有必要对数据进行筛选与剔除。为使指标数据在现有评价标准下具有良好的分化效果，引入差异系数β来刻画一组数据在空间上的相对波动程度^[12]，计算公式为

$\beta = \frac{{{S_j}}}{{\overline {{X_j}} }},$

(17)

式中：S_j为第j项指标数据的标准差；$\overline {{X_j}} $为第j项指标数据的均值。
此外，在上述步骤之后，还要考虑数据之间的相关性，利用皮尔逊相关系数分析数据两两之间的相关程度，剔除相关性较大的指标。
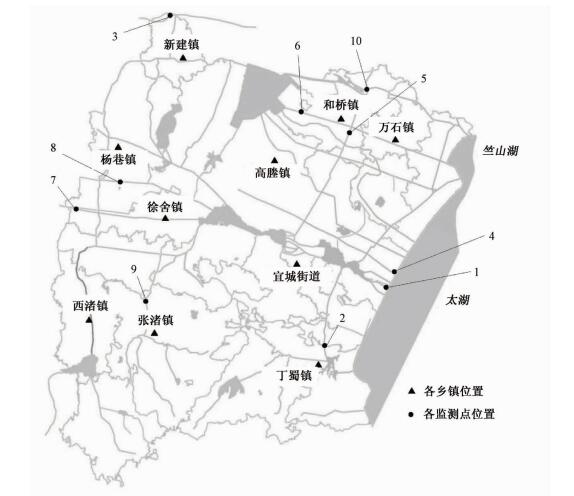
2 应用实例将模型应用于宜兴市地表水功能区评价，选取10个水功能区监测断面(见表 1)2015年水质监测数据作为评价样本，监测断面位置见图 1。宜兴市地表水功能区水质监测数据共包含17项指标，按式(17)计算各指标数据差异系数β，并以β≥0.4为标准，当指标β < 0.4认为分辨性差，对评价体系层次划分起到的分类效果不明显，剔除该指标。经计算，剔除5项，保留12项。再对剩下的12项指标进行相关性检验，结果见表 2。
Fig. 1

	Download: JPG larger image
图 1 宜兴市地表水功能区水质监测断面位置图 Fig. 1 Locations of Yixing ground water functional zone water quality monitoring sections 图 1 宜兴市地表水功能区水质监测断面位置图 Fig. 1 Locations of Yixing ground water functional zone water quality monitoring sections -->

Table 1

表 1 宜兴市地表水功能区水质监测项目Table 1 Yixing ground water functional zone water quality monitoring project 序号 功能区分类 水功能区名称 断面名称 水质目标 1 缓冲区 城东港宜兴缓冲区 陈东桥 Ⅲ 2 缓冲区 蠡河宜兴缓冲区 方溪大桥 Ⅲ 3 渔业用水区 中干河宜兴渔业、工业用水区 芳泉村 Ⅲ 4 缓冲区 官渎港宜兴缓冲区 官渎桥 Ⅳ 5 景观娱乐用水区 武宜运河宜兴景观娱乐、工业用水区 和桥桥 Ⅳ 6 景观娱乐用水区 殷村港宜兴景观娱乐、渔业用水区 南新桥 Ⅳ 7 景观娱乐用水区 南溪河宜兴景观娱乐、工业用水区 潘家坝 Ⅲ 8 渔业用水区 邮芳河宜兴渔业、工业用水区 塘东桥 Ⅲ 9 工业用水区 桃溪河宜兴工业、农业用水区 五洞桥 Ⅳ 10 渔业用水区 漕桥河宜兴市渔业、工业用水区 闸口 Ⅳ

表 1 宜兴市地表水功能区水质监测项目Table 1 Yixing ground water functional zone water quality monitoring project

Table 2

表 2 12项指标皮尔逊相关系数Table 2 12-indicators Pearson correlation coefficients 指标代号 1 2 3 4 5 6 7 8 9 10 11 12 1 1.00 0.55** 0.18 0.63** 0.40* 0.56** 0.07 0.04 -0.16 0.34* 0.19 0.31 2 0.55** 1.00 0.24 0.40* 0.84** 0.68** 0.30 0.26 0.31 0.16 0.03 0.33* 3 0.18 0.24 1.00 -0.06 0.24 0.28 0.12 0.00 0.17 0.01 -0.30 -0.19 4 0.63** 0.40* -0.06 1.00 0.25 0.30 -0.06 -0.06 -0.07 0.29 0.24 0.44** 5 0.40* 0.84** 0.24 0.25 1.00 0.54** 0.23 0.30 0.24 0.11 -0.04 0.24 6 0.56** 0.68** 0.28 0.30 0.54** 1.00 0.24 0.28 -0.02 0.22 0.13 0.31 7 0.07 0.30 0.12 -0.06 0.23 0.24 1.00 -0.04 0.17 0.16 0.22 0.25 8 0.04 0.26 0.00 -0.06 0.30 0.28 -0.04 1.00 0.07 0.01 -0.11 0.01 9 -0.16 0.31 0.17 -0.07 0.24 -0.02 0.17 0.07 1.00 -0.04 -0.41* -0.19 10 0.34* 0.16 0.01 0.29 0.11 0.22 0.16 0.01 -0.04 1.00 0.16 0.51** 11 0.19 0.03 -0.30 0.24 -0.04 0.13 0.22 -0.11 -0.41* 0.16 1.00 0.41* 12 0.31 0.33* -0.19 0.44** 0.24 0.31 0.25 0.01 -0.19 0.51** 0.41* 1.00 注：数字1~12分别表示指标：五日生化需氧量(BOD5)、氨氮(NH3-N)、铅、化学需氧量(COD)、总氮(TN)、总磷(TP)、铜、锌、镉、阴离子表面活性剂、硫化物、粪大肠菌群。*表示显著性水平为0.05，**表示显著性水平为0.01。

表 2 12项指标皮尔逊相关系数Table 2 12-indicators Pearson correlation coefficients

可以看出氨氮与总氮相关性系数高达0.84，并通过显著性水平为0.01的检验，因此剔除指标总氮。以剩下11个指标建立水质评价体系，评价等级标准见表 3。
Table 3

表 3 地表水水质指标分类等级标准Table 3 Ground water quality indicator standards set for the six classes 指标/(mg/L) Ⅰ Ⅱ Ⅲ Ⅳ Ⅴ 劣Ⅴ 生化需氧量 3 3 4 6 10 30 氨氮 0.15 0.50 1.00 1.50 2.00 4.00 铅 0.01 0.01 0.05 0.05 0.10 0.50 化学需氧量 15 15 20 30 40 60 总磷 0.02 0.10 0.20 0.30 0.40 0.60 铜 0.01 1.00 1.00 1.00 1.00 3.00 锌 0.05 1.00 1.00 2.00 2.00 4.00 镉 0.001 0.005 0.005 0.005 0.010 0.030 阴离子表面活性剂 0.2 0.2 0.2 0.3 0.3 0.5 硫化物 0.05 0.10 0.20 0.50 1.00 3.00 粪大肠菌群 200 2000 10000 20000 40000 80000 注：参考地表水环境质量标准基本项目标准限制(GB 3838—2002)，其中劣Ⅴ类限值在GB 3838—2002并没有，表中劣Ⅴ类限值是根据宜兴市水功能区实际监测情况拟定，具有地域性。实际操作中应适具体情况而定。

表 3 地表水水质指标分类等级标准Table 3 Ground water quality indicator standards set for the six classes

以城东港宜兴缓冲区陈东桥监测断面为例，按式(5)~式(10)计算其联系度矩阵
按式(11)~式(16)计算，并考虑随机观测误差权重的影响，对组合权重加以修正，得到最终权重向量W=[ω₁, …, ω_j, …, ω₁₁]=[0.1305, 0.2165, 0.0200, 0.2095, 0.1373, 0.0029, 0.0066, 0.0324, 0.0784, 0.0088, 0.1572]。将联系度矩阵μ与权重向量W相乘得到综合联系度矩阵Z

$\mathit{\boldsymbol{Z}} = {\mathit{\boldsymbol{\mu }}^{\rm{T}}} \cdot \mathit{\boldsymbol{W = }}\left[ {\begin{array}{*{20}{c}}{0.4329 + 0.1822{i^ - } + 0.3848{j^ - }}\\{0.2419 + 0.1051{i^ + } + 0.5034{i^ - } + 0.1496{j^ - }}\\{0.6932 + 0.0412{i^ + } + 0.1699{i^ - } + 0.0853{j^ + } + 0.0103{j^ - }}\\{0.8160 + 0.0825{i^ + } + 0.0197{i^ - } + 0.0819{j^ + }}\\{0.6087 + 0.2911{i^ + } + 0.1002{j^ + }}\\{0.6275 + 0.1999{i^ + } + 0.1727{j^ + }}\end{array}} \right].$

利用集对势shi(μ)判断水质结果：shi(μ)=a/c。当a/c>1时，描述为集对同势，表示评价样本与等级标准存在同一趋势；当a/c < 1，描述为集对反势，当a/c=1时，描述为集对均势。集对同势又可分为3种：当a>c>b时，为强同势; 当a>b>c时，为弱同势; 当b>a>c时，为微同势。
按上述定义计算陈东桥断面水质监测数据对应6个级别的集对势分别为：

${\rm{shi}}\left( {{\mu _1}} \right) = 1.1250,{\rm{shi}}\left( {{\mu _2}} \right) = 1.6175,$

${\rm{shi}}\left( {{\mu _3}} \right) = 7.2501,{\rm{shi}}\left( {{\mu _4}} \right) = 9.9661,$

${\rm{shi}}\left( {{\mu _5}} \right) = 6.0757,{\rm{shi}}\left( {{\mu _6}} \right) = 3.6340.$

进行归一化处理，得到水质结果对6个级别的趋同程度分别为：3.8%、5.5%、24.4%、33.6%、20.5%、12.2%，判断其水质级别为Ⅳ类。同样可以计算其余监测断面水质结果，见表 4。
Table 4

表 4 各水质监测断面模型计算结果Table 4 Model calculation results for different sections 监测断面 shi(μ1) shi(μ2) shi(μ3) shi(μ4) shi(μ5) shi(μ6) 陈东桥 1.1250 1.6175 7.2501 9.9661 6.0757 3.6340 方溪大桥 1.3925 1.6722 7.7821 9.4264 4.4560 3.4698 芳泉村 0.7467 0.5532 2.4905 4.3648 6.4440 5.1285 官渎桥 0.9864 1.0523 3.5606 6.3299 6.5335 4.2631 和桥桥 1.4729 1.7277 4.2566 6.7408 3.5195 3.1254 南新桥 1.4644 8.2933 9.4374 10.0802 3.7024 2.6264 潘家坝 1.2487 2.4910 8.4815 10.6700 4.9307 3.1722 塘东桥 1.1477 1.9676 8.5814 11.0002 4.4347 2.9319 五洞桥 1.5722 6.7195 9.4835 11.3507 3.4121 2.5411 闸口 0.8622 0.7423 4.9841 10.6968 7.5045 5.2483

表 4 各水质监测断面模型计算结果Table 4 Model calculation results for different sections

需要说明的是当不同级别的集对势存在相等或相近情况时，会影响判断结果。此时可以根据集对势的强弱，或者综合比较c₁、c₂的大小，强同势说明对等级趋同程度比较强，c₁较大说明对等级优反程度比较大，c₂较大说明对等级劣反程度比较大。如官渡桥断面shi(μ₄)=6.3299，shi(μ₅)=6.5335，两者数值比较接近，但shi(μ₅)为强同势，shi(μ₄)为弱同势，且μ₅中c₁、c₂均比较小，说明其等级优反、劣反程度比较小，等级距离比较近，因此综合考虑确定官渡桥断面水质级别为Ⅴ类。同样，根据上述判断原则可以得到其余断面水质结果。为验证模型对水质级别判断的合理性，另外采用人工神经网络^[2]、灰色理论法^[3]、投影寻踪法^[4]3种不确定性评价方法进行计算，并将结果进行比较，见表 5。
Table 5

表 5 4种方法评价结果比较Table 5 Comparison of evaluation results among the four different methods 断面名称 改进集对分析 人工神经网络 灰色理论法 投影寻踪法 陈东桥 Ⅳ Ⅲ Ⅳ Ⅳ 方溪大桥 Ⅳ Ⅳ Ⅳ Ⅳ 芳泉村 Ⅴ Ⅴ Ⅴ Ⅴ 官渎桥 Ⅴ Ⅴ Ⅴ Ⅴ 和桥桥 Ⅳ Ⅳ Ⅳ Ⅳ 南新桥 Ⅳ Ⅳ Ⅱ Ⅳ 潘家坝 Ⅳ Ⅳ Ⅳ Ⅳ 塘东桥 Ⅳ Ⅳ Ⅴ Ⅳ 五洞桥 Ⅳ Ⅳ Ⅳ Ⅴ 闸口 Ⅳ Ⅳ Ⅳ Ⅳ

表 5 4种方法评价结果比较Table 5 Comparison of evaluation results among the four different methods

可以看出，4种方法所得结果基本上一致，小部分断面存在差异。在陈东桥水质监测断面上，人工神经网络判断结果为Ⅲ类，其余3种方法结果均为Ⅳ类，此断面上，11项指标中有1项为Ⅰ类，4项为Ⅲ类，5项为Ⅳ类，1项为劣Ⅴ类，综合判断为Ⅳ类比较合适。在南新桥水质监测断面上，灰色理论法结果为Ⅱ类，其余3种方法为Ⅳ类，此断面上，11项指标中有5项Ⅱ类，3项Ⅳ类，3项Ⅴ类，1项劣Ⅴ类，综合判定为Ⅳ类比较合适。塘东桥水质监测断面灰色理论法结果、五洞桥水质监测断面投影寻踪法也是类似情况。可以看出，改进的集对分析模型对于水质判断结果是比较合理的。从模型评价结果来看，与宜兴市地表水功能区水质目标(见表 2)进行比较，选取的10个水功能区中，只有武宜运河宜兴景观娱乐、工业用水区，殷村港宜兴景观娱乐、渔业用水区，桃溪河宜兴工业、农业用水区，漕桥河宜兴市渔业、工业用水区4个水功能区达到水质目标要求，其余6个水功能区均未达标。
3 结论与展望1) 通过对传统集对分析模型进行改进，将同异反联系度概念进行延伸扩展，把差异度细分为优异与劣异，对立度细分为优反与劣反，可以使其更好适应于水质评价等级细化问题。将模型应用于宜兴市地表水功能区水质评价，并将结果与人工神经网络、灰色理论法、投影寻踪法的结果进行比较，发现改进的集对分析模型水质评价结果更符合实际情况，评价结果更可靠。选取的10个水功能区中，4个水质达标，6个水质不达标，水功能区评价结果不理想。
2) 水质评价原始指标数据复杂而冗余，利用差异系数与相关性进行指标进行筛选，剔除冗余的指标，取得了不错的效果。权重计算综合使用熵值法与超标倍数法，这样既能兼顾监测数据本身的效用值，又能突出超标因子的影响。同时考虑随机观测误差对权重的影响，利用误差权重对组合权重进行修正，使得权重分配合理性得以有效提高。
3) 模型应用还处在初步阶段，可能还存在不足之处，比如模型对于结果的量化区分度不高，当水质处于同一级别时，就较难进一步区分其优劣。这在以后的模型应用中有待于进一步研究与完善。
参考文献

[1]	王颖, 邵磊, 杨方廷, 等. 改进的集对分析水质综合评价方法[J]. 水力发电学报, 2012, 31(3): 99-106.
[2]	刘国东, 黄川友, 丁晶. 水质综合评价的人工神经网络模型[J]. 中国环境科学, 1998, 18(6): 35-38.
[3]	史晓新, 夏军. 水环境质量评价灰色模式识别模型及应用[J]. 中国环境科学, 1997, 17(2): 32-35.
[4]	张欣莉, 丁晶, 李祚泳, 等. 投影寻踪新算法在水质评价模型中的应用[J]. 中国环境科学, 2000, 20(2): 187-189. DOI:10.3321/j.issn:1000-6923.2000.02.022
[5]	李如忠. 水质评价理论模式研究进展及趋势分析[J]. 合肥工业大学学报(自然科学版), 2005, 28(4): 369-373. DOI:10.3969/j.issn.1003-5060.2005.04.008
[6]	杜明亮, 吴彬, 张宏, 等. 改进权重集对分析法在准东水质评价中的应用[J]. 人民黄河, 2014, 36(4): 62-64. DOI:10.3969/j.issn.1000-1379.2014.04.020
[7]	王栋, 朱元甡. 随机观测误差对水环境评价的影响[J]. 水利学报, 2003(10): 1-5. DOI:10.3321/j.issn:0559-9350.2003.10.001
[8]	赵克勤. 集对分析及其初步应用[M]. 杭州: 浙江科技出版社, 2000.
[9]	魏明华, 郑志宏, 黄强, 等. 基于改进SPA法的地下水环境模糊综合评判[J]. 水利学报, 2009, 40(10): 1204-1209. DOI:10.3321/j.issn:0559-9350.2009.10.008
[10]	代雪静, 田卫. 水质模糊评价模型中赋权方法的选择[J]. 中国科学院研究生院学报, 2011, 28(2): 169-176.
[11]	张晨, 王清, 陈剑平, 等. 金沙江流域泥石流的组合赋权法危险度评价[J]. 岩土力学, 2011, 32(3): 831-836. DOI:10.3969/j.issn.1000-7598.2011.03.032
[12]	范荣亮, 谢悦波, 付鹏, 等. 基于属性测度-联系数的节水型生态城市的健康评价[J]. 水利学报, 2009, 40(12): 1460-1466. DOI:10.3321/j.issn:0559-9350.2009.12.008