目前,国外****围绕滑靴副油膜动力学特性和能量损失机理展开研究[3, 4]。Schenk和Ivantysynova[5]考虑滑靴与油膜之间的流固耦合效应,分析弹性变形对滑靴副能量损失的影响。Kazama[6]考虑油液的黏温效应,建立滑靴副非等温油膜间隙模型,结果表明滑靴所受的压紧力和旋转速度是影响油膜温升特性的主要原因。Canbulut等[7, 8]建立人工神经网络模型分析滑靴副摩擦功率损失,结果表明滑靴的表面粗糙度、阻尼管直径以及作用面积与滑靴副摩擦功率损失密切相关。Bergada[9]和Kumar等[10]围绕滑靴环形密封槽内部流场的动静态特性展开研究,讨论不同工况下环形槽内流体的运动特征和涡流效应。国内****对高速高压下轴向柱塞泵滑靴副的润滑机理研究起步较晚[11, 12, 13, 14]。目前,大多数研究尚未深入阐释摩擦部件与油膜之间的能量损失特征,忽略了摩擦部件与油液之间的热传递途径以及温度对固体的物理性能参数的影响,但这些因素都会引起滑靴底面油膜温度升高,降低油膜厚度,影响滑靴的承载性能。
本文分析了滑靴副的功率损失来源以及热量传递途径,建立滑靴副热力学耦合模型。利用轴向柱塞泵综合性能试验台,开展柱塞泵温度特性试验,并对滑靴副热力学耦合模型的计算结果进行了验证。在此基础上,对比分析滑靴副油膜温升的变化规律,讨论滑靴的结构参数对其热力学特性的影响。
1 滑靴副的热力学耦合模型1.1 工作原理图 1所示为轴向柱塞泵结构图。当缸体随主轴旋转时,柱塞沿缸体向左运动时(0°~180°),缸体的工作腔容积减小,促使液压油从配流盘的排油槽流出,为泵的排油区,如A-A视图所示。同理,柱塞沿缸体向右运动时(180°~360°),油液通过配流盘的吸油槽,进入柱塞腔,为泵的吸油区。对滑靴而言,将柱塞腔内高压油经过阻尼管进入滑靴底面以产生液压反推力,平衡滑靴所受压紧力,并提供可靠的流体润滑,减小滑靴表面磨损。
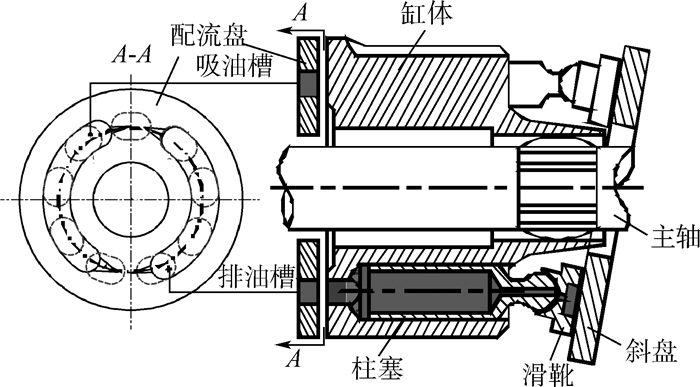 |
| 图 1 轴向柱塞泵结构图 Fig. 1 Structure scheme of axial piston pump |
| 图选项 |
1.2 油膜厚度方程图 2所示为滑靴副楔形油膜厚度。滑靴受到倾覆力矩的影响,导致滑靴与斜盘之间形成楔形油膜。其中,滑靴的倾覆角度和中心油膜厚度决定滑靴底面任一点油膜厚度,其表达式为
 |
| 图 2 滑靴副楔形油膜厚度 Fig. 2 Wedge oil film thickness of slipper pair |
| 图选项 |
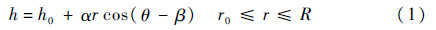
式中:h为油膜厚度;h0为中心油膜厚度;α为倾覆角度;θ为极角;β为倾斜方位角;r为极径;r0为滑靴内径;R为滑靴外径。
1.3 油膜压力控制方程根据Navier-Stokes方程和流量连续性方程,建立滑靴底面油膜压力场,其控制方程为
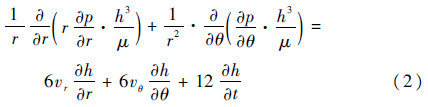
边界条件为
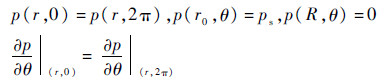
式中:μ为油液黏度;vr为油液的径向速度;vθ为油液的切向速度;Ps为滑靴油室压力;p为油膜压力;t为工作时间。
轴向柱塞泵在工作过程中,柱塞腔内高压油经过滑靴的阻尼管产生压力降后,进入滑靴油室,产生滑靴的支承反力。因此,考虑油液在阻尼管中的压力损失,滑靴油室压力为

式中:Pp为柱塞腔压力;l为阻尼管长度;d为阻尼管直径;λ为沿程阻力系数;ρ为油液密度;Qs为泄漏流量。
1.4 温度控制方程假设滑靴底面油膜处于热力学平衡状态,油膜的能量传递形式主要包括对流换热、传导换热以及热量耗散。忽略油液体积力和热辐射的影响,则油膜的能量方程[15]为
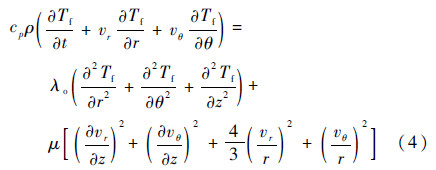
式中:λo为油液热传导系数;Tf为油膜温度;cp为油液的比热容;z为高度。
除了求解能量方程外,还需要求解滑靴和斜盘的热传导方程,其表达式为
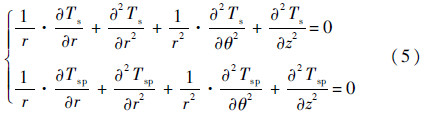
式中:Ts为滑靴温度;Tsp为斜盘温度。
1.5 油液的黏温关系本文采用32号液压油作为工作介质,温度范围为20~75℃。在常压工况下,压力对油液黏度的影响比较小,这里不考虑。但是油液黏度对温度变化十分敏感。表 1所示为不同温度下液压油的实际黏度。液压油的Reynolds黏温表达式为

表 1 不同温度下液压油的实际黏度Table 1 Practical hydraulic oil viscosity under different temperatures
| Tf/℃ | 20 | 30 | 40 | 50 | 60 | 75 |
| μ/(10-2Pa·s) | 6.75 | 4.19 | 3.19 | 2.21 | 1.57 | 1.21 |
表选项
2 滑靴副功率损失与热边界条件2.1 滑靴副功率损失滑靴副泄漏和黏性摩擦是油液温度升高的主要来源。滑靴副受到压力流和剪切流的影响,产生泄漏功率损失和黏性摩擦功率损失,转化成油液内能,表现为油膜温度升高。
图 3所示为油液的径向和切向流速。油液流速是影响滑靴副功率损失的主要参数。因此,油液的径向和切向流速为
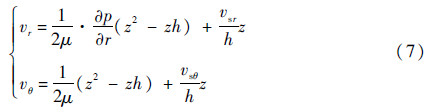
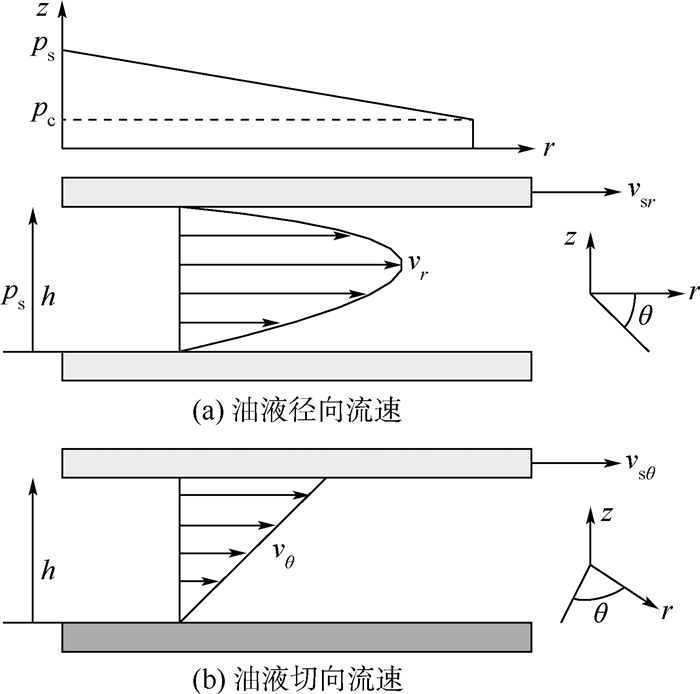 |
| 图 3 油液径向和切向流速 Fig. 3 Oil radial and tangential velocities |
| 图选项 |
式中:vsr为滑靴的径向运动速度;vsθ为滑靴的切向运动速度。
滑靴的径向和切向运动速度为

式中:ω为滑靴公转角速度,ω=2πnT/60,n为主轴转速,T为主轴旋转周期;ωs为滑靴自转角速度;δ为径向和切向运动速度之间的夹角;rb为滑靴支承面任意一点与缸体中心的距离。
滑靴支承面任意一点与缸体中心的距离可表示为

式中:φ为缸体转角;Rφ为任意缸体转角下滑靴中心到缸体中心之间的距离;Rd为柱塞的分布圆半径。
为了计算黏性摩擦功率损失,对油液的径向和切向应力进行求解,即为
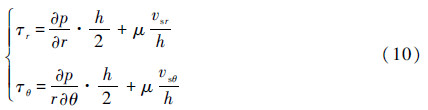
式中:τr为径向应力;τθ为切向应力。
摩擦力矩为
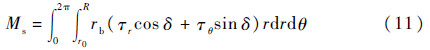
黏性摩擦功率损失为
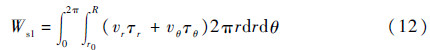
泄漏流量为

泄漏流量功率损失为
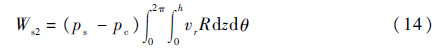
式中:Ws2为泄漏流量功率损失;pc为壳体油腔压力。
2.2 热边界条件图 4所示为滑靴副的热边界条件。滑靴、斜盘与油膜之间的热传导边界包括滑靴表面温度边界、斜盘表面温度边界、油膜温度的周向边界和油膜温度的径向边界。
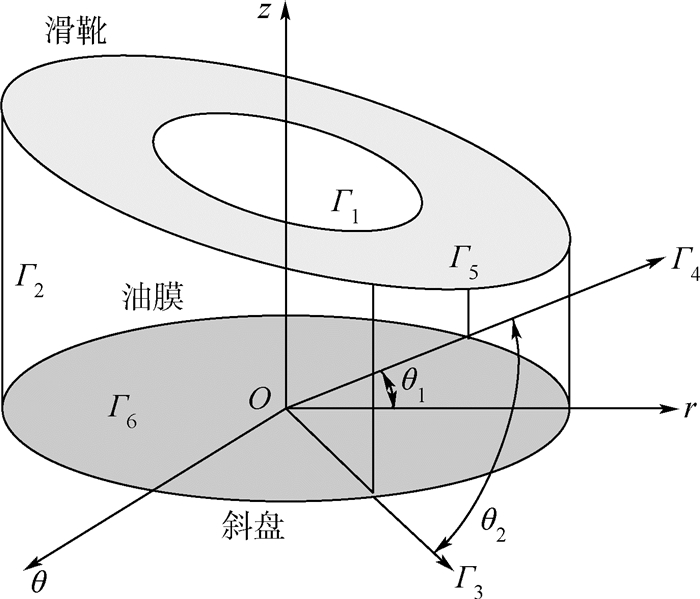 |
| Γ1—滑靴内腔油室与密封带的边界面;Γ2—油膜与壳体内腔油液的接触面;Γ3—θ1处油膜界面;Γ4—θ2处油膜界面;Γ5—滑靴密封带与油膜的接触面;Γ6—斜盘与油膜的接触面。 图 4 滑靴副的热边界条件 Fig. 4 Thermal boundary conditions of slipper pair |
| 图选项 |
滑靴副的热边界条件如下:
滑靴底面油膜的径向温度边界主要集中在滑靴内腔油室,为入口油液温度,其表达式为

式中:Tin为入口油液温度。
滑靴底面油膜温度的周向边界为油膜与壳体内腔油液耦合界面,其表达式为
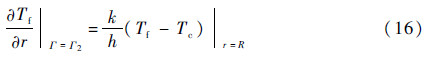
式中:k为油液换热系数;Tc为壳体回油温度。
油膜在圆周方向上的热量传递过程可以看作为连续热流传导过程,其热传导的表达式为
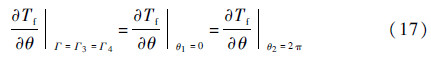
滑靴、斜盘与油膜之间的交界面都采用热流量连续边界条件。其中,滑靴与油膜之间的热传导边界主要包括以下3个部分。
1)滑靴油室与油膜的接触面
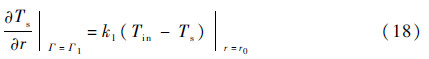
式中:k1为滑靴热传导系数。
2)滑靴外径与壳体油液的接触面
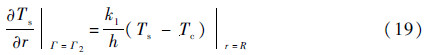
3)滑靴密封带与油膜的接触面
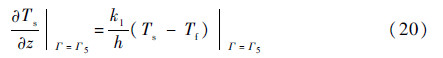
斜盘与油膜之间的热传导边界为斜盘与油膜的接触面,其表达式为
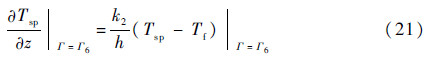
式中:k2为斜盘热传导系数。
3 理论结果及其分析本文以A4VTG90泵为研究对象,所涉及的主要参数与工况性能为:R=12.8 mm,r0=6.4 mm,d=1 mm,l=3.5 mm,k1=98 W/(m·℃);k2=67 W/(m·℃);ρ=860 kg/m3,k=0.26 W/(m·℃),cp=1 884 J/(kg·℃);pp=21 MPa,n=1 500 r/min,Tin=50℃。为了验证滑靴副热力学耦合模型的准确性,对比分析给定工况下滑靴副油膜温度的变化规律,讨论滑靴半径比和阻尼管长度直径比对油膜温度的影响。
3.1 油膜温度对比分析图 5所示为不同柱塞腔压力下滑靴副油膜温度场。从图 5(a)可知,滑靴处于排油区时,滑靴受到倾覆力矩的影响,滑靴底面形成楔形油膜,导致油膜温度场呈不均匀分布,且沿滑靴半径呈递减趋势,油膜温度约为47.5~50℃。其中,颜色较深处为油膜温度的最大值,说明该区域的油膜厚度最薄,容易发生偏磨磨损,而颜色较浅处为滑靴边缘,其原因是油膜与滑靴之间存在热传导过程,油膜温度沿半径方向存在温度差,但是滑靴内腔油室与滑靴边缘之间的温度差不超过2.5℃。从图 5(b)可知,当滑靴处于吸油区时,滑靴所受的正向压紧力减小,增强滑靴动压效应,增大滑靴的倾覆角度,此时油膜温度场在半径方向上的温度差发生改变,滑靴边缘处油膜温度为46℃。上述油膜温度变化特征表明滑靴底面油膜温度与柱塞腔压力成正比,随着柱塞腔压力减小,滑靴副泄漏流量和黏性摩擦减少,降低油液内能,表现为油膜温度降低。
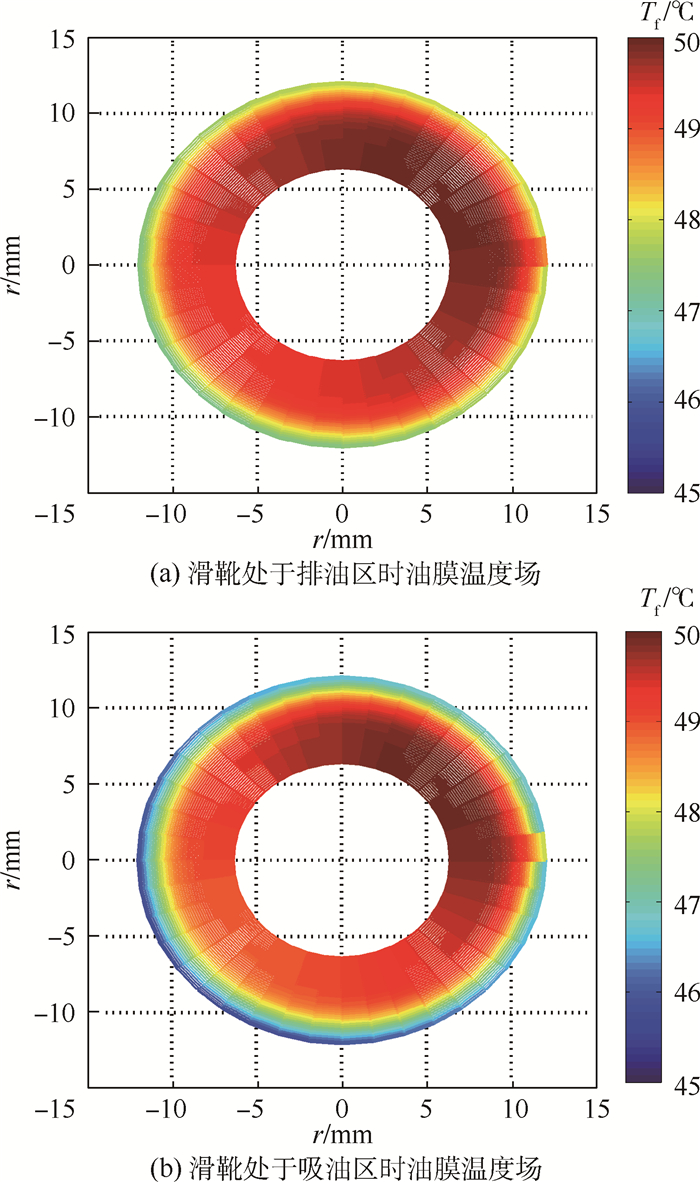 |
| 图 5 不同柱塞腔压力下滑靴副油膜温度场 Fig. 5 Oil film temperature field in slipper pair under different piston chamber pressures |
| 图选项 |
图 6所示为滑靴副油膜温度变化曲线。计算中,采用文献[16]中所给出的流体和滑靴的初始参数。结果表明油膜温度随缸体转角变化而发生改变,与试验结果[16]的变化趋势接近,数值相差为0.1~0.3℃,由于其采用剩余压紧力法设计了一个斜盘转动而缸体固定的柱塞泵简易装置,在柱塞腔压力为20 MPa和主轴转速为1 650 r/min下测试滑靴底面油膜温度,这个装置的缺点是滑靴因随缸体固定不动而缺少离心力,无法反映滑靴倾覆现象对油膜温升的影响,试验结果只反映滑靴因泄漏和滑动摩擦所造成的油膜温度变化,油膜温度变化趋于平滑,温度波动范围较小。本文考虑了滑靴的动压效应,对压力控制方程进行了修正,计算结果优于前者。当滑靴处于泵的排油区时,油液温度从46℃上升到50℃,这说明滑靴所受的正向压紧力增大,滑靴因泄漏和黏性摩擦产生的功耗损失增大,引起油液温度升高,同时滑靴受到离心力矩和倾覆力矩的影响,滑靴处于持续不稳定的承载状态,油膜温度产生波动。当滑靴处于泵的吸油区时,油液温度从50℃下降到46℃,这说明滑靴的正向压紧力减小,滑靴副功耗损失减小,引起油液温度降低。与文献[16]相比,在滑靴倾覆效应的影响下,理论油膜温度波动更加显著,尤其滑靴处于吸排油交替区时,滑靴底面流体动力压力场增强,楔形油膜厚度急剧下降,温升变化比较剧烈,在某种程度上加剧滑靴表面偏磨磨损。这些特征说明滑靴的动压效应与滑靴副功耗损失密切相关,改变油膜温度,且滑靴的结构参数与油膜温度之间存在映射关系,应予以重视。
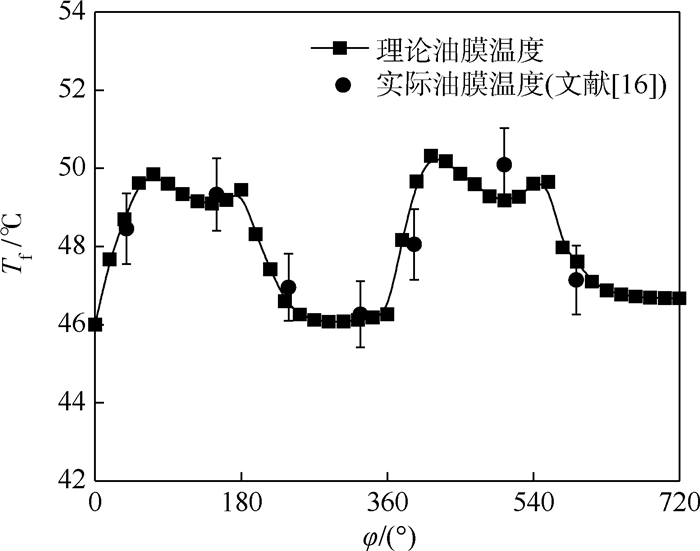 |
| 图 6 滑靴副油膜温度变化曲线 Fig. 6 Oil film temperature curve in slipper pair |
| 图选项 |
3.2 滑靴的半径比对油膜温度的影响图 7为不同柱塞腔压力下滑靴的半径比对油膜温度的影响。从图 7可以看出,油膜温度随滑靴的半径比增大而升高,且随柱塞腔压力增大而升高。当滑靴的半径比大于1.5时,随着柱塞腔压力增大,油膜温度的上升幅度明显增加,其原因是式(11)和式(13)中黏性摩擦力矩项和泄漏流量项与滑靴半径有关;当油液从滑靴的密封带中流出时,泄漏流量因半径比所引起的过流面积增大而明显增加,同时摩擦力矩与滑靴半径成正比,增加泄漏功耗和黏性摩擦功耗损失,最终表现为油膜温度升高,但对相同压力条件下不同滑靴半径比所增加的油膜温升幅度不尽相同。
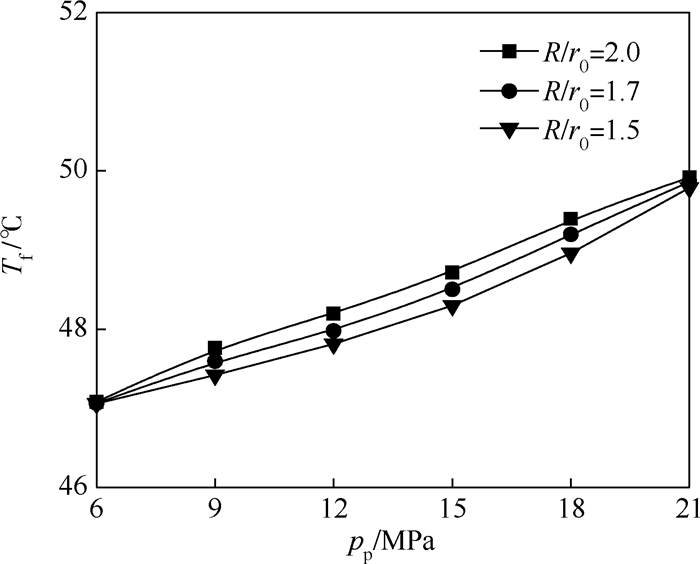 |
| 图 7 不同柱塞腔压力下滑靴半径比对油膜温度的影响 Fig. 7 Effects of slipper radius ratio on oil film temperature under different piston chamber pressures |
| 图选项 |
图 8为不同主轴转速下滑靴的半径比对油膜温度的影响。从图 8可以看出,油膜温度与主轴转速呈单调递增关系,且当主轴转速大于1 200 r/min时,油液温升显著增加,其原因是式(8)中滑靴的径向和切向运动速度与主轴转速呈正相关,影响滑靴底面油液的流动速度,且式(11)和式(13)中黏性摩擦力矩项和泄漏流量项与油液流速以及滑靴半径成正比。当主轴转速增大时,油液流速增加,滑靴副的泄漏功耗与黏性摩擦功耗增大,转化为油液内能,引起油液温度升高。
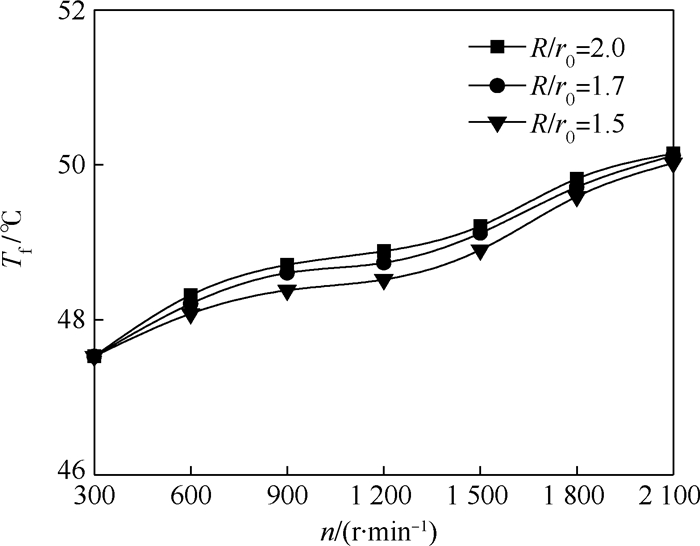 |
| 图 8 不同主轴转速下滑靴半径比对油膜温度的影响 Fig. 8 Effects of slipper radius ratio on oil film temperature under different shaft rotational speeds |
| 图选项 |
3.3 阻尼管长度直径比对油膜温度的影响图 9为不同柱塞腔压力下阻尼管长度直径比对油膜温度的影响。阻尼管长度直径比的增大将会引起油膜温度的升高。当阻尼管长度直径比大于3.50时,随着柱塞腔压力增大,油膜温度的上升幅度在0.2~0.8℃左右,其原因是式(3)中滑靴油室压力项与阻尼管长度直径比成反比,且滑靴副泄漏流量来自于柱塞腔内高压油,而阻尼管对油液起到节流作用。当阻尼管长度恒定时,泄漏流量随阻尼管直径减小而减小,且滑靴油室压力减小,在某种程度上抑制泄漏功率损失,降低油膜厚度,但是增大油膜的剪切应力,增加黏性摩擦功率损失,导致油膜温度的上升趋势明显加快。
 |
| 图 9 不同柱塞腔压力下阻尼管长度直径比对油膜温度的影响 Fig. 9 Effects of orifice length diameter ratio on oil film temperature under different piston chamber pressures |
| 图选项 |
图 10为不同主轴转速下阻尼管长度直径比对油膜温度的影响。油膜温度与主轴转速呈单调递增关系,不同主轴转速下阻尼管长度直径比对油膜温度的影响较小,其原因是滑靴的泄漏与黏性摩擦功耗损失与油液流动速度呈正相关,而阻尼管长度直径比与滑靴油室压力呈负相关,减少泄漏流量,对油膜温度起到一定的抑制作用。由此可知,阻尼管长度直径比的增大带来的泄漏功耗减少不足以补偿由主轴转速提高所带来的泄漏功耗和黏性摩擦功耗增大,引起油液温度升高。
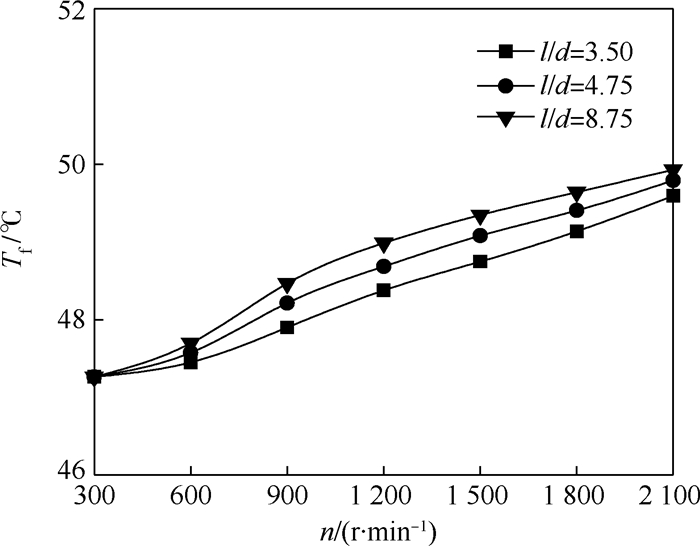 |
| 图 10 不同主轴转速下阻尼管长度直径比对油膜温度的影响 Fig. 10 Effects of orifice length diameter ratio on oil film temperature under different shaft rotational speeds |
| 图选项 |
4 试验结果及其分析图 11所示为A4VTG90液压泵和液压试验台。由于泵的内部空间紧凑,试验比较困难,且柱塞泵油液温升主要源于摩擦副因泄漏和黏性摩擦产生的发热量、缸体组件的自身发热以及泵的自搅发热,通过泄漏流量进入壳体内腔,所以选择测试泵的回油口温度,分析滑靴的结构参数与柱塞泵回油口温度之间的映射关系。与文献[16]相比,这种试验方法没有破坏滑靴底面油膜特征,考虑了滑靴的动压效应,降低试验难度,所测得的试验结果能反映滑靴结构参数对柱塞泵温升特性的影响。本试验工作介质为32号液压油,液压泵的转速范围为300~2 100 r/min,出口压力范围为6~21 MPa。
 |
| 图 11 A4VTG90液压泵和液压试验台 Fig. 11 A4VTG90 hydraulic pump and hydraulic test bench |
| 图选项 |
图 12所示为不同柱塞腔压力下油膜温度和回油口温度的对比。当主轴转速为1 500 r/min时,油膜温度与回油口温度随柱塞腔压力增大而升高,温度变化范围为47~50℃,这说明柱塞腔压力与油液温度存在耦合效应,柱塞腔压力的增大会增加摩擦副因功率损失所产生的发热量,引起油液温度升高。泵的回油口温度略高于油膜温度,其原因是在建模时只考虑滑靴产生的功率损失,没有涉及柱塞泵内柱塞副、配流副以及轴承发热的影响。不同柱塞腔压力下阻尼管长度直径比对油液温升的影响大于滑靴半径比的影响,当柱塞腔压力为12 MPa时,油液温度的上升幅值为0.4~0.7℃,这说明恒转速高压工况下阻尼管的长度直径比应取较小值,防止滑靴底面油膜温度过高,影响柱塞泵的散热效果。
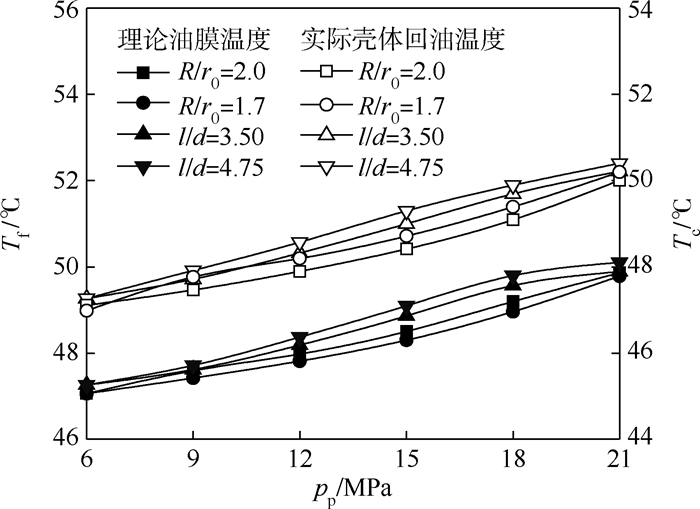 |
| 图 12 不同柱塞腔压力下油膜温度和回油口温度的对比 Fig. 12 Comparison of oil film temperature and outlet temperature under different piston chamber pressures |
| 图选项 |
图 13所示为不同主轴转速下油膜温度和回油口温度的对比。当柱塞腔压力为21 MPa时,油膜温度与回油口温度随主轴转速增大而升高;但在高转速(大于1 200 r/min)范围内,滑靴半径比对油膜温度的影响逐渐超过阻尼管长度直径比的影响,油液温度的上升幅值在0.3~0.7℃左右,其原因是滑靴油室压力与阻尼管长度直径比成反比,式(7)中压力梯度项减小,降低油液流动速度,在一定程度上抑制滑靴的泄漏功耗损失,降低油液温度,而式(12)和式(14)中油液流速项与滑靴半径比呈单调递增关系,增加滑靴副功耗损失,引起油液温度升高,这说明恒压高速工况下滑靴的半径比对滑靴副功率损失的影响更为显著,应尽量取较小值,降低油膜温度,应该引起重视。
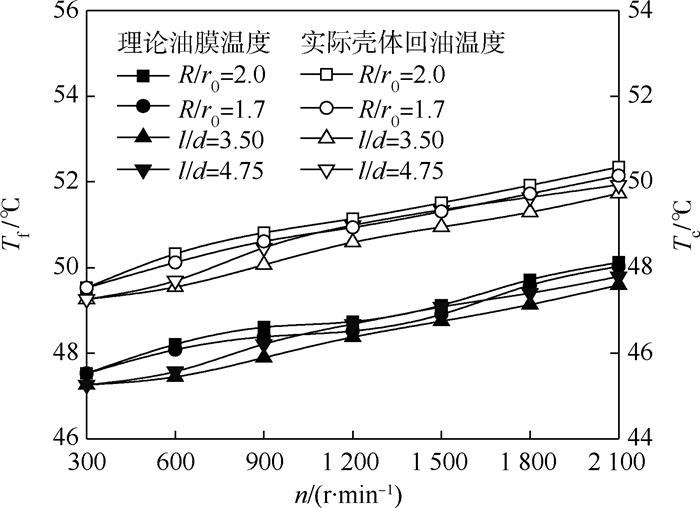 |
| 图 13 不同主轴转速下油膜温度与回油口温度的对比 Fig. 13 Comparison of oil film temperature and outlet temperature under different shaft rotational speeds |
| 图选项 |
5 结 论1)滑靴受到倾覆力矩的影响,滑靴与斜盘之间形成楔形油膜,增加滑靴副功率损失,影响滑靴和油膜之间的传热特征,导致油膜温度场呈不均匀分布,且沿滑靴半径方向呈递减趋势。油膜温度的最大值出现在滑靴底面油膜厚度最薄区域,容易引起滑靴偏磨磨损。油膜温度随柱塞腔压力变化而发生改变,油膜温度的最大值出现在泵的排油区。
2)恒压高速工况下滑靴半径比与滑靴底面油液流动速度呈单调递增关系,增加滑靴副的泄漏和黏性摩擦功率损失,引起油膜温度的上升幅度在0.3~0.7℃左右。因此,滑靴的半径比范围为1.5~2.0之间,应尽量取较小值,降低油膜温度,提高滑靴副润滑性能。
3)恒转速高压工况下阻尼管长度直径比与滑靴油室压力呈单调递减关系,降低油膜压力梯度,减小油液流动速度,对油膜温度起到一定的抑制作用,但是黏性摩擦功率损失因油膜厚度变薄而增大,对油膜温度的影响较为显著。因此,阻尼管的长度直径比范围为3.50~8.75之间,应取较小值,防止滑靴底面油膜温度过高,改善柱塞泵的散热效果。
参考文献
| [1] | LI C G, JIAO Z X.Thermal-hydraulic modeling and simulation of piston pump[J].Chinese Journal of Aeronautics,2006,19(4):354-358. |
| Click to display the text | |
| [2] | 付永领,李祝锋, 祁晓野,等.轴向柱塞式电液泵能量转化效率研究[J].机械工程学报,2014,50(14):204-211. FU Y L,LI Z F,QI X Y,et al.Research on the energy conversion efficiency of axial piston electro-hydraulic pump[J].Journal of Mechanical Engineering,2014,50(14):204-211(in Chinese). |
| Cited By in Cnki (3) | Click to display the text | |
| [3] | DADOUCHE A, FILLON M,BLIGOUD J.Experiments on thermal effects in a hydrodynamic thrust bearing[J].Tribology International,2000,33(3-4):167-174. |
| Click to display the text | |
| [4] | TADEUSZ Z. Testing the heating of the basic components of an axial multipiston pump[J].Measurement Science Review,2001,1(1):123-126. |
| [5] | SCHENK A, IVANTYSYNOVA M.An investigation of the impact of elastohydrodynamic deformation on power loss in the slipper swash plate interface[C]//Proceedings of 8th JFPS International Symposium on Fluid Power.Tokyo:JFPS,2011:228-234. |
| [6] | KAZAMA T. Thermohydrodynamic lubrication model applicable to a slipper of swashplate type axial piston pumps and motors(effects of operating conditions)[J].Tribology Online,2010,5(5):250-254. |
| Click to display the text | |
| [7] | CANBULUT F, SINANOGLU C,KOC E.Experimental analysis of frictional power loss of hydrostatic slipper bearings[J].Industrial Lubrication and Tribology,2012,61(3):123-131. |
| Click to display the text | |
| [8] | CANBULUT F, YILDIRIM S,SINANOGLU C.Design of an artificial neural network for analysis of frictional power loss of hydrostatic slipper bearings[J].Tribology Letters,2004,17(4):887-899. |
| Click to display the text | |
| [9] | BERGADA J M. Leakage and groove pressure of an axial piston pump slipper with multiple lands[J].Tribology Transactions,2008,51(4):469-481. |
| Click to display the text | |
| [10] | KUMAR S, BERGADA J M,WATTON J.Axial piston pump grooved slipper analysis by CFD simulation of three-dimensional NVS equation in cylindrical coordinates[J].Computers & Fluids,2009,38(6):648-663. |
| Click to display the text | |
| [11] | 刘洪,苑士华, 荆崇波,等.磨损轮廓与弹性变形对滑靴动态特性的影响[J].机械工程学报,2013,49(5):75-82. LIU H,YUAN S H,JING C B,et al.Effects of wear profile and elastic deformation on the slipper's dynamic characteristics[J].Journal of Mechanical Engineering,2013,49(5):75-82(in Chinese). |
| Cited By in Cnki (2) | Click to display the text | |
| [12] | 马纪明,李齐林, 任春宇,等.轴向柱塞泵滑靴副润滑磨损的影响因素分析[J].北京航空航天大学学报,2015,41(6):1-6. MA J M,LI Q L,REN C Y,et al.Wear analysis of a hydraulic axial pump swash plate/slipper pair[J].Journal of Beijing University of Aeronautics and Astronautics,2015,41(6):1-6(in Chinese). |
| Cited By in Cnki (4) | |
| [13] | 徐兵,李迎兵, 张斌,等.轴向柱塞泵滑靴副倾覆现象数值分析[J].机械工程学报,2010,46(20):161-168. XU B,LI Y B,ZHANG B,et al.Numerical simulation of overturning phenomenon of axial piston pump slipper pair[J].Journal of Mechanical Engineering,2010,46(20):161-168(in Chinese). |
| Cited By in Cnki (17) | |
| [14] | 汤何胜,訚耀保, 李晶.柱塞泵滑靴副间隙泄漏及摩擦转矩特性研究[J].华南理工大学学报(自然科学版),2014,42(7):74-79. TANG H S,YIN Y B,LI J.Clearance leakage and friction torque of slipper pair in axial piston pump[J].Journal of South China University of Technology(Natural Science Edition),2014,42(7):74-79(in Chinese). |
| Cited By in Cnki (3) | |
| [15] | SCHENK A, IVANTYSYNOVA M.A transient thermoelastohydrodynamic lubrication model of the slipper/swash plate in axial piston machines[J].Journal of Tribology,2015,137(7):031701-1-10. |
| Click to display the text | |
| [16] | KAZAMA T, SUZUKI M,SUZUKI K.Relation between sliding-part temperature and clearance shape of a slipper in swash plate axial piston motors[C]//Proceedings of 9th JFPS International Symposium on Fluid Power.Tokyo:JFPS,2014:382-389. |
