目前国内外相关研究中,探讨较多的是恒定应力加速试验评估方法,也有部分步进应力加速试验评估方法[10, 11, 12],鲜有步退应力加速试验评估方法的相关论述[13].对于高可靠、长寿命电子产品,虽然步进应力加速试验理论方法较为成熟,统计精度较高,却存在所需样本量较大、试验时间较长及在做步进应力加速贮存试验过程中常会遇到较低应力水平下产品的损伤效果不明显的问题等不足,严重影响到试验效率.步退加速寿命试验与步进加速寿命试验相比,存在失效率高、样本量少、试验设备简单的优点[13, 14, 15, 16, 17],进而成为加速贮存试验在工程应用中的一个重要的研究方向.文献[10, 11]给出了在指数分布场合下利用阿伦尼斯模型对步进应力加速寿命试验进行统计分析的方法;文献[12]给出了在指数分布场合下利用步进应力加速寿命试验的极大似然估计方法,并证明非线性方程组有唯一解;文献[17, 18]从多个角度通过Monte-Carlo仿真模拟对比分析了步进应力和步退应力加速试验的试验效率,论证了步退应力试验的效率优势和步退应力试验方法的有效性.但这几种方法的缺点是假设产品在整个加速应力范围内产品的寿命与应力之间均服从对数线性阿伦尼斯模型,未对阿伦尼斯模型的适用情况进行分析做出修正.
本文针对产品在高温下的非工作失效率接近于其工作失效率[9],而对数线性阿伦尼斯模型并不适用于拟合温度较高时产品的寿命与温度应力之间的关系,给出了描述寿命与温度关系的分段非线性阿伦尼斯模型.与对数线性阿伦尼斯模型相比,无需产品退化速率为对数线性化的假设,算法相对简单,因此提高了该模型的工程适用性.通过某雷达高度表的加速贮存试验评估结果表明,与对数线性阿伦尼斯模型相比,采用本文修正后的分段非线性阿伦尼斯模型能够得到更加准确的贮存寿命评估结果.
1 分段非线性阿伦尼斯模型1.1 模型假设
为了不失一般性,采用阿伦尼斯模型进行加速贮存试验寿命评估需要做如下假设[1]:
假设1 在正常应力水平S0和加速应力水平S1,S2,…,Sk下产品的寿命分布都服从指数分布,在应力Si下产品的寿命分布函数为
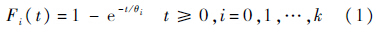
式中,θi为Si下产品的平均寿命,失效密度函数为
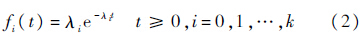
假设2 产品的平均寿命θi与所用的加速应力水平Si之间服从阿伦尼斯模型的关系:
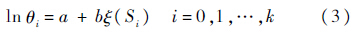
假设3 产品的剩余寿命仅依赖于当时已累积失效部分和当时的应力水平,而与累积方式无关.
1.2 加速模型阿伦尼斯模型[1]:
式中,θ为产品平均寿命;A为常数;Ea为失效机理的激活能;k=8.617×10－5eV,表示Boltzman常数;T为绝对温度，K.
由于在加速试验中,产品会经历高温下的加速试验,温度变化范围较大,在较低的温度范围内,产品的非工作失效率基本保持不变,而在高温范围内,产品的非工作失效率渐进接近产品的工作失效率[9],因此并不能判定阿伦尼斯模型在整个温度变化范围内都是对数线性关系(对1/T).如果仍然在整个温度范围内用对数线性阿伦尼斯模型来处理问题,就会出现较大偏差,有必要引进一种精度更高的寿命评估方法.因此,在高温时,提出下面的对数非线性阿伦尼斯修正模型[9]:
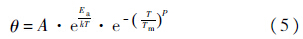
式中,Tm为产品失效机理发生改变的临界温度;P为形状参数.对式(4)和式(5)两边取对数,得到分段非线性阿伦尼斯模型:
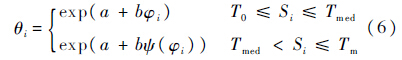
式中,a=lnA和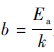
且b>0为待估参数;φi=1/Si为已知函数;T0为正常应力下的温度;
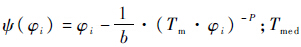为失效率发生较大变化的临界值.
根据指数分布下失效率与平均寿命的关系[1],得到:
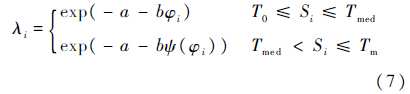
1.3 步退应力加速贮存试验设S1为试验初始加速应力水平,且S1>S2>…>Sk－1>Sk,ti(i=1,2,…，k－1)表示应力Si到Si+1的转换时刻,t0=0为试验开始时刻,tk为试验结束时刻.记第i个等级下第j个失效样本的失效时间为tij(i=1,2,…，k;j=1,2,…，ri)，对于定数截尾试验,有tij=tk.试验总失效数为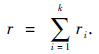
以Δi=ti－ti－1表示在Si下的试验时间.
2 贮存寿命评估模型2.1 试验时间折算数学模型步退应力试验的失效数据除最高应力水平以外都是多个应力水平共同作用的结果,即只有最高应力下的失效数据才是产品真正的寿命.因此如何对试验时间进行折算从而分离出完整寿命数据是步退应力试验分析的关键问题[19].
如果用G(tSk)表示S1,S2…，Sk应力水平下截止到t时刻产品的试验时间折算到Sk下的等效时间,则:
1) 应力水平S1作用下第j个故障产品的试验时间为G1j(t1jS1)=t1j,1≤j≤r1;
2) 应力水平Si,2≤i≤k作用下第j个故障产品的试验时间[12]为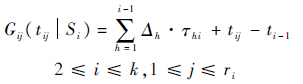
式中,
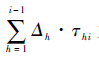为第i个应力水平下第j个故障产品在应力水平Si下的补偿量.进而得到第i个应力水平下第j个故障产品的试验时间的模型为
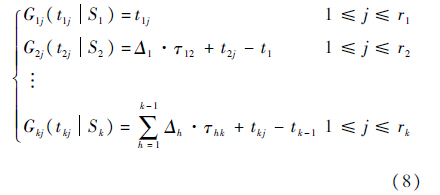
2.2 评估模型2.2.1 产品的寿命分布由假设1和3可知产品在步退应力加速寿命试验下的分布函数[1]为
第i个等级下第j个失效样本的失效概率密度函数[1]为
2.2.2极大似然估计模型对于低温(T0 < T ≤ Tmed)下产品平均寿命的极大似然估计的建模及求解可参考文献[12],在此只对高温(Tmed< T < Tm)下产品平均寿命的极大似然估计建模并进行求解.
对于n个产品进行步退应力加速贮存寿命试验,建立全样本的极大似然估计模型[12]如下: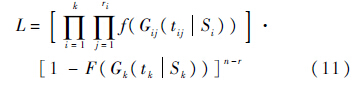 
结合前面的寿命分布函数和失效概率密度函数,得到模型的对数形式如下: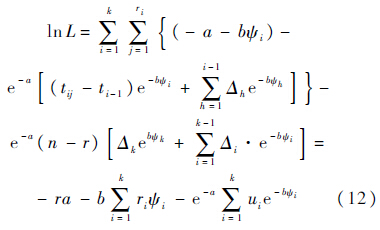 
式中
利用该对数似然方程,分别对参数a,b和P求偏导数,建立非线性方程组如下:
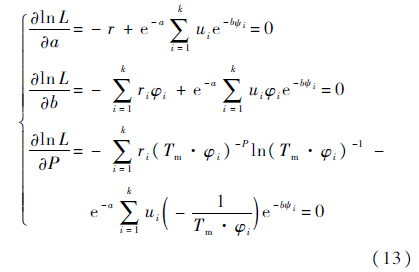
利用遗传算法进行特征提取,图 1为基于遗传算法的实现框架[20].
 |
| 图 1 基于遗传算法的实现框架Fig. 1 Implementation framework based on genetic algorithm |
| 图选项 |
基于遗传算法的求解过程[20]如下.
1) 确定决策变量和约束条件:
决策变量为a,b,P,约束条件为a<0,b>0,P>0.
2) 确定目标函数:
3) 求解目标函数,获得最优解.
2.2.3 正常应力水平下平均寿命θ0的极大似然估计利用遗传算法对式(13)求解得到待估计参数的估计值为(a,b,P),结合式(6)进而得到正常应力水平下参数θ0的极大似然估计(MLE,Maximum Likelihood Estimation)为
3 应用算例3.1 雷达高度表步退应力加速贮存试验某雷达高度表属于电子类产品,由主机与收、发天馈装置组成,主要元器件类别包含:电感器、电容器(钽电解、磁介质)、金属膜电阻器、连接器(SMA、低频航空插头)、微波单片、集成电路、导线、半柔性电缆等.其寿命服从指数分布,从外场的试验数据分析已知其平均故障间隔时间(MTBF)为604 800 h.根据试验应力的提高应以不改变产品在正常工作水平下的失效机理为准则,通过预试验已知雷达高度表在165℃的试验温度下均为电源模块失效,失效原因为高温使电源模块内印制板垂直向上方向上的聚氨酯橡胶发生较大形变,致使其灌封保护的个别焊点开裂,造成电源模块失效,确定Tm=438 K.且通过预试验得到雷达高度表在T>353 K时失效率较高,故确定Tmed=353 K.由于温度是影响电子产品在贮存期性能的主要应力,选择试验加速应力为温度应力,加速模型选择阿伦尼斯模型.
现欲考察雷达高度表在正常贮存温度(S0=298 K)条件下的寿命,由于雷达高度表是典型的高可靠长寿命产品,在常应力下其失效非常缓慢,用定数截尾(截尾数为1)步退应力加速寿命试验方法对其贮存寿命进行评估.
相应试验参数为:试验样本n=6,步退应力等级k=3,加速应力为S1=388 K,S2=378 K,S3=368 K,每个应力等级下的失效数均为1,即ri=1,i=1,2,3.各应力等级下故障产品的故障时间(即各应力等级转换时刻)分别为t1=2 160 h,t2=5 420 h,t3=11 820 h,则各应力水平下的试验时间分别是Δ1=t1=2 160 h,Δ2=t2－t1=3 260 h,Δ3=t3－t2=6 400 h.
3.2 贮存寿命评估3.2.1 基于分段非线性阿伦尼斯模型的贮存寿命评估结果结合式(13)和试验数据,得到加速应力Si(i=1,2,3)下试样的故障前时间折算到加速应力水平Si下的试验时间为t*i=(ti－ti－1)+
,利用遗传算法求解,得到加速模型中的参数估计值为a=－5.08,b=5 488.83,p=3,将估计结果(a,b,P)代入式(6)进而得到加速方程为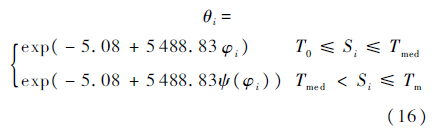
取正常贮存温度S0=298 K,得到正常贮存条件下产品的平均寿命θ1=620 880 h,失效率λ1=1/θ1=1.61×10－6.
3.2.2 基于对数线性阿伦尼斯模型的贮存寿命评估结果根据文献[12],加速应力Si(i=1,2,3)下试样的故障前时间折算到加速应力水平Si下的试验时间为
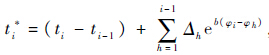,得到基于对数线性阿伦尼斯模型的步退应力加速贮存试验中加速模型的参数估计值a=－2.28,b=4 552.78.将估计结果(a,b)代入式(5)得到产品在自然贮存条件下的平均寿命的方程:θ2=exp(－2.28+4 552.78 φ0),进而得到产品在自然贮存条件下的平均寿命θ2=441 435 h,失效率为λ2=1/θ2=2.27×10－6.
3.3 结果分析1) 将基于分段非线性阿伦尼斯模型的加速贮存寿命评估方法得到的计算结果、基于对数线性阿伦尼斯模型加速贮存寿命评估方法得到的计算结果与产品的实际平均寿命和失效率进行对比分析,其误差结果如下式所示:
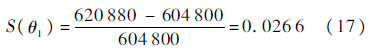
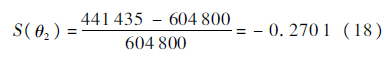
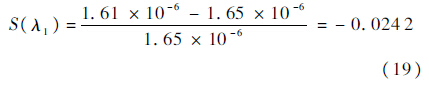
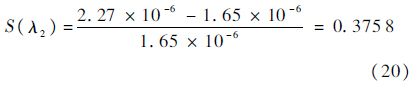
从式(17)~式(20)可以看出,基于对数线性阿伦尼斯模型评估得到的平均寿命θ2相对于实际平均寿命的误差为27.01%,失效率的误差为37.58%,评估结果偏差较大.而基于修正的分段非线性阿伦尼斯模型得到的平均寿命θ1相对于实际平均寿命的误差仅为2.66%,失效率的误差仅为2.42%,相对误差均控制在5%之内,其评估结果精确度远远高于基于对数线性阿伦尼斯模型评估得到的结果,评估结果精确度较高.
2) 结合式(6),得到基于分段非线性阿伦尼斯模型得到的失效率和基于对数线性阿伦尼斯模型得到的失效率随不同温度应力的变化趋势如图 2所示.
 |
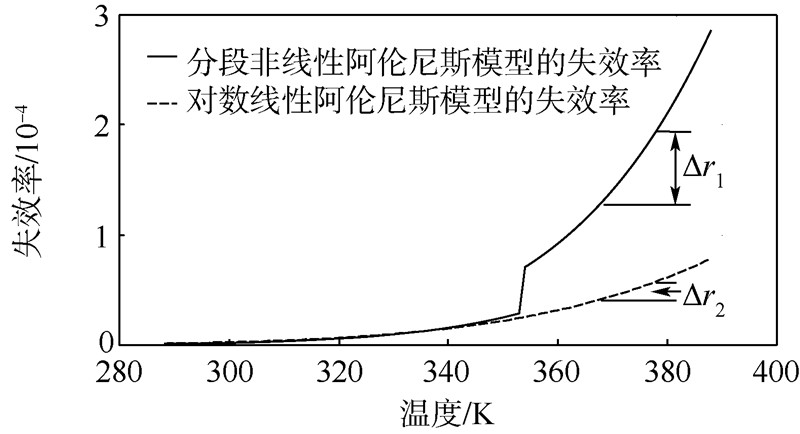| 图 2 失效率随温度变化的趋势图Fig. 2 Trend of failure rate changing with temperature |
| 图选项 |
从图 2可以看出,在低温阶段,基于对数线性阿伦尼斯模型的加速贮存寿命评估方法得到的失效率r2和基于分段非线性阿伦尼斯模型的加速贮存寿命评估方法得到的失效率r1随温度变化均较平缓,而在高温时,如从368~378 K,失效率r1的变化率为
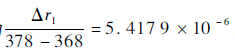,失效率r2的变化率为
,即失效率r1的变化率远大于失效率r2的变化率,基于分段非线性阿伦尼斯模型的加速贮存寿命评估方法更加符合电子产品在较低的温度范围时非工作失效率较小,而在高温范围时,其非工作失效率较大并渐进接近产品的工作失效率的现象.3) 将基于分段非线性阿伦尼斯模型的加速贮存寿命评估方法得到的可靠度R1、基于对数线性阿伦尼斯模型的加速贮存寿命评估方法得到的可靠度R2与产品外场得到的可靠度R0进行对比分析,可得其可靠度函数的对比如图 3所示.
 |
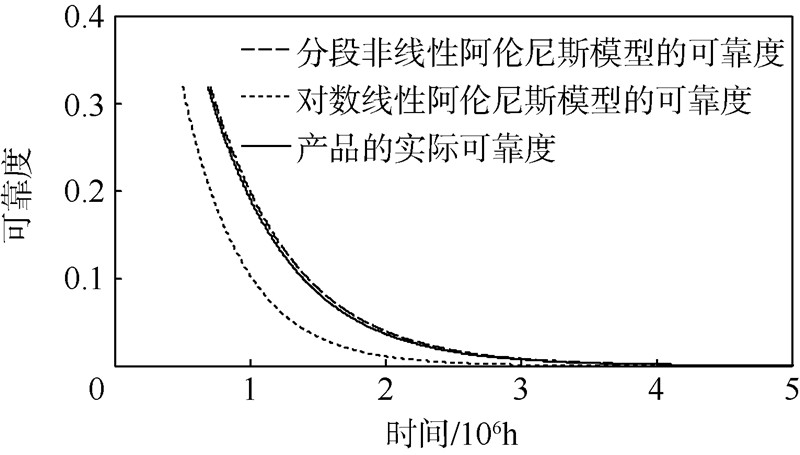| 图 3 不同方法得到的可靠度随时间变化趋势的对比Fig. 3 Comparison of reliability trends over time got by different ways |
| 图选项 |
从图 3中可以看出,基于分段非线性阿伦尼斯模型得到的可靠度函数R1与实际可靠度函数R0几乎重合,吻合度相对较高,进一步验证了本文中基于分段非线性阿伦尼斯模型的加速贮存寿命评估方法的有效性以及准确性.
3.4 Monte-Carlo仿真为进一步说明方法的合理性,利用Monte Carlo仿真试验数据并分析结果.根据贮存失效分布函数,产品的寿命服从指数分布,F(t)=1－e－t/θ,从变换抽样方法可得X=1－e－t/θ.由于X与1－X均为区间[0, 1]上服从均匀分布的随机数,可得T=－θ ln X即为服从参数θ的指数分布的随机变量.然后利用Monte Carlo仿真,得到仿真试验数据及相应的评估结果如表 1所示.表 1 Monte Carlo仿真及评估结果 Table 1 Monte Carlo simulation and evaluation results
| 序号 | 应力 | 仿真失效 时间/h | θ/h | 基于分段非线性 | 基于对数线性 | ||
| θ1/h | 偏差/% | θ2/h | 偏差/% | ||||
| 1 | Tm=433 K,Tmed=408 K S1=428 K,S2=418 K,S3=408 K | 288 624 912 | 120 960 | 125 860 | 4.05 | 106 265 | -12.15 |
| 2 | Tm=418 K,Tmed=363 K S1=388 K,S2=378 K,S3=368 K | 1 243 2 587 3 763 | 345 600 | 362 681 | 4.94 | 286 969 | -16.96 |
| 3 | Tm=431 K,Tmed=388 K S1=418 K,S2=408 K,S3=398 K | 2 184 3 192 4 320 | 2 420 000 | 2 562 538 | 5.89 | 1 950 800 | -19.39 |
表选项
从表 1可以看出,基于分段非线性阿伦尼斯模型的步退应力加速贮存试验评估方法得到的评估结果与仿真的偏差百分比控制在5%左右,其精度明显高于基于对数线性阿伦尼斯模型的步退应力加速贮存试验评估方法所得到的结果.
4 结 论1) 本文针对对数线性阿伦尼斯模型不能准确地拟合寿命与应力之间的关系,结合步退应力加速寿命试验的统计分析问题进行讨论,给出了一种基于分段非线性阿伦尼斯模型的步退应力加速贮存试验评估方法.
2) 通过对雷达高度表的步退应力加速贮存试验评估得到的平均寿命、失效率以及可靠度函数的对比分析,可以看出本文所研究的基于分段非线性阿伦尼斯模型的加速贮存寿命评估方法的结果误差在5%范围内,具有较好的适用性和较高的精确度.本文的基于分段非线性阿伦尼斯模型的加速贮存寿命评估方法能够有效地解决步退应力加速贮存寿命试验的统计分析问题,为武器装备定寿与延寿工程奠定了基础.
参考文献
| [1] | 茆诗松, 王玲玲.加速寿命试验[M].北京:科学出版社,1997:16-22. Mao S S,Wang L L.Accelerated life testing[M].Beijing:Science Press,1997:16-22(in Chinese). |
| [2] | 张春华,陈循, 温熙森.加速寿命试验技术综述[J].兵工学报,2004,25(4):485-490. Zhang C H,Chen X,Wen X S.A review of accelerated life testing technology[J].Acta Armamentarii,2004,25(4):485-490(in Chinese). |
| Cited By in Cnki (99) | Click to display the text | |
| [3] | Hartler G. Parameter estimation for the arrhenius model[J].IEEE Transactions on Reliability,1986,35(4):414-418. |
| Click to display the text | |
| [4] | Nelson W. Accelerated testing-statistical model,test plans and data analysis[M].New York:John Wiley & Sons,1990:496- 502. |
| [5] | Nelson W. Analysis of accelerated life test data-part I:the arrhenius model and graphical methods[J].IEEE Transactions on Electrical Insulation,1971,6(4):165-181. |
| Click to display the text | |
| [6] | Nelson W. Accelerated life testing step-stress models and data analysis [J].IEEE Transactions on Reliability,1980,29(2):103-108. |
| Click to display the text | |
| [7] | 李健,汪金华, 陆陪永.温度步进应力加速寿命试验研究[J].电子产品可靠性与环境试验,2007,25(1):1-4. Li J,Wang J H,Lu P Y.Research of temperature stepped stress accelerated life testing[J].Electronic Product Reliability and Environmental Testing,2007,25(1):1-4(in Chinese). |
| Cited By in Cnki (8) | |
| [8] | 李进,李传日. 加速寿命试验中修正阿伦尼斯加速因子的研究[J].电子产品可靠性与环境试验,2009(S1):38-42. Li J,Li C R.A study of the modified Arrhenius acceleration factor in acceleration life test[J].Electronic Product Reliability and Environmental Testing,2009(S1):38-42(in Chinese). |
| Cited By in Cnki (3) | |
| [9] | Coit D W, Priore M G.Impact of nonoperating periods on equipment reliability,RADC-1984-22232[R].Rome:IIT Research Institute,1984. |
| Click to display the text | |
| [10] | 茆诗松. 指数分布场合下步进应力加速寿命试验的统计分析[J].应用数学学报,1985,8(3):311-316. Mao S S.Statistical analysis of accelerated life testing-step-stress models under the exponential distribution case[J].Acta Mathematicae Applicatae Sinica,1985,8(3):311-316(in Chinese). |
| Cited By in Cnki (96) | Click to display the text | |
| [11] | 仲崇新,张志华. 指数分布场合定时和定数截尾步进应力加速寿命试验和统计分析[J].应用概率统计,1991,7(1):52-59. Zhong C X,Zhang Z H.Type-I censored and type-II censored step stress accelerated life test and statistical analysis under exponential distribution[J].Chinese Journal of Applied Probability and Statistics,1991,7(1):52-59(in Chinese). |
| Cited By in Cnki (36) | |
| [12] | 费鹤良,张学新. 指数分布场合下步进应力加速寿命试验的极大似然估计[J].应用数学学报,2004,17(3):398-404. Fei H L,Zhang X X.The maximum likelihood estimation of step stress accelerated life testing under exponential distribution situation[J].Acta Mathematicae Applicatae Sinica,2004,17(3): 398-404(in Chinese). |
| Cited By in Cnki (12) | |
| [13] | 李宪珊. 步退应力加速试验方法及其应用[J].强度与环境,2012,39(6):59-62. Li X S.Step down stress accelerated testing method and application[J].Structure & Environment Engineering,2012,39(6): 59-62(in Chinese). |
| Cited By in Cnki (2) | |
| [14] | 张春华. 步降应力加速寿命试验的理论和方法[D].长沙:国防科技大学,2002. Zhang C H.Theory and method of step down stress accelerated life testing[D].Changsha:National University of Defense Technology,2002(in Chinese). |
| Cited By in Cnki (27) | |
| [15] | 张春华,陈循, 温熙森.步降应力加速寿命试验(上篇)——方法篇[J].兵工学报,2005,26(5):661-665. Zhang C H,Chen X,Wen X S.Step-down-stress accelerated life testing-methodology[J].Acta Armamentarii,2005,26(5):661-665(in Chinese). |
| Cited By in Cnki (39) | Click to display the text | |
| [16] | 张春华,陈循, 温熙森.步降应力加速寿命试验(下篇)——统计分析篇[J].兵工学报,2005,26(5):666-669. Zhang C H,Chen X,Wen X S.Step-down-stress accelerated life testing-statistical analysis[J].Acta Armamentarii,2005,26(5): 666-669(in Chinese). |
| Cited By in Cnki (30) | Click to display the text | |
| [17] | 徐广,王蓉华. 步降应力加速寿命试验的效率分析[J].上海师范大学学报:自然科学版,2008,37(5):468-475. Xu G,Wang R H.Efficiency analysis of step-down-stress accelerated life testing[J].Journal of Shanghai Normal University:Natural Sciences,2008,37(5):468-475(in Chinese). |
| Cited By in Cnki (4) | |
| [18] | Wang R H, Sha N J,Gu B Q,et al.Comparison analysis of efficiency for step-down and step-pp stress accelerated life testing[J].IEEE Transactions on Reliability,2012,61(2):590-603. |
| Click to display the text | |
| [19] | 赵宇,杨军, 马小兵.可靠性数据分析[M].北京:国防工业出版社,2011:25-26. Zhao Y,Yang J,Ma X B.Data analysis of reliability[M].Beijing:National Defence Industry Press,2011:25-26(in Chinese). |
| [20] | 雷英杰,张善文, 李续武,等.遗传算法工具箱及应用[M].西安:西安电子科技大学出版社,2014:18-19. Lei Y J,Zhang S W,Li X W,et al.Genetic algorithm toolbox and its application[M].Xi'an:Xi'an University of Electronic Science and Technology Press,2014:18-19(in Chinese). |
