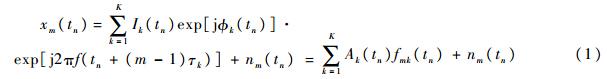
式中,Ik(tn)和
k(tn)分别表示tn时刻第k个信号的幅度和相位;nm(tn)表示tn时刻第m个阵元处的附加噪声,n=1,2,…,N表示快拍数,m=1,2,…,M表示阵元数.本文的目的是估计信号的方位Θ=(θ1,θ2,…,θk)T,而对信号的包络A={Ak(tn),∀ k,n}和噪声的方差不感兴趣.由Bayesian理论可知,信号方位Θ=(θ1,θ2,…,θk)T的后验概率密度函数为
文献[5]提出采样数据正交化算法解决式(2)的积分问题,首先将N次快拍数据分成Nb块,每块有N/Nb=nb个快拍数据.对每一个数据块进行正交化,对于第s个数据块有
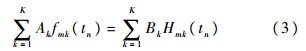
式中
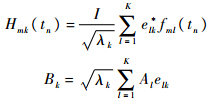
λk和ek=[e1k,e2k,…,eKk]T分别是矩阵F的特征值和特征向量，F是K×K维的矩阵,其元素定义为
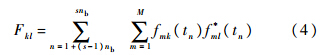
分别取噪声参数σ服从Jeffrey先验分布
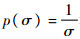和均匀先验分布p(σ)=1,即可得到后验概率密度为
式中
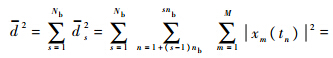
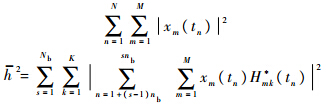
从式(5)可以看出,这是一个关于Θ的高维非线性的多峰值函数,要求它的全局最大值对应的方位角,通过对后验概率密度进行K维网格搜索得到全局最大峰值,计算量非常大,如果计算一个网格点的后验概率密度的计算量为Δ,那么K维的计算量为ΔK.所以尽管Bayesian方位估计方法的估计精度很高,但是其巨大的计算量是其实际应用的最大障碍.2 基于蚁群算法的Bayesian方法首先给出ACO-Bayesian方法的流程图如图 1所示.
 |
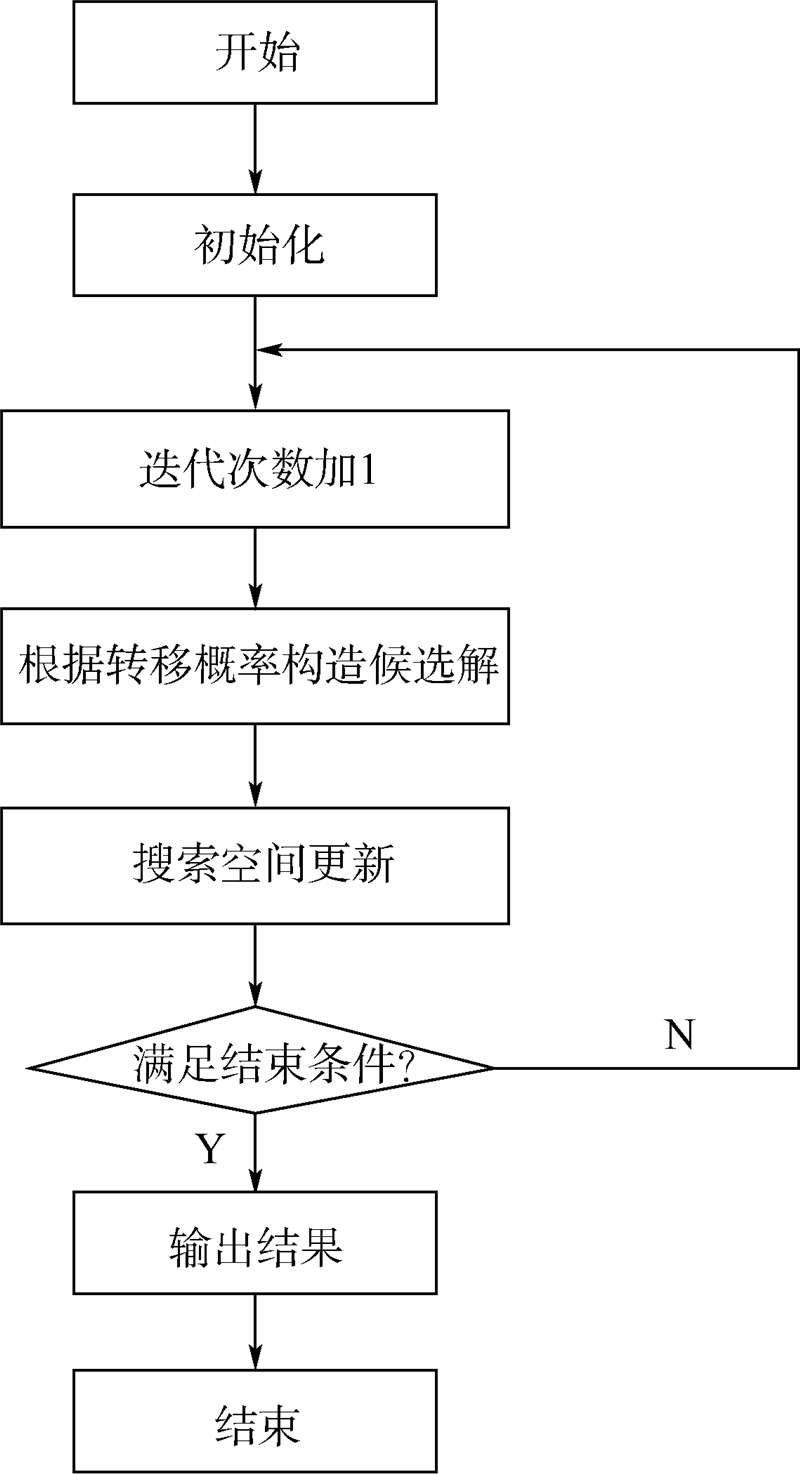| 图 1 ACO-Bayesian方法流程图Fig. 1 Flow chart of ACO-Bayesian method |
| 图选项 |
由于在文献[15]中已对蚁群算法的步骤有了详细的介绍,这里仅作原理性阐述.1) 初始化.首先根据均匀分布UK[θa,θb]从K维搜索空间得到一个抽样搜索空间(θ1θ2…θL),并将抽样搜索空间按照ACO-Bayesian方法的目标函数值(即式(5))从大到小降序排列.然后按照独立高斯分布N(1,q2L2)计算搜索空间对应的权值向量,每组解对应一个权值,最后将搜索空间及其对应的目标函数值和权值向量放入档案表中.2) 根据转移概率更新候选解.满足迭代循环条件时,每只蚂蚁以转移概率p(由式(6)计算)在整个搜索空间中选择一组解θl(每次迭代每只蚂蚁只需选择一次),然后构造以选中解为均值,档案表中所有解与选中解的平均距离为标准差(用信息素挥发系数对其进行修正)的高斯核函数如式(7),利用该高斯核函数对档案表中的所有解进行高斯核抽样得到候选解.
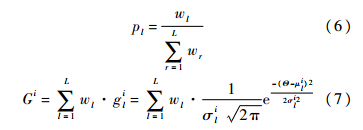
式中,Gi是对整个搜索空间Θ进行一次高斯核抽样值;wl(l=1,2,…,L)即是步骤1)计算的每一组解对应的权值,L是搜索空间的抽样个数;μli即是选中解;σli为用信息素ξ修正的整个搜索空间所有解与当前选中解的平均偏差.对K维搜索空间有
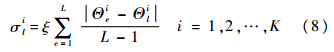
其中Θli表示当前选中解的第i个分量.3) 根据候选解更新搜索空间.计算候选解对应的目标函数值,并与档案表中的第1组解进行比较,若大于第1组解,则用候选解替换最后一组解(即目标函数值最小的解),同时给这个新添加的解赋权值,最后对新产生的搜索空间按照目标函数值f从大到小重新排序;若小于第1组解,则不作调整.4) 得到方位估计值.给定一个精度δ,若连续5次的方位估计值与前一次迭代结果的差值均小于δ,则迭代结束,方位估计结果为最后5次的迭代结果的均值.不满足迭代结束条件转步骤2).3 仿真结果与性能分析计算机仿真中采用均匀线列阵,阵元个数为12,采样频率为120 kHz,100次快拍,两目标入射方位角分别为±2°,归一化夹角为α=0.475 6.3.1 目标分辨概率和估计性能分析1) 两目标信噪比为0 dB时,Bayesian方法后验概率分布曲面如图 2所示,图 3(a)和图 3(b)分别是其二维等高线图和峰值点附近的放大图.可以清晰地看出Bayesian方法的后验概率分布曲面只有一个全局最大值点,该点对应的两个角度就是两目标方位的估计值,Bayesian方法是一个非线性的多维最优化的问题.
 |
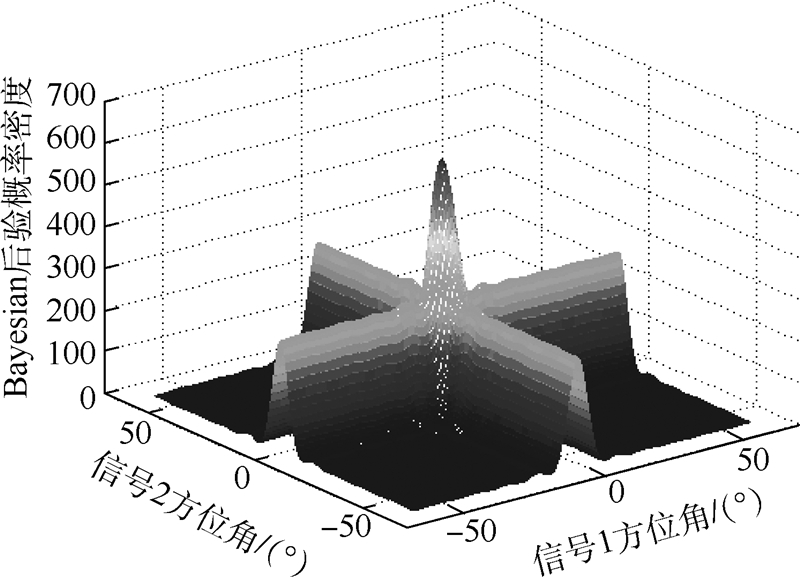| 图 2 后验概率曲面Fig. 2 Curved surface of posteriori probability |
| 图选项 |
 |
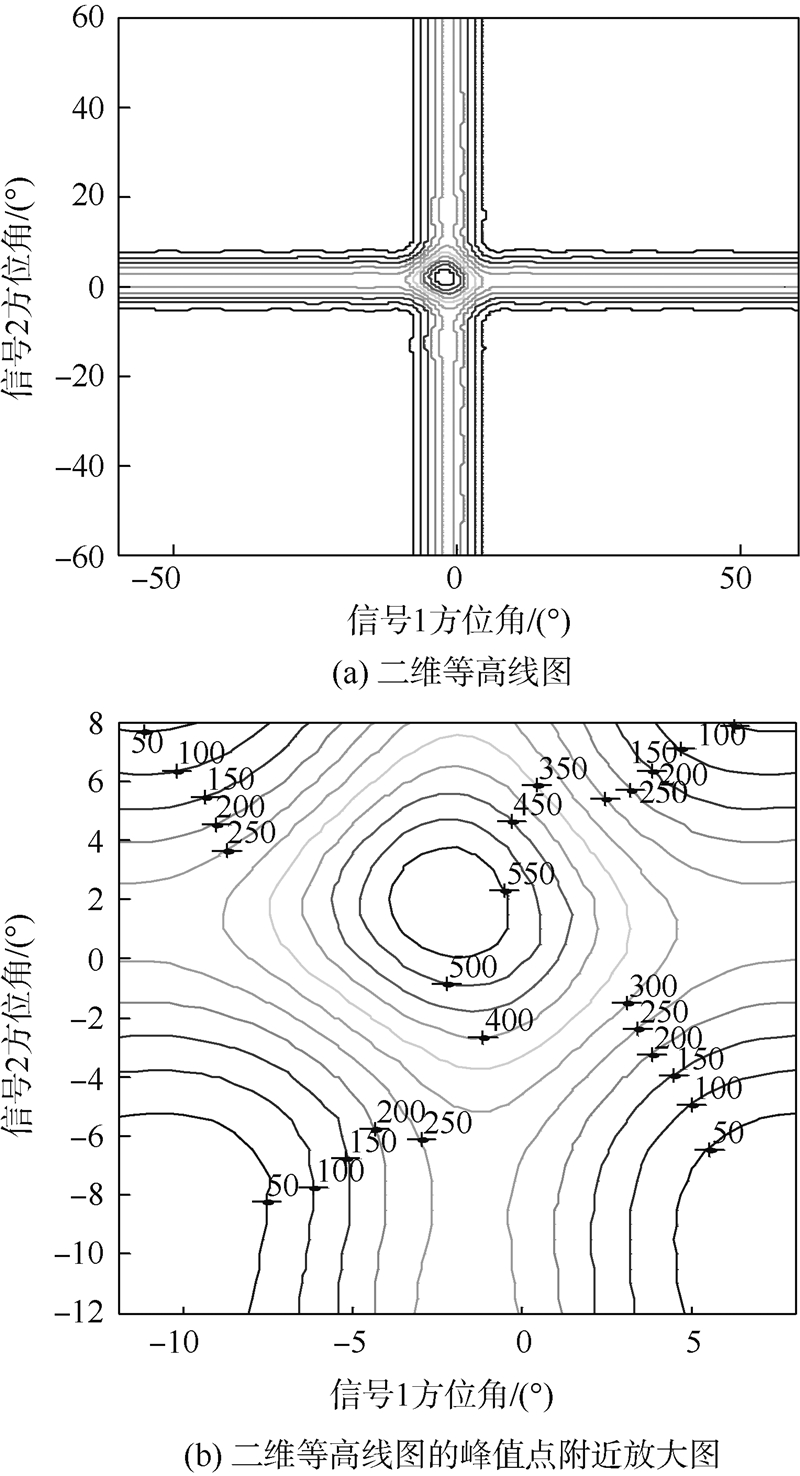| 图 3 二维等高线图和峰值点附近放大图Fig. 3 2-dimension contour and enlarged drawing near peak value points |
| 图选项 |
2) ACO-Bayesian方法方位估计结果与迭代次数的关系曲线(SNR=0 dB)如图 4所示,可以看出,在信噪比为0 dB的时候,ACO-Bayesian方法有优良的收敛性,可以收敛到最优解.
 |
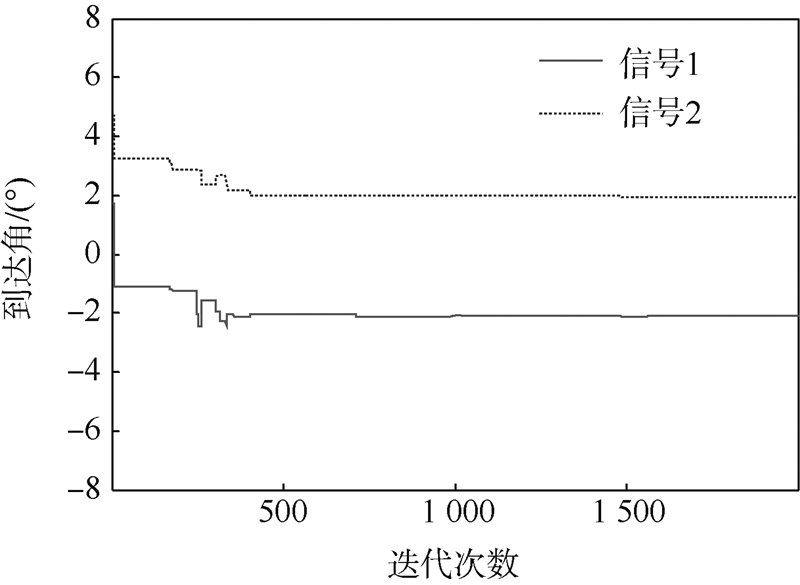| 图 4 收敛性分析Fig. 4 Convergence analysis |
| 图选项 |
3) 分析ACO-Bayesian方法的估计性能,并与Bayesian,MUSIC和MNM方法作对比实验,实验中参数设置如下:T=2,L=100,q=0.1,ξ=0.01,δ=0.001,[θa,θb]=[－60°,60°],做100次Monte Carlo实验,图 5是4种方法的分辨概率,可以看出ACO-Bayesian方法的分辨能力与Bayesian相当,优于MUSIC和MNM方法;图 6和图 7分别是信号1和信号2的估计均方根误差,为了更好地对几种方法的分辨精度进行对比,将由于信噪比过低MNM和MUSIC方法不能成功分辨时的误差标记为10,此时并不是指均方根误差为10,可以看出ACO-Bayesian方法估计性能明显优于MUSIC和MNM方法,信噪比高于-12 dB时,ACO-Bayesian和Bayesian方法的估计性能相当.
 |
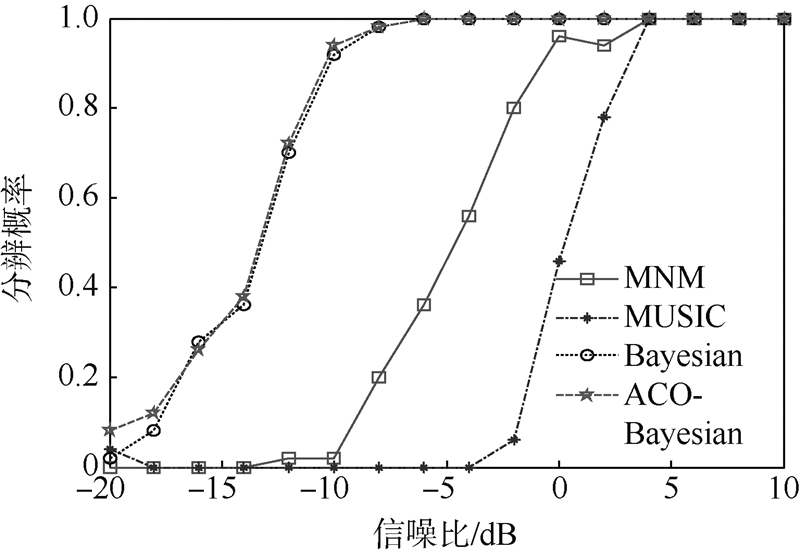| 图 5 分辨概率比较Fig. 5 Resolution probability comparison |
| 图选项 |
 |
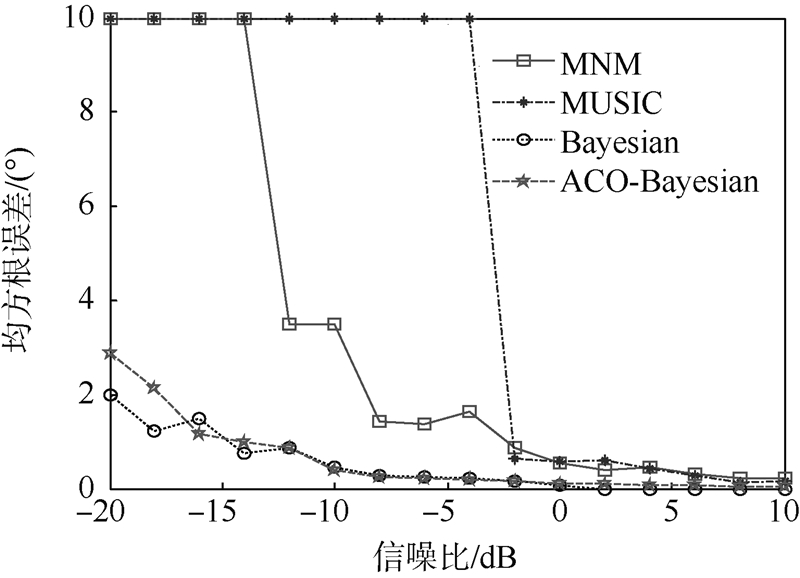| 图 6 信号1的均方根误差Fig. 6 RMSE (root mean squared error) of signal 1 |
| 图选项 |
 |
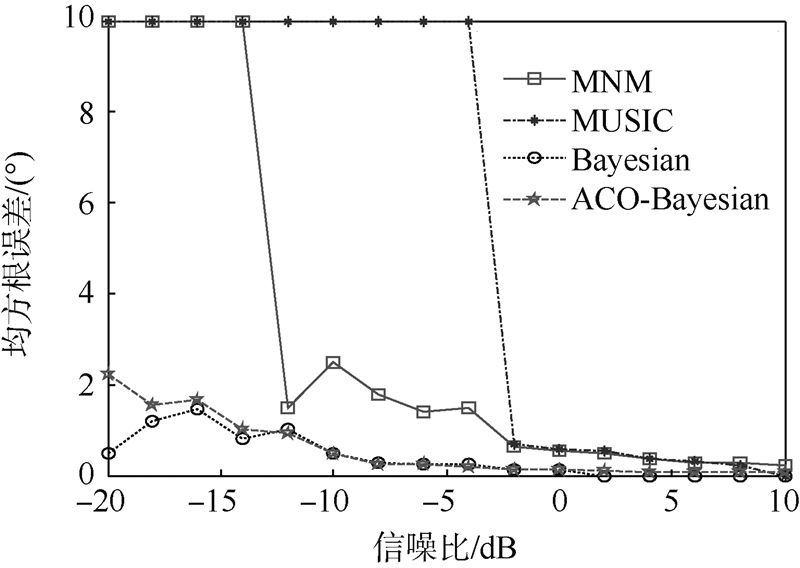| 图 7 信号2的均方根误差Fig. 7 RMSE (root mean squared error) of signal 2 |
| 图选项 |
3.2 计算复杂度分析如果计算一个网格点的后验概率密度的计算量为Δ,则Bayesian方法的计算复杂度为JB=[(θb－θa)/s]P×Δ,其中,[θa,θb]和s分别为Bayesian方法的角度搜索范围和搜索步长;而ACO-Bayesian方法的计算复杂度约为JAB≈(P×IP+L+CP×IP)×Δ,其中P,IP,L分别为ACO-Bayesian方法的信号个数、迭代次数和搜索空间抽样个数.对比Bayesian方法的P维搜索,ACO-Bayesian方法使用高斯核概率抽样技术,P×IP+L小于Bayesian方法P维搜索空间的网格数,而CP是ACO-Bayesian一次迭代高斯核概率抽样的计算量,远远小于P×IP+L.下面通过仿真对ACO-Bayesian方法的计算量进行分析,仿真模型和参数设置与第3节相同,做50次Monte Carlo实验,表 1给出了不同信噪比条件下ACO-Bayesian方法收敛到方位真实值附近所需要的平均迭代次数I2.表 1 不同信噪比条件下ACO-Bayesian方法的平均迭代次数 Table 1 Mean iteration times of ACO-Bayesian method in different SNR (signal to noise ratio) condition
| SNR/dB | -5 | 0 | 5 | 10 |
| 平均迭代次数 | 1 338.1 | 1 106.3 | 957.2 | 846.7 |
表选项
以信噪比为-5 dB为例,Bayesian方法和ACO-Bayesian的计算复杂度分别为JB=[(θb－θa)/s]K×Δ=57 600×Δ,JAB≈(T×IK+L+CK×IK)×Δ=4 114.3×Δ.由以上仿真结果可以看出,ACO-Bayesian方法保持了Bayesian方法的估计性能,且计算量大约是Bayesian方法的1/14,大大降低了运算量.4 水池实验验证依托20×8×7 m3大型消声水池(如图 8所示)开展高分辨方位估计实验对本文的快速方法进行验证,高分辨实验框图如图 9所示.
 |
| 图 8 大型消声水池Fig. 8 Noise elimination water tank |
| 图选项 |
 |
| 图 9 高分辨水池实验框图Fig. 9 Diagram of high resolution water tank experiment |
| 图选项 |
实验中采用6阵元均匀线列阵,系统采样频率为122 880 Hz,波束宽度约为16.9°,利用单源数据,按照15 dB信噪比合成夹角为不同波束宽度的双源信号.快拍数为4 000,统计10次,方位估计结果如表 2所示.可以看出,ACO-Bayesian最大后验概率方位估计快速方法的均方根误差与原方法相比,略有增加,但仍能正确估计出目标的方位,保持了原方法的高分辨能力,能正确估计夹角为1/5波束宽度的两目标.表 2 不同归一化夹角情况方位估计结果Table 2 DOA(direction of arrival) in different normalized angle
| 目标真实方位/(°) | 归一化夹角 | Bayesian | ACO-Bayesian | ||
| 平均值/(°) | RMSE/(°) | 平均值/(°) | RMSE/(°) | ||
| 13.0,-3.6 | 1 BW | 12.91,-3.41 | 0.45,0.46 | 12.89,-3.39 | 0.59,0.63 |
| -3.6,2.0 | 1/3 BW | -3.20,1.91 | 0.51,0.40 | -3.19,1.89 | 0.62,0.59 |
| 0,3.2 | 1/5 BW | -0.22,2.90 | 0.53,0.67 | -0.21,2.89 | 0.68,0.67 |
表选项
5 结 论Bayesian高分辨方位估计方法性能十分优越,但该方法理论复杂,本文针对该方法由于多重积分和多维非线性搜索而导致的计算量大、难以工程应用的问题,将连续蚁群算法与Bayesian方位估计方法相结合,提出了一种基于连续蚁群算法的Bayesian(ACO-Bayesian)方位估计新方法,给出了完整的理论过程,并进行了仿真性能分析和水池实验验证.仿真结果表明,ACO-Bayesian方法在保持Bayesian方法优良性能的同时,把Bayesian方法的计算量从((θb－θa)/s)K×Δ减少到(T×IK+L+CK×IK)×Δ,显著减少了计算复杂度,水池实验结果表明,ACO-Bayesian方法能正确估计夹角为1/5波束宽度的两目标,从而为Bayesian方位估计方法的工程应用提供了一种新方法.
参考文献
| [1] | 冯西安.水下目标高分辨方位估计技术研究[D].西安:西北工业大学,2004.Feng X A.Study on the high resolution DOA estimation techniques of underwater targets[D].Xi'an:Northwestern Polytechnical University,2004(in Chinese). |
| Cited By in Cnki (14) | |
| [2] | Tadaion A A,Derakhtian M,Gazor S,et al.A fast multiple-source detection and localization array signal processing algorithm using the spatial filtering and ML approach[J].IEEE Transactions on Signal Processing,2007,55(5):1815-1827. |
| Click to display the text | |
| [3] | Chen C E,Lorenzelli F,Hudson R E,et al.Stochastic maximum-likelihood DOA estimation in the presence of unknown nonuniform noise[J].IEEE Transactions on Signal Processing,2008,56(7):3038-3044. |
| Click to display the text | |
| [4] | Vorobyov S A,Gershman A B,Wong K M.Maximum likelihood direction-of-arrival estimation in unknown noise fields using sparse sensor arrays[J].IEEE Transactions on Signal Processing,2005,53(1):34-43. |
| Click to display the text | |
| [5] | Huang J G,Chen J F,Liu C M,et al.Bayesian approach to high resolution direction-of-arrival estimation[C]//Proceeding of the Fourth International Conference on Signal Processing.Piscataway,NJ:IEEE,1998:377-380. |
| Click to display the text | |
| [6] | Li X,Huang J G.Bayesian high resolution DOA estimator based on importance sampling[C]//Proceeding of Oceans 2005-Europe.Brest,France:Institute of Electrical and Electronics Engineers Computer Society,2005:611-615. |
| Click to display the text | |
| [7] | Djuric P M,Li H T.Bayesian spectrum estimation of harmonic signals[J].IEEE Signal Processing Letters,1995,2(11):213-215. |
| Click to display the text | |
| [8] | Viberg M,Swindlehurst A L.A Bayesian approach to auto-calibration for parametric array signal processing[J].IEEE Transactions on Signal Processing,1994,42(12):3495-3507. |
| Click to display the text | |
| [9] | Dorigo M.Optimization,learning and natural algorithms[D].Italy:Dipartimento di Elettronica,Politecnico di Milano,1992. |
| Click to display the text | |
| [10] | Socha K,Dorigo M.Ant colony optimization for continuous domains[J].European Journal of Operational Research,2008,185(3):1155-1173. |
| Click to display the text | |
| [11] | Dorigo M,Gambardella L M.Ant colony system:a cooperative learning approach to the traveling salesman problem[J].IEEE Transactions on Evolutionary Computation,1997,1(1):53-66. |
| Click to display the text | |
| [12] | Costa D,Hertz A.Ants can colour graphs[J].Journal of the Operational Research Society,1997,48(3):295-305. |
| Click to display the text | |
| [13] | Gagne C,Price W L,Gravel M.Comparing an ACO algorithm with other heuristics for the single machine scheduling problem with sequence-dependent setup times[J].Journal of the Operational Research Society,2002,53:895-906. |
| Click to display the text | |
| [14] | Corne D,Dorigo M,Glover F.New ideas in optimization[M].London,UK:McGraw-Hill,1999:63-76. |
| Click to display the text | |
| [15] | 焦亚萌,黄建国,韩晶.基于连续蚁群优化算法的小快拍加权子空间拟合快速算法[J].电子与信息学报,2011,33(4):972-976.Jiao Y M,Huang J G,Han J.Continuous ant colony optimization based weighted subspace fitting fast algorithm for DOA estimation with few snapshots[J].Journal of Electronics & Information Technology,2011,33(4):972-976(in Chinese) |
| Cited By in Cnki (8) |
