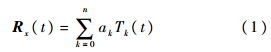
其中,Tk(t)为第1类切比雪夫多项式;ak为星历文件中的系数;t为标准化时间,大小在-1~1之间.对速度和加速度插值可由对式(1)做微分得到.设星历插值后的月心位置、速度和加速度分别R0,V0和A0.另外,通过星历插值还可以获得任意时刻从月固坐标系转换到地心惯性坐标系的3个天平动欧拉角.2 月基SAR对地观测模型的建立月基SAR与星载SAR对地观测模型的最大区别在于:①星载SAR姿态旋转一般采用3-1-2方式,而月基SAR采用3-1-3旋转方式.②星载SAR一般假设天线指向在星体坐标系内不变,利用卫星姿态控制指向,而月基SAR无法控制月球姿态,需直接调整控制指向的两个角度,这两个角度在月面站心坐标系内为高度角和方位角,在天球坐标系内为赤经和赤纬,它们与星下点离线角和斜视角可相互转化.③月基SAR需要考虑月球半径在姿态旋转时对天线位置的影响.下面首先介绍3个右手坐标系(图 1):①地心天球坐标系OE-xyz,x指向春分点,z指向天球北极,假设其为惯性坐标系.②月固坐标系,OL-x′y′z′,x′指向平均可见月盘中心或者也可以说是地球平均位置,同时也是月面经纬网的零点,z′指向月球北极.③地固坐标系,OE-x″y″z″,x″指向零度经线与赤道的交点,z″指向地球北极.
 |
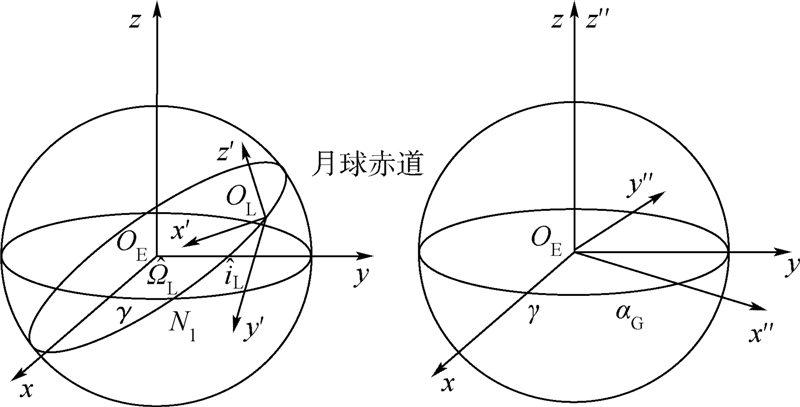| 图 1 3个右手坐标系,γ为春分点Fig. 1 Three right handed coordinates system in which γ is the vernal equinox |
| 图选项 |
通过3个欧拉角
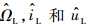的旋转可以将月固坐标系旋转到地心惯性坐标系,旋转矩阵为MLE.设月球赤道相对于地球赤道的升交点为N1,白道相对于黄道降交点为N2,3个欧拉角的天文学含义分别为N1的赤经,月球赤道相对于地球赤道的倾角以及月球起始子午线经过N2至N1的夹角[16].设Rx,Ry和Rz分别为绕x,y和z轴旋转的旋转矩阵,则
3个欧拉角的变率可取
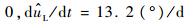为月球公转的平均角速度.通过旋转春分点格林尼治恒星时角αG可以将地固坐标系旋转到地心惯性坐标系,旋转矩阵为Mr,可以用来计算等效斜视角.由于变化量小或时间尺度过大的原因,本文未考虑地球章动、岁差和极移.dαG/dt=ωe,ωe为地球自转角速度.
月基SAR天线运动可以分解为两个部分:月球质心的运动和天线随月球自转的运动.由于月球在地心惯性坐标系中的位置、速度和加速度仅为时间的函数,因此本文不将其视为影响多普勒参数的自变量.能够影响月基SAR多普勒参数的量为:①天线在月球表面的位置;②波束角.因此对于月面上经纬度为(αa,δa)的点,它在月固坐标系下的天线位矢、速度和加速度为
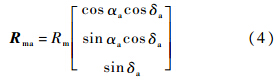
其中Rm=1 738 km为月球半径.
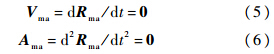
将它们转到月心惯性坐标系,再转到地心惯性坐标系后变为
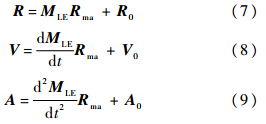
式(7)~式(9)表示天线在惯性系中的位置、速度和加速度,当然也可以用数值差分方法计算速度和加速度,两者最大速度误差约为7.2×10-5 m/s,最大加速度误差约为5.5×10-9 m/s2,对于多普勒参数计算完全可以忽略.3 波束指向月基SAR的一大优势是可以快速指向可见地球半球的任意位置,因此需要计算任意波束方向下的多普勒参数.空间中任意一个单位矢量都需要由两个角度控制,类似星载SAR系统,这两个角度一般可以转化为星下点离线角θn和斜视角θs.星下点离线角为波束与天线位置矢量的夹角.斜视角是波束与零多普勒面之间的夹角.当这两个角度确定后,波束中心视矢量RLOS就确定了,中心视矢量与大地椭球体的交点即为地面波束覆盖区中心.在地心惯性坐标系下,如果知道星下点离线角θn和斜视角θs,则可以得到以下两个方程:
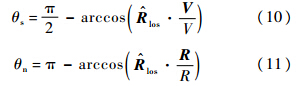
式(10)和式(11)构成两个圆锥面,两方程的解为两个曲面相交的单位矢量, z的大根表示左视,小根表示右视,以下计算以左视为例.在地心惯性坐标系中计算,由于地球自转效应的主导作用,此时的θs为实际斜视角,与等效斜视角存在一定差异;如果在地固坐标系中计算,可以得到总的等效斜视角,用θrs表示.地面波束中心矢量Rt、波束中心视矢量
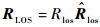和天线位置矢量R有如下关系: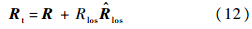
并且,Rt满足地球椭球方程:
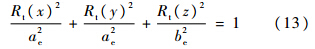
其中,ae为地球赤道半径6 378.137 km;be为地球极地半径6 356.752 km.根据以上关系可以得到一个二次方程,从而得到Rlos的值[9].星载SAR可以假设连接方式使得天线和星体的相对姿态保持一致,然而在月基SAR系统中,由于观测星下点离线角的限制和天平动的存在,天线指向必须不断调整以指向地球.由于月球轨道倾角较小,月基SAR的纬度覆盖完整度受到一定限制.表 1和图 2显示了θrs为零时θn对波束纬度覆盖的影响(改变波束与天线速度的夹角).可以看出,随着θn等差递增,波束入射角和照射纬度也呈现等差递增的规律,而且波束中心扫过的纬度跨度也很稳定.这个特点使观测计划的制定变得相对简单,只需根据月球与目标的纬度差用简单的线性关系来计算所需的离线角.另外,考虑到波束宽度,月基SAR至少能覆盖±75°之间的地区.2014年1月月球轨道倾角较小,约为20°,在其他倾角较大的月份,波束覆盖区域更大.表 1 月基SAR离线角对入射角和地面纬度的影响Table 1 Incident angle and terrestrial latitude related to moon-borne SAR off-nadir angle(°)
| θn | 波束中心入射角 | 最大纬度 | 最小纬度 | 纬度跨度 |
| 0.3 | 18.42 | 43.21 | -4.80 | 48.01 |
| 0.4 | 24.91 | 50.05 | 2.82 | 47.24 |
| 0.5 | 31.77 | 57.02 | 10.47 | 46.55 |
| 0.6 | 39.18 | 64.34 | 18.40 | 45.95 |
| 0.7 | 47.49 | 72.40 | 26.76 | 45.64 |
表选项
 |
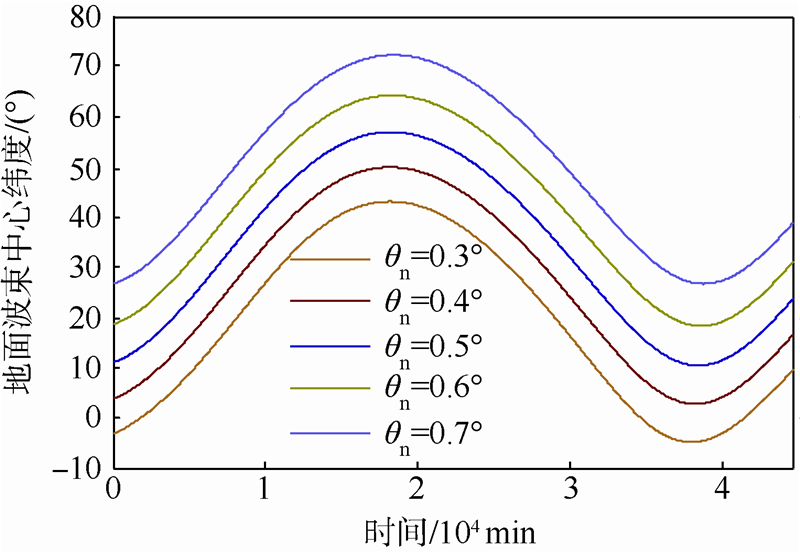| 图 2 θn与地面波束中心纬度沿轨变化关系Fig. 2 Relationship between terrestrial latitude of beam footprint center and θn along the orbit |
| 图选项 |
如果直接给定一个θs,那么波束会有大部分时间不能与地球椭球相交.由表 1可以看出,月基SAR的θn最好在0.3°~0.7°之间,而最大θs不应超过4°.图 3给出了月基SAR的θs沿轨从-4°变化到4°时地面波束中心的纬度变化情况(θn=0.5°),其整体形状与图 2类似.很明显需要通过沿轨不断变化θs可以使波束一直照射在地球上,而且还可以增加纬度照射范围以应对不同的观测需求.
 |
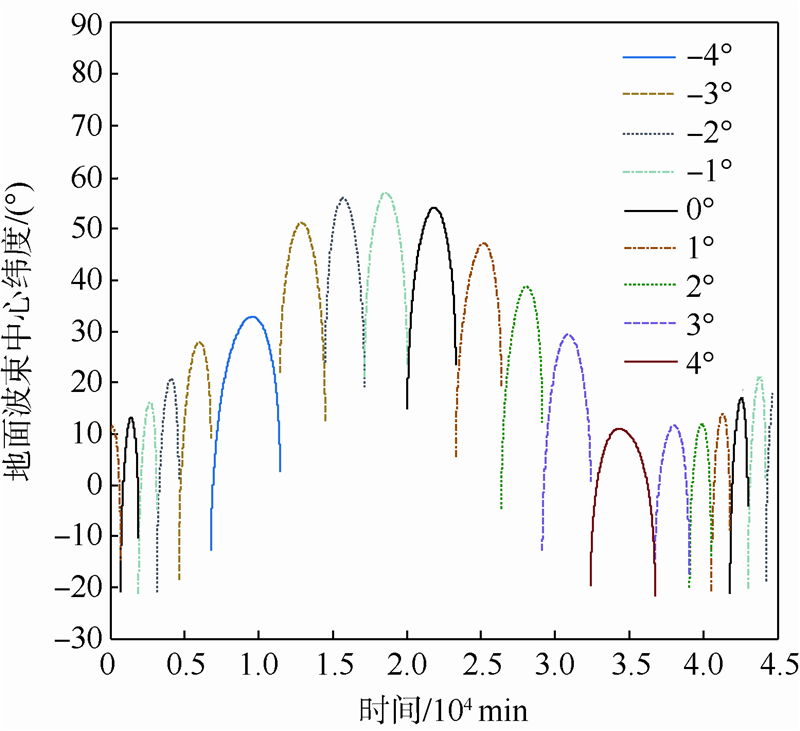| 图 3 θs与地面波束中心纬度沿轨变化关系Fig. 3 Relationship between terrestrial latitude of beam footprint center and θs along the orbit |
| 图选项 |
4 估算多普勒参数SAR多普勒中心频率可表示为
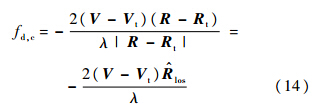
其中Vt为目标随地球自转的线速度.对式(14)进行微分,得到多普勒调频率的计算公式:
其中At为目标随地球自转的加速度.由于观测距离长,式中大括号里的第1项很小.通过式(14)和式(15)可以计算得到月基SAR的多普勒参数.文献[9,11]方法与本文的方法均为利用坐标系旋转进行计算,但本文方法做了适合月基SAR特点的改进:①考虑了天线位置与月心的差异;②直接利用离线角和斜视角定义天线方向更适合月基SAR的实际情况.下面探讨天线位置差异引入的计算误差.本文选择了6个点进行分析,分别是月面坐标为A(0,0),B(0,60),C(0,-60),D(60,0),E(-60,0)和F月心,θs=0°,θn=0.5°.图 4显示了计算结果,为了表现差异,仅给出了局部放大图.天线位置差异对多普勒中心频率计算的影响主要体现在:①多普勒中心频率曲线出现时移,最大时移均出现在D和E之间,大小为75~115 min;②曲线形状略有不同,B和C的差异相对更大,消除时移后仍可达数十赫兹.位置对多普勒调频率也有相似的影响,时移最大值也出现在D和E之间,而值的最大差异为0.002 Hz/s,出现在B和C之间.
 |
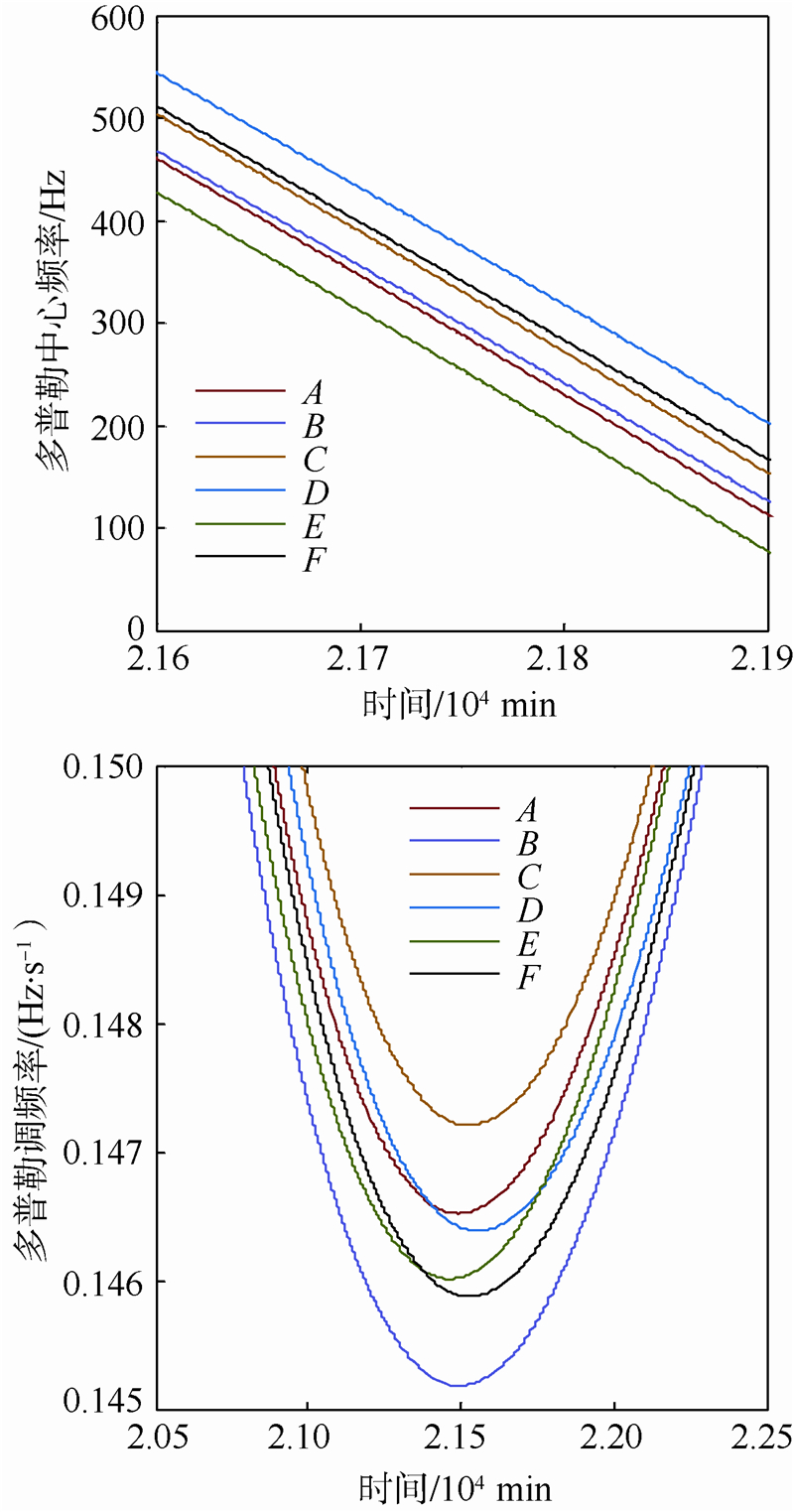| 图 4 月面位置对多普勒参数估算的影响Fig. 4 Doppler parameters estimation variance attributed to different selenographic position |
| 图选项 |
事实上,F点可以假设是一个放置在月心处的卫星,能够利用文献[9]中的方法以及式(14)和式(15) 进行估算,但需要注意天线指向.图 5显示了未经月面位置补偿的星载SAR估算方法中与经过月面位置补偿的本文方法之间多普勒调频率误差沿轨变化情况,参照点为F点(多普勒调频率误差为0).为了使曲线连续并消除角度定义上的差异,本图使用了零多普勒导引.六者最大误差出现在B和C之间,大小仍然为0.002 Hz/s.与F点相比,调频率误差最大值出现在C点,约0.001 5 Hz/s,而月面零点A的最大误差约为0.001 Hz/s.
 |
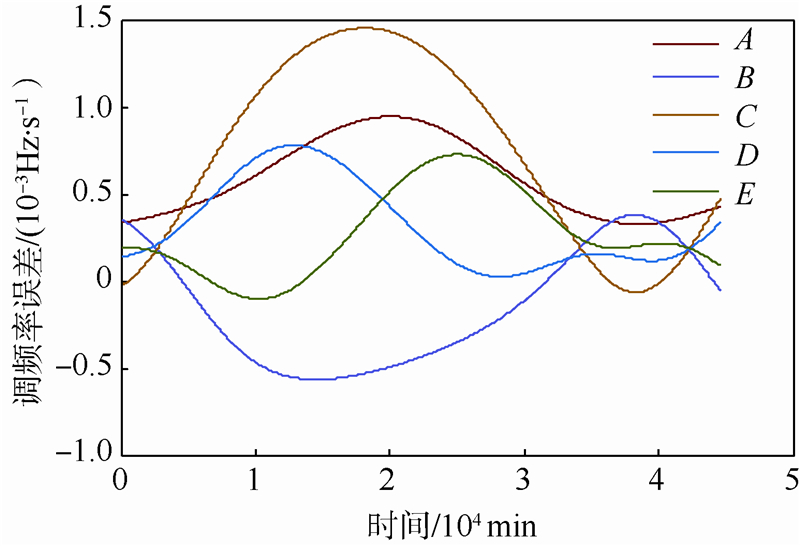| 图 5 零多普勒导引后的多普勒调频率误差Fig. 5 Doppler frequency rate error after zero Doppler steering |
| 图选项 |
由于月基SAR的合成时间相当长(10 min左右),如此误差仍然会对成像造成严重影响.多普勒中心频率的估计误差应该处于信号模糊比和SNR容许的损失范围之内.设时长为600 s,调频率为0.2 Hz/s,过采样率为1.2,则PRF=144 Hz,误差应小于7.2 Hz.另外,多普勒中心频率误差的差异还会造成图像畸变.月基SAR方位压缩中,2%的冲击响应展宽对应1.9×10-6 Hz/s的多普勒调频率误差.由此可见多普勒参数对天线放置位置十分敏感,而月面位置补偿也是十分必要的.5 结 论本文利用JPL星历通过插值和坐标转换构建了月基SAR对地观测几何模型.在此基础上,利用两个二次方程组,解算任意波束方向下的地面波束印记中心位置,再计算月基SAR的多普勒参数,得到如下结论:1)星历插值后,对旋转矩阵近似求导可获得天线在地心惯性坐标系下的运动参数,与高精度数值差分结果相比误差可以忽略.2)月基SAR的波束角需沿轨不断调整以指向地球,在星下点离线角为0.5°时,斜视角最大值约为4°.3)天线放置的位置会明显影响多普勒参数的计算值,中心频率偏差可超过一个PRF,调频率偏差在10-3量级.
参考文献
| [1] | Kiyo T,Jean P.Synthetic aperture radar imaging from an inclined geosynchronous orbit[J].IEEE T Geosci Remote Sens,1983,GE-21(3):324-329. |
| Click to display the text | |
| [2] | Prati C,Rocca F,Giancola D,et al.Passive geosynchronous SAR system reusing backscattered digital audio broadcasting signals[J].IEEE T Geosci Remote Sens,1998,36(6):1973-1976. |
| Click to display the text | |
| [3] | Bruno D,Hobbs S,Ottavianelli G.Geosynchronous synthetic aperture radar:concept design,properties and possible applications[J].Acta Astronaut,2006,59(1):149-156. |
| Click to display the text | |
| [4] | Fornaro G,Franceschetti G,Lombardini F,et al.Potentials and limitations of moon-borne SAR imaging[J].IEEE T Geosci Remote Sens,2010,48(7):3009-3019. |
| Click to display the text | |
| [5] | Guo H D,Ding Y X,Liu G,et al.Conceptual study of lunar-based SAR for global change monitoring[J].Science China:Earth Sciences,2014,57(8):1771-1779. |
| Click to display the text | |
| [6] | Moccia A,Renga A.Synthetic aperture radar for Earth observation from a lunar base:performance and potential applications[J].IEEE T Aero Elec Sys,2010,46(3):1034-1051. |
| Click to display the text | |
| [7] | Raney R K.Doppler properties of radars in circular orbits[J].International Journal of Remote Sensing Letters,1986,7(9):1153-1162. |
| Click to display the text | |
| [8] | Curlander J C,Mcdonough R N.Synthetic aperture radar system and signal processing[M].New York:Wiley,1991. |
| [9] | Cumming I G,Wong F H.Digital processing of synthetic,aperture radar data:algorithms and implementation[M].Boston:Artech House,2005. |
| [10] | 杨文付,曾涛,丁泽刚.基于星历数据的SAR多普勒参数计算[J].北京理工大学学报,2010,30(10):1221-1225.Yang W F,Zeng T,Ding Z G.Doppler parameters calculation of SAR based on satellite ephemeris[J].Transactions of Beijing Institute of Technology,2010,30(10):1221-1225(in Chinese). |
| Cited By in Cnki | |
| [11] | 文竹,周荫清,陈杰.高精度星载SAR多普勒参数估算方法[J].北京航空航天大学学报,2006,32(12):1418-1421.Wen Z,Zhou Y Q,Chen J.Accurate method to calculate space-borne SAR Doppler parameters[J].Journal of Beijing University of Aeronautics and Astronautics,2006,32(12):1418-1421(in Chinese). |
| Cited By in Cnki (1) | |
| [12] | 郑经波,宋红军,尚秀芹,等.地球同步轨道星载SAR多普勒特性分析[J].电子与信息学报,2011,33(4):810-815.Zheng J B,Song H J,Shang X Q,et al.Doppler properties analysis of GEO spaceborne SAR[J].Journal of Electronics & Information Technology,2011,33(4):810-815(in Chinese). |
| Cited By in Cnki (10) | |
| [13] | 赵秉吉,齐向阳,宋红军,等.基于椭圆轨道的Geo-SAR精确多普勒参数解析计算方法[J].电子与信息学报,2012,34(11):2642-2647.Zhao B J,Qi X Y,Song H J,et al.Accurate Doppler parameters estimation of Geo-SAR based on elliptical orbit[J].Journal of Electronics & Information Technology,2012,34(11):2642-2647(in Chinese). |
| Cited By in Cnki (4) | |
| [14] | Murphy T W.Lunar laser ranging:the millimeter challenge[J].Reports on Progress in Physics,2013,76(7):076901. |
| Click to display the text | |
| [15] | Standish E M.JPL planetary and lunar ephemerides,DE 405/LE 405[EB/OL],California:Jet Propulsion Laboratory,1998(1998-08-26)[2014-01-05]. |
| [16] | 郗晓宁,曾国强,任萱,等.月球探测器轨道设计[M].北京:国防工业出版社,2001.Xi X N,Zeng G Q,Ren X.Orbit design of lunar probe[M].Beijing:National Defense Industry Press,2001(in Chinese) |
