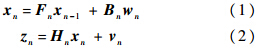
其中,
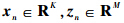为第n时刻状态和观测矢量;
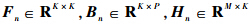为第n时刻的状态转移矩阵、过程噪声增益矩阵和量测矩阵.假定第n时刻过程噪声矢量wn∈RP,量测噪声矢量vn∈RM分布均为零均值高斯白噪声,即E{wn}=0,E{vn}=0;并假定两个噪声矢量互不相关,即对于任意的i,j满足E{wivjT}=0.Qn=E[wnwnT]为过程噪声协方差矩阵,Rn=E[vnvnT]为量测噪声协方差矩阵.对于时不变情况,状态空间模型的状态转移矩阵和观测矩阵简化为F和H.2 现有UFIR滤波器假定UFIR滤波器窗长为N,那么当得到第n时刻的量测时,从时刻m=n－N+1到时刻n之间的N个量测为可用量测.为了保证滤波器的因果性,必须满足m≥0,即n≥N－1.由文献[10]和文献[13]可得n时刻目标状态的估计值可以表示为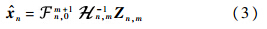
其中
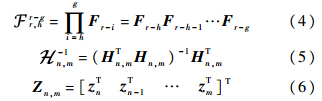
而
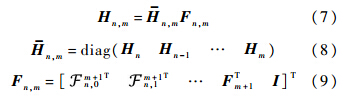
对于时不变系统而言,此时估计式简化为
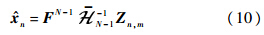
其中
而
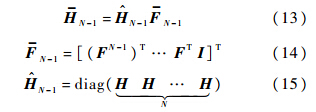
从上面的介绍可以看出,批处理UFIR滤波器能够在忽视噪声统计特性的情况下对信号进行滤波.更重要的是当N1时,UFIR滤波器是近似最优的.但另一方面,N的增大将引起矩阵和向量维数的增大，从而导致计算量急剧增加.迭代UFIR滤波器很好地解决了这一问题,由文献[14]可得迭代UFIR估计式为
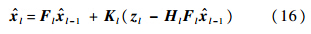
其中
其中Gl为第l时刻的广义噪声功率增益(GNPG)[15].初始条件
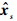和Gs通过批处理UFIR滤波器而得到: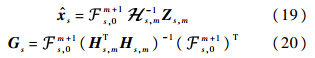
此时批处理窗长K<<N.其中s=m+K－1，迭代变量l从m+K到n.当l=n时,得到滤波器的估计值
n.对于时不变系统公式简化为
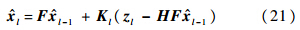
其中
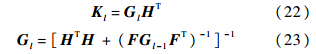
初始条件
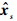和Gs同样可由窗长为K的时不变批处理UFIR滤波器得到: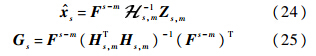
其中s=m+K－1,迭代变量l从m+K到n.3 改进迭代UFIR滤波器在机动目标跟踪中,机动的出现会使得量测数据与滤波数据产生较大偏差.所以偏差的大小能够反映出机动的情况.但从式(18)和式(23)可以看出GNPG只与状态转移矩阵和观测矩阵有关.而且迭代UFIR滤波器每一点的滤波结果都是由之前N－K个量测独立迭代得到的.这样不同时刻滤波过程中的GNPG具有一定的独立性,这使得对于GNPG的改变更加自由.所以本文通过量测数据与滤波数据的偏差定义广义噪声功率增益调整系数(γ)来自适应调整GNPG的值,以进一步提高UFIR滤波器的滤波效果.首先，由于机动只与量测与滤波结果偏差的大小有关而与符号无关,所以本文选取量测与滤波结果偏差的均方根作为描述机动的基本信息,第i时刻偏差的均方根表示为
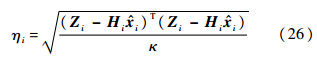
其中κ为目标运动的维数;Zi为第i时刻的量测数据;
i为第i时刻的滤波结果;Hi为状态空间模型的观测矩阵.其次，由于只有通过不同时刻偏差的比值才能反映出机动的情况,所以本文将上一时刻偏差的均方根作为基准,此时刻偏差的均方根与上一时刻的比值来反映机动的情况.并且考虑到迭代开始时的GNPG为初始批处理窗长K个时刻积累的结果,所以有理由对其开K次方.那么第i时刻与i－1时刻的比值表示为
最后，考虑到可能因为各种原因产生野值而造成滤波发散.又由于机动一般都会持续几秒甚至十几秒,所以本文采用对多时刻λ取均值的方法来消除野值的影响,同时这又不会影响对机动的描述.对于取均值的范围本文选取窗长的一半.l时刻的广义噪声功率增益调整系数表示为
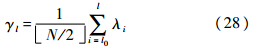
其中l0=l－N/2+1,N/2 表示取N/2的整数部分.由于必须满足l0≥m+K+1,即
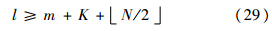
从而对广义噪声功率增益的调整只能从m+K+N/2 时刻开始.前述算法中的式(18)变为
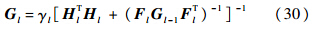
式(23)变为
从算法可以看出滤波过程中每个γ都开了K次方,这显然不是最佳的.因为随着迭代过程的进行,初始批处理长度的影响将不断减小.不过考虑批处理的影响程度随迭代次数增加而减小的程度很难度量,且更趋向于1的γ更能够保证滤波的收敛,这样每个γ都开最大次方似乎也是唯一的选择.不过乘上广义噪声增益调整系数必然将降低滤波的收敛速度,但这与在机动目标跟踪中丢失目标相比是可以接受的.从总体上看,随着迭代次数的增加,目标位置的协方差趋于减小.由于存在目标机动,所以改进算法能够被理解为:当此时刻的量测与滤波结果的偏差比前一时刻要大时,则有理由相信此时目标发生了机动,那么就应该增大GNPG赋予新息更高的权重,从而降低机动造成的滤波误差.而当此时刻偏差比前一时刻小时,表明滤波结果是准确的,那么适当减小新息的权重并不会影响滤波效果,同时GNPG的减小还能够加快滤波的收敛速度.4 机动目标跟踪仿真本文的仿真场景为一个机动目标加速-转弯场景.其中时刻1~时刻20为加速区,时刻20~时刻40为匀速区,时刻40~时刻70为转弯区,时刻70~时刻100为匀速区,如图 1所示.
 |
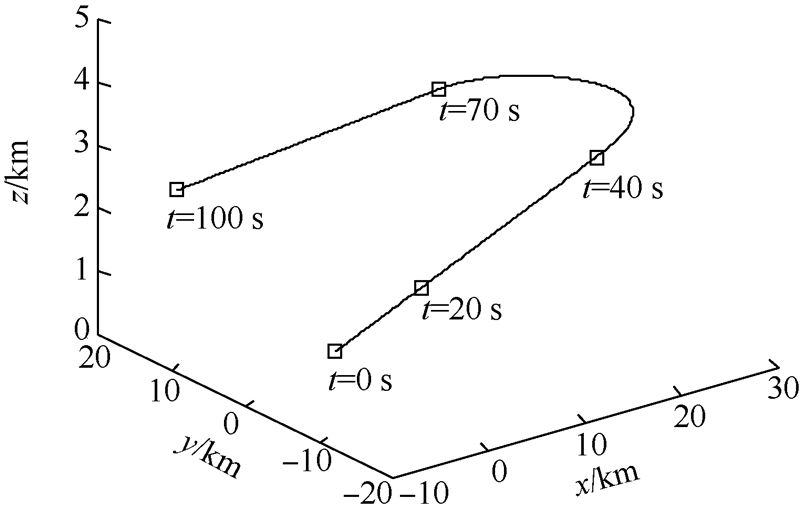| 图 1 机动目标仿真场景Fig. 1 Maneuvering target simulation scenario |
| 图选项 |
仿真系统描述为直角坐标系下的白噪声加速度模型.其中式(1)和式(2)中,状态x定义为xyz方向上的位移、速度和加速度的9维向量.
过程噪声协方差:
量测噪声协方差:
其中T为采样间隔,仿真中T=0.1.考虑到对现有的任何一种基于KF的机动目标跟踪算法(如CN,VD,IMM等),都可以按其原理设计对应的基于UFIR滤波器的跟踪算法,并且UFIR滤波器能够忽视噪声统计特性的优势依然存在.因此仿真中只对KF,UFIR滤波器及改进UFIR滤波器的性能进行了仿真对比.当目标轨迹被附加一个协方差为100的零均值高斯白噪声时,卡尔曼滤波器近似达到最优.通过计算求出此时UFIR滤波器的最优窗长Nopt=55[11,16],并取批处理长度K=5.100次蒙特卡洛所得35~55 s一段的位置均方根误差(RMSE)如图 2所示.
 |
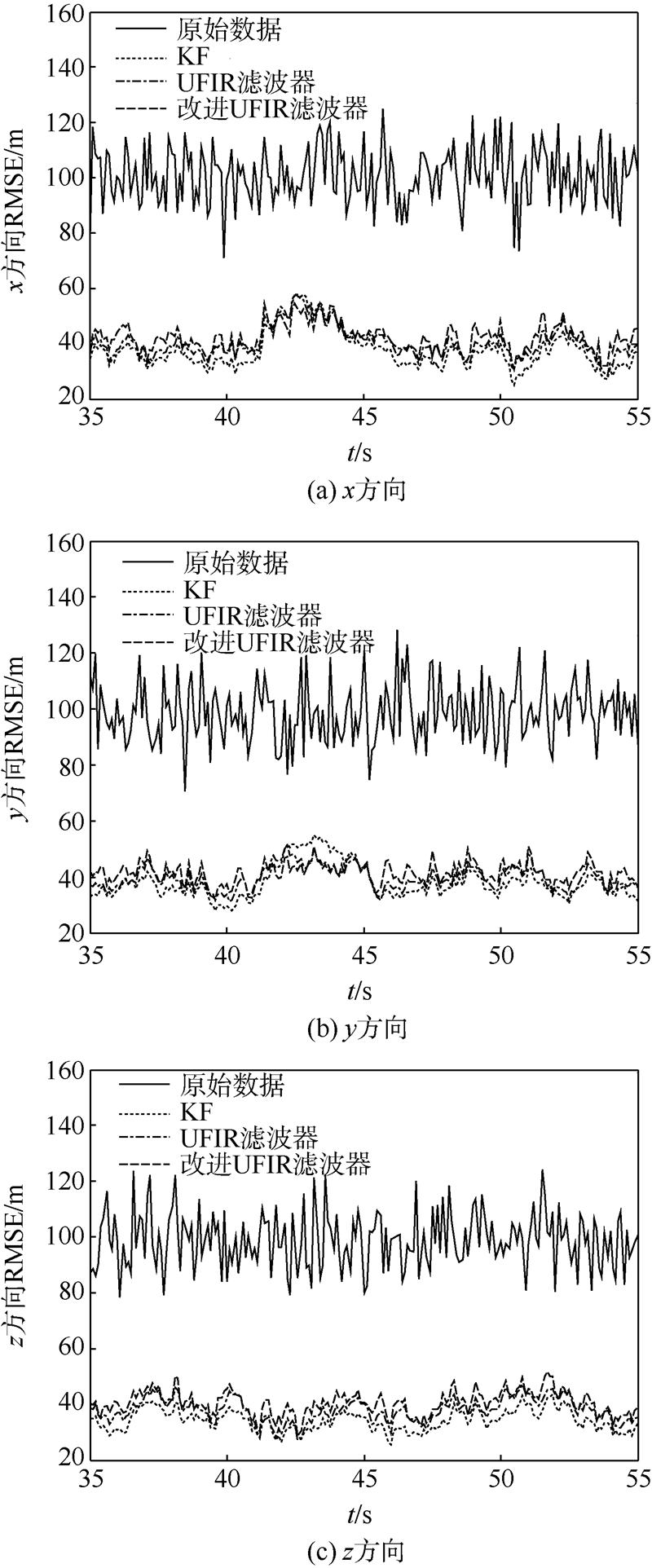| 图 2 噪声特性已知情况下的滤波器性能对比Fig. 2 Filter performances when noise statistics are known |
| 图选项 |
通过仿真可以发现,在噪声统计特性已知的情况下,KF的滤波性能比两种UFIR滤波器都好.而改进UFIR滤波器与现有UFIR滤波器在最优条件下的滤波效果是相似的.这也验证了在已知噪声统计特性的条件下,在LMMSE准则下KF是最优的,也是最佳的选择.由于在真实情况下，并不能准确预知目标的运动情况，此时假定的过程噪声统计特性可能并不准确.为了验证3种滤波器对于这种不准确情况的鲁棒性，将过程噪声协方差调整为16，此时仿真结果如图 3所示.
 |
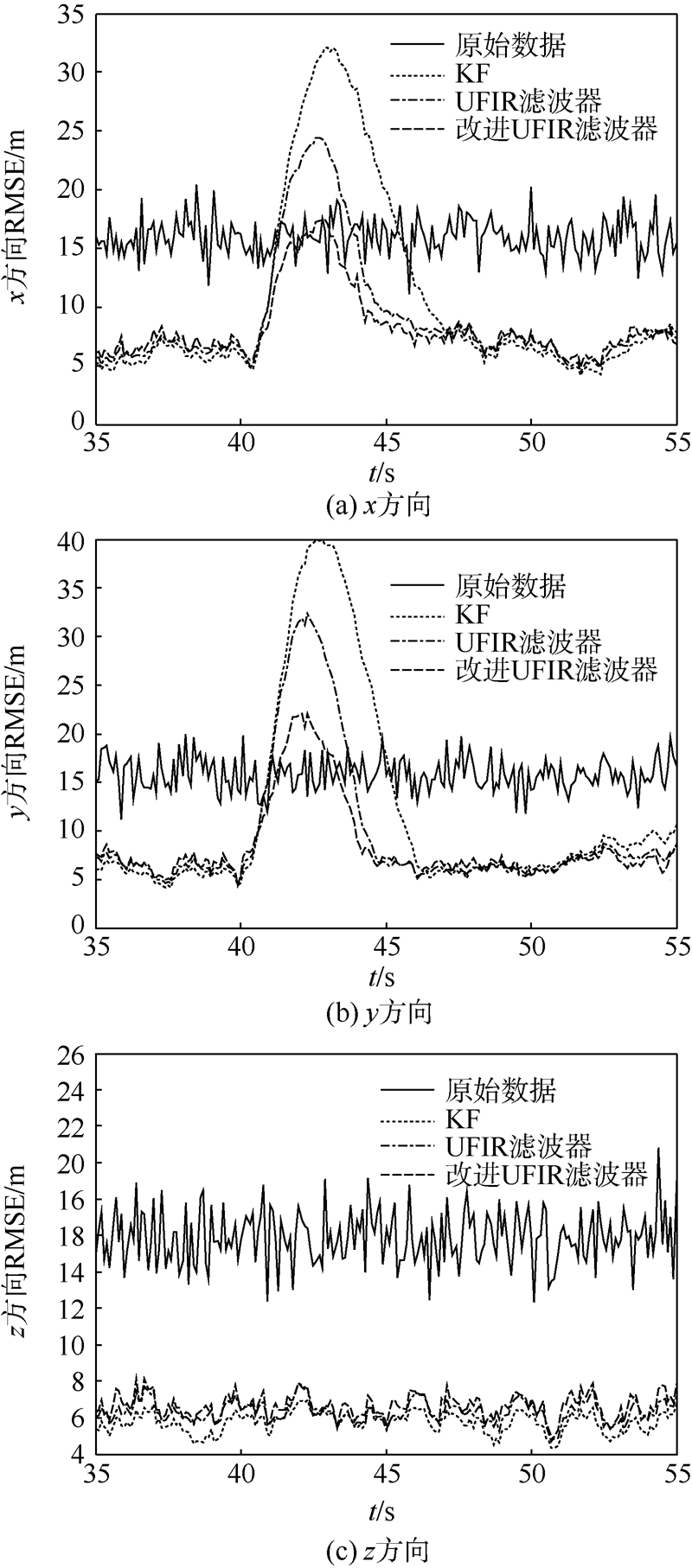| 图 3 噪声特性未知情况下的滤波器性能对比Fig. 3 Filter performances when noise statistics are unknown |
| 图选项 |
从仿真结果可以看出，由于此时假定的过程噪声统计特性并不准确，KF的估计误差显著增大.但UFIR滤波器由于在滤波过程中并不需要过程噪声统计特性的先验信息，对假定过程噪声统计特性不准确的情况表现出了更强的鲁棒性.并且改进UFIR滤波器由于能够利用量测与滤波结果之间的偏差来自适应调整新息增益矩阵，从而更好地适应了目标机动，获得了比现有UFIR滤波器更好的滤波性能.5 结 论本文将UFIR滤波器用于机动目标跟踪中,并针对现有UFIR滤波器的缺点提出了改进算法.仿真结果表明:1) 在已知初始条件和噪声统计分布的理想条件下,KF在LMMSE准则下比UFIR滤波器性能略优.2) 但当噪声发生变化即噪声统计分布未知时,UFIR滤波器相对于KF表现出了更强的鲁棒性.3) 本文提出的改进UFIR滤波器能够自适应调整新息增益矩阵,表现出了相比于现有UFIR滤波器更佳的滤波性能.4) UFIR滤波器的这些优势的代价就是迭代UFIR滤波器的计算量近似为KF的Nopt倍.
参考文献
| [1] | Houles A,Bar-Shalom Y.Multisensor tracking of a maneuvering target in clutter[J].IEEE Transactions on Aerospace and Electronic Systems,1989,25(2):176-188. |
| Click to display the text | |
| [2] | Bar-Shalom Y,Birmiwal K.Variable dimension filter for maneuvering target tracking[J].IEEE Transactions on Aerospace and Electronic Systems,1982,18(5):621-629. |
| Click to display the text | |
| [3] | Magrill D T.Optimal adaptive estimation of sampled stochastic processes[J].IEEE Transactions on Automatic Control,1965,10(4):434-439. |
| Click to display the text | |
| [4] | Nadarajah N,Tharmarasa R,McDonald M,et al.IMM forward filtering and backward smoothing for maneuvering target tracking[J].IEEE Transactions on Aerospace and Electronic Systems,2012,48(3):2673-2678. |
| Click to display the text | |
| [5] | Gibbs B.Advanced Kalman filtering,least-squares and modeling[M].New York:Wiley,2011. |
| Click to display the text | |
| [6] | Shmaliy Y S.An unbiased FIR filter for TIE model of a local clock in applications to GPS-based timekeeping[J].IEEE Transactions on Ultrasonics,Ferroelectrics,and Frequency Control,2006,53(5):862-869. |
| Click to display the text | |
| [7] | Kwon O K,Kwon W H,Lee K S.FIR filters and recursive forms for discrete-time state-space models[J].Automatica,1989,25(5):715-728. |
| Click to display the text | |
| [8] | Kwon W H,Kim P S,Han S H.A receding horizon unbiased FIR filter for discrete-time state space models[J].Automatica,2002,38(3):545-551. |
| Click to display the text | |
| [9] | Kwon W H,Kim P S,Park P.A receding horizon Kalman FIR filter for discrete time-invariant systems[J].IEEE Transactions on Automatic Control,1999,44(9):1787-1791. |
| Click to display the text | |
| [10] | Shmaliy Y S.An iterative Kalman-like algorithm ignoring noise and initial conditions[J].IEEE Transactions on Signal Processing,2011,59(6):2465-2473. |
| Click to display the text | |
| [11] | Ramirez-Echeverria F,Sarr A,Shmaliy Y S.Optimal memory for discrete-time FIR filters in state-space[J].IEEE Transactions on Signal Processing,2014,62(3):557-561. |
| Click to display the text | |
| [12] | Song T L,Speyer J L.A stochastic analysis of a modified gain extended Kalman filter with application to estimation with bearing only measurements[J].IEEE Transactions on Automatic Control,1985,AC-30(10):940-949. |
| Click to display the text | |
| [13] | Shmaliy Y S,Ibarra-Manzano O.Time-variant linear optimal finite impulse response estimator for discrete-time state-space models[J].International Journal of Adaptive Control and Signal Processing,2012,26(2):95-104. |
| Click to display the text | |
| [14] | Shmaliy Y S.Linear optimal FIR estimation of discrete time-invariant state-space models[J].IEEE Transactions on Signal Processing,2010,58(6):3086-3096. |
| Click to display the text | |
| [15] | Shmaliy Y S,Simon D.Iterative unbiased FIR state estimation: a review of algorithms[J].Eurasip Journal on Advances in Signal Processing,2013(1):1-16. |
| Click to display the text | |
| [16] | Simon D,Shmaliy Y S.Unified forms for Kalman and finite impulse response filtering and smoothing[J].Automatica,2013,49(6):1892-1899 |
| Click to display the text |
