所谓油箱惰化就是通过技术手段,使油箱上部空间气层中氧含量低于燃油蒸汽燃烧所需的浓度水平.油箱惰化系统主要由引气及处理、机载空气分离和油箱上部空间氧浓度控制3部分组成,其中,机载空气分离是其核心.而随着膜制备技术的进步,利用压力驱动下不同气体通过中空纤维膜时渗透率的不同来进行空气分离的方式已成为当前机载油箱惰化系统的首选方式.
针对中空纤维膜国内外已开展了大量的研究工作,如Pabby和Sirkar等[1, 2]对中空纤维膜技术以及萃取过程进行了综述分析;Ahmad等[3]对CO2分离膜的温度、压力特性进行了分析;Sohrabi等[4]建立了CO2在中空纤维膜中传输的数学模型并进行了数值模拟;Yoon等[5]对中空纤维膜的压降进行了研究;Katoh,Rezakazemi,Miramini等[6, 7, 8]对中空纤维膜分离过程进行了仿真分析;Shirazian和Atchariyawut等[9, 10]对中空纤维膜接触器的传质过程进行了研究;刘小芳等[11]对机载膜分离性能开展了实验研究;贺高红等[12]对中空纤维膜气体分离器性能建立了数学模型;冯诗愚等[13]对机载中空纤维膜的分离特性进行了分析.但在上述研究中,由于没有充分考虑飞机飞行因素对于膜性能的影响,其研究成果均不能直接指导飞机燃油箱惰化系统设计.
事实上,在实际飞行过程中,由于发动机引气压力、温度与飞行高度的变化,使得机载空气分离装置分离性能时刻发生着改变,即惰化油箱的富氮气体流量、浓度改变,这直接关系到油箱惰化的实际效果.因此,要开展飞机燃油箱惰化系统设计,首先必须掌握压力、温度对膜分离性能的影响,然后依据飞行包线内引气压力、温度、飞行高度变化规律来预测富氮气体流量、浓度的变化,并通过油箱上部空间氧浓度分布仿真计算来掌握实际油箱惰化情况.正是在上述背景条件下,作者开展了本文的研究工作.
本文通过搭建实验平台,对某型机载空气分离装置性能变化规律开展了实验研究,拟合了富氮气体流量与影响因素之间的计算关系式,并对其准确性进行了验证;在此基础上,分析了压力、温度、高度等因素对膜分离性能的影响,并计算获得了在整个飞行包线内富氮气体流量的变化规律.本文研究成果可为实际惰化系统设计奠定基础.
1 实验系统实验系统如图 1所示,它由大气环境模拟舱、机载中空纤维膜分离装置、气源设备及相关的测量、调节与控制仪器仪表组成.采用真空泵控制大气环境舱压力,实现对飞行高度的模拟;采用气源设备来模拟发动机不同的引气状态;采用氧分析仪及压力、温度和流量传感器来测试富氮气体浓度、流量等参数.
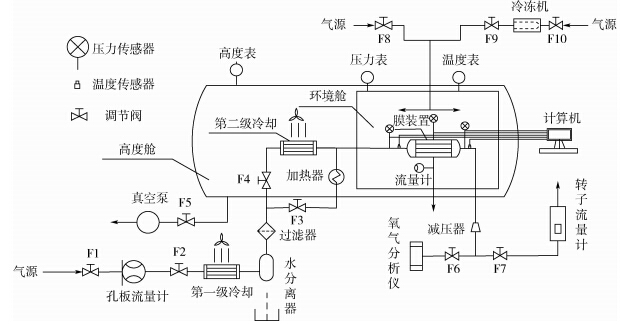 |
| 图 1 机载膜分离装置实验系统结构图Fig. 1 Experiment system structure of onboard membrane separation unit |
| 图选项 |
实验中,输入膜装置的压缩空气系统由压缩机储气罐、调压阀、孔板流量计、第一级冷却器、水分离器、过滤器、第二级冷却器、加热器等部件组成.供气流量由调节阀F1和F2控制,大小由孔板流量计测出.气体经第一级冷却后,由水分离器分离出水,再经过主路过滤器(AFF8B-06D)、油雾分离器(AM350-06D)和微雾分离器(AMD350-06D)三级过滤后进入膜分离装置,由于氧氮渗透速率的差异,氧气比氮气通过膜渗透的快,因此空气被分离成富氮气体和富氧气体.当需要加温或冷却时,分别开启调节阀F3或F4.采用真空泵与调节阀F5控制舱内高度.环境温度则由调节阀F8,F9,F10控制.需要加热时,打开F8,冷却时打开F9和F10.富氮气体流量控制是经减压阀稳压后,通过流量调节阀F7实现的,其输出流量由转子流量计计量,浓度由氧气浓度分析仪测量.
通过温度传感器、压力传感器与计算机的配合工作,可对每次实验中膜入口气体温度、压力,出口富氮气体温度、压力、环境温度及装置中减压阀出口压力进行自动记录.保持工作环境稳定2~3 min后,才记录结果.
在实验中,空气入口压力分别控制为0.3,0.4,0.5,0.6,0.7和0.8 MPa,出口处富氮气体浓度分别控制为98%,95%,91%,88%和85%,进气温度分别控制为50,70,80,100和115℃,高度分别控制为0,5,10,12 km.
2 实验结果及其处理2.1 实验结果实验共获取了120个点的实验数据,其部分实验结果如表 1所示.
表 1 实验结果Table 1 Experimental result
| 实验点 | 富氮浓度/% | 温度/℃ | 压力/MPa | 富氮流量/(kg·h-1) |
| 1 | 98 | 50 | 0.3 | 1.6 |
| 10 | 91 | 80 | 0.3 | 11.5 |
| 20 | 85 | 115 | 0.3 | 54.5 |
| 30 | 91 | 80 | 0.4 | 23.1 |
| 40 | 85 | 115 | 0.4 | 108.7 |
| 50 | 91 | 70 | 0.5 | 31.6 |
| 60 | 85 | 115 | 0.5 | 161.5 |
| 70 | 91 | 70 | 0.6 | 44.8 |
| 80 | 85 | 100 | 0.6 | 180.3 |
| 90 | 91 | 50 | 0.7 | 34.7 |
| 100 | 85 | 100 | 0.7 | 235.7 |
| 110 | 91 | 70 | 0.8 | 73.9 |
| 120 | 85 | 115 | 0.8 | 342.4 |
表选项
2.2 实验结果处理本文采用数学拟合方法对实验结果进行处理.所谓拟合是指已知某函数的若干离散值,通过调整该函数中的待定系数,使得该函数与已知值的相差最小.
数学拟合方法的难度在于函数的具体形式未知,特别是在有多个自变量的研究中,这个问题更为突出.考虑到实验数据较为完善,本文采用了非线性多项式拟合方法,所选择的拟合函数如下所示:

式中:t为引气温度,℃;p为膜入口压力,MPa;x为氮浓度,%;Q为富氮流量,kg/h.
由于Levenberg-Marquardt算法吸收了最速下降法和高斯-牛顿法的优点,成为了最有效的非线性拟合算法之一,因此,本文应用了该算法.
设拟合方程式为
 (t;P),式中t为自变量,P=(p1,p2,…,pn-1,pn)T为参数向量,n为参数个数.在给定m组测量数据(ti,yi),i=1,2,…,m中,根据卡方误差准则[14]:
(t;P),式中t为自变量,P=(p1,p2,…,pn-1,pn)T为参数向量,n为参数个数.在给定m组测量数据(ti,yi),i=1,2,…,m中,根据卡方误差准则[14]: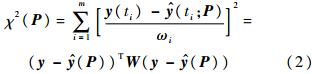
式中,ωi为误差;W为对角阵Wii=1/ω2i.
由Levenberg-Marquardt算法,有

式中,J代表
 /P;I为单位矩阵.
/P;I为单位矩阵.迭代的时候对参数向量P产生一个偏量h使χ2减小.当λ很大的时候,算法主要体现的是最速下降法,其特点是性能稳定和收敛.当接近极小点时,λ随之减小,算法主要体现高斯-牛顿算法,其特点是快速收敛到极小点.
拟合函数式系数如表 2所示.
表 2 拟合系数Table 2 Fitting coefficient
| 系数 | 数值/10-2 | 系数 | 数值/10-2 | 系数 | 数值/10-2 | 系数 | 数值/10-2 |
| a000 | -1.606 81 | a100 | -2.431 2 | a200 | -2.999 52 | a300 | -3.445 84 |
| a001 | -0.992 16 | a101 | -1.405 98 | a201 | -1.892 71 | a301 | -2.187 66 |
| a002 | 1.431 101 | a102 | -0.753 02 | a202 | -1.028 15 | a302 | -1.349 31 |
| a003 | 0.180 376 | a103 | -0.097 36 | a203 | -0.591 | a303 | -0.639 27 |
| a010 | 30.359 86 | a110 | 3.354 724 | a210 | -17.596 8 | a310 | -34.628 8 |
| a011 | 25.906 | a111 | 3.913 147 | a211 | -10.701 8 | a311 | -21.232 4 |
| a012 | 26.232 66 | a112 | 8.890 436 | a212 | -3.249 91 | a312 | -9.457 17 |
| a013 | 26.182 76 | a113 | 13.130 05 | a213 | 4.133 003 | a313 | -1.472 19 |
| a020 | -3.195 19 | a120 | 0.998 759 | a220 | 4.142 389 | a320 | -0.238 8 |
| a021 | 48.978 16 | a121 | -60.711 5 | a221 | -48.343 8 | a321 | 52.260 73 |
| a022 | 84.452 83 | a122 | -52.845 | a222 | -55.925 4 | a322 | 40.209 61 |
| a023 | 26.145 35 | a123 | -60.805 8 | a223 | -38.738 1 | a323 | 63.675 55 |
| a030 | -0.051 3 | a130 | -0.296 96 | a230 | 0.843 017 | a330 | -0.510 92 |
| a031 | 5.061 965 | a131 | -14.470 2 | a231 | 13.624 13 | a331 | -4.135 51 |
| a032 | 1.640 862 | a132 | -9.224 92 | a232 | 13.429 32 | a332 | -6.001 34 |
| a033 | 3.232 503 | a133 | -9.824 08 | a233 | 10.395 54 | a333 | -3.713 73 |
表选项
将表 2中的系数代入式(1)中,可在已知引气温度、压力和富氮浓度的情况下,求出富氮气体流量.
富氮气体流量拟合计算值与实验值的误差分析如图 2所示.
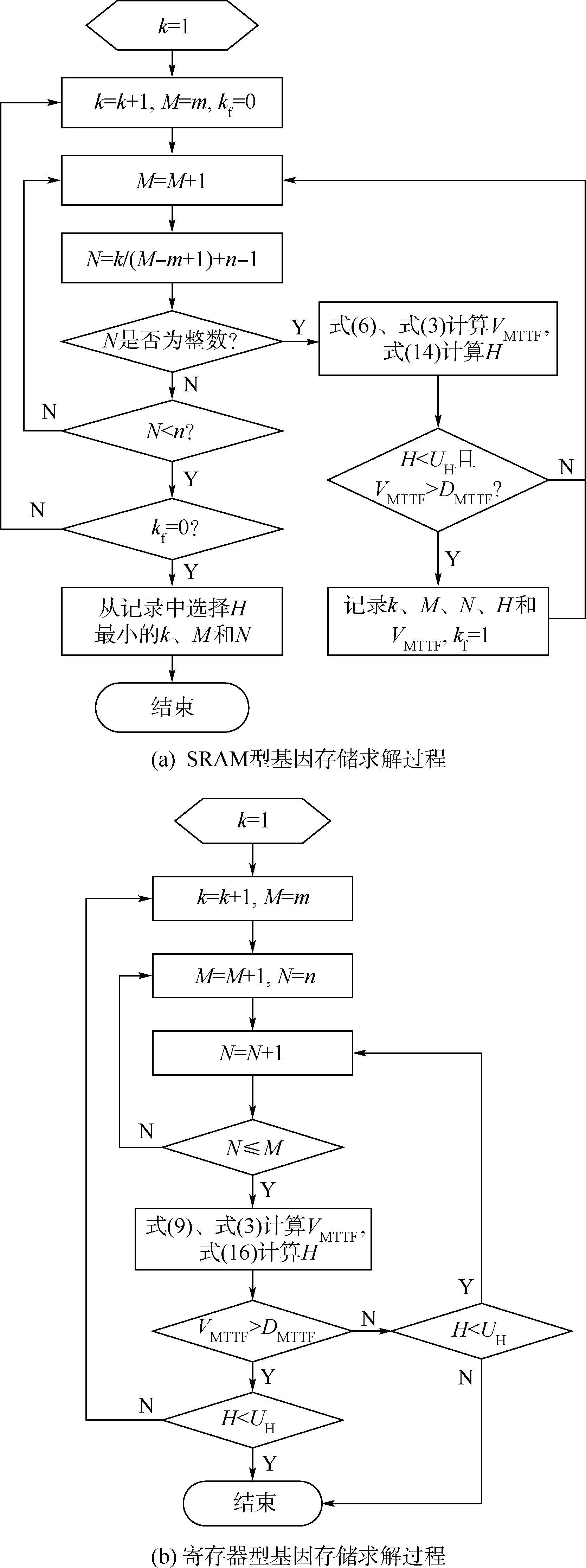 |
| 图 2 富氮气体流量拟合计算值与实验值的误差分析Fig. 2 Rich nitrogen flow error analysis of fitting calculation value and experimental value |
| 图选项 |
由图 2可见,在0~20 kg/h富氮气体流量内,拟合值与实验值偏差较大,尤其在小流量范围,其偏差更大,大约高达10%;随着富氮气体流量的增加,拟合值与实验值偏差缩小,其误差基本在3%的范围内,同时,根据拟合数据计算富氮流量均方根误差(RMSE)为3.2,其平均误差百分比为5.01%,这充分说明了本方程具有较好的准确性.
2.3 高度修正系数由于实验变量多,且实际工作中高度对分离性能的影响较小,为了降低拟合系数求解的难度,提高拟合公式的计算精度,在上述多项式拟合中,并没有考虑高度变化对富氮气体流量的影响,而是直接依据海平面状态下的实验数据开展拟合工作的.
为了充分反映飞行高度变化对富氮气体流量的影响,本文采用了高度修正系数来描述.
高度修正系数通过实验数据拟合得出,其拟合函数式为
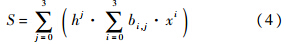
式中,S为高度修正系数;h为高度,km;x为富氮浓度.
其拟合系数如表 3所示.
表 3 高度修正系数拟合数值Table 3 Fitting value of altitude correction coefficient
| 系数 | 数值 | 系数 | 数值 |
| b00 | 4.984 0×100 | b20 | -8.319 9×10-2 |
| b01 | 1.707 5×10-1 | b21 | -8.572 8×10-1 |
| b02 | -1.302 3×100 | b22 | 1.389 0×100 |
| b03 | -1.939 1×10-1 | b23 | 2.647 1×10-1 |
| b10 | -3.732 3×10-1 | b30 | -3.461 7×100 |
| b11 | 2.719 2×10-2 | b31 | 6.604 5×10-1 |
| b12 | -1.730 8×10-1 | b32 | 1.018 6×10-1 |
| b13 | 1.829 2×10-1 | b33 | -2.546 1×10-1 |
表选项
引用高度修正系数后,实际富氮气体流量可采用下式计算.

通过验证计算,高度修正系数误差范围在5%以内,符合计算需要.
3 富氮气体流量影响因素研究3.1 温度对富氮流量的影响引气压力为0.5 MPa,高度为0 km,富氮浓度分别为98%,95%,91%,88%和85%时,引气温度对富氮流量的影响如图 3所示.
图 3可见,富氮流量随着引气温度的增加而增加.观察富氮浓度曲线变化可以看出,随着富氮浓度的降低,引气温度对富氮流量的影响加大.
 |
| 图 3 温度对富氮流量的影响Fig. 3 Effect of temperature on rich nitrogen flow |
| 图选项 |
3.2 浓度对富氮流量的影响温度为80℃,高度为0 km,引气压力分别为0.3,0.4,0.5,0.6,0.7和0.8 MPa时,富氮气体浓度对富氮流量的影响如图 4所示.
图 4可见:富氮流量随着富氮浓度的增加而减少;当在引气压力较大的时候,富氮流量随富氮浓度的变化更为明显.
 |
| 图 4 富氮浓度对富氮流量的影响Fig. 4 Effect of rich nitrogen concentration on rich nitrogen flow |
| 图选项 |
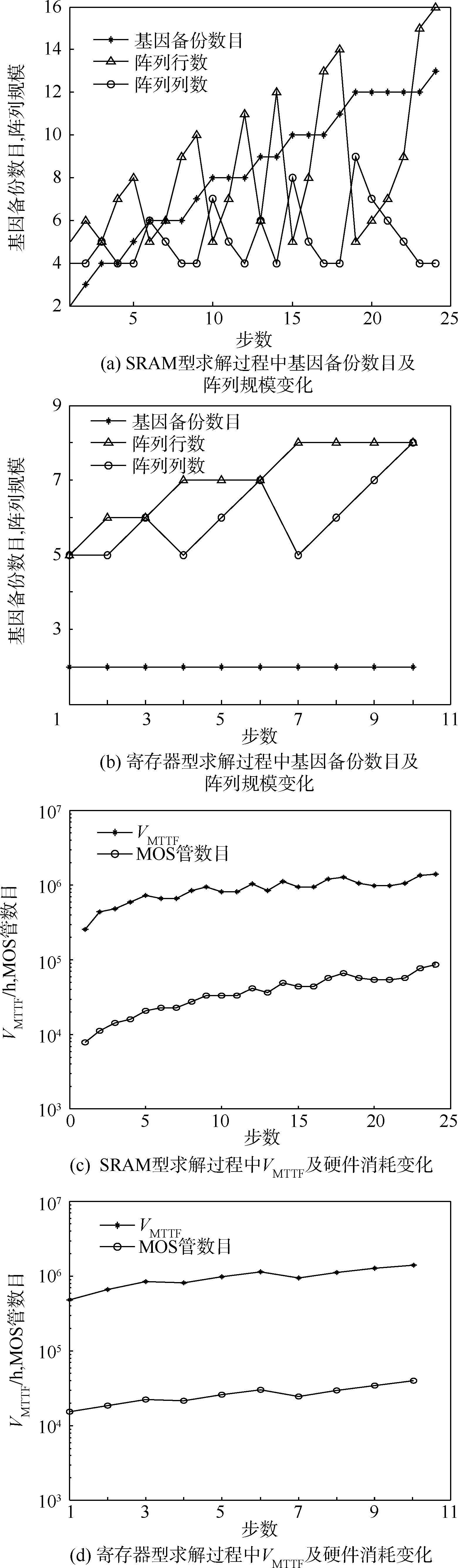
3.3 引气压力对富氮流量的影响富氮浓度为91%,高度为0 km,温度分别为50,70,80,90,100,115℃时,引气压力对膜分离性能的影响如图 5所示.
 |
| 图 5 压力对富氮流量的影响Fig. 5 Effect of pressure on rich nitrogen flow |
| 图选项 |
由图 5可以看出,富氮流量随着压力的增加而增加;温度越高,压力对富氮流量变化的影响越明显.
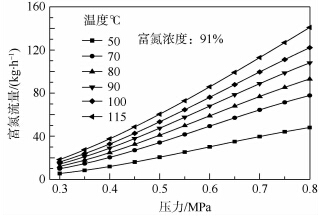
3.4 飞行高度对富氮流量的影响引气压力控制为0.7 MPa,引气温度控制为115℃,富氮气体浓度分别控制为98%,95%,91%,88%和85%时,高度对富氮流量的影响如图 6所示.由图中可以看出:富氮流量随着高度的增加而增加;但富氮浓度越高,高度对富氮流量的影响越小.
 |
| 图 6 高度对富氮流量的影响Fig. 6 Effect of altitude on rich nitrogen flow |
| 图选项 |
4 飞行包线下富氮气体流量研究本文以文献[15]中所提供的飞行包线为例,来研究在全飞行包线下富氮气体流量的变化规律.
文献[15]中所提供的引气压力、温度、富氮气体浓度及飞行高度与时间的变化关系见图 7.
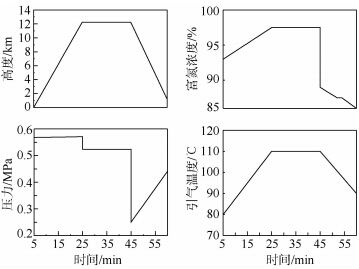 |
| 图 7 飞行包线下高度、压力、温度、浓度变化规律[15]Fig. 7 Variation law of altitude,pressure,temperature and concentration under flight envelope[15] |
| 图选项 |
根据上文所得的拟合公式,嵌入图 7所示参数,建立图 8所示的仿真模型开展计算,其计算结果与文献[15]中所给出的参考结果的比较如图 9所示.
 |
| 图 8 全飞行包线下仿真计算模型Fig. 8 Simulation calculation model of the flight envelope |
| 图选项 |
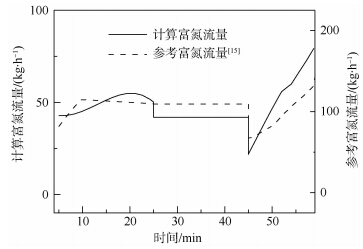 |
| 图 9 计算结果与参考结果对比Fig. 9 Result of calculation and reference |
| 图选项 |
由图 9中可以看出,本文的计算结果与参考结果总体的变化趋势十分吻合;而数值上的差距是由于本文所采用的分离膜材料特性与文献中的材料特性之间的差异造成的.
5 结 论1) 本文所获分离性能计算公式具有较好的准确性,可真实反映膜分离性能的变化规律.
2) 本文建立的分离性能模型可用于实际飞行包线下富氮气体流量的计算,可为惰化系统设计提供参考.
3) 高度、压力、温度与流量成正向关系;在压力、温度一定时,富氮浓度与流量成反向关系,当浓度增加时,其流量下降;且当富氮浓度越低、高度(温度、压力)越高时,对流量的影响越明显.
参考文献
| [1] | Pabby A K,Sastre A M.State-of-the-art review on hollow fibre contactor technology and membrane-based extraction processes[J].Journal of Membrane Science,2013,430:263-303. |
| Click to display the text | |
| [2] | Sirkar K K.Membranes,phase interfaces,and separations:novel techniques and membranes-an overview[J].Industrial and Engineering Chemistry Research,2008,47(15):5250-5266. |
| Click to display the text | |
| [3] | Ahmad F,Lau K K,Shariff A M,et al.Temperature and pressure dependence of membrane permeance and its effect on process economics of hollow fiber gas separation system[J].Journal of Membrane Science,2013,430:44-55. |
| Click to display the text | |
| [4] | Sohrabi M R,Marjani A,Moradi S,et al.Mathematical modeling and numerical simulation of CO2 transport through hollow-fiber membranes[J].Applied Mathematical Modelling,2011,35(1):174-188. |
| Click to display the text | |
| [5] | Yoon S H,Lee S H,Yeom I T.Experimental verification of pressure drop models in hollow fiber membrane[J].Journal of Membrane Science,2008,310(1-2):7-12. |
| Click to display the text | |
| [6] | Katoh T,Tokumura M,Yoshikawa H,et al.Dynamic simulation of multicomponent gas separation by hollow-fiber membrane module:nonideal mixing flows in permeate and residue sides using the tanks-in-series model[J].Separation and Purification Technology,2011,76:362-372. |
| Click to display the text | |
| [7] | Rezakazemi M,Niazi Z,Mirfendereski M,et al.CFD simulation of natural gas sweetening in a gas-liquid hollow-fiber membrane contactor[J].Chemical Engineering Journal,2011,168(3):1217-1226. |
| Click to display the text | |
| [8] | Miramini S A,Razavi S M R,Ghadiri M,et al.CFD simulation of acetone separation from an aqueous solution using supercritical fluid in a hollow-fiber membrane contactor[J].Journal of Membrane Science,2013,72:130-136. |
| Click to display the text | |
| [9] | Shirazian S,Moghadassi A,Moradi S.Numerical simulation of mass transfer in gas-liquid hollow fiber membrane contactors for laminar flow conditions[J].Simulation Modelling Practice andTheory,2009,17:708-718. |
| Click to display the text | |
| [10] | Atchariyawut S,Feng C,Wang R,et al.Effect of membrane structure on mass-transfer in the membrane gas-liquid contacting process using microporous PVDF hollow fibers[J].Journal of Membrane Science,2006,285:272-281. |
| Click to display the text | |
| [11] | 刘小芳,刘卫华,钱国诚,等.机载中空纤维膜富氮性能实验[J].航空动力学报,2012(5):976-980.Liu X F,Liu W H,Qian G C,et al.Experimentation on nitrogen-enriched characteristics of on-board hollow fibre membrane[J].Journal of Aerospace Power,2012(5):976-980(in Chinese). |
| Cited By in Cnki | Click to display the text | |
| [12] | 贺高红,徐仁贤,朱葆琳.中空纤维膜气体分离器的数学模型[J].化工学报,1994,45(2):162-167.He G H,Xun R X,Zhu B L.Mathematical model for hollow fiber membrane gas separator[J].Journal of Chemical Industry and Engineering,1994,45(2):162-167(in Chinese). |
| Cited By in Cnki (17) | |
| [13] | 冯诗愚,卢吉,刘卫华,等.机载制氮系统中空纤维膜分离特性[J].航空动力学报,2012,27(6):1332-1339.Feng S Y,Lu J,Liu W H,et al.Separation performance of hollow fiber membrane for on-board inerting gas generating system[J].Journal of Aerospace Power,2012,27(6):1332-1339(in Chinese). |
| Cited By in Cnki (1) | Click to display the text | |
| [14] | Gavin H P.The Levenberg-Marquardt method for nonlinear least squares curve-fitting problems[EB/OL].North Carolina:Duke University[2013-11-09].http://people.duke.edu/-hpgavin/ce281/lm.pdf. |
| Click to display the text | |
| [15] | Parker Aerospace.Fuel and inertingsystem COMAC C919 program,1ETP2090024T[R].Irvine:Parker Hannifin Corporation,2009:104-106 |
