大脑中神经元具有复杂的空间树突结构,并通过整合来自树突各处的时空输入信号实现信息处理。理解神经元树突信号整合是理解神经信息处理的基础。由于经典的神经元电缆模型不能解析处理具有复杂空间结构、包含非线性离子通道以及状态依赖的突触电流输入的真实生物学场景,因此如何定量刻画具有空间结构的神经元树突计算法则及其动力学性质是神经科学中的一个重要难题。
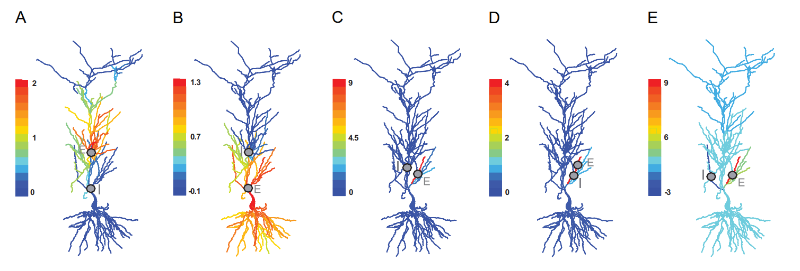
本工作通过建立具有空间树突结构的神经元膜电位动力学的偏微分方程组模型,并利用扰动理论推导得到了方程的解析解,借此可以准确描述神经元接收状态依赖的突触电流输入时膜电位的变化。并进一步推导得到了具有树突分枝结构的神经元整合时空突触输入信号所满足的双线性整合法则,该法则在符合真实生物学场景的神经元仿真模型中得到了验证。在此基础上,通过降维分析将原高维偏微分方程组动力学模型降维至仅描述细胞体处膜电位变化的一维常微分方程约化动力学模型。该约化模型可以有效刻画原偏微分方程组描述的神经元模型在胞体处的信息整合以及树突计算功能,从而为设计包含树突计算功能的神经元网络模拟快速算法和人工神经网络模型奠定了基础。本工作在课题组前期研究树突计算相关的多个工作的基础上,构建了系统而统一的数学理论和计算框架,对未来研究神经元树突计算和空间神经元动力学提供了新的数学工具和研究角度。
本工作由上海交通大学的李松挺、周栋焯、以及纽约大学的David McLaughlin教授合作完成,第一作者为李松挺教授,通讯作者为李松挺、周栋焯和David McLaughlin教授。本工作得到了国家自然科学基金委、科技部、上海市科委和教委等基金支持。
