近日，上海交通大学自然科学研究院/数学科学学院金石教授、李磊教授以及杜克大学数学系刘建国教授的论文《Random Batch Methods (RBM) for interacting particle systems》入选杂志《Journal of Computational Physics》新设立的Seminar Series 演讲。该篇论文被选为首批报告的论文之一， 将由金石教授于2021年11月1日进行宣讲。

《Journal of Computational Physics》是科学计算和应用数学最重要的杂志之一， 每年发表600余篇论文。为彰显该杂志的影响力，杂志从今年秋天起设立Journal of Computational Physics Seminar Series， 每月一次，由编委遴选过去五年内在该杂志发表的极具创新性或近年来产生过重要影响的论文。

Random Batch Methods (RBM) 是关于经典N-体粒子问题的一个新的随机算法。 描述这类问题的基本数学方程是牛顿第二定律，是物理和力学最基本的方程之一。 多体粒子问题在分子动力学， 天体物理， 材料科学， 生物和社会科学中的群体问题， 以及机器学习和数据科学中的统计采样等领域具有广泛的应用。 这类问题的难点是O(N²)的计算量， 由于N 常常达到百万至亿以上的量级， 这种计算量是当今计算机无法承受的。 针对此类问题，人们通常致力于构造O(N log N) 或者 O(N) 的计算方法，当选为上世纪十大算法的快速傅里叶变换(Fast Fourier Transform-FFT)和快速多极子方法(Fast Multiple Method—FMM)便是此类计算方法。

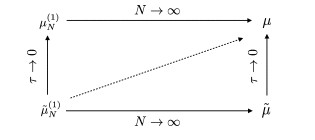
RBM巧妙和新颖地将机器学习中常用的随机梯度下降法中的随机分批思想用于多体粒子系统， 想法在于在每个计算步将N个粒子随机分成许多小组， 每组只有少量的粒子， 而粒子之间的相互作用只需在小组内进行即可，这样每步的计算量就降到了O(N)。 同时他们证明了该方法在平均场尺度下其均方误差不依赖于N, 这样就保证了虽然计算量降到了O(N)，计算时间却和N无关。
RBM及其推广方法目前已在分子动力学， 统计采样，量子多体问题， 生物和社会系统的群体共识模型等方面获得广泛的应用。 数学科学学院的徐振礼教授和自然科学研究院的洪亮教授团队也加入了这类方法的研究，并探索在生物医药领域的应用。 该研究群体发展的Random Batch Ewald 方法比目前广泛应用于分子动力学模拟方法的计算速度提高了一个数量级， 并且在万核CPU的平行效率达到近100%。
金石团队的工作得到了国家自然科学基金委和上海市科委的资助。