
 , 李志刚, 吴缀
, 李志刚, 吴缀 东北大学秦皇岛分校 控制工程学院, 河北 秦皇岛 066000
收稿日期:2021-03-19
基金项目:国家自然科学基金青年基金资助项目(61601104);中央高校基本科研业务费专项资金资助项目(N2023021)。
作者简介:单鹏(1985-),男,河南平舆人,东北大学讲师。
摘要:目前Whittaker Smoother(WS)算法应用广泛, 该算法的核心在于用整数阶微分来表示粗糙度.但整数阶微分表示过于单一, 不够灵活, 不能真实反映出信号的粗糙度.相反分数阶微分表示丰富, 可以更好地描述真实信号的粗糙度.因此, 本文用分数阶微分来改进WS算法, 使它更加灵活有效.采用Riemann-Liouvile(RL)和Grumwald-Letnikov(GL)两种不同的分数阶微分计算方法来实现分数阶WS算法.此外, 通过数学推导, 实现分数阶WS算法的自动选参.含有尖锐峰的核磁共振谱实验结果表明: 分数阶WS算法可以提取更多的真实信息; Marzipan红外光谱实验结果表明: 与原有整数阶WS算法相比, 光谱定量分析的精度更高.
关键词:分数阶微分光谱预处理光滑去噪定量分析偏最小二乘
Fractional Differential Whittaker Smoother
SHAN Peng, HE Nian

 , LI Zhi-gang, WU Zhui
, LI Zhi-gang, WU Zhui School of Control Engineering, Northeastern University at Qinhuangdao, Qinhuangdao 066000, China
Corresponding author: HE Nian, E-mail: HeNian_HN@163.com.
Abstract: At present, the Whittaker Smoother(WS)algorithm is widely used. The core of the algorithm lies in the use of integer-order differentiation to express roughness. However, the integer-order differential representation is single and not flexible enough to truly reflect the roughness of the signal. On the contrary, the fractional differential expression is flexible and can better describe the roughness of the real signal. Therefore, the fractional differentiation is used to improve the WS algorithm and make it more flexible and effective. As two fractional differential calculation methods, Riemann-Liouville(RL)and Grümwald-Letnikov(GL)are adopted to implement the fractional WS algorithm.Furthermore, the automatic parameter selection of the fractional WS algorithm is realized by mathematical derivation. The experimental results of the nuclear magnetic resonance spectrum with sharp peaks show that the fractional-order WS algorithm can extract more real information; additionally, the experimental results of Marzipan infrared spectra show that the precision of spectral quantitative analysis is higher compared with the original integer-order WS algorithm.
Key words: fractional differentionspectral preprocessingsmoothing and denoisingquantitative analysispartial least squares
现代光谱分析技术是一种通过分析物质的光谱来实现对物质类别及化学成分鉴定的方法, 是一项结合了光谱检测、数据处理、模式识别和计算机等多种理论和方法的综合性分析技术, 被广泛运用于生产生活中[1-3].因受到传感器、背景噪声、电路噪声以及随机误差等因素的影响, 噪声是光谱信号探测时无法避免的现象.光滑去噪成为光谱分析中一个重要的预处理步骤, 能够提高后续光谱分析算法的准确性和可靠性.光谱去噪算法得到了人们的广泛重视, 产生了多种从不同角度实现光滑去噪的算法, 从严格意义上可分成几类.
基于噪声与光谱信号的统计特性差异, 可采用平滑滤波来消除或减少噪声, 例如均值滤波、中值滤波、Kalman滤波、移动多项式平滑滤波等; 基于噪声与光谱信号的频率特征差异, 可采用傅里叶变换、小波变换[4]和经验模态分解[5](empirical mode decomposition, EMD)等; 基于噪声与信号波形之间的差异, 可采用形态滤波等.采用平滑滤波的算法需要人为设定一些参数(如移动窗口的宽度, 拟合阶次), 参数直接影响着算法的性能.具有代表性的算法有Savitzky-Golay(SG)多项式最小二乘法[6], SG对于一些较大的数据, 计算量变大, 不能快速计算出平滑序列; 需要人为设定一些参数, 且不能自动选择; 使用宽度固定的平滑窗口, 当平滑窗口宽度越大, 平滑效果越好, 但是光谱失真会越严重, 即会导致峰畸变或者丢失.
相较于SG算法, Whittaker Smoother(WS)算法[7]计算速度快、实现简单、可以通过快速计算留一交叉验证实现自动选参.WS算法采用整数阶微分(2或3阶)对真实信号的粗糙度进行约束, 并通过调节正则化参数λ来平衡粗糙度和保真度两个冲突的目标, 最终找到一个适当的平滑序列.用整数阶微分表示粗糙度简单有效, 但是这种表示是片面的, 所包含的信息量极为有限, 不能很好地描述问题.即整数阶微分表示不依赖于历史数据, 缺少全局相关性, 对于一些复杂连续过程整数阶往往不能很好地对其进行准确描述.
近些年来, 分数阶微分研究成为热点, 被广泛地应用于各个领域[8-12].在光谱分析领域, Toman等[13]提出用半阶导数对谱峰进行分辨; 卢小泉等[14]采用分数阶导数处理噪声信号; Kharintsev等[15]提出一种利用分数阶导数来提取光谱参数的方法; Mocak等[16]利用分数阶微分改善信号的分辨率; 李远禄等[17]提出一种基于分数阶微分的重叠峰分辨的方法; Li等[18]提出用分数阶导数结合Haar小波来分辨重叠的洛伦兹峰; 徐继刚等[19]利用分数阶导数处理油气红外光谱数据用来提高多元校正模型分析精度; 张东等[20]和田安红等[21]将分数阶微分应用在盐渍土高光谱数据预处理中, 表明分数阶微分对干旱荒漠区土壤光谱数据进行潜在信息挖掘是有效的; 本文通过分数阶微分来增强对真实光谱信号的粗糙度表示, 进一步提高平滑效果.本文将RL和GL分数阶微分定义引入WS算法中, 解决了在WS算法实际应用中存在的相关问题.实验采用偏最小二乘法对Marzipan在多种不同仪器下的光谱进行定量分析, 预测糖分和水分.实验结果表明分数阶WS算法比整数阶更加灵活有效, 光谱定量分析精度更高.
1 算法原理1.1 Whittaker Smoother算法原理WS算法: 对于一列长度为m, 等间距的噪声序列为y, 通过WS得到平滑序列为z.对于这两个序列, 有以下要求: ①对原始数据的保真度.通常用函数 s=∑i(yi-zi)2表示.②序列z的粗糙度.这里用z的一阶微分来表示,Δzi=zi-zi-1, 对其进行平方求和, 表示z的粗糙度: R=∑i(Δzi)2.然后, 平衡两个相互冲突的目标, 这两个目标的平衡组合记为Q=S+λR, λ是一个用户选择的数.惩罚最小二乘的思想是找出使Q最小的一个z的序列.记为
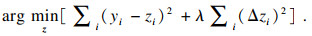 | (1) |
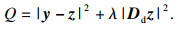 | (2) |
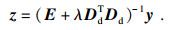 | (3) |
交叉验证: 令Sλ=(E+ λ D dT Dd) -1,
则z=(E+λD dT Dd) -1 y=Sλy.
其中,Sλ满足Sλ I=I, I为单位向量.
定义
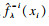
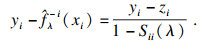 | (4) |
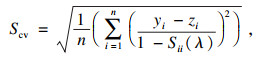 | (5) |
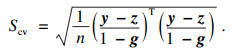 | (6) |
1.2 分数阶微分定义目前常用的主要有三种分数阶微分定义: Riemann-Liouvile, Grumwald-Letnikov, Caputo.本文选用前两种定义, 同样为避免大量繁杂的代数运算, 选择矩阵形式表示分数阶微分.
1.2.1 Riemann-Liouvile定义Kilicman等[23]给出Riemann-Liouvile微分运算矩阵:
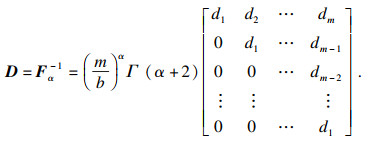 | (7) |
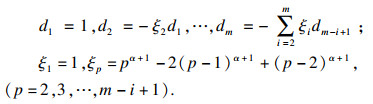 |
1.2.2 Grumwald-Letnikov定义Grumwald-Letnikov分数阶微分定义为
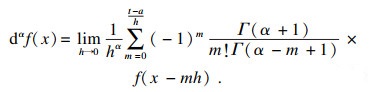 | (8) |
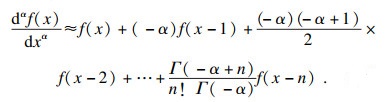 | (9) |
1.3 Fractional Differential Whittaker Smoother(FDWS)1.3.1 算法原理序列z的粗糙度R用分数阶微分来代替, 根据上文给出的分数阶微分矩阵可以写出各点的微分r=D α z,粗糙度为各点微分的平方和.目标函数Q=| y-z|2+ λ| Dα z|2, 序列z的表达式为
 |
1.3.2 交叉验证在引入分数阶微分后, 不能进行交叉验证.因单独的分数阶微分矩阵如DαRL, DαGL所得平滑矩阵Sλα不满足Sλα I=I.对分数阶微分矩阵作以下限制: 对于高阶微分矩阵, 只采用先整数阶微分再分数阶微分矩阵,记为D*=DαDd, 最后的平滑矩阵Sλ*基本满足Sλ* I=I条件限制, 存在极小的误差, 可以忽略.但是这种限制有一个缺陷, 小于一阶的运算矩阵没有包含进去.同样提出一种改进策略,对于小于1阶的微分运算矩阵做出限制: 先用整数一阶微分矩阵, 再用分数阶积分矩阵.所以最后的平滑矩阵基本满足Sλ I=I条件限制.
在一定的区间内, 通过交叉验证误差(选择相应的参数: 正则化系数λ、微分阶次α)可以选出一条较为理想的光滑信号, 而且在一定程度上还可以进行人工调参, 用户可根据需求选择.
2 实验2.1 实验条件实验在Windows 10操作系统下实现; 主要配置: Core I5 CPU主频2.50GHz, 8 GB RAM; 编程在Matlab, 2019a版下实现.
2.2 实验数据1) NMR数据: 该数据集是斯坦福大学开发的小波工具包(Wavelab toolbox)里所采用的经典数据集(见http://statweb.stanford.edu/~wavelab/),Eilers[7]曾对其进行光滑处理, 验证WS算法有效性.本文验证对尖锐峰信号的提取是否有效.
2) Marzipan数据集: 该数据集由7种光谱仪测量的32个Marzipan样品的近红外(NIR)或红外(IR)光谱组成, 用于水分和糖分浓度的预测(见http://www.models.life.ku.dk/Marzipan).本文选用5种光谱仪器的光谱数据进行光滑处理, 验证分数阶WS算法对后续光谱分析精度的影响.
2.3 FDWS_RL, FDWS_GL对比实验随着数据的增加, Dα的结构变得庞大, 对矩阵的存储以及计算造成了很大的负担.实际应用中, 以损失有限精度为代价, 提高计算速度是很有必要的.通过实验发现, 将Dα固定计算宽度, 构造成和Dα相似的结构, 计算速度变快, 同时光滑效果良好.实验发现DαRL适用于0-1阶, DαGL适用于任意阶.DαRL可通过D*=DαDd扩展至任意阶, DαGL同样可以用该方法表示任意阶.在计算整数n阶微分时, 会将前面n个点的微分省略掉, 分数阶固定计算宽度时同样存在该问题.当计算宽度过大时, 粗糙度将丢失过多开始部分的信息.例如分数阶计算宽度固定为40时, 前39个点没有微分.这导致在对信号进行光滑时, 前面39个点与原信号一致.若将这部分微分表示出来, 该部分仍有光滑作用, 用户可以根据需求去调整微分运算矩阵的结构.如图 1所示, Smoother 1为省略开始部分点的微分, Smoother 2(为方便观察, 向下平移了10个单位)为未省略开始部分点的微分, 均为2.1阶RL微分(整数2阶、分数0.1阶组合表示), λ=10, GL实验结果与之相似.
图 1(Fig. 1)
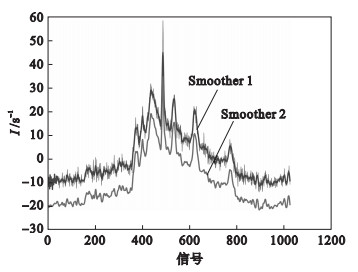 | 图 1 核磁共振谱的RL平滑Fig.1 RL smoothing of an NMR spectrum |
对光谱数据进行光滑处理的目的在于去除噪声的同时能够尽可能多地保留真实信息.整数阶WS算法在处理一些含有尖窄峰的信号时(如NMR光谱), 峰值信号丢失过多(见图 2放大图).与之相反, 分数阶在保证同样去噪效果下, 可以通过调节阶次, 来实现对真实尖峰信息的保留.通过图 2观察得到, 在一定的阶次范围内, 峰值信号的保留与微分矩阵的阶次成正比, 阶次越高, 保留的有用信息越多.此外, RL, GL两种计算方式实验结果差别不大.最后固定正则化系数(λ=10), 分别计算各阶次交叉验证均方根误差, 结果如表 1所示.观察发现, 均方根误差与阶次大致呈反比, 实验结果再次表明, 在一定范围内, 随着阶次越高, 保留的真实信息越多.
图 2(Fig. 2)
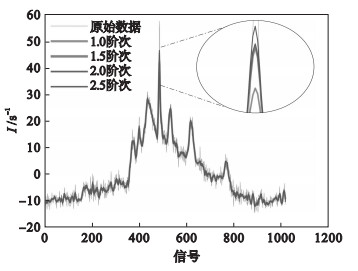 | 图 2 核磁共振谱的不同阶次的平滑Fig.2 Different order smoothing of an NMR spectrum |
表 1(Table 1)
| 表 1 交叉验证均方根误差 Table 1 Cross-validation root mean square error |
数据预处理主要是为了后续的光谱定量分析服务, 为了进一步验证分数阶微分对后续光谱定量分析精度的影响, 本文对Marzipan数据集进行实验.根据KS[24]算法将样本按3∶ 1比例划分, 24个样本作为训练集, 8个样本作为测试集, 采用偏最小二乘回归方法(PLS)[25]分别建立原始光谱、原始光谱+FDWS_RL(含整数阶)处理、原始光谱+FDWS_GL处理后的PLS模型.PLS采用5折交叉验证, 从1~15中选出最佳潜变量个数.测试集样本的均方根预测误差结果(见表 2, 表 3)表明: 5种仪器的光谱在光滑预处理后预测精度都有所提高, 其中Bomem, IA260仪器的光谱, 经过FDWS_RL光滑预处理后对糖分的预测精度显著提高, 两种光谱均方根预测误差分别由1.475, 3.579降到0.926, 0.488;Nit仪器下光谱对水分的均方根预测误差由0.423降到0.278.FDWS_GL实验结果与之相似.可以发现预测均方根误差最小值所对应的阶次均为分数阶, 反映出分数阶WS算法比整数阶更具有应用价值.从理论上讲, 分数阶WS阶次连续可调, 同时涵盖了整数阶, 因此光滑效果永远不会低于整数阶WS算法, 最差保持原有整数阶WS算法的光滑效果.实际实验结果同样表明, 用分数阶微分作光滑处理时, 能够有效地提取有用信号, 相较于整数阶WS算法可以进一步提高后期光谱分析算法的准确性.
表 2(Table 2)
| 表 2 PLS预测水分、糖分均方根误差(RL) Table 2 PLS predicts RMSE of moisture and sugar(RL) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
表 3(Table 3)
| 表 3 PLS预测水分、糖分均方根误差(GL) Table 3 PLS predicts RMSE of moisture and sugar(GL) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
3 结论1) 本文算法采用分数阶微分表示光谱的粗糙度, 使算法更加灵活, 表示更加丰富.
2) 分数阶WS算法比整数阶WS算法能保留更多的真实信息.在核磁共振谱的实验中得到证明.
3) 分数阶WS算法可以进一步提高后续光谱定量分析的精度, 同时表明对原始光谱数据进行光滑处理可以增强有效信号的相对强度, 提高光谱分析算法的准确性.在Marzipan红外光谱实验中得到证明.
参考文献
| [1] | Wilde A S, Hanghey S A, Galvin-king P, et al. The feasibility of applying NIR and FT-IR fingerprinting to detect adulteration in black pepper[J]. Food Control, 2019, 100: 1-7. DOI:10.1016/j.foodcont.2018.12.039 |
| [2] | Viderman D, Abdildin Y G. Near-infrared spectroscopy in neurocritical care: a review of recent updates[J]. World Neurosurgery, 2021, 151(5): 23-28. |
| [3] | Fan S, Zhong Q, Fauhl-Hassek C, et al. Classification of Chinese wine varieties using 1H NMR spectroscopy combined with multivariate statistical analysis[J]. Food Control, 2017, 88: 113-122. |
| [4] | Chen T H, Zhao S, Shao S Q, et al. Non-invasive diagnosis methods of coronary disease based on wavelet denoising and sound analyzing[J]. Saudi Journal of Biological Sciences, 2017, 24(3): 526-536. DOI:10.1016/j.sjbs.2017.01.023 |
| [5] | 赵肖宇, 方一鸣, 王志刚, 等. EEMD自适应去噪在拉曼光谱中的应用[J]. 光谱学与光谱分析, 2013, 33(12): 3255-3258. (Zhao Xiao-yu, Fang Yi-ming, Wang Zhi-gang, et al. Application of EEMD adaptive denoising in Raman spectroscopy[J]. Spectroscopy and Spectral Analysis, 2013, 33(12): 3255-3258. DOI:10.3964/j.issn.1000-0593(2013)12-3255-04) |
| [6] | Savitzky A, Golay M J E. Smoothing and differentiation of data by simplified least squares procedures[J]. Analytical Chemistry, 1964, 36(8): 1627-1639. DOI:10.1021/ac60214a047 |
| [7] | Eilers P H. A perfect smoother[J]. Analytical Chemistry, 2003, 75: 3631-3636. DOI:10.1021/ac034173t |
| [8] | 谢天婷, 张路, 王飞, 等. 双频驱动下分数阶过阻尼马达在空间对称势中的定向输运[J]. 物理学报, 2014, 63(23): 105-113. (Xie Tian-ting, Zhang Lu, Wang Fei, et al. The directional transport of a fractional overdamped motor in a space symmetric potential under dual-frequency drive[J]. Acta Physica Science, 2014, 63(23): 105-113.) |
| [9] | Oldham K B. Fractional differential equations in electrochemistry[J]. Advances in Engineering Software, 2010, 41(1): 9-12. DOI:10.1016/j.advengsoft.2008.12.012 |
| [10] | Smith A Z, Kartci A, Bran c ˇ ík L. Fractional-order lossy transmission line with skin effect using NILT method[C]//2017 40th International Conference on TSP. Barcelona: IEEE, 2017: 730-734. |
| [11] | Wu S L, Zhou T. Parareal algorithms with local time-integrators for time fractional differential equations[J]. Journal of Computational Physics, 2018(358): 135-149. |
| [12] | Allagui A, Freeborn T J, Elwakil A S, et al. Review of fractional-order electrical characterization of supercapacitors[J]. Journal of Power Sources, 2018, 400(1): 457-467. |
| [13] | Toman J, Brown S D. Peak resolution by semiderivative voltammetry[J]. Analytical Chemistry, 1981, 53(9): 1497-1504. DOI:10.1021/ac00232a046 |
| [14] | 卢小泉, 刘宏德, 张敏, 等. 分数导数结合傅里叶最小二乘拟合处理含噪音的重迭信号[J]. 分析化学, 2003(2): 143-147. (Lu Xiao-quan, Liu Hong-de, Zhang Min, et al. Fractional derivative combined with Fourier least squares fitting to deal with overlapping signals with noise[J]. Chinese Journal of Analytical Chemistry, 2003(2): 143-147. DOI:10.3321/j.issn:0253-3820.2003.02.004) |
| [15] | Kharintsev S, Salakhov M K. A simple method to extract spectral parameters using fractional derivative spectrometry[J]. Spectrochimica Acta Part A: Molecular & Biomolecular Spectroscopy, 2004, 60(8/9): 2125-2133. |
| [16] | Mocak J, Janiga I, Rievaj M, et al. The use of fractional differentiation or integration for signal improvement[J]. Measurement Science Review, 2007, 7(5): 39-42. |
| [17] | 李远禄, 于盛林, 郑罡. 基于分数阶微分的重叠峰分辨方法[J]. 中国科学(B辑: 化学), 2007, 4: 361-368. (Li Yuan-lu, Yu Sheng-lin, Zheng Gang. Overlapping peak resolution method based on fractional differential[J]. Science in China(Series B: Chemistry), 2007, 4: 361-368.) |
| [18] | Li Y L, Tang H Q, Chen H X. Fractional-order derivative spectroscopy for resolving simulated overlapped Lorenztian peaks[J]. Chemometrics & Intelligent Laboratory Systems, 2011, 107(1): 83-89. |
| [19] | 徐继刚, 冯新泸, 管亮, 等. 分数阶微分在红外光谱数据预处理中的应用[J]. 化工自动化及仪表, 2012, 39(3): 347-351. (Xu Ji-gang, Feng Xin-lu, Guan Liang, et al. Fractional differential application in reprocessing infrared spectral data[J]. Control and Instruments in Chemical Industry, 2012, 39(3): 347-351. DOI:10.3969/j.issn.1000-3932.2012.03.014) |
| [20] | 张东, 塔西甫拉提· 特依拜, 张飞, 等. 分数阶微分在盐渍土高光谱数据预处理中的应用[J]. 农业工程学报, 2014, 30(24): 151-160. (Zhang Dong, Tashpolat· Tiyip, Zhang Fei, et al. Application of fractional differential in preprocessing hyperspectral data of saline soil[J]. Transactions of the Chinese Society of Agricultural Engineering, 2014, 30(24): 151-160. DOI:10.3969/j.issn.1002-6819.2014.24.018) |
| [21] | 田安红, 熊黑钢, 赵俊三, 等. 分数阶微分对盐渍土野外光谱预处理精度提升的机理分析[J]. 光谱学与光谱分析, 2019, 39(8): 2495-2500. (Tian An-hong, Xiong Hei-gang, Zhao Jun-san, et al. Mechanism of improvement for pretreatment accuracy of field spectra of saline soil using fractional differention algorithm[J]. Spectroscopy and Spectral Analysis, 2019, 39(8): 2495-2500.) |
| [22] | Hastie T, Tibshirani R. Generalized additive models[M]. London: Chapman and Hall, 1990: 42-49. |
| [23] | Kilicman A, Zhour Z. Kronecker operational matrices for fractional calculus and some applications[J]. Applied Mathematics and Computation, 2007(187): 250-265. |
| [24] | Zhang L, Li G, Sun M, et al. Kennard-Stone combined with least square support vector machine method for noncontact discriminating human blood species[J]. Infrared Physics and Technology, 2017(86): 116-119. |
| [25] | Zheng J H, Song Z H, Ge Z Q. Probabilistic learning of partial least squares regression model: theory and industrial applications[J]. Chemometrics and Intelligent Laboratory Systems, 2016, 158(5): 80-90. |
