
 , 徐迪1,2, 李雷1,2, 马辉1,2
, 徐迪1,2, 李雷1,2, 马辉1,2 1. 东北大学 机械工程与自动化学院, 辽宁 沈阳 110819;
2. 东北大学 航空动力装备振动及控制教育部重点实验室, 辽宁 沈阳 110819
收稿日期:2020-10-13
基金项目:国家自然科学基金资助项目(11872148,U1908217);中央高校基本科研业务费专项资金资助项目(N2003012, N2003013,N180703018, N170308028);装备预研领域基金资助项目(61407200107)。
作者简介:罗忠(1978-),男,内蒙古商都人,东北大学教授,博士生导师。
摘要:针对涡轴发动机主轴轴承故障特征难以提取, 背景噪声干扰大的问题, 提出了改进二阶循环平稳解卷积(PSO-CYCBD)方法, 用于提取强噪声背景下的故障特征频率.该方法采用粒子群优化(PSO)算法对二阶循环平稳解卷积(CYCBD)方法中的滤波器长度参数进行寻优.首先, 基于故障轴承振动特点建立信号模型, 然后用PSO算法对包络谱故障特征比(FFR)进行最大化处理, 将得到的最优滤波器长度参数输入到CYCBD方法中, 对滤波后的信号进行包络谱分析, 提取故障特征频率.最后, 将提出的方法应用于实测信号中, 与传统包络谱分析相比提高了故障特征提取的效率和准确性, 从而验证了该方法的有效性.
关键词:故障诊断涡轴发动机主轴轴承粒子群优化二阶循环平稳解卷积
Bearing Fault Detection Based on Improved CYCBD Method
LUO Zhong1,2

 , XU Di1,2, LI Lei1,2, MA Hui1,2
, XU Di1,2, LI Lei1,2, MA Hui1,2 1. School of Mechanical Engineering & Automation, Northeastern University, Shenyang 110819, China;
2. Key Laboratory of Vibration and Control of Aero-Propulsion System, Ministry of Education, Northeastern University, Shenyang 110819, China
Corresponding author: LUO Zhong, E-mail: zhluo@mail.neu.edu.cn.
Abstract: Aiming at the problem that it is difficult to extract the fault features of the main shaft bearing of turboshaft engines, and that the background noise has a large interference, an improved second-order cyclostationary blind deconvolution (CYCBD) method is proposed to extract the fault feature frequency under strong noise background. In this method, particle swarm optimization (PSO) is used to optimize the filter length parameters for the CYCBD method. Firstly, the signal model is established based on the vibration characteristics of the fault bearing, and then the envelope spectrum fault feature ratio (FFR) is maximized by PSO algorithm. The optimal filter length parameter is input into the CYCBD method, and the envelope spectrum of the filtered signal is analyzed to extract the fault feature frequency. Finally, the proposed method is applied to the measured signal, and the efficiency and accuracy of fault feature extraction are improved compared with the traditional envelope spectrum analysis, which verifies the effectiveness of the method proposed.
Key words: fault diagnosisspindle bearing of turboshaft engineparticle swarm optimization(PSO)second-order cyclostationarity blind deconvolution(CYCBD)
轴承作为涡轴发动机转子系统的关键部件, 在发动机运行中起着至关重要的作用, 由于发动机内部结构复杂, 振动传感器只能布置在机匣上, 位置与滚动轴承距离较远.当故障发生时, 采集到的振动信号往往带有较强的背景噪声, 因此合理有效的降噪方法对故障诊断的发展十分重要[1].
在研究轴承故障特征的提取过程中, 对于解卷积方法的研究逐渐成为国内外的研究重点, Endo等[2]提出使用最小熵解卷积(MED)来增强解卷积能力, 从而检测齿轮局部故障. McDonald等[3-4]利用了故障的周期特性, 将最大相关峭度反卷积(MCKD)和多点最优最小熵解卷积(MOMED)方法用于检测轴承故障.胡爱军等[5]采用人工鱼群算法, 自适应得到MCKD的最优参数, 利用参数优化的MCKD算法实现滚动轴承多故障分析.为了进一步提高MCKD算法的降噪能力, Hong等[6]针对MCKD算法和多小波的局限性, 提出了一种定制平衡多小波和自适应MCKD相结合的旋转机械复合故障诊断方法.Buzzoni等[7]提出了一种基于最大化二阶循环平稳性, 用特征值分解算法迭代求解的解卷积方法(CYCBD).朱丹宸等[8]将CYCBD方法和互相关谱相结合, 并以最大谐波显著性指数(HSI)为依据, 自适应选取最优滤波器长度.
目前对于CYCBD方法的研究还有以下问题, 如使用CYCBD方法时人工设置参数会造成提取的故障特征不明显, 容易对轴承故障造成错误判断.但是CYCBD方法计算量较大, 最优滤波器长度参数难以通过遍历的方法寻找, 因此对于最优滤波器长度的搜寻方法, 需要展开进一步的研究.
根据上述情况, 提出PSO-CYCBD方法检测轴承故障, 该方法使用粒子群算法(PSO)得到最佳滤波器长度参数, 实现对CYCBD方法的优化.PSO-CYCBD方法能够自适应地对仿真信号和实测信号进行处理, 对滤波后的信号进行包络谱分析, 结果验证了该方法提取轴承故障特征的准确性, 提高了计算效率.
1 PSO-CYCBD方法1.1 CYCBD方法卷积方法[9]是故障特征提取的有效工具, CYCBD方法能够将具有循环平稳特性的故障冲击信号从噪声中提取出来.如式(1)所示, 其目的是从观测到的噪声信号x中恢复输入信号s0.
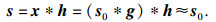 | (1) |
用矩阵表示离散信号的卷积为式(2)所示.
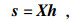 | (2) |
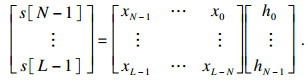 | (3) |
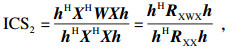 | (4) |
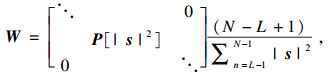 | (5) |
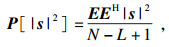 | (6) |
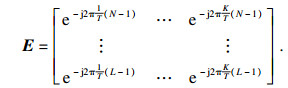 | (7) |
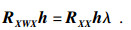 | (8) |
1) 初始化滤波器h.将收敛条件设定为
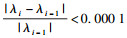
2) 由输入信号x和h计算加权相关矩阵W.
3) 求解式中特征值λ和滤波器h.
4) 返回2)中更新滤波器h, 重新计算直到λ收敛.
CYCBD方法的效果会受到滤波器长度N的影响, 较大的N会增加计算时间, 较小的N会使滤波效果不理想.因此, 本文对于参数N的取值范围限定在(1, 800), 对其使用粒子群优化算法求取最佳参数.
1.2 粒子群优化方法粒子群算法[10](PSO)是一种参数优化技术, 假设粒子群由n个粒子组成X=[X1, X2, …, Xn], 每个粒子由两个特征代表, 位置Xi=[xi1, xi2, …, xid, …, xiD], 以及速度Vi=[vi1, vi2, …, vid, …, viD], 其中D代表解的空间维数.Xi代表粒子的候选优化位置, Vi代表粒子搜寻的方向以及优化步长.通过跟踪每个粒子当前的最佳个体位置Pi=[Pi1, Pi2, …, Pid, …, PiD]以及当前整个种群的最佳群体位置Pg=[Pg1, Pg2, …, Pgd, …, PgD], 在每次迭代中更新每个粒子的位置和速度.优化过程中粒子的位置更新和速度更新按照式(10)和式(11)来进行.
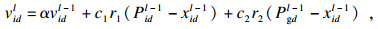 | (9) |
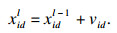 | (10) |
1.3 优化目标函数由于λ值会随着滤波器长度的增大而增大, 无法反映CYCBD解卷积的效果[11], 因此并不适合作为粒子群优化的目标函数, 本文采用包络谱的故障特征比(FFR)作为目标函数.
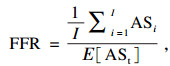 | (11) |
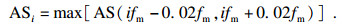 | (12) |
2 轴承故障仿真分析2.1 轴承故障模型为了说明PSO-CYCBD方法的有效性, 本文建立了一个故障轴承振动信号模型:
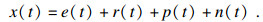 | (13) |
 | (14) |
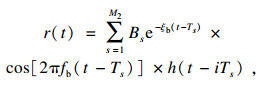 | (15) |
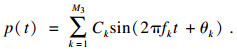 | (16) |
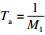
当模拟外圈故障建模时A(t)=1, 外圈故障特征频率fo=M1=73 Hz, 采样频率fs1=9 344 Hz, 其中各个参数的值如表 1所示.当建立内圈故障模型时, 内圈故障特征频率设为fi=93 Hz, 转频大小为fr=10 Hz, 幅值为A(t)=0.5(1-cos(2πfrt)), 其余参数与外圈故障相同.
表 1(Table 1)
| 表 1 轴承故障仿真参数 Table 1 Simulation parameters of bearing fault |
2.2 仿真信号处理结果对仿真信号添加高斯白噪声后, 外圈故障和内圈故障仿真信号的信噪比达到了-13 dB和-15 dB, 染噪后信号的时域图像如图 1a和图 2a所示.对其进行包络谱分析, 分别得到外圈故障和内圈故障信号的包络谱图 1b和图 2b.能够从图中看到仿真信号的外圈故障频率fo和内圈故障特征频率fi被淹没在噪声频率中, 无法分辨出来.
图 1(Fig. 1)
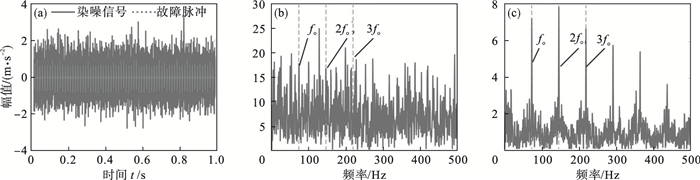 | 图 1 外圈故障仿真信号Fig.1 Simulated signals of bearing outer race fault (a)—外圈故障仿真时域信号;(b)—外圈故障仿真包络谱;(c)—PSO-CYCBD处理后包络谱(N=305). |
图 2(Fig. 2)
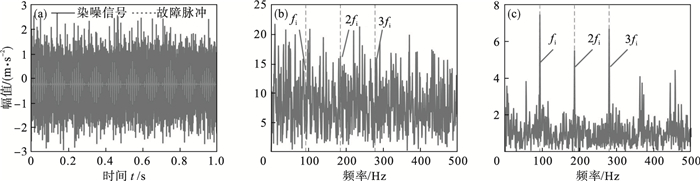 | 图 2 内圈故障仿真信号Fig.2 Simulated signals of bearing inner race fault (a)—内圈故障仿真时域信号;(b)—内圈故障仿真包络谱;(c)—PSO-CYCBD处理后包络谱(N=570). |
使用本文提出的PSO-CYCBD方法, 进行降噪处理, 经过粒子群算法优化后得到外圈故障的最优滤波器长度为N=305.图 1c为处理后信号的包络谱, 与原始信号的包络谱相比, 能够看到更为清晰的外圈故障频率fo=73 Hz, 干扰频率和噪声得到了降低.对内圈故障进行优化后的最优滤波器长度为N=570,图 2c为其包络谱.从结果看, 内圈故障频率fi以及相应的倍频谐波被清晰地提取出来, 验证了PSO-CYCBD方法的有效性.
3 实验验证3.1 PSO-CYCBD方法验证本文使用的轴承-转子故障试验台如图 3所示, 左端支承为健康轴承, 右端支承为故障轴承.
图 3(Fig. 3)
 | 图 3 故障轴承振动测试试验台Fig.3 Vibration test bench of fault bearing |
实验中采样频率设定为fs=20 kHz.外圈故障轴承型号为N205EM, 故障宽度为3 mm.内圈故障轴承型号为NU205EM, 故障宽度为1 mm.这些故障形态如图 4所示.其中外圈故障时域图像如图 5a所示, 内圈故障时域图像如图 5b所示.
图 4(Fig. 4)
 | 图 4 故障轴承Fig.4 Fault bearing (a)—外圈故障轴承;(b)—内圈故障轴承. |
图 5(Fig. 5)
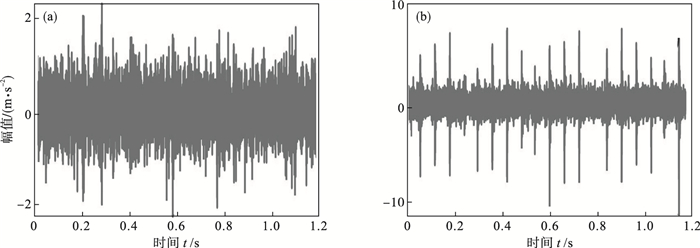 | 图 5 实验数据Fig.5 experimental data (a)—外圈故障时域图;(b)—内圈故障时域图. |
根据轴承的物理尺寸可以得到轴承外圈故障特征频率为fo=42.2 Hz, 轴承内圈故障特征频率为fi=128.2 Hz.通过时域信号, 得到轴承外圈故障的包络谱图 6a和内圈的包络谱图 7a.
图 6(Fig. 6)
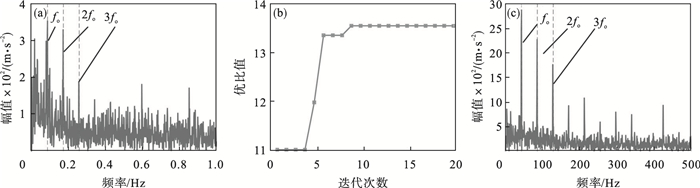 | 图 6 外圈故障PSO-CYCBD方法处理结果Fig.6 Results of applying PSO-CYCBD to the bearing outer race fault (a)—实测信号外圈故障包络谱;(b)—外圈故障PSO优化过程;(c)—处理后外圈故障包络谱(N=4). |
图 7(Fig. 7)
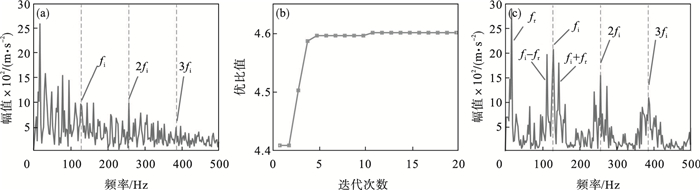 | 图 7 内圈故障PSO-CYCBD方法处理结果Fig.7 Results of applying PSO-CYCBD to the bearing inner race fault (a)—实测信号内圈故障包络谱;(b)—内圈故障PSO优化过程;(c)—处理后内圈故障包络谱(N=564). |
能够从图 6a中看出, 外圈故障频率受到与故障无关的频率干扰以及噪声影响, 因此直接通过对原始信号进行包络谱分析容易对故障造成误判.使用本文提出的PSO-CYCBD降噪方法对故障轴承振动信号进行处理, 经过粒子群优化后滤波器长度为4, PSO优化过程如图 6b所示, 图 6c为故障信号经过CYCBD方法滤波后的包络谱, 能够看到故障特征频率被清晰地提取出来.
图 7a为轴承内圈故障的包络谱, 能够看到故障特征频率被噪声淹没, 无法通过包络解调分离故障特征频率.使用CYCBD方法经PSO优化后滤波器长度为564, 优化过程如图 7a所示, 经过CYCBD方法解卷积后的包络谱为图 7c, 从图 7c中可以直观明显地看到故障特征频率, 同时也能够观察到内圈故障频率应该具有的边频特征[13].
从图 6c和图 7c的包络谱中能够看出本文使用的PSO-CYCBD方法能够从振动信号中提取到清晰的轴承故障特征频率, 成功诊断出故障.
3.2 不同滤波器长度对比验证为了说明本文使用的PSO算法对于CYCBD方法的优化效果, 分别将滤波器长度设定为N=100和N=800, 对内圈故障信号进行处理, 结果如图 8所示.
图 8(Fig. 8)
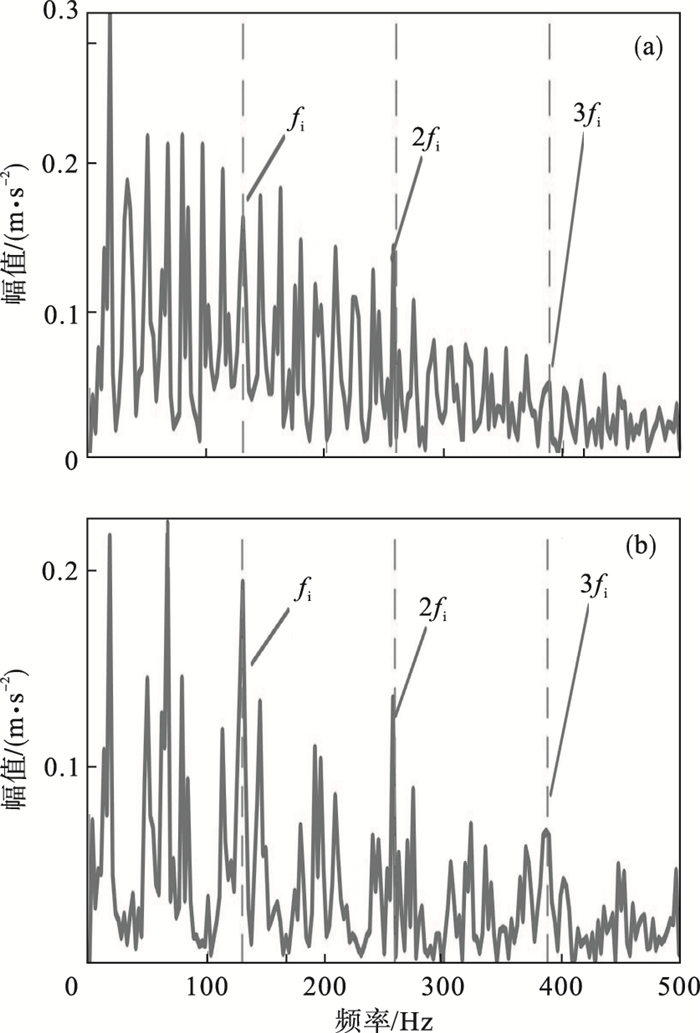 | 图 8 不同滤波器长度处理结果Fig.8 Processing results of different filter lengths (a)—处理后内圈故障包络谱(N=100);(b)—处理后内圈故障包络谱(N=800). |
图 8a中, 内圈故障频率被转动频率干扰, 而且故障频率的三次谐波不能清晰地分离出来, 很容易造成错误判断.图 8b中, 虽然能看到故障特征频率, 但无关的频率分量幅值较大.两种滤波器长度得到的滤波结果与图 7c相比差异明显, 通过上述结果能够看出PSO算法用于优化CYCBD方法的有效性.
4 结论1) 应用PSO算法对CYCBD方法进行优化, 避免了人工设置参数带来的影响, 在保证滤波效果的前提下, 与遍历寻优相比提高了计算效率.
2) 通过仿真与实验对所提的PSO-CYCBD方法进行了验证, 结果表明在外部存在随机冲击,并且故障有周期小范围波动的情况下, 该方法与传统包络谱分析相比能够更准确地提取出故障特征频率.
参考文献
| [1] | Robert B R, Jér?me A. Rolling element bearing diagnostics—a tutorial[J]. Mechanical Systems and Signal Processing, 2011, 25(2): 485-520. DOI:10.1016/j.ymssp.2010.07.017 |
| [2] | Endo H, Randall R. Enhancement of autoregressive model based gear tooth fault detection technique by the use of minimum entropy deconvolution filter[J]. Mechanical Systems and Signal Processing, 2006, 21(2): 906-919. |
| [3] | McDonald G, Qing Z. Multipoint optimal minimum entropy deconvolution and convolution fix: application to vibration fault detection[J]. Mechanical Systems and Signal Processing, 2017, 82: 461-477. DOI:10.1016/j.ymssp.2016.05.036 |
| [4] | McDonald G, Qing Z, Ming J. Maximum correlated Kurtosis deconvolution and application on gear tooth chip fault detection[J]. Mechanical Systems and Signal Processing, 2012, 33: 237-255. DOI:10.1016/j.ymssp.2012.06.010 |
| [5] | 胡爱军, 赵军. 基于自适应最大相关峭度解卷积的滚动轴承多故障诊断[J]. 振动与冲击, 2019, 38(22): 171-177. (Hu Ai-jun, Zhao Jun. Diagnosis of multiple faults in rolling bearings based on adaptive maximum correlated Kurtosis deconvolution[J]. Journal of Vibration and Shock, 2019, 38(22): 171-177.) |
| [6] | Hong L H, Liu X B, Zuo H Y. Compound faults diagnosis based on customized balanced multiwavelets and adaptive maximum correlated Kurtosis deconvolution[J]. Measurement, 2019, 146: 87-100. DOI:10.1016/j.measurement.2019.06.022 |
| [7] | Buzzoni M, Antoni J, D'Elia G. Blind deconvolution based on cyclostationarity maximization and its application to fault identification[J]. Journal of Sound and Vibration, 2018, 432: 569-601. DOI:10.1016/j.jsv.2018.06.055 |
| [8] | 朱丹宸, 张永祥, 何伟, 等. 基于自适应CYCBD和互相关谱的滚动轴承复合故障诊断方法[J]. 振动与冲击, 2020, 39(11): 116-122. (Zhu Dan-chen, Zhang Yong-xiang, He Wei, et al. Compound faults diagnosis of rolling element bearing using adaptive CYCBD and cross-correlation spectrum[J]. Journal of Vibration and Shock, 2020, 39(11): 116-122.) |
| [9] | Miao Y, Zhao M, Lin J, et al. Sparse maximum, harmonics-to-noise-ratio deconvolution for weak fault signature detection in bearings[J]. Measurement Science and Technology, 2016, 27(10): 105004. DOI:10.1088/0957-0233/27/10/105004 |
| [10] | 王东风, 孟丽. 粒子群优化算法的性能分析和参数选择[J]. 自动化学报, 2016, 42(10): 1552-1561. (Wang Dong-feng, Meng Li. Performance analysis and parameter selection of PSO algorithms[J]. Acta Automatica Sinica, 2016, 42(10): 1552-1561.) |
| [11] | 赵晓涛, 孙虎儿, 姚巍. 基于CYCBD和包络谱的滚动轴承微弱故障特征提取[J]. 机械传动, 2020, 44(4): 165-169. (Zhao Xiao-tao, Sun Hu-er, Yao Wei. Feature extraction of weak fault for rolling bearing based on CYCBD and envelope spectrum[J]. Journal of Mechanical Transmission, 2020, 44(4): 165-169.) |
| [12] | Wang Z, Zhou J, Wang J, et al. A novel fault diagnosis method of gearbox based on maximum Kurtosis spectral entropy deconvolution[J]. IEEE Access, 2019, 7: 29520-29532. DOI:10.1109/ACCESS.2019.2900503 |
| [13] | 马辉, 李鸿飞, 俞昆, 等. 含局部故障的滚动轴承动力学建模及振动分析[J]. 东北大学学报(自然科学版), 2020, 41(3): 343-348. (Ma Hui, Li Hong-fei, Yu Kun, et al. Dynamic modeling and vibration analysis of rolling bearings with local fault[J]. Journal of Northeastern University(Natural Science), 2020, 41(3): 343-348.) |
