
 , 李禹雄
, 李禹雄 东北大学 机械工程与自动化学院, 辽宁 沈阳 110819
收稿日期:2020-07-23
基金项目:国家自然科学基金资助项目(51975110); “兴辽英才计划”项目(XLYC1907171); 中央高校基本科研业务费专项资金资助项目(N2003005)。
作者简介:丁鹏飞(1996-),男,辽宁朝阳人,东北大学博士研究生;
黄贤振(1982-),男,山东定陶人,东北大学教授,博士生导师。
摘要:车削加工参数的随机性会影响直径误差, 因此,本文提出一种细长轴直径误差可靠性灵敏度分析方法.通过剪切区模型和几何分析法建立直径误差模型, 采用Kriging方法重构细长轴车削加工误差与切削参数的函数关系, 然后采用蒙特卡罗方法进行可靠性灵敏度分析, 据此评价各参数对直径误差的影响程度.研究结果表明: 切削速度、刀具前角和直径增加, 系统可靠性增高; 切削深度、切削宽度、刀架与刀具间距离和轴的长径比增加, 系统可靠性降低.研究结果能为降低车削加工细长轴直径误差提供理论依据.
关键词:细长轴加工切削力直径误差Kriging可靠性灵敏度
Reliability Sensitivity Analysis of Turning Error for Slender Shaft
DING Peng-fei, WANG Chang-li, HUANG Xian-zhen

 , LI Yu-xiong
, LI Yu-xiong School of Mechanical Engineering & Automation, Northeastern University, Shenyang 110819, China
Corresponding author: HUANG Xian-zhen, E-mail: xzhhuang@mail.neu.edu.cn.
Abstract: The randomness of turning parameters will affect the diameter error. So, a reliability sensitivity analysis method for the diameter error of slender shaft is proposed. The shear zone model and geometric analysis method are used to establish the diameter error model. Kriging method is used to reconstruct the functional relationship between the machining error and the cutting parameters of slender shaft. The reliability sensitivity analysis is carried out by using the Monte Carlo method, and the influence degree of each parameter on the diameter error is evaluated. The results show that the system reliability increases with the increasing of cutting speed, tool rake angle and diameter, while it decreases with the increasing of cutting depth, cutting width, distance between tool holder and tool, and length diameter ratio of the slender shaft. The research results can provide theoretical basis for reducing the diameter error of slender shaft.
Key words: slender shaft machiningcutting forcediameter errorKrigingreliability sensitivity
细长轴类工件在加工过程中由于切削力的作用会发生弯曲变形, 这种变形改变了原有的工件特性, 产生直径误差, 从而影响工件的尺寸精度, 增加加工难度[1].因此, 建立动态模型来预测车削过程中直径误差的变化具有重要意义.
文献[2]考虑刀具界面润滑, 建立切削局部摩擦系数随切削条件和最小润滑参数变化的力学模型.文献[3]采用离散傅立叶变换和最小二乘直线拟合逼近车削曲面, 得到最终的直线度误差.文献[4]通过正运动学和实际逆运动学建立了蜗杆车削齿形误差预测与补偿模型.文献[5]基于多体理论和齐次变换矩阵, 建立了选择性运动学误差模型.
以上研究为细长轴加工误差的可靠性灵敏度分析奠定了基础, 但这些模型中使用的加工参数是确定的.实际过程中由于制造环境中的不确定性因素, 加工条件往往具有随机性和不确定性.本文提出一种细长轴车削加工过程中直径误差的预测方法, 将剪切区切削力计算和误差几何分析法[6-7]进行结合, 采用Kriging法分析了细长轴加工误差的可靠性灵敏度, 并通过数值计算验证了该方法的正确性和有效性.
1 误差模型建立加工过程中剪切过程是复杂的, 基于文献[8]中的理论, 主剪切带可分成两个不等的截面, 如图 1和图 2所示.
图 1(Fig. 1)
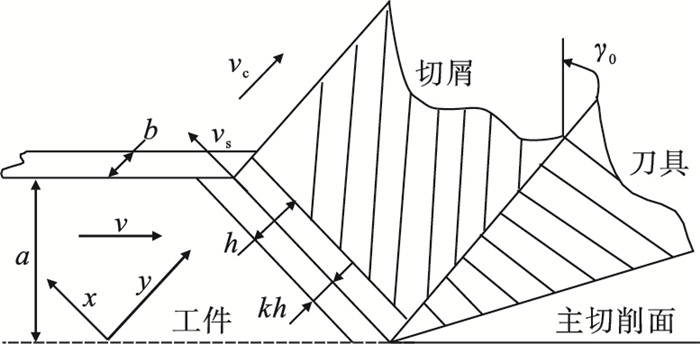 | 图 1 不等剪切带模型Fig.1 Unequal shear zone model |
图 2(Fig. 2)
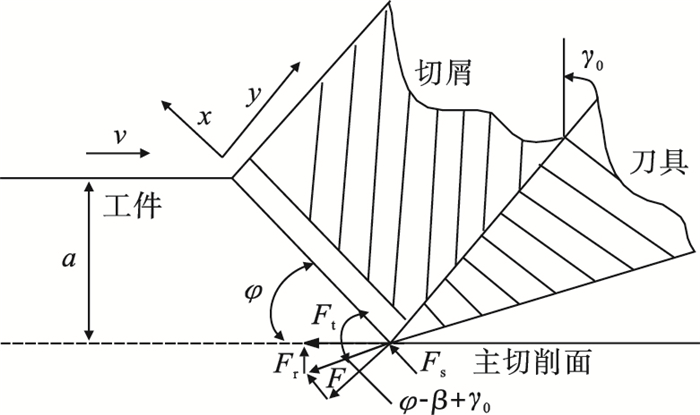 | 图 2 切削力示意图Fig.2 Schematic diagram of cutting force |
图 1,图 2中: v为切削速度; vc为切屑速度; vs为切屑剪切速度; a为切削深度; γ0为前角; h为剪切带厚度; k为不等系数; b为切削宽度; Fs为剪切力.用Merchant方程[9]近似剪切角值, 可以得到剪切角φ、平均摩擦系数f及摩擦角β:
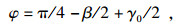 | (1) |
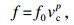 | (2) |
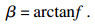 | (3) |
 | (4) |
通过求解剪应力τ, 可求解加工过程中的剪切力Fs、主切削力Ft和刀具进给力Fr:
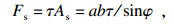 | (5) |
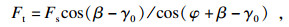 | (6) |
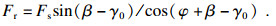 | (7) |
考虑机床中心位移、工件和机床的变形对车削工件直径的影响, 采用几何分析方法[11]预测车削工件的加工误差.由于细长轴工件的长径比大, 在普通车床上加工细长轴需要一个支撑装置, 支撑的目的是防止使用工具时细长轴发生偏移.支撑装置连接在机床支架上, 并随支架一起移动, 整体分析如图 3所示.
图 3(Fig. 3)
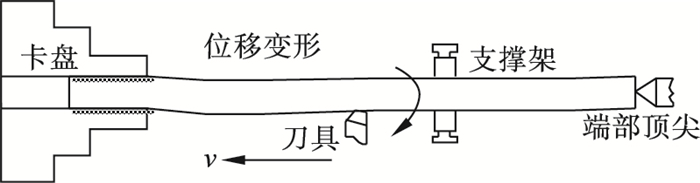 | 图 3 加工示意图Fig.3 Schematic diagram of machining |
工件受到三个切削力分量作用: 切向力Ft、径向力Fr和轴向力Fa.工件和车刀的挠度可以在x-y剖面上进行分析, 如图 4所示.由于轴向力Fa对径向变形的影响很小, 因此在本文中忽略其影响.
图 4(Fig. 4)
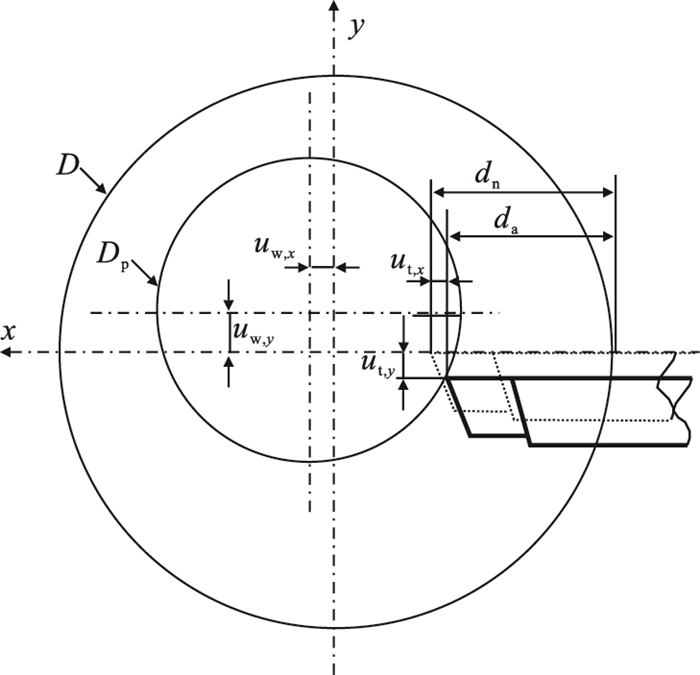 | 图 4 横截面示意图Fig.4 Schematic diagram of the cross section |
机床、工件和刀具在切削力的作用下都会发生变形, 基于整个系统的弹性变形, 对车削操作进行几何分析.由于刀具挠度ut, x和ut, y远小于细长轴挠度, 故式(8)中的ut, x和ut, y可以忽略, 简化为式(9):
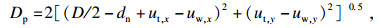 | (8) |
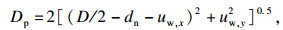 | (9) |
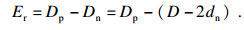 | (10) |
将细长轴分别在x-z平面和y-z平面上进行有限元分析[7].细长轴夹持在卡盘和端部顶尖之间, 卡盘的一端固定, 另一端受约束, 从动件的支撑增强了细长轴的径向刚度, 但与卡盘或顶部相比, 从动件刚度较小, 因此可以将从动件支架视为弹簧.综上所述, 车削系统的整体力学模型如图 5所示.其中kx和ky分别是x-z和y-z平面上从动件的面内刚度.
图 5(Fig. 5)
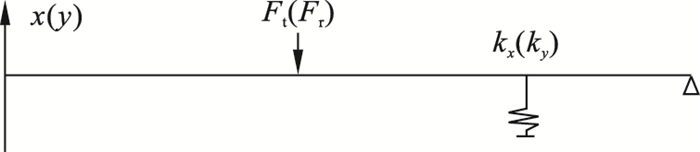 | 图 5 车削的整体力学模型Fig.5 Overall mechanical model of the turning |
1.1 x-z平面分析细长轴在x-z平面的受力情况如图 6所示.
图 6(Fig. 6)
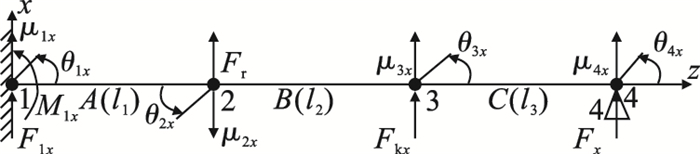 | 图 6 x-z平面单元Fig.6 x-z plane unit |
将整个工件分为A, B, C三个单元.相应的单位长度为l1, l2和l3.节点1~4分别代表卡盘作用点、刀具切削点、支撑刀架的作用点和顶尖端的作用点, 每个节点上的力分别为F1x, Fr, Fkx和F4x.节点3处的支撑力可采用Fkx=kfx×u3x计算, 根据Q=K×σ(Q是荷载向量, K是刚度矩阵, σ是位移向量) 可得
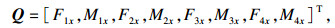 | (11) |
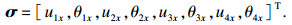 | (12) |
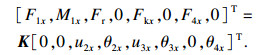 | (13) |
图 7(Fig. 7)
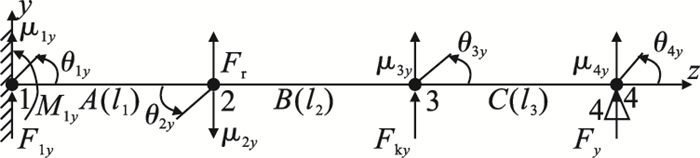 | 图 7 y-z平面单元Fig.7 y-z plane unit |
图中,u2x和u2y分别表示工件在切削点x和y方向的位移.因此, 式(14)中的u2x即为式(9)中的uw, x; 式(15)中的u2y为式(9)中的uw, y.
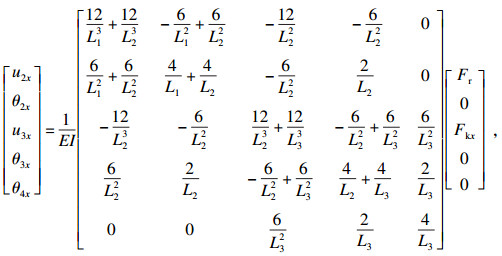 | (14) |
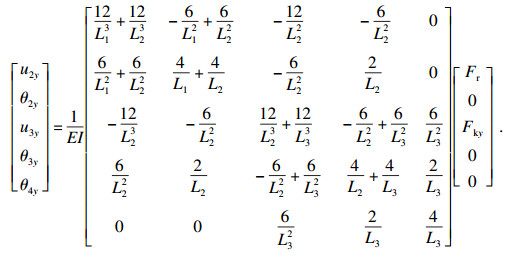 | (15) |
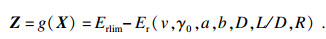 | (16) |
 | (17) |
图 8(Fig. 8)
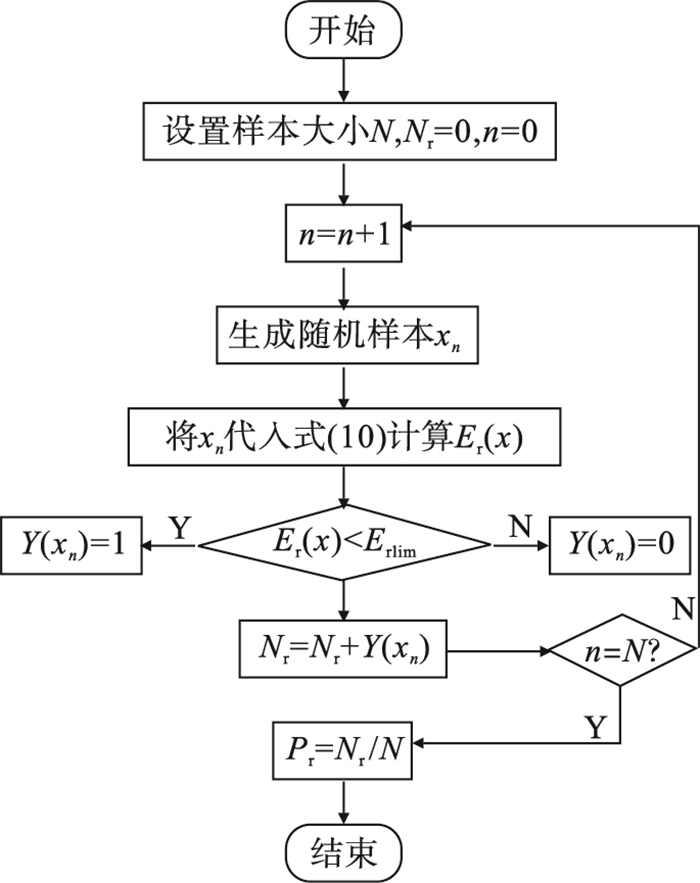 | 图 8 蒙特卡罗流程图Fig.8 Monte Carlo flow chart |
根据误差模型随机变量的分布特征生成相应的样本点; 对随机变量样本点按照图 8流程进行仿真计算, 得到系统的响应特性; 利用所建立的极限方程, 通过蒙特卡罗模拟确定随机变量样本点的可靠性概率.为了保证结果的准确性, 需要进行大量的实验.假设实验次数为N, Nr是满足极限状态的实验次数.可靠性概率表示为
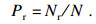 | (18) |
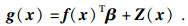 | (19) |
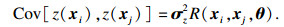 | (20) |
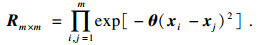 | (21) |
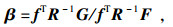 | (22) |
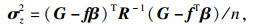 | (23) |
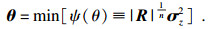 | (24) |
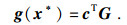 | (25) |
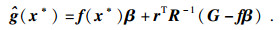 | (26) |
2.3 可靠性灵敏度分析可靠性灵敏度是失效概率对基本随机变量的均值和标准差的偏导数[18].设定随机变量xi的分布参数是θxi(k)(i=1, 2, …, n; k=1, 2, …, m;k为第i个变量xi的分布参数的个数).分布参数的失效概率积分方程的偏导数为灵敏度:
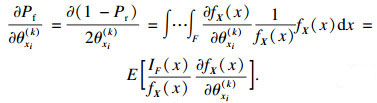 | (27) |
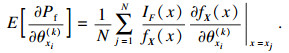 | (28) |
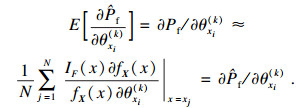 | (29) |
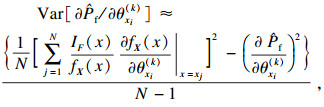 | (30) |
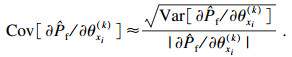 | (31) |
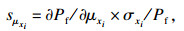 | (32) |
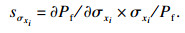 | (33) |
图 9(Fig. 9)
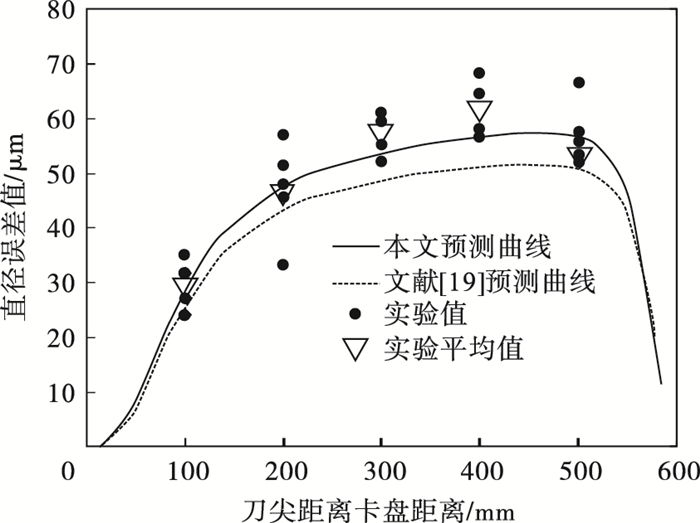 | 图 9 直径误差结果对比Fig.9 Comparison of diameter error results |
图 9给出了本文方法得到的加工误差值随刀尖至卡盘距离变化的预测曲线、文献[19]中的实验曲线和预测曲线; 可以看出, 本文的预测曲线更接近于实验值, 说明本文建立的模型是精确的.
3.2 加工误差可靠性及灵敏度分析算例加工分析的一个重要部分是计算失效概率, 因为它可以直接量化输入参数不确定性对结构响应的影响.本文使用拉丁超立方体法抽取105个随机样本进行蒙特卡罗模拟, 再用Kriging法进行计算; 将计算结果与蒙特卡罗法所得结果进行对比.分析流程如图 10所示.
图 10(Fig. 10)
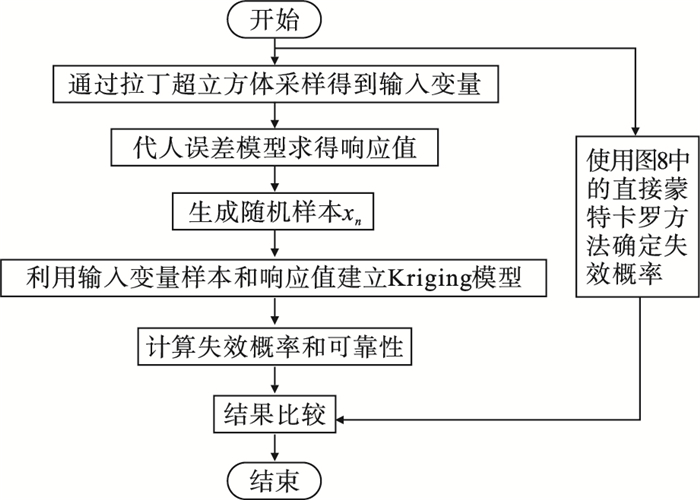 | 图 10 两种方法的对比Fig.10 Comparison of the two methods |
计算过程所需的固定参数和考虑随机性的设计变量的概率特性如表 1和表 2所示.为验证Kriging与蒙特卡罗模型结果的一致性, 设参数γ0, a, b, D, L/D, R的变异系数为0.05, 均服从正态分布; 设误差极限Erlim=0.2 mm.采用Kriging法和蒙特卡罗法计算细长轴车削加工误差的可靠性并绘制曲线, 结果如图 11所示.
表 1(Table 1)
| 表 1 固定参数值 Table 1 Fixed parameter values | ||||||||||||||||||||||||||||||||||||||||||||||||
表 2(Table 2)
| 表 2 随机概率特征 Table 2 Probability characteristics of random variables | |||||||||||||||||||||||||||||||||
图 11(Fig. 11)
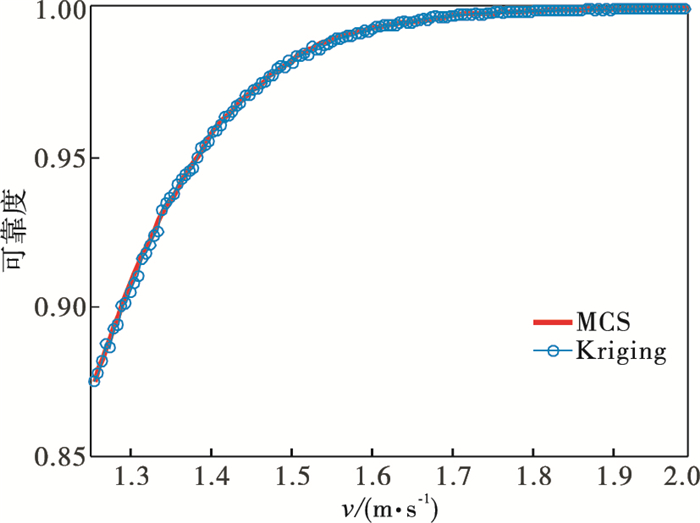 | 图 11 直径误差可靠性随速度变化曲线Fig.11 Curve of diameter error reliability with speed |
由图 11可以看出, 当车削速度大于1.8 m/s时, 系统的可靠性约为1.0, 并且蒙特卡罗法与Kriging法得到的可靠性曲线吻合良好, 即相互证明了准确性.为了探讨随机变量的变化对误差值的影响程度, 对随机变量进行了可靠性灵敏度分析, 结果如图 12和图 13所示.
图 12(Fig. 12)
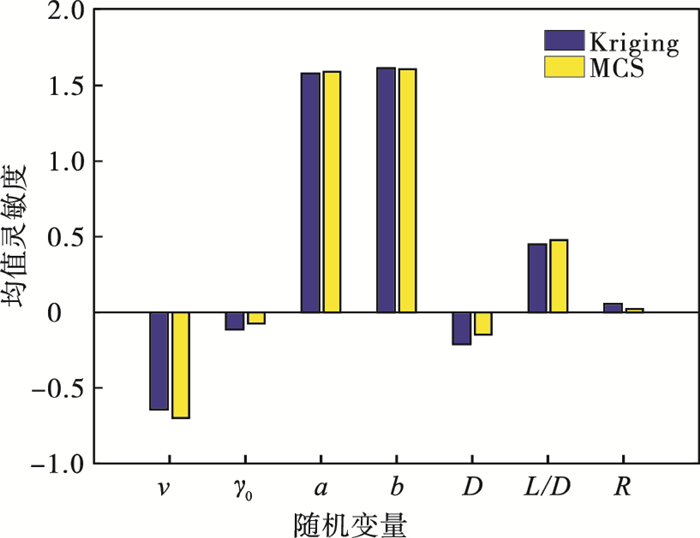 | 图 12 均值灵敏度分析Fig.12 Sensitivity analysis of meanvalues |
图 13(Fig. 13)
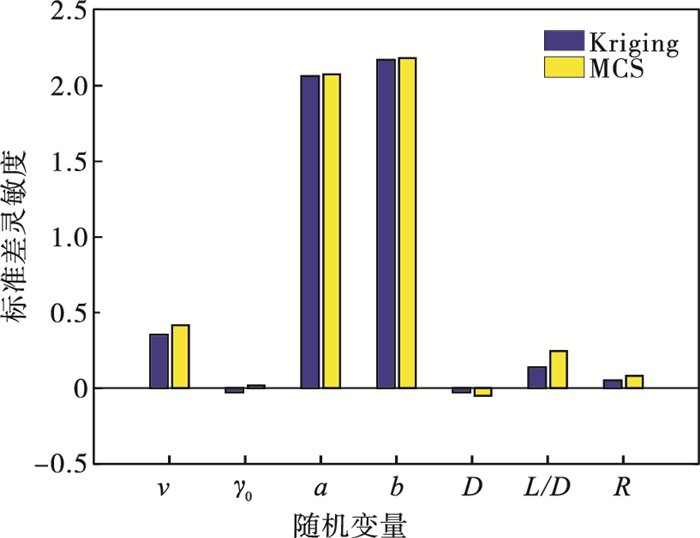 | 图 13 标准差灵敏度分析Fig.13 Sensitivity analysis of standard deviation |
为进一步讨论图 12和图 13的正确性, 本文对每个参数进行单一变量控制分析, 将所得结果排列成折线图, 如图 14所示.
图 14(Fig. 14)
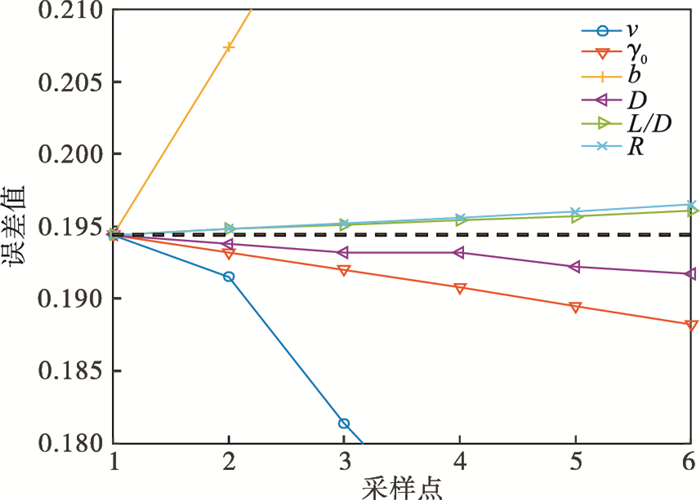 | 图 14 采样点随机变量对应的误差值Fig.14 Error values of random variables at different sampling points |
从图 14可以看出, 所得结果与灵敏度分析直方图分析结果一致.结果表明: 提高切削速度v、刀具前角γ0和细长轴直径D都会减小细长轴加工误差; 反之, 增大切削深度a、切削宽度b、刀架与刀具的距离R和长径比L/D, 细长轴加工误差增大.
4 结论1) 本文建立了细长轴车削加工误差模型, 采用Kriging方法重构模型进行误差可靠性灵敏度分析.该方法考虑了参数的随机性, 使车削过程的预测与工程实际相吻合, 大大提高细长轴车削加工误差的预测精度; 与直接蒙特卡罗法所用时间(1.01×104 s)相比, Kriging模型预测细长轴加工误差所需的时间(40.9 s)更少, 提高了概率分析和计算的效率.
2) 提高切削速度、增加刀具角度和细长轴直径可以减小细长轴加工误差, 提高细长轴直径失效可靠性; 而随着切削深度、切削宽度、刀架与刀具的距离、长径比的增加, 细长轴加工误差增大, 车削系统的失效可靠性降低.其中, 切削深度和切削宽度对系统的影响最大, 切削速度和长径比的影响次之, 刀具前角和刀架与刀具之间距离的影响较小.因此, 在分析细长轴直径误差时, 应着重测量影响较大的变量, 以此进行分析.
参考文献
| [1] | Huang P, Lee W B, Chan C Y. Investigation of the effects of spindle unbalance induced error motion on machining accuracy in ultra-precision diamond turning[J]. International Journal of Machine Tools and Manufacture, 2015, 94: 48-56. DOI:10.1016/j.ijmachtools.2015.04.007 |
| [2] | Behera B C, Ghosh S, Rao P V. Modeling of cutting force in MQL machining environment considering chip tool contact friction[J]. Tribology International, 2018, 117: 283-295. DOI:10.1016/j.triboint.2017.09.015 |
| [3] | Cao Y L, Liu T, Ye X F, et al. Lathe errors identification based on surface topography analysis after turning[J]. Precision Engineering, 2016, 46: 243-253. DOI:10.1016/j.precisioneng.2016.05.003 |
| [4] | Ding S, Song Z Q, Wu W, et al. Geometric error modeling and compensation of horizontal CNC turning center for TI worm turning[J]. International Journal of Mechanical Sciences, 2019, 167: 105266. |
| [5] | Li D, Jiang X, Tong Z, et al. Kinematics error compensation for a surface measurement probe on an ultra-precision turning machine[J]. Micromachines, 2018, 9(7): 334-341. DOI:10.3390/mi9070334 |
| [6] | Li B L, Wang X L, Hu Y J, et al. Analytical prediction of cutting forces in orthogonal cutting using unequal division shear-zone model[J]. International Journal of Advanced Manufacturing Technology, 2011, 54: 431-443. DOI:10.1007/s00170-010-2940-8 |
| [7] | 韩荣第, 郭建亮. 加跟刀架的细长轴车削加工尺寸误差的仿真[J]. 南京航空航天大学学报, 2005, 37(B11): 108-112. (Han Rong-di, Guo Jian-liang. Simulation of dimensional error in turning slender shaft with heel rest[J]. Journal of Nanjing University of Aeronautics and Astronautics, 2005, 37(B11): 108-112.) |
| [8] | Tounsi N, Vincenti J, Otho A, et al. From the basic mechanics of orthogonal metal cutting toward the identification of the constitutive equation[J]. International Journal of Machine Tools and Manufacture, 2002, 42(12): 1373-1383. DOI:10.1016/S0890-6955(02)00046-9 |
| [9] | Dudzinski D, Molinari A. A modeling of cutting for viscoplastic materials[J]. International Journal of Mechanical Sciences, 1997, 39(4): 369-389. DOI:10.1016/S0020-7403(96)00043-4 |
| [10] | Fang N. A quantitative sensitivity analysis of cutting performances in orthogonal machining with restricted contact and flat-faced tools[J]. Journal of Manufacturing Science and Engineering, 2004, 126(2): 408-411. DOI:10.1115/1.1643081 |
| [11] | Mayer J R R, Phan A V, Cloutier G. Prediction of diameter errors in bar turning: a computationally effective model[J]. Applied Mathematical Modelling, 2000, 24(12): 943-956. DOI:10.1016/S0307-904X(00)00027-5 |
| [12] | 谢里阳. 机械可靠性理论、方法及模型中若干问题评述[J]. 机械工程学报, 2014, 50(14): 27-35. (Xie Li-yang. Review of some problems in mechanical reliability theory, method and model[J]. Journal of Mechanical Engineering, 2014, 50(14): 27-35.) |
| [13] | Huang X, Jia F, Zhang Y, et al. Prediction of surface location error in milling considering the effects of uncertain factors[J]. Mechanical Sciences, 2017, 8(2): 385-392. DOI:10.5194/ms-8-385-2017 |
| [14] | Sun Z L, Wang J, Li R, et al. LIF: a new Kriging based learning function and its application to structural reliability analysis[J]. Reliability Engineering & System Safety, 2017, 157: 152-165. |
| [15] | Kim S H, Na S W. Response surface method using vector projected sampling points[J]. Structural Safety, 1997, 19(1): 3-19. DOI:10.1016/S0167-4730(96)00037-9 |
| [16] | Gao Y, Turng L S, Wang X. Adaptive geometry and process optimization for injection molding using the Kriging surrogate model trained by numerical simulation[J]. Advances in Polymer Technology, 2010, 27(1): 1-16. |
| [17] | Huang X Z, Li Y X, Zhang Y M, et al. A new direct second-order reliability analysis method[J]. Applied Mathematical Modelling, 2018, 55: 68-80. DOI:10.1016/j.apm.2017.10.026 |
| [18] | 杨周, 张义民. 不完全概率信息下机械零部件的可靠性灵敏度设计[J]. 东北大学学报(自然科学版), 2008, 29(7): 1012-1015. (Yang Zhou, Zhang Yi-min. Reliability-based sensitivity design of mechanical components depending on incomplete information on probability[J]. Journal of Northeastern University(Natural Science), 2008, 29(7): 1012-1015. DOI:10.3321/j.issn:1005-3026.2008.07.026) |
| [19] | Guo J L, Han R D. A united model of diametral error in slender bar turning with a follower rest[J]. International Journal of Machine Tools & Manufacture, 2006, 46(9): 1002-1012. |
