
 , 王璐, 程军娜, 田济荣
, 王璐, 程军娜, 田济荣 中国海洋大学 信息科学与工程学院, 山东 青岛 266100
收稿日期:2020-08-18
基金项目:国家自然科学基金资助项目(61701462);山东省自然科学基金资助项目(ZR2014FQ027);中央高校基本科研业务费专项资金资助项目(201513015)。
作者简介:张娜(1980-),女,山东青岛人,中国海洋大学讲师,博士。
摘要:基于距离选通成像时间切片间的相关性, 提出分布式压缩感知三维成像方法, 有效解决了三维成像庞大数据量与硬件存储性能的冲突.根据相关性构建基于联合稀疏模型的分布式压缩模型, 辅助重构部分时间切片.设计一种自适应距离选通方法, 根据设定阈值自适应调整选通时间, 无需距离先验信息, 增加了系统灵活性.结果表明: 平均采样率为0.15时, 该方法的成像质量比传统方法提高11.124 dB, 成像距离的平均误差降低6.240.分布式成像方法能够有效减少时间切片冗余信息的采集, 为距离选通三维成像提供了一种新的思路.
关键词:计算成像水下三维成像分布式压缩感知自适应距离选通成像联合稀疏模型
Adaptive Range-Gated 3D Imaging Based on Distributed Compressed Sensing
ZHANG Na

 , WANG Lu, CHENG Jun-na, TIAN Ji-rong
, WANG Lu, CHENG Jun-na, TIAN Ji-rong School of Information Science and Engineering, Ocean University of China, Qingdao 266100, China
Corresponding author: ZHANG Na, E-mail: baiquanbaiquan@126.com.
Abstract: Based on the correlation between time slices of range-gated imaging, a distributed compressed sensing 3D imaging method was proposed, which solved the conflict between a large amount of data and hardware storage performance in 3D imaging. According to the correlation, a distributed compression model based on the joint sparse model was constructed to assist the reconstruction of partial time slices. An adaptive range-gated method was designed, and the gated time was adaptively adjusted according to the set threshold, without distance prior information, which increases system flexibility. The results show that when the average sampling rate is 0.15, the imaging quality of this method is 11.124 dB higher than that of the traditional method, and the average error of imaging distance is reduced by 6.240. The distributed imaging method can effectively reduce the collection of time slice redundant information, providing a new idea for range-gated 3D imaging.
Key words: computational imagingunderwater three-dimensional imagingdistributed compressed sensingadaptive range-gated imagingjoint sparse model
距离选通切片式成像方法是一种对特定距离目标实现三维重建的成像方法, 因其成像距离远、成像系统适应性强等特点而被广泛应用在水下、精确制导、夜视安防等领域[1].其中, 基于多帧水下距离选通三维重构方法[2]能够在降低后向散射噪声的基础上根据时间切片复原深度信息, 距离分辨率好, 在水下领域应用较为广泛, 但切片式成像方法存在的数据量大和实时性差的问题限制了在成像设备受限的水下场景的进一步扩展.针对采集数据量问题, 具有低采样率特点的压缩感知[3-5]将该成像方法引领到新的研究方向.研究人员通过将距离信息加入压缩感知三维成像计算[6-7]及对距离信息进行编码[8]实现压缩感知三维成像以减少计算量, 或使用压缩感知技术改进飞行时间三维成像来降低采集时间[9-11], 研究取得了一定的效果.然而以上研究只是在单个时间切片层面上应用压缩感知理论, 完成对物体各个时间切片的独立压缩采样重构, 虽然在一定程度上减少了采集数据量, 但是却忽略了时间切片间的空间关联信息.
通过对自然物体三维信息的观察研究发现, 其时间切片间具有一定关联[8], 而分布式压缩感知正是为了解决多信号内部及信号间关联性重构问题[12-14].本文设计了一种分布式压缩感知距离选通三维成像方法.利用分布式压缩感知原理框架, 通过多时间切片联合稀疏模型对时间切片间的关联性进行建模, 利用高采样率时间切片辅助重构低采样率时间切片.时间切片联合稀疏度小于时间切片单个切片稀疏度的加和, 时间切片关联信息辅助重构低采样率时间切片, 该方法能够以更低的采样率采样, 解决三维成像采样率与存储空间的矛盾.针对距离选通硬件灵活性差的问题, 本文提出了一种自适应距离选通成像方法, 该方法根据设定阈值, 自适应选择选通时间, 增加了系统灵活性.
1 分布式压缩感知模型1.1 分布式压缩感知压缩感知数学表达式为[14-16]
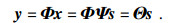 |
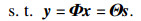 |
主要重构算法: 基于求解最小l0范数的贪婪算法, 将最小l0范数转化为最小l1范数求解的凸优化算法, 根据阈值选择原子的阈值化方法, 需要结构化采样及构造特殊观测矩阵的组合方法, 类似于主成分分析的统计优化方法, 采用lp范数求解非凸优化方法[17-19].
以上压缩感知重构算法针对单一信号, 只考虑了信号自身稀疏特性, 并不适合多信号重构问题[20-23].在无线传感器网络领域, Baron等[13]提出了分布式压缩感知理论, 将网络信号内部及信号间的关联性分为三种联合稀疏模型(joint sparse model, JSM), 并提出对应的联合重构算法.实验表明联合重构算法可以显著节省测量数目.分布式压缩感知对多信号独立压缩测量联合重建的模型[13]如图 1所示.
图 1(Fig. 1)
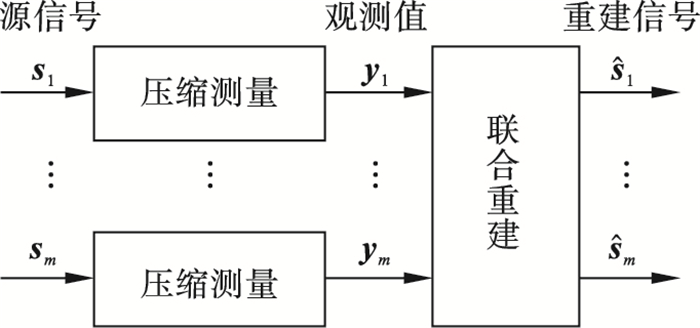 | 图 1 分布式压缩感知基本模型Fig.1 Basic model of distributed compressed sensing |
1.2 基于联合稀疏模型的分布式压缩感知模型研究表明, 三维成像过程中不同距离处的图像(也称为时间切片)具有相关性[9, 13-14], 以根据时间切片特点得到的足球为例, 简单证实其时间切片间的相关性.第16张时间切片与前后15张时间切片的结构相似度如图 2所示.该相关性符合JSM-2模型, 因此构建基于时间切片的联合稀疏模型.同一物体的两个相邻时间切片分别用xt和xt+1表示, 其中t是瞬时时间, xt和xt+1具有相同的稀疏度:
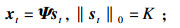 | (1) |
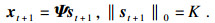 | (2) |
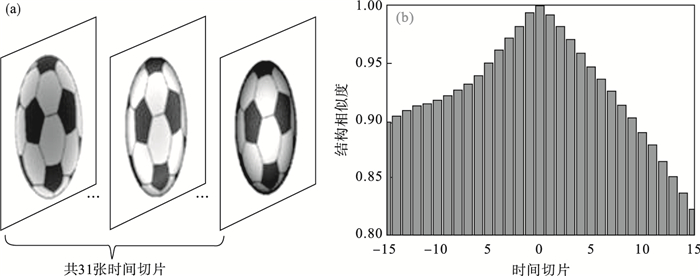 | 图 2 时间切片间结构相似度Fig.2 Structural similarity between time slices (a)—时间切片;(b)—结构相似度曲线. |
式中: st和st+1分别是xt和xt+1在稀疏基Ψ下的稀疏表示, ‖st‖0=‖st+1‖0=K.
根据联合稀疏模型, 结合时间切片间关联性特点设计分布式压缩感知算法(DCS-SPL)模型框架, 如图 3所示.
图 3(Fig. 3)
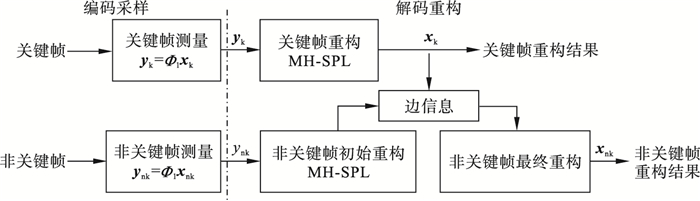 | 图 3 分布式压缩感知算法模型框架Fig.3 Distributed compressed sensing algorithm model framework |
在多假设预测平滑投影Landwebers算法(MH-SPL)[24]的启发下, 结合时间切片间的空间稀疏特点, 提出基于联合稀疏模型的分布式压缩感知(DCS-SPL)模型, 对时间切片关联性进行建模, 利用关联信息辅助重构低采样率时间切片.编码采样端, 时间切片被编码为关键帧和非关键帧, 利用高低不同的采样率得到采样值.在解码重构端, 关键帧的重构利用MH-SPL重构, 非关键帧首先采用MH-SPL初始重构, 然后结合生成的关联信息(边信息)进行最终重构.
非关键帧最终重构部分过程: 假设y为x的测量值, x为信号x的初始重构,
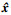
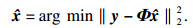 | (3) |
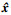
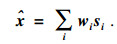 |
优化式(3)可知
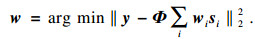 |
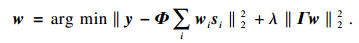 |
2 基于分布式压缩感知的自适应距离选通三维成像方法搭建的成像系统如图 4所示.
图 4(Fig. 4)
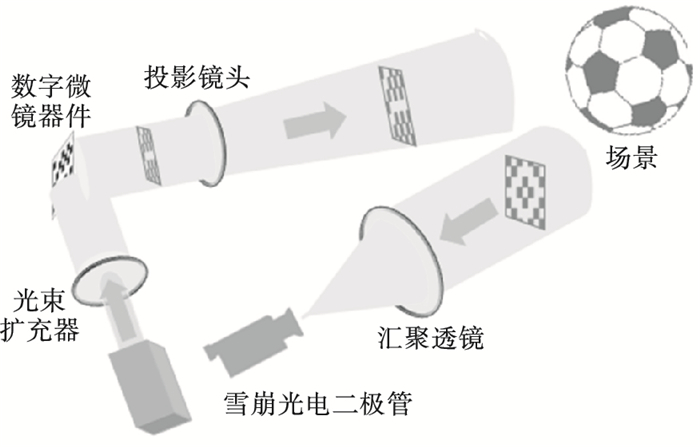 | 图 4 成像系统示意图Fig.4 Schematic diagram of imaging system |
激光器发射激光经光束扩充器照射在数字微镜器件(digital micromirror device, DMD)上, DMD加载采样矩阵对激光光束进行空间调制, 调制后的光束经过投影镜头投影在目标场景, 经场景反射后反射光经过汇聚透镜聚集在雪崩光电二极管(avalanche photon diode, APD), 由APD接收器接收反射总光强, 由计算机计算重构三维目标, 具体过程如图 5所示.
图 5(Fig. 5)
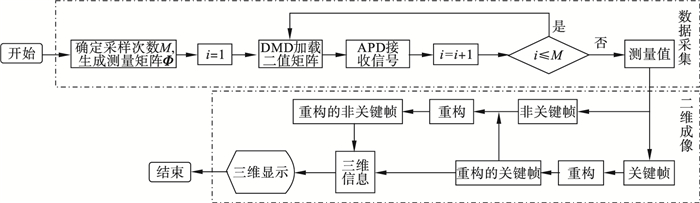 | 图 5 基于分布式压缩感知的水下三维成像流程图Fig.5 Underwater 3D imaging flow chart based on distributed compressed sensing |
数据采集阶段, 结合提出的自适应距离选通方法确定采样策略.
由于物体呈现立体状态, 因此到探测器的距离存在差异, 物体反射光到达接收器的时间不同, APD接收器在不同时间接收到物体不同部分表面反射回来的光强.提出自适应距离选通方法, 根据APD接收信号情况设定阈值, 自适应选择选通时间处的光强信号不仅有效抑制了后向散射, 而且解决了距离选通需要预先估计物体成像距离从而在硬件上实现开闭的问题, 增加了系统灵活性.
APD接收M次DMD调制的光强信号, 处理后得最终采样值y, 如图 6所示.T为设定阈值; yi=[yi(1), yi(2), …, yi(n)]为第i次采样值; yj=[y1(j), y2(j), …, yM/L(j)]∈RM/L为第j个有效值对应的M/L次测量得到的信号; yj为时间tj对应距离处的目标测量值, yj=Φx(j)=ΦΨs(j), 经过重构算法, 即可得到时间tj对应距离处的图像.M和L分别对应关键帧和非关键帧应用不同采样率得到的采样值个数.Δ为提取间隔, 根据实际分辨率需要, 等间隔(Δ)提取对应时间的光强.
图 6(Fig. 6)
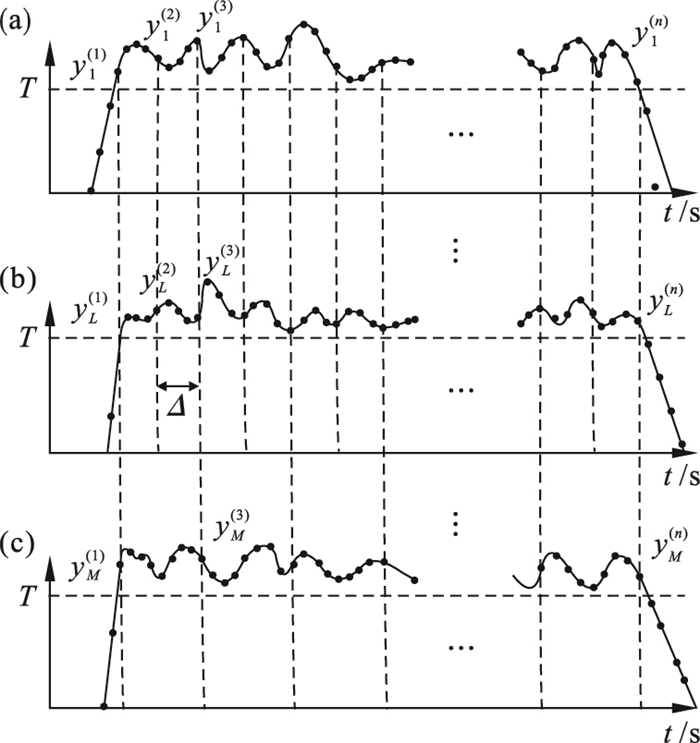 | 图 6 分布式压缩感知采样Fig.6 Distributed compressed sensing sampling (a)—第一次测量;(b)—第L次测量;(c)—第M次测量. |
三维成像过程包括时间切片的重构及三维信息获取与重建, 如图 7所示.采用DCS-SPL模型获取的时间切片如图 7a所示; 以时间切片中圈出的两个像素点A(a, b), B(a, b)为例, 经过处理, A, B两点随时间变化曲线如图 7b所示; 采用质心法求得A, B像素点处的强度值xA(a, b), xB(c, d), 取强度值处的时间tA, tB对应的距离dA, dB作为像素点处的距离信息, 距离信息和强度信息如图 7c所示; 利用目标物体强度信息和距离信息即可重构出如图 7d所示的三维物体.
图 7(Fig. 7)
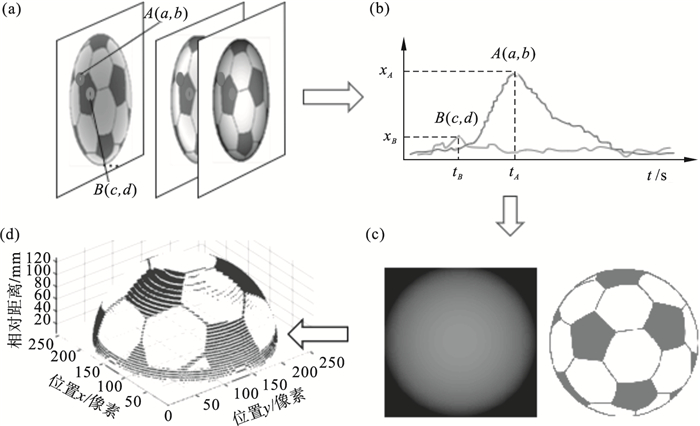 | 图 7 目标物体三维成像过程Fig.7 3D imaging process of target (a)—重构时间切片; (b)—像素点拟合曲线; (c)—距离图和强度图; (d)—重建的三维物体. |
搭建的三维成像系统,采用单像素探测器接收总光照强度, 抗扰动性强, 更易于远距离成像; 利用距离选通原理进行成像, 有效抑制后向散射等噪声, 适用于网状障碍物成像, 同时提出自适应距离选通方法提高了系统的灵活性; 采用分布式压缩方式, 显著降低了数据量, 在实时三维成像上提供了一种新的角度.
3 实验与分析3.1 三维成像实验选择足球作为目标三维物体进行实验, 分辨率为256×256, 三维距离信息根据距离分辨率进行了设置, 同时为了美观及视觉感受, 显示了相对距离, 如图 8a所示; 实际距离经过简单计算即可获取, 强度图像如图 8b所示.
图 8(Fig. 8)
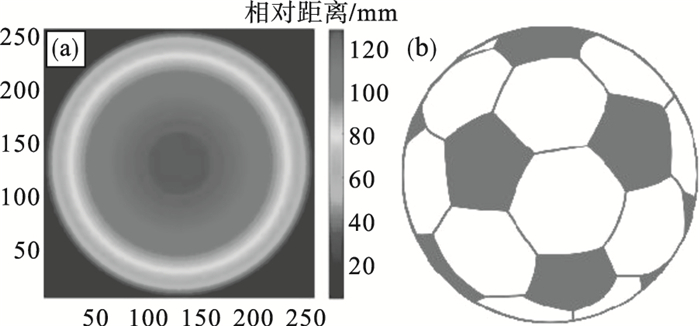 | 图 8 场景图像Fig.8 Scene image (a)—距离图像;(b)—强度图像. |
根据距离分辨率设定了32个时间切片, 提出的分布式压缩感知成像方法以关键帧: 非关键帧=1∶1进行编码, 采样率为0.2∶0.1.
该三维成像系统能够有效减少冗余信息的采集, 衡量标准可以转换为相同采集数据量下的重构质量, 以分布式压缩感知成像的平均采样率作为对比方法的采样率(在本次实验中为0.15)对场景进行成像, 对比方法选取经典的正交匹配追踪算法(OMP)、全变差增广拉格朗日交替方向算法(TVAL3)、压缩感知算法(CS-SPL).不同成像结果如图 9, 图 10所示.图 9表示不同的强度图像、距离图像及物体三维呈现结果.图 10算法表示距离误差图像及放大10倍后的误差图像.表 1统计了不同成像方法在不同采样率下的评价结果, 包括重构强度图像的PSNR和结构相似度(SSIM)、重构距离图像的误差均值和均方误差(MSE).
图 9(Fig. 9)
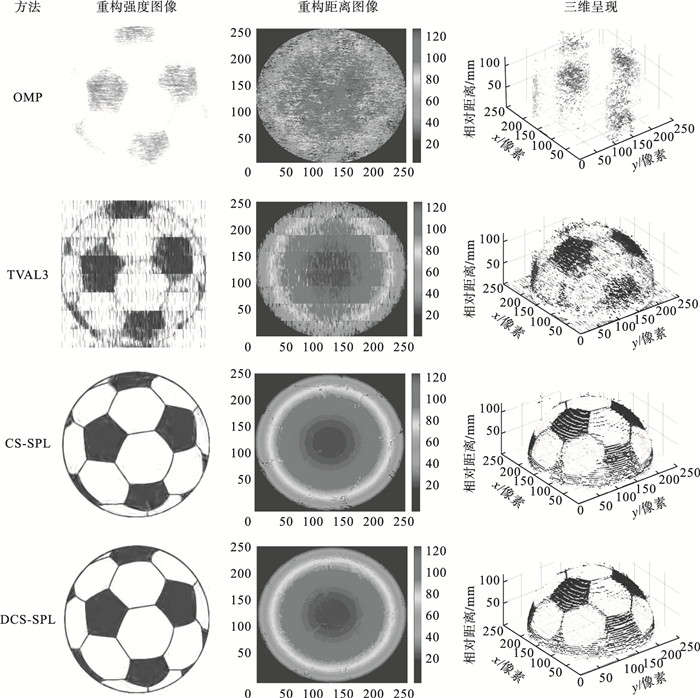 | 图 9 不同成像方法在0.15的平均采样率下的成像结果Fig.9 Imaging results of different imaging methods at an average sampling rate of 0.15 |
图 10(Fig. 10)
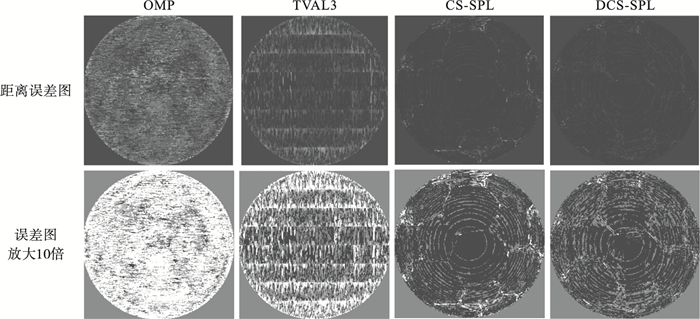 | 图 10 不同成像方法在0.15的平均采样率下的距离误差结果Fig.10 Range error results of different imaging methods at an average sampling rate of 0.15 |
表 1(Table 1)
| 表 1 不同成像方法的评价指标 Table 1 Evaluation index of different imaging methods |
以关键帧数量: 非关键帧数量=1∶3的分组情况计算, DCS-SPL和CS-SPL采用不同采样率的成像结果如图 11所示.其中, 横坐标表示平均采样率, 左侧纵坐标表示峰值信噪比(PSNR), 右侧纵坐标表示均方误差(MSE).′*′和′+′分别表示DCS-SPL和CS-SPL的强度图像随采样率变化的PSNR曲线, ′○′和′◇′分别代表对应的距离图像的均方误差(MSE)随采样率的变化.
图 11(Fig. 11)
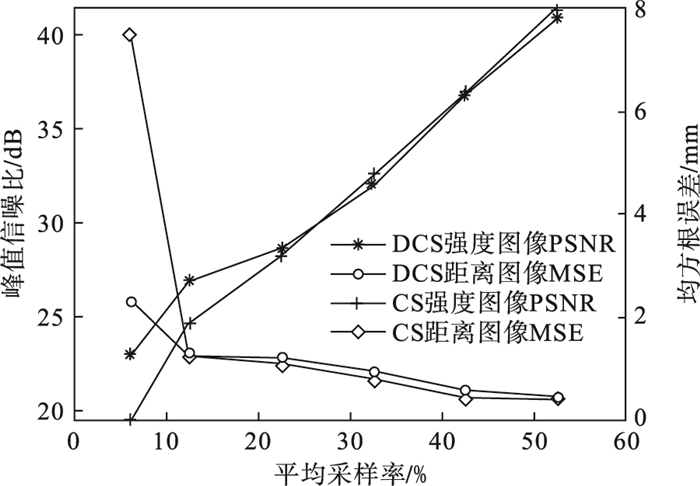 | 图 11 DCS-SPL和CS-SPL不同采样率的实验结果Fig.11 Experimental results of different sampling rates of DCS-SPL and CS-SPL |
3.2 分析与讨论在重构三维物体图像的质量方面, 由图 9中重构强度图像可知, 平均采样率为0.15时, DCS-SPL成像结果表现最佳, 其次是CS-SPL, 相比之下, OMP和TVAL3成像结果表现不佳.由表 1中4种方法在不同采样率下的重构强度图像的PSNR和SSIM结果可知, DCS-SPL在不同采样率, 重构质量均达到最高水平; 其次是CS-SPL, 相对而言, 与DCS-SPL重构质量相差不大;OMP和TVAL3重构质量与DCS-SPL相差较大, 特别是OMP, 平均采样率为0.125时, 与DCS-SPL的PSNR结果差值达到19.255 dB, 是OMP结果的2.43倍, 与SSIM的结果相差0.733.平均采样率为0.125时, DCS-SPL比传统方法平均PSNR高出11.124 dB. DCS-SPL时间切片重构质量高于其他三种成像方法,优势在于其利用了相邻时间切片间的空间关联信息, 在原有采样率的基础上, 增添了时间切片相关信息, 从而提高了重构质量.值得一提的是, 在平均采样率逐步增加的情况下, CS-SPL与DCS-SPL的成像质量差距逐渐减少, 原因在于分布式辅助重构的思想, 在采样率较低时效果会很明显.随着采样率的增加, 采样数据包含的信息足已重构出质量好的结果, 这种情况下, 采用分布式辅助重构的增强效果就会减弱, 图 11中峰值信噪比的变化趋势间接证实了这一点.因此, DCS-SPL在采样率较低的情况下成像效果优于采样率偏高的情况.
在重建三维物体距离精度上, 由图 9中重建距离图像、图 10中距离误差图像以及放大10倍的距离误差图像可知, 在平均采样率为0.15时, 结果与重构的强度图像所得结论一致, DCS-SPL距离精度最高.DCS-SPL重建距离误差图像,在正常视觉效果下,只在边缘处存在细微的偏差, 误差放大10倍后, 误差视觉效果仍是所有方法中最好的.CS-SPL重建距离精度仅次于DCS-SPL, 误差图像在正常视觉下, 在边缘处有偏差; OMP与TVAL3的误差图像即使在正常视觉效果下,距离误差也非常明显, 尤其是OMP, 重建距离图像基本没有距离信息.由表 1中重构距离图像的误差均值和MSE可知, DCS-SPL在不同采样率下的误差均值及均方误差均最小, 造成该结果的原因在于获取三维物体距离信息的过程中, 重构的时间切片图像质量影响其距离精度, 质量越高, 重构距离精度越高.由图 11可知, 在平均采样率增加的同时, CS-SPL与DCS-SPL的距离均方误差也在逐步减小, 原因在于距离信息的获取依赖重构质量, 重构质量随平均采样率的增加所提高的幅度有限.
实验表明基于分布式压缩感知的三维成像方法能够减少采集三维物体时间切片冗余信息, 从而降低三维成像方法对采集数据量的依赖性, 保证在相同采样率下得到最好的重建结果.
4 结论1) 本文提出的分布式压缩感知三维物体成像方法, 通过联合稀疏模型对时间切片间关联性建模, 获取时间切片相关信息辅助低采样率时间切片重构, 从而提高成像重构质量, 有效利用时间切片的空间关联信息降低三维时间切片成像方法对采集数据量的依赖性.
2) 在数据采集阶段, 根据接收信号情况设定阈值自适应选择选通时间的成像方法, 解决了距离选通成像方法需要预先估计目标距离、硬件实现难的问题.分布式压缩感知水下三维成像方法不仅能够抑制散射噪声, 而且有效减少时间切片冗余信息的采集, 具有灵活性好、抗扰动性强的特点.该方法可应用于水下网状障碍物成像、水下实时三维成像等领域.
参考文献
| [1] | Wang X, Liu X, Ren P, et al. Underwater three-dimensional range-gated laser imaging based on triangular-range-intensity profile spatial-correlation method[C]//Optoelectronic Imaging & Multimedia Technology IV. Beijing, 2016: 1-6. |
| [2] | 李海兰, 王霞, 金伟其, 等. 基于多帧水下距离选通图像的三维重构方法[J]. 光学学报, 2010, 30(12): 3464-3470. (Li Hai-lan, Wang Xia, Jin Wei-qi, et al. 3-dimersional reconstruction based on underwater range gated images[J]. Acta Optica Sinica, 2010, 30(12): 3464-3470.) |
| [3] | An Y, Zhang Y, Guo H, et al. Compressive sensing based three-dimensional laser imaging with dual illumination[J]. IEEE Access, 2019, 7: 25708-25717. DOI:10.1109/ACCESS.2019.2900449 |
| [4] | Sejdi E, Orovi I, Stankovi S. Compressive sensing meets time-frequency: an overview of recent advances in time-frequency processing of sparse signals[J]. Digital Signal Processing, 2017, 77: 22-35. |
| [5] | Rani M, Dhok S B, Deshmukh R B. A systematic review of compressive sensing: concepts, implementations and applications[J]. IEEE Access, 2018, 6: 4875-4894. DOI:10.1109/ACCESS.2018.2793851 |
| [6] | De Kort D W, Hertel S A, Appel M, et al. Under-sampling and compressed sensing of 3D spatially-resolved displacement propagators in porous media using APGSTE-RARE MRI[J]. Magnetic Resonance Imaging, 2019, 56: 24-31. DOI:10.1016/j.mri.2018.08.014 |
| [7] | 孙梦阳. 基于距离编码的压缩传感激光三维成像的研究[D]. 哈尔滨: 哈尔滨工业大学, 2017. (Sun Meng-yang. Research on laser 3D imaging of compressed sensing based on range encoding[D]. Harbin: Harbin Institute of Technology, 2017. ) |
| [8] | 张硕. 基于压缩感知的三维成像方法研究[D]. 杭州: 浙江大学, 2013. (Zhang Shuo. Research on 3D imaging method based on compressive sensing[D]. Hangzhou: Zhejiang University, 2013. ) |
| [9] | Sun M J, Edgar M P, Gibson G M, et al. Single-pixel three-dimensional imaging with time-based depth resolution[J]. Nature Communications, 2016, 7: 1-7. |
| [10] | Edger M, Sun M, Spalding G, et al. First-photon 3D imaging with a single pixel camera[C]// Frontiers in Optics 2016. Rochester: Optical Society of America. 2016. https: //doi.org/10.1364/FIO.2016.FF1D.2. |
| [11] | Sun M, Zhang J. Single-pixel imaging and its application in three-dimensional reconstruction: a brief review[J]. Sensors, 2019, 19(3): 732. DOI:10.3390/s19030732 |
| [12] | Chen X, Zhang Y, Qi R. Block sparse signals recovery algorithm for distributed compressed sensing reconstruction[J]. Journal of Information Processing Systems, 2019, 15(2): 410-421. |
| [13] | Baron D, Duarte M F, Wakin M B, et al. Distributed compressive sensing[EB/OL]. (2009-01-22)[2020-06-18]. https://arxiv.org/abs/0901.3403. |
| [14] | 王伟. 基于距离选通门控切片激光成像精度的实验研究[D]. 哈尔滨: 哈尔滨工业大学, 2015. (Wang Wei. Experimental research of range accuracy on range-gated time slice laser imaging[D]. Harbin: Harbin Institute of Technology, 2015. ) |
| [15] | Donoho D. For most large underdetermined systems of linear equations, the minimal near-solution approximates the sparsest near-solution[J]. Communications on Pure and Applied Mathematics, 2006, 59(6): 797-829. DOI:10.1002/cpa.20132 |
| [16] | Wu J, Liu Z, Tan S, et al. Computational spectral imaging based on random modulation and compressed sensing reconstruction algorithm[C]// Digital Holography and Three-Dimensional Imaging. Heidelberg: Optical Society of America, 2016. https://doi.org/10.1364/3D.2016.JT3A.37. |
| [17] | Li M, Yan L, Yang R, et al. Fast single-pixel imaging based on optimized reordering Hadamard basis[J]. Acta Physica Sinica, 2019, 68(6): 87-94. |
| [18] | Baraniuk R, Davenport M, Devore R, et al. A simple proof of the restricted isometry property for random matrices[J]. Constructive Approximation, 2008, 28(3): 253-263. DOI:10.1007/s00365-007-9003-x |
| [19] | 和志杰, 杨春玲, 汤瑞东. 视频压缩感知中基于结构相似的帧间组稀疏表示重构算法研究[J]. 电子学报, 2018, 46(3): 544-553. (He Zhi-jie, Yang Chun-ling, Tang Rui-dong. Research on structural similarity based on inter-group sparse representation in video compression sensing[J]. Acta Electronica Sinica, 2018, 46(3): 544-553. DOI:10.3969/j.issn.0372-2112.2018.03.005) |
| [20] | Zhu J, Lim S H, Gastpar M. Communication versus computation: duality for multiple-access channels and source coding[J]. IEEE Transactions on Information Theory, 2018, 65(1): 292-301. |
| [21] | Elzouki D, Dumitrescu S, Chen J. Lattice-based robust distributed source coding[J]. IEEE Transactions on Information Theory, 2019, 6(3): 1764-1781. |
| [22] | Liu B, Gui G, Matsushita S, et al. Compressive sensing-based adaptive sparse multipath channel estimation[J]. Journal of Advanced Computational Intelligence and Intelligent Informatics, 2017, 21(1): 153-158. DOI:10.20965/jaciii.2017.p0153 |
| [23] | Guggenmos M, Sterzer P, Cichy R M. Multivariate pattern analysis for MEG: a comparison of dissimilarity measures[J]. Neuroimage, 2018, 173: 434-447. DOI:10.1016/j.neuroimage.2018.02.044 |
| [24] | Chen C, Tramel E W, Fowler J E. Compressed-sensing recovery of images and video using multi-hypothesis predictions[C]//Signals, Systems and Computers(ASILO-MAR). Pacific Grove, 2011: 1193-1198. |
