周雅夫1,2,刘邵勋1,2,孙宵宵1,2,黄立建1,2,连静1,2
(1.工业装备结构分析国家重点实验室(大连理工大学),辽宁 大连 116024; 2.大连理工大学 运载工程与力学学部汽车工程学院,辽宁 大连 116024)
摘要:
为准确量化车用动力电池老化程度,提升其行业利用率,实现电池的全生命周期剩余寿命（Remaining useful life, RUL）的精确预测,提出一种基于多系数模型的车用动力电池全生命周期寿命预测方法。该方法融合重组了传统的经验指数模型和改进后的多项式回归模型,重组后的模型能在实验数据分析的基础上追踪电池全生命周期内的寿命退化趋势。该方法采用粒子滤波（Particle filter, PF）思想在线调整模型参数,设计了针对动力电池不同状态,不同容量种类的算例预测电池的RUL,通过改进多项式回归模型,传统经验指数模型以及多系数模型的预测精度对比评估模型。实验结果表明:相较于经验指数模型和改进后的多项式回归模型,本文提出的多系数模型针对电池容量衰减具有更好的拟合能力；结合粒子滤波算法,该模型无论是对在役电池还是退役电池均具有高精度的寿命预测结果。该方法对不同容量的动力电池均能准确预测电池失效时间,在电池梯次利用行业具有一定的适用性。
关键词: 动力电池 寿命预测 粒子滤波 融合模型 容量衰减
DOI：10.11918/202007052
分类号:TM911
文献标识码:A
基金项目:国家重点研发计划(2018YFE0105100)
Prediction method for full lifetime of vehicle power battery
ZHOU Yafu1,2,LIU Shaoxun1,2,SUN Xiaoxiao1,2,HUANG Lijian1,2,LIAN Jing1,2
(1.State Key Laboratory of Structural Analysis for Industrial Equipment (Dalian University of Technology), Dalian 116024, Liaoning, China; 2.School of Automotive Engineering, Faculty of Vehicle Engineering and Mechanics, Dalian University of Technology, Dalian 116024, Liaoning, China)
Abstract:
A full lifetime capacity prediction method for vehicle power batteries was proposed, so as to accurately quantify the aging degree of automotive power batteries, improve the utilization rate of batteries, and achieve accurate prediction of the remaining useful life (RUL) in the whole life cycle of batteries. By integrating the traditional empirical exponential model and the improved polynomial regression model, the proposed method could track the degradation trend of battery life cycle based on the analysis of experimental data. The particle filter (PF) was adopted to adjust the model parameters online. Experiments were carried out to predict the RUL of power batteries with different states and capacities. The model was evaluated by comparing the prediction accuracy of different models. Experimental results show that the proposed model had a stronger ability in battery capacity attenuation tracking than that of the traditional empirical exponential model and the improved polynomial regression model. Combined with particle filter algorithm, the method achieved high-precision prediction results for both in-service and retired batteries. Besides, the method could accurately predict the failure time of power batteries with different capacities, which has a wide applicability in battery cascade utilization.
Key words: power batteries life prediction particle filtering fusion model capacity attenuation
周雅夫, 刘邵勋, 孙宵宵, 黄立建, 连静. 车用动力电池全生命周期寿命预测方法[J]. 哈尔滨工业大学学报, 2022, 54(6): 37-44. DOI: 10.11918/202007052.
ZHOU Yafu, LIU Shaoxun, SUN Xiaoxiao, HUANG Lijian, LIAN Jing. Prediction method for full lifetime of vehicle power battery[J]. Journal of Harbin Institute of Technology, 2022, 54(6): 37-44. DOI: 10.11918/202007052.
基金项目 国家重点研发计划(2018YFE0105100) 作者简介 周雅夫(1962—), 男, 教授, 博士生导师;
连静(1980—), 女, 副教授, 博士生导师 通信作者 连静, lianjing@dlut.edu.cn 文章历史 收稿日期: 2020-07-10
Abstract Full text Figures/Tables PDF
车用动力电池全生命周期寿命预测方法
周雅夫1,2, 刘邵勋1,2, 孙宵宵1,2, 黄立建1,2, 连静1,2
1. 工业装备结构分析国家重点实验室(大连理工大学), 辽宁 大连 116024;
2. 大连理工大学 运载工程与力学学部汽车工程学院, 辽宁 大连 116024
收稿日期: 2020-07-10
基金项目: 国家重点研发计划(2018YFE0105100)
作者简介: 周雅夫(1962—), 男, 教授, 博士生导师; 连静(1980—), 女, 副教授, 博士生导师
通信作者: 连静, lianjing@dlut.edu.cn
摘要: 为准确量化车用动力电池老化程度, 提升其行业利用率, 实现电池的全生命周期剩余寿命(Remaining useful life, RUL)的精确预测, 提出一种基于多系数模型的车用动力电池全生命周期寿命预测方法。该方法融合重组了传统的经验指数模型和改进后的多项式回归模型, 重组后的模型能在实验数据分析的基础上追踪电池全生命周期内的寿命退化趋势。该方法采用粒子滤波(Particle filter, PF)思想在线调整模型参数, 设计了针对动力电池不同状态, 不同容量种类的算例预测电池的RUL, 通过改进多项式回归模型, 传统经验指数模型以及多系数模型的预测精度对比评估模型。实验结果表明: 相较于经验指数模型和改进后的多项式回归模型, 本文提出的多系数模型针对电池容量衰减具有更好的拟合能力; 结合粒子滤波算法, 该模型无论是对在役电池还是退役电池均具有高精度的寿命预测结果。该方法对不同容量的动力电池均能准确预测电池失效时间, 在电池梯次利用行业具有一定的适用性。
关键词: 动力电池 寿命预测 粒子滤波 融合模型 容量衰减
Prediction method for full lifetime of vehicle power battery
ZHOU Yafu1,2, LIU Shaoxun1,2, SUN Xiaoxiao1,2, HUANG Lijian1,2, LIAN Jing1,2
1. State Key Laboratory of Structural Analysis for Industrial Equipment (Dalian University of Technology), Dalian 116024, Liaoning, China;
2. School of Automotive Engineering, Faculty of Vehicle Engineering and Mechanics, Dalian University of Technology, Dalian 116024, Liaoning, China
Abstract: A full lifetime capacity prediction method for vehicle power batteries was proposed, so as to accurately quantify the aging degree of automotive power batteries, improve the utilization rate of batteries, and achieve accurate prediction of the remaining useful life (RUL) in the whole life cycle of batteries. By integrating the traditional empirical exponential model and the improved polynomial regression model, the proposed method could track the degradation trend of battery life cycle based on the analysis of experimental data. The particle filter (PF) was adopted to adjust the model parameters online. Experiments were carried out to predict the RUL of power batteries with different states and capacities. The model was evaluated by comparing the prediction accuracy of different models. Experimental results show that the proposed model had a stronger ability in battery capacity attenuation tracking than that of the traditional empirical exponential model and the improved polynomial regression model. Combined with particle filter algorithm, the method achieved high-precision prediction results for both in-service and retired batteries. Besides, the method could accurately predict the failure time of power batteries with different capacities, which has a wide applicability in battery cascade utilization.
Keywords: power batteries life prediction particle filtering fusion model capacity attenuation
近年来，为应对传统化石燃料枯竭和环境恶化等问题，锂离子电池被广泛应用于新能源汽车、航空航天、电网以及储能等领域。锂离子电池的老化程度极大地影响其供电设施的工作性能，若不能及时了解电池老化程度，电动汽车和储能设施将无法正常运行。受限于现有技术，难以直接测量在役的锂离子电池老化程度，因此建立准确的电池健康、RUL预测机制对于电池管理和梯次利用尤为重要。现阶段较为常用的方法是建立模型来描述电池的老化行为[1-3]。
物理模型和经验模型是现阶段两种主要的描述电池老化行为的方法，其均是通过数学语言描述电池的物理、化学或者数理关系建立电池容量、内阻或其他能表达电池特性的参数表达式。目前国内外对在汽车在役电池(电池容量80%以上)容量衰减的建模研究已经比较成熟，存在多种方法，具体包括：1)基于电池内部化学机理建立的模型，文献[4-5]着重分析了锂电池固体电解质膜(Solid electrolyte interface, SEI)随着电池老化的溶解恢复的过程，建立了用于描述电池容量变化的机理模型，然而在锂离子电池实际使用过程中，复杂的工作环境导致其老化过程呈现强非线性，此过程会增大固定参数的电池机理模型的预测误差。2)通过等效电路模型的电池老化建模，文献[6]利用电路元件建立了用于描述电池的等效电路模型(Equivalent circuit model, ECM)，该模型以电池老化容量衰减与内阻之间的关系，从而以外推的方式精确预测出电池的RUL，文献[7-8]通过采用了一种组合式的等效电路模型，找到了在电池衰老过程中关于电流和电压的过渡方程表达式，文献[9]分析了电池荷电状态(State of charge, SOC)的动态变化过程，建立了线性模型实现了SOC的精确预测。3)通过大量电池衰减的实测数据建立经验模型，该类方法一般能够精确预测电池状态，但受限于数据获取条件，其广泛应用往往需要结合相应的智能算法。文献[10-11]通过分析电池的内部阻抗数据变化，建立电池阻抗变化的数据集，分别结合自回归滑动平均模型(Autoregressive moving average model, ARMA)和人工神经网络(Artificial neural network, ANN)等智能方法对电池RUL进行预测，文献[12-14]是通过分析电池的容量衰减数据，采用了经验二次多项式或指数函数作为电池容量衰减模型，并利用粒子滤波方法改变观测方程参数对电池容量进行预测，文献[15]从电池容量保持率的角度对电池寿命分析，用高斯函数总结了其容量与剩余寿命的关系，同时利用外推法实现了RUL的预测，文献[16]提出的贝叶斯模型用于衡量卫星锂电池二元性能以及寿命数据，文献[17]将数据驱动利用到了电池的寿命预测，文献[18-19]采用了机器学习算法识别电池老化实现电动汽车电池寿命的优化，文献[20]通过建立单粒子模型分析锂离子电池老化过程，文献[21-22]则通过分析电池充电过程中数据变化，建立经验模型预测电池寿命。现有对电池RUL的预测方法多集中于对在役电池的预测，鲜有预测退役动力电池的RUL相关的文献，为实现电池剩余价值的最大化利用，本文提出了针对车用动力电池的全生命周期寿命预测方法。
本文通过分析电池全寿命周期的容量衰减实验数据，在传统经验模型的基础上进行改进融合，提出了用于表征电池容量与充放循环关系的多系数模型，利用多组电池容量衰减数据验证该模型的表征能力。采用粒子滤波思想通过不断更新模型参数以实现对电池的容量预测和追踪，从在役电池(容量衰减到80%)和退役电池(容量80%衰减到50%)两个方面进行实验，从而实现对车用动力电池全生命周期的寿命预测。
1 模型的构建 1.1 基础经验模型的分析验证目前，二阶指数函数和二次多项式是被广泛用于电池容量衰减预测的基本经验模型[23]，本文首先对传统二次多项式模型进行改进，原二次多项式经验模型的数学表达式为
$C=\sigma_{1} \times k^{2}+\sigma_{2} \times k+\sigma_{3}$ (1)
式中：σ1、σ2、σ3为模型中的待定参数, k为电池循环次数, C为电池容量。相比于传统二次多项式，式(1)对电池容量衰减有更强的表征能力，如图 1、表 1所示，故本文采用三次多项式用于模型重组。
Fig. 1
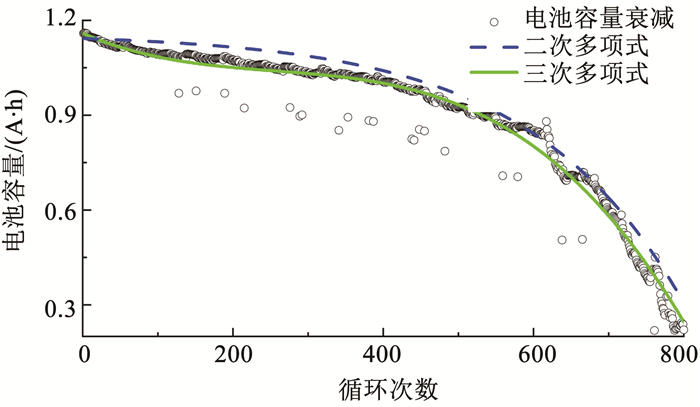图 1 经验模型拟合对比图 Fig. 1 Fitting results of improved model 表 1
表 1 拟合效果对比 Tab. 1 Comparison of fitting effects 模型类型 相关系数 均方根误差 二次多项式 0.928 6 0.035 1
三次多项式 0.966 9 0.062 4
表 1 拟合效果对比 Tab. 1 Comparison of fitting effects
三次多项式和二阶指数函数经验模型的表达式分别为:
$\mathrm{A} : \quad\ \ C=\alpha_{1} \times n^{3}+\alpha_{2} \times n^{2}+\alpha_{3} \times n+\alpha_{4}$ (2)
$\mathrm{B}: \quad C=b_{1} \times \exp \left(b_{2} \times n\right)+b_{3} \times \exp \left(b_{4} \times n\right)$ (3)
式中：C为电池计算容量, n为电池在标准充放电条件下的循环次数, α1, α2, α3, α4, b1, b2, b3, b4为模型中的参数。
电池容量预测模型是实现电池RUL预测的基础，其对电池全生命周期容量的拟合效果直接关乎预测是否准确。本文中利用相关系数(R2)与均方跟误差(Root mean squared error, RMSE)表征模型与容量衰减曲线之间的匹配度。量纲一的比值R2的计算方法如下：
$R^{2}=\frac{\mathrm{SSR}}{\mathrm{SST}}=\frac{(\mathrm{SST}-\mathrm{SSE})}{\mathrm{SST}}=1-\frac{\mathrm{SSE}}{\mathrm{SST}}$ (4)
式中：回归平方和(Sum of squares due to regression, SSR)为预测数据与原始实验数据均值差值的平方和，总偏差平方和(Total sum of squares, SST)为原始实验数据与数据均值差值的平方和，两者关系如下式描述：
$\mathrm{SSR}=\sum\limits_{i=1}^{n} \omega_{i}\left(\hat{y}_{i}-\bar{y}\right)^{2}$ (5)
式中：ωi为每个预测点对应实际实验值的权重,
$\mathrm{SST}=\sum\limits_{i=1}^{n} \omega_{i}\left(y_{i}-\bar{y}\right)^{2}$ (6)
式中: ωi为每个预测点对应实际实验值的权重, yi表征电池相应循环中的实测容量值。
相关系数(R2)是一种拟合效果的有效衡量工具。由式(4)可知，其取值范围为[0, 1]，当R2越趋近于1，表示模型变量越能合理解释原始数据，该模型的数据拟合结果置信程度越高。RMSE是一种表征两组数据偏差的有效工具，其表达式为
$\operatorname{RMSE}=\sqrt{\frac{1}{n} \sum\limits_{i=1}^{n}\left(y_{i}-\bar{y}\right)^{2}}$ (7)
图 2(a)~图 2(d)分别为每100次循环中，模型A和B计算电池容量数据与A组电池实际数据的相关系数与均方根误差的变化图。
Fig. 2
图 2 每百次循环中的模型A, B对电池数据匹配情况 Fig. 2 Matching results of model A and model B in every 100-cycle 从每百次循环的R2和RMSE值的变化可以看出，模型A, B对A组电池全局容量拟合效果不是恒定的，其整体呈变化趋势。为保证预测模型对于电池容量衰减有全局稳定的拟合效果，实现对电池全生命周期的容量预测和追踪，本文将对模型A，B拆分重组以构建新模型。
1.2 新模型的选型在模型A中，α4为常数项，其取值接近电池容量的标称容量值，该模型本质上是通过前3项(α1×n3+α2×n2+α3×n)的取值变化使模型A的计算结果收敛于实际的电池容量；在模型B中，b3×exp(b4×n)函数值远大于b1×exp(b2×n)的值，其原理类似于模型A。
本文采取的方法是将模型中的变量和常数项进行区分，根据其占模型结果的比重进行重组得出新的组合模型，并根据实际的拟合结果以及预测精度判断新组合模型的应用效果。拆分重组后的4种模型的表达式如下：
$\mathrm{C}: C_{1}=\alpha_{1} \times n^{3}+\alpha_{2} \times n^{2}+\alpha_{3} \times n+b_{3} \cdot \exp \left(b_{4} \cdot n\right)$ (8)
$\mathrm{D}: \qquad\qquad\qquad C_{2}=b_{1} \cdot \exp \left(b_{2} \cdot n\right)+\alpha_{4}$ (9)
$\mathrm{E}: C_{3}=\alpha_{1} \times n^{3}+\alpha_{2} \times n^{2}+\alpha_{3} \times n+b_{1} \cdot \exp \left(b_{2} \cdot n\right)$ (10)
$\mathrm{F}: \qquad\qquad\qquad C_{4}=b_{3} \cdot \exp \left(b_{4} \cdot n\right)+\alpha_{4}$ (11)
式中：模型中的C均为模型计算电池容量, n为电池循环次数。
在表 2中，模型C和模型D对实测数据的表征效果优于模型E和F，结合表 1数据可以得出模型C, D在吻合度上的优势。仅从对数据的表征能力上足以体现组合模型C的优点，所以本文增加了不同模型对电池RUL的预测结果以筛选两组组合模型。
表 2
表 2 模型匹配度对比 Tab. 2 Comparison of model results 电池 模型A 模型B 模型C 模型D 模型E 模型F RMSE R2 RMSE R2 RMSE R2 RMSE R2 RMSE R2 RMSE R2
A1 0.023 91 0.929 24 0.024 54 0.928 89 0.003 12 0.973 41 0.031 15 0.905 89 0.041 95 0.765 74 0.059 87 0.615 87
A2 0.014 03 0.959 09 0.019 12 0.958 74 0.003 35 0.995 61 0.030 82 0.934 35 0.042 57 0.739 78 0.055 63 0.598 78
A3 0.016 65 0.978 47 0.010 07 0.978 11 0.002 02 0.975 89 0.013 45 0.932 83 0.055 99 0.694 25 0.053 15 0.587 45
A4 0.019 55 0.963 75 0.009 36 0.973 43 0.002 19 0.985 04 0.014 80 0.932 99 0.050 24 0.772 35 0.063 87 0.556 59
A5 0.010 81 0.973 56 0.010 16 0.961 25 0.001 76 0.989 35 0.018 13 0.918 06 0.037 82 0.861 35 0.065 69 0.546 58
A6 0.011 39 0.964 731 0.010 06 0.964 37 0.002 79 0.989 79 0.018 04 0.929 75 0.035 63 0.869 87 0.068 54 0.540 21
表 2 模型匹配度对比 Tab. 2 Comparison of model results
2 粒子滤波对参数的修正在实际应用中，电池容量衰减模型不能充分体现结果的可靠性，由固定参数的容量衰减模型获得的预测结果难以具有代表性。为保证电池容量衰减预测的准确性，模型的参数还需要新的算法实现参数的不断更新以保证自身鲁棒性。PF因其非参数化、非高斯化等特点被广泛应用于解决此类非线性问题[24-25]。本文以观测模型为基础，依靠PF思想修正观测模型参数，实现不同种类电池容量的精确预测。
粒子滤波作为蒙特卡洛仿真的近似贝叶斯滤波算法，基于计算粒子的均值精确实现后验概率估计[26-28]。该方法利用离散的粒子采样均值计算代替积分计算以获得系统预测结果。
2.1 计算步骤由模型C例，即容量预测时认为其容量表达式为：
$Z(\kappa)=\nu_{1} \times \kappa^{3}+\nu_{2} \times \kappa^{2}+\nu_{3} \times \kappa+\nu_{4} \cdot \exp \left(\nu_{5} \cdot \kappa\right)$ (12)
式中：Z为预测电池的容量, κ为电池在标准协议下的充放电实验循环次数, 模型的计算容量Z和系统的状态变量ν1, ν2, ν3, ν4, ν5含有未知方差的白噪声。表 3是模型C，D预测实验过程中各个参数的初始值。
表 3
表 3 不同电池预测方程初始值 Tab. 3 Initial values of parameters in prediction function 模型参数 模型C 模型D 在役 退役 在役 退役
ν1 -1.030×10-8 -4.880×10-9 - -1.200×10-9
ν2 5.010×10-6 3.920×10-6 - 1.237×10-6
ν3 1.040×10-3 1.210×10-3 - 6.580×10-4
ν4 1.122 1.131 - 1.291
ν5 -3.060×10-4 -2.440×10-4 - -2.560×10-3
表 3 不同电池预测方程初始值 Tab. 3 Initial values of parameters in prediction function
式(12)中需要估计的参数可表达为
$V(\kappa)=\left[\nu_{1}(\kappa), \nu_{2}(\kappa), \nu_{3}(\kappa), \nu_{4}(\kappa), \nu_{5}(\kappa)\right]$ (13)
此时的状态方程为:
$\begin{aligned}&\nu_{1}(n+1)=\nu_{1}(n)+W \nu_{1}(n), W \nu_{1} \sim N(0, M) \\&\nu_{2}(n+1)=\nu_{2}(n)+W \nu_{2}(n), W \nu_{2} \sim N(0, M) \\&\nu_{3}(n+1)=\nu_{3}(n)+W \nu_{3}(n), W \nu_{3} \sim N(0, M) \\&\nu_{4}(n+1)=\nu_{4}(n)+W \nu_{4}(n), W \nu_{4} \sim N(0, M) \\&\nu_{5}(n+1)=\nu_{5}(n)+W \nu_{5}(n), W \nu_{5} \sim N(0, M)\end{aligned}$ (14)
式中：ν1(n+1), …, ν5(n+1)为预测模型中所有状态参数在n+1时刻的状态, W∈RWN表示的是系统的过程噪声符合方差为M，均值为0的高斯分布。以模型C为例，电池容量衰减模型中的观测方程则可表达为
$\begin{aligned}Q(\kappa)=& \nu_{1} \times \kappa^{3}+\nu_{2} \times \kappa^{2}+\nu_{3} \times \kappa+\\& \nu_{4} \cdot \exp \left(\nu_{5} \cdot \kappa\right)+\zeta(\kappa)\end{aligned}$ (15)
2.2 重要性采样首先根据p(Vκ|Q1∶ κ)状态方程得出p(Vκ|Q1∶ κ-1)的值，即根据状态方程κ时刻的取值，配合过程噪声生成系统在κ+1时刻的状态。由于过程噪声的随机性，系统在κ+1时刻的状态可以被分布成大量的采样，此时这些采样点组成的数集可以被称为粒子集。
2.3 校正阶段在完成粒子集的设定后，其更新公式如下:
$\omega_{\kappa}^{i}=\omega_{\kappa-1}^{i} p\left(Q_{\kappa} \mid V_{\kappa-1}^{i}\right)$ (16)
式中：ωκi(i=1, 2, 3, 4, 5, …, N)为与所选粒子关联的权重，N为粒子初始化时设置的总个数。
对所有的粒子校正环节后，进行归一化权值操作。式(17)为第κ充放循环中粒子i的权重取值大小。
$\widetilde{\omega}_{\kappa}^{i}=\omega_{\kappa}^{i} / \sum\limits_{i=1}^{N} \omega_{\kappa}^{i}$ (17)
2.4 重采样阶段重采样过程中，粒子的保留或去除取决于其自身权值大小。系统的真实状态V(κ)在依据权值大小对粒子取舍后获得。
重采样后的粒子可以代表电池系统容量真实的概率分布，根据此概率分布，结合基于序列的后验期望估算方法，可以得到下一时刻电池容量的后验期望I(Gκ)。
$I\left(G_{\kappa}\right)=\int G_{\kappa}\left(V_{\kappa}\right) p\left(V_{\kappa} \mid Q_{1: \kappa}\right) \mathrm{d} V_{\kappa}$ (18)
在下一轮滤波中，直接将重采样后的粒子输入到状态方程中，就能够获得粒子集对应的电池容量衰减量的观测集，即新一轮滤波的粒子集。
最后，在完成了设定滤波阶段的循环次数后，需预测的第κ+1时刻的电池容量的表达式为
$Q_{\kappa+1}=\sum\limits_{i=1}^{N} \omega_{\kappa}^{i} Q_{\kappa}$ (19)
对于退役电池的寿命预测，采用的方法是将测量的状态向量以及其当前的后验分布P(Vn|Q1∶ κ)投射到所有可能的未来路径当中，每个容量的轨迹分布由相应的模型表达式计算，当前循环次数的容量分布计算以及RUL期望值为:
$P\left(V_{\kappa} \mid Q_{1: \kappa}\right) =\sum\limits_{i=1}^{N} \omega_{\kappa}^{i}\left(Q_{\kappa+1}-Q_{\kappa+1}^{i}\right)$ (20)
$\mathrm{RUL}_{\kappa} =\sum\limits_{i=1}^{N} \operatorname{RUL}_{\kappa}^{i} \omega_{\kappa}^{i}$ (21)
3 电池寿命预测验证 3.1 试验中的充放电条件参与实验的电池为A, B两组不同容量的电池，所有电池的参数见表 4。其在实验中均采用恒电流充放电法；首先使用0.5 C电流充电，直至被测电池到达上截止电压，随后保持电池电压不变，充电电流将缓慢降低到0.05 A以下；当电池放电时，恒流放电至电压降为2.7 V，从而实现电池充放电的一次循环。图 3为电池A1, B1的容量衰减图。
表 4
表 4 电池各项参数 Tab. 4 Battery parameters 电池 容量/mAh 质量/g 尺寸/mm 正极材料 上截止电压/V A 1 150 21.1 5.4×33.6×50.6 LiCoO2 4.2
B 1 350 27.5 6.0×37.2×50.6 LiCoO2 4.2
表 4 电池各项参数 Tab. 4 Battery parameters
Fig. 3
图 3 电池A1，B1容量衰减实测图 Fig. 3 Capacity attenuation of batteries A1 and B1 3.2 电池寿命预测验证本文首先将电池(A5，A6)作为在役电池数据集对粒子滤波容量预测算法以及容量衰减模型进行验证，选取电池充放循环试验的前300次，即电池的寿命衰减到为其正常寿命的1/3为训练阶段，利用后续阶段作为电池预测阶段并对比模型C和D的滤波预测结果。预测精度的检验标准定为预测误差和标准差(Standard deviation，STD)。标准差用于衡量预测值与实际值的偏差，当RUL预测结果在置信区间内时，一个小的STD值代表着较窄的RUL预测区间，也就代表着较高的置信水平。
各模型的预测结果如图 4所示，以在役电池A5的容量衰减预测结果为例：选取电池标称容量的80%为失效阈值，观测方程为模型A和D时的预测结果相似，两者预测动力电池A5容量到达设定的失效阈值时间均提前与实际测量值约30个标准充放循环；观测方程为模型B时，预测电池A5到达设定的失效阈值时间点晚于实测值约40个充放循环；观测方程为模型C时，预测电池A5与实测值基本吻合，预测失效时间滞后于实测值3个充放循环。在表 5中，+为预测电池失效时间滞后；-为预测电池失效时间提前；STD为预测结果与容量真实值的偏差。由表 5中的两组电池容量衰减预测结果可知，模型C的预测结果STD值分别为1.03%和0.80%；平均误差均为0.9%。其整体预测曲线较接近原始电池容量衰减数据。
Fig. 4
图 4 在役电池A5，A6 RUL预测结果 Fig. 4 RUL prediction results of in-service batteries A5 and A6 表 5
表 5 4种模型预测结果总结 Tab. 5 Summary of prediction results of four models 电池 模型A 模型B 模型C 模型D 预测精度 STD 平均误差/% 预测精度 STD 平均误差/% 预测精度 STD 平均误差/% 预测精度 STD 平均误差/%
A5 -30 0.024 18 2.3 +40 0.011 51 5.5 +3 0.010 31 0.9 -30 0.024 03 4.3
A6 +30 0.019 13 1.5 +∞ 0.032 34 9.5 +2 0.008 47 0.9 -50 0.021 31 3.1
表 5 4种模型预测结果总结 Tab. 5 Summary of prediction results of four models
综合图 4以及表 5、6的结果分析，在原始经验模型A、B和重组观测模型C、D中，模型C的预测结果无论是整体逼近真实值效果，还是最后的失效时间预测均大幅度高于其他参与对比模型，故选择模型C进行退役电池寿命预测，将其预测结果与传统经验模型A和B的预测结果进行比较，验证本文提出模型对于电池在役阶段和退役阶段均具有较高的预测精度。
表 6
表 6 退役电池预测结果总结 Tab. 6 Summary of prediction results of retired batteries 电池 模型A 模型B 模型C 预测精度 STD 平均误差/% 预测精度 STD 平均误差/% 预测精度 STD 平均误差/%
A5 +∞ 0.146 310 3.5 -70 0.774 09 11.2 -10 0.042 49 2.7
A6 +50 0.010 676 6.2 -70 0.086 33 9.6 +5 0.047 02 2.3
B1 -∞ - - +200 0.154 52 5.0 +10 0.021 48 1.1
B2 -80 0.895 870 2.8 +∞ - - +1 0.020 77 0.7
表 6 退役电池预测结果总结 Tab. 6 Summary of prediction results of retired batteries
动力电池A5, A6, B1和B2的退役阶段容量衰减预测结果如图 5所示，图 6是模型C对动力电池A5，A6和B1，B2的退役阶段的容量预测过程中系数的变化曲线。
Fig. 5
图 5 3种模型退役电池RUL预测结果对比 Fig. 5 Comparison of RUL prediction results of retired batteries by three models Fig. 6
图 6 退役电池预测系数变化 Fig. 6 Parameters changes in retired batteries 以模型C为例，观测方程为模型C时，电池A5到达失效阈值的预测时间提前实验测量失效时间约10个充放循环；电池A6到达失效阈值的预测时间稍滞后于实验测量失效时间约5个充放循环，且两组预测误差均较低，分别为2.7%和2.3%；在对电池B1退役阶段容量衰减预测中，到达失效阈值预测时间滞后于实测数据约10个标准充放循环；对电池B1退役阶段容量衰减预测中，其预测曲线与实测曲线贴合程度较好，到达失效时间预测值稍滞后于实测值1个标准充放循环。电池B1和B2的预测误差分别为1.1%和0.7%。从实验结果可知，相比于传统多项式模型和指数函数模型，采用模型C为观测方程对不同类别的电池容量衰减预测精度均有较大的提升，该结果证明了该组合模型用于预测电池容量衰减的有效性。
4 结论1) 本文提出的融合模型吸收了现有经验模型的优点，对电池全生命周期容量衰减具有更强的保证能力，通过对不同电池容量衰减数据吻合度分析证明了该模型的可行性和有效性。
2) 在基于粒子滤波的在役电池容量预测实验中，该模型能对在役电池实现精确的寿命预测，预测误差小于2%，误差均值小于1%。
3) 该方法不仅适用于在役动力电池寿命预测，在研究较少的退役电池寿命预测实验中，对不同容量的电池寿命预测也具有较高的精度，预测误差小于5%，误差均值小于3%，有助于电池梯次使用行业的发展。
参考文献
[1] NEUBAUER J, PESARAN A. The ability of battery second use strategies to impact plug-in electric vehicle prices and serve utility energy storage applications[J]. Journal of Power Sources, 2011, 196(23): 10351. DOI:10.1016/j.jpowsour.2011.06.053
[2] VISWANATHAN V V, KINTNER-MEYER M. Second use of transportation batteries: Maximizing the value of batteries for transportation and grid services[J]. IEEE Transactions on Vehicular Technology, 2011, 60(7): 2963. DOI:10.1109/TVT.2011.2160378
[3] 陶志军, 贾晓峰. 中国动力电池回收利用产业商业模式研究[J]. 汽车工业研究, 2018(10): 33. DOI:10.3969/j.issn.1009-847X.2018.10.006
[4] BEAK K W, HONG E S, CHA S W. Capacity fade modeling of a Lithium-ion battery for electric vehicles[J]. International Journal of Automotive Technology, 2015, 16(2): 309. DOI:10.1007/s12239-015-0033-2
[5] RAMESH S, KRISHNAMURTHY B. A mathematical model to study capacity fading in lithium ion batteries: Formation and dissolution reactions[J]. Journal of the Electrochemical Society, 2015, 162(4): A545. DOI:10.1149/2.0221504jes
[6] SCHMIDT A P, BITZER M, IMRIE A W, et al. Model-based distinction and quantification of capacity loss and rate capability fade in Li-ion batteries[J]. Journal of Power Sources, 2010, 195(22): 7634. DOI:10.1016/j.jpowsour.2010.06.011
[7] 林甜甜, 陈自强, 刘健. 基于等幅度充电时间的锂离子电池健康状态估计[J]. 装备环境工程, 2018, 15(12): 75.
LIN Tiantian, CHEN Ziqiang, LIU Jian. Health state estimation of lithium-ion battery based on equal time interval charging[J]. Equipment Environmental Engineering, 2018, 15(12): 75. DOI:10.7643/issn.1672-9242.2018.12.012
[8] SCIPIONI R, J?RGENSEN P S, STROE D I, et al. Complementary analyses of aging in a commercial LiFePO 4/graphite 26650 cells[J]. Electrochemical Acta, 2018, 284: 454. DOI:10.1016/j.electacta.2018.07.124
[9] COUTO L D, SCHORSCH J, JOB N, et al. State of health estimation for lithium-ion batteries based on an equivalent-hydraulic model: An iron phosphate application[J]. Journal of Energy Storage, 2019, 21: 259. DOI:10.1016/j.est.2018.11.001
[10] WENG Caihao, FENG Xuning, SUN Jing, et al. State-of-health monitoring of lithium-ion battery modules and packs via incremental capacity peak tracking[J]. Applied Energy, 2016, 180: 360. DOI:10.1016/j.apenergy.2016.07.126
[11] MA Zeyu, YANG Ruixin, WANG Zhenpo. A novel data-model fusion state-of-health estimation approach for lithium-ion batteries[J]. Applied Energy, 2019, 237: 836. DOI:10.1016/j.apenergy.2018.12.071
[12] WANG Zengkai, ZENG Shengkui, GUO Jianbin, et al. State of health estimation of lithium-ion batteries based on the constant voltage charging curve[J]. Energy, 2019, 167: 661. DOI:10.1016/j.energy.2018.11.008
[13] ABRAHAM D P, KNUTH J L, DEES D W, et al. Performance degradation of high-power lithium-ion cells—Electrochemistry of harvested electrodes[J]. Journal of Power Sources, 2007, 170(2): 465. DOI:10.1016/j.jpowsour.2007.03.071
[14] ZHANG Lingling, MA Yulin, CHENG Xinqun, et al. Degradation mechanism of over-charged LiCoO2/ mesocarbon microbeads battery during shallow depth of discharge cycling[J]. Journal of Power Sources, 2016, 329: 255. DOI:10.1016/j.jpowsour.2016.08.030
[15] YANG Xiaoguang, LENG Yongjun, ZHANG Guangsheng, et al. Modeling of lithium plating induced aging of lithium-ion batteries: Transition from linear to nonlinear aging[J]. Journal of Power Sources, 2017, 360: 28. DOI:10.1016/j.jpowsour.2017.05.110
[16] LAI Xin, GAO Wenkai, ZHENG Yuejiu, et al. A comparative study of global optimization methods for parameter identification of different equivalent circuit models for Li-ion batteries[J]. Electrochimica Acta, 2019, 295: 1057. DOI:10.1016/j.electacta.2018.11.134
[17] SEVERSON K A, ATTIA P M, JIN N, et al. Data-driven prediction of battery cycle life before capacity degradation[J]. Nature Energy, 2019, 4(5): 383. DOI:10.1038/s41560-019-0356-8
[18] ZHANG Yunwei, TANG Qiaochu, ZHANG Yao, et al. Identifying degradation patterns of lithium-ion batteries from impedance spectroscopy using machine learning[J]. Nature Communications, 2020, 11(1): 1706. DOI:10.1038/s41467-020-15235-7
[19] ATTIA P M, GROVER A, JIN N, et al. Closed-loop optimization of fast-charging protocols for batteries with machine learning[J]. Nature, 2020, 578(7795): 397. DOI:10.1038/s41586-020-1994-5
[20] RECHKEMMER S K, ZANG Xiaoyun, ZHANG Weimin, et al. Empirical Li-ion aging model derived from single particle model[J]. The Journal of Energy Storage, 2019, 21: 773. DOI:10.1016/j.est.2019.01.005
[21] ZHENG Yuejiu, WANG Jingjing, QIN Chao, et al. A novel capacity estimation method based on charging curve sections for lithium-ion batteries in electric vehicles[J]. Energy, 2019, 185: 361. DOI:10.1016/j.energy.2019.07.059
[22] ZHENG Xiujuan, FANG Huajing. An integrated unscented Kalman filter and relevance vector regression approach for lithium-ion battery remaining useful life and short-term capacity prediction[J]. Reliability Engineering & System Safety, 2015, 144: 74. DOI:10.1016/j.ress.2015.07.013
[23] XING Yinjiao, MA E W M, TSUI K L, et al. An ensemble model for predicting the remaining useful performance of lithium-ion batteries[J]. Microelectronics Reliability, 2013, 53(6): 813. DOI:10.1016/j.microrel.2012.12.003
[24] WEI Jingwen, DONG Guangzhong, CHEN Zonghai. Remaining useful life prediction and state of health diagnosis for lithium-ion batteries using particle filter and support vector regression[J]. IEEE Transactions on Industrial Electronics, 2017, 65(7): 5634. DOI:10.1109/TIE.2017.2782224
[25] ANDRE D, NUHIC A, SOCZKA-GUTH T, et al. Comparative study of a structured neural network and an extended Kalman filter for state of health determination of lithium-ion batteries in hybrid electric vehicles[J]. Engineering Applications of Artificial Intelligence, 2013, 26(3): 951. DOI:10.1016/j.engappai.2012.09.013
[26] PATIL M A, TAGADE P, HARIHARAN K S, et al. A novel multistage Support Vector Machine based approach for Li ion battery remaining useful life estimation[J]. Applied Energy, 2015, 159: 285. DOI:10.1016/j.apenergy.2015.08.119
[27] LIU Datong, ZHOU Jianbao, LIAO Haitao, et al. A health indicator extraction and optimization framework for lithium-ion battery degradation modeling and prognostics[J]. IEEE Transactions on Systems Man & Cybernetics Systems, 2015, 45(6): 915. DOI:10.1109/TSMC.2015.2389757
[28] HE Wei, WILLIARD N, OSTERMAN M, et al. Prognostics of lithium-ion batteries based on Dempster-Shafer theory and the Bayesian Monte Carlo method[J]. Journal of Power Sources, 2011, 196(23): 10314. DOI:10.1016/j.jpowsour.2011.08.040
